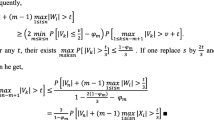On Collisions Times of ‘Self-Sorting’ Interacting Particles in One-Dimension with Random Initial Positions and Velocities

Abstract

We investigate a one-dimensional system of N particles, initially distributed with random positions and velocities, interacting through binary collisions. The collision rule is such that there is a time after which the N particles do not interact and become sorted according to their velocities. When the collisions are elastic, we derive asymptotic distributions for the final collision time of a single particle and the final collision time of the system as the number of particles approaches infinity, under different assumptions for the initial distributions of the particles’ positions and velocities. For comparison, a numerical investigation is carried out to determine how a non-elastic collision rule, which conserves neither momentum nor energy, affects the median collision time of a particle and the median final collision time of the system.

Appendices

Appendix: 1 Proof of Proposition 1

Suppose at the time of a collision, in addition to the change in velocity, the labels of particles are also switched. Unlike the case of elastic collisions, the path of a particle in space-time is not a straight line. Instead, individual particles follow piecewise linear trajectories where the slope of each segment changes by a factor of $1-\epsilon$ after each intersection with another path. Again, let $\ell _i(t)$ denote the position of the ith particle and $\tau _{i,\star _1}<\tau _{i,\star _2}<\dots$ denote the times when the path of particle i intercepts the path of another particle. Then

$$\begin{aligned} \ell _i(t) = {\left\{ \begin{array}{ll} X_i +t V_i &{} 0<t \le \tau _{i,\star _1} \\ (X_i+\tau _{i,\star _1} V_1) + (t-\tau _{i,\star _1}) (1-\epsilon ) V_i &{} \tau _{i,\star _1} < t \le \tau _{i,\star _2} \\ \vdots \end{array}\right. } \end{aligned}$$

As was the case for elastic collisions, the collection of intersection times of the trajectories of particles (now piecewise linear) is in one-to-one correspondence with the collection of collision times. Therefore, for a system to have infinitely many collision times, there must be two paths which intersect infinitely many times. In the case $\epsilon = 1$, two particles remain fixed together following their collision so that they cannot collide a second time and the existence of a final collision time is thus trivial. As such, we focus on the case where $\epsilon < 1.$ Then, since the initial velocities are continuous random variables, it follows that for all $1\le i < j \le N$ and $k,m \in \{0,1,2,\dots \}$, $(1-\epsilon )^k V_i \ne (1-\epsilon )^m V_j$ almost surely which ensures that any two paths which intersect do so by crossing one another a.s.

We now assume the paths $\ell _1$ and $\ell _2$ intersect infinitely often and derive a contradiction. Since the paths cross, we may choose two successive intersection times, $s_1^{(2)}<s_2^{(2)}$, such that $\ell _1(t) > \ell _2(t)$ for $t\in (s_1^{(2)},s_2^{(2)})=\mathbb {S}^{(2)}.$ It may be the case that a third path also intersects $\ell _1$ and $\ell _2$ at time $s_1^{(2)}$ or $s_2^{(2)}$. However, we may relabel the paths so that a ternary intersection does not alter the velocities of paths $\ell _1$ and $\ell _2$ on the open interval $\mathbb {S}^{(2)}.$

For example, suppose $\ell _3$ also intersects with $\ell _1$ and $\ell _2$ at $s_1^{(2)}$ or $s_2^{(2)}$. There are two possibilities. Firstly, $\ell _3$ does not intersect $\ell _1$ or $\ell _2$ on the interval $(s_1^{(2)},s_2^{(2)}).$ Thus, $\ell _3$ will not alter the velocities of $\ell _1,\ell _2$ on this interval and so will not influence the time, $s_2^{(2)}$, when $\ell _1$ and $\ell _2$ intersect again.

Secondly, $\ell _3$ could intersect either $\ell _1$ or $\ell _2$ at a second time $s\in (s_1^{(2)},s_2^{(2)}).$ For instance, suppose $\ell _3$ intersects with $\ell _1$ at times s and $s_2^{(2)}$, and that $\ell _3$ does not intersect $\ell _2$ on the interval $(s,s_2^{(2)}).$ We can then relabel the paths and times so that, $\ell _1$ and $\ell _2$ (formerly $\ell _1$ and $\ell _3$), intersect at successive times $s_1^{(2)}$ and $s_2^{(2)}$ (formerly s and $s_2^{(2)}$). Then on the interval $(s_1^{(2)},s_2^{(2)})$, the path $\ell _3$ (formerly $\ell _2$) intersects with neither $\ell _1$ nor $\ell _3$. Other possibilities are handled similarly. As a result of this choice, on the closed interval $\overline{\mathbb {S}^{(2)}}$, any path which crosses both $\ell _1$ and $\ell _2$ does so an equal number of times.

Let us return to case where $\ell _1$ and $\ell _2$ intersect at successive times $s_2^{(1)}$ and $s_2^{(2)}$ and $\ell _1(t)>\ell _2(t)$ for $t\in \mathbb {S}^{(2)}$. Furthermore, assume these paths are chosen so that there is no other path which intersects both $\ell _1$ or $\ell _2$ at $s_1^{(2)}$ or $s_2^{(2)}$ and either $\ell _1$ or $\ell _2$ at another time in the interval $\mathbb {S}^{(2)}.$ Let

$$\begin{aligned} u_i^+ = \lim _{h\rightarrow 0^+}\frac{\ell _i(s_1^{(2)}+h)-\ell _i(s_1^{(2)})}{h}, \quad i=1,2 \end{aligned}$$

be the velocities of particles 1 and 2 immediately after their collision at $s_1^{(2)}.$ Let

$$\begin{aligned} U_i^- = \lim _{h\rightarrow 0^-}\frac{\ell _i(s_2^{(2)}+h)-\ell _i(s_2^{(2)})}{h}, \quad i=1,2 \end{aligned}$$

be the velocities of particles 1 and 2 immediately before their collision at $s_2^{(2)}.$ Since $\ell _1(t) > \ell _2(t)$ for $t\in \mathbb {S}^{(2)}$ and the paths cross a.s., it follows that

$$\begin{aligned} u_1^+>u_2^+ \quad \text { and } \quad U_1^- < U_2^- \quad \text { a.s}. \end{aligned}$$

(A.1)

We note that the velocities of both paths 1 and 2 must be of the same sign since $U_i^-$ is related to $u_i^+$ by the equation $U_i^-=(1-\epsilon )^{k_i}u_i^+$ where $(1-\epsilon )^{k_1}>0$ and $k_i$ is the number of additional path intersections of i during $\mathbb {S}^{(2)}$.

Consider the path intersections involving $\ell _1$ on the interval $\mathbb {S}^{(2)}$ (Fig. 10). There are two possibilities. (1) A path, (shown as a dotted, red line in Fig. 10), crosses both $\ell _1$ and $\ell _2$ (the dashed, blue lines in Fig. 10) k times, and alters the velocities of both particles by a multiplicative factor of $(1-\epsilon )^k.$ Alternatively, (2) a path may only intersect $\ell _1$ leaving the velocity of particle 2 unchanged (the solid black line in Fig. 10).

Fig. 10

Paths $\ell _1$ and $\ell _2$ are shown as dashed, blue lines. The dotted red line serves as an example of a path which intersects both $\ell _1$ and $\ell _2$. A path which intersects $\ell _1$ twice without hitting $\ell _k$ (shown as a solid black line) implies the existence of another ‘nested’ path, $\ell _{k+1}$, also crossing $\ell _1$ twice but between the times, $s_1^{(k)}<s_2^{(k)}$, when $\ell _{k}$ hits $\ell _1$ (Color figure online)

If only $k_1$ intersections of the first type occur, then

$$\begin{aligned} U_1^-=u_1^+(1-\epsilon )^{k_1} > u_2^+(1-\epsilon )^{k_1}=U_2^- \end{aligned}$$

which contradicts the assumption that $U_1^- < U_2^-.$ Indeed, $\ell _1$ and $\ell _2$ must experience a different number of intersections, $k_1$ and $k_2$ respectively, so that

$$\begin{aligned} U_1^- = (1-\epsilon )^{k_1}u_1^+ < (1-\epsilon )^{k_2} u_2^+ = U_2^-. \end{aligned}$$

The details of the ordering of $k_1$ and $k_2$ depend on both the sign of $u_1^+,u_2^+$ and on the sign of $\epsilon .$ However, we may assume without loss of generality that $k_1 > k_2 \ge 0.$

Thus, there must be a path which intersects $\ell _1$ at least twice without intersecting $\ell _2$. Call it $\ell _3$. Again, we may choose successive intersection times, $s_1^{(3)} < s_2^{(3)}$ in $\mathbb {S}^{(2)},$ such that $\ell _1(t)>\ell _3(t)$ and repeat the preceding argument (Fig. 10).

As such, the existence of a kth path with successive intersections of $\ell _1$ at times $s_1^{(k)}<s_2^{(k)}$ then implies the existence of a $(k+1)$th path which has successive intersections with $\ell _1$ on a subinterval $\mathbb {S}^{(k+1)}=(s_1^{(k+1)},s_2^{(k+1)})\subset (s_1^{(k)},s_2^{(k)})=\mathbb {S}^{(k)}$. By construction, $\ell _2,\dots ,\ell _k$ cannot collide with $\ell _1$ on $\mathbb {S}^{(k+1)}$. Through induction we reach a contradiction as this requires an $(N+1)$th path in a system with only N paths.

Appendix 2: Proof of Theorem 3

In this case, let $\mu _N =\mu N \log (N)$. We now proceed by splitting the integrals g(X, V, N), again with the aim of extracting the O(1 / N) components of the integrals within g(X, V, N) as $N\rightarrow \infty$.

$$\begin{aligned} g(X,V,N)= & {} \bigg [1 - \int _0^\infty f_v(V+w)F_x(X-\mu N \log N w)dw \nonumber \\&- \int _{-\infty }^0f_v(V+w)[1-F_x(X-\mu N \log N w)]dw \bigg ]^{N-1}\nonumber \\= & {} \bigg [1-\int _0^\infty \bigg (f_v(V+w)F_x(X-\mu N \log N w) \nonumber \\&+ f_v(V-w)[1-F_x(X+\mu N \log N w)]\bigg ) dw \bigg ]^{N-1}\nonumber \\= & {} \bigg [1- \int _0^{\frac{1}{N\sqrt{\log N}}} \bigg (f_v(V+w)F_x(X-\mu N \log N w) \nonumber \\&+ f_v(V-w)[1-F_x(X+\mu N \log N w)]\bigg ) dw \nonumber \\&- \int _{\frac{1}{N\sqrt{\log N}}}^\infty \bigg (f_v(V+w)F_x(X-\mu N \log N w) \nonumber \\&+ f_v(V-w)[1-F_x(X+\mu N \log N w)]\bigg ) dw \bigg ]^{N-1}{.} \end{aligned}$$

(B.1)

The first integral in Eq. (B.1) over the interval $(0,\frac{1}{N\sqrt{\log N}})$ is $O(\frac{1}{N\sqrt{\log N}})$. In the remaining integral, we first make the change of variables $w\mapsto N\log N w.$

$$\begin{aligned}&\int _{\frac{1}{N\sqrt{\log N}}}^\infty \bigg (f_v(V+w)F_x(X-\mu N \log N w) \nonumber \\&\qquad + f_v(V-w)[1-F_x(X+\mu N \log N w)]\bigg ) dw \nonumber \\&\quad =\frac{1}{N\log N}\int _{\sqrt{\log N}}^\infty \bigg [ f_v\big (V+\frac{w}{N\log N}\big ) F_x(X- \mu w) \nonumber \\&\qquad + f_v\big (V-\frac{w}{N \log N}\big )[1-F_x(X+\mu w)] \bigg ] dw{.} \end{aligned}$$

(B.2)

Since $w > \sqrt{\log N}$, we can make use of the scalings from Eq. (4.14) for $F_x(X-\mu w)$ and $1-F_x(X+\mu w)$ valid for $\alpha =1$ and continue the preceding calculation.

$$\begin{aligned}&\frac{1}{N\log N}\int _{\sqrt{\log N}}^\infty \bigg [ f_v\big (V+\frac{w}{N\log N}\big ) F_x(X- \mu w) \nonumber \\&\qquad + f_v\big (V-\frac{w}{N \log N}\big )[1-F_x(X+\mu w)] \bigg ] dw\nonumber \\&\quad =\frac{1}{N\log N}\int _{\sqrt{\log N}}^\infty \bigg [ \frac{ f_v\big (V+\frac{w}{N\log N}\big )}{\pi (\mu w -X)}\bigg (1+\frac{O(1)}{(\mu w -X)^2} \bigg ) \nonumber \\&\qquad + \frac{f_v\big (V-\frac{w}{N \log N}\big )}{\pi (\mu w +X)}\bigg (1+\frac{O(1)}{(\mu w+X)^2}\bigg ) \bigg ] dw \nonumber \\&\quad = \frac{1}{N\log N}\int _{\sqrt{\log N}}^{N\sqrt{\log N}} \bigg [ \frac{ f_v\big (V+\frac{w}{N\log N}\big )}{\pi (\mu w -X)}\bigg (1+\frac{O(1)}{(\mu w -X)^2} \bigg ) \nonumber \\&\qquad + \frac{f_v\big (V-\frac{w}{N \log N}\big )}{\pi (\mu w +X)}\bigg (1+\frac{O(1)}{(\mu w+X)^2}\bigg ) \bigg ]dw \nonumber \\&\qquad +\frac{1}{N\log N}\int _{N\sqrt{\log N}}^\infty \bigg [ \frac{ f_v\big (V+\frac{w}{N\log N}\big )}{\pi (\mu w -X)}\bigg (1+\frac{O(1)}{(\mu w -X)^2} \bigg ) \nonumber \\&\qquad + \frac{f_v\big (V-\frac{w}{N \log N}\big )}{\pi (\mu w +X)}\bigg (1+\frac{O(1)}{(\mu w+X)^2}\bigg ) \bigg ] dw{.} \end{aligned}$$

(B.3)

We now bound the integral over the interval $(N\sqrt{\log N}, \infty )$.

$$\begin{aligned}&\frac{1}{N\log N}\int _{N\sqrt{\log N}}^\infty \frac{ f_v\big (V\pm \frac{w}{N\log N}\big )}{\pi (\mu w \mp X)}\bigg (1+\frac{O(1)}{(\mu w \mp X)^2} \bigg )dw \nonumber \\&\quad \le \frac{1}{\pi (\mu N\sqrt{\log N} \mp X)}\bigg (1+\frac{O(1)}{(\mu N\sqrt{\log N} \mp X)^2} \bigg )\nonumber \\&\cdot \frac{1}{N\log N}\int _{N\sqrt{\log N}}^\infty f_v\big (V\pm \frac{w}{N\log N}\big )dw \nonumber \\&\quad = \frac{1}{\pi (\mu N\sqrt{\log N} \mp X)}\bigg (1+\frac{O(1)}{(\mu N\sqrt{\log N} \mp X)^2} \bigg ) \bigg (\pm F_v(\infty ) \mp F_v\big (V\pm \frac{1}{\sqrt{\log N}}\big )\bigg ) \nonumber \\&\quad = O\bigg (\frac{1}{N\sqrt{\log N}}\bigg ){.} \end{aligned}$$

(B.4)

To review, at this point we have shown that as N tends to infinity

$$\begin{aligned} g(X,V,N) =&\bigg [1 - \frac{1}{N\log N}\int _{\sqrt{\log N}}^{N\sqrt{\log N}} \frac{ f_v\big (V+\frac{w}{N\log N}\big )}{\pi (\mu w -X)}\bigg (1+\frac{C}{(\mu w -X)^2} \bigg )dw \\&- \frac{1}{N\log N}\int _{\sqrt{\log N}}^{N\sqrt{\log N}}\frac{f_v\big (V-\frac{w}{N \log N}\big )}{\pi (\mu w +X)}\bigg (1+\frac{C'}{(\mu w+X)^2}\bigg ) dw \\&+ O\bigg (\frac{1}{N\sqrt{\log N}}\bigg )\bigg ]^{N-1}{.} \end{aligned}$$

The remaining integrals over the interval $(\sqrt{\log N},N\sqrt{\log N})$ account for O(1 / N) terms which give rise to the exponential, $e^{-\frac{2f_v(V)}{\pi \mu }}$ from the theorem. Note that the correction terms, $C/(\mu w \pm X)^2$, from the scaling in Eq. (4.14) give rise to corrections of the order $C/\log N$ in the following display.

$$\begin{aligned}&\int _{\sqrt{\log N}}^{N\sqrt{\log N}} \frac{ f_v\big (V+\frac{w}{N\log N}\big )}{\pi (\mu w -X)}\bigg (1+\frac{O(1)}{(\mu w -X)^2} \bigg )dw \nonumber \\&\quad = \bigg (1+\frac{O(1)}{\log N}\bigg )\int _{\sqrt{\log N}}^{N\sqrt{\log N}} \frac{ f_v\big (V+\frac{w}{N\log N}\big )}{\pi (\mu w -X)}\nonumber \\&\int _{\sqrt{\log N}}^{N\sqrt{\log N}}\frac{f_v\big (V-\frac{w}{N \log N}\big )}{\pi (\mu w +X)}\bigg (1+\frac{O(1)}{(\mu w+X)^2}\bigg ) dw \nonumber \\&\quad = \bigg (1+\frac{O(1)}{\log N}\bigg ) \int _{\sqrt{\log N}}^{N\sqrt{\log N}}\frac{f_v\big (V-\frac{w}{N \log N}\big )}{\pi (\mu w +X)} dw. \end{aligned}$$

(B.5)

The correction in Eq. (B.5) therefore will be of order $O(1/\log N)$. Now focus on the integrals

$$\begin{aligned} \frac{1}{N\log N} \int _{\sqrt{\log N}}^{N\sqrt{\log N}}\frac{f_v\big (V\pm \frac{w}{N \log N}\big )}{\pi (\mu w \mp X)}dw \end{aligned}$$

and deduce a limit. We apply the change of variable $w\mapsto \frac{1}{N\sqrt{\log N}} w$.

$$\begin{aligned} \frac{1}{N\log N} \int _{\sqrt{\log N}}^{N\sqrt{\log N}}\frac{f_v\big (V\pm \frac{w}{N \log N}\big )}{\pi (\mu w \mp X)}dw = \frac{1}{\sqrt{\log N}} \int _{\frac{1}{N}}^1 \frac{f_v\big (V\pm \frac{w}{\sqrt{\log N}}\big )}{\pi ({\mu } N\sqrt{\log N} w \mp X)} dw {.}\nonumber \\ \end{aligned}$$

(B.6)

By the assumption that $f_v$ is continuous, it is uniformly continuous on the interval $[V,V+1]$. Thus $f_v\big (V\pm \frac{w}{\sqrt{\log N}}\big ) = f_v(V) +o(1)$ as $N\rightarrow \infty .$ Then,

$$\begin{aligned} \frac{1}{\sqrt{\log N}} \int _{\frac{1}{N}}^1 \frac{f_v\big (V\pm \frac{w}{\sqrt{\log N}}\big )}{\pi (\mu N\sqrt{\log N} w \mp X)} dw= & {} \frac{1}{\sqrt{\log N}} \int _{\frac{1}{N}}^1 \frac{f_v(V)+o(1)}{\pi ({\mu } N\sqrt{\log N} w \mp X)} dw\nonumber \\= & {} \frac{f_v(V)+o(1)}{\pi \mu N \log N} \log |\pi \mu N \sqrt{\log N} w \mp X|\bigg |_{w=1/N}^{w=1} \nonumber \\= & {} \frac{f_v(V)}{\pi \mu N} + o(1/N){.} \end{aligned}$$

(B.7)

Thus, as $N\rightarrow \infty$

$$\begin{aligned} g(X,V,N)= \bigg [1-\frac{2f_v(V)}{\pi \mu N} + o\bigg (\frac{1}{N}\bigg )\bigg ]^{N-1} \rightarrow \exp \bigg (-\frac{2f_v(V)}{\pi \mu } \bigg ) {\qquad \text {as } N \rightarrow \infty ,} \end{aligned}$$

(B.8)

which concludes the proof.

Appendix 3: Proof of Theorem 6

In this case, we take $z_N(t) = t N^2 \log N$. We need only show the following two requirements of the limit law are satisfied:

$$\begin{aligned}&\left( {\begin{array}{c}N\\ 2\end{array}}\right) P(\tau _{1,2}> tN^2 \log N ) \rightarrow \frac{2}{\pi t} \int _\mathbb {R} f_v^2 (V) dV \\&N^3 P(\tau _{1,2}> tN^2 \log N , \tau _{2,3} >t N^2 \log N ) \rightarrow 0{.} \end{aligned}$$

The previous statements follow naturally from the asymptotic results derived in the proof of Theorem 3. Again, from Eq. (4.21) with $z_N(t) = t N^2 \log N.$

$$\begin{aligned} \left( {\begin{array}{c}N\\ 2\end{array}}\right) P(\tau _{1,2} > tN^2 \log N )= & {} \left( {\begin{array}{c}N\\ 2\end{array}}\right) \bigg (\int _{\mathbb {R}^2}f_x(X)f_v(V) \int _0^\infty f_v(w+V)F_x(X \nonumber \\&-t wN^2 \log N) dwdXdV \nonumber \\&+\int _{\mathbb {R}^2}f_x(X)f_v(V) \int _{-\infty }^0 f_v(w+V) (1 \nonumber \\&-F_x(X-t w N^2 \log N ))dw dX dV \bigg ) {.} \end{aligned}$$

(C.1)

In the proof of Theorem 3, it was shown that for large N,

$$\begin{aligned} \int _0^\infty f_v(w+V)F_x(X-tN\log N w) dw= & {} \frac{f_v(V)}{\pi t {N}} + o(N^{-1}) \nonumber \\ \int _{-\infty }^0 f_v(w+V) (1-F_x(X-t N\log N w))dw= & {} \frac{f_v(V)}{\pi t N}+ o(N^{-1}){.} \end{aligned}$$

(C.2)

Replacing $N \log N$ with ${2} N^2\log N$ and t with t / 2 in the previous statement, we have the following relationship for large N.

$$\begin{aligned} \left( {\begin{array}{c}N\\ 2\end{array}}\right) P(\tau _{1,2} > tN^2 \log N )= & {} \left( {\begin{array}{c}N\\ 2\end{array}}\right) \int _{\mathbb {R}^2} f_x(X)f_v(V) \bigg (\frac{{4} f_v(V)}{\pi t N^2} + o(N^{-2})\bigg ) dX dV \nonumber \\\rightarrow & {} \frac{{2}}{\pi t} \int _\mathbb {R} f_v^2(V) dv {\qquad \text {as } N \rightarrow \infty .} \end{aligned}$$

(C.3)

For the second requirement, we make use of the same asymptotic expansion as in Eq. (C.2).

$$\begin{aligned}&N^3P(\tau _{1,2}>N^2\log N t , \tau _{2,3} >N^2\log N t ) \nonumber \\&\quad =N^3 \int _{\mathbb {R}^2}f_x(X)f_v(V) \bigg (\int _0^\infty f_v(w+V)F_x(X-tw N^2\log N ) dw \nonumber \\&\qquad + \int _{-\infty }^0 f_v(w+V) (1-F_x(X-tw N^2\log N))dw\bigg )^2 dX dV \nonumber \\&\quad = N^3 \int _{\mathbb {R}^2}f_x(X)f_v(V) \bigg (\frac{{4}}{\pi t N^2} f_v(V) + o(N^{-2})\bigg )^2 dXdV \nonumber \\&\quad = \frac{{16}}{\pi {^2} t{^2} N} \int _\mathbb {R}f_v{^3}(V) dV +o(N^{-1}) \rightarrow 0 {\qquad \text {as } N \rightarrow \infty ,} \end{aligned}$$

(C.4)

which completes the proof.

Appendix 4: Counterexample to the Proof of Theorem 4 when $E|X|<\infty$, $E|X|^{3/2}=\infty$

In the proof of Theorem 4, we verified the two requirements

$$\begin{aligned}&\left( {\begin{array}{c}N\\ 2\end{array}}\right) P\bigg (\tau _{1,2} > \left( {\begin{array}{c}N\\ 2\end{array}}\right) t \bigg ) \rightarrow \frac{1}{t} \bigg (\int _{\mathbb {R}}f_v{^2}(V) dV\bigg ) \int _{\mathbb {R}^2} |X-y|f_x(X)f_x(y) dXdy \end{aligned}$$

(D.1)

$$\begin{aligned}&N^3P\bigg (\tau _{1,2}> {\left( {\begin{array}{c}N\\ 2\end{array}}\right) t}, \tau _{2,3}>\left( {\begin{array}{c}N\\ 2\end{array}}\right) t\bigg ) \rightarrow 0 \end{aligned}$$

(D.2)

as $N\rightarrow \infty$. Recall that Eq. (D.1) followed from the assumption that $E|X_1|<\infty$ and the continuity and boundedness of $f_v$. However, Eq. (D.2) required the additional assumption that $E|X_1|^{3/2}< \infty .$

Suppose the initial positions of particles are distributed with a density

$$\begin{aligned} f_x(x) = \frac{C_\alpha }{1+|x|^{1+\alpha }} \end{aligned}$$

for $\alpha \in (1,3/2]$. In this case, $E|X_1|<\infty$, but $E|X_1|^{3/2}$ does not exist. We now proceed to show Eq. (D.2) is not satisfied for this choice of density for the initial position. From the proof of Theorem 4, recall

$$\begin{aligned}&N^3P\bigg (\tau _{1,2}> z_N(t), \tau _{2,3}>\left( {\begin{array}{c}N\\ 2\end{array}}\right) t\bigg ) \\&\quad =\,N^3\int _{\mathbb {R}^2} f_x(X)f_v(V) \bigg ( \int _0^\infty f_v(w+V)F_x\bigg ( X-\left( {\begin{array}{c}N\\ 2\end{array}}\right) tw\bigg ) dw \\&\qquad + \int _0^\infty f_v(V-w)\bigg [1-F_x\bigg (X + \left( {\begin{array}{c}N\\ 2\end{array}}\right) tw\bigg )\bigg ] dw \bigg )^2dX dV \end{aligned}$$

which is bounded below by

$$\begin{aligned}&N^3\int _{\mathbb {R}^2} f_x(X)f_v(V)\bigg (\int _0^\infty f_v(V-w)\bigg [1-F_x\bigg (X + \left( {\begin{array}{c}N\\ 2\end{array}}\right) tw\bigg )\bigg ] dw \bigg )^2dXdV \\&\quad =\,N^3\int _{\mathbb {R}} f_v(V)\int _0^\infty f_v(V-w_1)\int _0^\infty f_v(V-w_2) \\&\qquad \times \int _{\mathbb {R}}f_x(X)\bigg [1-F_x\bigg (X+\large {\left( {\begin{array}{c}N\\ 2\end{array}}\right) }tw_1\bigg )\bigg ]\bigg [1-F_x\bigg (X+\left( {\begin{array}{c}N\\ 2\end{array}}\right) tw_2\bigg )\bigg ]dXdw_1dw_2dV{.} \end{aligned}$$

Furthermore, we can restrict the region of integration to $w_1,w_2\in (1,2)$ and $X< -N(N-1) t$. In this case, $X+\left( {\begin{array}{c}N\\ 2\end{array}}\right) tw\le 0$. Thus, by the symmetry of $f_x$, it follows that $1-F_x(X+\left( {\begin{array}{c}N\\ 2\end{array}}\right) tw) \ge 1/2$. Then,

$$\begin{aligned}&N^3P\bigg (\tau _{1,2}> z_N(t), \tau _{2,3}>\left( {\begin{array}{c}N\\ 2\end{array}}\right) t\bigg ) \\&\quad \ge N^3\int _{\mathbb {R}}f_v(V)\int _0^\infty f_v(V-w_1)\int _0^\infty f_v(V-w_2) \\&\qquad \times \int _{\mathbb {R}}f_x(X)\bigg [1-F_x\bigg (X+\large {\left( {\begin{array}{c}N\\ 2\end{array}}\right) }tw_1\bigg )\bigg ]\bigg [1-F_x\bigg (X+\left( {\begin{array}{c}N\\ 2\end{array}}\right) tw_2\bigg )\bigg ]dXdw_1dw_2dV \\&\quad \ge N^3 \int _{-\infty }^{-N(N-1)t} f_x(X) \cdot \frac{1}{2}\cdot \frac{1}{2} dX \cdot \int _\mathbb {R}f_v(V)\int _1^2 f_v(V-w_1) dw_1 \nonumber \\&\qquad \int _1^2f_v(V-w_2) dw_2 dV \\&\quad =\, CN^3\int _{-\infty }^{-N(N-1)t}f_x(X)dX{.} \end{aligned}$$

For $z \ll -1$, $\int _{-\infty }^{z}f_x(z) dz \approx \frac{1}{|z|^\alpha }.$ In this case, we have assumed $\alpha \in (1,3/2]$ so that as $N\rightarrow \infty$,

$$\begin{aligned} CN^3 \int _{-\infty }^{-N(N-1)t}f_x(X)dX \rightarrow \frac{C}{t^\alpha } \frac{N^3}{N^{2\alpha }}> 0. \end{aligned}$$

Thus, Eq. (D.2) is not satisfied. As such, the proof of Theorem 4 does not apply for this choice of density for the initial position of particles.