Moment Closure Approximations of the Boltzmann Equation Based on $\varphi$-Divergences

Abstract

This paper is concerned with approximations of the Boltzmann equation based on the method of moments. We propose a generalization of the setting of the moment-closure problem from relative entropy to $\varphi$-divergences and a corresponding closure procedure based on minimization of $\varphi$-divergences. The proposed description encapsulates as special cases Grad’s classical closure based on expansion in Hermite polynomials and Levermore’s entropy-based closure. We establish that the generalization to divergence-based closures enables the construction of extended thermodynamic theories that avoid essential limitations of the standard moment-closure formulations such as inadmissibility of the approximate phase-space distribution, potential loss of hyperbolicity and singularity of flux functions at local equilibrium. The divergence-based closure leads to a hierarchy of tractable symmetric hyperbolic systems that retain the fundamental structural properties of the Boltzmann equation.

1 Introduction

The Boltzmann equation describes the molecular dynamics of fluid flows based on their one-particle phase-space distribution. The equation encapsulates all conventional macroscopic flow models, as its limit solutions correspond to solutions of the compressible Euler and Navier–Stokes equations [4, 17], the incompressible Euler and Navier–Stokes equations [19, 37], the incompressible Stokes equations [38] and the incompressible Navier–Stokes–Fourier system [36]; see [50] for an overview. The Boltzmann equation is uniquely suited to describe transitional molecular/continuum flows and the corresponding rarefaction effects, by virtue of its inherent characterization of deviations of the velocity distribution from local equilibrium. Rarefaction effects are essential in multitudinous applications, e.g. problems involving large mean free paths in high-altitude flows and hypobaric applications such as chemical vapor deposition; see [13, 56] and references therein for further examples. Moreover, the perpetual trend toward miniaturization in science and technology renders accurate descriptions of fluid flows in the transitional regime of fundamental technological relevance, e.g. in nanoscale applications, micro-channel flows or porous-media flows [54]. The Boltzmann equation moreover provides a prototype for other models for collective behavior of large ensembles of particles, for instance, in semi-conductors [26], plasmas, fusion and fission devices [43], and dispersed-particle flows [47–49].

Numerical approximation of the Boltzmann equation poses a formidable challenge, on account of its high dimensional setting: in D spatial dimensions, the one-particle phase-space is 2D dimensional. The corresponding computational complexity of conventional discretization methods, such as finite-element methods with uniform meshes, is prohibitive. Numerical approximations of the Boltzmann equation have been predominantly based on particle methods, such as DSMC [6, 7]. Convergence proofs for these methods [63] however convey that their computational cost is prohibitive in the fluid-dynamical limit. Moreover, DSMC can be inefficient, because it is inherent to the underlying Monte-Carlo process that the approximation error decays only as ${n^{-\frac{1}{2}}}$ as the number of simulation molecules, n, increases; see, for instance, [32, Thm. 5.14]. Efficient computational modeling of fluid flows in the transitional molecular/continuum regime therefore remains an outstanding challenge.

The method of moments [20, 35, 56, 61] provides an alternative approximation technique for the Boltzmann equation. The method of moments is a general statistical approximation technique which identifies parameters of an approximate distribution based on its moments [41]. Application of the method of moments to the Boltzmann equation yields an evolution equation for the moments of the phase-space distribution. Moment-based approximations are generally consistent with a restricted interest in functionals of the distribution associated with macroscopic properties of the fluid. The method of moments is closely related to extended thermodynamics; see, for instance, [16, 44]. A recent extension to the method of moments are the regularized moment methods, in which the moment method is combined with a perturbative approximation in the Knudsen number [31, 55, 57].

Intrinsic to the method of moments is an approximation of the moment-closure relation that completes the evolution equation for the moments. Moment-closure approximations for the Boltzmann equation were originally conceived by Grad [20]. Grad’s closure relies on an expansion of the one-particle distribution in Hermite polynomials. For a linear Boltzmann equation extended with exogenous forcing, it has been shown that the distribution in Grad’s moment equations converges to the distribution of the underlying kinetic model as the order of the moment approximation tends to infinity, and to the solution of a corresponding drift-diffusion model in the macroscopic limit, i.e. as the Knudsen number tends to zero [51]. Grad’s moment systems are impaired by two essential deficiencies, however, viz. the potential occurrence of inadmissible locally negative distributions and potential loss of hyperbolicity [11, 59]. Levermore [35] has developed a moment-closure procedure based on constrained entropy minimization, similar to Dreyer’s maximum-entropy closure in extended thermodynamics [16]. The entropy minimization procedure formally leads to an exponential closure. Levermore’s moment systems retain the fundamental structural properties of the Boltzmann equation, viz., conservation of mass, momentum and energy, Galilean invariance and entropy dissipation. Moreover, the moment systems form a hierarchy of symmetric hyperbolic systems and the corresponding distributions are non-negative. It was later shown by Junk [27], however, that Levermore’s moment-closure procedure is impaired by a realizability problem, in that there exist moments for which the minimum-entropy distribution is non-existent. Moreover, the fluxes in Levermore’s moment systems may become arbitrarily large in the vicinity of (local) equilibrium. Recent results by Junk [28], Schneider [52] and Pavan [46] convey that potential non-existence of solutions to the entropy-minimization problem can be avoided by relaxing the constraints to allow inequalities in the highest-order moments. Moreover, the solution to the relaxed entropy minimization problem coincides with the solution to the original constrained entropy minimization problem if the latter admits a solution. The relaxation of the entropy-minimization problem however generally engenders the loss of a one-to-one correspondence between the moments and the distribution. Moreover, relaxation of the entropy minimization problem does not resolve the potential singularities in the flux function, as these singularities are intrinsic to the exponential form of the closure relation. Another fundamental complication, pertaining to the implementation of moment systems based on exponential closure, is that the resulting formulation requires the evaluation of moments of exponentials of polynomials of, in principle, arbitrary order. It is generally accepted that the derivation of closed-form expressions for such moments is intractable, and accurate approximation of the moments is a notoriously difficult problem; see, for instance, [34].

In this paper we consider alternative moment-closure relations for the Boltzmann equation, based on approximations of the exponential function derived from truncations of its standard limit definition, $\exp (\cdot )=\lim _{n\rightarrow \infty }(1+\cdot /n)^n$. It is to be noted that closure relations derived from a series-expansion definition of the exponential have received scant attention before, e.g. by Brini and Ruggeri [12]. Our motivation for considering the limit definition instead of the series-expansion definition for constructing the moment closures is based on the direct availability of a corresponding inverse relation for higher order approximations. We propose a generalization of the setting of the moment-closure problem from Kullback–Leibler divergence [33] (i.e relative entropy) to the class of $\varphi$-divergences [14]. The considered $\varphi$-divergences constitute an approximation to the Kullback–Leibler divergence in the vicinity of (local) equilibrium. It will be shown that the approximate-exponential closure relation can be derived via constrained minimization of a corresponding $\varphi$-divergence. The proposed description encapsulates as special cases Grad’s closure relation and Levermore’s entropy-based closure relation. For even order approximations of the exponential, the closure relation engenders non-negative phase-space distributions. Moreover, the corresponding moment systems are symmetric hyperbolic and tractable, in the sense that the formulation only requires the evaluation of higher-order moments of Gaussian distributions. The moment systems furthermore dissipate a $\varphi$-divergence relative to a suitable reference distribution, analogous to the dissipation of relative entropy of the Boltzmann equation, provided that the collision operator dissipates the corresponding $\varphi$-divergence. We will show that the class of collision operators that dissipate appropriate $\varphi$-divergences includes the standard BGK [5] and generalized BGK [35] operators.

The remainder of this paper is organized as follows. Section 2 surveys, for completeness, well known structural features of the Boltzmann equation to be retained in the developed moment system approximation. Section 3 introduces concepts relevant to moment systems. We will establish that moment systems can alternatively be construed as Galerkin subspace approximations of the Boltzmann equation in renormalized form, and review the conventional moment closures of Grad [20] and Levermore [35] and their shortcomings in this setting. Section 4 presents a novel tractable moment closure relation based on $\varphi$-divergence minimization. It will be shown that the corresponding closed system of moment equations are well-posed and retain the structural features of the Boltzmann equation. To investigate the approximation properties of the new moment-system approximation and the most important implementation aspects, viz. solution of the minimization problem and integration of moments of the resulting approximate distribution, Sect. 5 considers elementary one-dimensional numerical experiments. Finally, Sect. 6 presents a concluding discussion.

2 Structural Properties of the Boltzmann Equation

2.1 The Boltzmann Equation

Consider a monatomic gas, i.e. a gas composed of a single species of identical classical particles, contained in a fixed spatial domain $\Omega \subset \mathbb {R}^D$. Kinetic theory describes the state of such a gas by a non-negative (phase-space) density $f=f(t,{\varvec{x}},{\varvec{v}})$ over the single-particle phase space $\Omega \times \mathbb {R}^D$. The evolution of f is considered to be governed by the Boltzmann equation,

$$\begin{aligned} \partial _t f + v_i\partial _{x_i} f=\mathcal {C}(f) \end{aligned}$$

(1)

where the collision operator $f\mapsto \mathcal {C}(f)$ acts only on the ${\varvec{v}}=(v_1,\ldots ,v_D)$ dependence of f locally at each $(t,{\varvec{x}})$ and the summation convention applies to repeated indices. The collision operator is assumed to possess certain conservation, symmetry and dissipation properties, viz., conservation of mass, momentum and energy, invariance under Galilean transformations and dissipation of appropriate entropy functionals. These fundamental properties of the collision operator are treated in further detail below. Our treatment of the conservation and symmetry properties is standard (see, for instance, [35]) and is presented merely for coherence and completeness. For the entropy-dissipation property, we consider a generalization of the usual (relative) entropy to $\varphi$-divergences [14], to enable an exploration of the moment-closure problem in an extended setting; see Sect. 4.

2.2 Conservation and Invariance Properties

To elaborate the conservation properties of the collision operator, let $\langle \cdot \rangle$ denote integration in the velocity dependence of any scalar, vector or matrix valued measurable function over D-dimensional Lebesgue measure. A function $\psi :\mathbb {R}^D\rightarrow \mathbb {R}$ is called a collision invariant of $\mathcal {C}$ if

$$\begin{aligned} \langle \psi \,\mathcal {C}(f) \rangle = 0 \qquad \forall f\in \mathscr {D}(\mathcal {C}), \end{aligned}$$

(2)

where $\mathscr {D}(\mathcal {C})\subset {}L^1(\mathbb {R}^D,\mathbb {R}_{\ge {}0})$ denotes the domain of $\mathcal {C}$, which we consider to be a subset of the almost everywhere nonnegative Lebesgue integrable functions on $\mathbb {R}^D$. Equation (1) associates a scalar conservation law with each collision invariant:

$$\begin{aligned} \partial _t\langle \psi f\rangle +\partial _{x_i} \langle v_i \psi f \rangle = 0 \end{aligned}$$

(3)

We insist that $\{1,v_1,\ldots ,v_D,|{\varvec{v}}|^2\}$ are collision invariants of $\mathcal {C}$ and that the span of this set contains all collision invariants, i.e.

$$\begin{aligned} \langle {}\psi \,\mathcal {C}(f)\rangle =0\quad \forall {}f\in \mathscr {D}(\mathcal {C}) \quad \Leftrightarrow \quad \psi \in \mathrm {span}\{1,v_1,\ldots ,v_D,|{\varvec{v}}|^2\}=:\mathbb {E}. \end{aligned}$$

The moments $\langle {}f\rangle$, $\langle {}v_if\rangle$ and $\langle {}|{{\varvec{v}}}|^2f\rangle$, correspond to mass-density, the (components of) momentum-density and energy-density, respectively. Accordingly, the conservation law (3) implies that (1) conserves mass, momentum and energy.

The assumed symmetry properties of the collision operator pertain to commutation with translational and rotational transformations. In particular, for all vectors ${\varvec{u}}\in \mathbb {R}^D$ and all orthogonal tensors $\mathcal {O}:\mathbb {R}^D\rightarrow \mathbb {R}^D$, we define the translation transformation $\mathcal {T}_{{\varvec{u}}}:\mathscr {D}(\mathcal {C})\rightarrow \mathscr {D}(\mathcal {C})$ and the rotation transformation $\mathcal {T}_{\mathcal {O}}:\mathscr {D}(\mathcal {C})\rightarrow \mathscr {D}(\mathcal {C})$ by:

$$\begin{aligned} (\mathcal {T}_{{\varvec{u}}}f)({\varvec{v}})&=f({\varvec{u}}-{\varvec{v}}) \qquad \forall {}f\in \mathscr {D}(\mathcal {C})\\ (\mathcal {T}_{\mathcal {O}}f)({\varvec{v}})&=f(\mathcal {O}^{*}{\varvec{v}}) \qquad \forall {}f\in \mathscr {D}(\mathcal {C}) \end{aligned}$$

with $\mathcal {O}^{*}$ the Euclidean adjoint of $\mathcal {O}$. Note that the above transformations act on the ${\varvec{v}}$-dependence only. It is assumed that $\mathcal {C}$ possesses the following symmetries:

$$\begin{aligned} \mathcal {C}(\mathcal {T}_{{\varvec{u}}}f)=\mathcal {T}_{{\varvec{u}}}\mathcal {C}(f),\qquad \mathcal {C}(\mathcal {T}_{\mathcal {O}}f)=\mathcal {T}_{\mathcal {O}}\mathcal {C}(f) \end{aligned}$$

(4)

The symmetries (4) imply that (1) complies with Galilean invariance, i.e. if $f(t,{\varvec{x}},{\varvec{v}})$ satisfies the Boltzmann equation (1), then for arbitrary ${{\varvec{u}}}\in \mathbb {R}^D$ and arbitrary orthogonal $\mathcal {O}:\mathbb {R}^D\rightarrow \mathbb {R}^D$, so do $f(t,{\varvec{x}} - {{\varvec{u}}}t,{{\varvec{v}}}-{{\varvec{u}}})$ and $f(t,\mathcal {O}^{*}{{\varvec{x}}},\mathcal {O}^{*}{{\varvec{v}}})$.

2.3 Dissipation Properties

The entropy dissipation property of $\mathcal {C}$ is considered in the extended setting of [35, Sect. 7], from which we derive the following definition: a convex function $\eta :\mathbb {R}_{\gneq {}0}\rightarrow \mathbb {R}$ is called an entropy density for $\mathcal {C}$ if

$$\begin{aligned} \langle \eta '(f)\,\mathcal {C}(f) \rangle \le 0, \qquad \forall f\in \mathscr {D}(\mathcal {C}) \end{aligned}$$

(5)

with $\eta '(f)$ the derivative of $\eta (f)$, and if for every $f\in \mathscr {D}(\mathcal {C})$ the following equivalences hold:

$$\begin{aligned} \mathcal {C}(f) = 0 \quad \Leftrightarrow \quad \langle \eta '(f)\,\mathcal {C}(f)\rangle = 0 \quad \Leftrightarrow \quad \eta '(f)\in \mathbb {E}\end{aligned}$$

(6)

Relation (5) implies that $\mathcal {C}$ dissipates the local entropy $\langle \eta (\cdot )\rangle$, which leads to an abstraction of Boltzmann’s H-theorem for (1), asserting that solutions of the Boltzmann equation (1) satisfy the local entropy-dissipation law:

$$\begin{aligned} \partial _t\langle \eta (f) \rangle +\partial _{x_i} \langle v_i \eta (f) \rangle = \langle \mathcal {C}(f)\, \eta '(f)\rangle \le 0\,. \end{aligned}$$

(7)

The functions $\langle \eta (f) \rangle$, $\langle v_i \eta (f) \rangle$ and $\langle \eta '(f)\, \mathcal {C}(f)\rangle$ are referred to as entropy density, entropy flux and entropy-dissipation rate, respectively. The first equivalence in (6) characterizes local equilibria of $\mathcal {C}$ by vanishing entropy dissipation, while the second equivalence indicates the form of such local equilibria. For spatially homogeneous initial data, $f_0$, Eqs. (5) and (6) suggest that equilibrium solutions, $f_{\mathrm {eq}}$, of (1) are determined by:

$$\begin{aligned} f_{\mathrm {eq}}={{\mathrm{arg\,min}}}\big \{\langle \eta (f)\rangle :f\in \mathscr {D}(\mathcal {C}),\langle f {\varvec{\psi }}\rangle =\langle {}f_0{\varvec{\psi }}\rangle \}, \end{aligned}$$

(8)

Equation (8) identifies equilibria as minimizers¹ of the entropy, subject to the constraint that the invariant moments are identical to the invariant moments of the initial distribution.

We will admit distributions that vanish on sets with nonzero measure. To accommodate such distributions, we introduce an auxiliary non-negativity condition on the collision operator, in addition to (5) and (6). The non-negativity condition insists that $\mathcal {C}(f)$ cannot be negative on zero sets of f:

$$\begin{aligned} \mathcal {C}(f)\big |_{\mathbb {R}^D\setminus \mathrm {supp}(f)}\ge {}0 \end{aligned}$$

(9)

Condition (9) encodes that the collision operator cannot create locally negative distributions. It can be verified that (9) holds for a wide range of collision operators, including the BGK operator [5], the multi-scale generalization of the BGK operator introduced in [35], and all collision operators that are characterized by a (non-negative) collision kernel.

2.4 Divergence-Based Entropies

The standard definition of entropy corresponds to a density $f\mapsto {}f\log {}f$, possibly augmented with $f\psi$ where $\psi \in \mathbb {E}$ is any collision invariant. It is to be noted that for Maxwellians $\mathcal {M}$, i.e. distributions of the form

$$\begin{aligned} \mathcal {M}({{\varvec{v}}}):= \mathcal {M}_{(\varrho ,{{\varvec{u}}},T)}({{\varvec{v}}}) := \frac{\varrho }{(2\pi {}RT)^{\frac{D}{2}}}\exp \left( -\frac{|{\varvec{v}}-{\varvec{u}}|^2}{2RT}\right) \end{aligned}$$

(10)

for some $(\varrho , {{\varvec{u}}}, T)\in \mathbb {R}_{>0}\times \mathbb {R}^D\times \mathbb {R}_{>0}$ and a certain gas constant $R\in \mathbb {R}_{>0}$, it holds that $\log \mathcal {M}\in \mathbb {E}$. Therefore, the relative entropy $\langle {}f\log {}(f/\mathcal {M})\rangle$ of f with respect to some suitable $\mathcal {M}$ is equivalent to $\langle {}f\log {}f\rangle$ in the sense of dissipation characteristics. The physical interpretation of the entropy $\langle {}f\log {}f\rangle$, due to Boltzmann [8–10], is that of a measure of degeneracy of macroscopic states, i.e. of the number of microscopic states that are consistent with the macroscopic state as described by the one-particle marginal, f. In the context of information theory, Shannon [53] showed that for discrete probability distributions, the density $f\mapsto {}f\log {}f$ is uniquely defined by the postulates of continuity, strong additivity and the property that $m\eta (1/m)<n\eta (1/n)$ whenever $n<m$. These postulates ensure that for discrete probability distributions the entropy yields a meaningful characterization of information content and, accordingly, rationalize an interpretation of entropy as a measure of the uncertainty or, conversely, information gain pertaining to an observation represented by the corresponding probability distribution [25].

Kullback and Leibler [33] generalized Shannon’s definition of information to the abstract case and identified the divergence²

$$\begin{aligned} D_{\text {KL}}(\mu _1|\mu _2)=\int f_1\log (f_1/f_2)\,d\nu \end{aligned}$$

(11)

as a distance between mutually absolutely continuous measures $\mu _1$ and $\mu _2$, both absolutely continuous with respect to the measure $\nu$ with Radon–Nikodym derivatives $f_1=d\mu _1/d\nu$ and $f_2=d\mu _2/d\nu$. The Kullback–Leibler divergence characterizes the mean information for discrimination between $\mu _1$ and $\mu _2$ per observation from $\mu _1$. Noting that the Kullback–Leibler divergence (11) coincides with the relative entropy of $f_1$ with respect to $f_2$, the relative entropy $\langle {}f\log (f/\mathcal {M})\rangle$ can thus be understood as a particular measure of the divergence of the one-particle marginal relative to the reference (or background) distribution $\mathcal {M}$. Kullback–Leibler divergence was further generalized by Csiszár [14] and Ali et al. [2], who introduced a general class of distances between probability measures, referred to as $\varphi$-divergences, of the form:

$$\begin{aligned} D_{\varphi }(\mu _1|\mu _2)=\int f_2\,\varphi ({f_1}/{f_2})\,d\nu \end{aligned}$$

(12)

where $\varphi$ is some convex function subject to $\varphi (1)=\varphi '(1)=0$ and $\varphi ''(1)>0$. Note that the Kullback–Leibler divergence corresponds to the specific case $\varphi _{\text {KL}}(\cdot )=(\cdot )\log (\cdot )$.

In this work, we depart from the standard (relative) entropy for (1) and instead consider entropies based on particular $\varphi$-divergences. These $\varphi$-divergences generally preclude the usual physical and information-theoretical interpretations, but still provide a meaningful entropy density in accordance with (5) and (6). The considered $\varphi$-divergences yield a setting in which entropy-minimization based moment-closure approximations to (1) are not impaired by non-realizability, exhibit bounded fluxes in the vicinity of equilibrium, and are numerically tractable.

Remark 1

Implicit to our adoption of $\varphi$-divergence-based entropies is the assumption that such entropies comply with (5) and (6) for a meaningful class of collision operators. It can be shown that the class of admissible collision operators includes the BGK operator [5]:

$$\begin{aligned} \mathcal {C}_{\mathrm {BGK}}(f) = -\tau ^{-1}(f-\mathcal {E}_f) \end{aligned}$$

(13)

where $\tau \in \mathbb {R}_{>0}$ is a relaxation time and $\mathcal {E}_{(\cdot )}$ corresponds to the map $f_0\mapsto f_{\mathrm {eq}}$ defined by (8). The Kuhn–Tucker optimality conditions associated with (8) convey that $\eta '(\mathcal {E}_f)\in \mathbb {E}$ and, therefore, $\langle {}\eta '(\mathcal {E}_f)(f-\mathcal {E}_f)\rangle =0$. The dissipation inequality (5) then follows from the convexity of $\eta (\cdot )$:

$$\begin{aligned} \langle \eta '(f)\, \mathcal {C}_{\mathrm {BGK}}(f) \rangle = -\tau ^{-1}\big \langle \big (\eta '(f)-\eta '(\mathcal {E}_f)\big )(f-\mathcal {E}_f)\big \rangle \le 0 \end{aligned}$$

(14)

Moreover, because equality in (14) holds if and only if $f=\mathcal {E}_f$, the condition $\langle \eta '(f)\,\mathcal {C}_{\mathrm {BGK}}(f)\rangle =0$ implies that $f=\mathcal {E}_f$, which in turn yields $\mathcal {C}_{\mathrm {BGK}}(f)=0$ and $\eta '(f)\in \mathbb {E}$. The equivalences in (6) are therefore also verified. A similar result holds for the multi-scale generalization of the BGK operator introduced in [35]; see Appendix.

3 Moment Systems

Moment systems are approximations of the Boltzmann equation based on a finite number of velocity-moments of the one-particle marginal. An inherent aspect of moment equations derived from (1) is that low-order moments are generally coupled with higher-order ones, and consequently a closed set of equations for the moments cannot be readily formulated. Therefore, a closure relation is required.

3.1 General Derivation and the Moment-Closure Problem

To derive the moment equations from (1) and elaborate on the corresponding moment-closure problem, let $\mathbb {M}$ denote a finite-dimensional subspace of D-variate polynomials and let $\{m_i({\varvec{v}})\}_{i=1}^M$ represent a corresponding basis. Denoting the column M-vector of these basis elements by ${\varvec{m}}$, it holds that the moments $\{\langle {}{m_i}f\rangle \}_{i=1}^M$ of the one-particle marginal satisfy:

$$\begin{aligned} \partial _t\langle {\varvec{m}} f\rangle +\partial _{x_i}\langle v_i{\varvec{m}} f\rangle = \langle {\varvec{m}}\mathcal {C}(f)\rangle \end{aligned}$$

(15)

It is to be noted that we implicitly assume in (15) that f resides in

$$\begin{aligned} \mathbb {F}:= & {} \Big \{f\in {}\mathscr {D}(\mathcal {C}):mf\in {L}^1\big (\mathbb {R}^{D}\big ),\,{\varvec{v}} mf\in {L}^1\big (\mathbb {R}^{D},\mathbb {R}^D\big ),\,m\mathcal {C}(f)\in {}L^1\big (\mathbb {R}^D\big ) \nonumber \\&\quad \text { for all }m\in \mathbb {M}\Big \} \end{aligned}$$

(16)

almost everywhere in the considered time interval (0, T) and the spatial domain $\Omega$. This assumption has been confirmed in specific settings of (1) but not for the general case; see [35, Sect. 4] and the references therein for further details.

The moment-closure problem pertains to the fact that (15) provides only M relations between $(2+D)M$ independent variables, viz., the densities $\langle {} m_i f\rangle$, the flux components $\langle {}v_i m_i f\rangle$ and the production terms $\langle m_i\mathcal {C}(f)\rangle$. Therefore, $(1+D)M$ auxiliary relations must be specified to close the system. Generally, moment systems are closed by expressing the fluxes and production terms as a function of the densities. Moment systems are generally closed by constructing an approximation to the distribution function from the densities and then evaluating the fluxes and production terms for the approximate distribution. Denoting by $\mathbb {A}\subseteq \mathbb {R}^M$ a suitable class of moments, a function $\mathcal {F}:\mathbb {A}\rightarrow \mathbb {F}$ must be specified such that $\mathcal {F}$ realizes the moments in $\mathbb {A}$, i.e. $\langle {\varvec{m}}\mathcal {F}({\varvec{\rho }})\rangle ={\varvec{\rho }}$ for all ${\varvec{\rho }}\in \mathbb {A}$, and $\mathcal {F}(\langle {}{\varvec{m}} f\rangle )$ constitutes a suitable (in a sense to be made more precise below) approximation to the solution f of the Boltzmann equation (1). Approximating the moments in (15) by ${\varvec{\rho }}\approx \langle {\varvec{m}} f\rangle$ and replacing f in (15) by the approximation $\mathcal {F}({\varvec{\rho }})$, one obtains the following closed system for the approximate moments:

$$\begin{aligned} \partial _t{\varvec{\rho }}+\partial _{x_i}\langle v_i{\varvec{m}} \mathcal {F}({\varvec{\rho }})\rangle =\langle {\varvec{m}} \mathcal {C}(\mathcal {F}({\varvec{\rho }}))\rangle . \end{aligned}$$

(17)

The closed moment system (17) is essentially defined by the polynomial subspace, $\mathbb {M}$, and the closure relation, $\mathcal {F}$. A subspace/closure-relation pair $(\mathbb {M},\mathcal {F})$ is suitable if the corresponding moment system (17) is well posed and retains the fundamental structural properties of the Boltzmann equation (1) as described in Sect. 2, viz., conservation of mass, momentum and energy, Galilean invariance and dissipation of an entropy functional. Auxiliary conditions may be taken into consideration, e.g. that the fluxes and production terms can be efficiently evaluated by numerical quadrature.

3.2 Reinterpretation via Renormalization and Galerkin Approximation

Moment systems can alternatively be conceived of as Galerkin subspace-approximations of the Boltzmann equation (1) in renormalized form. This Galerkin-approximation interpretation can for instance prove useful in constructing error estimates for (17) and in deriving structural properties. In addition, the Galerkin-approximation interpretation conveys that smooth functionals of approximate distributions obtained from moment systems, such as velocity moments, generally display superconvergence under hierarchical-rank refinement, in accordance with the Babuška–Miller theorem; see [3] and also Sect. 5.

We consider the subspace $\mathbb {M}$ and introduce a function $\beta :\mathbb {M}\rightarrow \mathbb {F}$, referred to as a renormalization map. Denoting by $V((0,T)\times \Omega ;\mathbb {M})$ a suitable class of functions from $(0,T)\times \Omega$ into $\mathbb {M}$, the moment system (17) can be recast into the Galerkin form:

$$\begin{aligned}&{ Find}\, g\in {}V\big ((0,T)\times \Omega ;\mathbb {M})\big ):\nonumber \\&\qquad \qquad \big \langle m\partial _t \beta (g)\big \rangle +\big \langle mv_i\partial _{x_i}\beta (g)\big \rangle = \big \langle m\mathcal {C}(\beta {}(g))\big \rangle \quad \forall m\in {}\mathbb {M},\text { a.e. }(t,{\varvec{x}})\in (0,T)\times \Omega .\nonumber \\ \end{aligned}$$

(18)

To elucidate the relation between (17) and (18), we associate to the renormalization map $\beta :\mathbb {M}\rightarrow \mathbb {F}$ a function $\mathcal {F}_{\beta }:\mathscr {D}(\mathcal {F}_{\beta })\rightarrow \mathbb {F}$ such that $\mathcal {F}_{\beta }({\varvec{\rho }})=\beta {}(g_{{\varvec{\rho }}})$ with $g_{{\varvec{\rho }}}$ according to $\langle {\varvec{m}}\beta {}(g_{{\varvec{\rho }}})\rangle ={\varvec{\rho }}$. The domain $\mathscr {D}(\mathcal {F}_{\beta })$ is implicitly restricted to moments ${\varvec{\rho }}\in \mathbb {R}^M$ that can be realized by some $g\in \mathbb {M}$. The equivalence between the Galerkin formulation (18) and the moment system (17) now follows immediately by noting that $\{m_i\}_{i=1}^M$ constitutes a basis of $\mathbb {M}$ and inserting $g_{{\varvec{\rho }}}$ for g in (18).

The Galerkin form (18) facilitates a unified treatment of moment-closure systems. In the remainder of this section we review the celebrated moment closures of Levermore [35] and Grad [20] in the context of the Galerkin form (18), to provide a basis for the subsequent divergence-based moment closures in Sect. 4. We note that other closure relations exist, e.g. based on Pearson distributions [60]. However, these closures do not generally possess a hierarchical structure, i.e. the renormalization map for these closures is non-generic and specifically connected to a particular subspace $\mathbb {M}$, and are outside the scope of this treatise.

3.3 Levermore’s Entropy-Based Moment Closure

The moment-closure relation of Levermore [35] is essentially characterized by the renormalization map:

(19)

For this closure relation, a subspace $\mathbb {M}$ is considered to be admissible if it satisfies:

• (1) $\mathbb {E}\subseteq \mathbb {M}$;

• (2) $\mathbb {M}$ is invariant under the actions of $\mathcal {T}_{{\varvec{u}}}$ and $\mathcal {T}_{\mathcal {O}}$;

• (3) $\mathbb {M}_c:=\{m\in \mathbb {M}: \left\langle \exp (m)\right\rangle <\infty \}$ has a nonempty interior in $\mathbb {M}$.

The first condition insists that $\mathbb {M}$ contains the collision invariants, which ensures that the moment system imposes conservation of mass, momentum and energy. These conservation laws must be obeyed if any fluid-dynamical approximation is to be recovered. The second condition dictates that for all $m\in \mathbb {M}$, all ${\varvec{u}}\in \mathbb {R}^D$ and all orthogonal tensors $\mathcal {O}$ it holds that $m({\varvec{u}}-(\cdot ))\in \mathbb {M}$ and $m(\mathcal {O}^{*}(\cdot ))\in \mathbb {M}$. This condition ensures that the moment system exhibits Galilean invariance. As argued by Junk [29], rotation and translation invariant finite dimensional spaces are necessarily composed of multivariate polynomials. The third condition requires that $\mathbb {M}$ contains functions m such that $\beta (m(\cdot ))$ is Lebesgue integrable on $\mathbb {R}^D$. For $\beta (\cdot )=\exp (\cdot )$ and $\mathbb {M}$ composed of multivariate polynomials, this condition implies that the highest-order terms in any variable in $\mathbb {M}$ must be of even order. The subset $\mathbb {M}_c$ then corresponds to a convex cone, consisting of all polynomials in $\mathbb {M}$ for which the highest-order terms in any variable are of even order and have a negative coefficient. One can infer that $\exp (\cdot )$ maps $\mathbb {M}_c$ to distributions with bounded moments and fluxes, i.e. $g\in \mathbb {M}_c$ implies $|\langle {}m\beta (g)\rangle |<\infty$ and $|{{\varvec{v}}}m\beta (g)\rangle |<\infty$ for all $m\in \mathbb {M}$.

In [35] the moment-closure relation associated with (19) is derived by minimization of the entropy with density $\eta _{\mathrm {L}}(f):=f\log {}f-f$, subject to the moment constraint. Specifically, considering any admissible subspace $\mathbb {M}$, Levermore formally defines the closure relation ${\varvec{\rho }}\mapsto \mathcal {F}_{\mathrm {L}}({\varvec{\rho }})$ according to:

$$\begin{aligned} \mathcal {F}_{\mathrm {L}}({\varvec{\rho }}):= {{\mathrm{arg\,min}}}_{f\in \mathbb {F}} \big \{\langle f\log f - f\rangle :\langle {\varvec{m}} f \rangle ={\varvec{\rho }}\big \} \end{aligned}$$

(20)

To elucidate the fundamental properties of the closure relation (20), we consider an admissible subspace $\mathbb {M}$ and we denote by $\mathbb {D}$ the collection of all $f\in \mathbb {F}$ that yield moments ${\varvec{\rho }}=\langle {\varvec{m}} f\rangle$ for which the minimizer in (20) exists. The operator $\mathcal {F}_{\mathrm {L}}(\langle {\varvec{m}}(\cdot )\rangle ):\mathbb {D}\rightarrow \mathbb {I}$ is idempotent and its image $\mathbb {I}\subset \mathbb {D}$ admits a finite-dimensional characterization. In particular, it holds that $\log \mathbb {I}$ coincides with the convex cone $\mathbb {M}_c$. The idempotence of the operator $\mathcal {F}_{\mathrm {L}}(\langle {\varvec{m}}(\cdot )\rangle )$ and its injectivity in $\mathbb {D}$ imply that (20) corresponds to a projection. This projection is generally referred to as the entropic projection [23]. A second characterization of (20) follows from the following sequence of identities, which holds for any $f\in \mathbb {F}$ such that $\langle {\varvec{m}} f\rangle ={{\varvec{\rho }}}$ and all Maxwellian distributions, $\mathcal {M}=\exp (\psi )$ with $\psi \in \mathbb {E}$:

$$\begin{aligned} \langle {}f\log (f/\mathcal {M})\rangle= & {} \langle {}f(\log {}f-\psi )\rangle = \langle {}f\log {}f-f\rangle +\langle {}f(1-\psi )\rangle \nonumber \\= & {} \langle {}f\log {}f-f\rangle +{{\varvec{\alpha }}}\cdot {{\varvec{\rho }}} \end{aligned}$$

(21)

for some ${\varvec{\alpha }}\in \mathbb {R}^M$. Noting that ${\varvec{\alpha }}\cdot {\varvec{\rho }}$ is independent of f, one can infer from (11) and (21) that $\mathcal {F}_{\mathrm {L}}$ according to (20) is the distribution in $\mathbb {F}$ that is closest to equilibrium in the Kullback–Leibler divergence, subject to the condition that its moments $\langle {\varvec{m}} (\cdot )\rangle$ coincide with ${\varvec{\rho }}$. Similarly, it can be shown that $\mathcal {F}_{\mathrm {L}}$ according to (20) minimizes $\langle {}f\log {}f\rangle$ subject to $\langle {\varvec{m}} f\rangle ={\varvec{\rho }}$. Therefore, the information interpretation of the entropy $\langle {}f\log {}f\rangle$ (see Sect. 2) enables a third characterization of (20), viz. as the least-biased distribution given the information $\langle {\varvec{m}}(\cdot )\rangle ={\varvec{\rho }}$ on the moments.

The exponential form of the renormalization map (19) can be derived straightforwardly by means of the Lagrange multiplier method. Provided it exists, the minimizer of the constrained minimization problem (20) corresponds to a stationary point of the Lagrangian $(f,{\varvec{\alpha }})\mapsto \langle {}f\log {}f-f{}\rangle +{\varvec{\alpha }}\cdot ({\varvec{\rho }}-\langle {}{\varvec{m}} f\rangle )$. The stationarity condition implies that $\log {}f-{\varvec{\alpha }}\cdot {\varvec{m}}$ vanishes, which conveys the exponential form $f=\exp ({\varvec{\alpha }}\cdot {\varvec{m}})$. It is to be noted that the Lagrange multipliers have to comply with an admissibility condition related to integrability. In particular, ${\varvec{\alpha }}\cdot {\varvec{m}}$ must belong to the convex cone $\mathbb {M}_c$.

In [35] it is shown that moment systems with closure $\mathcal {F}_{\mathrm {L}}$ yield quasi-linear symmetric hyperbolic systems for the Lagrange multipliers. Application of the chain rule to (17) with $\mathcal {F}_{\mathrm {L}}({\varvec{\rho }})=\exp ({\varvec{\alpha }}\cdot {\varvec{m}})$ (with, implicitly, ${\varvec{\rho }}=\langle {\varvec{m}}\exp ({\varvec{\alpha }}\cdot {\varvec{m}})\rangle$) yields:

$$\begin{aligned} {{\varvec{A}}}_0({\varvec{\alpha }})\frac{\partial {{\varvec{\alpha }}}}{\partial {}t} +\sum _{i=1}^D{{\varvec{A}}}_i({\varvec{\alpha }})\frac{\partial {\varvec{\alpha }}}{\partial {}x_i} = {{\varvec{s}}}({\varvec{\alpha }}) \end{aligned}$$

(22)

with ${{\varvec{A}}}_0({\varvec{\alpha }})=\langle {\varvec{m}} \otimes {\varvec{m}} \exp ({\varvec{\alpha }}\cdot {\varvec{m}})\rangle$, ${{\varvec{A}}}_i({\varvec{\alpha }})=\langle v_i{\varvec{m}} \otimes {\varvec{m}} \exp ({\varvec{\alpha }}\cdot {\varvec{m}})\rangle$ and ${{\varvec{s}}}({\varvec{\alpha }})= \langle {\varvec{m}} \, \mathcal {C}(\exp ({\varvec{\alpha }}\cdot {\varvec{m}}))\rangle$. The symmetry of ${{\varvec{A}}}_i$ $(i=0,1,\ldots ,D)$ and the positive definiteness of ${{\varvec{A}}}_0$ are evident. By virtue of its quasi-linear symmetric hyperbolicity, the system (22) is at least linearly well posed [35]. Moreover, under auxiliary conditions on the initial data, local-in-time existence of solutions can be established; see, for instance, [39].

Levermore’s moment systems retain the fundamental structural properties of the Boltzmann equation. The conservation properties and Galilean invariance are direct consequences of conditions 1 and 2 on the admissible subspaces, respectively. Dissipation of the entropy $\langle {}\eta _{\mathrm {L}}(\cdot )\rangle$ can be inferred from the Galerkin formulation (18), noting that for (19) it holds that $\log \beta _{\mathrm {L}}(\cdot ):\mathbb {M}\rightarrow \mathbb {M}$. Hence, if g complies with (18) in conjunction with (19) then the following identity holds on account of Galerkin orthogonality:

$$\begin{aligned} \langle {}\log \beta _{\mathrm {L}}(g)\,\partial _t\beta _{\mathrm {L}}(g)\rangle +\langle {}\log \beta _{\mathrm {L}}(g)\,v_i\partial _{x_i}\beta _{\mathrm {L}}(g)\rangle =\langle \log \beta _{\mathrm {L}}(g)\,\mathcal {C}(\beta _{\mathrm {L}}(g))\rangle \end{aligned}$$

(23)

The left-hand side of this identity coincides with $\partial _t\langle \eta _{\mathrm {L}}(\beta (g))\rangle +\partial _{x_i}\langle {}v_i\eta _{\mathrm {L}}(\beta _{\mathrm {L}}(g))\rangle$, while the right-hand side equals $\langle {}\mathcal {C}(\beta _{\mathrm {L}}(g))\,\eta _{\mathrm {L}}'(\beta _{\mathrm {L}}(g))\rangle$. For g according to (18), the distribution $\beta _{\mathrm {L}}(g)$ thus obeys the entropy dissipation relation (7) with entropy density $\eta _{\mathrm {L}}$.

Levermore’s consideration of entropy-based moment-closure systems in [35], as well as the above exposition, implicitly rely on existence of a solution to the moment-constrained entropy minimization problem (20). It was however shown by Junk in the series of papers [27–29] that for super-quadratic $\mathbb {M}$ the closure relation (20) is impaired by non-realizability, i.e. a minimizer of (20) may be non-existent. Moreover, the class of local equilibrium distributions generally lies on the boundary of the set of degenerate densities. In [27], Junk also establishes that the flux $\langle v_i{\varvec{m}} \beta _{\mathrm {L}}(g)\rangle$ can become unbounded in the vicinity of equilibrium, thus compromising well-posedness of (22). The singularity of the fluxes moreover represents a severe complication for numerical approximation methods; see also [42].

The realizability problem of Levermore’s entropy-based moment closure has been extensively investigated; see, in particular, [24, 27–29, 46, 52]. In [24, 29, 46] it has been shown that the set of degenerate densities is empty if and only if the set $\{{\varvec{\alpha }}\in \mathbb {R}^M:{\varvec{m}} \exp ({\varvec{\alpha }}\cdot {\varvec{m}})\in {}L^1(\mathbb {R}^D,\mathbb {R}^M)\}$ of Lagrange multipliers associated with integrable distributions is open. This result implies that degenerate densities are unavoidable for super-quadratic polynomial spaces, because the Lagrange multipliers associated with equilibrium are then located on the boundary of the above set; see also [24]. To bypass the realizability problem, Schneider [52] and Pavan [46] considered the following relaxation of the constrained entropy-minimization problem:

$$\begin{aligned} {{\mathrm{arg\,min}}}_{f\in \mathbb {F}}\{\langle {}f\log {}f-f\rangle :\langle {\varvec{m}} f\rangle \le ^{*}{\varvec{\rho }}\} \end{aligned}$$

(24)

where the binary relation $\le ^{*}$ connotes that the highest order moments of the left member are bounded by the corresponding moments of the right member. The relaxation of the highest-order-moment constraints serves to accommodate that minimizing sequences $\{f_n\}\subset \mathbb {F}$ subject to the constraint $\langle {}{\varvec{m}} f_n\rangle ={\varvec{\rho }}$ converge (in the topology of absolutely integrable functions) to an exponential density with inferior highest-order moments; see [24, 27, 28, 46, 52]. The analyses in [46, 52] convey that the relaxed minimization problem indeed admits a unique solution, corresponding to an exponential distribution. The exponential closure can therefore be retained if the closure relation is defined by (24) instead of (20). It is to be noted however that the closure relation (24) does not generally provide a bijection between the Lagrange multipliers and the moments. Moreover, the aforementioned singularity of fluxes near equilibrium is also inherent to (24).

Another formidable obstruction to the implementation of numerical approximations of Levermore’s moment-closure systems are the exponential integrals that appear in (17). The evaluation of moments of exponentials of super-quadratic polynomials is generally accepted to be intractable, and accurate approximation of such moments is algorithmically complicated and computationally intensive; see, in particular, [34, Sect. 12.2] and [27, Sect. 6].

3.4 Grad’s Hermite-Based Moment Closure

In his seminal paper [20], Grad proposed a moment-closure relation based on a factorization of the one-particle marginal in a Maxwellian distribution and a term expanded in Hermite polynomials; see also [21, Sect. V]. The expansion considered by Grad writes:

$$\begin{aligned} f(t,{\varvec{x}},{\varvec{c}})\approx \mathcal {M}({\varvec{c}}) \sum _{k=0}^{n}\sum _{{\varvec{i}}_k}\frac{1}{k!}a_{{\varvec{i}}_k}^{(k)}({\varvec{x}},t)\mathscr {H}_{{\varvec{i}}_k}^{(k)}({\varvec{c}}), \end{aligned}$$

(25)

where ${\varvec{c}}$ denotes peculiar velocity, ${\varvec{i}}_k=(i_1,i_2,\ldots ,i_k)$ is a multi-index with sub-indices ${i_{(\cdot )}}\in \{1,2,\ldots ,D\}$, ${{a_{{\varvec{i}}_k}^{(k)}}}$ are the polynomial expansion coefficients and ${{\mathscr {H}{}_{{\varvec{i}}_k}^{(k)}}}$ are D-variate Hermite polynomials of degree k:

$$\begin{aligned} \mathscr {H}{}^{(k)}_{{\varvec{i}}_k}({\varvec{x}}) = \frac{(-1)^k}{\omega (|{\varvec{x}}|)}\frac{\partial ^k\omega (|{\varvec{x}}|)}{\partial {}x_{i_1}\partial {}x_{i_2}\cdots \partial {}x_{i_k}} \quad \text {with}\quad \omega (s)=\frac{1}{(2\pi )^{d/2}}\exp (-s^2/2). \end{aligned}$$

(26)

The Maxwellian in (25) can either correspond to a prescribed local or global Maxwellian, or it can form part of the approximation; see [20, 21]. In the latter case, the coefficients associated with invariant moments are fixed and it holds that ${a^{(0)}=1}$, ${a^{(1)}_i=0}$ and ${a^{(2)}_{ii}=1}$. By virtue of the specific properties of Hermite polynomials, moments of Grad’s approximate distribution (25) can be evaluated in closed-form.

The linear hull of the Hermite polynomials ${\{\mathscr {H}^{(k)}_{{\varvec{i}}}\}_{0\le {}k\le {}n}}$ coincides with the class of D-variate polynomials of degree at most n. The Hermite polynomials in (26) do not provide a basis of the polynomials, however, on account of linear dependence; evidently, the Hermite polynomial in (26) is invariant under permutations of its indices. In [20], uniqueness of the coefficients in (25) is restored by imposing auxiliary symmetry conditions on the coefficients.

Grad’s moment systems can be conveniently conceived of as Galerkin approximations of the Boltzmann equation in renormalized form in accordance with (18). For a prescribed Maxwellian, the renormalization map simply corresponds to

(27)

Incorporation of the Maxwellian in (25) in the approximation can be represented by the alternative renormalization map:

(28)

where $\Pi _{\mathbb {E}}:\mathbb {M}\mapsto \mathbb {E}$ denotes the orthogonal projection onto the space of collision invariants and $\mathrm {Id}$ represents the identity operator. The embedding $\mathbb {E}\subseteq \mathbb {M}$ implies that $\Pi _{\mathbb {E}}\mathbb {M}=\mathbb {E}$ and $(\mathrm {Id}-\Pi _{\mathbb {E}})\mathbb {M}=\mathbb {M}\setminus \mathbb {E}$. Hence, the projection in (28) provides a separation of $\mathbb {M}$ into $\mathbb {E}$ and its orthogonal complement.

It is notable that the renormalization maps (27) and (28) can be conceived of as a linearization of Levermore’s exponential closure relation in the vicinity of a Maxwellian. In particular, setting $\psi =\log \mathcal {M}\in \mathbb {E}$, the following identities hold pointwise:

$$\begin{aligned} \exp (g)=\exp (\psi )\exp (g-\psi )=\mathcal {M}\exp (g-\psi )=\mathcal {M}\big (1+(g-\psi )+O(|g-\psi |^2)\big )\nonumber \\ \end{aligned}$$

(29)

as $(g-\psi )\rightarrow {}0$. To derive the renormalization map (27) for a prescribed Maxwellian, it suffices to note that $1+g-\psi \in \mathbb {M}$. To infer the renormalization map (28) if the Maxwellian is retained in the approximation, we note that by setting $\psi =\Pi _{\mathbb {E}}g$ and omitting the remainder in (29), we obtain (28).

For a prescribed global Maxwellian $\mathcal {M}$, Grad’s moment systems dissipate the entropy $\eta _{\chi ^2}(f) := \frac{1}{2}\mathcal {M}(f/\mathcal {M}-1)^2$, provided that $\eta _{\chi ^2}$ represents an entropy density for the collision operator under consideration. It can for example be shown that $\eta _{\chi ^2}$ is generally a suitable entropy density for collision operators linearized about $\mathcal {M}$ (see [22]) and for BGK collision operators. Dissipation of the entropy $\langle \eta _{\chi ^2}\rangle$ relative to the global Maxwellian $\mathcal {M}$ can be directly inferred from the Galerkin formulation (18), by noting that for the renormalization map $\beta _{\mathrm {G}}$ in (27) it holds that:

$$\begin{aligned} \eta _{\chi ^2}'(\beta _{\mathrm {G}}(g))=\beta _{\mathrm {G}}(g)/\mathcal {M}-1=g-1\in \mathbb {M}\end{aligned}$$

(30)

Hence, ${\eta _{\chi ^2}'}$ resides in the test space $\mathbb {M}$ in (18) and dissipation of ${\langle \eta _{\chi ^2}\rangle }$ follows from Galerkin orthogonality. The entropy $\langle \eta _{\chi ^2}(f)\rangle$ is associated with the $\varphi _{\chi ^2}$-divergence of f relative to $\mathcal {M}$ with $\varphi _{\chi ^2}(s)=\frac{1}{2}(s-1)^2$; cf. (12). Grad’s moment-closure relation can in fact be obtained by minimization of the $\varphi _{\chi ^2}$-divergence subject to the moment constraints:

$$\begin{aligned} \mathcal {F}_{\mathrm {G}}({\varvec{\rho }})={{\mathrm{arg\,min}}}_{f\in \mathbb {F}}\big \{\big \langle \mathcal {M}\varphi _{\chi ^2}(f/\mathcal {M})\big \rangle :\langle {\varvec{m}} f\rangle ={\varvec{\rho }}\big \} \end{aligned}$$

(31)

The minimization problem (31) is not impaired by the realizability problem inherent to (20), because the moment functionals $\langle {}m(\cdot )\rangle$ are continuous in the topology corresponding to $\langle {}\eta _{\chi ^2}\rangle$.

If the Maxwellian is retained in the approximation in accordance with the renormalization map (28), then an entropy for the corresponding moment systems can be non-existent or its derivation is intractable. However, for any entropy density $\eta$ for the collision operator, the following identity holds by virtue of the Galerkin-orthogonality property of $\beta :=\beta (g)$ in (18):

$$\begin{aligned} \begin{array}{ll} \partial _t\langle \eta (\beta )\rangle + \partial _{x_i}\langle {}v_i\eta (\beta )\rangle &{}= \langle (\eta '(\beta )-m)\partial _t\beta \rangle + \langle (\eta '(\beta )-m)v_i\partial _{x_i}\beta \rangle \\ &{}\phantom {=}- \langle (\eta '(\beta )-m)\mathcal {C}(\beta )\rangle + \langle \eta '(\beta )\mathcal {C}(\beta )\rangle \end{array} \end{aligned}$$

(32)

for arbitrary $m\in \mathbb {M}$. Equation (32) implies that solutions to Grad’s moment systems dissipate any entropy $\langle \eta \rangle$ for the collision operator up to $\inf _{m\in \mathbb {M}}\Vert \eta '(\beta (g))-m\Vert$, in some suitable norm $\Vert \cdot \Vert$. For example, introducing the condensed notation $g_0=\Pi _{\mathbb {E}}g$, $g_1=(\mathrm {Id}-\Pi _{\mathbb {E}})g$ and the convex functional $\eta :\mathbb {E}\times \mathbb {M}\setminus \mathbb {E}\rightarrow \mathbb {R}$ according to

$$\begin{aligned} \eta (g_0,g_1)=(g_0-1)e^{g_0}(1+g_1)+e^{g_0}g_1(1+g_1) \end{aligned}$$

(33)

the renormalization map in (28) corresponds to $\beta (g)=e^{g_0}(1+g_1)$ and it holds that

$$\begin{aligned} \begin{array}{ll} d\eta (g_0,g_1)&{}=(g_0+g_1)e^{g_0}(1+g_1)\,dg_0+(g_0+2g_1)e^{g_0}\,dg_1\\ &{}=(g_0+g_1)(\partial _{g_0}\beta \,dg_0+\partial _{g_1}\beta \,dg_1)+g_1e^{g_0}\,dg_1\\ &{}=(g_0+g_1)\,d\beta +g_1e^{g_0}\,dg_1 \end{array} \end{aligned}$$

(34)

Considering that $g_0+g_1\in \mathbb {M}$, it follows from (32) that if $\eta$ in (33) is an entropy density for the collision operator, then Grad’s moment systems with renormalization map (28) dissipate $\eta$ up to $O(g_1)$ as $g_1$ vanishes (in some appropriate norm). Note that $g_1$ vanishes at equilibrium.

Grad’s moment-closure relation exhibits several fundamental deficiencies that may cause breakdown of the physical and mathematical structure of the corresponding moment system for large deviations from equilibrium. First, the expansion (25) admits inadmissible, locally negative distributions. Second, if the Maxwellian is retained in the approximation in accordance with (28), the corresponding moment systems are generally non-symmetric and hyperbolicity is not guaranteed. It has been observed in [11, 59] that Grad’s moment-closure systems can indeed exhibit complex characteristics and loss of hyperbolicity. Recently, regularization procedures have been introduced to restore the hyperbolicity of Grad’s moment systems. However, these regularizations generally disrupt the conservation properties of the moment system.

4 Divergence-Based Moment Closures

4.1 Renormalizations Based on Deformed Exponentials

In this section we present a novel moment-closure relation based on an approximation of the exponential function. The considered approximation is derived from truncations of the standard limit definition of the exponential $\exp (\cdot ):={\lim _{n\rightarrow \infty } (1 + (\cdot )/n)^n\approx (1 + (\cdot )/N)^N}$. It is noteworthy that unlike the exponential function, in the limit as $v\rightarrow -\infty$ the truncated exponential as well as its derivative do not vanish. The former condition is needed to preserve the decay properties of the exponential function while the latter condition is needed to preserve the same absolute maximum and minimum as the exponential. Moreover, as opposed to the exponential function, the truncated exponential can be negative if N is odd. Several approximations of the exponential function that preserve the aforementioned properties of the exponential have been proposed in the literature; see, for example, [30, 45, 62] and references therein. These so-called deformed exponentials can generally serve to construct moment-closure renormalization maps, with properties depending on the particular form of the deformed exponential and the construction. In [62], Tsallis proposed the q-exponential:

$$\begin{aligned} \widetilde{\exp }_q (x) := \big (1+ (1-q)x\big )^{1/(1-q)}_+ \end{aligned}$$

(35)

with $q\ne {}1$ and $(\cdot )_+ = \frac{1}{2}(\cdot )+\frac{1}{2}|\cdot |$ the non-negative part of a function extended by 0. The q-exponential in (35) is related to the non-negative part of the truncated limit definition of the exponential by $1-q=1/N$. We will consider renormalization maps of the form

(36)

with $\mathcal {M}$ a prescribed distribution, e.g. a local or global Maxwellian. The renormalization map $\beta _N$ can then be construed as an approximation to the exponential renormalization map about the Maxwellian distribution $\mathcal {M}$. We will establish that the distribution (36) can be derived as the minimizer of a modified entropy that approximates the Kullback–Leibler divergence near $\mathcal {M}$ and that belongs to the class of $\varphi$-divergences. In addition, we will show that the resulting moment system overcomes the aforementioned deficiencies of Grad’s and Levermore’s moment systems, while retaining the fundamental properties of the Boltzmann equation presented in Sect. 2.

The renormalization map (36) engenders the following moment-closure relation:

$$\begin{aligned} \mathcal {F}_N({\varvec{\rho }}):= \mathcal {M} \ \widetilde{\exp }_q({\varvec{\alpha }}\cdot {\varvec{m}}) = \mathcal {M} \left( 1+\frac{{\varvec{\alpha }}\cdot {\varvec{m}}}{N}\right) ^N_+ \end{aligned}$$

(37)

where the moment densities ${\varvec{\rho }}$ and the coefficients ${\varvec{\alpha }}$ are related by ${\varvec{\rho }}=\langle {\varvec{m}}\,\mathcal {M}\,\widetilde{\exp }_q({\varvec{\alpha }}\cdot {\varvec{m}})\rangle$. Given a polynomial subspace $\mathbb {M}\supseteq \mathbb {E}$ with a Galilean-group property (admissibility conditions 1 and 2 in Sect. 3.3), the moment system corresponding to (36) conforms to (17) with, in particular, the moment-closure relation $\mathcal {F}_N$ according to (37).

4.2 Connection to Closure Relations of Levermore and Grad

To elucidate some of the characteristics of the renormalization map (36), we regard it in comparison with the renormalization maps (19) and (27) associated with Levermore’s exponential moment-closure relation and Grad’s moment-closure relation with a prescribed Maxwellian prefactor, respectively.

To compare the renormalization map (36) to the renormalization map (19) associated with Levermore’s closure relation, we note that by virtue of the vector-space structure of $\mathbb {M}\supseteq \mathbb {E}$, for an arbitrary Maxwellian distribution $\mathcal {M}$ it holds that $\log \mathcal {M}+\mathbb {M}=\mathbb {M}$. Hence, for $g\in \mathbb {M}$, the renormalization map (19) can be equivalently expressed as $g\mapsto \exp (\log \mathcal {M}+g)$. In the limit $N\rightarrow \infty$, we obtain for (36):

$$\begin{aligned} \lim _{N\rightarrow \infty }\beta _N(g)=\mathcal {M}\lim _{N\rightarrow \infty }\Big (1+\frac{g}{N}\Big )^N_+=\mathcal {M}\exp (g)=\exp (\log \mathcal {M}+g) \end{aligned}$$

(38)

Equation (38) implies that in the limit $N\rightarrow \infty$, the renormalization map in (36) coincides with the exponential renormalization map associated with Levermore’s moment-closure relation. For finite N, the moments $\langle {}m\beta _N(g)\rangle$ and fluxes $\langle {}mv\beta _N(g)\rangle$ with $m,g\in \mathbb {M}$ correspond to piecewise-polynomial moments of the Gaussian distribution $\mathcal {M}$. The evaluation of such moments is tractable (see Remark 2 below), as opposed to the evaluation of moments and fluxes for the exponential renormalization map. In addition, for super-quadratic approximations $\mathbb {M}\supset \mathbb {E}$, the exponential renormalization map associated with Levermore’s closure can lead to singular moments and fluxes in the vicinity of equilibrium, i.e. as g approaches $\mathbb {E}$. The fundamental underlying problem is the realizability problem; see Sect. 3.3 and [27]. Accordingly, one can form sequences $\{g_n\}$ such that $\exp (g_n)\rightarrow \mathbb {E}$ (in the $L^1$ topology) while there exist $m\in \mathbb {M}$ such that $|\langle {}m{}\exp (g_n)\rangle |\rightarrow \infty$ or $|\langle {}m{}v\exp (g_n)\rangle |\rightarrow \infty$. One can infer that due to the exponential decay of the prefactor $\mathcal {M}$ and the polynomial form of the renormalization map in (36), moments and fluxes corresponding to (36) are non-singular near equilibrium.

To compare (36) to the renormalization map (27) corresponding to Grad’s moment-closure relation with a prescribed Maxwellian prefactor, we note that by virtue of the vector-space structure of $\mathbb {M}\supseteq \mathbb {E}$, it holds that $1+\mathbb {M}=\mathbb {M}$. Hence, for $g\in \mathbb {M}$, the renormalization map (27) can be equivalently expressed as $\beta _{\mathrm {G}}:g\mapsto \mathcal {M}(1+g)$. Comparison of $\beta _N$ and $\beta _{\mathrm {G}}$ then imparts that $\beta _1=(\beta _{\mathrm {G}})_+$, i.e. for $N=1$ the renormalization map $\beta _N$ in (36) coincides with the non-negative part of the renormalization in Grad’s closure, extended by zero. Therefore, the renormalization map (36) avoids the potential negativity of the approximate distribution inherent to Grad’s closure and corresponding loss of hyperbolicity.

Remark 2

Computing moments of the closure relation (36) involves computing the roots of the polynomial ${\varvec{\alpha }}\cdot {\varvec{m}}+N$. In the multidimensional case, such roots may be difficult to compute since the problem is under-determined and the roots may form curves (2D) and surfaces (3D) of, in principle, arbitrary shape. However, when ${\varvec{\alpha }}\cdot {\varvec{m}}+N$ is of even maximal degree and the highest order coefficients are of the same sign, subdivision schemes (see for example [40] and references therein) may be used to approximate the positive part of ${\varvec{\alpha }}\cdot {\varvec{m}}+N$ since its zero sets are either empty or correspond to isolated points or closed loops. For the following choice of subspace hierarchies, ${\varvec{\alpha }}\cdot {\varvec{m}}+N$ is of even maximal degree and the highest order coefficients are of the same sign

$$\begin{aligned} \mathbb {M}&= \text {span}\{1,\ {\varvec{v}},\ |{\varvec{v}}|^2\}\end{aligned}$$

(39)

$$\begin{aligned} \mathbb {M}&= \text {span}\{1,\ {\varvec{v}},\ {\varvec{v}} \vee {\varvec{v}},\ {\varvec{v}}\vee {\varvec{v}}\vee {\varvec{v}},\ |{\varvec{v}}|^4\}\end{aligned}$$

(40)

$$\begin{aligned}&\vdots \end{aligned}$$

(41)

$$\begin{aligned} \mathbb {M}&= \text {span}\{1,\ {\varvec{v}},\ {\varvec{v}} \vee {\varvec{v}},\ {\varvec{v}}\vee {\varvec{v}}\vee {\varvec{v}},\ {\varvec{v}}\vee {\varvec{v}}\vee {\varvec{v}}\vee {\varvec{v}},\ {\varvec{v}}\vee {\varvec{v}}\vee {\varvec{v}}\vee {\varvec{v}}\vee {\varvec{v}},\ \ldots ,\ |{\varvec{v}}|^{2k}\} \end{aligned}$$

(42)

4.3 Conservation, Invariance and Dissipation Properties

The moment system corresponding to (36) retains conservation of mass, momentum and energy as well as Galilean invariance. The conservation properties can be directly deduced from the Galerkin form (18) of the moment system, by noting that $\mathbb {E}$ is contained in the test space $\mathbb {M}$, in accordance with admissibility condition 1 in Sect. 3.3. Galilean invariance is an immediate consequence of admissibility condition 2.

Contrary to Levermore’s moment system, the moment system with renormalization map (36) does not generally dissipate the relative entropy $\langle {}f\log {}(f/\mathcal {M})\rangle$, because the inverse of $\beta _N(\cdot )$ does not correspond to $\log (\cdot )$ and, therefore, $\log \beta _N(g)$ does not generally belong to the test space $\mathbb {M}$ for $g\in \mathbb {M}$; cf. Sect. 3.3. Under appropriate conditions on the collision operator (see Sect. 2), the moment system closed by (36) does however dissipate a modified relative entropy. To determine a suitable entropy function for the moment system with renormalization map (36) relative to some global Maxwellian distribution, $\mathcal {M}$, we observe that:

$$\begin{aligned} \beta _N^{-1}(\cdot )= \displaystyle {N\bigg (\frac{(\cdot )}{\mathcal {M}}\bigg )^{1/N}-N} \end{aligned}$$

(43)

provides an inverse of $\beta _N$ according to (36) on the support of $\beta _N$. In particular, it holds that:

$$\begin{aligned} \beta ^{-1}_N\big (\beta _N(g)\big ) ={\left\{ \begin{array}{ll} g\quad &{}\text {if }g\ge {}-N\\ -N\quad &{}\text {otherwise} \end{array}\right. } \end{aligned}$$

(44)

The expression in (43) yields an approximation to the natural logarithm, corresponding to the inverse of the approximation of the exponential function in (36) for $g\ge {}-N$. This approximate logarithm is eligible as the derivative of an entropy density associated with the moment system with renormalization (36). Defining the entropy density as

$$\begin{aligned} \eta _N(f)=f\bigg (\frac{N^2}{1+N}\bigg (\frac{f}{\mathcal {M}}\bigg )^{1/N} - N\bigg )+\mathcal {M}\frac{N}{1+N} \end{aligned}$$

(45)

it holds that $\eta _N'(\cdot )=\beta _N^{-1}(\cdot )$. The constant in (45) has been selected such that $\eta _N(\mathcal {M})$ vanishes. The entropy corresponding to (45) can be cast in the form of a relative entropy associated with a $\varphi$-divergence, in accordance with (12). To this end, we introduce

$$\begin{aligned} \varphi _N(\cdot )=(\cdot )\bigg (\frac{N^2}{1+N}(\cdot )^{1/N} - N\bigg )+\frac{N}{1+N} \end{aligned}$$

(46)

and note that $\eta _N(f)=\mathcal {M}\varphi _N(f/\mathcal {M})$. Convexity of the function $\varphi _N$ and of the corresponding entropy density $\eta _L$ follows by direct computation:

$$\begin{aligned} \varphi _N''(\cdot )=(\cdot )^{(1-N)/N} \end{aligned}$$

(47)

Therefore, $\varphi _N''$ is strictly positive on $\mathbb {R}_{>0}$. Moreover, it holds that $\varphi _N(1)=0$. To establish that solutions to the moment system with renormalization map (36) dissipate the entropy corresponding to the density (45), we consider a solution $\beta _N(g)$ of the moment system and note that the chain rule yields:

$$\begin{aligned} \partial _t\big \langle \eta _N(\beta _N(g))\big \rangle + \partial _{x_i}\big \langle {}v_i\eta _N(\beta _N(g))\big \rangle = \big \langle {}\eta _N'(\beta _N(g))\,\partial _t\beta _N(g)\big \rangle + \big \langle {}\eta _N'(\beta _N(g))\,v_i\partial _{x_i}\beta _N(g)\big \rangle \nonumber \\ \end{aligned}$$

(48)

The velocity integral in the right member of (48) can be separated into contributions from $\mathrm {supp}(\beta _N(g))$ and its complement, $\mathbb {R}^D{\setminus }\mathrm {supp}(\beta _N(g))$. On $\mathrm {supp}(\beta _N(g))$ it holds that $\eta '_N(\beta _N(g))=g$. On its complement, g is strictly less than $-N$ and it follows from (36) that $\partial _t\beta _N(g)$ and $\partial _{x_i}(\beta _N(g))$ vanish. Equation (48) therefore implies:

$$\begin{aligned} \partial _t\big \langle \eta _N(\beta _N(g))\big \rangle + \partial _{x_i}\big \langle {}v_i\eta _N(\beta _N(g))\big \rangle = \big \langle {}g\,\partial _t\beta _N(g)\big \rangle + \big \langle {}g\,v_i\partial _{x_i}\beta _N(g)\big \rangle \end{aligned}$$

(49)

Noting that $g\in \mathbb {M}$, we infer from the Galerkin form of the moment system in (18) and the fact that g coincides with $\eta '_N(\beta _N(g))$ on $\mathrm {supp}(\beta _N(g))$ that

$$\begin{aligned}&\partial _t\big \langle \eta _N(\beta _N(g))\big \rangle + \partial _{x_i}\big \langle {}v_i\eta _N(\beta _N(g))\big \rangle = \big \langle {}g{}\,\mathcal {C}(\beta _N(g))\big \rangle \nonumber \\&\qquad \qquad \qquad = \big \langle {}\eta _N'(\beta _N(g))\,\mathcal {C}(\beta _N(g))\big \rangle + \int _{\mathbb {R}^D\setminus \mathrm {supp}(\beta _N(g))}\big (g({\varvec{v}})-\eta _N'(0)\big )\,\mathcal {C}(0)\,d{\varvec{v}} \end{aligned}$$

(50)

If $\eta _N(\cdot )$ according to (45) is an entropy density for the collision operator $\mathcal {C}$ under consideration, then the first term in the ultimate expression in (50) is non-positive on account of (5). The derivative of the entropy density in (45) satisfies $\eta '_N(0)=-N$. Moreover, because $g<-N$ on $\mathbb {R}^D\setminus \mathrm {supp}(\beta _N(g))$ and by virtue of the non-negativity condition on the collision operator according to (9), the second term in the ultimate expression in (50) is also non-positive. Solutions of the moment system therefore comply with a local entropy-dissipation relation analogous to (7):

$$\begin{aligned} \partial _t\big \langle \eta _N(\beta _N(g))\big \rangle + \partial _{x_i}\big \langle {}v_i\eta _N(\beta _N(g))\big \rangle \le {}0 \end{aligned}$$

(51)

The entropy dissipation relation (51) extends to renormalization maps of the form (36) with suitable non-uniform background distributions. For a non-uniform distribution $\mathcal {M}$, an additional contribution to the right hand side of (50) appears, conforming to

$$\begin{aligned} \Big \langle \big (\varphi _N(\beta /\mathcal {M})-(1/\mathcal {M})\varphi '_N(\beta /\mathcal {M})\big )\big (\partial _t\mathcal {M}+v_i\partial _{x_i}\mathcal {M}\big )\Big \rangle \end{aligned}$$

(52)

with $\varphi _N$ according to (46). The production term in (52) indeed vanishes if $\mathcal {M}$ corresponds to a global Maxwellian background distribution. However, (52) does not generally disappear for non-uniform background distributions, which could disrupt the entropy dissipation relation (51). Equation (52) conveys that the entropy dissipation relation (51) is retained for suitable choices of $\mathcal {M}$, such as free streaming Maxwellian distributions and solutions to the Vlasov equation; see also [1].

4.4 Derivation via $\varphi$-Divergence Minimization

The moment-closure relation (37) can be derived by minimization of the $\varphi _N$-divergence subject to the moment constraint; cf. the definition of Levermore’s closure relation according to (20). Consider the constrained minimization problem:

$$\begin{aligned} \mathcal {F}_{N}({\varvec{\rho }}):= & {} {{\mathrm{arg\,min}}}_{f\in \mathbb {F}} \Big \{\langle \eta _N(f)\rangle :\langle {\varvec{m}} f \rangle ={\varvec{\rho }}\Big \} \nonumber \\= & {} {{\mathrm{arg\,min}}}_{f\in \mathbb {F}} \Big \{\big \langle \mathcal {M}\varphi _N(f/\mathcal {M})\big \rangle :\langle {\varvec{m}} f \rangle ={\varvec{\rho }}\Big \} \end{aligned}$$

(53)

Formally, the solution to (53) can be obtained by the method of Lagrange multipliers. The minimizer in (53) corresponds to a stationary point of the Lagrangian $(f,{\varvec{\alpha }})\mapsto \langle \eta _N(f)\rangle +{\varvec{\alpha }}\cdot ({\varvec{\rho }}-\langle {{\varvec{m}}}f\rangle )$. The stationarity condition implies that $\eta _N'(f)-{\varvec{\alpha }}\cdot {\varvec{m}}=0$ and, on account of (43), that $\beta _N^{-1}(f)={\varvec{\alpha }}\cdot {\varvec{m}}$. It follows directly that the minimizer in (53) is of the form $\mathcal {F}_{N}({\varvec{\rho }})=\beta _N({\varvec{\alpha }}\cdot {\varvec{m}})$ in conformity with (37).

As opposed to the entropy minimization problem (20) underlying Levermore’s closure relation, the minimization problem (53) is well posed. Existence of a solution to the minimization problem (53) can be deduced from results for generalized projections for non-negative functions by Csiszár in [15]. In [15] it is shown that the minimization problem

$$\begin{aligned} \inf \bigg \{\int {}f_2(v)\,\varphi \big (f_1(v)/f_2(v)\big )\,\nu (d{}v):f_1\in \mathbb {X}\bigg \} \end{aligned}$$

(54)

over a constrained set of non-negative functions,

$$\begin{aligned} \mathbb {X}=\bigg \{f:\int {}a_j(v)\,f(v)\,\nu (d{}v)=\rho _j,\,j\in \mathbb {J}\bigg \} \end{aligned}$$

(55)

for certain countable functions $\{a_j\}_{j\in \mathbb {J}}$, possesses a minimizer belonging to $\mathbb {X}$ provided that the following (sufficient) conditions hold:

• (1) $\mathbb {X}$ is a convex set of non-negative functions and the infimum in (54) is finite;

• (2) $\lim _{s\rightarrow \infty } \varphi '(s) = \infty$;

• (3) $\int \varphi ^{*}(\xi |a_j(v)|)f_2(v)\,\nu (dv)$ is finite for all $\xi >0$ and $j\in \mathbb {J}$.

The function $\varphi ^{*}$ in condition 3 corresponds to the convex conjugate of $\varphi$. Comparison conveys that (53) conforms to (54) and (55) with $f_2=\mathcal {M}$, $\nu (\cdot )$ Lebesgue measure and $\{a_j\}_{j\in \mathbb {J}}$ a monomial basis of $\mathbb {M}$. Convexity of the constrained distributions follows from the linearity of the moment constraints. Finiteness of the infimum is ensured by the fact that the infimum over the constrained set is bounded from below by the infimum over the unconstrained set, and the latter attains its minimum of 0 for $f=\mathcal {M}$. The minimization problem (53) thus complies with condition 1. Compliance with condition 2 follows from $\varphi _N'(s)=Ns^{1/N}-N$ and $\lim _{s\rightarrow \infty }s^{1/N}=\infty$. To verify condition 3, we note that the convex conjugate of $\varphi _N$ is:

$$\begin{aligned} \varphi _N^{*}(t)=\sup _{s\in \mathbb {R}_{\ge 0}}\big (st-\varphi _N(s)\big )=\frac{N}{1+N}\left( \bigg (1+\frac{t}{N}\bigg )^{N+1}_+-1\right) \end{aligned}$$

(56)

Condition 2 therefore translates into the requirement that

$$\begin{aligned} \big \langle \mathcal {M}\varphi ^{*}_N\big (\xi |m_j|\big )\big \rangle = \frac{N}{1+N}\left\langle \mathcal {M}\bigg (1+\frac{\xi |m_j|}{N}\bigg )^{N+1}_+-\mathcal {M}\right\rangle \end{aligned}$$

(57)

is bounded. By virtue of the exponential decay of the prefactor $\mathcal {M}$ and the fact that $|m_j|^{N+1}$ increases only polynomially, the expressions in (57) are indeed finite for any $\xi >0$. The minimization problem (53) therefore also satisfies condition 3. It is notable that the minimization problem (20) pertaining to Levermore’s moment closure satisfies conditions 1 and 2 but violates condition 3.

4.5 Symmetric Hyperbolicity

To establish that the closure relation (37) leads to a symmetric-hyperbolic system, we insert (37) into the generic form of moment systems (17), and note that application of the chain rule and product rule leads to a system of the form (22) with:

$$\begin{aligned} {{\varvec{A}}}_0({\varvec{\alpha }})&=\left\langle {\varvec{m}} \otimes {\varvec{m}}\, \mathcal {M}\left( 1+\frac{{\varvec{\alpha }}\cdot {\varvec{m}}}{N}\right) _+^{N-1}\right\rangle \end{aligned}$$

(58a)

$$\begin{aligned} {{\varvec{A}}}_i({\varvec{\alpha }})&= \left\langle v_i{\varvec{m}} \otimes {\varvec{m}} \,\mathcal {M}\left( 1+\frac{{\varvec{\alpha }}\cdot {\varvec{m}}}{N}\right) _+^{N-1}\right\rangle \end{aligned}$$

(58b)

$$\begin{aligned} {{\varvec{s}}}({\varvec{\alpha }})&= \left\langle {\varvec{m}} \, \mathcal {C}\bigg (\mathcal {M}\left( 1+\frac{{\varvec{\alpha }}\cdot {\varvec{m}}}{N}\right) _+^{N}\bigg )\right\rangle - \left\langle {\varvec{m}} \, \left( 1+\frac{{\varvec{\alpha }}\cdot {\varvec{m}}}{N}\right) _+^{N} \bigg (\frac{\partial \mathcal {M}}{\partial {}t}+\sum _{i=1}^Dv_i\frac{\partial \mathcal {M}}{\partial {}x_i}\bigg )\right\rangle \end{aligned}$$

(58c)

The symmetry of ${{\varvec{A}}}_0,\ldots ,{{\varvec{A}}}_D$ is evident. Positive-definiteness of ${{\varvec{A}}}_0$ follows from:

$$\begin{aligned} {\varvec{\gamma }}\cdot \left\langle {\varvec{m}} \otimes {\varvec{m}} \,\mathcal {M}\left( 1+\frac{{\varvec{\alpha }}\cdot {\varvec{m}}}{N}\right) ^{N-1}_+\right\rangle {\varvec{\gamma }} = \left\langle ({\varvec{\gamma }}\cdot {\varvec{m}} )^2\mathcal {M}\left( 1+\frac{{\varvec{\alpha }}\cdot {\varvec{m}}}{N}\right) ^{N-1}_+\right\rangle \ge {}0 \end{aligned}$$

(59)

The inequality in (59) reduces to an equality if and only if ${\varvec{\gamma }}=0$ or ${\varvec{\alpha }}\cdot {\varvec{m}} =-N$. The latter case is pathological, because ${\varvec{\alpha }}\cdot {\varvec{m}} =-N$ implies that $\mathcal {F}_{N}({\varvec{\rho }})=0$.

The second component of the production term ${{\varvec{s}}}({{\varvec{\alpha }}})$, i.e. the term representing the contribution of $\partial _t\mathcal {M}+v_i\partial _{x_i}\mathcal {M}$ to the production, may cause blow up of solutions to the hyperbolic system (17) with (58) in the limit $t\rightarrow \infty$. Hence, the hyperbolic character of (17) with (58) ensures stability of solutions only in finite time. If $\mathcal {M}$ corresponds to a global Maxwellian, then $\partial _t\mathcal {M}+v_i\partial _{x_i}\mathcal {M}$ vanishes and the stability provided by hyperbolicity also holds in the ad-infinitum limit.

It is noteworthy that, as opposed to Grad’s moment-closure relation according to (28), the background distribution $\mathcal {M}$ in our moment-closure relation (36) is independent of the moments. The Gaussian in Grad’s closure relation (28) corresponds to the local equilibrium distribution, which bears an implicit local dependence on the moments. This dependence leads to asymmetry of the flux Jacobian and loss of hyperbolicity of the corresponding Grad moment system. The pre-factor $\mathcal {M}$ in (36) is independent of the moments, but can be $(t,{\varvec{x}})$-dependent. Such $(t,{\varvec{x}})$-dependence of $\mathcal {M}$ generally leads to contributions to the production term in the corresponding moment system conforming to (58c), but does not compromise the symmetry and hyperbolic character of the moment system. Let us note that in addition to the moment-closure relation corresponding to (28), Grad also considered moment-closure relations with a prescribed global or local Maxwellian in accordance with (27); see [21, Sects. 28–30].

5 Numerical Results for the 1D Spatially Homogeneous Boltzmann-BGK Equation

5.1 Test-Case Setup

To illustrate the elementary properties of the moment-system approximation (18) with the divergence-based closure relation encoded by the renormalization map (36), this section presents numerical computations for the spatially homogeneous Boltzmann-BGK equation in 1D:

$$\begin{aligned}&\partial _tf =-\tau ^{-1}(f-\mathcal {E}_f)\end{aligned}$$

(60a)

$$\begin{aligned}&f(0,v)=f_0(v) \end{aligned}$$

(60b)

for some given initial distribution $f_0$. The corresponding moment system writes:

$$\begin{aligned} \partial _t \langle {\varvec{m}} \mathcal {F}_{N}\rangle&= -\tau ^{-1}\big \langle {\varvec{m}}( \mathcal {F}_N-\mathcal {E}_{ \mathcal {F}_N})\big \rangle \end{aligned}$$

(61a)

$$\begin{aligned} \mathcal {F}_{N}(0,v)&= (\mathcal {F}_{N})_0(v) \end{aligned}$$

(61b)

with $\mathcal {F}_{N}$ according to (37) and $(\mathcal {F}_{N})_0$ defined by the minimization problem (53) subject to the moments corresponding to the initial distribution:

$$\begin{aligned} (\mathcal {F}_{N})_0:= & {} {{\mathrm{arg\,min}}}_{f\in \mathbb {F}}\big \{\langle \eta _N(f)\rangle :\langle {\varvec{m}} f \rangle =\langle {\varvec{m}} f_0 \rangle \big \} \nonumber \\= & {} \big \{f\in \mathbb {F}:f=\beta _N(g),g\in \mathbb {M},\langle {\varvec{m}} f \rangle =\langle {\varvec{m}} f_0 \rangle \big \} \end{aligned}$$

(62)

The systems in (60) and (61) represent initial-value problems for the ordinary differential equations (60a) and (61a). It can be verified by substitution that the solutions of the initial-value problems in (60) and (61) are, respectively,

$$\begin{aligned}&f(t,v) =e^{-t/\tau } f_0 + \big (1-e^{-t/\tau }\big )\mathcal {E}_f \end{aligned}$$

(63a)

$$\begin{aligned}&\mathcal {F}_N(t,v) = e^{-t/\tau } (\mathcal {F}_{N})_0 + \big (1-e^{-t/\tau }\big ) \mathcal {E}_{\mathcal {F}_N} \end{aligned}$$

(63b)

Indeed, noting that $\mathcal {E}_f=\mathcal {E}_{f_0}$ is independent of t, for f(t, v) according to (63a) we obtain:

$$\begin{aligned} \partial _tf=-\tau ^{-1}e^{-t/\tau }(f_0-\mathcal {E}_f) = -\tau ^{-1}(f-\mathcal {E}_f) \end{aligned}$$

(64)

in accordance with (60a). Moreover, one can infer that $f(0,v)=f_0(v)$ and, hence, (63a) satisfies (60). Similarly, it can be shown that (63b) complies with (61). The constraints in the minimization problem in (62) impose ${\mathcal {E}_{f_0}= \mathcal {E}_{(\mathcal {F}_{N})_0}}$. Based on the expressions for the solutions in (63), it then follows that:

$$\begin{aligned} \big \Vert f(t,\cdot )-\mathcal {F}_{N}(t,\cdot )\big \Vert = e^{-t/\tau }\big \Vert f_0 -(\mathcal {F}_{N})_0\big \Vert \end{aligned}$$

(65)

in any suitable norm. Equation (65) conveys that the accuracy of the approximation of $f(t,\cdot )$ by $\mathcal {F}_{N}(t,\cdot )$ at any time $t>0$ depends exclusively on the accuracy of the approximation of the initial condition $f_0$ by $(\mathcal {F}_{N})_0$ according to (62). In the remainder of this section we therefore restrict our considerations to numerical examples that illustrate the approximation properties of $\varphi _N$-divergence minimizers and to properties of the projection problem (62).

We consider approximations of the distributions:

$$\begin{aligned} f_1(v)&= \frac{e^{-\frac{1}{2}(v - 2)^2}}{\sqrt{2 \pi }} +\frac{e^{-\frac{1}{2}(v + 2)^2}}{\sqrt{2 \pi }}, \end{aligned}$$

(66a)

$$\begin{aligned} f_2(v)&= \frac{e^{-\frac{1}{2}(v - 2)^2}}{\sqrt{2 \pi }} +\frac{e^{-\frac{1}{4}(v + 2)^2}}{\sqrt{4 \pi }}, \end{aligned}$$

(66b)

$$\begin{aligned} f_3(v)&= \frac{e^{-2(v - 2)^2}}{\sqrt{\pi /2}} +\frac{e^{-\frac{4}{3}v^2}}{\sqrt{3\pi /4}}+\frac{e^{-(v + 2)^2}}{\sqrt{\pi }} \end{aligned}$$

(66c)

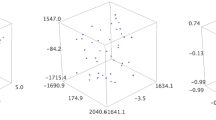
by means of moment-constrained $\varphi _2$-divergence minimizers in polynomial spaces of increasing order. The distributions in (66), plotted in Fig. 1, correspond to distributions of increasing complexity, viz., a symmetric bi-modal distribution, a non-symmetric bi-modal distribution and a non-symmetric tri-modal distribution, respectively.³

Fig. 1

Distributions $f_1$ (left), $f_2$ (center) and $f_3$ (right) according to (66) and the corresponding approximations with $k=3$ (dotted), $k=6$ (dash-dot) and $k=15$ (dashed) moments obtained from the moment-constrained $\varphi$-divergence minimization problem (62)

5.2 Numerical Aspects

For the pre-factor $\mathcal {M}$ in the renormalization map (36) and, accordingly, in the relative entropy $\langle \eta _2(f)\rangle =\langle \mathcal {M}\varphi _2(f/\mathcal {M})\rangle$ associated with the $\varphi _2$-divergence in (46), we select the global equilibrium distribution ${\mathcal {E}_{f_0}}$.

The approximation $\mathcal {F}_2:=\mathcal {F}_2^i$ to $f:=f_i$ is determined by the minimization problem (62). Denoting by $\mathbb {M}_k=\mathrm {span}\{1,v,\ldots ,v^{k-1}\}$ the space of polynomials of degree $k-1$, the minimization problem in (62) with $k\ge {}3$ moment constraints engenders the nonlinear-projection problem:

$$\begin{aligned} \mathcal {F}_2=\mathcal {M}\left( 1+\frac{g}{N}\right) ^{N}_+,\,g\in \mathbb {M}_k: \qquad \bigg \langle {}m\mathcal {M}\Big (1+\frac{g}{2}\Big )^{2}_+\bigg \rangle = \big \langle {}mf\big \rangle \qquad \forall {}m\in \mathbb {M}_k \end{aligned}$$

(67)

Expanding $g(v)=\alpha _i{}v^{i-1}={\varvec{\alpha }}\cdot {{\varvec{m}}}(v)$, Equation (67) corresponds to a nonlinear algebraic system for the coefficients ${\varvec{\alpha }}$. To evaluate the integrals in (61), we first determine the roots of the polynomial $(1+{\varvec{\alpha }}\cdot {{\varvec{m}}}/2)$ and then establish the limits of the positive parts to compute the corresponding contributions to the moments of $\mathcal {M}(1+{\varvec{\alpha }}\cdot {{\varvec{m}}}/2)_+^2$. The integrals in (67) are evaluated by applying a suitable transformation of the integration variable and invoking the following rule:

$$\begin{aligned} \int _{v_0}^{v_1} e^{-v^2} v^k \, dv= & {} \frac{1}{2} \left( \Gamma \left( \frac{1+k}{2}\right) -\Gamma \left( \frac{1+k}{2},v_1^2\right) \right) \text {sign}^{1+k}(v_1) \nonumber \\&-\frac{1}{2}\left( \Gamma \left( \frac{1+k}{2}\right) -\Gamma \left( \frac{1+k}{2},v_0^2\right) \right) \text {sign}^{1+k}(v_0) \end{aligned}$$

(68)

where $-\infty \le v_0 \le \infty$ and $-\infty \le v_1 \le \infty$ and $\Gamma (\cdot )$ and $\Gamma (\cdot ,\cdot )$ are the complete and incomplete gamma functions respectively.

The coefficients ${\varvec{\alpha }}$ are extracted from the system (67) by means of the Newton method. It is to be noted that $(1+g/2)^2_+$ is Fréchet differentiable with respect to g by virtue of the fact that, evidently, changes in the sign of $1+g/2$ occur only at roots. A consistent Jacobian for the tangent problems in the Newton method is provided by:

$$\begin{aligned} \frac{d}{d{\varvec{\alpha }}} \bigg \langle {{\varvec{m}}}\,\mathcal {M}\Big (1+\frac{{\varvec{\alpha }}\cdot {{\varvec{m}}}}{2}\Big )^2_+\bigg \rangle = \bigg \langle {{\varvec{m}}}\otimes {{\varvec{m}}}\,\mathcal {M}\Big (1+\frac{{\varvec{\alpha }}\cdot {{\varvec{m}}}}{2}\Big )_+\bigg \rangle =:{{\varvec{J}}}({{\varvec{\alpha }}}). \end{aligned}$$

(69)

The Jacobian matrix ${{\varvec{J}}}({{\varvec{\alpha }}})$ in the right member of (69) can be identified as a symmetric-positive definite matrix and, hence, the tangent problems in the Newton method are well posed. The Jacobian is however of Hankel-type and it becomes increasingly ill-conditioned as the number of moments increases; see for example [18, 58]. Consequently, the convergence behavior of the Newton process deteriorates for higher-moment systems.

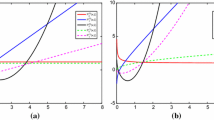
To illustrate the dependence of the convergence behavior of the Newton process on the number of moments, Fig. 2 (left) plots the ratio of the 2-norm of the update in the Newton process, $\Vert \delta {\varvec{\alpha }}\Vert _2$, over the 2-norm of the solution vector, ${\Vert {\varvec{\alpha }}^{(n+1)}\Vert _2}$, versus the number of iterations for polynomial orders $k=7,9,11,13$ for the three test distributions in (66). The ratio $\Vert \delta {\varvec{\alpha }}\Vert _2/\Vert {\varvec{\alpha }}^{(n+1)}\Vert _2$ can be conceived of as the relative magnitude of the update vector. Figure 2 (right) plots an approximation of the corresponding infinity-norm condition numbers, $\varkappa _{\infty }({{\varvec{\alpha }}})=\Vert {{\varvec{J}}}({{\varvec{\alpha }}})\Vert _{\infty }\Vert {{\varvec{J}}}^{-1}({{\varvec{\alpha }}})\Vert _{\infty }$, of the Jacobian matrices. The results in Fig. 2 convey that the condition number increases significantly as the number of moments increases. For $k=7$ the condition number is approximately $10^3$, while for $k=13$ the condition number exceeds $10^5$ and can even reach $10^{10}$. For high-order approximations, the convergence behavior of the Newton process is generally slow and non-monotonous. However, in all cases the relative update can be reduced to a tolerance of $10^{-4}$.

Fig. 2

Convergence of the Newton process for the nonlinear projection problem (67) and conditioning of the corresponding Jacobian matrices: (left) relative magnitude of the Newton update, $\Vert \delta {\varvec{\alpha }}\Vert _2/\Vert {\varvec{\alpha }}^{(n+1)}\Vert _2$, versus the number of iterations for $k=7,9,11,13$ and for distributions (66a) (top), (66b) (center) and (66c) (bottom); (right) corresponding $\infty$-norm condition numbers, $\varkappa _{\infty }({{\varvec{\alpha }}}^{(n)})$, of the Jacobian matrices according to (69)

5.3 Approximation Properties

To illustrate the approximation properties of the moment method with closure relation (37), Fig. 3 (left) plots the $L^1(\mathbb {R})$-norm of the relative error in the approximation $\mathcal {F}_2^i$ to the distribution $f_i$ ($i=1,2,3$) according to (66) and Fig. 3 (right) the corresponding relative error in the cosine moment,

$$\begin{aligned} \mathrm {err}_1= \frac{\Vert f_i-\mathcal {F}^i_2\Vert _{{L}^1(\mathbb {R})}}{\Vert f_i\Vert _{\mathbb {L}^1(\mathbb {R})}}, \qquad \mathrm {err}_2=\frac{|\langle \cos (\cdot ) f_i\rangle - \langle \cos (\cdot )\mathcal {F}^i_2\rangle |}{|\langle \cos (\cdot )f_i\rangle |}, \end{aligned}$$

(70)

respectively. The cosine moment does not have any physical significance and only serves to investigate the super-convergence properties of the approximation in accordance with the Babuška–Miller theorem [3]; see Sect. 3. A non-polynomial moment has been selected to examine the convergence behavior, because for any polynomial moment $\langle \sigma {}f_i\rangle$ with $\sigma \in \mathbb {M}_l$ the approximation $\langle \sigma \mathcal {F}_2^i\rangle$ provided by the k-moment approximation $\mathcal {F}^i_2$ is exact for all $k\ge {}l$, on account of the constraints in (62).

Figure 3 (left) indicates that $\Vert f_i-\mathcal {F}_2^i\Vert _{L^1(\mathbb {R})}$ converges exponentially with increasing k, i.e., there exist positive constants C and $\zeta$ such that $\Vert f_i-\mathcal {F}_2^i\Vert _{L^1(\mathbb {R})}\le {}C\zeta ^{-k}$. In particular, $\zeta \approx {}10^{-0.13}\approx 0.74$ for the bi-modal distributions $f_1$ and $f_2$ and $\zeta \approx 10^{-0.085}\approx 0.82$ for the tri-modal distribution $f_3$. Comparison of the left and right panels in Fig. 3 conveys that the approximation of the cosine moment indeed converges at a higher rate than the $L^1(\mathbb {R})$-norm of the approximation itself. Figure 3 (right) conveys that the cosine moment converges at a rate of $\zeta \approx 10^{-0.58}\approx 0.26$ for both the bi-modal distributions $f_1,f_2$ and the tri-modal distribution $f_3$.

Fig. 3

Approximation properties of the moment method with closure relation (37): (left) convergence of the relative error in the $L^1(\mathbb {R})$-norm $\mathrm {err}_1$ according to (70) for $f_1,f_2$ and $f_3$ in (66); (right) corresponding convergence of the relative error in the cosine moment, $\mathrm {err}_2$

Fig. 4

Illustration of the effect of a misinformative pre-factor on the approximation properties of the moment method with closure relation (35): relative error (70) in the approximation of sample distribution (66c) with a pre-factor $\mathcal {M}=\mathcal {M}_{\rho _3,u+\delta u,T_3}$ corresponding to a shifted global equilibrium distribution, for $k=3,5,\ldots ,13$

In the moment-closure approximation (67) of the sample distributions (66), the pre-factor has been selected as the global equilibrium (10) corresponding to each sample distribution. These global equilibria can be determined explicitly, by virtue of the availability of the underlying distributions. In general, however, the underlying distribution is not explicitly available. The question that then imposes itself, is how the pre-factor should be selected and how sensitive the approximation is with respect to the pre-factor. In this context, it is important to note that the pre-factor, $\mathcal {M}$, appears in the moment-constrained $\varphi$-divergence minimization (53) as a background measure. This background measure can be conceived of as prior information on the solution of (1), locally at $(t,{\varvec{x}})$, before the information encoded in the moments is accounted for. The solution to (53) can be understood as the corresponding posterior. In general, any prior carries subjective or objective⁴ information. A subjective prior is more (mis-)informative about the posterior than an objective one. A Maxwellian prior qualifies as subjective for posteriors of the form (37), in view of the fact that the exponential decay or growth of Maxwellians exceeds that of polynomials. Hence, the behavior of the posterior (37) as $|{\varvec{v}}|\rightarrow \infty$ is completely determined by the prior $\mathcal {M}$, and not by the information encoded in the moments. To illustrate the consequences of a misinformative subjective prior, we reconsider the approximation of the sample distribution (66c) by means of (67), in which the prior, $\mathcal {M}=\mathcal {M}_{\rho _3,u_3+\delta u, T_3}$, corresponds to the global equilibrium distribution in accordance with (66c), shifted by $\delta u$. Figure 4 plots the relative error in the approximate distribution, $\mathrm {err}_1$ according to (70), versus the shift, $\delta {}u$. The figure conveys that a shift in the pre-factor yields a detrimental effect on the accuracy of the approximation. It is to be noted, however, that convergence under k-refinement is retained.

If credible prior information is not available, it is more appropriate to select the pre-factor in accordance with an objective prior, e.g. uniform (Lebesgue) measure. Moreover, it is not sensible to construct high-rank moment systems based on unreliable prior information. Instead, the hierarchy of the moment systems can be exploited to update prior information, i.e. the pre-factor for each moment system beyond $k=3$ can be extracted from the solution to a lower-rank moment system. It is to be noted that a pre-factor corresponding to a solution of the Euler equations corresponds to a specific instance of such a hierarchical procedure.

6 Conclusion

To avoid the realizability problem inherent to the maximum-entropy closure relation for moment-system approximations of the Boltzmann equation, we proposed a new class of closure relations based on $\varphi$-divergence minimization. We established that $\varphi$-divergences provide a natural generalization of the usual relative-entropy setting of the moment-closure problem. It was shown that minimization of certain $\varphi$-divergences leads to suitable closure relations and that the corresponding moment-constrained $\varphi$-divergence minimization problems are not impaired by the realizability problem inherent to minimization of the Kullback–Leibler divergence. Moreover, if the collision operator under consideration dissipates a $\varphi$-divergence, then the corresponding minimal-divergence moment-closure systems retain the fundamental structural properties of the Boltzmann equation, namely, conservation of mass, momentum and energy, Galilean invariance, and dissipation of an entropy, sc. the $\varphi$-divergence. For suitable $\varphi$-divergences, the closure relation yields non-negative approximations of the one-particle marginal. Divergence-based moment systems are generally symmetric hyperbolic, which implies linear well-posedness.

We inferred that moment systems can alternatively be conceived of as Galerkin approximations of a renormalized Boltzmann equation. We considered moment systems based on a renormalization map composed of Tsallis’ q-exponential. This renormalization map is concomitant with a $\varphi$-divergence corresponding to the anti-derivative of the inverse q-exponential, which yields a natural approximation to relative entropy. The evaluation of moments of the q-exponential, elementary in numerical methods for the corresponding moment system, is tractable, as opposed to the evaluation of moments of exponentials of arbitrary-order polynomials, connected with maximum-entropy closure.

Numerical results have been presented for the one-dimensional spatially homogeneous Boltzmann-BGK equation. The nonlinear projection problem associated with the moment-constrained $\varphi$-divergence minimization problems was solved by means of Newton’s method. We observed that the condition number of the Jacobian matrices in the tangent problems generally deteriorates as the number of moments increases. Nevertheless, in all considered cases approximations up to at least 15 moments could be computed. We observed that the q-exponential approximation converges exponentially in the $L^1(\mathbb {R})$-norm with increasing number of moments. Moreover, we demonstrated that functionals of the approximate distribution display super convergence, in accordance with the Babuška–Miller theorem for Galerkin approximations.

Appendix: Generalized BGK Collision Operator

In [35], Levermore introduced a class of multiscale generalizations of the BGK collision operator based on a finite sequence of increasingly constrained entropic projections of the form (20). In particular, given an admissible space of polynomials $\mathbb {M}$, consider a sequence of nested subspaces $\{\mathbb {M}_k\}_{k=1}^K$ with $\mathbb {M}_0=\mathbb {E}$ and strictly contained in $\mathbb {M}$, i.e. $\mathbb {E}=\mathbb {M}_1\subset \mathbb {M}_2\subset \cdots \subset \mathbb {M}_K\subset \mathbb {M}$. For each k and $f\in \mathbb {F}$, let $f\mapsto \mathcal {F}^k(f)=:\mathcal {F}^k$ be the $\mathbb {M}_k$-moments constrained entropic projection of f,

$$\begin{aligned} \mathcal {F}^k(f):= {{\mathrm{arg\,min}}}_{g\in \mathbb {F}} \big \{\langle \eta (g)\rangle :\langle m g \rangle =\langle m f \rangle ,\,\forall {}m\in \mathbb {M}_k\big \}, \end{aligned}$$

(71)

with $\eta (g)=g\log {}g-g$, under the assumption that (71) admits a solution for each k. Based on the sequence of projections $\{\mathcal {F}^k\}_{k=1}^K$, one can define a multiscale relaxation operator:

$$\begin{aligned} \mathcal {C}(f) = -\theta _K(f-\mathcal {F}^K)-\sum _{k=1}^{K-1}\theta _k(\mathcal {F}^{k+1}-\mathcal {F}^{ k}) \end{aligned}$$

(72)

with $\{\theta _k\}_{k=1}^{K}$ an increasing sequence of positive relaxation rates depending on f. The relaxation rate $\theta _k$ with $k\in \{1,2,\ldots ,K-1\}$ constitutes the rate at which $\mathcal {F}^{k+1}$ decays to $\mathcal {F}^{k}$, while $\theta _K$ is the rate at which f decays to $\mathcal {F}^K$. In [35] it is shown that the Prandtl number can be controlled via the relaxation rates.

The above construction of the generalized BGK operator can be extended to $\varphi$-divergences. To this end, consider an arbitrary $\varphi$-divergence and let $f\mapsto \mathcal {F}^k(f)=:\mathcal {F}^k$ denote the corresponding divergence-minimization projection according to (71), i.e. $\mathcal {F}^k$ is defined by (71) with $\eta (\cdot )=\mathcal {M}\varphi ((\cdot )/\mathcal {M})$. Based on the projections $\mathcal {F}^k$, an extended BGK operator can be defined analogous to (72). To establish that $\eta '(\cdot )=\varphi '((\cdot /\mathcal {M})$ corresponds to an entropy density for the generalized BGK operator, we first note that the (strong) convexity of $\eta$ implies:

$$\begin{aligned} (\eta '(s)-\eta '(t))(s-t)\big \rangle \ge 0 \end{aligned}$$

(73)

for all s, t in the domain of $\eta$ and equality in (73) holds if and only if $s=t$. Rearranging the sum in (72) yields:

$$\begin{aligned} \mathcal {C}(f)= -\theta _1\big (f-\mathcal {F}^1\big ) -\sum _{k=1}^{K-1}\big (\theta _{k+1}-\theta _{k}\big )\big (f-\mathcal {F}^{k+1}\big ) \end{aligned}$$

(74)

From the minimization problem (71) we infer that for all k it holds that $\eta '(\mathcal {F}^k)\in \mathbb {M}_k$ and $\langle {}m(f-\mathcal {F}^k)\rangle =0$ for all $m\in {}\mathbb {M}_k$. Hence, $\langle \eta '(\mathcal {F}^k)f\rangle -\langle \eta '(\mathcal {F}^k)\mathcal {F}^k\rangle =0$ yields a partition of zero for all k. From (74) and the aforementioned partition of zero, we obtain

$$\begin{aligned} \big \langle \eta '(f)\mathcal {C}(f)\big \rangle= & {} -\,\theta _1\big \langle \eta '(f)\big (f-\mathcal {F}^1\big )\big \rangle -\,\sum _{k=1}^{K-1}\big (\theta _{k+1}-\theta _{k}\big )\big \langle \eta '(f)\big (f-\mathcal {F}^{k+1}\big )\big \rangle \nonumber \\= & {} -\,\theta _1\big \langle \big (\eta '(f)-\eta '(\mathcal {F}^1\big )\big (f-\mathcal {F}^1\big )\big \rangle \nonumber \\&-\sum _{k=1}^{K-1}\big (\theta _{k+1}-\theta _{k}\big )\big \langle \big (\eta '(f)-\eta '(\mathcal {F}^{k+1})\big )\big (f-\mathcal {F}^{k+1}\big )\big \rangle \end{aligned}$$

(75)

From $\theta _1>0$ and $\theta _{k+1}>\theta _k$ ($k=1,\ldots ,K-1$), and the convexity of $\eta (\cdot )$ according to (73) we conclude that $\eta$ and $\mathcal {C}$ satisfy the dissipation relation (5), i.e. $\langle \eta '(f)\mathcal {C}(f)\rangle \le {}0$ for all admissible f. To verify the second prerequisite relation between $\eta$ and $\mathcal {C}$, viz., the equivalence of the statements in (6), we first observe that the implication (6)${}_{(i)}$ $\Rightarrow$ (6)${}_{(ii)}$ is trivial. To validate the reverse implication in (6), we note that (6)${}_{(ii)}$ in combination with the convexity of $\eta$ according to (73) and the ultimate expression in (75) implies that ${(\eta '(f)-\eta '(\mathcal {F}^k))(f-\mathcal {F}^k)}$ vanishes almost everywhere for all $k=1,\ldots ,K$. This, in turn, implies that $f=\mathcal {F}^1=\cdots =\mathcal {F}^K$. Condition (6)${}_{(i)}$ then follows directly from (74). To verify the implication (6)${}_{(ii)}$ $\Rightarrow$ (6)${}_{(iii)}$, we note that ${\mathcal {F}^k}$ according to (71) satisfies ${\eta '(\mathcal {F}^k)\in \mathbb {M}_k}$ for all k. Recalling that (6)${}_{(ii)}$ implies $f={\mathcal {F}^1}$, we infer $\eta '(f)\in \mathbb {M}_1=\mathbb {E}$ in accordance with (6)${}_{(iii)}$. Finally, the reverse implication (6)${}_{(iii)}$ $\Rightarrow$ (6)${}_{(ii)}$ follows immediately from (74) and the moment constraints in (71).