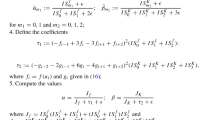Skip to main content
Springer Nature Link
Log in

High Order Finite Difference Multi-resolution WENO Method for Nonlinear Degenerate Parabolic Equations

  • Published:
Journal of Scientific Computing Aims and scope Submit manuscript

Abstract

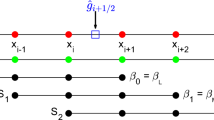
In this paper, we propose a new finite difference weighted essentially non-oscillatory (WENO) scheme for nonlinear degenerate parabolic equations which may contain non-smooth solutions. An alternative formulation is designed to approximate the second derivatives in a conservative form. In this formulation, the odd order derivatives at half points are used to construct the numerical flux, instead of the usual practice of reconstruction. Moreover, the multi-resolution WENO scheme is designed to circumvent the negative ideal weights and mapped nonlinear weights that appear when applying the standard WENO idea. We will describe the scheme formulation and present numerical tests for one- and two-dimensional, demonstrating the designed high order accuracy and non-oscillatory performance of the schemes constructed in this paper.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Abedian, R., Adibi, H., Dehghan, M.: A high-order weighted essentially non-oscillatory (WENO) finite difference scheme for nonlinear degenerate parabolic equations. Comput. Phys. Commun. 184(8), 1874–1888 (2013)

    Article  MathSciNet  Google Scholar 

  2. Alt, H.W., Luckhaus, S.: Quasilinear elliptic-parabolic differential equations. Math. Z. 183(3), 311–341 (1983)

    Article  MathSciNet  Google Scholar 

  3. Arbogast, T., Huang, C.-S., Zhao, X.: Finite volume weno schemes for nonlinear parabolic problems with degenerate diffusion on non-uniform meshes. J. Comput. Phys. 399, 108921 (2019)

    Article  MathSciNet  Google Scholar 

  4. Aregba-Driollet, D., Natalini, R., Tang, S.: Explicit diffusive kinetic schemes for nonlinear degenerate parabolic systems. Math. Comput. 73(245), 63–94 (2004)

    Article  MathSciNet  Google Scholar 

  5. Aronson, D. G.: The porous medium equation. In Nonlinear diffusion problems, pp. 1–46. Springer, Berlin (1986)

  6. Balsara, D.S., Shu, C.-W.: Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J. Comput. Phys. 160(2), 405–452 (2000)

    Article  MathSciNet  Google Scholar 

  7. Barenblatt, G.I.: On self-similar motions of a compressible fluid in a porous medium. Akad. Nauk SSSR. Prikl. Mat. Meh 16(6), 79–6 (1952)

    MathSciNet  Google Scholar 

  8. Berger, A.E., Brezis, H., Rogers, J.C.: A numerical method for solving the problem \(u_t-\Delta f(u)=0\). RAIRO. Anal. Numér. 13(4), 297–312 (1979)

    Article  MathSciNet  Google Scholar 

  9. Bessemoulin-Chatard, M., Filbet, F.: A finite volume scheme for nonlinear degenerate parabolic equations. SIAM J. Sci. Comput. 34(5), B559–B583 (2012)

    Article  MathSciNet  Google Scholar 

  10. Buckley, S.E., Leverett, M., et al.: Mechanism of fluid displacement in sands. Trans. AIME 146(01), 107–116 (1942)

    Article  Google Scholar 

  11. Cavalli, F., Naldi, G., Puppo, G., Semplice, M.: High-order relaxation schemes for nonlinear degenerate diffusion problems. SIAM J. Numer. Anal. 45(5), 2098–2119 (2007)

    Article  MathSciNet  Google Scholar 

  12. Christlieb, A., Guo, W., Jiang, Y., Yang, H.: Kernel based high order explicit unconditionally stable scheme for nonlinear degenerate advection-diffusion equations. J. Sci. Comput. 82(3), 52 (2020)

    Article  MathSciNet  Google Scholar 

  13. Duyn, C.Y., Peletier, L.: Nonstationary filtration in partially saturated porous media. Arch. Ration. Mech. Anal. 78(2), 173–198 (1982)

    Article  MathSciNet  Google Scholar 

  14. Gottlieb, S., Shu, C.-W., Tadmor, E.: Strong stability-preserving high-order time discretization methods. SIAM Rev. 43(1), 89–112 (2001)

    Article  MathSciNet  Google Scholar 

  15. Jiang, G.-S., Shu, C.-W.: Efficient implementation of weighted eno schemes. J. Comput. Phys. 126(1), 202–228 (1996)

    Article  MathSciNet  Google Scholar 

  16. Jiang, Y., Shu, C.-W., Zhang, M.: An alternative formulation of finite difference weighted ENO schemes with lax-wendroff time discretization for conservation laws. SIAM J. Sci. Comput. 35(2), A1137–A1160 (2013)

    Article  MathSciNet  Google Scholar 

  17. Jiang, Y., Shu, C.-W., Zhang, M.: Free-stream preserving finite difference schemes on curvilinear meshes. Methods Appl. Anal. 21(1), 1–30 (2014)

    MathSciNet  MATH  Google Scholar 

  18. Kurganov, A., Tadmor, E.: New high-resolution central schemes for nonlinear conservation laws and convection-diffusion equations. J. Comput. Phys. 160(1), 241–282 (2000)

    Article  MathSciNet  Google Scholar 

  19. Levy, D., Puppo, G., Russo, G.: Compact central weno schemes for multidimensional conservation laws. SIAM J. Sci. Comput. 22(2), 656–672 (2000)

    Article  MathSciNet  Google Scholar 

  20. Liu, X.-D., Osher, S., Chan, T.: Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115(1), 200–212 (1994)

    Article  MathSciNet  Google Scholar 

  21. Liu, Y., Shu, C.-W., Zhang, M.: On the positivity of linear weights in WENO approximations. Acta Math. Appl. Sin. Engl. Ser. 25(3), 503–538 (2009)

    Article  MathSciNet  Google Scholar 

  22. Liu, Y., Shu, C.-W., Zhang, M.: High order finite difference WENO schemes for nonlinear degenerate parabolic equations. SIAM J. Sci. Comput. 33(2), 939–965 (2011)

    Article  MathSciNet  Google Scholar 

  23. Lu, Y., Jger, W.: On solutions to nonlinear reactiondiffusionconvection equations with degenerate diffusion. J. Differ. Equ. 170(1), 1–21 (2001)

    Article  Google Scholar 

  24. Magenes, E., Nochetto, R., Verdi, C.: Energy error estimates for a linear scheme to approximate nonlinear parabolic problems. ESAIM Math. Modell. Numer. Anal. Modél. Math. Anal. Numér. 21(4), 655–678 (1987)

    Article  MathSciNet  Google Scholar 

  25. Muskat, M., Wyckoff, R. D. et al.: Flow of homogeneous fluids through porous media. (1937)

  26. Nochetto, R., Schmidt, A., Verdi, C.: A posteriori error estimation and adaptivity for degenerate parabolic problems. Math. Comput. 69(229), 1–24 (2000)

    Article  MathSciNet  Google Scholar 

  27. Nochetto, R.H., Verdi, C.: Approximation of degenerate parabolic problems using numerical integration. SIAM J. Numer. Anal. 25(4), 784–814 (1988)

    Article  MathSciNet  Google Scholar 

  28. Otto, F.: L1-contraction and uniqueness for quasilinear elliptic-parabolic equations. J. Differ. Equ. 131(1), 20–38 (1996)

    Article  Google Scholar 

  29. Shu, C.-W.: High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 51(1), 82–126 (2009)

    Article  MathSciNet  Google Scholar 

  30. Shu, C.-W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes. J. Comput. Phys. 77(2), 439–471 (1988)

    Article  MathSciNet  Google Scholar 

  31. Shu, C.-W., Osher, S.: Efficient implementation of essentially non-oscillatory shock-capturing schemes. II. J. Comput. Phys. 83(1), 32–78 (1989)

    Article  MathSciNet  Google Scholar 

  32. Wang, Y., Zhu, J.: A new type of increasingly high-order multi-resolution trigonometric weno schemes for hyperbolic conservation laws and highly oscillatory problems. Computers and Fluids, p. 104448 (2020)

  33. Zeldovich, Y. B., Kompaneets, A.: Towards a theory of heat conduction with thermal conductivity depending on the temperature. Collection of papers dedicated to 70th birthday of Academician AF Ioffe, Izd. Akad. Nauk SSSR, Moscow, pp. 61–71 (1950)

  34. Zhang, Q., Wu, Z.-L.: Numerical simulation for porous medium equation by local discontinuous galerkin finite element method. J. Sci. Comput. 38(2), 127–148 (2009)

    Article  MathSciNet  Google Scholar 

  35. Zhu, J., Shu, C.-W.: A new type of multi-resolution weno schemes with increasingly higher order of accuracy. J. Comput. Phys. 375, 659–683 (2018)

    Article  MathSciNet  Google Scholar 

  36. Zhu, J., Shu, C.-W.: A new type of multi-resolution weno schemes with increasingly higher order of accuracy on triangular meshes. J. Comput. Phys. 392, 19–33 (2019)

    Article  MathSciNet  Google Scholar 

  37. Zhu, J., Shu, C.-W.: A new type of third-order finite volume multi-resolution weno schemes on tetrahedral meshes. J. Comput. Phys. 406, 109212 (2020)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, University of Science and Technology of China, Hefei, 230026, Anhui, People’s Republic of China

    Yan Jiang

Authors
  1. Yan Jiang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Yan Jiang.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Research is supported by NSFC Grant 11901555.

Appendix A: Smoothness Indicator \(\beta _r\)

Appendix A: Smoothness Indicator \(\beta _r\)

Here, we give the formulas of smoothness indicator \(\beta _r, r=1, 2, 3, 4\):

$$\begin{aligned} \beta _1&= \left( g_{j-1} - g_{j} \right) ^2, \end{aligned}$$
(A.1)
$$\begin{aligned} \beta _2&= \frac{781}{720} \left( g_{j-1} - 3 g_{j} + 3 g_{j+1} - g_{j+2} \right) ^2 + \frac{13}{48} \left( g_{j-1} - g_{j} - g_{j+1} + g_{j+2} \right) ^2 \nonumber \\&\quad + \left( g_{j-1} - g_{j} \right) ^2 , \end{aligned}$$
(A.2)
$$\begin{aligned} \beta _3&= \frac{21520059541}{19838649600} ( g_{j-2} - 5 g_{j-1} + 10 g_{j} - 10 g_{j+1} + 5 g_{j+2} - g_{j+3} )^2 \nonumber \\&\quad + \frac{1}{440858880} ( 1851 g_{j-2} - 31123 g_{j-1} + 84114 g_{j} - 84114 g_{j+1} + 31123 g_{j+2} - 1851 g_{j+3} )^2 \nonumber \\&\quad + \frac{1}{2246400} ( 131 g_{j-2} - 1173 g_{j-1} + 1042 g_{j} + 1042 g_{j+1} - 1173 g_{j+2} + 131 g_{j+3} )^2 \nonumber \\&\quad + \frac{1421461}{5241600} ( g_{j-2} - 3 g_{j-1} + 2 g_{j}+ 2 g_{j+1} - 3 g_{j+2} + g_{j+3} )^2 +(-g_{j} + g_{j+1})^2 , \end{aligned}$$
(A.3)
$$\begin{aligned} \beta _4 =&1.4041259062317264 g_{j-3}^2 - 19.009155271319045 g_{j-3} g_{j-2}\nonumber \\&\quad + 66.50902509852973 g_{j-2}^2 + 54.339909801618134 g_{j-3} g_{j-1}\nonumber \\&\quad - 390.9402172389724 g_{j-2} g_{j-1} + 590.6133168359419 g_{j-1}^2\nonumber \\&\quad - 85.00749694374984 g_{j-3} g_{j} + 625.8186587734967 g_{j-2} g_{j}\nonumber \\&\quad - 1938.8377490285563 g_{j-1} g_{j} + 1633.1518037432388 g_{j}^2 \nonumber \\&\quad + 78.6410569694366 g_{j-3} g_{j+1} - 590.180193745405 g_{j-2} g_{j+1}\nonumber \\&\quad + 1868.4913145573562 g_{j-1} g_{j+1} - 3225.229198069056 g_{j} g_{j+1}\nonumber \\&\quad + 1633.1518037432388 g_{j+1}^2 - 43.07675485182256 g_{j-3} g_{j+2} \nonumber \\&\quad + 328.5879072717406 g_{j-2} g_{j+2} - 1059.7910441832473 g_{j-1} g_{j+2}\nonumber \\&\quad + 1868.4913145573562 g_{j} g_{j+2} - 1938.8377490285563 g_{j+1} g_{j+2}\nonumber \\&\quad + 590.6133168359419 g_{j+2}^2 + 12.957946502914096 g_{j-3} g_{j+3} \nonumber \\&\quad - 100.25299648951443 g_{j-2} g_{j+3} + 328.5879072717406 g_{j-1} g_{j+3}\nonumber \\&\quad - 590.180193745405 g_{j} g_{j+3} + 625.8186587734967 g_{j+1} g_{j+3}\nonumber \\&\quad - 390.9402172389724 g_{j+2} g_{j+3} + 66.50902509852973 g_{j+3}^2 \nonumber \\&\quad - 1.6537580195408403 g_{j-3} g_{j+4}+ 12.957946502914096 g_{j-2} g_{j+4}\nonumber \\&\quad - 43.07675485182256 g_{j-1} g_{j+4} + 78.6410569694366 g_{j} g_{j+4}\nonumber \\&\quad - 85.00749694374984 g_{j+1} g_{j+4} + 54.339909801618134 g_{j+2} g_{j+4} \nonumber \\&\quad - 19.009155271319045 g_{j+3} g_{j+4} + 1.4041259062317264 g_{j+4}^2 . \end{aligned}$$
(A.4)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jiang, Y. High Order Finite Difference Multi-resolution WENO Method for Nonlinear Degenerate Parabolic Equations. J Sci Comput 86, 16 (2021). https://doi.org/10.1007/s10915-020-01382-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10915-020-01382-y

Keywords