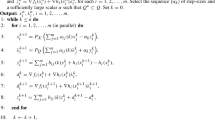1 Introduction

We consider problems of the form

$$\begin{aligned} \min _{y \in {\mathbb {R}}^n} f(y)=\sum _{i=1}^{N} f_i(y), \end{aligned}$$
(1)

where \(f_i : {\mathbb {R}}^n \rightarrow {\mathbb {R}}\) are strongly convex local cost functions. A decentralized optimization framework is considered, more precisely, we assume decentralized but connected network of N nodes.

Distributed consensus optimization over networks has become a mainstream research topic, e.g., [2,3,4, 6, 9, 11], motivated by numerous applications in signal processing [13], control [16], Big Data analytics [23], social networks [1], etc. Various methods have been proposed in the literature, e.g., [22, 24, 28,29,30,31, 33,34,35, 37].

While early distributed (sub)gradient methods exhibit several useful features, e.g., [18], they also have the drawback that they do not converge to the exact problem solution when applied with a constant step-size; that is, for exact convergence, they need to utilize a diminishing step-size [39]. To address this issue, several different mechanisms have been proposed. Namely, in [25] two different weight-averaging matrices at two consecutive iterations are used. A gradient-tracking technique where the local updates are modified so that they track the network-wide average gradient of the nodes’ local cost functions is proposed and analyzed in [12, 21]. The authors of [2] incorporate multiple consensus steps per each gradient update to obtain the convergence to the exact solution.

In this paper we investigate a different strategy to develop a novel class of exact distributed methods by employing quadratic penalty approach. The method is defined by the standard reformulation of distributed problem (1) into constrained problem in \( {\mathbb {R}}^{nN} \) with constraints that penalize the differences in local approximations of the solution. The reformulated constrained problem is then solved by a quadratic penalty method. Given that the sequence of penalty subproblems is quadratic, we employ a fixed point linear solver to find zeroes of the corresponding gradients. Thus, we abbreviated the method as EFIX – Exact Fixed Point.

The proposed approach is as follows. The constrained distributed problem in \( {\mathbb {R}}^{nN} \) is reformulated by adding a quadratic penalty term that penalizes the differences of solution estimates at neighbouring nodes across the network. Then the sequence of penalty problems are solved inexactly, wherein the corresponding penalty parameters increase over time to make the algorithm exact. The algorithm parameters, the penalty parameter sequence and the levels of inexactness of the (inner) penalty problems, are designed such that the overall algorithm exhibits efficient behaviour. We consider two types of strongly convex objective functions - quadratic and generic strongly convex function. For quadratic objective function the subproblems are quadratic, while in the generic case we approximate the objective function at the current iteration with a quadratic model. Solving these problems boils down to finding zeroes of the gradients, i.e. to solving systems of linear equations and one can employ any distributed linear solver like fixed point iterative methods. The proposed framework is general and we exemplify it by employing the Jacobi Over-Relaxation (JOR) method for solving the penalty subproblems. Numerical tests on both simulated and real data sets demonstrate that the resulting algorithms are (at least) comparable with existing alternatives like [21, 36] in terms of the required computational and communication costs, as well as the required knowledge of global system parameters such as the global (maximal) Lipschitz constant of the local gradients L, strong convexity constant \(\mu \) and the network parameters.

From the theoretical point of view the following results are established. First, for the quadratic cost functions, we show that either a sequence generated by the EFIX method is unbounded or it converges to the exact solution of the original problem (1). The worst-case complexity result of order \({{\mathcal {O}}}(\epsilon ^{-1})\) is proved. For strongly convex costs with Lipschitz continuous gradients, the obtained result corresponds to the well-known result in the classical, centralized optimization - if the iterative sequence converges then its limit is the solution of the original problem. Admittedly, this result is weaker than what is known for existing alternatives like, e.g., [21], but are enough to theoretically certify the methods and are in line with the general theory of quadratic penalty methods; see, e.g., [19]. Numerical examples nevertheless demonstrate advantages of the proposed approach. Moreover, the convergence results of the proposed method are obtained although the Linear Independence Constraint Qualification, LICQ is violated.

It is worth noting that penalty approaches have been studied earlier in the context of distributed consensus optimization, e.g., [14, 15, 27, 40]. The authors of [40] allow for nondifferentiable costs, but their analysis relies on Lagrange multipliers and the distance from a closed, convex feasible set which plays a crucial role in the analysis. In [27], a differentiable exact penalty function is employed, but the problem under consideration assumes local constraints and separable objective function. Moreover, LICQ is assumed to hold. In our case, separating the objective function yields the constrained optimization problem (2) where the LICQ is violated. The authors of [15] consider more general problems with possibly nondiffrenetiable part of the objective function and linear constraints and provide the analysis for the decentralized distributed optimization problems (Section 4 of [15]). They show the convergence to an exact solution by carefully designing the penalty parameters and the step size sequence. The proposed algorithm boils down to the distributed gradient with time-varying step sizes. The convergence is of the order \({{\mathcal {O}}}(1/\sqrt{k})\), i.e., \({{\mathcal {O}}}(1/k)\) for the accelerated version. We notice that EFIX algorithm needs the gradient calculations only in the outer iterations, whenever the penalty parameter is increased and a new subproblem is generated, which makes it computationally less demanding. The numerical efficiency of the method in [15] is not documented to the best of out knowledge, although the convergence rate results are very promising. The strong convexity is not imposed in [15], and possibilities for relaxation of convexity requirements in EFIX are going to be the subject of further research. The algorithm presented in [14] is also based on penalty approach. A sequence of subproblems with increasing penalty parameters is defined and solved by accelerated proximal gradient method. Careful adjustment of algorithmic parameters yields a better complexity result than the results presented here. However, with respect to existing work, the proposed EFIX framework is more general in terms of the subsumed algorithms and can accommodate arbitrary R-linearly-converging solver for quadratic penalty subproblems. Finally, another important advantage of EFIX is the robustness with respect to algorithmic parameters.

The paper is organized as follows. In Sect. 2 we give some preliminaries. EFIX method for quadratic problems is defined and analyzed in Sect. 3. The analysis is extended to general convex case in Sect. 4 and the numerical results for both quadratic and general case are presented in Sect. 5. Some conclusions are drawn in Sect. 6. All proofs are moved to the Appendix.

2 Preliminaries

The notation we will use further is the following. With \( {\mathbb {A}}, {\mathbb {B}}, \ldots \) we denote matrices in \( {\mathbb {R}}^{nN \times nN} \) with block elements \( {\mathbb {A}} = [A_{ij}], \; A_{ij} \in {\mathbb {R}}^{n \times n} \) and elements \( a_{ij} \in {\mathbb {R}}. \) The vectors of corresponding dimensions will be denoted as \( {\mathbf {x}} \in {\mathbb {R}}^{nN} \) with sub-blocks \( x_i \in {\mathbb {R}}^n \) as well as \( y \in {\mathbb {R}}^n. \) The vector (matrix) norm \( \Vert \cdot \Vert \) is the Euclidean (spectral) norm.

Let us specify more precisely the setup we consider here. The network of connected computational nodes is represented by a graph \(G=(V, E)\), where V is the set of nodes \(\{1,\ldots ,N\}\) and E is the set of undirected edges (i, j). Denote by \(O_i\) the set of neighbors of node i and let \(\bar{O_i}=O_i \bigcup \{i\}.\) Let W and \( L=I-W \) denote the communication matrix and the corresponding Laplacian matrix. The communication matrix W is a weighted adjacency matrix of G with additional properties as stated in Assumption 1 below. We also define augmented communication matrix \({\mathbb {W}}=W \otimes I \in {\mathbb {R}}^{nN \times nN}\) and augmented weighted Laplacian matrix \( {\mathbb {L}}={\mathbb {I}}- {\mathbb {W}},\) where \({\mathbb {I}}\in {\mathbb {R}}^{nN \times nN} \) is the identity matrix and \( \otimes \) denotes the Kronecker product. The properties of the communication matrix W are stated as follows.

A 1

The matrix \( W \in {\mathbb {R}}^{N \times N} \) is symmetric, doubly stochastic and

$$\begin{aligned} w_{ij} > 0 \text{ if } j\in {\bar{O}}_i, \; w_{ij} = 0 \text{ if } j \notin {\bar{O}}_i \end{aligned}$$

The network G is connected and undirected.

Let us assume that each of N nodes has its local cost function \(f_i\) and has access to the corresponding derivatives of this local function. Under the assumption A1, the problem (1) has the equivalent form

$$\begin{aligned} \min _{{\mathbf {x}} \in {\mathbb {R}}^{nN}} F({\mathbf {x}}):=\sum _{i=1}^{N} f_i(x_i) \quad \text{ s. } \text{ t. } \quad {\mathbb {L}}^{1/2} {\mathbf {x}}=0, \end{aligned}$$
(2)

where \({\mathbf {x}}=(x_1;\ldots ;x_N) \in {\mathbb {R}}^{nN}. \) Notice that under Assumption A1 the constraint \( {\mathbb {L}}^{1/2} {\mathbf {x}}=0\) is actually stating that the feasible vectors \({\mathbf {x}}= (x_1;\ldots ;x_N)\) have the property \( x_i = x_j, \; i,j=1,\ldots ,N.\) Hence, the equivalence of (1) and (2) is in the following sense. Let us denote by \( y^* \in {\mathbb {R}}^n \) the solution of (1). Then \( {\mathbf {x}}^* = (y^*,\ldots ,y^*) \in {\mathbb {R}}^{nN} \) is a solution of (2). Conversely, let \({\mathbf {x}}^*\) be the solution to (2). Then, \({\mathbf {x}}^* = (y^*\ldots .,y^*)\), where \(y^*\) is the solution to (1). Now, the quadratic penalty reformulation of this problem associated with graph G is

$$\begin{aligned} \min _{{\mathbf {x}} \in {\mathbb {R}}^{nN}} \Phi _{\theta } ({\mathbf {x}}):=F({\mathbf {x}}) +\frac{\theta }{2} {\mathbf {x}}^T {\mathbb {L}}{\mathbf {x}}, \end{aligned}$$
(3)

where \(\theta >0\) is the penalty parameter. Clearly, each solution of (3) depends on the value of \( \theta \). Given that the quadratic penalty is not exact, to achieve equivalence we need \( \theta \rightarrow \infty . \) Otherwise, for any fixed value of \( \theta \) one can show that the solution of (3), say \( {\tilde{x}} \in {\mathbb {R}}^{nN}\) has the property that for any \(i=1,..,N\), there holds \( \Vert {\tilde{x}}_i - y^*\Vert = {{{\mathcal {O}}}}(\theta ). \) For further details one can see [38]. The EFIX method proposed in the sequel follows the sequential quadratic programming framework where the sequence of problems (3) with increasing values of the penalty parameters are solved approximately. Therefore, asymptotically we reach an exact solution of (1) as the penalty parameter goes to infinity. The communication matrix W influences the rate of convergence of the method but given that \( {\mathbb {W}} {\mathbf {x}} = {\mathbf {x}} \) is the constraint that ensures \( x_1=x_2 =\ldots =x_N \) for all W that satisfy A1, it does not influence the equivalence of the reformulation, i.e., equivalence of the problems (1) and (2). Regarding the influence of matrix W on the relation between (2) and (3), it can be shown that, for a fixed \(\theta \), the difference between the solutions of (2) and (3) is on the order \({{\mathcal {O}}}(1/(1-\lambda _2))\), where \(\lambda _2\) is the modulus of the second largest in modulus eigenvalue of W. See, e.g., Theorem 4 in [38] or equations (7) and (8) in [7].

3 EFIX-Q: Quadratic problems

Quadratic costs are very important subclass of problems that we consider. One of the typical example is linear least squares problem which comes from linear regression models, data fitting etc. We start the analysis with the quadratic costs given by

$$\begin{aligned} f_i(y)=\frac{1}{2} (y-b_i)^T B_{ii} (y-b_i), \end{aligned}$$
(4)

where \(B_{ii} = B_{ii}^T\in {\mathbb {R}}^{n \times n}, b_i \in {\mathbb {R}}^n\). Let us denote by \({\mathbb {B}}=diag(B_{11},\ldots ,B_{NN})\) the block-diagonal matrix and \({\mathbf {b}}=(b_1;\ldots ;b_N) \in {\mathbb {R}}^{n N}\). Then, the penalty function defined in (3) with the quadratic costs (4) becomes

$$\begin{aligned} \Phi _{\theta }({\mathbf {x}})= \frac{1}{2} ({\mathbf {x}}-{\mathbf {b}})^T {\mathbb {B}}({\mathbf {x}}-{\mathbf {b}})+ \frac{\theta }{2} {\mathbf {x}}^T{\mathbb {L}}{\mathbf {x}}\end{aligned}$$

and

$$\begin{aligned} \nabla \Phi _{\theta }({\mathbf {x}})= ({\mathbb {B}}+\theta {\mathbb {L}}) {\mathbf {x}}-{\mathbb {B}}{\mathbf {b}}. \end{aligned}$$

Thus, solving \(\nabla \Phi _{\theta }({\mathbf {x}})=0\) is equivalent to solving the linear system

$$\begin{aligned} {\mathbb {A}}(\theta ) {\mathbf {x}}={\mathbf {c}}, \quad {\mathbb {A}}(\theta ):={\mathbb {B}}+\theta {\mathbb {L}}, \quad {\mathbf {c}}:={\mathbb {B}}{\mathbf {b}}. \end{aligned}$$
(5)

Clearly, matrix \( {\mathbb {A}}(\theta ) \) depends on parameter theta as well as a number of matrices and vectors derived from \( {\mathbb {A}}\) below. To simplify the notation we will omit \( \theta \) further on if \( \theta \) is a generic parameter and place it whenever \( \theta \) has some specific value. Under the following assumptions, this system can be solved in a distributed, decentralized manner by applying a suitable linear solver. To make the presentation more clear we concentrate here on the JOR method, without loss of generality.

A 2

Each function \(f_i, \; i=1,\ldots , N \) is \(\mu \)-strongly convex.

This assumption implies that the diagonal elements of Hessian matrices \(B_{ii}\) are positive, bounded by \(\mu \) from below. This can be easily verified by the fact that \(y^T B_{ii} y\ge \mu \Vert y\Vert ^2\) for \(y=e_j, j=1,\ldots ,n\) where \(e_j\) is the j-th column of the identity matrix \( I \in {\mathbb {R}}^{n \times n}. \) Clearly, the diagonal elements of \({\mathbb {A}}\) are positive. Moreover, \({\mathbb {A}}\) is positive definite with minimal eigenvalue bounded from below with \(\mu \). Therefore, for arbitrary \( {\mathbf {x}}_0 \in {\mathbb {R}}^{nN} \) and \( {\mathbb {A}}, {\mathbf {c}}\) given in (5), we can define the JOR iterative procedure as

$$\begin{aligned} {\mathbf {x}}^{k+1}= & {} {\mathbb {M}}{\mathbf {x}}^k+{\mathbf {p}}, \end{aligned}$$
(6)
$$\begin{aligned} {\mathbb {M}}= & {} q {\mathbb {D}}^{-1}{\mathbb {G}}+(1-q){\mathbb {I}}, \quad {\mathbf {p}}=q {\mathbb {D}}^{-1} {\mathbf {c}}, \end{aligned}$$
(7)

where \({\mathbb {D}}\) is a diagonal matrix with \(d_{ii}=a_{ii}\) for all \(i=1,\ldots ,nN\), \({\mathbb {G}}={\mathbb {D}}-{\mathbb {A}}\), \({\mathbb {I}}\) is the identity matrix and q is the relaxation parameter. The structure of \( {\mathbb {A}}\) and \( {\mathbb {M}}\) makes the iterative method specified in (6) completely distributed assuming that each node i has the corresponding (block) row of \( {\mathbb {M}},\) and thus we do not need any additional adjustments of the linear solver to the distributed network.

The JOR method (6)-(7) can be stated in the distributed manner as follows. Notice that the blocks of \( {\mathbb {A}}\) are given by

$$\begin{aligned} A_{ii}=B_{ii}+\theta (1-w_{ii})I, \quad \text{ and } \quad A_{ij}=-\theta w_{ij}I \quad \text{ for } i \ne j. \end{aligned}$$
(8)

Therefore, we can represent JOR iterative matrix \({\mathbb {M}}\) in similar manner, i.e., \({\mathbb {M}}=[M_{ij}]\) where

$$\begin{aligned} M_{ii}=q D_{ii}^{-1}G_{ii}+(1-q)I, \quad M_{ij}=q \theta w_{ij} D_{ii}^{-1} \quad \text{ for } \quad i \ne j, \end{aligned}$$
(9)

and \({\mathbf {p}}=(p_1;\ldots ;p_N)\) is calculated as

$$\begin{aligned} p_i=q D_{ii}^{-1}B_{ii} b_i. \end{aligned}$$
(10)

Thus, each node i can update its own vector \(x_i\) by

$$\begin{aligned} x_i^{k+1}=\sum _{j \in {\bar{O}}_i}M_{ij} x^k_j+p_i. \end{aligned}$$
(11)

Notice that (11) requires only the neighbouring \( x_j^k, \) and the corresponding elements of \( M_{ij}, j \in {\bar{O}}_j, \) i.e. the method is fully distributed.

The convergence interval for the relaxation parameter q is well known in this case, see e.g. [8].

Lemma 3.1

Suppose that the assumptions A1-A2 are satisfied. Then the JOR method converges for all \(q \in (0,2/\sigma ({\mathbb {D}}^{-1}{\mathbb {A}}))\), with \( \sigma ({\mathbb {D}}^{-1}{\mathbb {A}}))\) being the spectral radius of \( ({\mathbb {D}}^{-1}{\mathbb {A}})).\)

Lemma 3.1 gives the interval for relaxation parameter q that ensures that the spectral radius of \( {\mathbb {M}}\) is smaller than 1 and hence gives the sufficient and necessary condition for convergence. Estimating the spectral radius of \( {\mathbb {D}}^{-1}{\mathbb {A}}\) is not an easy task in general and several results are derived for specific matrix classes that specify the interval for q such that a sufficient condition for convergence holds, i.e. values of q that give \( \Vert {\mathbb {M}}\Vert _p < \rho \le 1 \) for \( p=1,2,\infty \).

Let us now estimate the interval stated in Lemma 3.1. We have

$$\begin{aligned} \sigma ({\mathbb {D}}^{-1}{\mathbb {A}}) \le \Vert {\mathbb {D}}^{-1}{\mathbb {A}}\Vert \le \Vert {\mathbb {D}}^{-1}\Vert \Vert {\mathbb {A}}\Vert . \end{aligned}$$

Since the diagonal elements of \(B_{ii}\) are positive and \( {\mathbb {D}}\) is the diagonal matrix with elements \( d_{ii} = b_{ii} + \theta \ell _{ii}, i=1,\ldots , nN, \) with \( {\mathbb {L}}=[\ell _{ij}] \in {\mathbb {R}}^{nN \times nN},\) we can upper bound the norm of \( {\mathbb {D}}^{-1} \) as follows

$$\begin{aligned} \Vert {\mathbb {D}}^{-1}\Vert \le \frac{1}{\theta (1-{\bar{w}})}, \end{aligned}$$

where \({\bar{w}}:=\max _i w_{ii}<1\). On the other hand,

$$\begin{aligned} \Vert {\mathbb {A}}\Vert \le \Vert {\mathbb {B}}\Vert +2 \theta \le \max _i l_i+2 \theta :=L+2 \theta , \end{aligned}$$

where \(l_i\) is the largest eigenvalue of \(B_{ii}\). So, the convergence interval for the relaxation parameter can be set as

$$\begin{aligned} q\in \left( 0,\frac{2\theta (1-{\bar{w}})}{L+2 \theta }\right) . \end{aligned}$$
(12)

Alternatively, one can use the infinity norm and obtain a bound as above with \({\bar{B}}:=\max _{i} \Vert B_{ii}\Vert _{\infty }\) instead of L.

The iterative matrix \({\mathbb {M}}\) depends on the penalty parameter and the EFIX algorithm we define further on solves a sequence of penalty problems defined by a sequence of penalty parameters \( \theta _s, s=0,1,\ldots . \) Thus (12) can be updated for each penalty subproblem, defined with a new penalty parameter. However the upper bound in (12) is monotonically increasing with respect to \(\theta \), so one can set \(q \in (0,2 \theta _0 (1-{\bar{w}})/ (L+2 \theta _0))\) without updating with the change of \( \theta . \) In the test presented in Sect. 5 we use \(\theta _0=2 L\), which further implies that the JOR parameter can be fixed to any positive value smaller than \(4(1-{\bar{w}})/5\).

The globally convergent algorithm for problem (1) with quadratic functions (4) is given below. In each subproblem we have to solve a linear system of type (5). The algorithm is designed such that these linear systems are solved within an inner loop defined by (11). The penalty parameters \( \{\theta _{s}\} \) with the property \( \theta _{s} \rightarrow \infty , \; s \rightarrow \infty , \) and the number of inner iterations k(s) of type (11) are assumed to be given. Also, we assume that the relaxation parameters q(s) are defined by a rule that fulfills (12). Thus, for given \( \theta _{s} \) the linear system \( {\mathbb {A}}(\theta _{s}) {\mathbf {x}} = {\mathbf {c}} \) is solved approximately in each outer iteration, with the iterative matrix

$$\begin{aligned} {\mathbb {M}}(\theta _{s}) = q(s) {\mathbb {D}}^{-1} {\mathbb {G}}+ (1-q(s)){\mathbb {I}}. \end{aligned}$$

The global constants L and \( {\bar{w}}\) are needed for updating the relaxation parameter in each iteration but the nodes can settle them through initial communication at the beginning of iterative process. Thus, they are also treated as input parameters for the algorithm. Notice that constants L and \({\overline{w}}\) represent maxima of certain scalar quantities distributed across nodes in the network. Let us consider L, while similar arguments hold for \({\overline{w}}\) as well. Assuming that each node i knows the Lipschitz constant \(l_i\) of \(\nabla f_i\), then each node can obtain L after the nodes perform a distributed algorithm to calculate L that can be taken as \(L=\max _i l_i\). There are several ways to calculate maximum in a fully distributed way inexpensively, e.g., [26]. Such algorithm converges in \({\mathcal {O}} (diam)\) iterations (communication rounds), where diam is the network diameter.

Algorithm EFIX-Q.

Given: \(\{\theta _{s}\}, \) \( x_i^0 \in {\mathbb {R}}^{n}, i=1,\ldots ,N\), \(\{k(s)\} \subset {\mathbb {N}}, L, {\bar{w}}. \) Set \(s=0\).

  1. S1

    Set \( k = 0 \) and choose q according to (12) with \(\theta =\theta _{s}. \) Let \( {\mathbb {M}}= {\mathbb {M}}(\theta _{s}), z_i^0 = x_i^{s}, i=1,\ldots ,N. \)

  2. S2

    For each \(i=1,\ldots , N \) compute the new local solution estimates

    $$\begin{aligned} z_i^{k+1}=\sum _{j \in {\bar{O}}_i} M_{ij} z^{k}_j+p_i \end{aligned}$$

    and set \( k =k+1. \)

  3. S3

    If \(k<k(s)\) go to step S2. Else, set \( {\mathbf {x}}^{s+1} = (z_1^k,\ldots ,z_N^k), \; s=s +1\) and go to step S1.

The above algorithm relies on distributed implementation of the fixed point solver JOR. Thus each node has a set of local information, to be more specific each node i has the corresponding ith block-row of the matrix \({\mathbb {M}} \) and the corresponding vector \( p_i. \) In fact, having in mind the structure of matrix \({\mathbb {M}}\), one can see that each node i, besides the input parameters, only needs to store the following: the Hessian of the local cost function, i.e., \(B_{ii} \in {\mathbb {R}}^{n \times n}\); the vector \(b_{i} \in {\mathbb {R}}^{n}\); and the weights \((w_{i1},w_{i2},\ldots ,w_{iN}) \in {\mathbb {R}}^N\), i.e., the ith row of the matrix W. For instance, notice that the block \(M_{ij}\) of the matrix \({\mathbb {M}}\) can be derived from the stored data since it varies through j directly with \(w_{ij}\) and \(D_{ii}\) is the diagonal matrix with the diagonal which coincides with the diagonal of \(A_{ii}=B_{ii}+\theta (1-w_{ii})I\). Additionally, node i can also store the vectors \(p_i, diag(D^{-1}_{ii}) \in {\mathbb {R}}^n\) and the matrix \(M_{ii}\in {\mathbb {R}}^{n \times n}\) in order to avoid unnecessary calculations within inner iterations. Each node computes \( z_{i}^{k+1}\) in Step 2, using \( z_{j}^{k} , j \in {\bar{O}}_i\) from its neighbors and computing \( M_{ij} z_{j}^k \) and after that transmits the new approximation \( z_{i}^{k+1}\) to the neighbors. Thus, at each iteration, each node i sends to its immediate neighbors in graph G vector \( z_{i}^{k+1} \in {\mathbb {R}}^n\) and receives the corresponding estimates of the neighboring nodes \( z_{j}^{k+1}\in {\mathbb {R}}^n, j \in O_i\).

Our analysis relies on the quadratic penalty method, so we state the framework algorithm (see [19] for example). We assume again that the sequence of penalty parameters \( \{\theta _s\} \) has the property \( \theta _s \rightarrow \infty \) and that the tolerance sequence \(\{\varepsilon _s\}\) is such that \(\varepsilon _s \rightarrow 0\).

Algorithm QP.

Given: \(\{\theta _{s}\}, \; \{\varepsilon _s\}.\) Set \( s=0. \)

  1. S1

    Find \({\mathbf {x}}^s\) such that

    $$\begin{aligned} \Vert \nabla \Phi _{\theta _{s}}({\mathbf {x}}^s)\Vert \le \varepsilon _s. \end{aligned}$$
    (13)
  2. S2

    Set \(s=s+1\) and return to S1.

Let us demonstrate that the EFIX-Q fits into the framework of Algorithm QP, that is given a sequence \(\{\varepsilon _s\}\) such that \(\varepsilon _s \rightarrow 0, \) there exists a proper choice of the sequence \( \{k(s)\} \) such that (13) is satisfied for all penalty subproblems.

Lemma 3.2

Suppose that the assumptions A1-A2 are satisfied. If \( \Vert \nabla \Phi _{\theta _{s}}({\mathbf {x}}^s)\Vert \le \varepsilon _s \) then \(\Vert \nabla \Phi _{\theta _{s+1}}({\mathbf {x}}^{s+1})\Vert \le \varepsilon _{s+1}\) for

$$\begin{aligned} k(s)=\Bigg \lceil \Big |\frac{ \log (\mu \varepsilon _{s+1})-\log (L+2 \theta _{s+1})(\varepsilon _s+2{\bar{c}})}{\log (\rho _{s+1})} \Big |\Bigg \rceil , \end{aligned}$$
(14)

where \( \rho _{s+1} \) is a constant such that \(\Vert {\mathbb {M}}(\theta _{s+1})\Vert \le \rho _{s+1}<1\) and \({\bar{c}}=\Vert {\mathbf {c}}\Vert \).

The previous lemma shows that EFIX-Q fits into the framework of quadratic penalty methods presented above if we assume \(\varepsilon _s \rightarrow 0\) and set k(s) as in (14), with \( \{{\mathbf {x}}^s\} \) being the outer iterative sequence of Algorithm EFIX-Q. Notice that the inner iterations (that rely on the JOR method) stated in steps S2-S3 of EFIX-Q can be replaced with any solver of linear systems or any optimizer of quadratic objective function which can be implemented in decentralized manner and exhibits linear convergence with factor \(\rho _s\). Moreover, it is enough to apply a solver with R-linear convergence, i.e., any solver that satisfies

$$\begin{aligned} \Vert {\mathbf {z}}^{k}-{\mathbf {x}}^*_{\theta _{s+1}}\Vert \le C_{s+1} \Vert {\mathbf {x}}^{s}-{\mathbf {x}}^*_{\theta _{s+1}}\Vert \rho ^{k}_{s+1}, \end{aligned}$$

where \(C_{s+1}\) is a positive constant. In this case, the slightly modified k(s) with \((L+2 \theta _{s+1})\) multiplied with \(C_{s+1}\) in (14) fits the proposed framework.

Although the LICQ does not hold for (2), following the steps of the standard proof and modifying it to cope with LICQ violation, we obtain the global convergence result presented below.

Theorem 3.1

Suppose that the assumptions A1-A2 are satisfied. Assume that \(\varepsilon _s \rightarrow 0\) and k(s) is defined by (14). Let \(\{{\mathbf {x}}^{s}\} \) be a sequence generated by algorithm EFIX-Q. Then, either the sequence \(\{{\mathbf {x}}^{s}\} \) is unbounded or it converges to a solution \({\mathbf {x}}^*\) of the problem (2) and \(x_i^*\) is the solution of problem (1) for every \(i=1,\ldots ,N\).

The previous theorem states that the only requirement on \(\{\varepsilon _s\}\) is that it is a positive sequence that tends to zero. On the other hand, quadratic penalty function is not exact penalty function and the solution \({\mathbf {x}}^*_{\theta }\) of the penalty problem (3) is only an approximation of the solution \(y^*\) of problem (1). Moreover, it is known (see Corollary 9 in [38]) that for every \(i=1,\ldots ,N,\) there holds

$$\begin{aligned} e^1_{i, \theta }:=\Vert x^*_{i,\theta }-y^*\Vert ={\mathcal {O}}(\theta ^{-1}). \end{aligned}$$

More precisely, denoting by \(\lambda _2\) the second largest eigenvalue of W in modulus, we have

$$\begin{aligned} e^1_{i, \theta _{s}}\le \frac{L J}{\theta _{s}\kappa (1-\lambda _2)}\sqrt{4-2 \kappa \theta _{s}^{-1}}+\frac{J}{\theta _{s} (1-\lambda _2)}, \end{aligned}$$
(15)

where \(\kappa =\mu L/(\mu +L)\) and \(J=\sqrt{2 L f(0)}\) since the optimal value of each local cost function is zero. Thus, looking at an arbitrary node i and any outer iteration s we have

$$\begin{aligned} \Vert x_i^s-y^*\Vert \le \Vert x_i^s- x^*_{i,\theta _{s}}\Vert + \Vert x^*_{i,\theta _{s}}-y^*\Vert :=e^2_{i, \theta _{s}}+e^1_{i, \theta _{s}}. \end{aligned}$$
(16)

So, there is no need to solve the penalty subproblem with more accuracy than \( e^1_{i, \theta }\) - the accuracy of approximating the original problem. Therefore, using (27) and (15) and balancing these two error bounds we conclude that a suitable value for \(\varepsilon _s,\) see (27), can be estimated as

$$\begin{aligned} \varepsilon _s=\mu \Bigg (\frac{L J}{\theta _{s}\kappa (1-\lambda _2)}\sqrt{4-2 \kappa \theta _{s}^{-1}}+\frac{J}{\theta _{s} (1-\lambda _2)}\Bigg ) \end{aligned}$$
(17)

Similar idea of error balance is used in [39], to decide when to decrease the step size.

Assume that we define \(\varepsilon _s\) as in (17) Together with (27) we get

$$\begin{aligned} \Vert x_i^s- x^*_{i,\theta _{s}}\Vert ={{{\mathcal {O}}}}\left( \frac{1}{\theta _{s}}\right) . \end{aligned}$$

Furthermore, using (15) and (16) we obtain

$$\begin{aligned} \Vert x_i^s-y^*\Vert ={{{\mathcal {O}}}}\left( \frac{1}{\theta _{s}}\right) . \end{aligned}$$

Therefore, the following result concerning the outer iterations holds.

Proposition 3.1

Suppose that the assumptions of Theorem 3.1 hold and that \(\varepsilon _s\) is defined by (17). Let \(\{{\mathbf {x}}^{s}\} \) be a bounded sequence generated by EFIX-Q . Then for every \(i=1,\ldots ,N\) there holds

$$\begin{aligned} \Vert x_i^s-y^*\Vert ={{{\mathcal {O}}}}\left( \frac{1}{\theta _{s}}\right) . \end{aligned}$$

The complexity result stated below for the special choice of penalty parameters, \( \theta _s = s \) can be easily derived using the above Proposition.

Corollary 3.1

Suppose that the assumptions of Proposition 3.1 hold and \(\theta _{s}=s\) for \(s = 1,2,\ldots \).

Then after at most

$$\begin{aligned} {\bar{s}}=\left\lceil \frac{2J(3+2L/\mu )}{(1-\lambda _2)}\epsilon ^{-1}\right\rceil \end{aligned}$$

iterations we have \(\Vert x_i^{{\bar{s}}}-y^*\Vert \le \epsilon \) for all \(i=1,\ldots ,N\) and any \(\epsilon >0\), where J and \(\lambda _2\) are as in (15).

Notice that the number of outer iterations \({\bar{s}}\) to obtain the \(\epsilon \)-optimal point depends directly on J, i.e., on f(0) and the Lipschitz constant L. Moreover, it also depends on the network parameters - recall that \(\lambda _2\) represents the second largest eigenvalue of the matrix W, so the complexity constant can be diminished if we can chose the matrix W such that \(\lambda _2\) is as small as possible for the given network.

4 EFIX-G: Strongly convex problems

In this section, we consider strongly convex local cost functions \(f_i\) that are not necessarily quadratic. The main motivation comes from machine learning problems such as logistic regression where the Hessian is easy to calculate and, under regularization, satisfies Assumption A2. The main idea now is to approximate the objective function with a quadratic model at each outer iteration s and exploit the previous analysis. Instead of solving (13), we form a quadratic approximation \(Q_{s}({\mathbf {x}})\) of the penalty function \(\Phi _{\theta _{s}}({\mathbf {x}})\) defined in (3) as

$$\begin{aligned} Q_{s}({\mathbf {x}}):= & {} F({\mathbf {x}}^{s-1})+\nabla ^T F({\mathbf {x}}^{s-1})({\mathbf {x}}-{\mathbf {x}}^{s-1})+\nonumber \\&+ \frac{1}{2} ({\mathbf {x}}-{\mathbf {x}}^{s-1})^T \nabla ^2 F({\mathbf {x}}^{s-1})({\mathbf {x}}-{\mathbf {x}}^{s-1})+\frac{\theta _{s}}{2} {\mathbf {x}}^T {\mathbb {L}}{\mathbf {x}}\end{aligned}$$
(18)

and search for \({\mathbf {x}}^s\) that satisfies

$$\begin{aligned} \Vert \nabla Q_{s} ({\mathbf {x}}^s)\Vert \le \varepsilon _s. \end{aligned}$$
(19)

In other words, we are solving the system of linear equations

$$\begin{aligned} {\mathbb {A}}_s {\mathbf {x}}={\mathbf {c}}_s, \end{aligned}$$

where

$$\begin{aligned} {\mathbb {A}}_s:= & {} \nabla ^2 F({\mathbf {x}}^{s-1})+\theta _{s}{\mathbb {L}}, \\ {\mathbf {c}}_s:= & {} \nabla ^2 F({\mathbf {x}}^{s-1}) {\mathbf {x}}^{s-1}-\nabla F({\mathbf {x}}^{s-1}) . \end{aligned}$$

Under the stated assumptions, \({\mathbb {A}}_s\) is positive definite with eigenvalues bounded with \(\mu \) from below and the diagonal elements of \({\mathbb {A}}_s\) are strictly positive. Therefore, using the same notation and formulas as in the previous section with \(\nabla ^2 f_i(x_i^{s-1})\) instead of \(B_{ii}\) in (8) we obtain the same bound for the JOR parameter, (12).

Before stating the algorithm, we repeat the formulas for completeness. The matrix \({\mathbb {A}}_s=[A_{ij}]\) has blocks \(A_{ij} \in {\mathbb {R}}^{n \times n}\) given by

$$\begin{aligned} A_{ii}=\nabla ^2 f_i(x_i^{s-1})+\theta _s (1-w_{ii})I, \quad \text{ and } \quad A_{ij}=-\theta _{s} w_{ij}I \quad \text{ for } i \ne j. \end{aligned}$$
(20)

The JOR iterative matrix is \({\mathbb {M}}_s=[M_{ij}]\) where

$$\begin{aligned} M_{ii}=q_s D_{ii}^{-1}G_{ii}+(1-q)I, \quad M_{ij}=q_s \theta _{s} w_{ij} D_{ii}^{-1} \quad \text{ for } \quad i \ne j, \end{aligned}$$
(21)

and the vector \({\mathbf {p}}_s=(p_1;\ldots ;p_N)\) is calculated as \({\mathbf {p}}_s=q {\mathbb {D}}_s^{-1} {\mathbf {c}}_s\), where \({\mathbb {D}}_s\) is a diagonal matrix with \(d_{ii}=a_{ii}\) for all \(i=1,\ldots ,nN\) and \({\mathbb {G}}_s={\mathbb {D}}_s-{\mathbb {A}}_s\), i.e.,

$$\begin{aligned} p_i=q D_{ii}^{-1}c_i, \quad \text{ where } \quad c_i=\nabla ^2 f_i(x_i^{s-1})x_i^{s-1}-\nabla f_i(x_i^{s-1}). \end{aligned}$$
(22)

The algorithm presented below is a generalization of EFIX-Q and we assume the same initial setup: the global constants L and \( {\bar{w}} \) are known, the sequence of penalty parameters \( \{\theta _s\} \) and the sequence of inner iterations counters \( \{k(s)\} \) are input parameters for the algorithm.

Algorithm EFIX-G.

Input: \(\{\theta _{s}\}, \) \( x_i^0 \in {\mathbb {R}}^{n}, i=1,\ldots ,N\), \(\{k(s)\} \subset {\mathbb {N}}, L, {\bar{w}}. \) Set \(s=0\).

  1. S1

    Each node i sets q according to (12) with \(\theta =\theta _{s}. \)

  2. S2

    Each node calculates \(\nabla f_i(x_i^{s})\) and \(\nabla ^2 f_i(x_i^{s})\). Define \( {\mathbb {M}}= {\mathbb {M}}_s \) given by (21), \( z_i^0 = x_i^{s}, i=1,\ldots ,N \) and set \(k=0\).

  3. S3

    For \( i =1,\ldots , N \) update the solution estimates

    $$\begin{aligned} z_i^{k+1}=\sum _{j \in {\bar{O}}_i} M_{ij} z^{k}_j+p_i \end{aligned}$$

    and set \( k =k+1. \)

  4. S4

    If \(k<k(s)\) go to step S3. Else, set \( {\mathbf {x}}^{s+1} = (z_1^k;\ldots ;z_N^k), \; s=s +1\) and go to step S1.

The algorithm differs from the quadratic case EFIX-Q in step S2, where the gradients and the Hessians are calculated in a new point at every outer iteration. Each node i, besides the input parameters, stores the weights \((w_{i1},w_{i2},\ldots ,w_{iN}) \in {\mathbb {R}}^N\). Moreover, it calculates the Hessian of the local cost function \(\nabla ^2 f_i(x_i^{s}) \in {\mathbb {R}}^{n \times n}\) and the corresponding gradient \(\nabla f_i(x_i^{s}) \in {\mathbb {R}}^{n}\) at each outer iteration and stores them through the inner iterations. Similarly to the EFIX-Q case, node i can also store the vectors \(p_i, diag(D^{-1}_{ii}) \in {\mathbb {R}}^n\) and the matrix \(M_{ii}\in {\mathbb {R}}^{n \times n}\) calculated at each outer iteration in order to avoid unnecessary calculations within the corresponding inner iterations. At each iteration, each node exchanges the current estimates of the solution (vectors \(z_j^{k}\)) with its immediate neighbors as explained in EFIX-Q case.

Following the same ideas as in the proof of Lemma 3.2, we obtain the similar result under the following additional assumption.

A 3

For each \(y \in {\mathbb {R}}^n\) there holds \(\Vert \nabla ^2 f_i(y)\Vert \le l_i\), \(i=1,\ldots ,N\).

Notice that this assumption implies that \(\Vert \nabla ^2 F({\mathbf {x}})\Vert \le L:=\max _{i} l_i\).

Lemma 4.1

Suppose that Assumptions A1-A3 hold. If \( \Vert \nabla Q_{s} ({\mathbf {x}}^s)\Vert \le \varepsilon _s\) holds then \(\Vert \nabla Q_{s+1}({\mathbf {x}}^{s+1})\Vert \le \varepsilon _{s+1}\) for

$$\begin{aligned} k(s)=\Bigg \lceil \Big |\frac{ \log (\mu \varepsilon _{s+1})-\log (L+2 \theta _{s+1})(\varepsilon _s+{\bar{c}}_s+{\bar{c}}_{s+1})}{\log (\rho _{s+1})} \Big |\Bigg \rceil , \end{aligned}$$
(23)

where \( \rho _{s+1} \) is a constant such that \(\Vert {\mathbb {M}}_{s+1}\Vert \le \rho _{s+1}<1\) and \({\bar{c}}_s=\Vert {\mathbf {c}}_s\Vert \).

The Lemma above implies that EFIX-G is a penalty method with the penalty function Q instead of \(\Phi , \) i.e., with (19) instead of (13). Notice that due to assumption A2, without loss of generality we can assume that the functions \(f_i\) are nonnegative and thus the relation between \(\varepsilon _s\) and \(\theta _{s}\) can remain as in (17). We have the following convergence result which corresponds to the classical statement in centralized optimization, [19].

Theorem 4.1

Let the assumptions A1-A3 hold. Assume that \( \{{\mathbf {x}}^s\} \) is a sequence generated by Algorithm EFIX-G such that k(s) is defined by (23) and \(\varepsilon _s \rightarrow 0. \) If \( \{{\mathbf {x}}^s\} \) is bounded then every accumulation point of \( \{{\mathbf {x}}^s\} \) is feasible for the problem (2). Furthermore, if \( \lim _{s \rightarrow \infty } {\mathbf {x}}^s = {\mathbf {x}}^* \) then \( {\mathbf {x}}^* \) is the solution of problem (2), i.e., \(x_i^*\) is the solution of problem (1) for every \(i=1,\ldots ,N\).

5 Numerical results

5.1 Quadratic case

We test EFIX-Q method on a set of quadratic functions (4) defined as in [12]. Vectors \(b_i\) are drawn from the Uniform distribution on [1, 31], independently from each other. Matrices \(B_{ii}\) are of the form \(B_{ii}=P_i S_i P_i\), where \(S_i\) are diagonal matrices with Uniform distribution on [1, 101] and \(P_i\) are matrices of orthonormal eigenvectors of \(\frac{1}{2} (C_i+C_i^T)\) where \(C_i\) have components drawn independently from the standard Normal distribution.

The network is formed as follows, [12]. We sample N points randomly and uniformly from \([0,1] \times [0,1]\). Two points are directly connected if their distance, measured by the Euclidean norm, is smaller than \(r=\sqrt{\log (N)/N}\). The graph is connected. Moreover, if nodes i and j are directly connected, we set \(w_{i,j}=1/\max \{deg(i),deg(j)\}\), where deg(i) stands for the degree of node i and \( w_{i,i}=1-\sum _{j\ne i}w_{i,j}\). We test on graphs with \(N=30\) and \(N=100\) nodes.

The error metrics is the following

$$\begin{aligned} e(x^k):=\frac{1}{N} \sum _{i=1}^{N}\frac{\Vert x_i^k-y^*\Vert }{\Vert y^*\Vert }, \end{aligned}$$
(24)

where \(y^*\ne 0\) is the exact (unique) solution of problem (1).

The parameters are set as follows. The Lipschitz constant is calculated as \(L=\max _{i} l_i\), where \(l_i\) is the largest eigenvalue of \(B_{ii}\). The strong convexity constant is calculated as \(\mu =\min _{i} \mu _i\), where \(\mu _i>0\) is the smallest eigenvalue of \(B_{ii}\).

The proposed method is denoted by EFIX-Q k(s) balance to indicate that we use the number of inner iterations given by (14) where \( L, \mu , {\bar{c}}\) are calculated at the initial phase of the algorithm and imposing (17) to balance two types of errors as discussed in Sect. 3. The initial value of the penalty parameter is set to \(\theta _0=2L\). The choice is motivated by the fact that the usual step size bound in many gradient-related methods is \(\alpha <1/(2L)\) and \(1/\alpha \) corresponds to the penalty parameter. Hence, we set \(\theta \ge 2L\). Further, the penalty parameter is updated by \(\theta _{s+1}=(s+1) \theta _{s}\). The inner solver used at Step 3 of EFIX-Q method is the Jacobi method, i.e., JOR method with \( q=1. \) In the quadratic case, the Jacobi method converged and the bounds derived in (12) were not needed. The Jacobi method (JOR method in general) is used to solve the sequence of quadratic problems up to accuracy determined \(\{ \varepsilon _s \}. \) Clearly, the precision, measured by \( \varepsilon _s \) determines the computational costs. On the other hand it is already discussed that the error in solving a particular quadratic problem should not be decreased too much given that the quadratic penalty is not an exact method and hence each quadratic subproblem is only an approximation of the original constrained problem, depending on the penalty parameter \( \theta _s \). Therefore, we tested several choices of the inner iteration counter and parameter update, to investigate the error balance and its influence on the convergence. The method abbreviated as EFIX-Q k(s) is obtained with \(\varepsilon _0=\theta _0= 2L \), \(\varepsilon _s=\varepsilon _0/s\) for \(s>0\), and k(s) defined by (14). Furthermore, to demonstrate the effectiveness of k(s) stated in (14) we also report the results from the experiments where the inner iterations are terminated only if (13) holds, i.e. without a predefined sequence k(s). We refer to this method as EFIX-Q stopping. Notice that the exit criterion of EFIX-Q is not computable in the distributed framework and the test reports here are performed only to demonstrate the effectiveness of (14).

The proposed method is compared with the state-of-the-art method [17, 21] abbreviated as DIGing 1/(mL), where 1/(mL) represents the step size, i.e., \(\alpha =1/(mL)\) for different values of \(m \in \{2,3,10,20,50,100\}\). This method is defined as follows

$$\begin{aligned} x_i^{k+1}=\sum _{j=1}^{N} w_{ij} x_j^k-\alpha u_i^k, \; u_i^{k+1}=\sum _{j=1}^{N} w_{ij} u_j^k+ B_{ii} (x_i^{k+1}-x_i^{k}), u_i^0=\nabla f_i(x_i^0). \end{aligned}$$

We model the total computational cost by counting the total number of n-dimensional SPs (scalar products of two n-dimensional real vectors) per node evaluated during the algorithm run, i.e., we let the unit computational cost be a single n-dimensional SP evaluation. Here, we model a single N-dimensional scalar product computational cost as \(\xi :=N/n\) unit costs. Thus, the computational cost of DIGing method per node, per iteration, can be estimated to \(n+2n \xi \) since \(\sum _{j} w_{ij} x_j^k\) takes \(n \xi \) unit computational costs (n N-dimensional SPs) as well as \(\sum _{j} w_{ij} u_j^k\), and \(B_{ii} (x_i^{k+1}-x_i^{k})\) takes n unit computational costs (n n-dimensional SPs). In the sequel, we refer to unit computational costs as SPs.

In order to compare the costs, we unfold the proposed EFIX-Q method considering all inner iterations consecutively (so k below is the cumulative counter for all inner iterations) as follows

$$\begin{aligned} x_i^{k+1}=q D_{ii}^{-1} G_{ii} x_i^k+(1-q)x_i^k+q \theta D_{ii}^{-1} \sum _{i \ne j} w_{ij} x_j^k+q D_{ii}^{-1} B_{ii} b_i. \end{aligned}$$

Since \(D_{ii}\) is a diagonal matrix, \(q D_{ii}^{-1} G_{ii} x_i^k\) takes \(n+1\) SPs and \(D_{ii}^{-1} \sum _{i \ne j} w_{ij} x_j^k\) takes \(1+n \xi \) SPs. Moreover, \(B_{ii} b_i\) is calculated only once, at the initial phase, so \(D_{ii}^{-1} B_{ii} b_i\) costs only 1 SPs (unit costs). Thus, the cost of EFIX-Q method can be estimated to \(n+3+n \xi \) SPs per node, per iteration. The difference between EFIX-Q and DIGing can be significant especially for larger value of N, given the relative difference between quantities 3 and \( n \xi =N. \) Moreover, DIGing method requires at each iteration the exchange of two vectors, \(x_j\) and \(u_j\) among all neighbors, while EFIX requires only the exchange of \(x_j\), so it is 50\(\%\) cheaper than the DIGing method in terms of communication costs per iteration.

We set \({\mathbf {x}}^0=0\) for all the tested methods and consider \(n=10\) and \(n=100\). Figure 1 presents the errors \(e({\mathbf {x}}^k)\) throughout iterations k for \( N = 30 \) and \( N = 100. \) The results for different values of n appear to be very similar and hence we report only the case \( n = 100. \)

Fig. 1
figure 1

The EFIX methods (dotted lines) versus the DIGing method, error (24) propagation through iterations for \( n=100\), \(N=30\) (left) and \( n=100\), \(N=100\) (right)

Full size image

Comparing the number of iterations of all considered methods, from Fig. 1 one can see that EFIX-Q methods are highly competitive with the best DIGing method in the case of \(N=30\). Furthermore, EFIX-Q outperforms all the convergent DIGing methods in the case of \(N=100\). Moreover, we can see that EFIX-Q k(s) balance behaves similarly to EFIX-Q stopping, so the number of inner iterations k(s) given in Lemma 3.2 is well estimated. Also, EFIX-Q k(s) balance improves the performance of EFIX-Q k(s) and the balancing of errors yields a more efficient method.

We compare the tested methods in terms of computational costs, measured by scalar products and communication costs as well. The results are presented in Fig. 2 where we compare EFIX-Q k(s) balance with the best convergent DIGing method in the cases \(n=10, N=30\) (top) and \(n=100, N=100\) (bottom). The results show clear advantages of EFIX-Q, especially in the case of larger n and N.

Fig. 2
figure 2

The proposed method (dotted line) versus the DIGing method, error (24) and the computational cost (left) and communications (right) for \(n=10\), \(N=30\) (top) and \(n=100\), \(N=100\) (bottom)

Full size image

5.2 Strongly convex problems

EFIX-G method is tested on the binary classification problems for data sets: Mushrooms [32] (\(n=112\), total sample size \(T=8124\)), CINA0 [5] (\(n=132\), total sample size \(T=16033\)) and Small MNIST [20] (\(n=100\), total sample size \(T=7603\)). For each of the problems, the data is divided across 30 nodes of the graph described in Sect. 5.1 The logistic regression with the quadratic regularization is used and thus the local objective functions are of the form

$$\begin{aligned} f_i(y)=\sum _{j \in J_i} \log (1+e^{-\zeta _j d_j^T y})+\frac{\mu }{2}\Vert y\Vert ^2:=\sum _{j \in J_i} {\tilde{f}}_j(y), \end{aligned}$$

where \(J_i\) collects the indices of the data points assigned to node i, \(d_j \in {\mathbb {R}}^n \) is the corresponding vector of attributes and \(\zeta _j \in \{-1,1\}\) represents the label. The gradient and the Hessian of \({\tilde{f}}_j(y)\) are given by

$$\begin{aligned} \nabla {\tilde{f}}_j(y)= & {} \frac{1-\psi _j(y)}{\psi _j(y)}\zeta _j d_j+\mu y, \; \nabla ^2 {\tilde{f}}_j(y)=\frac{\psi _j(y)-1}{\psi ^2_j(y)}d_j d^T_j+\mu I, \\ \psi _j(y):= & {} 1+e^{-\zeta _j d_j^T y}. \end{aligned}$$

Thus, evaluating the gradient of \({\tilde{f}}_i(y)\) costs 1 SPs. Also, we estimate the cost of calculating the Hessian of \({\tilde{f}}_i(y)\) with n/2 SPs. Moreover, \((\psi _j(y)-1)/\psi ^2_j(y) \in (0,1)\) and thus all the local cost functions are \(\mu \)-strongly convex. The data is scaled in a such way that the Lipschitz constants \(l_i\) are 1 and thus \(L=1+\mu \). We set \(\mu =10^{-4}\).

We test EFIX-G k(s) balance, the counterpart of the quadratic version EFIX-Q k(s) balance, with k(s) defined by (23). The JOR parameter \(q_s\) is set according to (12), more precisely, we set \(q=2 \theta _{s} (1-{\bar{w}})/(L+2 \theta _{s})\). We report here that, unlike the quadratic case, Jacobi method did not converge and we had to use the estimate (12). A rough estimation of \({\bar{c}}_s\) is s \(3L\sqrt{N}\) since

$$\begin{aligned} \Vert {\mathbf {c}}_s\Vert \le \Vert \nabla ^2 F({\mathbf {x}}^{s-1})\Vert \Vert {\mathbf {x}}^{s-1}\Vert +\Vert \nabla F({\mathbf {x}}^{s-1})-\nabla F({\tilde{{\mathbf {x}}}})\Vert \le L 3 \max \{ \Vert {\mathbf {x}}^{s-1}\Vert , \Vert {\tilde{{\mathbf {x}}}}\Vert \}, \end{aligned}$$

where \({\tilde{{\mathbf {x}}}}\) is a stationary point of the function F. The remaining parameters are set as in the quadratic case.

Since the solution is unknown in general, the different error metric is used - the average value of the original objective function f across the nodes’ estimates

$$\begin{aligned} v({\mathbf {x}}^k)=\frac{1}{N} \sum _{i=1}^{N} f(x_i^k)=\frac{1}{N} \sum _{i=1}^{N} \sum _{j=1}^{N} f_j(x_i^k). \end{aligned}$$
(25)

We compare the proposed method with DIGing which takes the following form for general, non-quadratic problems

$$\begin{aligned} x_i^{k+1}=\sum _{j=1}^{N} w_{ij} x_j^k-\alpha u_i^k, \; u_i^{k+1}=\sum _{j=1}^{N} w_{ij} u_j^k+ \nabla f_i (x_i^{k+1})-\nabla f_i(x_i^{k}), u_i^0=\nabla f_i(x_i^0). \end{aligned}$$

For each of the data sets we compare the methods with respect to iterations, communications and computational costs (scalar products). The communications of the DIGing method are twice more expensive than for the proposed method, as in the quadratic case. Denote \({{\tilde{\xi }}}=|J_i|/n\). The computational cost of the DIGing method is estimated to \(2 n \xi +n {\tilde{\xi }}+|J_i|\) SPs per iteration, per node: weighted sum of \(x_j^k\) (\(n \xi \) SPs); weighted sum of \(u_j^k\) (\(n \xi \) SPs); evaluating \(\nabla f_i(x_i^{k})\) (\(n{\tilde{\xi }}+|J_i|\) SPs) because evaluating of each gradient \(\nabla {\tilde{f}}_j(x_i^k), j \in J_i\) costs 1 SP (for \(d_j^Tx_i^k\) needed for calculating \(\psi _j(x_i^{k})\)) and evaluating the gradient \(\nabla f_i(x_i^{k})\) takes the weighted sum of \(d_j\) vectors

$$\begin{aligned} \nabla f_i(x_i^{k})=\sum _{j \in J_i} \frac{1-\psi _j(x_i^{k})}{\psi _j(x_i^{k})}\zeta _j d_j+\mu x_i^{k}, \end{aligned}$$

which costs \(n {\tilde{\xi }}\) SPs (n \(|J_i|\)-dimensional scalar products). On the other hand, the cost of EFIX-G k(s) balance per node remains \(n \xi +n+3\) scalar products at each inner iteration while in the outer iterations (s) we have additional \(|J_i|+2n {{\tilde{\xi }}}+{\tilde{\xi }} n^2/2\) scalar products for evaluating Hessian (\({\tilde{\xi }} n^2/2\)) and \(c_i\) given by

$$\begin{aligned} c_i=\sum _{j \in J_i} \frac{\psi _j(x_i^{s-1})-1}{\psi ^2_j(x_i^{s-1})}d_j d^T_j x_i^{s-1} + \mu x_i^{s-1} -\nabla f_i(x_i^{s-1}), \end{aligned}$$

i.e., in order to evaluate \(c_i\) we have \(|J_i|\) scalar products of the form \(d^T_j x_i^{s-1}\), a weighted sum od \(d_j\) vectors which costs \(n{\tilde{\xi }}\) SPs and the gradient \(\nabla f_i(x_i^{s-1})\) which costs only \(n{\tilde{\xi }}\) SPs since the scalar products \(d^T_j x_i^{s-1}\) are already evaluated and calculated in the first sum.

The results are presented in Fig. 3, (y-axes is in the log scale). The first column contains graphs for EFIX - G k(s) balance and all DIGing methods with error metrics through iterations. Obviously, the EFIX -G method is either comparable or better in comparison with DIGing methods in all tested problems, except for Small MNIST dataset . To emphasize the difference in computational costs we plot in column two the graphs of error metrics with respect to SPs for EFIX -G and the two best DIGing method. The same is done in column three of the graph for the communication costs.

Fig. 3
figure 3

The proposed method (dotted line) versus the DIGing method on Mushrooms (top), CINA0 (middle) and Small MNIST data set (bottom)

Full size image

5.3 Additional comparisons

We provide additional comparisons with the very recent algorithm termed OPTRA in [36], as a further representative of state of the art. The authors of [36] show that, up to universal constants and in the smooth convex (non strongly convex) setting, OPTRA matches theoretical lower complexity bounds in terms of communication and computation, with respect to oracles as defined in [36]. Also, the numerical examples in [36] show that OPTRA is competitive with several state of the art alternatives. Therefore, we compare EFIX also with OPTRA. We perform tests on well connected communication matrix W defined at the beginning of Sect. 5.1 and on ring structure represented by \(W_{ring} \) communication matrix to examine the behavior on the network which is not well connected. In this case, we set diagonal elements of \( W_{ring} \) to 0.5 and the relevant (nonzero) off-diagonal elements are 0.25.

All the parameters for EFIX methods are the same as in the previous two subsections and we consider the same set test problems. We test OPTRA algorithm with number of inner consensus iterations set to \(K=2\) and the parameter which influences the step size set to \(\nu =100\). The choice was motivated by the the numerical results presented in [36]. The total number of (outer) iterations along which the algorithms will be run is set to \(T=200\). This is also the number of EFIX overall (total number of inner) iterations. Notice that this is relevant for OPTRA as certain OPTRA’s parameters explicitly depend on T. On the other hand, for EFIX, no parameter depends on T.

The metrics and the cost measures are retained as in the previous subsections. Using the same logic, we conclude that the communication cost of each OPTRA iteration is 2K (i.e., 2K times more costly that EFIX iteration). This comes from the fact that each OPTRA iteration calls the inner procedure named AccGossip two times and each AccGossip performs K consensus steps. For the quadratic case, the computational cost (in SPs) is \(2Kn \xi +n\) per node per iteration - the cost of calculating the gradient is n SPs per node and the of each consensus step is \(n \xi \) SPs. For the logistic regression case, the cost of calculating the gradient is \(n {\tilde{\xi }}+|J_i|\) SPs and we obtain the total cost of \((2K\xi +1)n+|J_i|+n {\tilde{\xi }}\) SPs per node, per iteration.

Fig. 4
figure 4

The proposed method (dotted line) versus the OPTRA methods on strongly convex quadratic functions (\(n=100, N=30\)) on well connected graph represented by W (left) and ring graph represented by \(W_{ring}\) (right)

Full size image
Fig. 5
figure 5

The proposed method (dotted line) versus the OPTRA methods on Mushrooms (top), CINA0 (middle) and Small MNIST data set (bottom) on well connected graph with 30 nodes

Full size image
Fig. 6
figure 6

The proposed method (dotted line) versus the OPTRA methods on Mushrooms (top), CINA0 (middle) and Small MNIST data set (bottom) on ring graph with 30 nodes

Full size image

The results are presented at Figs. 4, 5 and 6. Figure 4 represents the results obtained on quadratic costs for the two types of communication graphs and \( n=100, N=30 \). Figures 5 and 6 correspond to logistic regression problem with datasets Small MNIST, Mushrooms and CINA0. Figure 5 represents the results on well connected graph, while Fig. 6 deals with the ring graph.

Notice that, for the considered iteration horizon T, OPTRA achieves a very precise final accuracy for certain experiments, like for datasets Small MNIST and Mushrooms in Figs. 5 and 6 (top and bottom rows). On the other hand, OPTRA seems to saturate at a plateau or progresses very slowly on other experiments, like for the quadratic case in Fig. 4. This behavior is not in contradiction with the theory of OPTRA in [36], where the authors are concerned with providing the number of iterations needed to reach a prescribed finite accuracy, and are not concerned with asymptotic convergence as k tends to infinity. (See Theorem 7 in [36]). Both methods exhibit initial oscillatory behavior on CINA0 dataset in Figs. 5 and 6 (middle), but it seems that EFIX stabilizes sooner, while OPTRA continues to oscillate. So, for CINA0 dataset, EFIX method outperforms OPTRA. On the other hand, after the initial advantage of EFIX in terms of communication costs and iterations, OPTRA takes the lead and outperforms EFIX. The advantage of OPTRA is obvious in terms of computational costs measured in SPs (Figs. 5 and 6, middle). Notice that the conclusions are rather similar on both tested graphs. Taking into account all the presented results, the tested methods appear to be competitive.

We also comment on an advantage of EFIX with respect to OPTRA in terms of parameter tuning. Notice that for each problem at hand, we apply the same universal rules to set the EFIX parameters. In contrast, OPTRA has a free parameter \(\nu >0\) that seems to be difficult to tune. In terms of guidelines for setting \(\nu \), reference [36] suggests (up to universal constants) a theoretical optimized value of \(\nu \). For such value of \(\nu \), OPTRA achieves the lower complexity bounds with respect to the oracle defined in [36]; however, the optimized value of \(\nu \) depends on the gradient of the cost function at the solution and is hence difficult to specify. Reference [36] does not give guidelines how to approximate the optimized value of \(\nu \), but it rather hand-tunes \(\nu \) for each given data set and each given network. Another advantage of EFIX over OPTRA is that OPTRA’s parameters \(\tau \) and \(\gamma \) depend on the total iteration budget T. In other words, for different total iteration budgets T, OPTRA parameters should be set differently. In contrast, EFIX parameters are set universally irrespective of a value of T set beforehand.

6 Conclusions

The quadratic penalty framework is extended to distributed optimization problems. Instead of standard reformulation with quadratic penalty for distributed problems, we define a sequence of quadratic penalty subproblems with increasing penalty parameters. Each subproblem is then approximately solved by a distributed fixed point linear solver. In the paper we used the Jacobi and Jacobi Over-Relaxation method as the linear solvers, to facilitate the explanations. The first class of optimization problems we consider are quadratic problems with positive definite Hessian matrices. For these problems we define the EFIX-Q method, discuss the convergence properties and derive a set of conditions on penalty parameters, linear solver precision and inner iteration number that yield an iterative sequence which converges to the solution of the original, distributed and unconstrained problem. Furthermore, the complexity bound of \( {{{\mathcal {O}}}}(\epsilon ^{-1}) \) is derived. In the case of strongly convex generic function we define EFIX-G method. It follows the reasoning for the quadratic problems and in each outer iteration we define a quadratic model of the objective function and couple that model with the quadratic penalty. Hence, we are again solving a sequence of quadratic subproblems. The convergence statement is weaker in this case but nevertheless corresponds to the classical statement in the centralized penalty methods - we prove that if the sequence converges then its limit is a solution of the original problem. The method is dependent on penalty parameters, precision of the linear solver for each subproblem and consequently, the number of inner iterations for subproblems. As quadratic penalty function is not exact, the approximation error is always present and hence we investigated the mutual dependence of different errors. A suitable choice for the penalty parameters, subproblem accuracy and inner iteration number is proposed for quadratic problems and extended to the generic case. The method is tested and compared with the state-of-the-art first order exact method for distributed optimization, DIGing. It is shown that EFIX is comparable with DIGing in terms of error propagation with respect to iterations and that EFIX computational and communication costs are lower in comparison with DIGing methods. EFIX is also compared to recently developed primal-dual method - OPTRA. The comparison is made on both well connected and weekly connected graphs and the EFIX method proves to be at least competitive with the tested counterpart with respect to practical performance, while the advantage of EFIX lies in universal parameter settings.