High-throughput determination of high-quality interdiffusion coefficients in metallic solids: a review

Zhong, Jing; Chen, Li; Zhang, Lijun

doi:10.1007/s10853-020-04805-1

High-throughput determination of high-quality interdiffusion coefficients in metallic solids: a review

1000th Issue
Published: 19 May 2020

Volume 55, pages 10303–10338, (2020)
Cite this article

Download PDF

Journal of Materials Science Aims and scope Submit manuscript

High-throughput determination of high-quality interdiffusion coefficients in metallic solids: a review

Download PDF

3648 Accesses
35 Citations
1 Altmetric
Explore all metrics

Abstract

Accurate interdiffusion coefficients of composition and temperature dependence are significantly important for understanding different materials processes. However, the high-throughput determination of high-quality interdiffusion coefficients, especially in multicomponent systems, has been sustaining as a challenge in materials community. This review dealt with a comprehensive summarization of the recent progress in this field, aiming at advancing a scientific routine for realizing the high-throughput determination of high-quality interdiffusion coefficients in metallic solids. First, an introduction of traditional Matano-based approaches and their recent development was given. Second, the numerical inverse methods were described, with a focus on the recently developed pragmatic numerical inverse method and related public toolkits. Potential strategies for resolving the problems about accuracy and uniqueness of the solutions to the numerical inverse methods were highlighted. The combination of numerical inverse method and diffusion multiple technique was highly proposed for high-throughput determination of interdiffusion coefficients in metallic solids with any number of components. After that, the case studies on the high-throughput determination of interdiffusivity matrices in the real Ni-based, high-entropy/high-entropy superalloys were demonstrated. Discussion on the substitution of Re in Ni-based single-crystal superalloys and the sluggish diffusion in high-entropy/high-entropy superalloys was also carried out. Fourth, the general idea for the uncertainty quantification was proposed in order to obtain high-quality interdiffusion coefficients, followed by the introduction of recent progress on the uncertainty quantification in both Matano-based methods and numerical inverse methods. Finally, the conclusions were drawn, and the future trends in diffusion community were also pointed out.

Automation of diffusion database development in multicomponent alloys from large number of experimental composition profiles

Article Open access 01 March 2021

High-throughput measurements of interdiffusivity matrices in face centered cubic Ni–Al–Mo alloys at 1273–1473 K

Article 01 June 2017

High-Throughput Determination of Composition-Dependent Interdiffusivity Matrices and Atomic Mobilities in fcc Cu-Ni-Al Alloys by Combining Diffusion Couple Experiments with HitDIC Modeling

Article 24 March 2021

Introduction

Interdiffusion, which occurs in the presence of chemical potential gradient and results in net transport of mass, is an omnipresent but important phenomenon in a variety of materials processes, e.g., solidification, solid solution, aging, corrosion, mutual interaction between coatings and matrix, and so on [1,2,3,4,5,6]. Accurate interdiffusion coefficients (or interdiffusivities) are necessary for comprehensive understanding of these materials processes that helps to improve the property and performance of the target materials [7,8,9]. Moreover, accurate interdiffusion coefficients are also important parameters encountered in numerous equations of physics and chemistry [10, 11], and different types of numerical simulations based on Fick’s law for quantitative characterization of various physical, chemical and materials processes [12,13,14,15,16,17,18,19]. In general, the interdiffusion coefficient, also known as the chemical diffusion coefficient, is composition- and temperature-dependent. In a binary system, there is only one unique type of interdiffusion coefficient, while in a ternary system, a 2 × 2 interdiffusivity matrix (two main and two cross interdiffusivities) exists. As the component number increases, the size of such interdiffusion matrix increases dramatically, not to mention that they are composition- and temperature-dependent. Accordingly, it is really a challenge for efficient storage and usage of interdiffusivity matrix of composition and temperature dependence in industrial materials that are typically multicomponent [14, 15].

Of special significance lies in the concept of atomic mobility [20], which was introduced to efficiently reduce the complexity of storage and usage of the sophisticated interdiffusion coefficient matrices. The atomic mobilities are represented by its underlying physical/mathematic models [20,21,22,23,24], and the related model parameters can be assessed on the basis of the experimental diffusivity data phase by phase in the framework of the CALculation of PHAse Diagram (CALPHAD) technique [25] and stored in the atomic mobility database phase by phase [26,27,28]. From atomic mobility database together with the consistent thermodynamic database, one can calculate interdiffusivities of the corresponding system at any compositions and temperatures. The key point for establishment of accurate atomic mobility database for the target materials is attributed to the large amount of high-quality experimental diffusion coefficients, especially for the ones due to their efficient determination, in individual phase. However, to acquire large amount of high-quality interdiffusion coefficients, especially in multicomponent systems, is still very challenging.

The first challenge originates from the keyword “high-quality.” Because most of the literature reports are devoted to the investigations of interdiffusion coefficients in different metallic solids, we restrict the target materials to be metallic solids in this manuscript. For metallic solids, the solid-state single-phase diffusion couple technique is widely used to determine the interdiffusion coefficients. The intuitive demonstration of the preparation of solid/solid diffusion couple and the basic procedure for evaluation of interdiffusion coefficients are presented in Fig. 1. For more detailed information on the diffusion couple technique, one can refer to some nice publications [29,30,31,32]. Ideally, the standard diffusion couple technique in combination with the electron probe microanalysis (EPMA) and some other advanced techniques [30] can result in high-quality experimental composition profiles (note: they are actually a series of scattering data points). However, one should bear in mind that (1) the effect of grain boundary diffusion should be eliminated. One can either utilize the single-crystal samples or employ the long enough homogenization period and/or high enough homogenization temperature to let the grains grow large enough (i.e., at least longer than the diffusion distance during the subsequent annealing stage of diffusion couple) for polycrystal samples and (2) the effect of preparation methods for diffusion couple on the composition profiles at the initial state should be also considered. This is a very tricky task. A typical treatment is to have a relatively long annealing period to ease the effect of the initial composition profiles on the finally evaluated interdiffusion coefficients. Moreover, another superior treatment is from the very recent work by Chen et al. [32], who included the initial composition profiles as the initial state in the numerical inverse method. With the measured high-quality composition profiles, two more preconditions should be fulfilled in order to further determine the high-quality interdiffusion coefficients, i.e., the reasonable computational method for the evaluation of interdiffusion coefficient and that for the quantification of uncertainties.

Currently, the computational methods widely used for calculating interdiffusion coefficient in the literature can be divided into two categories. The first category includes the Boltzmann–Matano [33] and other related methods [34,35,36,37,38,39,40]. However, it is very difficult to apply the traditional Matano-based methods to evaluate the interdiffusion coefficients in quaternary and higher-order systems. Recently, some efforts have been made to extend their applicable capability, for instance, the pseudo-binary and pseudo-ternary methods developed by Paul and his colleagues [39,40,41]. One more important point related to the computational methods is that the adopted fitting function for the composition profile entails the influence on the obtained results. Considering the diversity of the experimental composition profiles, there are a variety of options for the fitting functions [42,43,44,45,46,47]. Even for one set of composition profiles, different fitting functions may lead to different interdiffusion coefficients [48]. Thus, it is of general interest to find a common function for all types of composition profiles in diffusion community. The second category refers to the numerical inverse methods [49,50,51,52,53,54], of which the essence is to solve an inverse problem. To take the experimental composition profiles as the result of a functional of interdiffusion coefficient matrices, such a functional is inversely determined by minimizing the misfit between the model-predicted and experimental composition profiles [55]. The advantage of the numerical inverse method rests with its computational efficiency and general applicability in systems with any number of components, but the accuracy for the interdiffusivities obtained from the numerical inverse method strongly depends on the numerical algorithms and convergence, which attracts the recent research interests.

The uncertainty quantification is critically important for high-quality interdiffusion coefficients, which, however, has been neglected in most publications in the literature. To quantify the uncertainties for the determined interdiffusion coefficients, all the error sources generated during the calculation procedure, like the experimental measurement and fitting of the composition profiles, and their propagation to the finally evaluated interdiffusion coefficients. There are some trials on the evaluation of uncertainties in the literature, but most of them focused on the binary systems [55,56,57]. It is still very challenging to develop a general but reasonable approach to quantify the uncertainties, especially in multicomponent systems [58].

The second challenge comes with the keyword “large amount,” which should be equivalent to the “high-throughput.” That is to say, it is necessary to perform the high-throughput determination of interdiffusion coefficients, which can efficiently provide large amount of data for assessing the atomic mobilities in each phase. It also fits well with the aims of the popular Materials Genome Initiative (MGI) projects nowadays [59,60,61]. The “high-throughput” determination should be achieved in both experimental and computational aspects. In the experimental aspect, the usage of advanced diffusion multiple technique [62], which is an assembly of numbers of subdiffusion couples, can provide relatively much more experimental composition data at once, compared with the single diffusion couple. As for the computational aspect, the numerical inverse method, which can retrieve the composition- and temperature-dependent interdiffusion coefficients along the entire diffusion path of diffusion multiple/couple, may realize this goal [54].

Consequently, this review is devoted to a comprehensive summary of all the efforts on high-throughput determination of high-quality interdiffusion coefficients in metallic solids in the literature, especially for the recent progress from our research group and others, aiming at advancing a scientific routine for realizing the high-throughput determination of high-quality interdiffusion coefficients in metallic solids. In this review, no attempt will be made on the experimental aspects that are already settled well, and only the computational aspects, including the computational methods for calculation of interdiffusion coefficient and quantification of the uncertainty oriented at high-throughput determination of high-quality interdiffusion coefficients in metallic solids.

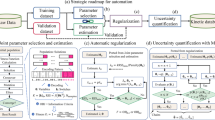
The structure of this review is spread out as follows: In the next two sections, the hierarchical timelines of the two categories of computation methods, i.e., Matano-based and numerical inverse methods, for the calculation of interdiffusion coefficients in metallic solids are first introduced. Latest developments of different methods are highlighted in the respective sections. Thereafter, several typical application cases with the features of high efficiency and high quality in determination of interdiffusion coefficients in Ni-based superalloys, face-centered cubic (fcc) high-entropy alloys and newly developed fcc AlCoCrFeNiTi high-entropy superalloys are demonstrated in “Case studies on high-throughput determination of interdiffusion coefficients” section. Discussion on the related diffusion properties, including the possible substitution of Re in Ni-based single-crystal superalloys and the sluggish diffusion in high-entropy/high-entropy superalloys, is also carried out. In “Uncertainty quantification for high-quality interdiffusion coefficients” section, summary and highlights on quantifying the uncertainties of the interdiffusion coefficients evaluated using the two categories of calculation methods are speculatively laid out. Finally, the conclusions of this review are drawn. Furthermore, the future development directions related to the high-throughput determination of high-quality interdiffusion coefficients in metallic solids are also pointed out.

Matano-based methods and their new developments

Boltzmann–Matano and other related methods

As early as 1933, Matano proposed a method to approach the initial contact interface and applied it to determine the composition-dependent interdiffusion coefficient of the Cu–Ni systems together with the Boltzmann analysis [33], bringing forth the well-known Boltzmann–Matano method. Taking a single phase in one hypothetical A-B binary system (here, B is chosen as solvent) as an example, the interdiffusion coefficient $\tilde{D}_{{{\text{AA}}}}^{{\text{B}}}$ (also equals $\tilde{D}_{{{\text{BB}}}}^{{\text{A}}}$) can be retrieved using

$$ \tilde{D}_{{{\text{AA}}}}^{{\text{B}}} = - \tilde{J}_{{\text{A}}} /\left( {\frac{{{\text{d}}c_{{\text{A}}} }}{{{\text{d}}x}}} \right) $$

(1)

where ${\text{c}}_{{\text{A}}}$ is the composition of component A, x is the distance and $\tilde{J}_{{\text{A}}}$ is the interdiffusion flux of component A, denoted as

$$ \tilde{J}_{{\text{A}}} = \frac{1}{2t}\mathop \smallint \limits_{{c_{{\text{A}}}^{{\text{L}}} {\text{ or}} c_{{\text{A}}}^{{\text{R}}} }}^{{c_{{\text{A}}} }} \left( {x - x_{{\text{M}}} } \right){\text{d}}c_{{\text{A}}} $$

(2)

Here, t is the diffusion time, $c_{{\text{A}}}^{{\text{L}}}$ and $ c_{{\text{A}}}^{{\text{R}}}$ are, respectively, the terminal compositions on the left and right sides of the semi-infinite diffusion couple and $x_{{\text{M}}}$ denotes the location of Matano position that can be evaluated according to

$$ \mathop \smallint \limits_{{c_{{\text{A}}}^{{\text{L}}} { }}}^{{c_{{\text{A}}}^{{\text{R}}} }} \left( {x - x_{{\text{M}}} } \right){\text{d}}c = 0 $$

(3)

For the past more than 80 years, the Boltzmann–Matano method has been successfully applied to determine the composition-dependent interdiffusion coefficients from the experimental composition profiles in a variety of binary systems. However, one should bear in mind that when the composition approaches $c_{{\text{A}}}^{{\text{L}}}$ and/or $ c_{{\text{A}}}^{{\text{R}}}$ in the semi-infinite diffusion couple, the numerator and denominator terms in Eq. (1) become 0, and thus the numerical problems always exist for the interdiffusion coefficients calculated using the Matano-based methods.

In order to get rid of extra complexity for evaluation of the Matano plane, Sauer and Freise [36] modified the Boltzmann–Matano method and evaluated the interdiffusion flux via

$$ \tilde{J}_{{\text{A}}} = \frac{{c_{{\text{A}}}^{{\text{L}}} - c_{{\text{A}}}^{{\text{R}}} }}{2t}\left[ {Y_{{\text{A}}}^{{\prime }} \mathop \smallint \limits_{ - \infty }^{{l^{\prime}}} \left( {1 - Y_{{\text{A}}} } \right){\text{d}}x + \left( {1 - Y_{{\text{A}}}^{{\prime }} } \right)\mathop \smallint \limits_{{l^{\prime}}}^{ + \infty } Y_{{\text{A}}} {\text{d}}x} \right] $$

(4)

instead of Eqs. (2) and (3). In Eq. (4), a normalized parameter $Y_{{\text{A}}}$ defined as $\left( {c_{{\text{A}}} - c_{{\text{A}}}^{{\text{L}}} } \right)/\left( {c_{{\text{A}}}^{{\text{R}}} - c_{{\text{A}}}^{{\text{L}}} } \right)$ was introduced to suspend the necessity of Matano plane. $l^{{\prime }}$ and $Y_{{\text{A}}}^{{\prime }}$ denote the position and the normalized composition at the desired position or composition. But it can be seen from the definition of $Y_{{\text{A}}}$ that the Sauer–Freise method is not applicable to the case in which $c_{{\text{A}}}^{{\text{L}}} = c_{{\text{A}}}^{{\text{R}}}$.

However, in a single phase of one hypothetical A–B–C ternary system (i.e., assuming C to be solvent, and A/B to be solutes), the Fick’s first law can be expressed as

$$ \tilde{J}_{{\text{A}}} = - \tilde{D}_{{{\text{AA}}}}^{{\text{C}}} \frac{{{\text{d}}c_{{\text{A}}} }}{{{\text{d}}x}} - \tilde{D}_{{{\text{AB}}}}^{{\text{C}}} \frac{{{\text{d}}c_{{\text{B}}} }}{{{\text{d}}x}} $$

(5)

$$ \tilde{J}_{{\text{B}}} = - \tilde{D}_{{{\text{BA}}}}^{{\text{C}}} \frac{{{\text{d}}c_{{\text{A}}} }}{{{\text{d}}x}} - \tilde{D}_{{{\text{BB}}}}^{{\text{C}}} \frac{{{\text{d}}c_{{\text{B}}} }}{{{\text{d}}x}} $$

(6)

Here, $\tilde{D}_{{{\text{AA}}}}^{{\text{C}}}$ and $\tilde{D}_{{{\text{BB}}}}^{{\text{C}}}$ are two main interdiffusion coefficients, while $\tilde{D}_{{{\text{AB}}}}^{{\text{C}}}$ and $\tilde{D}_{{{\text{BA}}}}^{{\text{C}}}$ are two cross ones. Thus, for a ternary system, there are four independent unknowns, but only two equations [i.e., Eqs. (5) and (6)] for one diffusion couple. For determining the interdiffusivity matrix in the ternary system, Kirkaldy and Young [34] extended the Boltzmann–Matano method to the ternary systems by carefully designing two diffusion couples of which diffusion paths have at least one common intersection point, as schematically shown as, for example, Points S₁ and/or S₂ in Fig. 2. At the common intersection point, one can have another two equations like Eqs. (5) and (6). Then, the four unknowns in the ternary interdiffusivity matrix can be explicitly solved. If the interdiffusion fluxes in Eqs. (5) and (6) are solved by the Boltzmann–Matano method [i.e., Eqs. (2) and (3)], one can refer it to be the Matano–Kirkaldy method [34]. However, if those are solved by the Sauer–Freise method, one can refer it to be the Whittle–Green method [63]. Though either the Matano–Kirkaldy or the Whittle–Green method has been widely used to determine the interdiffusion coefficients in ternary systems for the past years [45, 46, 64,65,66,67,68,69,70,71,72,73], there are two major constraints for this type of methods. One suffers from their low efficiency because only one set of interdiffusivity matrices at one intersection point can be obtained for two diffusion couples. For the sake of the composition-dependent interdiffusion coefficients in a ternary system, a large number of diffusion couples should be designed and prepared. However, the other constraint is owing to the difficulty in applying these types of methods in quaternary and higher-order systems since it seems impossible to design the diffusion couples with a common intersection in quaternary and higher-order systems.

In order to overcome the dilemma, some efforts have been made to extend the applicability of the traditional Matano-based methods. The first successful trial was from Dayananda and Sohn [35] in 1999, who proposed one approach for evaluating the average interdiffusion coefficients over specifically selected distance/composition ranges along the diffusion path of a single diffusion couple. One code, namely MultiDiFlux, was accordingly developed by Dayananda and his colleagues [74]. With the Daynanada–Sohn method, the amount of diffusion couples can be largely decreased, and the computational efficiency increases. However, only limited average interdiffusion coefficients can be determined, and their reliability depends largely on its variation within the specified composition range, which limits the wide application of the Daynanada–Sohn method. For the purpose of determining the composition-dependent interdiffusion coefficients in a ternary system using a single diffusion couple, Cermak and Rothova [75] extended the Daynanada–Sohn method [35] by making the distance/composition interval sufficiently small. With a sufficiently small interval, the authors [75] claimed that the average interdiffusion coefficients can approach the truly composition-dependent values with an arbitrary required accuracy. However, Cheng et al. [76] mathematically verified that the interdiffusivities evaluated by the Cermak–Rothova method [75] are still the average ones, but not the truly composition-dependent values. Another important contribution to the extension of Matano-based methods is from Morral and his colleagues [38, 77, 78], who introduced the concept of the square root diffusivity, and its relation to the interdiffusion coefficient in ternary and higher-order systems. However, according to such square root method, the composition interval over the diffusion couple should be small enough, and the resultant interdiffusion coefficients are constant. Similar to the average interdiffusion coefficient, the evaluated constant interdiffusion coefficients limit the wide applicability of the square root method considering its low efficiency.

It should be noted that all the above-mentioned Matano methods neglect the molar volume variance of the components in a concerned system. Such simplification is valid for most alloys with finite solubility range. In case that significant molar volume change with the concentration is asserted, one might refer to Wagner’s method [37], which is not introduced in detail here because (1) the accurate composition-dependent volume change in most alloys, especially in multicomponent alloys, is absent, and (2) no good numerical solution to address the problem with the composition-dependent molar volume variance is available currently [79,80,81,82].

Pseudo-binary and pseudo-ternary approaches

With the carefully designed pseudo-binary diffusion couple, Paul et al. [39, 82] proposed the pseudo-binary method for evaluating the composition-dependent interdiffusion coefficients in ternary and higher-order systems using the single diffusion couple. More recently, Paul et al. [40] further developed the pseudo-ternary method for evaluation of interdiffusion coefficients in quaternary and higher-order systems. The emergence of the pseudo-binary and pseudo-ternary methods provides the incredible convenience for evaluating the interdiffusion coefficients in multicomponent systems.

Taking a hypothetical ternary A–B–C system as an example, the typical diffusion paths of the pseudo-binary diffusion couples are illustrated as P₄ and P₅ in Fig. 2. It can be clearly seen from Fig. 2 that only the compositions of two solute components (i.e., A and C for P₄, while A and B for P₅) vary, while that of the third solvent component strictly keeps as constant over the diffusion distance. According to the pseudo-binary method [41], the compositions of the two solute components are, respectively, normalized by dividing by the summation of their compositions along the diffusion path (e.g., N_v = N_A + N_C for P₄, while N_v = N_A + N_B for P₅). Taking the solute component A for instance, its modified composition reads as $M_{A} = N_{A} /N_{v}$. Here, all the Ns denote the mole quantity. With the modified compositions, the interdiffusion coefficients in one pseudo-binary system can be thus evaluated referring to the computation procedure of the interdiffusion flux of A similar to the Sauer–Freise method,

$$ \tilde{J}_{{\text{A}}} = \frac{{M_{{\text{A}}}^{{\text{L}}} - M_{{\text{A}}}^{{\text{R}}} }}{{2tV_{{\text{m}}} }}\left[ {Y_{{M_{{\text{A}}} }}^{*} \mathop \smallint \limits_{ - \infty }^{{l^{*} }} \left( {1 - Y_{{M_{{\text{A}}} }} } \right){\text{d}}x + \left( {1 - Y_{{M_{{\text{A}}} }}^{*} } \right)\mathop \smallint \limits_{{l^{*} }}^{ + \infty } Y_{{M_{{\text{A}}} }} {\text{d}}x} \right] $$

(7)

where the $Y_{{M_{{\text{A}}} }}$ is noted as $\left( {M_{{\text{A}}} - M_{{\text{A}}}^{{\text{L}}} } \right)/\left( {M_{{\text{A}}}^{{\text{R}}} - M_{{\text{A}}} } \right)$, $l^{*}$ and $Y_{{M_{{\text{A}}} }}^{*}$ denote the position and normalized parameter at the desired composition. One example for demonstration of pseudo-binary method originated from Esakkiraja et al. [41] is illustrated in Fig. 3. The experimental composition profiles of all the components in both Al–Mn(Ni) and Al–Mn(NiCoFe) pseudo-binary diffusion couples annealed at 1100 °C for 25 h are, respectively, displayed in Fig. 3a, b. As can be seen, only the components Al and Mn develop the composition gradient over the diffusion region, indicating the strictly pseudo-binary Al–Mn(90Ni) and Al-Mn(30Ni + 30Co + 30Fe) diffusion couples. The interdiffusion coefficients as a function of N_Mn of the two pseudo-binary systems evaluated using the pseudo-binary method are presented in Fig. 3c. It can be seen in Fig. 3c that quite similar values of the interdiffusion coefficients are obtained in the two quasi-binary systems, resulting in a conclusion that the addition of constant Co and Fe components makes very small influence on the derived composition-dependent interdiffusion coefficients [41].

In the framework of the pseudo-ternary method, two pseudo-ternary diffusion couples with three varying components are required. Their diffusion paths of the three varying components projecting over an isothermal section (like P₂ and P₃ in Fig. 2) should have at least one common intersection point, similar to the one in ternary systems, i.e., S₁, as illustrated in Fig. 2. The compositions of the three varying components should be modified following the similar strategy as in the pseudo-binary method, and the modified composition profiles of the three components are then fitted separately [40]. One more additional step in the pseudo-ternary method is required to take the average value of the composition profiles of all the components with constant composition [41]. With the modified compositions, the interdiffusion fluxes for the solute components in the pseudo-ternary systems can be thus calculated according to Eq. (7). Meanwhile, the two equations similar to Eqs. (5) and (6) can be deduced based on the modified compositions as [40],

$$ \tilde{J}_{{\text{A}}} = - \tilde{D}_{{{\text{AA}}}}^{{\text{C}}} \frac{{{\text{d}}M_{{\text{A}}} }}{{{\text{d}}x}} - \tilde{D}_{{{\text{AB}}}}^{{\text{C}}} \frac{{{\text{d}}M_{{\text{B}}} }}{{{\text{d}}x}} $$

(8)

$$ \tilde{J}_{{\text{B}}} = - \tilde{D}_{{{\text{BA}}}}^{{\text{C}}} \frac{{{\text{d}}M_{{\text{A}}} }}{{{\text{d}}x}} - \tilde{D}_{{{\text{BB}}}}^{{\text{C}}} \frac{{{\text{d}}M_{{\text{B}}} }}{{{\text{d}}x}} $$

(9)

for one pseudo-ternary diffusion couple. Here, A, B and C are the components with varying compositions alongside the diffusion region of the fictitious A–B–C pseudo-ternary systems. After that, the standard Whittle–Green method can be utilized to compute the interdiffusion coefficients at the common intersection point of every two pseudo-ternary diffusion couples. A demonstration of the pseudo-ternary method in a real case from Esakkiraja et al. [41] is presented in Fig. 4. As can be seen, the measured composition profiles and their diffusion paths of the ternary Co–Fe–Ni and pseudo-ternary Co–Fe–Ni(Mo) diffusion couples annealed at 1100 °C for 100 h are displayed. The interdiffusion coefficient matrices of the ternary Ni–Co–Fe system and the pseudo-ternary Ni–Co–Fe (Mo) system at the corresponding intersection points along the diffusion paths can be then calculated [41]. The recently developed pseudo-binary and pseudo-ternary methods act as the important extension of the traditional Matano-based methods and can be employed to evaluate the interdiffusion coefficients in quaternary and higher-order systems, e.g., the high-entropy alloys [40, 41]. However, one should bear in mind that the strict pseudo-binary and/or pseudo-ternary diffusion couples need to be carefully designed if the pseudo-binary and/or pseudo-ternary methods are to be used. Moreover, according to the recent comment by Belova and Murch [83], one should be careful about the difference between the interdiffusion coefficients evaluated using the pseudo-binary/-ternary method and the actual ones, especially in multicomponent systems.

Development of fitting functions

Besides the computational method itself, the fitting and smoothing procedure is yet another important topic for evaluating the high-quality interdiffusion coefficients by means of the Boltzmann–Matano method and other related methods. Generally, the scattered experimental composition profiles measured from the diffusion couples are under-qualified for integration and differentiation, which are mandatory for the Boltzmann–Matano method and other related methods. For remedying such problem, the preset functions are usually employed to smooth and fit the composition profiles, which are further utilized to calculate the interdiffusion fluxes, slope of the composition profiles, and so on.

In general, any functions which can provide satisfactory fitting goodness to the experimental composition profiles are acceptable. The commonly adopted categories of the fitting functions in the literature include the error function [42, 84] and its superposition [43, 44], Boltzmann function (logistic function) [47] and its superposition [54], nested exponential function [46], pseudo-Fermi function [85], other manually constructed polynomial function [45], and so on. The advantages of these functions lie in the convenience of implementation, though they are considered to be prone to over-fitting [48]. One example was given by Zhong et al. [54], in which the interdiffusion coefficients of fcc Cu–Sn alloys at 873 K were evaluated using the Boltzmann–Matano method based on the same composition profile but fitted with different fitting functions, including the single, double and triple Boltzmann functions, as presented in Fig. 5. As shown in Fig. 5, the experimental composition profile due to Xu et al. [86] can be well reproduced by different fitting functions. However, different fitting functions may lead to different fitting degrees, resulting in the interdiffusion coefficients with noticeable difference. A single Boltzmann function tends to produce the average interdiffusion coefficient, while the superposition of the Boltzmann function generally produces the complicated relation between the interdiffusion coefficient and composition.

Very recently, Wei and Zhang [48] proposed that the category of the distribution functions is superior to other types of functions and can give reasonable fitting goodness to all types of composition profiles, thus resulting in reliable interdiffusion coefficients in different cases. According to Wei and Zhang [48], the normal, pseudo-normal, skew-normal, pseudo-skew-normal distribution functions can be employed for the simple $\tilde{D}\sim c$ relations, including the simple symmetrical, monotonic and simple unsymmetrical ones. Other than those simple ones, the superposed distribution functions should be used. As for the cases with uphill diffusion, the combined superposition of the distribution functions (i.e., probability distribution function and cumulative distribution function) may be chosen. A glance at superiority of distribution function is illustrated in Fig. 6, as originally reported by Wei and Zhang [48]. The ideal experimental points were generated from a preset $\tilde{D}\sim c$ relation, i.e., $\tilde{D}$ = 0.02 + 0.004c (unit: $\tilde{D}$ μm²/s; $\tilde{c}$ atomic percent) at a diffusion time of 10,000 s (see detail in original publication [48]). As can be seen in Fig. 6a, two types of functions, i.e., a specific error function developed by Kavakbasi et al. [84], and the distribution function developed by Wei and Zhang [48], can give very good fitting to ideal experimental data since the correlation coefficients are both extremely close to unity. However, the calculated interdiffusivities using the Boltzmann–Matano method but with different fitting functions show certain differences. As shown in Fig. 6b, the calculated composition-dependent interdiffusivities based on the distribution function can nicely reproduce the preset $\tilde{D}\sim c$ relation over the investigated composition range and present a slightly better result than those based on the specific error function [84]. The reason is that the distribution functions possess the ability to restrict the symmetry and complexity of the predicted interdiffusion fluxes and slopes providing interdiffusion coefficients of similar complexity to the nature of the materials [48]. Thus, the Matano-based methods in combination with the distribution functions can serve as the general solution for accurate determination of diffusion coefficients.

Numerical inverse methods

General development

Up to now, the foremost contribution to reasoning the interdiffusion coefficients of multicomponent systems is from the numerical inverse method. The numerical inverse method falls into the category of inverse problem or inverse coefficient problem. In fact, the inverse problem, as a well-studied topic in mathematics, is about reasoning the causes from the observations [87,88,89,90]. With the initial state of a diffusion couple and the composition-dependent interdiffusion coefficients, the predictions to the composition profiles of a diffusion couple can be imitated or simulated, namely the forward problem. In practice, the diffusion couple or diffusion multiple method together with the composition measurement techniques (like EPMA) provides the observations of the composition profiles. The inverse methods basically perform the reasoning of the coefficients in the governing equations by adapting the coefficients of interest to produce the predictions, which should agree satisfactorily with the observations, as illustrated in Fig. 7. The inverse problem can be generally cast into the framework of the PDE-constrained optimization problem,

$$ \theta = \arg \mathop {\min }\limits_{\theta } \sum\limits_{l} {\left\| {\tilde{c}_{l} - c_{l} \left( \theta \right) } \right\|} _{2}^{2} $$

(10)

subject to

$$ \frac{{\partial c_{k} }}{\partial t} = \nabla \left( {\mathop \sum \limits_{j = 1}^{n - 1} \tilde{D}_{kj}^{n} \left( \theta \right)\nabla c_{j} } \right)\;\;{\text{in}}\;\Omega \;{\text{for}}\;{\text{all}}\;{\text{solutes}} $$

(11)

$$ \nabla c_{k} = 0\;in\;\partial \Omega $$

(12)

where $\tilde{c}_{l}$ denotes the experimental composition profile, while $c_{l}$ is the prediction to the composition profiles using the extended Fick’s second law. It should be noted that the initial condition for the Fick’s second law in Eq. (11) is generally set as the initial state of the diffusion couple before annealing [32]. By resolving the unknowns $\theta$ in Eq. (10), the interdiffusion coefficients can thereby be determined based on the assessed values of $\theta$. Generally, the numerical inverse methods for calculating the interdiffusion coefficients distinguish from each other concerning their motivation for different diffusion properties, i.e., either merely reasoning the phenomenological interdiffusion coefficients or reasoning the parameters of physical significance like atomic mobility. What’s more, such method is named as the “numerical” inverse method because it relies on the intensive numerical iterations and computation resources, though analytic results for the interdiffusion coefficients might be provided.

In 2002, Bouchet and Mevrel [49, 91] applied the numerical inverse method to evaluate the interdiffusion coefficients in ternary systems. In their work, the polynomial equation was employed to model the relation of the interdiffusion coefficients with the composition [49]. Moreover, Bouchet and Mevrel’s work is featured with its treatment to solve the diffusion equations of a ternary system, following the convention proposed by Fujita and Gosting [92] on usage of the Boltzmann’s similarity variable. Fujita and Gosting’s convention can give an exact solution of the equations for free diffusion in three-component systems [92] and provide incredible convenience for making predictions to the composition profiles, assuming that the volume change on mixing and the concentration dependence of the diffusion coefficients are negligible. However, it is well known that for most practical systems, the interdiffusion coefficients are generally considered as composition dependent. To overcome such a constraint, Bouchet and Mevrel converted the partial differential equations of the Fick’s second law for a ternary system into the ordinary differential equations and made predictions to the composition profiles based on the reformulated equations [49]. With the predictions, the genetic algorithm was adopted by Bouchet and Mevrel for reasoning the coefficients of preset polynomial equation related to the interdiffusion coefficients so as to mimic the experimental composition profiles with the satisfactory fitting goodness. As claimed by Bouchet and Mevrel [49], a quite strict convergence criterion was applied though the finally obtained predictions deviate against the originally imitated composition profiles to a certain degree.

The so-called forward simulation method was developed by Zhao’s group [51, 93,94,95,96], aiming at recovering the interdiffusion coefficients for multiple phases from the composition profiles of single-phase and/or reactive diffusion couples/multiples. Such forward simulation method also falls to the category of numerical inverse method, as processes of this method accord with the essence of inverse problem. Different from the general inverse problems related to the Fick’s laws, the forward simulation method cooperates with the internal solver for the moving boundary problem or sharp interface model for the predictions of the composition profiles in the reactive diffusion couples/multiples. Accordingly, an open-source package, implemented with Python language, for the forward simulation method was also released in 2019 [94]. Though the forward simulation is advanced in calculating the interdiffusion coefficients for single phase or multiple phases in the diffusion couples/multiples, it is currently limited to the binary systems [51, 93,94,95,96]. It is worth mentioning that the diffusion multiple technique has been frequently adopted in Zhao’s group [95, 96] to provide the possibility for high-throughput determination of interdiffusion coefficients in the single/multiple phases of the diffusion multiples. One typical application in Ni–Mo system from Zhao’s group [94] is displayed in Fig. 8. It can be seen from the figure that based on the experimental composition profiles in one Ni/Mo reactive diffusion couple annealed at 1100 °C for 800 h, the composition-dependent interdiffusion coefficients of different phases in the Ni–Mo system at 1100 °C evaluated from the forward simulation method are in good agreement with those derived from the Sauer–Freise method.

In 2014, a pragmatic numerical inverse method for retrieving the composition-dependent interdiffusion coefficients in ternary systems was developed in the present authors’ group [52] and then augmented into one for the systems with any number of components [53]. In the pragmatic numerical inverse method, the composition- and temperature-dependent interdiffusion coefficients are related to the atomic mobilities, which are expressed in the CALPHAD-type formalism [20], following the conventional Manning’s equation [97, 98]. The real CALPHAD thermodynamic descriptions may be used for providing the thermodynamic factor, which can promote the evaluation of the physical atomic mobilities. However, whether the realistic CALPHAD thermodynamic descriptions are used or not does not affect the accuracy of the obtained interdiffusion coefficients. In favor of robotizing the procedures to retrieve the reliable composition-dependent interdiffusivities from the experimental composition profiles of single or multiple diffusion couples, a free-accessible C++ code for High-throughput Determination of Interdiffusion Coefficients (HitDIC) [54] was developed based on the pragmatic numerical inverse method and released worldwide in 2017 through the Web site: https://hitdic.com/. For the past years, the pragmatic numerical inverse method (using HitDIC) has been widely applied in different series of alloys with any number of components [99,100,101,102] and will be specifically introduced in the “Pragmatic numerical inverse method and HitDIC software” section.

A similar reasoning strategy was also adopted by Kucza et al. [50, 103], who applied the numerical inverse method to evaluate the tracer diffusion coefficients from the measured composition profiles of the single-phase diffusion couples. The CALPHAD-type thermodynamic descriptions were employed by Kucza et al. [50, 103] for the sake of evaluating derivatives of the chemical potential with respect to composition. But in many cases that no CALHAD thermodynamic descriptions are available in the literature, the authors [103] utilized the Miedema model [104, 105] to provide the thermodynamic parameters, which should be not so accurate as those from the CALPHAD assessment. For the kinetic part, Kucza et al. [50, 103] introduced a coefficient matrix of which the parameters characterize the diffusion interactions among the components of the target system. The tracer diffusivities were then roughly approximated by the linear dependence on the evaluated coefficient matrix, of which the terms were assumed as constants [50, 103]. What’s more, a program based on the Mathcad platform was also developed by the authors [50, 103]. It should be noted that this method was only used by Kucza et al. [50, 103] to evaluate the tracer diffusivities, instead of the interdiffusion coefficients. Moreover, the accuracy of their obtained tracer diffusivities strongly depends on the quality of thermodynamic descriptions.

In addition, a more recent piece of work was from Gaertner et al. [106], who introduced a concept of pairwise mobility, which was claimed by the authors to be quite fit for high-entropy alloys and can be reduced to the atomic mobility. In their numerical inverse method, both the experimental tracer and chemical diffusion concentration profiles were employed to retrieve the parameters in pairwise mobilities. It is worth mentioning that with the tracer diffusion experiments, the quality of the obtained tracer diffusivities/mobilities can be ensured. Thus, the method from Gaertner et al. [106] is superior to the one proposed by Kucza et al. [50, 103]. But again, no interdiffusion coefficients were predicted by Gaertner et al. [106]. Moreover, the meticulous details on the modeling of the inverse processes, which is very important for the reliability of the assessed parameters to be shown in “Pragmatic numerical inverse method and HitDIC software” section, were also absent in Ref. [106].

Pragmatic numerical inverse method and HitDIC software

In the framework of the pragmatic numerical inverse method, the interdiffusion coefficients in the target system can be represented by following the conventional Manning equation [97, 98] as

$$ \tilde{D}_{ij}^{n} = RT\left( {M_{i} {\Phi }_{ij}^{n} - x_{i} \mathop \sum \limits_{k} M_{k} {\Phi }_{kj}^{n} } \right) + S $$

(13)

where R is the gas constant, T the absolute temperature, S the contribution of wind vacancy effect and ${\Phi }_{ij}^{n}$ the thermodynamic factor given as

$$ {\Phi }_{ij}^{n} = \frac{{x_{k} }}{RT}\left( {\frac{{\partial \mu_{k} }}{{\partial x_{j} }} - \frac{{\partial \mu_{k} }}{{\partial x_{n} }}} \right) $$

(14)

In fact, there are different forms of S available in the studies [97, 98, 107,108,109]. For the atomic mobility $M_{k}$, the CALPHAD-type formalism proposed in Refs. [20, 21]. was adopted,

$$ M_{k} = \frac{1}{RT}{\exp}\left( {\frac{{{\Phi }_{{\text{k}}} }}{RT}} \right){}_{{}}^{mg} {\Omega } $$

(15)

where the mobility parameter ${\Phi }_{{\text{k}}}$ can be expanded with the Redlich–Kister polynomial

$$ {\Phi }_{{\text{k}}} = \mathop \sum \limits_{i} x_{i} {\Phi }_{k}^{i} + \mathop \sum \limits_{i} \mathop \sum \limits_{j > i} x_{i} x_{j} \left[ {\mathop \sum \limits_{r}^{m} {}^{r}{\Phi }_{k}^{i,j} \left( {x_{i} - x_{j} } \right)^{r} } \right] + $$

$$ \mathop \sum \limits_{i} \mathop \sum \limits_{j > i} \mathop \sum \limits_{k > j} x_{i} x_{j} x_{k} \left[ {\mathop \sum \limits_{r} v_{r}^{ijk} {}^{r}{\Phi }_{k}^{i,j,k} } \right] + \cdots $$

(16)

where ${\Phi }_{k}^{i}$, ${}_{ }^{r} {\Phi }_{k}^{i,j}$ and ${}_{ }^{r} {\Phi }_{k}^{i,j,k}$ represent the contribution of unary, binary and ternary systems and $v_{r}^{ijk}$ is represented as $x_{r} + \left( {1 - x_{i} - x_{j} - x_{k} } \right)/3$. As proposed by Chen et al. [52], the unary parameter ${\Phi }_{k}^{i}$ can be fixed if the corresponding self- and impurity diffusion coefficients in the unary system are known, while the interaction parameters, i.e., ${}_{ }^{r} {\Phi }_{k}^{i,j}$, ${}_{ }^{r} {\Phi }_{k}^{i,j,k}$…, are adjustable ones, which are assessed based on the measured composition profiles. In Eq. (15), ${}_{{}}^{mg} {\Omega }$ is a factor denoting the ferromagnetic contribution into the atomic mobility [21].

Different from the general numerical inverse methods in which only the experimental composition profiles are considered in the objective function, both experimental composition and interdiffusion flux profiles were considered in the objective functions of the pragmatic numerical inverse method [53]. The general modeling of multiobjective problem can thus be given as [54]

$$ \epsilon^{2} \left( \theta \right) = \left\{ {\frac{{w_{x} }}{{n_{i} }}\mathop \sum \limits_{i}^{n} w_{i} \mathop \sum \limits_{j}^{{C_{i} }} \mathop \sum \limits_{k}^{{N_{i,j} }} \frac{{\left| {x_{k}^{i,j} - \tilde{x}_{k}^{i,j} } \right|^{2} }}{{N_{i,j} }},\frac{{w_{J} }}{{n_{i} }}\mathop \sum \limits_{i}^{n} w_{i} \mathop \sum \limits_{j}^{{C_{i} }} \mathop \sum \limits_{k}^{{N_{i,j} }} \frac{{\left| {J_{k}^{i,j} - \tilde{J}_{k}^{i,j} } \right|^{2} }}{{N_{i,j} }}, \ldots } \right\} $$

(17)

where $w_{i}$ is the weight of the ith diffusion couple, $C_{i}$ the number of components for the ith diffusion couple, $N_{i}$ the number of experimental points in the ith diffusion couple, w_x and w_J the weights for composition and flux, respectively. The objective function in Eq. (17) is the average of the deviation between the predictions and the observations, according to the number of diffusion couples ($n_{i}$), components ($C_{i}$) and the experimental data points ($N_{i,*}$), measuring the average misfit related to a single experiment point. The default values of the weights, i.e., w_i, are set to be 1, and they can be customized according to the importance and reliability of the experimental properties. Scaling is generally in need as the magnitude of deviation contributed from the different experimental sources is remarkable, while w_x and w_J are responsible for rescaling different types of experimental properties. Consideration of multiple optimization criteria falls to the multiobjective problem, which can be also resolved with the readily proposed PDE-constrained optimization framework, providing profound stability and uniqueness for the desired computation results. One nice example is demonstrated in Fig. 9, in which the model-predicted composition profiles and interdiffusion fluxes of solute B in a hypothetical A–0.01B/A–0.99B (in mole fraction) binary diffusion couple, annealed at a certain temperature for 7200 s, based on five different sets of binary interdiffusivities, are presented. It can be inferred from Fig. 9 that the interdiffusion fluxes, being more sensitive to the fitting goodness than the composition profiles, are then suggested as one of the promising alternatives as the optimization criteria [53].

Despite the incredible superiority of numerical inverse method, the popularity of such a method has been limited due to its complexity of implementation. In 2017, the HitDIC software for the high-throughput determination of interdiffusion coefficients was released, which fully demonstrates the powerful capability of the numerical inverse method to reason the interdiffusion coefficients of multicomponent systems [54]. Figure 10 presents the computational framework of HitDIC. As indicated in Fig. 10, the composition profiles of all the diffusion couples are handled by the observation module, while the thermodynamic and atomic mobility databases are utilized by the simulation module. Computation of the deviations between the observations and predictions generated by observation and simulation module, respectively, is processed by the error module, producing overall metric of fitting goodness. Minimization process is executed under the optimization module to pursue satisfactory values of the parameters of interest in the atomic mobility database, which minimizes the cost function provided by the error module. Once the values of the parameters of interest are determined, the interdiffusion coefficients with respect to the composition can be further evaluated according to Eqs. (13)–(16). Briefly, HitDIC program is designed to execute over the readily made project by users; meanwhile, usage and demonstration of the HitDIC software are also available in https://hitdic.com.

Accuracy and uniqueness of the solutions in the numerical inverse methods

Accuracy and uniqueness of solutions in the numerical inverse methods remain as thoughtful concerns, beyond efforts on accounting for existence. The accuracy infers the deviation of the calculated values from the true ones, while the uniqueness arises from the possibility of having multiple equivalent solutions.

First, in the aspect of accuracy of the solutions, the interdiffusion coefficients evaluated by means of numerical inverse method in different benchmarks and practical study cases are usually compared with the results due to the Boltzmann–Matano method and other related methods, from the early work by Bouchet and Mevrel [49] to more recent ones [8, 95, 99, 110,111,112]. A profound evidence of the equivalence of the two methods, i.e., numerical inverse method and Boltzmann–Matano method, is from Xu et al. [99]. As illustrated in Fig. 11, based on the same sets of experimental composition profiles, the interdiffusion coefficients of fcc Ag–In binary alloys at 873 K, 973 K and 1073 K were calculated by using both the Boltzmann–Matano method with distribution functions and the numerical inverse method with HitDIC. As can be seen in the figure, very good agreement between the interdiffusion coefficients evaluated using the two methods is obtained, indicating that the accuracy of the interdiffusion coefficients evaluated by means of the numerical inverse method can be guaranteed. Moreover, similar conclusion can be drawn in ternary systems, as demonstrated in Fig. 12. The interdiffusion coefficients of fcc Ag–In–Cu alloys at 1073 K are evaluated based on the same sets of experimental composition profiles using both the Matano–Kirkaldy method with distribution functions and the numerical inverse method with HitDIC and compared with each other in Fig. 12. Again, very good consistency in the main and cross interdiffusion coefficients of fcc Ag–In–Cu alloys evaluated using the two methods can be clearly seen.

Second, the uniqueness of the solutions in the numerical inverse methods can trace back to the nature of the inverse problems. Inverse problems are typically ill-posed, and the deduced reason, i.e., the desired interdiffusion coefficients for the Fick’s second law, is sensitive to the variation in the original dataset, i.e., the experimental composition profiles, or having multiple feasible solutions. Such an essence of being ill-posed cannot be generally resolved using the advanced optimization algorithms which are insufficient to sort out the “best” from the equivalent ones. However, enriching the diffusion information for inverse problem, e.g., increasing the number of diffusion couples being concerned and/or adopting interdiffusion fluxes as addition optimization criterion, does help reduce the severity of being ill-posed or limit the possible solutions. When sufficient diffusion couples are supplied, numerical inverse method is able to come up with interdiffusion coefficients which are independent with level of noises contained by the experimental data [53, 54].

Beyond enriching experimental data, one convention adopted frequently in the community of inverse problem is to apply prior assumptions to restrict the solutions [89], like the parameter selection and regularization. Taking the numerical inverse method proposed by Chen et al. [52] as an example, the model for “atomic mobility” parameters is subject to a nested model, i.e., Eq. (16). Following the CALPHAD convention, it is assumed that the less interaction parameters are utilized that the better generality of the assessed values of the interaction parameters. The problem arises as it is hard to balance between the extrapolation and explanatory capability of the proposed models. The criteria regarding both the objectives, e.g., information criteria [113], are therefore required to weigh between the fitting goodness and the number of effective parameters for the sake of joint parameter selection and parameter estimation. The satisfactory solution is further obtained by resolving the reformulated optimization problem with a proposed criterion as the surrogated objective. The regularization is generally served as another tool for preventing overfitting while improving the generality of the assessed model and estimated parameters [114, 115]. The generality is of special importance for CALPHAD modeling, which always emphasizes the parameters of lower order systems for extrapolating and predicting the states and properties of higher order ones. Similar to the parameter selection, a surrogated objective function is formulated by introducing penalty on L₁/L₂ norm to the original objective function.

Overall, for the lower order systems, i.e., binary and ternary systems, the extensive efforts have proved the validity and accuracy of both the Matano-based methods and the numerical inverse methods, while question remains for the higher order systems. Uniqueness of the solutions in numerical inverse methods is also partly addressed though the applications of advanced mathematical theorem remain to be detailed.

Case studies on high-throughput determination of interdiffusion coefficients

Ni-based superalloys

Ni-based superalloys represent one of the most essential materials for aeroengine applications due to their outstanding high-temperature mechanical properties and creep/oxidation resistance [116]. The creep deformation behavior of Ni-based single-crystal superalloys controls the service life of turbine blades [117], which significantly benefits from the alloying effect due to the complex constitution of superalloy. According to the empirical and/or semiempirical relations proposed in Refs.[117,118,119,120], the interdiffusion coefficients of solutes are one of the key factors determining the creep resistance of the Ni-based superalloys. For the purpose of optimizing and even improving the creep properties of Ni-based superalloys, accurate determination of interdiffusion coefficients in Ni-based superalloys is invaluable and indispensable. For the past decades, extensive researches have been devoted to this direction. The readers can refer to the very recent summary of the current status of the interdiffusion databank in the Ni-based superalloy by Zhang et al. [31] for detailed information. Here, only a demonstration on how to perform the high-throughput determination of interdiffusion coefficients in Ni-based superalloys, as well as some meaningful results, is given as follows.

As summarized above, a combination of the numerical inverse method and diffusion multiple technique can be used for high-throughput determination of interdiffusion coefficients in the target systems. Taking fcc Ni–Al–Cr system by Chen and Zhang [121] as an example, a fcc Ni–Al–Cr diffusion multiple was carefully prepared by means of the hot-pressing technique and subject to annealing at 1173 K for 180 h. The backscattered electron (BSE) image for the microstructure of the fcc Ni–Al–Cr diffusion multiple is demonstrated in Fig. 13. As can be seen, with single/multiple ensemble, one set of binary Ni–Cr composition profiles and four sets of ternary Ni–Al–Cr composition profiles at 1173 K can be harvested, as shown in Fig. 14. In the calculation procedure, the advantages of using atomic mobility parameters with physical meaning as the fitting parameters in the pragmatic numerical inverse method were applied to evaluate the composition-dependent interdiffusion coefficient matrix surface in Ni-rich fcc Ni–Al–Cr systems at 1173 K, as displayed in Fig. 15. The validation of the obtained interdiffusion coefficients can be verified by the consistency between the model-predicted composition profiles in the diffusion multiple and the experimental ones. Moreover, it should be noted that all the measured composition profiles in ternary Ni–Al–Cr system were addressed simultaneously in the same optimization process, resulting in one self-consistent set of atomic mobilities for fcc Ni–Al–Cr phase at 1173 K. Such self-consistent set of atomic mobilities together with the thermodynamic descriptions can be used to predict the reasonable interdiffusion coefficients over much wider composition range.

Furthermore, inspired with a common sense that lower diffusion ability might lead to better creep resistance of the desired alloy system, Chen et al. [8, 110, 122, 123] performed a series of experimental measurements of interdiffusion coefficients in fcc Ni–X and Ni–Al–X alloys (X = Ta, W, Re, Os, Ir or Pt) to discover potential substitutional elements for Re in the new-generation single-crystal Ni-based superalloys. For binary systems, the diffusion couple technique in combination with the Matano-based methods was employed to determine the composition- and temperature-dependent interdiffusion coefficients in fcc Ni–X systems. As for the ternary systems, multiple diffusion couples together with HitDIC software in the framework of pragmatic numerical inverse method were utilized to conduct the high-throughput measurement of composition- and temperature-dependent interdiffusivity matrices in fcc Ni–Al–X systems. The reliability of the determined interdiffusivities was validated by comprehensively comparing the model-predicted profiles of composition or interdiffusion flux for each diffusion couple with the corresponding experimental data. Moreover, the comparison with the interdiffusivities evaluated using the traditional Matano–Kirkaldy method as well as those from the literature and in boundary binary systems was conducted. Reliable interdiffusion coefficients over the concerned composition ranges were therefore obtained. The typical results of fcc Ni–Al–Re and Ni–Al–Os systems are presented in Fig. 16, in which the three-dimensional main interdiffusivity surfaces, i.e., $\tilde{D}_{{{\text{AlAl}}}}^{{{\text{Ni}}}}$, $\tilde{D}_{{{\text{ReRe}}}}^{{{\text{Ni}}}}$ in fcc Ni–Al–Re system, and $\tilde{D}_{{{\text{AlAl}}}}^{{{\text{Ni}}}}$, $\tilde{D}_{{{\text{OsOs}}}}^{{{\text{Ni}}}}$ in fcc Ni–Al-Os system, at 1473 K, 1523 K and 1573 K, are included. From such 3D interdiffusivity surfaces, one can clearly see the change in the main interdiffusivities with the compositions of solutes, and also temperature. A comprehensive comparison of the evaluated interdiffusion coefficients in binary fcc Ni–X and ternary fcc Ni–Al–X alloys is illustrated in Fig. 17. As can be seen, in binary systems, the diffusion rate of Os is always lower than that of Re over the investigated temperature range i.e., from 1473 to 1573 K, while in ternary systems, the diffusion rate of Re is lower than that of Os at 1473 K and 1523 K but is slightly higher at 1573 K. Thus, in terms of diffusion coefficients, it was highly proposed that Os might be the potential substitute for Re in the new-generation Ni-based single-crystal superalloys [8], which triggers the subsequent extensive studies on the Ni-based superalloys with element Os [124, 125].

High-entropy alloys

The high-entropy alloys, or multiprinciple element alloys, which open a new door for exploring the novel alloys, are gaining more and more attention in materials community nowadays. It was reported that the sluggish diffusion is responsible for endowing the high-entropy alloys with outstanding properties at high temperatures, e.g., mechanical, magnetic and electrochemical characteristics [126]. In 2003, Tsai et al. [127] performed the first measurement of diffusivities in fcc CoCrFeMnNi high-entropy alloys by using the quasi-binary diffusion couples together with the Boltzmann–Matano method, and their results supported the core effect of sluggish diffusion in high-entropy alloys. However, Paul [128] commented on the method used by Tsai et al. [127] and questioned their derived diffusion data. Thus, whether the sluggish diffusion exists in the high-entropy alloys is still in question. In order to reveal the nature of diffusion behaviors in high-entropy alloys, it is necessary to perform large amount of accurate measurement of diffusivities in high-entropy alloys, as one of the research hot spots in the materials community [8, 9, 102, 103, 127, 129,130,131,132,133]. All the related literature reports up to now can be divided into two categories. The major one contributes to the determination of interdiffusion coefficients in fcc high-entropy alloys [8, 9, 102, 103, 127, 129,130,131,132,133], while the minor one contributes to the measurement of tracer diffusion coefficients in high-entropy alloys [134,135,136].

Since 2017, the diffusion multiple technique combined with the HitDIC software has been employed to conduct the high-throughput determination of interdiffusion coefficients in three types of high-entropy alloys, including fcc CoCrFeMnNi [129], fcc AlCoCrFeNi [100] and fcc CoCrCuFeNi [101]. The typical results in fcc CoCrFeMnNi and CoCrCuFeNi high-entropy alloys are presented in Figs. 18 and 19, respectively. Chen et al. [129] prepared a CoCrFeMnNi diffusion multiple schematically displayed in Fig. 18a using the hot-pressing technique. After annealing at 1373 K for 120 h, four groups of composition profiles in fcc CoCrFeMnNi high-entropy alloys were measured from such a diffusion multiple using EPMA technique. The corresponding quinary main interdiffusivities in the Co–Cr–Fe–Mn–Ni HEAs at 1373 K are determined by the pragmatic numerical inverse method and shown in Fig. 18b. As for fcc CoCrCuFeNi high-entropy alloys, a simplified sandwich-type diffusion multiple, schematically displayed in Fig. 19a, was employed by Wang et al. [101]. In total, three such sandwich diffusion multiples were prepared and subjected to annealing at 1273, 1323 and 1373 K for 72 h. The typical results of the composition profiles, interdiffusion fluxes and interdiffusion coefficients are presented in Fig. 19b.

With the determined numbers of interdiffusion coefficients in different fcc high-entropy alloys, a comprehensive comparison with those in the lower-order systems was also performed by Chen et al. [129], as shown in Fig. 20. In terms of the interdiffusion coefficients, it can be found that the binary interdiffusivities are larger than the ternary ones and are much larger than the ones for quinary systems. When it comes to the tracer diffusion coefficients, the tracer diffusivities of Ni in quinary alloys are lower than the data in binary alloys but larger than the values in ternary and quaternary alloys. Thus, it was concluded that the sluggish diffusion characteristic of Co–Cr–Fe–Mn–Ni HEAs exists from the point of view of interdiffusion coefficients, rather than the tracer diffusion coefficients [129]. Moreover, a similar conclusion was also drawn by Wang et al. [101] for the fcc Co–Cr–Cu–Fe–Ni HEAs.

The over-detailed discussion is avoided here to focus on the motivation and vision of the subject of this manuscript. More elaborative demonstrations on revealing the sluggish diffusion effect of the high-entropy alloys can be referred in the extensive investigations from the materials community [7, 100, 101, 103, 127, 130, 134, 135].

High-entropy superalloys

To develop novel superalloys with lower density and lower cost is one of the ultimate goals in the high-temperature materials technology. In 2015, Yeh et al. [137] reported a novel superalloy, i.e., AlCoCrFeNiTi-based high-entropy superalloy (HESA), which owns the composition space in between the traditional Ni-based superalloys and HEAs. HESAs were found to possess comprehensive mechanical properties attributed to their similar microstructure to the conventional Ni-based superalloys (i.e., fcc-γ and L1₂-γ′ precipitates) in combination with the similar properties to the traditional high-entropy alloys (HEAs). Meanwhile, with few or even no refractory elements, HESAs are with much lower density as well as lower cost than the traditional superalloys. In order to further validate whether such novel HESAs can be a candidate for substituting the traditional Ni-based superalloys, the creep resistance, which was reported to be related to diffusivities in the γ matrix [138], is one key factor. Thus, there is also a need to measure the accurate interdiffusion coefficients in the fcc AlCoCrFeNiTi alloys.

Very recently, Chen et al. [102] employed the similar sandwich diffusion multiple technique together with HitDIC software to conduct the high-throughput determination of composition-dependent interdiffusivities in fcc AlCoCrFeNiTi alloys over the composition range of HESAs. The three sets of measured composition profiles, due to the prepared sandwich diffusion multiple annealed at 1473 K for 32 h, are shown in Fig. 20a, while the calculated main interdiffusion coefficients of Al, Co, Cr, Fe and Ti at 1473 K along the three diffusion paths are displayed in Fig. 20b. Furthermore, the comparison of the main interdiffusivities in fcc AlCoCrFeNiTi HESA with the literature data in fcc Ni–X (X–Al, Co, Cr, Fe, Ti) alloys [139,140,141], fcc Ni–Y (Y–Re, Mo, W, Ta, Rh, Os, Ir, Nb, Ru, Pd and Pt) alloys [110, 123, 142,143,144] and fcc Ni–Al–X (X = Re, Mo, W, Ta, Rh, Os and Ir) alloys [8, 110, 111] is illustrated in Fig. 21. As clearly indicated in Fig. 21, the interdiffusivities in fcc AlCoCrFeNiTi HESAs are lower than those in Ni-based superalloys with most refractory elements, but higher than those with Ir, Re and Os.

Uncertainty quantification for high-quality interdiffusion coefficients

As stated above, extensive efforts have been made to develop different programs of high usability and availability for the high-throughput determination of interdiffusion coefficients by means of the Matano-based methods and numerical inverse methods and to apply those methods in determination of the interdiffusion coefficients for various systems. However, the uncertainty quantification for the obtained interdiffusion coefficients yet remains an another thoughtful concern. Unfortunately, in most publications available [64,65,66,67,68,69,70,71,72,73], the uncertainty quantification was simply neglected due to its complexity. In this section, the approaches for quantifying the interdiffusion coefficients evaluated from the two types of methods, including Matano-based methods and the numerical inverse methods, are summarized.

Uncertainty quantification for Matano-based methods

Up to now, only several reports about quantifying uncertainties of the interdiffusion coefficients in binary systems have been covered [55, 56]. In 2007, Ben Abdellah et al. [55] made a first attempt to quantify the uncertainty of interdiffusion coefficients in binary system evaluated using the Boltzmann–Matano method. However, Ben Abdellah et al. [55] considered the error sourced from the measurement of composition to be constant. Moreover, uncertainty propagation through the fitting procedure was not taken into account, as well as the uncertainty sourced from the determination of the Matano plane. Later, Lechelle et al. [56] advanced the uncertainty of interdiffusion coefficients in the framework of the Boltzmann–Matano method considering both fitting and experimental errors together with their propagation in the evaluation of interdiffusion coefficients. But the fitting function for composition profiles is prescribed by Lechelle et al. [56], and thus derived parameters and relation to the uncertainties are not generalized with other fitting functions, e.g., distribution functions. As a broad generalization, such reports generally calculate interdiffusion coefficients based on Boltzmann–Matano method and its variances and quantified the uncertainty from the frequentist point of view. The uncertainty propagated from sources to the results is measured by means of the mathematical relations between the sources of uncertainty and the interdiffusion coefficients, while quantifying the quantity of uncertainties together with the derivatives of mathematical relations. Another alternative for quantifying the uncertainty of various computation processes can be fulfilled from the point of view of Bayesian inference. Boettinger et al. [57] performed the analysis of uncertainty differently by using the Gaussian process to simulate the effect of the noises on the calculated interdiffusion coefficients, belonging to the category of Bayesian inference. New efforts on quantifying the uncertainties among the interdiffusion coefficients from the point of view of frequentist and Bayesian inference [145] are subsequently summarized as follows.

One of the pioneering researches on promoting a general framework on quantifying the uncertainties of the interdiffusion coefficients in binary, ternary and multicomponent systems was recently conducted by Wu et al. [146] based on the Matano-based methods together with the distribution functions. Notably, the generation and propagation of various errors, various kinds of fitting functions and evaluation methods were comprehensively addressed. A demonstration of the work by Wu et al. [146] can be inferred from a benchmark test in a fictitious binary system demonstrated in Fig. 22. As shown in Fig. 22a, an ideal set of composition profiles was imitated by Fick’s second law combined with the explicit finite difference scheme based on the preset $\tilde{D}\sim c$ relation, i.e., $\tilde{D} = 10^{ - 14} \left[ {2 + {\ln}\left( {536c + 1} \right)} \right]$, where the unit of interdiffusion coefficient is $m^{2} /s$, while that of composition is atomic fraction. A level of noise ($\delta = 2.0 \times 10^{ - 3}$) was also imposed in the simulated profiles to mimic the “experimental” composition profiles. Then, the ideal composition profile was used to retrieve the composition-dependent interdiffusion coefficients using both the Boltzmann–Matano and Sauer–Freise methods together with the distribution function. The resultant interdiffusion coefficients are displayed in Fig. 22d for a direct comparison with the “true” values, i.e., the preset $\tilde{D}\sim c$ relation. Meanwhile, the man-made noise among the “experimental” data was propagated into the subsequent fitting and computation procedures. Consequent confidence interval of the Matano position is further calculated and imposed in Fig. 22a based on the smoothed composition profiles, taking the error propagation among fitting processes into consideration as well. Knowledge of uncertainty of the Matano position is considerable, which is to be resolved for the Boltzmann–Matano method. Confidence interval for the slopes and interdiffusion fluxes can also be calculated according to the formalism of error propagation, as illustrated in Fig. 22b, c. It is worthy of mentioning that the estimated confidence intervals due to the two different approaches for the evaluation of the interdiffusion fluxes distinguish from each other, as shown in Fig. 22c. Thus, the distinguishable difference among the confidence interval of the interdiffusion fluxes is finally inherited by the evaluated confidence interval for the interdiffusion coefficients, shown in Fig. 22d. It can be clearly seen in Fig. 22d that the evaluated interdiffusion coefficients using the Boltzmann–Matano and Sauer–Freise methods are exactly the same and consistent with the true values, which locate well in the confidence intervals of the evaluated interdiffusion coefficients using the two methods.

Application of the proposed framework in a practical study case was also reported by Wu et al. [146], where the interdiffusion coefficients as well as the confidence interval of the fcc CoCrFeMnNi alloys at 1273 K were evaluated, as illustrated in Fig. 23. In Fig. 23a, a good fitting goodness is obtained for the smoothed composition profiles based on the distribution function. By means of the pseudo-binary method, the interdiffusion coefficients in the pseudo-binary system were subsequently computed in Fig. 23b, together with the evaluated confidence intervals. Moreover, the evaluated interdiffusion coefficients by Paul et al. [128] were also superimposed for a direct comparison. As shown in Fig. 23b, the calculated interdiffusion coefficients using the pseudo-binary method together with the distribution function agree well with the results by Paul et al. [128], which also lie well over the determined confidence intervals.

As demonstrated in Fig. 22, different methods for evaluation of interdiffusion coefficients result in different confidence intervals due to the different propagation paths of the errors. When it comes to the effect of different fitting functions, the similar result can be also found, as demonstrated in Fig. 24. In Fig. 24a, another set of ideal “experimental” composition profiles was generated by following the same strategy adopted in Fig. 22a but with different preset $\tilde{D}\sim c$ relation, composition range and noise level. Different fitting functions, e.g., the distribution function, double-superimposed Boltzmann function and double-superimposed error function, were employed to fit the ideal composition profile. As shown in Fig. 24a, all the functions tend to produce similar fitting goodness to the imitated composition profiles. With the composition profiles fitted using different fitting functions, the interdiffusion coefficients were then evaluated using the Sauer–Freise method, as shown in Fig. 24b. With the framework for uncertainty quantification developed by Wu et al. [146], the uncertainties can be quantified for the evaluated interdiffusion coefficients due to different fitting functions, as also included in Fig. 24b. As clearly indicated in Fig. 24b, based on the same Sauer–Freise method, the evaluated interdiffusion coefficients due to the distribution function agree best with the preset $\tilde{D}\sim c$ relation, and the corresponding confidence intervals are also the narrowest. But one more important note concerns that the preset $\tilde{D}\sim c$ relation well locates over the evaluated confidence intervals of the interdiffusion coefficients due to all types of fitting functions, indicating the reliability of the general framework on uncertainty quantification developed by Wu et al. [146].

Uncertainty quantification for numerical inverse methods

Distinguishing from the canonical methods, the numerical inverse method does not rely on explicit mathematical relations from the experimental composition profiles to the finally obtained interdiffusion coefficients, which is merely a least square problem constrained by the diffusion equations, i.e., Eq. (11). Consequently, from the frequentist point of view, the estimation of the confidence levels of the model parameters in the inverse problems is difficult as the inverse processes are usually extremely non-linear and non-differentiable. Different from the perspective of such classical statistics, Bayesian inference generally provides the incredible convenience for tackling complex analytical problems, irrespective of the computation processes and the size of data [147,148,149,150]

The latest effort endeavoring to quantify the uncertainty of “atomic mobility” parameter was from the present authors [58]. The Metropolis–Hasting algorithm was adopted by Zhong et al. [58] in order to draw the posterior distributions of the “atomic mobility” parameters, i.e., in the fcc Ni–Al–Ta alloy, as shown in Fig. 25. Generally, the “atomic mobility” parameters with the determined uncertainties can be applied for profiling the uncertainty of the interdiffusion coefficients, together with the thermodynamic descriptions. As a fact that “atomic mobility” is more favorable of being stored in the kinetic database, such a backward propagation process is not intended to be demonstrated in the current context. Nevertheless, Bayesian inference is able to come up with the probability density proportional to a known function, to which the explicit relation and derivatives with respect to the concerned parameters are not the prerequisite. However, the Markov chain Monte Carlo algorithm, i.e., Metropolis–Hasting algorithm, usually converges slowly. Sufficient iterations for random walks, i.e., 10000 for problem with three parameters of interest, are demanded to offer a good representation of the target posterior distribution. Therefore, the convergence diagnostics is helpful in preventing the unexpected waste of computing resources and time, as well as offering convincing evidence for the assessed values and uncertainty for the parameters of interest.

Taking fcc Ni–Al–Ta alloys as an example, the characteristics of the chains [145], i.e., between sequence variance, within sequence variance and potential scale reduction factor, can be calculated, respectively, as shown in Fig. 26. Generally, the multiple chains are in need of providing diverse starting points guaranteeing convergence to global optimal, while ten chains have been constructed for this study case of the fcc Ni–Al–Ta alloy. Alternative algorithms [151,152,153], other than the naive Metropolis–Hasting algorithm, usually rely on a more complicated theory and are harder to implement, but they usually suffer less from autocorrelation and converge faster. Such advanced algorithms would be indispensable when the number of the concerned parameters grows, especially for the multicomponent systems and multiprinciple component systems.

Currently, the Bayesian inference with the Metropolis–Hasting algorithm has been implemented in latest version of HitDIC software. In terms of determining the atomic mobility parameters, the accurate thermodynamic description is always the prerequisite in order to retain the physical meaning of the concerned parameters. The same convention applies to the quantification of the uncertainty of the atomic mobility parameters, which undergo simultaneous process for the determination of the concerned interaction parameters [58].

Conclusions and perspectives

In this review, all the literature efforts on the computational aspects for evaluation of interdiffusion coefficients in metallic solids were comprehensively summarized, with a focus on two keywords, i.e., “high-quality” and “high-throughput.” The traditional Matano-based methods together with the recently developed pseudo-binary/ternary approaches and distribution functions, the numerical inverse methods, especially the pragmatic numerical inverse method and HitDIC software as well as their applications in several real cases, and the uncertainty quantification approaches were introduced and discussed. It can be finally concluded that the recent fascinating progress makes the high-throughput determination of high-quality interdiffusion coefficients in metallic solids feasible now. Moreover, the reliable high-throughput computational methods/tools and the resultant high-quality interdiffusivity databank, together with the diffusion multiple technique for high-throughput measurement, generally constitute the solid infrastructures of the MGI [59, 60], ICME [154], and even machine learning projects for novel materials design. With this review, the following two major conclusions can be reached:

(1) The pseudo-binary and pseudo-ternary approaches enrich the family of the Matano-based methods and can be used to evaluate the interdiffusion coefficients in multicomponent systems by carefully designing the pseudo-binary and -ternary diffusion couples. Then, the integration of the Matano-based methods, the distribution functions and the uncertainty quantification facilitate the determination of “high-quality” interdiffusion coefficients in metallic solids with any number of components.

(2) The numerical inverse method has the natural advantage in high-throughput determination of the composition- and temperature-dependent interdiffusion coefficients in metallic solids, especially in multicomponent systems. With the careful strategies on ensuring the accuracy and uniqueness of the solutions, and uncertainty quantification, the numerical inverse method (and related software) can be utilized to perform the high-throughput determination of high-quality interdiffusion coefficients in metallic solids with any number of components in combination with the advanced diffusion multiple technique.

As demonstrated in this review, great progress on high-throughput determination of high-quality interdiffusion coefficients in metallic solids has been achieved. In pursuance of further advance this field, the following points are highly recommended to follow up:

The first point remains under further improvement in the uncertainty quantification approach for the pragmatic numerical inverse method. In the recent publication by Zhong et al. [58], only the error source from the composition profiles and its propagation was considered. With a view to fully characterize all the error sources, the uncertainty generated from the calculation of thermodynamic factors due to the thermodynamic descriptions and its propagation should be included. In fact, there are some reports on quantification of the thermodynamic interaction parameters for the CALPHAD-type thermodynamic databases [155,156,157,158]. Therefore, accommodation of propagation of the uncertainties from the thermodynamic description into the atomic mobility is considerable.

The second point is the automation of all the procedures in the evaluation of interdiffusion coefficients using the numerical inverse method. The demand for automation is mainly due to the problem with uniqueness of results from the numerical inverse method. The potential parameter selection and estimation procedures are to be conducted to fulfill the accuracy and generality of the evaluated kinetic descriptions, e.g., the optimization techniques combined with the information criteria. The computation utilities, e.g., HitDIC, are to be developed and advanced for facilitating a user-friendly workflow with the advanced techniques and methods.

The third point is to realize the novel alloy design by integrating the established interdiffusivity databank and the machine learning technique. In recent years, large datasets of high quality for diffusion properties, supported by high-throughput experiments combined with the advanced computation approaches and the increasing computing power, grow rapidly, as reviewed in this manuscript. The fact that datasets for diffusion properties are sparse in the high-dimension composition space is urging on advanced techniques beyond intuitive understanding the potential effects on the materials performance. For superalloys, as well as other systems, a deep abstraction over the readily obtained interdiffusion coefficients, together with other physical properties, toward mechanical and performance properties, like the creep resistance, is one of the promising innovations on promoting the materials design.

References

Boettinger WJ, Coriell SR, Greer A et al (2000) Solidification microstructures: recent developments, future directions. Acta Mater 48:43–70
Article CAS Google Scholar
Shewmon P (2016) Diffusion in solids, 2nd edn. Springer, Switzerland
Book Google Scholar
Warnken N, Ma D, Drevermann A et al (2009) Quantitative simulations of microstructure evolution in single crystal superalloys during solution heat treatment. Int Heat Treat Surf Eng 3:40–44
Article Google Scholar
Xia X, Peng Y, Zhang J et al (2019) Precipitation and growth behavior of γ′ phase in Ni₃Al-based superalloy under thermal exposure. J Mater Sci 54:13368–13377. https://doi.org/10.1007/s10853-019-03821-0
Article CAS Google Scholar
Ta N, Zhang L, Li Q et al (2018) High-temperature oxidation of pure Al: kinetic modeling supported by experimental characterization. Corros Sci 139:355–369
Article CAS Google Scholar
Barda H, Rabkin E (2020) Metal hetero-diffusion along the metal-ceramic interfaces: A case study of Au diffusion along the Ni-sapphire interface. Acta Mater 186:242–249
Article CAS Google Scholar
Divinski SV, Pokoev AV, Esakkiraja N, Paul A (2018) A mystery of “sluggish diffusion” in high-entropy alloys: the truth or a myth? In: Diffusion foundations. Trans Tech Publ, New York, pp 69–104
Chen J, Zhang L, Lu X-G (2018) Screening of possible re-substitutional elements in single-crystal Ni-based superalloys: a viewpoint from interdiffusion coefficients in Ni–Al–X Ternaries. Metall Mater Trans A 49:2999–3010
Article CAS Google Scholar
Zhang L, Du Y, Steinbach I et al (2010) Diffusivities of an Al–Fe–Ni melt and their effects on the microstructure during solidification. Acta Mater 58:3664–3675
Article CAS Google Scholar
Sutherland W (1905) LXXV. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. Lond Edinb Dublin Philos Mag J Sci 9:781–785
Article CAS Google Scholar
Einstein A (1905) On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat. Ann Phys 17:549–560
Article CAS Google Scholar
Borgenstam A, Höglund L, Ågren J, Engström A (2000) DICTRA, a tool for simulation of diffusional transformations in alloys. J Phase Equilib 21:269–280
Article CAS Google Scholar
Chen Q, Wu K, Sterner G, Mason P (2014) Modeling precipitation kinetics during heat treatment with Calphad-based tools. J Mater Eng Perform 23:4193–4196
Article CAS Google Scholar
Zhang L, Chen Q (2017) CALPHAD-type modeling of diffusion kinetics in multicomponent alloys. In: Handbook of solid state diffusion, vol 1, Elsevier, Amsterdam, pp 321–362
Zhang L (2018) Diffusion foundations vol 15: modeling of diffusion and diffusion-controlled phase transformations in alloys. Trans Tech Publications Limited, New York
Steinbach I (2009) Phase-field models in materials science. Model Simul Mater Sci Eng 17:073001
Article CAS Google Scholar
Bellemans I, Moelans N, Verbeken K (2018) Phase-field modelling in extractive metallurgy. Crit Rev Solid State 43:417–454
Article CAS Google Scholar
Steinbach I, Zhang L, Plapp M (2012) Phase-field model with finite interface dissipation. Acta Mater 60:2689–2701
Article CAS Google Scholar
Zhang L, Steinbach I (2012) Phase-field model with finite interface dissipation: extension to multi-component multi-phase alloys. Acta Mater 60:2702–2710
Article CAS Google Scholar
Andersson J, Ågren J (1992) Models for numerical treatment of multicomponent diffusion in simple phases. J Appl Phys 72:1350–1355
Article CAS Google Scholar
Jönsson B (1992) On ferromagnetic ordering and lattice diffusion: a simple model. Z Metallkd 83:349–355
Google Scholar
Helander T, Ågren J (1999) A phenomenological treatment of diffusion in Al–Fe and Al–Ni alloys having B2-bcc ordered structure. Acta Mater 47:1141–1152
Article CAS Google Scholar
Hallström S, Höglund L, Ågren J (2011) Modeling of iron diffusion in the iron oxides magnetite and hematite with variable stoichiometry. Acta Mater 59:53–60
Article CAS Google Scholar
Zhang L, Chen Q (2016) Revisiting the phenomenological model for effect of chemical ordering on diffusion. Intermetallics 70:72–81
Article CAS Google Scholar
Kaufman L, Bernstein H (1970) Computer calculation of phase diagrams. Academic Press, New York
Google Scholar
Sundman B, Jansson B, Andersson J-O (1985) The Thermo-Calc databank system. Calphad 9:153–190
Article CAS Google Scholar
Zhang L, Du Y, Ouyang Y et al (2008) Atomic mobilities, diffusivities and simulation of diffusion growth in the Co–Si system. Acta Mater 56:3940–3950
Article CAS Google Scholar
Zhang L, Du Y, Chen Q et al (2010) Atomic mobilities and diffusivities in the fcc, L12 and B2 phases of the Ni–Al system. Int J Mater Res 101:1461–1475
Article CAS Google Scholar
Kodentsov AA, Bastin GF, van Loo FJJ (2007) Application of diffusion couples in phase diagram determination. In: Methods for phase diagram determination. Elsevier, Amsterdam, pp 222–245
Kodentsov A, Paul A (2017) Diffusion couple technique: a research tool in materials science. In: Handbook of solid state diffusion, vol 2, Elsevier, Amsterdam, pp 207–275
Zhang LJ, Chen J, Chen WM et al (2017) Interdiffusion databanks of γ, γ′ and β phases in NiAl-based ternary systems. Diffus Found 13:136–166
Article CAS Google Scholar
Chen W, Li Q, Zhang L (2017) A novel approach to eliminate the effect of external stress on interdiffusivity measurement. Materials 10:961
Article CAS Google Scholar
Matano C (1933) On the relation between the diffusion-coefficients and concentrations of solid metals. Jpn J Appl Phys 8:109–113
CAS Google Scholar
Kirkaldy JS, Young DJ (1987) Diffusion in the condensed state. Institute of Metals, London
Google Scholar
Dayananda MA, Sohn YH (1999) A new analysis for the determination of ternary interdiffusion coefficients from a single diffusion couple. Metall Mater Trans A 30:535–543
Article Google Scholar
Sauer F, Freise V (1962) Diffusion in binären Gemischen mit Volumenänderung. Zeitschrift für Elektrochemie, Berichte der Bunsengesellschaft für physikalische Chemie 66:353–362
CAS Google Scholar
Wagner C (1969) The evaluation of data obtained with diffusion couples of binary single-phase and multiphase systems. Acta Metall 17:99–107
Article CAS Google Scholar
Thompson MS, Morral JE (1986) The square root diffusivity. Acta Metall 34:2201–2203
Article CAS Google Scholar
Paul A (2013) A pseudobinary approach to study interdiffusion and the Kirkendall effect in multicomponent systems. Philos Mag 93:2297–2315
Article CAS Google Scholar
Esakkiraja N, Paul A (2018) A novel concept of pseudo ternary diffusion couple for the estimation of diffusion coefficients in multicomponent systems. Scripta Mater 147:79–82
Article CAS Google Scholar
Esakkiraja N, Pandey K, Dash A, Paul A (2019) Pseudo-binary and pseudo-ternary diffusion couple methods for estimation of the diffusion coefficients in multicomponent systems and high entropy alloys. Philos Mag 99:2236–2264
Article CAS Google Scholar
Fuller CS, Ditzenberger JA (1956) Diffusion of donor and acceptor elements in silicon. J Appl Phys 27:544–553
Article CAS Google Scholar
Nikitin AG, Spichak SV, Vedula YS, Naumovets AG (2009) Symmetries and modelling functions for diffusion processes. J Phys D: Appl Phys 42:055301
Article CAS Google Scholar
Wang J, Li N, Wang C et al (2016) Computational study of atomic mobility in hcp Mg–Al–Zn ternary alloys. Calphad 54:134–143
Article CAS Google Scholar
Liu D, Zhang L, Du Y et al (1073K) Ternary diffusion in Cu-rich fcc Cu–Al–Si alloys at 1073K. J Alloys Compd 566:156–163
Article CAS Google Scholar
Cheng K, Liu D, Zhang L et al (2013) Interdiffusion and atomic mobility studies in Ni-rich fcc Ni−Al−Mn alloys. J Alloys Compd 579:124–131
Article CAS Google Scholar
Xu H, Chen W, Zhang L et al (2015) High-throughput determination of the composition-dependent interdiffusivities in Cu-rich fcc Cu–Ag–Sn alloys at 1073 K. J Alloys Compd 644:687–693
Article CAS Google Scholar
Wei M, Zhang L (2018) Application of distribution functions in accurate determination of interdiffusion coefficients. Sci Rep 8:5071
Article CAS Google Scholar
Bouchet R, Mevrel R (2002) A numerical inverse method for calculating the interdiffusion coefficients along a diffusion path in ternary systems. Acta Mater 50:4887–4900
Article CAS Google Scholar
Kucza W (2012) A combinatorial approach for extracting thermo-kinetic parameters from diffusion profiles. Scr Mater 66:151–154
Article CAS Google Scholar
Zhang Q, Zhao J-C (2013) Extracting interdiffusion coefficients from binary diffusion couples using traditional methods and a forward-simulation method. Intermetallics 34:132–141
Article CAS Google Scholar
Chen W, Zhang L, Du Y et al (2014) A pragmatic method to determine the composition-dependent interdiffusivities in ternary systems by using a single diffusion couple. Scripta Mater 90–91:53–56
Article CAS Google Scholar
Chen W, Zhong J, Zhang L (2016) An augmented numerical inverse method for determining the composition-dependent interdiffusivities in alloy systems by using a single diffusion couple. MRS Commun 6:295–300
Article CAS Google Scholar
Zhong J, Chen W, Zhang L (2018) HitDIC: A free-accessible code for high-throughput determination of interdiffusion coefficients in single solution phase. Calphad 60:177–190
Article CAS Google Scholar
Ben Abdellah A, Gasser JG, Bouziane K et al (2007) Experimental procedure to determine the interdiffusion coefficient of miscibility gap liquid alloys: case of GaPb system. Phys Rev B 76:174203
Article CAS Google Scholar
Lechelle J, Noyau S, Aufore L et al (2012) Volume interdiffusion coefficient and uncertainty assessment for polycrystalline materials. Diffus Fund 17:1–39
Google Scholar
Boettinger WJ, Williams ME, Moon K-W et al (2017) Interdiffusion in the Ni–Re system: evaluation of uncertainties. J Phase Equilib Diffus 38:750–763
Article CAS Google Scholar
Zhong J, Zhang L, Wu X et al (2020) A novel computational framework for establishment of atomic mobility database directly from composition profiles and its uncertainty quantification. J Mater Sci Technol 48:163–174
Article Google Scholar
McDowell DL, Kalidindi SR (2016) The materials innovation ecosystem: a key enabler for the materials genome initiative. MRS Bull 41:326–337
Article Google Scholar
Agrawal A, Choudhary A (2016) Perspective: Materials informatics and big data: realization of the “fourth paradigm” of science in materials science. APL Mater 4:053208
Article CAS Google Scholar
de Pablo JJ, Jackson NE, Webb MA et al (2019) New frontiers for the materials genome initiative. NPJ Comput Mater 5:41
Article Google Scholar
Zhao J-C, Zheng X, Cahill DG (2005) High-throughput diffusion multiples. Mater Today 8:28–37
Article CAS Google Scholar
Whittle D, Green A (1974) The measurement of diffusion coefficients in ternary systems. Scripta Metall 8:883–884
Article CAS Google Scholar
Li J, Liu T, Chen W et al (2014) Interdiffusion coefficients and atomic mobilities in fcc Cu–Fe–Mn alloys. J Min Metall B 50:93–99
Article Google Scholar
Kuang D, Liu D, Chen W et al (2016) Interdiffusion in bcc_B2 Ni–Al–Cu alloys at 1 173 K. Int J Mater Res 107:597–604
Article CAS Google Scholar
Ugaste Ü, Kodentsov AA, Van Loo F (2013) Concentration dependence of interdiffusion coefficients in Cu–Fe–Ni system. Phys Met Metallogr 114:54–62
Article Google Scholar
Chang H, Xu G, Lu X-G et al (2015) Experimental and phenomenological investigations of diffusion in Co–Al–W alloys. Scripta Mater 106:13–16
Article CAS Google Scholar
Chen J, Liu Y, Sheng G et al (2015) Atomic mobilities, interdiffusivities and their related diffusional behaviors in fcc Co–Cr–Ni alloys. J Alloys Compd 621:428–433
Article CAS Google Scholar
Moon K-W, Campbell C, Williams M, Boettinger W (2016) Diffusion in FCC Co-rich Co–Al–W Alloys at 900 and 1000 C. J Phase Equilib Diffus 37:402–415
Article CAS Google Scholar
Tripathi A, Middleton S, Lavernia EJ et al (2018) Ternary interdiffusion in β (BCC) phase of the Ti–Al–Nb system. J Phase Equilib Diffus 39:841–852
Article CAS Google Scholar
Wang C, Qin S, Lu Y et al (2018) Interdiffusion and atomic mobilities in fcc Co–Cr–Mo alloys. J Phase Equilib Diffus 39:437–445
Article CAS Google Scholar
Wang Y, Wang J, Wang H et al (2018) Thermodynamic description of the Ni–Mo–W system and interdiffusion study of its fcc phase. Calphad 61:165–172
Article CAS Google Scholar
Bai W, Xu G, Yang Z et al (2019) Diffusivities and atomic mobilities in bcc TiNbTa alloys. Calphad 65:299–315
Article CAS Google Scholar
Day KM, Ram-Mohan LR, Dayananda MA (2005) Determination and assessment of ternary interdiffusion coefficients from individual diffusion couples. J Phase Equilib Diffus 26:579–590
Article CAS Google Scholar
Cermak J, Rothova V (2003) Concentration dependence of ternary interdiffusion coefficients in Ni3Al/Ni3Al–X couples with X=Cr, Fe, Nb and Ti. Acta Mater 51:4411–4421
Article CAS Google Scholar
Cheng K, Chen W, Liu D et al (2014) Analysis of the Cermak-Rothova method for determining the concentration dependence of ternary interdiffusion coefficients with a single diffusion couple. Scripta Mater 76:5–8
Article CAS Google Scholar
Morral JE (1984) Rate constants for interdiffusion. Scripta. Metall 18:1251–1256
CAS Google Scholar
Morral JE, Hopfe WD (2014) Validation of multicomponent diffusivities using one diffusion couple. J Phase Equilib Diffus 35:666–669
Article CAS Google Scholar
Sekerka RF (2004) Similarity solutions for a binary diffusion couple with diffusivity and density dependent on composition. Prog Mater Sci 49:511–536
Article CAS Google Scholar
Rohrberg D, Spitzer K-H, Dörrer L et al (2008) Interdiffusion in ternary Fe–Cr –Al alloys with variable molar volume. Mater High Temp 25:247–255
Article CAS Google Scholar
Santra S, Paul A (2015) Role of the molar volume on estimated diffusion coefficients. Metall Mater Trans A 46:3887–3899
Article CAS Google Scholar
Santra S, Paul A (2015) Estimation of intrinsic diffusion coefficients in a pseudo-binary diffusion couple. Scripta Mater 103:18–21
Article CAS Google Scholar
Belova IV, Murch GE (2019) Comments on “Experimental assessment of the thermodynamic factor for diffusion in CoCrFeNi and CoCrFeMnNi high entropy alloys”. Scripta Mater 172:110–112
Article CAS Google Scholar
Tas Kavakbasi B, Golovin IS, Paul A, Divinski SV (2018) On the analysis of composition profiles in binary single-phase diffusion couples: systems with a strong compositional dependence of the interdiffusion coefficient. Defect Diffus Forum 383:23–30
Article Google Scholar
Rabkin E, Semenov V, Winkler A (2002) Percolation effects during interdiffusion in the Cu–NiAl system. Acta Mater 50:3229–3239
Article Google Scholar
Xu H, Zhang L, Cheng K et al (2017) Reassessment of atomic mobilities in fcc Cu–Ag–Sn system aiming at establishment of an atomic mobility database in Sn–Ag–Cu–In–Sb–Bi–Pb solder alloys. J Electron Mater 46:2119–2129
Article CAS Google Scholar
Beck JV, Blackwell B, Clair CR Jr (1985) Inverse heat conduction: ill-posed problem. Wiley, New York
Google Scholar
Keung YL, Zou J (1998) Numerical identifications of parameters in parabolic systems. Inverse Prob 14:83–100
Article Google Scholar
Tarantola A (2005) Inverse problem theory and methods for model parameter estimation. Society for Industrial and Applied Mathematics, Paris
Book Google Scholar
Rappaz M, Rappaz M, Bellet M, Deville MO (2010) Numerical modeling in materials science and engineering. Springer, Berlin
Google Scholar
Bouchet R, Mevrel R (2003) Calculating the composition-dependent diffusivity matrix along a diffusion path in ternary systems: Application to β-(Ni, Pt) Al. Calphad 27:295–303
Article CAS Google Scholar
Fujita H, Gosting LJ (1956) An exact solution of the equations for free diffusion in three-component systems with interacting flows, and its use in evaluation of the diffusion coefficients. J Am Chem Soc 78:1099–1106
Article CAS Google Scholar
Zhu L, Chen Z, Zhong W et al (2019) Measurement of diffusion coefficients in the bcc phase of the Ti–Sn and Zr–Sn binary systems. Metall Mater Trans A 50:1409–1420
Article CAS Google Scholar
Chen Z, Zhang Q, Zhao J-C (2019) pydiffusion: a python library for diffusion simulation and data analysis. J Open Res Softw 7:13
Article Google Scholar
Eastman CM, Zhao J-C (2019) Phase equilibria and diffusion in the Ni–Cr–Pt system at 1200° C. J Phase Equilib Diffus 40:542–552
Article CAS Google Scholar
Zhong W, Hooshmand MS, Ghazisaeidi M et al (2020) An integrated experimental and computational study of diffusion and atomic mobility of the aluminum–magnesium system. Acta Mater 189:214–231
Article CAS Google Scholar
Manning JR (1970) Cross terms in the thermodynamic diffusion equations for multicomponent alloys. Metall Mater Trans B 1:499–505
Article CAS Google Scholar
Manning JR (1971) Correlation factors for diffusion in nondilute alloys. Phys Rev B 4:1111–1121
Article Google Scholar
Xu H, Cheng K, Zhong J et al (2019) Determination of accurate interdiffusion coefficients in fcc Ag–In and Ag–Cu–In alloys: a comparative study on the Matano method with distribution function and the numerical inverse method with HitDIC. J Alloys Compd 798:26–34
Article CAS Google Scholar
Li Q, Chen W, Zhong J et al (2017) On sluggish diffusion in Fcc Al–Co–Cr–Fe–Ni high-entropy alloys: an experimental and numerical study. Metals 8:16
Article CAS Google Scholar
Wang R, Chen W, Zhong J, Zhang L (2018) Experimental and numerical studies on the sluggish diffusion in face centered cubic Co–Cr–Cu–Fe–Ni high-entropy alloys. J Mater Sci Technol 34:1791–1798
Article Google Scholar
Chen S, Li Q, Zhong J et al (2019) On diffusion behaviors in face centered cubic phase of Al–Co–Cr–Fe–Ni–Ti high-entropy superalloys. J Alloys Compd 791:255–264
Article CAS Google Scholar
Kucza W, Dąbrowa J, Cieślak G et al (2018) Studies of “sluggish diffusion” effect in Co–Cr–Fe–Mn–Ni, Co–Cr–Fe–Ni and Co–Fe–Mn–Ni high entropy alloys; determination of tracer diffusivities by combinatorial approach. J Alloys Compd 731:920–928
Article CAS Google Scholar
Takeuchi A, Inoue A (2000) Calculations of mixing enthalpy and mismatch entropy for ternary amorphous alloys. Mater Trans JIM 41:1372–1378
Article CAS Google Scholar
Takeuchi A, Inoue A (2010) Mixing enthalpy of liquid phase calculated by miedema’s scheme and approximated with sub-regular solution model for assessing forming ability of amorphous and glassy alloys. Intermetallics 18:1779–1789
Article CAS Google Scholar
Gaertner D, Abrahams K, Kottke J et al (2019) Concentration-dependent atomic mobilities in FCC CoCrFeMnNi high-entropy alloys. Acta Mater 166:357–370
Article CAS Google Scholar
Belova IV, Murch GE (2001) Behaviour of the diffusion vacancy-wind factors in the concentrated random alloy. Philos Mag A 81:1749–1758
Article CAS Google Scholar
Belova IV, Murch GE (2010) The nature of the vacancy-wind effect occurring in diffusion via six-jump-cycles in B2 intermetallics. Defect Diffus Forum 297–301:1218–1225
Article CAS Google Scholar
Belova IV, Ahmed T, Sarder U et al (2017) The Manning factor for direct exchange and ring diffusion mechanisms. Philos Mag 97:230–247
Article CAS Google Scholar
Chen J, Zhang L (2018) Composition-dependent interdiffusivity matrices in face centered cubic Ni–Al–X (X = Rh and W) alloys at 1423, 1473 and 1523 K: a high-throughput experimental measurement. Calphad 60:106–115
Article CAS Google Scholar
Wen S, Tang Y, Zhong J et al (2017) High-throughput measurements of interdiffusivity matrices in face centered cubic Ni–Al–Mo alloys at 1273–1473 K. J Mater Res 32:2188–2201
Article CAS Google Scholar
Deng S, Chen W, Zhong J et al (2017) Diffusion study in bcc_A2 Fe–Mn–Si system: experimental measurement and CALPHAD assessment. Calphad 56:230–240
Article CAS Google Scholar
Konishi S, Kitagawa G (2008) Information criteria and statistical modeling. Springer, New York
Book Google Scholar
Poggio T, Torre V, Koch C (1985) Computational vision and regularization theory. Nature 317:314–319
Article CAS Google Scholar
Girosi F, Jones M, Poggio T (1995) Regularization theory and neural networks architectures. Neural Comput 7:219–269
Article Google Scholar
Reed RC (2008) The superalloys: fundamentals and applications. Cambridge University Press, Cambridge
Google Scholar
Ma A, Dye D, Reed R (2008) A model for the creep deformation behaviour of single-crystal superalloy CMSX-4. Acta Mater 56:1657–1670
Article CAS Google Scholar
Zhu Z, Basoalto H, Warnken N, Reed RC (2012) A model for the creep deformation behaviour of nickel-based single crystal superalloys. Acta Mater 60:4888–4900
Article CAS Google Scholar
Dyson BF, Gibbons TB (1987) Tertiary creep in nickel-base superalloys: analysis of experimental data and theoretical synthesis. Acta Metall 35:2355–2369
Article CAS Google Scholar
Dyson BF (2009) Microstructure based creep constitutive model for precipitation strengthened alloys: theory and application. Mater Sci Tech-Lond 25:213–220
Article CAS Google Scholar
Chen W, Zhang L (2018) High-throughput determination of interdiffusivities for Ni–Al–Cr Alloys at 1173 K through a combination of diffusion multiple and numerical inverse method. Defect Diffus Forum 383:36–42
Article Google Scholar
Chen J, Zhang L, Zhong J et al (2016) High-throughput measurement of the composition-dependent interdiffusivity matrices in Ni-rich fcc Ni–Al–Ta alloys at elevated temperatures. J Alloys Compd 688:320–328
Article CAS Google Scholar
Chen J, Xiao J, Zhang L, Du Y (2016) Interdiffusion in fcc Ni–X (X = Rh, Ta, W, Re and Ir) alloys. J Alloys Compd 657:457–463
Article CAS Google Scholar
Lin Y, Li G, Wei M et al (2019) Isothermal section of Ni-Al-Os, isothermal tetrahedron and projection of Ni–Al–Cr–Os systems in Ni-rich region at 1200° C. Calphad 66:101636
Article CAS Google Scholar
Lin Y, Wei M, Li G, Zhang L (2018) Phase equilibria and microhardness of As-cast and annealed Ni–Al–Os alloys in Ni-rich region. J Phase Equilib Diffus 39:944–952
Article CAS Google Scholar
Yeh J-W, Chen S-K, Lin S-J et al (2004) Nanostructured high-entropy alloys with multiple principal elements: novel alloy design concepts and outcomes. Adv Eng Mater 6:299–303
Article CAS Google Scholar
Tsai K-Y, Tsai M-H, Yeh J-W (2013) Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys. Acta Mater 61:4887–4897
Article CAS Google Scholar
Paul A (2017) Comments on “Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys” by KY Tsai, MH Tsai and JW Yeh, Acta Materialia 61 (2013) 4887–4897. Scripta Mater 135:153–157
Article CAS Google Scholar
Chen W, Zhang L (2017) High-throughput determination of interdiffusion coefficients for Co–Cr–Fe–Mn–Ni high-entropy alloys. J Phase Equilib Diffus 38:457–465
Article CAS Google Scholar
Dąbrowa J, Zajusz M, Kucza W et al (2019) Demystifying the sluggish diffusion effect in high entropy alloys. J Alloys Compd 783:193–207
Article CAS Google Scholar
Kulkarni K, Chauhan GPS (2015) Investigations of quaternary interdiffusion in a constituent system of high entropy alloys. AIP Adv 5:097162
Article CAS Google Scholar
Dąbrowa J, Kucza W, Cieślak G et al (2016) Interdiffusion in the FCC-structured Al–Co–Cr–Fe–Ni high entropy alloys: experimental studies and numerical simulations. J Alloys Compd 674:455–462
Article CAS Google Scholar
Verma V, Tripathi A, Kulkarni KN (2017) On interdiffusion in FeNiCoCrMn high entropy alloy. J Phase Equilib Diffus 38:445–456
Article CAS Google Scholar
Vaidya M, Trubel S, Murty BS et al (2016) Ni tracer diffusion in CoCrFeNi and CoCrFeMnNi high entropy alloys. J Alloys Compd 688:994–1001
Article CAS Google Scholar
Vaidya M, Pradeep KG, Murty BS et al (2018) Bulk tracer diffusion in CoCrFeNi and CoCrFeMnNi high entropy alloys. Acta Mater 146:211–224
Article CAS Google Scholar
Mohan MG, Vaidya M, Murty BS et al (2020) Tracer diffusion in ordered pseudo-binary multicomponent aluminides. Scripta Mater 178:227–231
Article CAS Google Scholar
Yeh A, Tsao T, Chang Y et al (2015) Developing new type of high temperature alloys–high entropy superalloys. Int J Min Met Mater 1:107
Google Scholar
Oruganti R, Shukla A, Nalawade S et al (2019) A microstructure-based model for creep of gamma prime strengthened nickel-based superalloys. J Eng Mater Technol 141:011001
Article CAS Google Scholar
Yamamoto T, Takashima T, Nishida K (1980) Interdiffusion in the zeta-solid solution of a Ni–Al system. Trans JIM 21:601–608
Article Google Scholar
Jung S, Yamane T, Minamino Y et al (1992) Interdiffusion and its size effect in nickel solid solutions of Ni–Co, Ni–Cr and Ni–Ti systems. J Mater Sci Lett 11:1333–1337
Article CAS Google Scholar
Ustad T, Sørum H (1973) Interdiffusion in the Fe–Ni, Ni–Co, and Fe–Co systems. Phys Stat Sol (a) 20:285–294
Article CAS Google Scholar
Chen J, Zhang C, Wang J et al (2015) Thermodynamic description, diffusivities and atomic mobilities in binary Ni–Os system. Calphad 50:118–125
Article CAS Google Scholar
Karunaratne MSA, Reed RC (2003) Interdiffusion of the platinum-group metals in nickel at elevated temperatures. Acta Mater 51:2905–2919
Article CAS Google Scholar
Karunaratne M, Reed R (2005) Interdiffusion of niobium and molybdenum in nickel between 900–1300 C. In: Defect and Diffusion forum. Trans Tech Publ, New York, pp 420–425
McElreath R (2016) Statistical rethinking: a Bayesian course with examples in R and Stan. CRC Press/Taylor & Francis Group, Boca Raton
Google Scholar
Wu X, Zhong J, Zhang L (2020) A general approach to quantify the uncertainty of interdiffusion coefficients in binary, ternary and multicomponent systems evaluated using Matano-based methods. Acta Mater 188:665–676
Article CAS Google Scholar
Lu H, Shen Q, Chen J et al (2019) Parallel multiple-chain DRAM MCMC for large-scale geosteering inversion and uncertainty quantification. J Petro Sci Eng 174:189–200
Article CAS Google Scholar
Foreman-Mackey D, Hogg DW, Lang D, Goodman J (2013) emcee : the MCMC hammer. Publ Astron Soc Pac 125:306–312
Article Google Scholar
Covington TR, Robinan Gentry P, Van Landingham CB et al (2007) The use of Markov chain Monte Carlo uncertainty analysis to support a Public Health Goal for perchloroethylene. Regul Toxicol Pharm 47:1–18
Article CAS Google Scholar
Geyer CJ (2011) Introduction to Markov Chain Monte Carlo. In: Handbook of Markov Chain Monte Carlo. https://www.taylorfrancis.com/. Accessed 5 Oct 2019
Duane S, Kennedy AD, Pendleton BJ, Roweth D (1987) Hybrid Monte Carlo. Phys Lett B 195:216–222
Article CAS Google Scholar
Goodman J, Weare J (2010) Ensemble samplers with affine invariance. CAMCoS 5:65–80
Article Google Scholar
Wang F, Landau DP (2001) Efficient, multiple-range random walk algorithm to calculate the density of states. Phys Rev Lett 86:2050–2053
Article CAS Google Scholar
National Research Council (2008) Integrated computational materials engineering: a transformational discipline for improved competitiveness and national security. National Academies Press, Washington, DC
Google Scholar
Bocklund B, Otis R, Egorov A et al (2019) ESPEI for efficient thermodynamic database development, modification, and uncertainty quantification: application to Cu–Mg. MRS Commun 9:618–627
Article CAS Google Scholar
ESPEI: extensible self-optimizing phase equilibria infrastructure, https://github.com/PhasesResearchLab/ESPEI, assessed 2020-02-06.
Paulson NH, Bocklund BJ, Otis RA et al (2019) Quantified uncertainty in thermodynamic modeling for materials design. Acta Mater 174:9–15
Article CAS Google Scholar
Honarmandi P, Duong TC, Ghoreishi SF et al (2019) Bayesian uncertainty quantification and information fusion in CALPHAD-based thermodynamic modeling. Acta Mater 164:636–647
Article CAS Google Scholar
Cui Y, Jiang M, Ohnuma I et al (2008) Computational study of atomic mobility in Co–Fe–Ni ternary fcc alloys. J Phase Equilib Diffus 29:312–321
Article CAS Google Scholar
Million B, Kučera J (1971) Concentration dependence of nickel diffusion in nickel–cobalt alloys. Czech J Phys 21:161–171
Article CAS Google Scholar
Million B, Růžičková J, Velíšek J, Vřeštál J (1981) Diffusion processes in the Fe–Ni system. Mater Sci Eng 50:43–52
Article CAS Google Scholar
Rothman S, Nowicki L, Murch G (1980) Self-diffusion in austenitic Fe–Cr–Ni alloys. J Phys F 10:383–398
Article CAS Google Scholar

Download references

Acknowledgements

The financial support from the National Key Research and Development Program of China (Grant No. 2016YFB0301101) and the Youth Talent Project of Innovation-driven Plan at Central South University (Grant No. 2019XZ027) is acknowledged. Jing Zhong acknowledges the support from the Fundamental Research Funds for the Central Universities of Central South University (Grant No. 2018zzts129). Lijun Zhang is extremely grateful to the family members for their company and the communication editor, Prof. Philip Nash, and the reviewers for their unselfish dedication on this review during the unpredictable COVID-19 all over the world. The authors also would like to thank Ph.D. candidates Miss Li Qi, Miss Shiyao Chen and Mr. Xiaoke Wu from Central South University for kindly offering/fixing the original digital figures.

Author information

Authors and Affiliations

State Key Laboratory of Powder Metallurgy, Central South University, Changsha, 410083, Hunan, People’s Republic of China
Jing Zhong, Li Chen & Lijun Zhang

Authors

Jing Zhong
View author publications
You can also search for this author in PubMed Google Scholar
Li Chen
View author publications
You can also search for this author in PubMed Google Scholar
Lijun Zhang
View author publications
You can also search for this author in PubMed Google Scholar

Contributions

LZ conceived the presented idea and provided necessary materials. LC provided the necessary materials and helped with the revision. JZ and LZ wrote the article. All authors discussed the results and commented on the manuscript.

Corresponding author

Correspondence to Lijun Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zhong, J., Chen, L. & Zhang, L. High-throughput determination of high-quality interdiffusion coefficients in metallic solids: a review. J Mater Sci 55, 10303–10338 (2020). https://doi.org/10.1007/s10853-020-04805-1

Download citation

Received: 12 February 2020
Accepted: 07 May 2020
Published: 19 May 2020
Issue Date: August 2020
DOI: https://doi.org/10.1007/s10853-020-04805-1

Use our pre-submission checklist

Avoid common mistakes on your manuscript.

High-throughput determination of high-quality interdiffusion coefficients in metallic solids: a review

Abstract

Similar content being viewed by others

Automation of diffusion database development in multicomponent alloys from large number of experimental composition profiles

High-throughput measurements of interdiffusivity matrices in face centered cubic Ni–Al–Mo alloys at 1273–1473 K

High-Throughput Determination of Composition-Dependent Interdiffusivity Matrices and Atomic Mobilities in fcc Cu-Ni-Al Alloys by Combining Diffusion Couple Experiments with HitDIC Modeling

Introduction

Matano-based methods and their new developments

Boltzmann–Matano and other related methods