Introduction

Fast high-temperature dilatometry is widely used in materials science for the characterization of phase transformations and for studying precipitation kinetics in ferrous alloys. For the study of such processes in light-weight alloys at much lower temperatures, the method of primary choice usually is differential scanning calorimetry (DSC) owing to its ease of use and its versatility. For the sake of sensitivity, DSC is commonly applied using time-linear heating, i.e., under non-isothermal conditions; however, this requires more complex procedures of analysis. Compared to DSC, which is based on the heat flow, i.e., the rate of change of a variable, dilatometry directly measures the volume, i.e., a state variable where the measuring signal is independent of the heating rate. Therefore, dilatometry remains sensitive also under long-term isothermal measurement conditions [1,2,3,4].

Recently, a highly stable, non-contact dilatometer was developed that enables measurements of relative length changes \(\Delta L/L (t)\) under isothermal conditions in the sub-\(10^{-5}\) regime with minimized drift over times as long as \(10^6\) s [5]. This advanced technique opened up the possibility for quantitative studies of precipitation phenomena which are associated with tiny relative length changes that occur on long timescales and which so far have not been accessible. In order to demonstrate the potentials of this technique especially for assessing technologically relevant processes, a commercial grade Al–Mg–Si alloy (EN AW-6060) was used as a suitable model system [6]. On the one hand, the complex precipitation sequence of this alloy involves metastable phases, and on the other hand, the precipitation sequence of this alloy has been subject of comprehensive research before (for reviews see, e.g., Refs. [7, 8]). In conclusion, the merit of the current experimental approach can easily be demonstrated by comparison with data readily available. As outlined in a preceding paper [6] by the authors’ group, from in situ measurements of relative length change, the amount of the metastable coherent \(\beta ''\)-phase and the semicoherent \(\beta '\)-phase as well as of the stable \(\beta \)-phase has been determined previously on an absolute scale. There, the observed length change associated with each of the different phases could quantitatively be correlated with the theoretically expected contributions of the length change arising, on the one hand, from the volume excess of the precipitates, and on the other hand, from the volume change of the matrix due to the removal of solute atoms from the Al matrix [6]. This finding already demonstrated that high-precision isothermal dilatometry enables a quantitative volumetric identification of precipitates in dilute alloys.

In the present paper, in order to exploit the full potentials of this dilatometric measuring technique, not only the maximum values of the length changes are considered for determining the amount of precipitates, but also the isothermal behavior of the entire relative length change variation \(\Delta L/L (t)\) with time t will analytically be analyzed to study the kinetics of the precipitation processes. The analysis is performed in the framework of the Johnson-Mehl-Avrami-Kolomogorov (JMAK) theory which was found to be suitable to grasp major kinetic features even for complex precipitation sequences in Al alloys [9]. Although it is evident that detailed insight into precipitation processes in Al alloys on an atomistic scale ultimately requires more advanced models (see, e.g., Refs. [10,11,12,13]), the application of simple models, like JMAK, allows a direct and analytical fit to experimental data.

The characteristic features of the \(\Delta L/L (t)\) dilatometer curves also allows to derive time–temperature–precipitation (TTP) diagrams. For ferrous metals comprehensive atlases of transformation diagrams already exist [14], a proper amount of which has been assembled based on dilatometry data. For nonferrous metals and in particular for light-weight alloys such as aluminum alloys, available data only cover a few selected chemical compositions [15]. For instance, in situ differential scanning calorimetry (DSC) has been applied to study TTP diagrams in Al alloys [16] and in a more recent work dilatometry has been performed under cooling conditions providing significant data in the field of precipitation analysis in Al alloys [17]. However, dilatometric measurements on this kind of alloys have so far been restricted to relatively highly alloyed Al alloys as used in the study mentioned before or to steels [18, 19] which both exhibit volume changes upon precipitation much larger compared to that ones of the Al alloy investigated in this work. Here, we present a direct way to study isothermal TTP diagrams for comparably low-alloyed Al alloys making use of isothermal high-precision dilatometry.

Experimental procedure

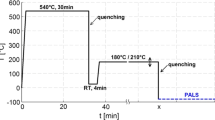
The dilatometer measurements were performed in a high-stability non-contact dilatometer based on two-beam Michelson interferometry. A detailed description of the self-developed dilatometer and of the measurement procedure for the Al alloy is given elsewhere by Luckabauer et al. [5] and Hengge et al. [6], respectively. Summarizing briefly, the studies were performed on cylindrical-shaped samples (length: 20 mm, diameter: 5.7 mm) of commercial grade EN AW-6060 Al–Mg–Si alloy. The compositions of the main elements were confirmed by optical emission spectroscopy and a Mg content of 0.65 at.%, a Si content of 0.52 at.%, and additional traces of primarily Fe (0.11 at.%) were determined. For each measurement run, a solution annealing was performed inside the dilatometer at 540 \(^{\circ }\)C for 30 min with then subsequent quenching in a helium gas stream, then holding at 32 \(^{\circ }\)C for 4 min, and a final fast heat-up (100 \(^{\circ }\)C/min) to temperatures between 170 \(^{\circ }\)C and 260 \(^{\circ }\)C for the isothermal precipitation treatment. Unless otherwise stated the difference between the sample’s length right after the heating step to aging temperatures and its actual length standardized to the its length at room temperature is termed as \(\Delta L/L\). Prior to the whole experiment series, the sample was annealed at 540 \(^{\circ }\)C for 24 h to obtain a fully recrystallized microstructure.

Hardness measurements (EMCO-TEST DuraJet, Brinell method) as standard characterization technique of the progress of precipitation were also performed for comparison.

Experimental results

Figure 1
figure 1

Reproducability of length change measurements and correlation with hardness. Relative length change \(\Delta L/L\) in dependence of time t measured at the aging temperature of 180 \(^\circ \)C and the corresponding Brinell hardness, HBW, measured upon ex situ aging at 180 \(^\circ \)C (black triangle, right-scale axis). Except for the lowest HBW value the size of the error bars are within the size of the symbol

Full size image
Figure 2
figure 2

Variation with aging temperature. Relative length change \(\Delta L/L\) in dependence of time t measured at the quoted aging temperature (unit \(^{\circ }\)C)

Full size image

Figure 1 shows relative length change curves \(\Delta L/L\) obtained during aging in dependence of time t at 180 \(^\circ \)C measured for multiple repetitions of the entire measuring sequence comprising solution annealing, quenching, and aging. The good agreement of the various \(\Delta L/L (t)\)-curves demonstrates the high reproducibility of the measurements and the high stability of the dilatometer. The variation of the Brinell hardness, HBW, also shown in Fig. 1, exhibits a maximum at about the same aging time as that of \(\Delta L/L\).

The characteristic variation of the \(\Delta L/L (t)\) curves upon isothermal aging for various temperatures between 170 \(^\circ \)C and 260 \(^\circ \)C is shown in Fig. 2. For all temperatures except 260 \(^\circ \)C, the relative length change \(\Delta L/L\) first increases in the range of several \(10^{-5}\) and then subsequently decreases. The maximum in length is shifted to higher values and longer times with decreasing annealing temperature. For 260 \(^\circ \)C or 240 \(^\circ \)C none or only a tiny length increase occurs prior to the decrease. For 240 \(^\circ \)C, 230 \(^\circ \)C, and 210 \(^\circ \)C, where the minimum value of \(\Delta L/L\) is reached during the measuring interval, the differences between the respective \(\Delta L/L\)-maxima and -minima are very similar and are in the range of \(6 \times 10^{-5}\). For 170 \(^\circ \)C, 180 \(^\circ \)C, and 200 \(^\circ \)C the \(\Delta L/L\)-minimum is not yet being reached during the time span of the measurement.

Analysis

Quantitative identification of precipitation sequence

As outlined by the authors in a preceding paper [6] that was focused on the maximum values of the length changes only, the observed increase in the length is due to the formation of the metastable coherent \(\beta ''\)-phase and the decrease in the length results from the formation of the metastable semicoherent \(\beta '\)-phase. This conclusion is based on a comparison with available literature data and in particular based on the clear correlation between the aging characteristics of the length change and the hardness (Fig. 1). In fact, the hardness increase is due to the \(\beta ''\)-phase as manifested in the hardness maximum [20]. In the subsequent, so-called overaging regime, which coincides with the regime of length decrease, the metastable \(\beta '\)-phase is reported to be the predominant phase [21]. A length increase upon precipitation of the \(\beta ''\)-phase and a length decrease upon \(\beta '\)-precipitation turns out to be the result of the counterbalance between the volume expansion due to the formation of the precipitates and the volume contraction of the Al matrix due to the removal of solute atoms from the matrix. For the formation of \(\beta ''\) which is considered to be Mg\(_4\)Al\(_3\)Si\(_4\) (see Ref. [6] and references therein), a net expansion occurs since in this case the Mg atoms that expand the Al matrix and the solved Si atoms that contracts the Al matrix contribute in equal amounts to the precipitates so that the expansion due to the formation of \(\beta ''\) exceeds that of the matrix contraction. Even though the specific volume of \(\beta '\)-precipitates, which are supposed to consist of Mg\(_9\)Si\(_5\), is higher than that of \(\beta ''\), a net contraction occurs upon \(\beta '\)-precipitation because the matrix contraction due to the removal of the lattice-expanding Mg atoms dominates (see [6]). This analysis of the various length change contributions does not only yield the correct quantitative amounts for the metastable phases \(\beta ''\) and \(\beta '\), but also that of the final, stable \(\beta \)-phase which can well be observed at higher temperatures within time spans accessible here (see [6]). For the details of the analysis the reader is referred to Ref. [6].

Analysis of precipitation kinetics

In a next step going beyond the consideration of the absolute change of the \(\Delta L/L\)-curves in the following a central topic will addressed, namely the quantitative analysis of the \(\Delta L/L(t)\)-curves with respect to the underlying kinetics.

For the rates of formation \(\dot{c}_{\beta ''}\) for \(\beta ''\) and \(\dot{c}_{\beta '}\) for \(\beta '\) we use the following approach for the rate equations:

$$\begin{aligned}&\dot{c}_{\beta ''} (t) = k_1 \Bigl \{ c_0 - \Bigl [ c_{\beta ''}(t) + c_{\beta '}(t) \Bigr ] \Bigr \} - k_2 c_{\beta ''}(t) \, , \end{aligned}$$
(1)
$$\begin{aligned}&\dot{c}_{\beta '}(t) = k_2 c_{\beta ''}(t) \, , \end{aligned}$$
(2)

where \(c_{\beta '', \beta '}\) and \(k_{1,2}\) are the atomic fractions and formation rates for the precipitate phases \(\beta ''\) and \(\beta '\), respectively, and the parameter \(c_0\) denotes the maximum amount of precipitates which is finally attained. Equation (1) corresponds to JMAK kinetics for the formation of \(\beta ''\) (Avrami exponent of \(n =1\)) combined with a second term dealing with the transformation to the \(\beta '\)-phase. The rate ansatz according to Eq. (2) describes a situation where \(\beta '\) is formed by transformation of \(\beta ''\), a notion which is in line with the literature [21, 22] and which will be extended below for elevated temperature.

For the initial conditions \(c_{\beta ''}(t=0) = c_{\beta '} (t=0) = 0\) the solutions for \(\beta ''\) (Eq. 1) and \(\beta '\) (Eq. 2) read:

$$\begin{aligned}&c_{\beta ''}(t) = \displaystyle c_0 \frac{k_1}{k_2 - k_1} \, \Bigl \{ \exp (-k_1 \, t) - \exp (-k_2 \, t) \Bigr \} \, , \end{aligned}$$
(3)
$$\begin{aligned}&c_{\beta '}(t) = \displaystyle c_0 \frac{1}{k_2 - k_1} \, \Bigl \{ - k_2 \exp (-k_1 \, t) + k_1 \exp (-k_2 t) \Bigr \} + c_0 \, . \end{aligned}$$
(4)

And the total amount of precipitates \(\beta _{tot}(t)\) is given by

$$\begin{aligned} c_{\beta ,tot}(t) = c_{\beta ''}(t) + c_{\beta '}(t) = c_0 \Bigl [ 1 - \exp (-k_1 \, t) \Bigr ] \, . \end{aligned}$$
(5)

According to Eq. (5), irrespective of a mutual transformation of \(\beta ''\) and \(\beta '\), the formation of the total amount of precipitates is governed by the rate constant \(k_1\). Since \(c_0\) represents the limiting value of \(c_{\beta '}\) (Eq. 4), a value of \(c_0 = 0.0101\) is taken which was derived for the maximum amount of the \(\beta '\)-phase, and which is slightly less than the value of 0.0113 derived for \(\beta ''\) (see Ref. [6]).

For fitting the \(\Delta L/L\)-curves, the coefficients \((\Delta L/L)/c\) for the variation of \(\Delta L/L\) with \(c_{\beta ''}\) and \(c_{\beta '}\) are taken from our previous work [6]. Then a fraction of 0.0101 for \(\beta '\) corresponds to \(\Delta L/L = -0.71 \times 10^{-4}\), i.e., a coefficient \((\Delta L/L)/c = - 7.03 \times 10^{-3}\). For \(\beta ''\), \(\Delta L/L = 0.39 \times 10^{-4}\) is obtained for a maximum fraction of 0.0113 [6], corresponding to \((\Delta L/L)/c = 3.35 \times 10^{-3}\). This finally yields the fit curve

$$\begin{aligned} \frac{\Delta L}{L} (t) = 3.35 \times 10^{-3} \, c_{\beta ''}(t) - 7.03 \times 10^{-3} \, c_{\beta '}(t) \, , \end{aligned}$$
(6)

with \(c_{\beta ''}(t)\), \(c_{\beta '}(t)\) according to Eqs. (3) and (4). Fitting the experimental \(\Delta L/L(t)\)-curves yields for each aging temperature the two rates \(k_1\) and \(k_2\) as the only fit parameters. The values of \(k_1\) and \(k_2\) deduced from the analyses of the \(\Delta L/L(t)\)-curves for the various isothermal temperatures are shown in Fig. 3 in an Arrhenius representation. It is evident that for high temperatures the two-rate fit is inappropriate, since the \(\Delta L/L(t)\)-decrease without preceding increase, e.g., for 240 \(^{\circ }\)C (Fig. 2) would imply a rate \(k_1\) at this temperature that is lower than those at the lower temperatures (see crosses in Fig. 3). As characteristic for metastable precipitation phenomena, this indicates that for the high temperatures, in addition to a \(\beta ''\rightarrow \beta '\) transformation, \(\beta '\)-precipitates may also form directly. In the rate equation system above (Eqs. 1, 2), a direct formation of \(\beta '\) (concentration: \(c_{\beta '_\mathrm{dir}}\)) can be considered in a straightforward manner by an additional rate equation

$$\begin{aligned} \dot{c}_{\beta '_{\mathrm{dir}}} (t) = k_3 \Bigl \{ c_0 - \Bigl [ c_{\beta ''}(t) + c_{\beta '}(t) + c_{\beta '_{\mathrm{dir}}} (t) \Bigr ] \Bigr \} \end{aligned}$$
(7)

and a corresponding extension of Eq. (1) by the summand \(c_{\beta '_{\mathrm{dir}}} (t)\) within the angular shaped brackets. The solution for this three-rates approach reads

$$\begin{aligned}&c_{\beta ''}(t) = \displaystyle c_0 \frac{k_1}{k_2 - (k_1+k_3)} \, \Bigl \{ \exp (-(k_1 + k_3) \, t) - \exp (-k_2 \, t) \Bigr \} \, , \end{aligned}$$
(8)
$$\begin{aligned}&c_{\beta '}(t) = \displaystyle c_0 \frac{1}{k_2 - (k_1+k_3)} \, \Bigl \{ - \frac{k_2 k_1}{k_1+k_3} \exp \Bigl (-(k_1+k_3) \, t\Bigr ) + k_1 \exp (-k_2 t) \Bigr \} + c_0 \frac{k_1}{k_1+k_3} \, . \end{aligned}$$
(9)
$$\begin{aligned}&c_{\beta '_{\mathrm{dir}}}(t) = \displaystyle c_0 \frac{k_3}{k_1+k_3} \, \Bigl \{1 - \exp (-(k_1+k_3) \, t) \Bigr \}\, , \end{aligned}$$
(10)

which for \(k_3 = 0\) contains as special case the two-rates solutions (Eqs. 3, 4). As shown in Fig. 3, the rate \(k_3\) for the direct formation of \(\beta '\) starts to exceed the rate \(k_2\) of the \(\beta '' \rightarrow \beta '\) transformation at 200 \(^\circ \hbox {C}\) and steeply increases for higher temperatures, demonstrating that in this temperature regime direct \(\beta \)-formation prevails.

Fitting the experimental \(\Delta L/L(t)\)-curves with the three-rates solutions by replacing \(c_{\beta '}(t)\) in Eq. (6) by \([c_{\beta '}(t) + c_{\beta '_{\mathrm{dir}}}(t)]\) yields pretty similar rates \(k_1\) and \(k_2\) for \(T < 240\) \(^{\circ }\)C as the two-rates solution (see Fig. 3). From linear fits of the three-rates solutions including \(T = 240\) \(^{\circ }\)C, the activation energies \(Q_1 =(0.90\pm 0.30)\) eV and \(Q_2 =(1.42\pm 0.28)\) eV can be deduced for the reactions rates \(k_1\) and \(k_2\), respectively. As shown in Fig. 4 for representative temperatures, the present model according to Eq. (6) yields fits that reasonably well match to the experimental \(\Delta L/L\)-curves.

Figure 3
figure 3

Arrhenius plot of precipitation kinetics. Arrhenius representation of reaction rates \(k_1\) (blue), \(k_2\) (red), \(k_3\) (black, empty circle) determined from fitting the \(\Delta L/L\)-curves according to the present model as well as Arrhenius representation of the temporal shift of the peak maxima (green, diamond) of the \(\Delta L/L\)-curves (Fig. 2) with varying temperature T according Eq. (11). \(k_1\) (blue, two-rates fit: \(\times \), three-rates fit: filled inverted triangle), \(k_2\) (red, two-rates fit: \(+\), three-rates fit: filled circle)

Full size image
Figure 4
figure 4

Fit of \(\Delta L/L\)-curves (solid lines) according to the present model (Eq. 6). Dotted lines: corresponding experimental curves (cf. Fig. 2). The aging temperature (unit \(^{\circ }\)C) are quoted. \(T = 200, 220\) \(^{\circ }\)C: two-rates fit (Eqs. 3, 4); \(T = 240\) \(^{\circ }\)C: three-rates fit (Eqs. 8–10)

Full size image

For the sake of completeness, in addition to the above deduced kinetics, as derived from fitting of the \(\Delta L/L\)-curves, a simple kinetic analysis can be obtained from the temporal shift of the peak maxima of the \(\Delta L/L\)-curves. For this purpose the time t corresponding to each peak maximum of \(\Delta L/L\) (Fig. 2) is plotted in Fig. 3 in an Arrhenius representation with varying temperature T, i.e.,

$$\begin{aligned} \frac{1}{t} = \frac{1}{t_0} \exp \Bigl ( - \frac{Q_\mathrm{eff}}{k_B T} \Bigr ) \, , \end{aligned}$$
(11)

where \(t_0^{-1}\) denotes a pre-exponential factor and \(Q_\mathrm{eff}\) the activation energy. From the linear fit of the data (Fig. 3), a value \(Q_\mathrm{eff} = (1.13 \pm 0.07)\) eV is deduced for the activation energy. This value is between those obtained for \(k_{1}\) and \(k_{2}\) (Fig. 3, see discussion).

TTP diagram

From the \(\Delta L/L(t)\)-curves a time–temperature–precipitation (TTP) diagram can be constructed. In the following, data points of the isothermal TTP diagram will at first be derived directly from the \(\Delta L/L(t)\)-curve and then from the fitted data obtained in the preceding section.

Figure 5
figure 5

Isothermal TTP diagram. Time–temperature–precipitation (TTP) characteristic for the formation of \(\beta ''\)- and \(\beta '\)-precipitates in AW 6060. Filled symbols refer to data directly taken from \(\Delta L/L\)-curves (maxima: \(\beta ''\); mimina: \(\beta '\); see text); crossed symbols denote the values deduced from the fit with two rates \(k_{1,2}\) (see crossed symbols in Fig. 6a, b). The dotted lines show the threshold values for reaching 60 % of the maximum concentration of \(\beta ''\) and \(\beta '\) (see filled symbols in Fig. 6a, b). The numbered data points (empty symbols) refer to data taken from literature (see Table 1)

Full size image
Figure 6
figure 6

Evolution of the formation of precipitates \(\beta '\) (a) and \(\beta ''\) (b) with time for various temperatures according to fit of present model with two rates \(k_{1,2}\) (Eqs. 3, 4). The symbols marked with a cross correspond to the maximum (a) or to a fraction of 0.98 (b) of the relative concentration \(c_{\beta ',\beta ''}/c_0\); the filled symbols mark 60 % of the maximum concentration

Full size image

The temperature T and time t associated with each extremum of the \(\Delta L/L(t)\)-curves define one set of data points in the time–temperature–precipitation (TTP) diagram. The maxima of the \(\Delta L/L(t)\)-curves (Fig. 2) correspond to the respective temperature and time where the metastable \(\beta ''\)-phase attains its maximum amount. For the metastable \(\beta '\)-phase the characteristic T- and t-values are given by the onset where the minimum of \(\Delta L/L(t)\) is reached. The corresponding data points of the isothermal TTP diagram, which can directly be constructed in this way from the dilatometer measurements, are shown in Fig. 5 as filled symbols.

Additionally, isothermal TTP data for \(c_{\beta ''}(t)\) and \(c_{\beta '}(t)\) can also be derived from the fitted values \(k_1\), \(k_2\) and the corresponding linear interpolations according to an Arrhenius behavior (Fig. 3) by making use of the relation between \(c_{\beta ''}(t)\), \(c_{\beta '}(t)\) and \(k_1\), \(k_2\) (Eqs. 3, 4).Footnote 1 Corresponding sets of \(c_{\beta ''}(t)\)- and \(c_{\beta '}(t)\)-curves for various temperatures are shown in Fig. 6, which yield the TTP data depicted in Fig. 5. For \(\beta ''\), the TTP data points are taken from the maxima of the \(c_{\beta ''}(t)\)-curves (see crossed symbols in Fig. 6a); for \(\beta '\) the TTP data points correspond to \(c_{\beta '} = 0.98\) (see crossed symbols in Fig. 6b).

From the \(c_{\beta ''}(t)\)- and \(c_{\beta '}(t)\)-plots in Fig. 6 also the time span, after which any other fraction of precipitates is reached, can be determined directly. For the sake of illustration, the threshold values for reaching 60 % of the maximum concentration of \(\beta ''\) and \(\beta '\) are also shown in Fig. 5.

Discussion

The analysis in the preceding section demonstrates that high-precision dilatometry serves as sensitive tool for the quantitative analysis of precipitation processes even if they are associated with only tiny length changes and even if they occur on long timescales. The \(\beta '' \rightarrow \beta '\) transformation in Al–Mg–Si alloys, which could be resolved in detail here, is hardly accessible by other thermal techniques as stated, e.g., for standard DSC [16]. Also with standard dilatometry upon linear heating, the formation of \(\beta ''\) in Al–Si–Mg alloys is much weaker discernible [23].

The substantially enhanced sensitivity in the present studies allowed a detailed kinetic analysis. Here, the sign inversion of the relative length change upon \(\beta '' \rightarrow \beta '\) transformation, which arises from the interplay between the precipitate and matrix volume, turned out as a particular feature of dilatometry that brings additional specificity for the precipitate characterization. The deduced activation energies are similar to those found earlier for Al–Si–Mg alloys [23]; they also can be considered as characteristic for metastable precipitates in Al alloys [24, 25]. The quantitative analysis confirms that the \(\Delta L/L\)-maximum arises from the competing effects of expansion and contraction due to \(\beta ''\)- and \(\beta '\)-formation, respectively. Since the coefficients of expansion due to the formation of \(\beta ''\) and the contraction due to the formation of \(\beta '\) are different (see Eq. 6), it is evident that the maxima arising from the sum of these contributions is shifted to earlier times compared to the time when a maximum amount of \( \beta ''\)-phase is present. Therefore, the activation energy \(Q_\mathrm{eff}\) deduced above from the time shift of the maximum of the length increase with aging temperature can be considered as an effective value, at most. These maxima should therefore also not be conceptually intermixed with those occurring upon heat release in DSC. Since the coefficients of expansion due to the formation of \(\beta ''\) and the contraction due to the formation of \(\beta '\) are different (see Eq. 6), it is evident that the maximum arising from the sum of these contributions is shifted to earlier times compared to the point when the \(\beta ''\)-phase attains its maximum value. From this point of view, it is also quite clear that the value of activation energy \(Q_\mathrm{eff}\) lays between those of the rates \(k_1\) and \(k_2\) for the formation of \(\beta ''\)- and \(\beta '\)-formation, respectively. One should also note that the \(\Delta L/L\)-maximum for each temperature can be well described by the present model (Eq. 6); however, this is not the case for the minimum which starts to occur toward the end of each measuring run (Fig. 2). These minima are due to a further transformation process of the \(\beta '\)-precipitates. A quantitative kinetic description of this process on the basis of a model correspondingly extended by a further rate constant would, however, require measurements for even longer aging times well exceeding \(10^5\) s.

Finally, we will address the attractive potentials of dilatometry for constructing TTP diagrams. The part of the isothermal TTP diagram presented here (Fig. 5) focuses on the technologically most relevant range of temperatures for the formation of \(\beta ''\) and \(\beta '\). It nicely summarizes that at low aging temperatures and short aging times, first the \(\beta ''\)-phase is formed, which transforms into the \(\beta '\)-phase at higher temperatures. The good agreement between the data points deduced directly from the extrema of the \(\Delta L/ L\)-curves and the data points deduced from the model fit (Fig. 5) confirm the assumption made above that the extrema of the dilatometric curves represent the respective maximum concentration of \(\beta ''\) and \(\beta '\). However, for \(\beta ''\) at elevated temperatures the corresponding \(\Delta L/ L\)-maximum occurs at slightly lower temperatures compared to the calculated \(c_{\beta ''}\)-maximum. This arises from the opposing contribution of \(\beta ''\) and \(\beta '\) to the overall volume change and the fact that with increasing temperature the onset of \(\beta '\)-formation is more strongly shifted to shorter times compared to that of \(\beta ''\). As demonstrated by the lines representing 60 % of already formed phase (Fig. 5), the data obtained from fitting the \(\Delta L/ L\)-curves allow to determine the relative amount of \(\beta ''\) and \(\beta '\) at any desired point in the isothermal TTP diagram, i.e., for specific technologically relevant heat treatment condition. It should be noted that this type of isothermal TTP diagram, which has been obtained starting from supersaturated solid solution by a heating step to the respective aging temperature has to be distinguished from the TTP diagrams obtained from dilatometric curves under, e.g., cooling conditions [17].

For comparison, four data points extracted from TEM investigations taken from the literature are included in the diagram (Fig. 5). According to those studies, the maximum amounts of \(\beta ''\) and \(\beta '\) prevail for the temperatures and times quoted in Table 1, whereby the samples have been subjected to equivalent isothermal heat treatment. These data points fit remarkably well to the present results obtained by dilatometry.

Table 1 Data points of the TTP diagram (see Fig. 5) that have been extracted from literature. The number (No.) corresponds to the number in that figure
Full size table

The characteristic C-curve in the TTP diagram should, in principle, also be detectable with dilatometry. This requires an appropriate adjustment of the heating unit in order to monitor the very early stage of the precipitation processes in the first hundreds of seconds of aging. The focus of the present work, however, laid on long range isothermal aging condition.

It becomes evident from the discussion above that the direct access to the application-relevant TTP diagrams marks a highly attractive feature of the present simple kinetic analysis. However, it is also apparent that the presented high-precision dilatometry with its particular length change characteristics upon multi-step precipitation processes provides a superior experimental database which is highly suitable for advanced modeling as well.