Quantifying the distributions of dislocation spacings and cell sizes

Abstract

A new method is proposed to quantify the local dislocation spacings on sections displaying the intersections of dislocation lines. The method was applied to dislocation structures in single crystals of CaF₂ introduced by deformation at elevated temperature and made visible by etch pits. The method yields the frequency distributions and the spatial distributions of dislocation spacings. For cellular dislocation structures the method provides a quantitative and objective characterization in terms of frequency distribution of dislocation spacings in cell boundaries and cell interiors and of cell size.

Introduction

One of the greatest successes of materials science is the discovery that plastic deformation is carried by dislocations, constituting the linear defects of the crystalline structure at the boundaries of slipped areas. The parameters of the dislocation structure are fundamental for description of crystal plasticity and strength on a microstructural basis. In view of this fact one might expect that the quantification of the dislocation structure is a standard in plasticity research. However, this is generally not the case. Dislocation structure characterization is regarded too difficult a task and too far from practical application to be a standard effort in the investigations of plastic deformation. The complex arrangement of the dislocation lines in three-dimensional space and the large effort related with high-resolution techniques of visualizing dislocations are discouraging researchers. If dislocation structures are treated at all, they are usually treated in qualitative terms only. However, one needs quantification of the dislocation structure to make full use of its relation to deformation rate and strength.

Dislocations are stored in crystals in two ways [1, 2]. In the beginning of deformation of a material with low initial dislocation density and more than one active slip system, individual dislocations move and form a cellular structure [1, 2]. In the following, these are addressed as free dislocations to distinguish them from the dislocations being part of planar networks at the boundaries between neighboring subgrains which are misoriented by low angles; the latter dislocations may be regarded as being geometrically necessary in the sense of providing the subgrain misorientations. The subgrain structure results from spatial fluctuation of the activity of glide on a given system [3]. It develops in the transition to the steady state of plastic deformation, that is, in the late stages of work hardening at constant rate and in primary creep, and superimposes on the structure of free dislocations [1, 4, 5].

The parameters of the dislocations structure are obtained from observations on plane sections of the deformed material where the intersections of dislocation lines are made visible by a suitable technique, so that free dislocations appear as points in the section and subgrain boundaries as quasicontinuous lines of points. The (sub-) grain size is relatively easy to measure as the average subgrain intercept along a test line. It is directly related to the subgrain boundary area per crystal volume [6]. Quantification of the distribution of spacings of free dislocations is more demanding. In the following we will treat the existing methods of deriving dislocation spacing distributions and propose a new one which is rather simple, avoids the shortcomings and disadvantages of the existing methods and, in addition, allows one to objectively characterize the cell size.

Local dislocation spacings

Methods of determination

To characterize the spacing between dislocations, the test line must be expanded into a test strip of finite width Z (see [7]) as shown in Fig. 1. In transmission electron microscopy (TEM) the strip corresponds to a cross section of a thin foil [7, 8], so that Z equals the foil thickness. This section is viewed edge on so that only the projections Y of the spacings between intersections of dislocations with the strip area can be determined. In the following the intersection points are denoted as dislocations for brevity.

Fig. 1

Dislocations intersect a section at the points marked by filled circles. Within a strip of width Z (shaded) the projected dislocation spacing is Y. The dark gray element has N = 2 dislocations lying on its left borderline; all light gray elements have N = 1

Brandon and Komen [7] proposed to estimate the cumulative frequency F(Y) of projected spacings Y along a test strip by dividing the test strip into equal segments of width Δ (see Fig. 1) and determining Y either, for Y < Δ, as the average spacing of dislocations in a segment or, for Y > Δ, from the number of segments between neighboring dislocations. The Y-distribution is not expected to be independent of Z, as an increasing number of close neighborhoods are disrupted when the strip is made thinner, causing a continuous systematic stretch of F(Y) to larger Y.

Odén et al. [8] avoided the Z-problem associated with the Y-method by a slight modification of the definition of the local dislocation spacing. The local area per dislocation intersection point is $Z\cdot Y_{i}/N_{i}$ where N _i is the number of dislocations located on the starting edge (with respect to the direction of propagation, e.g. from left to right) of the ith strip segment (see Fig. 1). It is relatively independent of Z, as Y _i increases when Z is reduced. The local density of dislocations is obtained as $\varrho_i = 2\,{N_i}/(Z\cdot Y_i) ;$ the factor of 2 converts intersections per area to length per volume. The local dislocation spacing is defined as

$$ L_i \equiv \varrho_i^{-0.5} = \sqrt{\frac{Z\,Y_i}{2\,N_i}}\,. $$

(1)

Odén et al. [8] showed that the frequency distribution of spacings L can be correlated to that of the links of dislocations in a three-dimensional network (Frank network). They determined L from TEM micrographs; Lin et al. [9] used the method of Odén et al. [8] to determine L from test strips in light-optical micrographs of sections where the intersections of dislocations are marked by etch pits.

Both methods described so far use only part of the information available from an etched section due to projection of the strip onto a line. More information can be obtained by measuring the spacing l _i of next nearest neighbors directly from a section. Figure 2 shows the chain of nearest neighbors in a test strip of width Z. It starts at half the width Z on the left end of the test strip and makes the shortest connection to the next neighbor in the strip without moving to the left.

Fig. 2

Directional linear chain of nearest neighbors within a strip of width Z

Example

Single crystals of CaF₂ were used as model material. Their dislocation mobility decreases dramatically with decreasing temperature, turning the material completely brittle at room temperature, so that dislocation structures introduced at elevated temperature deformation are frozen in during cooling under load [5, 10]. In addition, the room temperature brittleness facilitates preparation of planar {111}-sections by cleaving under mild thermal stresses [5, 10]. The crystals were deformed in uniaxial compression in 〈111〉 direction [5, 10]. In this crystal orientation three slip systems experience equal resolved shear stresses. As usual, the multiple slip conditions lead to development of a strongly cellular dislocation structure.

The methods of determining the distribution of dislocation spacings described above were applied to the cellular structures of free dislocations generated by a small amount of deformation at high temperature (Table 1). The dislocation structures were revealed by producing dislocation etch pits on cleavage planes. From atomic force or light-optical micrographs of the etched sections linear montages were assembled. Coordinates of etch pits corresponding to free dislocations were obtained within a strip of width Z ₀ extending along the montage, using an open-source digitizer software [11]. Figure 3a shows part of the montage for example 1 of Table 1. To test the influence of strip width, the digitized area was subdivided into 2ⁿ parallel and non-overlapping strips of equal width $Z=Z_{0}/2^n$ with n = 0,1,...,5. The resulting length distributions were then accumulated from the 2ⁿ independent strips. Figure 3b and c shows two examples of l-chains in single strips with different Z. For the sake of comparison the real dislocation structure was transformed into a random structure of same dislocation density (Fig. 3d) by moving each digitized etch pit to a new random position.

Table 1 Deformation conditions (stress σ, strain ε), tested section area A _test, number N _etch of counted etch pits, and average dislocation spacing δ of analyzed examples

Fig. 3

(a) Typical detail of linear montage of atomic force micrographs, with height $Z_{0}=70\;\upmu\hbox{m}$, of etched dislocation structure from example 1 in Table 1. Chains of nearest neighbors at spacing l in single strips of width (b) $Z=Z_{0}/2^{4}=4.4\,\upmu\hbox{m}$ and (c) Z = Z ₀ in digitized structure of (a). (d) Structure of (a) after randomization of etch-pit positions

Figure 4 shows the frequency distributions of Y according to the procedure proposed by Brandon and Komen [7] for two values of Z. As expected (see above), the Y-distribution is not independent of Z, simply because Y → ∞ as Z → 0. One also observes a significant influence of the grid width Δ: the distribution curves develop a kink at Y = Δ.

Fig. 4

Cumulative frequency F of projected dislocation spacings Y after Brandon and Komen [7] for the section of Fig. 3a for two different values of strip width (corresponding to foil thickness in case of TEM) $Z=Z_{0}/2^n$ and seven levels of grid width Δ varying in steps of factor 2

The L-distributions are only weakly dependent on Z. This holds for the real case (Fig. 5a) as well as for the randomized structure (Fig. 5c) and is most clearly seen from the relation between Z and the distribution characteristics presented in Fig. 6a and c, which also show that the average spacing $\bar{L}$ is about 0.8 δ where

$$ \delta\equiv \varrho^{-0.5}= \sqrt{\frac{Z\,\sum_{i}Y_i}{2\,\sum_{i}N_i}}\,. $$

(2)

is the average dislocation spacing defined in analogy to Eq. 1. When Z becomes large, Y becomes smaller than the resolution limit given by the pixel size of the digital micrograph. Then the stepwise increase of Y in units of pixel size causes a systematic error in F(L) for low L. This error becomes marked in the present light-optical observations for L < 3 μm as exemplified in Fig. 5c. It was corrected by modifying the measured dislocation positions by a scatter vector of random orientation and magnitude from zero to half the pixel size. The significant improvement of the L-data by superposition of scatter is obvious from the more consistent results for F(L) for L-values coming close to the resolution limit of the underlying micrograph ($0.18\,\upmu\rm m$ pixel size in the present case).

Fig. 5

Cumulative frequency F versus dislocation spacings for different $Z=Z_{0}/2^n$ (see ordinates of Fig. 6); (a) L and (b) l for dislocation structure corresponding to Fig. 3a, (c) L and (d) l for random structure corresponding to Fig. 3d. Stepped gray curves in (c) result from original L-method [9] without smoothing by subpixel scattering (see text)

Fig. 6

(a–d) Relation between width Z of test strips and characteristics of distributions of Fig. 5(a–d): L, l at cumulative frequencies F = 0.16, 0.5 and 0.84, mean values $\bar{L}, \bar{l}$

A more facetted picture emerges for the nearest neighbor spacing l. F(l) depends significantly on Z (Figs. 5b, d and 6b, d). The l-chain in the wide strip of Fig. 3c has attained its limiting form because Z is sufficiently large, so that each nearest neighbor is reached and further increase of Z does not alter the chain. Here the average segment length $\bar{l}$ virtually coincides with the average dislocation spacing δ (Fig. 6b, d). By contrast, the chain in the narrow strip of Fig. 3b misses next nearest neighbors lying outside the test strip. The regions with short spacings l are less affected by a decrease of Z than the regions with long l. This explains why the right shift of F(l) with decreasing Z to larger values is distinctly more pronounced for larger l.

The distributions F(l) in Fig. 5b deviate more strongly from log-normal symmetry than the other three distributions (Fig. 5a, c, d). This is confirmed by the fact that l _0.84/l _0.5 is significantly larger than l _0.5/l _0.16 in Fig. 6b in contrast to the other cases. This deviation from symmetry can be explained by the cellularity of the dislocation structure (Fig. 3a), leading to a preferential selection of small l in cell boundaries along the connecting chain (Fig. 3b, c).

Characterization of cellular dislocation structures

Distribution of dislocation spacings in cell boundaries and cell interiors

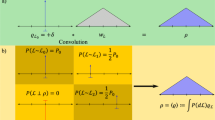
The information contained in F(l) may be used for a quantitative characterization of the cell structure. In the following, a simple segment-pooling method is presented which allows one to separate F(l) into two additive parts describing the cell boundaries (subscript b) and the cell interiors (subscript i):

$$ F(l)=\phi_{\rm b}\,F_{\rm b}(l) + (1-\phi_{\rm b})\,F_{\rm i}(l) \,; $$

(3)

ϕ_b and (1 − ϕ_b) are the fractions of boundary and interior segments, respectively. We start from the assumption that the distribution F _b(l) of boundary segments between nearest dislocation neighbors is symmetrical in Fig. 7a. This is supported by the ubiquity of log-normal distributions of microstructural spacings in materials and by the fact that F(L) is close to log-normal. To determine ϕ_b, the procedure outlined in Fig. 7a is applied. The thin line for ϕ = 0 represents F(l). Mirroring its branch with 0 ≤ F ≤ ϕ/2 at the point F = ϕ/2 yields a symmetrical curve. For instance, setting ϕ = ϕ_b as shown at the right ordinate yields the dashed line ϕ_b F _b as frequency distribution of the short boundary segments and the thick line (1 − ϕ_b)F _i as frequency distribution of the remaining long segments (see Eq. 3). Systematic variation of ϕ yields the thin lines (1 − ϕ)F _i(l). For large ϕ these lines dip into the field of negative values (hatched area in Fig. 7a). As 1 − ϕ > 0, these must result from F _i(l) < 0. However, negative values of the cumulative probability F _i are physically meaningless and must be excluded. ϕ_b is taken to be the maximum possible ϕ, for which occurrences of F _i(l) < 0 are still negligible. In the example of Fig. 7a this is the case for ϕ = ϕ_b = 0.54 ± 0.05.

Fig. 7

(a) (1 − ϕ)F _i for long segments l in cell interior, obtained by splitting F(l) of Fig. 5b according to Eq. 3 and setting ϕ_b = ϕ = 0.0, 0.1, … ,0.9. Thick lines show ϕ F _b and (1 − ϕ)F _i for maximum ϕ = ϕ_b without significant occurrences of F _i < 0 (hatched area). See text for details. (b) Variation of medians l _b,0.5 and l _i,0.5 of F _b(l) and F _i(l) with strip width $Z=Z_{0}/2^n$

The procedure of determining F _b(l) and F _i(l) is robust against variations of strip width Z. This is seen from Fig. 7b. It shows that the medians l _b,0.5 and l _i,0.5 of the frequency distributions F _b(l) and F _i(l) remain essentially constant, as long as Z > 2 δ. The slight decrease of l _b,0.5 and l _i,0.5 with decreasing Z is associated with a slight systematic decrease of ϕ_b, resulting from the increasing deviation from symmetry of the F(l)-curves in Fig. 5c. This effect is rather small compared to typical experimental scatter. For Z < 3 δ, however, one finds a systematic increase of l _i,0.5 with decreasing Z owing to the change in the shapes of the F(l)-curves of Fig. 5b discussed above.

The above separation procedure was applied in a formal manner also to the random dislocation distribution of Fig. 3d. In contrast to the case of the cellular structure, an increase of l _b,0.5 with decreasing Z was found for the random structure. This qualitative difference is related to and thereby confirms the absence of cellularity in the random structure.

Cell size

The knowledge of the spacing distribution in cell boundaries and cell interiors opens the opportunity to objectively identify cell boundaries at large and determine their spacings. Figure 8a shows a clearly cellular dislocation structure; the narrow strip of width Z ₀ served as sampling area. The width Z < Z ₀ of the test strips is small compared to the estimate of cell size. This is necessary to avoid the l-chain following the curved cell boundary traces; if this would happen, the l-chain would miss the cell interiors and the linear cell intercept c could not be determined.

Fig. 8

Cell structure formed in case 2 of Table 1; (a) detail of montage of light-optical micrographs with l-chain in strip of width $Z=Z_{0}/3=2.2\;\upmu\hbox{m}\approx \delta$; (b) l as function of position y along the strip for the chain in (a); segment pooling (see text) results in alternating sequence of cell interiors (white) and cell boundaries (gray)

Separation of the F(l)-distributions measured in the test strips according to Eq. 3 for values of Z ≥ δ yielded the medians l _b,0.5 and l _i,0.5 of F _b(l) and F _i(l) shown in Fig. 8b; they are virtually independent of Z as in Fig. 7b. Figure 8b shows the spatial variation of l in the chain of Fig. 8a with location y along the test strip. These segments may indicate a cell boundary, if one or more consecutive l-values fall below a certain limit, given for instance by l _b,0.5 or by δ. The numbers N _b of boundaries identified in these ways are shown in Fig. 9. It is seen that N _b increases steeply with strip width Z, far beyond the result N _b = 18 of visual inspection of the micrographs with subjective boundary identification on the basis of the dislocation pattern as a whole. The reason lies in the increasing number of consecutive segments in the chain which still belong to a single boundary. Since the spacings in a boundary naturally fluctuate around l _b,0.5, an additional (virtual) boundary is identified, whenever a single segment (or a group of neighboring ones) happens to be longer than the selected threshold.

Fig. 9

Number N _b of boundaries in test strip of Fig. 8a as function of strip width Z with boundary identification by l < l _b,0.5, by l < δ, and by the segment-pooling scheme (see text) in comparison to result from visual inspection

This boundary fragmentation problem is avoided by complementing the identification of cell boundaries by the identification of cell interiors where l exceeds a certain limit, chosen as l _i,0.5, and using the condition that each pair of neighboring boundaries must enclose the interior of a single cell (and vice versa). To fulfill the latter condition, those segments, which cannot immediately be identified as either a boundary segment or a cell interior segment, need to be classified.

This is done according to the following segment-pooling scheme. A sequence of segments l, which lie between two cell interior segments and do not belong to a cell boundary, is regarded to belong to the same cell interior as the enclosing segments. Analogously, a sequence of segments, which lie between two cell boundary segments and do not belong to a cell interor, is regarded to belong to the same cell boundary as the enclosing segments. Finally, a sequence of segments, which lie in between a boundary segment and a cell interior segment, is separated into two halves which are regarded to belong to the adjacent cell boundary and interior, respectively. This scheme transforms the l-chain into an alternating sequence of cell interiors and boundaries in the direction y along the test strip (Fig. 8b). Figure 9 shows that the numbers N _b of cell boundaries derived from pooling of segments come close to the visual result and vary only weakly with test strip width Z. In contrast to the visual identification of boundaries, the proposed method has the advantage of being an objective one, independent of the observer.

After identifying the cell boundaries, the lengths of cell intercepts c are obtained as the distances of neighboring boundaries in y-direction (Fig. 8b), if the exact location of each cell boundary is defined. As a reasonable definition we chose the center of the sequence of l-segments belonging to a single boundary. Open ends on both sides of the strip were combined to represent one cell.

The resulting c-distributions are plotted in Fig. 10. Consistent with the visual impression obtained from Fig. 8, there is excellent agreement between F(c) obtained from three adjacent strips of the type shown in Fig. 8a with $Z=Z_{0}/3\approx\delta$ and from visual inspection. This indicates that the proposed l-pooling scheme yields an objective criterion for identification of cell boundaries, which is not in conflict with the visual impression of an experienced observer. The ratio of cell size (average cell segment length) $\bar{c}$ to average dislocation spacing δ is about 20; this is the expected order of magnitude (see data for Cu in Figs. 8–10 in [1]).

Fig. 10

Frequency distributions of cell intercepts c determined by segment-pooling scheme in test strip of Fig. 8a with Z = Z ₀ and $Z=Z_{0}/3$ (average c from three adjacent strips) in comparison to result of visual inspection

Increasing the strip width by a factor of three to Z = Z ₀ has only a small influence on F(c). Thus the method is rather stable against limited variation of Z. The somewhat lower frequency of occurrence of small l in a strip with larger Z may be connected to the fact that larger Z gives somewhat more opportunity for the chain to run along boundaries and circumvent short cell intercepts.

Concluding remarks

A new method for determining local dislocation spacings is proposed. It is applicable to sections where the intersections of dislocations are made visible, for instance by the etch pit technique. The local spacings are defined as the shortest segments between intersection points forming a directed chain along a test strip of suitable width. The new method is easier to use and, due to its sensitivity to the width of the test strip, delivers more information than the conventional link-length method [8, 9] based on the average area per dislocation. In particular, it allows one to objectively characterize cellular dislocation structures by the frequency distributions of dislocation spacings in cell boundaries and cell interiors. These distributions yield the spatial arrangement of cell boundaries, from which the distribution of cell intercepts and the cell size can be obtained.

The restriction of magnification in light-optical observation of dislocation etch pits can be overcome by atomic force microscopy. In principle, it appears possible to apply the new method also to transmission electron microscopic micrographs, by combining information on sections parallel and perpendicular to the electron beam for foils of different thickness; however, this was beyond the scope of the present work.

Once the coordinates of the dislocations (intersection points) in a test section have been obtained in digital form, the processing of the data for full, objective quantification of the dislocation structure including its cellularity is an easy task which can be performed in a semiautomatic manner by a computer program.