Modelling off-axis ply matrix cracking in continuous fibre-reinforced polymer matrix composite laminates

Abstract

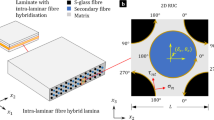
The fracture process of composite laminates subjected to static or fatigue tensile loading involves sequential accumulation of intra- and interlaminar damage, in the form of transverse cracking, splitting and delamination, prior to catastrophic failure. Matrix cracking parallel to the fibres in the off-axis plies is the first damage mode observed. Since a damaged lamina within the laminate retains certain amount of its load-carrying capacity, it is important to predict accurately the stiffness properties of the laminate as a function of damage as well as progression of damage with the strain state. In this paper, theoretical modelling of matrix cracking in the off-axis plies of unbalanced symmetric composite laminates subjected to in-plane tensile loading is presented and discussed. A 2-D shear-lag analysis is used to determine ply stresses in a representative segment and the equivalent laminate concept is applied to derive expressions for Mode I, Mode II and the total strain energy release rate associated with off-axis ply cracking. Dependence of the degraded stiffness properties and strain energy release rates on the crack density and ply orientation angle is examined for glass/epoxy laminates. Suitability of a mixed mode fracture criterion to predict the cracking onset strain is also discussed.

Appendices

Appendix A

Variation of the out-of-plane shear stresses has the form

$$ \sigma_{j3}^{(2)} =\frac{\tau_j} {h_2} x_3, \quad 0\leqslant \vert x_3 \vert \leqslant h_2, \quad j=1,2, \quad \sigma_{j3}^{(1)} =\frac{\tau_j} {h_1} (h-x_3),\quad h_2 \leqslant \vert x_3 \vert \leqslant h $$

(24)

Constitutive equations for the out-of-plane shear stresses are

$$ \left\{{{\begin{array}{ll} {\sigma_{13}^{(k)}} \\ {\sigma_{23}^{(k)}} \\ \end{array}}} \right\}\approx \left[ {{ \begin{array}{ll} {Q_{55}^{(k)}} & {Q_{45}^{(k)}} \\ {Q_{45}^{(k)}} & {Q_{44}^{(k)}} \\ \end{array}}} \right]\frac{\partial} {\partial x_3} \left\{ {{\begin{array}{ll} {u_1^{(k)}} \\ {u_2^{(k)}} \\ \end{array}}} \right\},\quad i=1,2 $$

(25)

After substituting Eq. (25) into Eq. (24), multiplying them by x ₃ and by h−x ₃ respectively and integrating with respect to x ₃ we get

$$ \frac{h_1} {3}\left\{{{\begin{array}{ll} {\tau_1} \\ {\tau_2} \\ \end{array}}} \right\}=\left[ {{\begin{array}{ll} {{\hat Q}_{55}^{(1)}} & {{\hat Q}_{45}^{(1)}} \\ {{\hat Q}_{45}^{(1)}} & {{\hat Q}_{44}^{(1)}} \\ \end{array}}} \right]\left({\left\{{{\begin{array}{ll} {{\tilde u}_1^{(1)}} \\ {{\tilde u}_2^{(1)}} \\ \end{array}}} \right\}-\left\{{{\begin{array}{ll} {U_1} \\ {U_2} \\ \end{array}}} \right\}} \right) $$

(26a)

$$ \frac{h_2} {3}\left\{ {{\begin{array}{ll} {\tau_1} \\ {\tau_2} \\ \end{array}}} \right\}=\left[ {{\begin{array}{ll} {{\hat Q}_{55}^{(2)}} & {{\hat Q}_{45}^{(2)}} \\ {{\hat Q}_{45}^{(2)}} & {{\hat Q}_{44}^{(2)}} \\ \end{array}}} \right]\left({\left\{{{\begin{array}{ll} {U_1} \\ {U_2} \\ \end{array}}}\right\}-\left\{ {{\begin{array}{ll} {{\tilde u}_1^{(2)}} \\ {{\tilde u}_2^{(2)}} \\ \end{array}}}\right\}} \right) $$

(26b)

Here {U _j }={u ⁽¹⁾ _j }| _{x_3 =h_2} ={u ⁽²⁾ _j }| _{x_3 =h_2},   j=1,2 are the in-plane displacements at the interface. After rearranging Eqs. (26a) and (26b) become

$$ \left\{ {{\begin{array}{ll} {{\tilde u}_1^{(1)}} \\ {{\tilde u}_2^{(1)}} \\ \end{array}}} \right\}-\left\{ {{\begin{array}{ll} {{\tilde u}_1^{(2)}} \\ {{\tilde u}_2^{(2)}} \\ \end{array}}} \right\}=\left({\frac{h_1} {3}\left[ {{\begin{array}{ll} {{\hat Q}_{55}^{(1)}} & {{\hat Q}_{45}^{(1)}} \\ {{\hat Q}_{45}^{(1)}} & {{\hat Q}_{44}^{(1)}} \\ \end{array}}} \right]^{-1}} \right.\left. {+\frac{h_2} {3}\left[ {{\begin{array}{ll} {{\hat Q}_{55}^{(2)}} & {{\hat Q}_{45}^{(2)}} \\ {{\hat Q}_{45}^{(2)}} & {{\hat Q}_{44}^{(2)}} \\ \end{array}}} \right]^{-1}} \right)\left\{ {{\begin{array}{ll} {\tau_1} \\ {\tau_2} \\ \end{array}}} \right\} $$

(27)

Inversion of Eq. (27) leads to

$$ \left\{ {{\begin{array}{ll} {\tau_1} \\ {\tau_2} \\ \end{array}}} \right\}=\left[ {{\begin{array}{ll} {K_{11}} & {K_{12}} \\ {K_{21}} & {K_{22}} \\ \end{array}}} \right]\left({\left\{ {{\begin{array}{ll} {{\tilde u}_1^{(1)}} \\ {{\tilde u}_2^{(1)}} \\ \end{array}}} \right\}-\left\{ {{\begin{array}{ll} {{\tilde u}_1^{(2)}} \\ {{\tilde u}_2^{(2)}} \\ \end{array}}} \right\}} \right), $$

(28a)

$$ \left[ {{\begin{array}{ll} {K_{11}} & {K_{12}} \\ {K_{21}} & {K_{22}} \\ \end{array}}} \right]=\left({\frac{h_1} {3}\left[ {{\begin{array}{ll} {{\hat Q}_{55}^{(1)}} & {{\hat Q}_{45}^{(1)}} \\ {{\hat Q}_{45}^{(1)}} & {{\hat Q}_{44}^{(1)}} \\ \end{array}}} \right]^{-1}} \right.\left. {+\frac{h_2} {3}\left[ {{\begin{array}{ll} {{\hat Q}_{55}^{(2)}} & {{\hat Q}_{45}^{(2)}} \\ {{\hat Q}_{45}^{(2)}} & {{\hat Q}_{44}^{(2)}} \\ \end{array}}} \right]^{-1}} \right)^{-1} $$

(28b)

Appendix B

On applying the constitutive equations, inverse to Eq. (4), the generalised plane strain condition ${\tilde \varepsilon}_{11}^{(1)} ={\tilde \varepsilon}_{11}^{(2)}$ becomes

$$ S_{11}^{(1)} {\tilde \sigma}_{11}^{(1)} +S_{12}^{(1)} {\tilde \sigma}_{22}^{(1)} +S_{16}^{(1)} {\tilde \sigma}_{12}^{(1)} ={\hat S}_{11}^{(2)} {\tilde \sigma}_{11}^{(2)} +{\hat S}_{12}^{(2)} {\tilde \sigma}_{22}^{(2)} $$

(29)

where ${\hat S}_{ij}^{(k)}$ are the compliances for the kth layer. Using the laminate equilibrium equations, Eq. (5), stresses in the 1st layer can be excluded, so that

$$ {\tilde \sigma}_{11}^{(2)} =a_{22} {\tilde \sigma}_{22}^{(2)} +a_{12} {\tilde \sigma}_{12}^{(2)} +b{\bar \sigma}_x, $$

(30)

$$ a_{22} =-\frac{{\hat S}_{12}^{(1)} +\chi {\hat S}_{12}^{(2)}} {{\hat S}_{11}^{(1)} +\chi {\hat S}_{11}^{(2)}}, \quad a_{12} =-\frac{{\hat S}_{16}^{(1)}} {{\hat S}_{11}^{(1)} +\chi {\hat S}_{11}^{(2)}}, \quad \chi =\frac{h_1} {h_2}, $$

$$ b=(1+\chi)\frac{({\hat S}_{11}^{(1)} \cos^2\theta +{\hat S}_{12}^{(1)} \sin^2\theta -{\hat S}_{16}^{(1)} \sin\theta \cos\theta)}{{\hat S}_{11}^{(1)} +\chi {\hat S}_{11}^{(2)}} $$

Finally, strain differences are expressed in terms of stresses as

$$ \left\{ {{\begin{array}{ll} {{\tilde \gamma}_{12}^{(1)} -{\tilde \gamma}_{12}^{(2)}} \\ {{\tilde \varepsilon}_{22}^{(1)} -{\tilde \varepsilon}_{22}^{(2)}} \\ \end{array}}} \right\}=-\frac{1}{\chi} \left[ {{\begin{array}{ll} {L_{11}} & {L_{12}} \\ {L_{21}} & {L_{22}} \\ \end{array}}} \right]\left\{ {{\begin{array}{ll} {{\tilde \sigma}_{12}^{(2)}} \\ {{\tilde \sigma}_{22}^{(2)}} \\ \end{array}}} \right\}+\frac{1}{\chi} \left\{ {{\begin{array}{ll} {M_1} \\ {M_{12}} \\ \end{array}}} \right\}{\bar \sigma}_x $$

(31)

Here

$$ L_{11} ={\hat S}_{66}^{(1)} +a_{12} {\hat S}_{16}^{(1)} +\chi {\hat S}_{66}^{(2)}, \quad L_{12} ={\hat S}_{26}^{(1)} +a_{22} {\hat S}_{16}^{(1)} $$

$$ L_{21} ={\hat S}_{26}^{(1)} +a_{12} {\hat S}_{12}^{(1)} +\chi a_{12} {\hat S}_{12}^{(2)},\quad L_{22} ={\hat S}_{22}^{(1)} +a_{22} {\hat S}_{12}^{(1)} +\chi ({\hat S}_{22}^{(2)}+a_{22} {\hat S}_{12}^{(2)})$$

$$ M_1 =(1+\chi)\left[ {({\hat S}_{16}^{(1)} +a_{12} {\hat S}_{11}^{(2)})\cos^2\theta} \right.+({\hat S}_{26}^{(1)} +a_{12} {\hat S}_{12}^{(1)})\sin^2\theta \left. {-({\hat S}_{66}^{(1)} +a_{12} {\hat S}_{16}^{(1)})\sin\theta \cos\theta} \right] $$

$$ M_2 =(1+\chi)\left[ {({\hat S}_{12}^{(1)} +a_{22} {\hat S}_{11}^{(1)})\cos^2\theta +} \right.({\hat S}_{22}^{(1)} +a_{22} {\hat S}_{12}^{(1)})\sin^2\theta -\left. {({\hat S}_{26}^{(1)} +a_{22} {\hat S}_{16}^{(1)})\sin\theta \cos\theta} \right] $$

Substitution into the equilibrium equations, Eq. (3), yields the following coupled 2nd order differential equations

$$ \frac{{\rm d}^2}{{\rm d}x_2^2} \left\{ {{\begin{array}{ll} {{\tilde \sigma}_{12}^{(2)}} \\ {{\tilde \sigma}_{22}^{(2)}} \\ \end{array}}} \right\}-\frac{1}{h_1} \left[ {{\begin{array}{ll} {K_{11}} & {K_{12}} \\ {K_{12}} & {K_{22}} \\ \end{array}}} \right]\;\left({\left[ {{\begin{array}{ll} {L_{11}} & {L_{12}} \\ {L_{12}} & {L_{22}} \\ \end{array}}} \right]\left\{ {{\begin{array}{ll} {{\tilde \sigma}_{12}^{(2)}} \\ {{\tilde \sigma}_{22}^{(2)}} \\ \end{array}}} \right\}+\left\{ {{\begin{array}{ll} {M_1} \\ {M_2} \\ \end{array}}} \right\}{\bar \sigma}_x} \right)=0$$

(32)

This set of equations is uncoupled at the expense of increasing the order of differentiation, resulting in a fourth order non-homogeneous ordinary differential equation.