Skip to main content
SpringerLink
Log in

\(\tilde{A}\) and \(\tilde{D}\) type cluster algebras: triangulated surfaces and friezes

  • Published:
Journal of Algebraic Combinatorics Aims and scope Submit manuscript

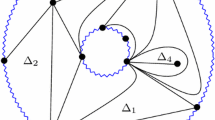
Abstract

By viewing \(\tilde{A}\) and \(\tilde{D}\) type cluster algebras as triangulated surfaces, we find all cluster variables in terms of either (i) the frieze pattern (or bipartite belt) or (ii) the periodic quantities previously found for the cluster map associated with these frieze patterns. We show that these cluster variables form friezes which are precisely the ones found by Assem–Dupont by applying the cluster character to the associated cluster category.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21

Similar content being viewed by others

Data Availability

Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.

References

  1. Assem, I., Dupont, G.: Friezes and a construction of the Euclidean cluster variables. J. Pure Appl. Algebra 215(10), 2322–2340 (2011)

    Article  MathSciNet  Google Scholar 

  2. Assem, I., Reutenauer, C., Smith, D.: Friezes. Adv. Math. 225(6), 3134–3165 (2010)

    Article  MathSciNet  Google Scholar 

  3. Auslander, M.: Representation theory of Artin algebras II. Comm. Algebra 1(4), 269–310 (1974)

    Article  MathSciNet  Google Scholar 

  4. Baur, K., Parsons, M.J., Tschabold, M.: Infinite friezes. European J. Combin. 54, 220–237 (2016)

    Article  MathSciNet  Google Scholar 

  5. Bernstein, I.N., Gel’fand, I.M., Ponomarev, V.A.: Coxeter functors and Gabriel’s theorem. Russian Math. Surveys 28(2), 17 (1973)

    Article  MathSciNet  Google Scholar 

  6. Buan, A.B., Marsh, B.R., Reineke, M., Reiten, I., Todorov, G.: Tilting theory and cluster combinatorics. Adv. Math. 204(2), 572–618 (2006)

    Article  MathSciNet  Google Scholar 

  7. Caldero, P., Chapoton, F.: Cluster algebras as Hall algebras of quiver representations. Comment. Math. Helv. 81(3), 595–616 (2006)

    Article  MathSciNet  Google Scholar 

  8. Caldero, P., Keller, B.: From triangulated categories to cluster algebras II. Ann. Sci. Éc. Norm. Supér. (4) 39(6), 983–1009 (2006)

    Article  MathSciNet  Google Scholar 

  9. Conway, J.H., Coxeter, H.S.M.: Triangulated polygons and frieze patterns. Math. Gaz. 57(400), 87–94 (1973)

    Article  MathSciNet  Google Scholar 

  10. Coxeter, H.S.M.: Frieze patterns. Acta Arith 18(1), 297–310 (1971)

    Article  MathSciNet  Google Scholar 

  11. Crawley-Boevey, Wi.: Lectures on representations of quivers, Lectures in Oxford (1992)

  12. Dupont, G.: Cluster multiplication in regular components via generalized Chebyshev polynomials. Algebr. Represent. Theory 15(3), 527–549 (2012)

    Article  MathSciNet  Google Scholar 

  13. Fomin, S., Shapiro, M., Thurston, D.P.: Cluster algebras and triangulated surfaces. Part I: cluster complexes. Acta Math. 201(1), 83–146 (2008)

    Article  MathSciNet  Google Scholar 

  14. Fomin, S., Zelevinsky, A.: Cluster algebras I: foundations. J. Amer. Math. Soc. 15(2), 497–529 (2002)

    Article  MathSciNet  Google Scholar 

  15. Fomin, S., Zelevinsky, A.: Cluster algebras IV: coefficients. Compos. Math. 143(1), 112–164 (2007)

    Article  MathSciNet  Google Scholar 

  16. Fordy, A.P., Hone, A.: Discrete integrable systems and Poisson algebras from cluster maps. Comm. Math. Phys. 325(2), 527–584 (2014)

    Article  MathSciNet  Google Scholar 

  17. Fordy, A.P., Marsh, B.R.: Cluster mutation-periodic quivers and associated Laurent sequences. J. Algebraic Combin. 34(1), 19–66 (2011)

    Article  MathSciNet  Google Scholar 

  18. Gabriel, P.: Unzerlegbare darstellungen I. Manuscripta Math. 6(1), 71–103 (1972)

    Article  MathSciNet  Google Scholar 

  19. Gabriel, P.: Auslander-reiten sequences and representation-finite algebras. In: Representation Theory I, pp. 1–71. Springer, Berlin (1980)

  20. Gabriel, P., Riedtmann, C.: Group representations without groups. Comment. Math. Helv. 54(1), 240–287 (1979)

    Article  MathSciNet  Google Scholar 

  21. Holm, T., Jørgensen, P.: \({SL}_2\)-tilings and triangulations of the strip. J. Combin. Theory Ser. A 120(7), 1817–1834 (2013)

    Article  MathSciNet  Google Scholar 

  22. Hügel, L.A.: An introduction to Auslander-Reiten theory, Lecture notes. ICTP Trieste (2006)

  23. Keller, B.: Cluster algebras, quiver representations and triangulated categories. arXiv preprint arXiv:0807.1960 (2008)

  24. Keller, B., Scherotzke, S.: Linear recurrence relations for cluster variables of affine quivers. Adv. Math. 228(3), 1842–1862 (2011)

    Article  MathSciNet  Google Scholar 

  25. Morier-Genoud, S., Ovsienko, V., Tabachnikov, S.: 2-frieze patterns and the cluster structure of the space of polygons. Ann. Inst. Fourier 62(3), 937–987 (2012)

    Article  MathSciNet  Google Scholar 

  26. Muir, T.: A Treatise on the Theory of Determinants: With Graduated Sets of Exercises. Macmillan, London (1882)

    MATH  Google Scholar 

  27. Pallister, J.: Linear relations and integrability for cluster algebras from affine quivers. Glasg. Math. J. 1–38 (2020)

  28. Pallister, J.: Linearisability and integrability of discrete dynamical systems from cluster and LP algebras. Ph.D. thesis, University of Kent (2020)

Download references

Acknowledgements

The author thanks Andy Hone, Rei Inoue and Philipp Lampe for helpful discussions and advice. This paper was improved thanks to advice from anonymous reviewers. This research was carried out while the author was a recipient of a Japan Society for the Promotion of Science (JSPS) postdoctoral fellowship and was supported by JSPS KAKENHI Grant Number 21F20788.

Author information

Authors and Affiliations

  1. Department of Mathematics and Informatics, Faculty of Science, Chiba University, Chiba, Japan

    Joe Pallister

Authors
  1. Joe Pallister
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Joe Pallister.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Pallister, J. \(\tilde{A}\) and \(\tilde{D}\) type cluster algebras: triangulated surfaces and friezes. J Algebr Comb 56, 1163–1202 (2022). https://doi.org/10.1007/s10801-022-01152-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10801-022-01152-z

Keywords

Mathematics Subject Classification

Search

Navigation