Skip to main content
SpringerLink
Log in

A Fractional Schrödinger Equation and Its Solution

  • Published:
International Journal of Theoretical Physics Aims and scope Submit manuscript

Abstract

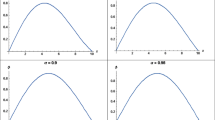
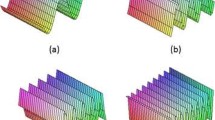
This paper presents a fractional Schrödinger equation and its solution. The fractional Schrödinger equation may be obtained using a fractional variational principle and a fractional Klein-Gordon equation; both methods are considered here. We extend the variational formulations for fractional discrete systems to fractional field systems defined in terms of Caputo derivatives to obtain the fractional Euler-Lagrange equations of motion. We present the Lagrangian for the fractional Schrödinger equation of order α. We also use a fractional Klein-Gordon equation to obtain the fractional Schrödinger equation which is the same as that obtained using the fractional variational principle. As an example, we consider the eigensolutions of a particle in an infinite potential well. The solutions are obtained in terms of the sines of the Mittag-Leffler function.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Schrödinger, E.: Quantisierung als Eigenwert Problem (Erste Mitteilung). Ann. Phys. 79, 734 (1926)

    Article  Google Scholar 

  2. Nelson, E.: Quantum Fluctuations. Princeton University Press, Princeton (1985)

    MATH  Google Scholar 

  3. Nelson, E.: Derivation of Schrödinger equation from Newtonian mechanics. Phys. Rev. 150, 1079 (1966)

    Article  ADS  Google Scholar 

  4. Hall, M.J.W., Reginatto, M.: Schrödinger equation from an exact uncertainty principle. J. Phys. A 35, 3289 (2002)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  5. Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, New York (1974)

    MATH  Google Scholar 

  6. Miller, K.S., Ross, B.: An Introduction to the Fractional Integrals and Derivatives-Theory and Applications. Wiley, New York (1993)

    Google Scholar 

  7. Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)

    Book  MATH  Google Scholar 

  8. Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)

    MATH  Google Scholar 

  9. Zaslavsky, G.M.: Hamiltonian Chaos and Fractional Dynamics. Oxford University Press, Oxford (2005)

    MATH  Google Scholar 

  10. Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)

    MATH  Google Scholar 

  11. Magin, R.L.: Fractional Calculus in Bioengineering. Begell House, Reading (2006)

    Google Scholar 

  12. Mainardi, F., Luchko, Yu., Pagnini, G.: The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 4(2), 153 (2001)

    MATH  MathSciNet  Google Scholar 

  13. Riewe, F.: Nonconservative Lagrangian and Hamiltonian mechanics. Phys. Rev. E 53, 1890 (1996)

    Article  MathSciNet  ADS  Google Scholar 

  14. Klimek, M.: Fractional sequential mechanics-models with symmetric fractional derivative. Czechoslov. J. Phys. 51, 1348 (2001)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  15. Agrawal, O.P.: Formulation of Euler-Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 272, 368 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  16. Muslih, S.I., Baleanu, D.: Hamiltonian formulation of systems with linear velocities within Riemann-Liouville fractional derivatives. J. Math. Anal. Appl. 304, 599 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  17. Baleanu, D., Muslih, S.I.: Lagrangian formulation of classical fields within Riemann-Liouville fractional derivatives. Phys. Scr. 72(2–3), 119 (2005)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  18. Rabei, E.M., Nawafleh, K.I., Hijjawi, R.S., Muslih, S.I., Baleanu, D.: The Hamilton formalism with fractional derivatives. J. Math. Anal. Appl. 327, 891 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  19. Dong, J.P., Xu, M.Y.: Some solutions to the space fractional Schrödinger equation using momentum representation method. J. Math. Phys. 48, 072105 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  20. Naber, M.: Time fractional Schrödinger equation. J. Math. Phys. 45, 3339 (2004)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  21. Wang, S.W., Xu, M.Y.: Generalized fractional Schrödinger equation with space-time fractional derivatives. J. Math. Phys. 48, 043502 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  22. Laskin, N.: Lévy flights over quantum paths. Commun. Nonlinear. Sci. Numer. Simul. 12, 2 (2007)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  23. Laskin, N.: Fractional quantum mechanics. Phys. Rev. E 62, 3135 (2000)

    Article  ADS  Google Scholar 

  24. Muslih, S.I., Agrawal, O.P., Baleanu, D.: A fractional Dirac equation and its solution. J. Phys. A, Math. Gen. 45(3), 055203 (2010)

    Article  MathSciNet  ADS  Google Scholar 

  25. Goldstein, H.: Classical Mechanics. Addison-Wesley, Reading (1980)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Southern Illinois University, Carbondale, IL, 62901, USA

    Sami I. Muslih & Om P. Agrawal

  2. Department of Mathematics and Computer Sciences, Faculty of Arts and Sciences, Çankaya University, 06530, Ankara, Turkey

    Dumitru Baleanu

Authors
  1. Sami I. Muslih
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Om P. Agrawal
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dumitru Baleanu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dumitru Baleanu.

Additional information

S.I. Muslih is on leave of absence from Al-Azhar University-Gaza.

D. Baleanu is on leave of absence from Institute of Space Sciences, P.O. Box, MG-23, 76900, Magurele-Bucharest, Romania.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Muslih, S.I., Agrawal, O.P. & Baleanu, D. A Fractional Schrödinger Equation and Its Solution. Int J Theor Phys 49, 1746–1752 (2010). https://doi.org/10.1007/s10773-010-0354-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10773-010-0354-x

Keywords

Search

Navigation