Appendix A: Transformed elastic stiffness constants of a diamond cubic mono-crystalline plate
The non-vanishing elastic stiffness constants, \({c}^{\prime }_{ij}\), with respect to the rotated coordinate system, \(\hbox {x }[1\bar{{1}}0]\), \(\hbox {y }[111]\), \(\hbox {z }[\bar{{1}}\bar{{1}}2]\) and referred to in Eq. (1) can be expressed in terms of their counterparts, , determined with respect to the edges, [100], [010], [001], of a diamond cubic crystal as follows:
$$\begin{aligned} \begin{aligned}&{c}^{\prime }_{11} ={c}^{\prime }_{33} =\frac{1}{2}\left( {c_{11} +c_{12} } \right) +c_{66} , \\&{c}^{\prime }_{22} =\frac{1}{3}\left( {c_{11} +2c_{12} +4c_{66} } \right) ,\\&{c}^{\prime }_{44} ={c}^{\prime }_{66} =\frac{1}{3}\left( {c_{11} -c_{12} +c_{66} } \right) , \\&{c}^{\prime }_{55} =\frac{1}{6}\left( {c_{11} -c_{12} +4c_{66} } \right) , \\&{c}^{\prime }_{12} ={c}^{\prime }_{23} =\frac{1}{3}\left( {c_{11} +2c_{12} -2c_{66} } \right) , \\&{c}^{\prime }_{13} =\frac{1}{6}\left( {c_{11} +5c_{12} -2c_{66} } \right) ,\\&{c}^{\prime }_{14} =-\frac{1}{3\sqrt{2}}\left( {c_{11} -c_{12} -2c_{66} } \right) , \\&{c}^{\prime }_{34} =-{c}^{\prime }_{56} =\frac{1}{3\sqrt{2}}\left( {c_{11} -c_{12} -2c_{66} } \right) . \end{aligned} \end{aligned}$$
(78)
Appendix B: Details of the derivation of the solution for a \((111)[\bar{{1}}\bar{{1}}2]\times [1\bar{{1}}0]\) through-crack under mixed mode I+II+III loading
Some of the details of the mathematical derivation of the solution, involving complex roots, for a diamond cubic crystal plate, weakened by \((111)[\bar{{1}}\bar{{1}}2]\times [1\bar{{1}}0]\) through-crack and subjected to mode I/II loading (Sect. 3), are presented here. The components of displacement that satisfy the equilibrium equations (1) can be expressed in the following form:
$$\begin{aligned}&u(x,y,z) = ( \overline{{\overline{{D}}}}_1 i\sin ( {kz} )+ \overline{{\overline{{D}}}}_2 \cos ( {kz} ) ) ( {ik} )^{s}\nonumber \\&\quad \times \, [ \overline{{A}}_1( {x+(\xi +i\eta )y} )^{s} + \overline{{A}}_2 ( {x+(\xi -i\eta )y} )^{s}\nonumber \\&\quad +\,\overline{{A}}_3 ( {x+(-\xi +i\eta )y} )^{s}+ \overline{{A}}_4 ( {x+(-\xi -i\eta )y} )^{s}\nonumber \\&\quad +\,\overline{{A}}_5 (x+i\zeta y)^{s} + \overline{{A}}_6 (x-i\zeta y)^{s} ],\end{aligned}$$
(79a)
$$\begin{aligned}&v(x,y,z) = ( \overline{{\overline{{D}}}}_1 i\sin ( {kz} )+ \overline{{\overline{{D}}}}_2 \cos ( {kz} ) ) ( {ik} )^{s}\nonumber \\&\quad \times \, [ \overline{{B}}_1 ( {x+(\xi +i\eta )y} )^{s} + \overline{{B}}_2 ( {x+(\xi -i\eta )y} )^{s}\nonumber \\&\quad +\, \overline{{B}}_3 ( {x+(-\xi +i\eta )y} )^{s} +\overline{{B}}_4 ( {x+(-\xi -i\eta )y} )^{s}\nonumber \\&\quad +\,\overline{{B}}_5 (x+i\zeta y)^{s} + \overline{{B}}_6 (x-i\zeta y)^{s} ],\end{aligned}$$
(79b)
$$\begin{aligned}&w(x,y,z) = ( \overline{{\overline{{D}}}}_1 i\sin ( {kz} )+ \overline{{\overline{{D}}}}_2 \cos ( {kz} ) )( {ik} )^{s}\nonumber \\&\quad \times \, [ \overline{{C}}_1 ( {x+(\xi +i\eta )y})^{s}+\overline{{C}}_2 ( {x+(\xi -i\eta )y} )^{s}\nonumber \\&\quad \, + \overline{{C}}_3 ( {x+(-\xi +i\eta )y} )^{s} +\overline{{C}}_4 ( {x+(-\xi -i\eta )y} )^{s}\nonumber \\&\quad \,+ \overline{{C}}_5 (x+i\zeta y)^{s} + \overline{{C}}_6 (x-i\zeta y)^{s} ], \end{aligned}$$
(79c)
where \(\overline{{A}}_k , \overline{{B}}_k , \overline{{C}}_k , \hbox {k} = 1,\ldots ,6\), are undetermined coefficients. It may be noted that \(\overline{{B}}_k\) and \(\overline{{C}}_k\) can be expressed in terms of the corresponding \(\overline{{A}}_k , \hbox {k} = 1,\ldots ,6\), by using Eq. (9), as given below:
$$\begin{aligned} \overline{{B}}_1&= \left( {H_1 + iH_2 } \right) \overline{{A}}_1 ,\end{aligned}$$
(80a)
$$\begin{aligned} \overline{{B}}_2&= \left( {H_1 - iH_2 } \right) \overline{{A}}_2 ,\end{aligned}$$
(80b)
$$\begin{aligned} \overline{{B}}_3&= \left( {H_3 + iH_4 } \right) \overline{{A}}_3,\end{aligned}$$
(80c)
$$\begin{aligned} \overline{{B}}_4&= \left( {H_3 - iH_4 } \right) \overline{{A}}_4,\end{aligned}$$
(80d)
$$\begin{aligned} \overline{{B}}_5&= \left( {H_5 + iH_6 } \right) \overline{{A}}_5 ,\end{aligned}$$
(80e)
$$\begin{aligned} \overline{{B}}_6&= \left( {H_5 - iH_6 } \right) \overline{{A}}_6 , \end{aligned}$$
(80f)
$$\begin{aligned} \overline{{C}}_1&= \left( {{H}^{\prime }_1 + i{H}^{\prime }_2 } \right) \overline{{A}}_1,\end{aligned}$$
(81a)
$$\begin{aligned} \overline{{C}}_2&= \left( {{H}^{\prime }_1 - i{H}^{\prime }_2 } \right) \overline{{A}}_2 ,\end{aligned}$$
(81b)
$$\begin{aligned} \overline{{C}}_3&= \left( {{H}^{\prime }_3 + i{H}^{\prime }_4} \right) \overline{{A}}_3 ,\end{aligned}$$
(81c)
$$\begin{aligned} \overline{{C}}_4&= \left( {{H}^{\prime }_3 - i{H}^{\prime }_4 } \right) \overline{{A}}_4,\end{aligned}$$
(81d)
$$\begin{aligned} \overline{{C}}_5&= \left( {{H}^{\prime }_5 + i{H}^{\prime }_6 } \right) \overline{{A}}_5 ,\end{aligned}$$
(81e)
$$\begin{aligned} \overline{{C}}_6&= \left( {{H}^{\prime }_5 - i{H}^{\prime }_6 } \right) \overline{{A}}_6, \end{aligned}$$
(81f)
in which
$$\begin{aligned} H_1&= -\frac{\left\{ {\left( {a_1 \!+\!{a}^{\prime }_1 } \right) \left( {c_1 \!+\!{c}^{\prime }_1 } \right) +\left( {b_1 \!+\!{b}^{\prime }_1 } \right) \left( {d_1 \!+\!{d}^{\prime }_1 } \right) } \right\} }{\left\{ {\left( {c_1 \!+\!{c}^{\prime }_1 } \right) ^{2}\!+\!\left( {d_1 \!+\!{d}^{\prime }_1 } \right) ^{2}} \right\} },\end{aligned}$$
(82a)
$$\begin{aligned} H_2&= -\frac{\left\{ {\left( {b_1 \!+\!{b}^{\prime }_1 } \right) \left( {c_1 \!+\!{c}^{\prime }_1 } \right) \!-\!\left( {a_1 \!+\!{a}^{\prime }_1 } \right) \left( {d_1 \!+\!{d}^{\prime }_1 } \right) } \right\} }{\left\{ {\left( {c_1 \!+\!{c}^{\prime }_1 } \right) ^{2} \!+\!\left( {d_1 \!+\!{d}^{\prime }_1 } \right) ^{2}} \right\} },\end{aligned}$$
(82b)
$$\begin{aligned} H_3&= -\frac{\left\{ {\left( {a_1 \!-\!{a}^{\prime }_1 } \right) \left( {c_1 \!-\!{c}^{\prime }_1 } \right) \!+\!\left( {b_1 \!-\!{b}^{\prime }_1 } \right) \left( {d_1 \!-\!{d}^{\prime }_1 } \right) } \right\} }{\left\{ {\left( {c_1 \!-\!{c}^{\prime }_1 } \right) ^{2} \!+\!\left( {d_1 \!-\!{d}^{\prime }_1 } \right) ^{2}} \right\} },\end{aligned}$$
(82c)
$$\begin{aligned} H_4&= \frac{\left\{ {\left( {b_1 \!-\!{b}^{\prime }_1 } \right) \left( {c_1 \!-\!{c}^{\prime }_1 } \right) \!-\!\left( {a_1 -{a}^{\prime }_1 } \right) \left( {d_1 \!-\!{d}^{\prime }_1 } \right) } \right\} }{\left\{ {\left( {c_1 \!-\!{c}^{\prime }_1 } \right) ^{2} \!+\!\left( {d_1 \!-\!{d}^{\prime }_1 } \right) ^{2}} \right\} },\end{aligned}$$
(82d)
$$\begin{aligned} H_5&= \frac{\left\{ {e_1 g_1 +f_1 h_1 } \right\} }{\left( {g_1 ^{2}+h_1 ^{2}} \right) },\end{aligned}$$
(82e)
$$\begin{aligned} H_6&= \frac{\left\{ {f_1 g_1 -e_1 h_1 } \right\} }{\left( {g_1 ^{2}+h_1 ^{2}} \right) }, \end{aligned}$$
(82f)
$$\begin{aligned} {H}^{\prime }_1&= -\frac{\left\{ {a_2 c_2 +b_2 d_2 } \right\} }{\left\{ {c_2 ^{2}+d_2 ^{2}} \right\} },\end{aligned}$$
(83a)
$$\begin{aligned} {H}^{\prime }_2&= \frac{\left\{ {a_2 d_2 -b_2 c_2 } \right\} }{\left\{ {c_2 ^{2}+d_2 ^{2}} \right\} },\end{aligned}$$
(83b)
$$\begin{aligned} {H}^{\prime }_3&= -\frac{\left\{ {e_2 g_2 +f_2 h_2 } \right\} }{\left\{ {g_2 ^{2}+h_2 ^{2}} \right\} },\end{aligned}$$
(83c)
$$\begin{aligned} {H}^{\prime }_4&= \frac{\left\{ {e_2 h_2 -f_2 g_2 } \right\} }{\left\{ {g_2 ^{2}+h_2 ^{2}} \right\} },\end{aligned}$$
(83d)
$$\begin{aligned} {H}^{\prime }_5&= -\frac{\left\{ {{c}^{\prime }_{14} +{c}^{\prime }_{56} H_5 } \right\} }{\left\{ {{c}^{\prime }_{55} -{c}^{\prime }_{44} \zeta ^{2}} \right\} },\end{aligned}$$
(83e)
$$\begin{aligned} {H}^{\prime }_6&= -\frac{{c}^{\prime }_{56} \left\{ {\zeta +H_6 } \right\} }{\left\{ {{c}^{\prime }_{55} -{c}^{\prime }_{44} \zeta ^{2}} \right\} }, \end{aligned}$$
(83f)
where
$$\begin{aligned} a_1&= {c}^{\prime }_{11} {c}^{\prime }_{44} +{c}^{\prime }_{55} {c}^{\prime }_{66} +{c}^{\prime }_{44} {c}^{\prime }_{66} \left( {\xi ^{2}-\eta ^{2}} \right) \nonumber \\&\quad +{c}^{\prime }_{11} {c}^{\prime }_{55} \frac{\left( {\xi ^{2}-\eta ^{2}} \right) }{\left( {\xi ^{2}+\eta ^{2}} \right) ^{2}}, \end{aligned}$$
(84a)
$$\begin{aligned} {a}^{\prime }_1 =-\left( {{c}^{\prime }_{14} +{c}^{\prime }_{56} } \right) ^{2}\xi , \end{aligned}$$
(84a')
$$\begin{aligned} b_1 =-\frac{2{c}^{\prime }_{11} {c}^{\prime }_{55} \xi \eta }{\left( {\xi ^{2}+\eta ^{2}} \right) ^{2}}+2{c}^{\prime }_{44} {c}^{\prime }_{66} \xi \eta , \end{aligned}$$
(84b)
$$\begin{aligned} {b}^{\prime }_1 =-\left( {{c}^{\prime }_{14} +{c}^{\prime }_{56} } \right) ^{2}\eta , \end{aligned}$$
(84b')
$$\begin{aligned} c_1 =\left( {{c}^{\prime }_{12} +{c}^{\prime }_{66} } \right) \left\{ {{c}^{\prime }_{55} +{c}^{\prime }_{44} \left( {\xi ^{2}-\eta ^{2}} \right) } \right\} -{c}^{\prime }_{14} {c}^{\prime }_{56},\nonumber \\ \end{aligned}$$
(84c)
$$\begin{aligned} {c}^{\prime }_1 =-{{{c}^{\prime }_{56}}^{2}}\xi , \end{aligned}$$
(84c')
$$\begin{aligned} d_1 =2{c}^{\prime }_{44} \left( {{c}^{\prime }_{12} +{c}^{\prime }_{66} } \right) \xi \eta , \end{aligned}$$
(84d)
$$\begin{aligned} {d}^{\prime }_1 =-{{{c}^{\prime }_{56}}^{2}}\eta , \end{aligned}$$
(84d')
$$\begin{aligned} e_1&= \left( {{c}^{\prime }_{11} -{c}^{\prime }_{66} \zeta ^{2}} \right) \left( {{c}^{\prime }_{55} -{c}^{\prime }_{44} \zeta ^{2}} \right) /\zeta ^{2},\end{aligned}$$
(84e)
$$\begin{aligned} f_1&= \left( {{c}^{\prime }_{14} +{c}^{\prime }_{56} } \right) ^{2}\zeta ,\end{aligned}$$
(84f)
$$\begin{aligned} g_1&= \left( {{c}^{\prime }_{12} +{c}^{\prime }_{66} } \right) \left( {{c}^{\prime }_{55} -{c}^{\prime }_{44} \zeta ^{2}} \right) -{c}^{\prime }_{14} {c}^{\prime }_{56} ,\end{aligned}$$
(84g)
$$\begin{aligned} h_1&= -{{{c}^{\prime }_{56}}^{2}}\zeta , \end{aligned}$$
(84h)
$$\begin{aligned} a_2&= {c}^{\prime }_{14} +{c}^{\prime }_{56} \left( {\xi +H_1 } \right) ,\end{aligned}$$
(85a)
$$\begin{aligned} b_2&= {c}^{\prime }_{56} \left( {H_2 +\eta } \right) ,\end{aligned}$$
(85b)
$$\begin{aligned} c_2&= {c}^{\prime }_{55} +{c}^{\prime }_{44} \left( {\xi ^{2}-\eta ^{2}} \right) ,\end{aligned}$$
(85c)
$$\begin{aligned} d_2&= 2{c}^{\prime }_{44} \xi \eta ,\end{aligned}$$
(85d)
$$\begin{aligned} e_2&= {c}^{\prime }_{14} -{c}^{\prime }_{56} \left( {\xi -H_3 } \right) ,\end{aligned}$$
(85e)
$$\begin{aligned} f_2&= {c}^{\prime }_{56} \left( {H_4 +\eta } \right) ,\end{aligned}$$
(85f)
$$\begin{aligned} g_2&= c_2 ,\end{aligned}$$
(85g)
$$\begin{aligned} h_2&= -d_2. \end{aligned}$$
(85h)
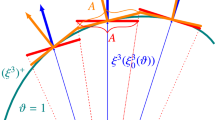
The corresponding stress field can easily be obtained from Eq. (79). It is convenient to express the components of the displacement vector and stress tensor, in terms of the cylindrical polar coordinate system \((\hbox {r}, \uptheta , \hbox {z})\); see Fig. 2. Expressing
$$\begin{aligned}&\rho \cos (\psi ) = r \left( {\cos (\theta )+\xi \sin (\theta )} \right) , \nonumber \\&{\rho \sin (\psi ) = r \left( {\eta \sin (\theta )} \right) }, \end{aligned}$$
(86a)
$$\begin{aligned}&{\rho }^{\prime } \cos ({\psi }^{\prime }) = r \left( {\cos (\theta )-\xi \sin (\theta )} \right) ,\nonumber \\&{{\rho }^{\prime } \sin ({\psi }^{\prime }) = r \left( {\eta \sin (\theta )} \right) ,} \end{aligned}$$
(86b)
$$\begin{aligned}&{\rho }^{\prime \prime } \cos ({\psi }^{\prime \prime }) = r \cos (\theta ),\nonumber \\&{{\rho }^{\prime \prime } \sin ({\psi }^{\prime \prime }) = r \left( {\zeta \sin (\theta )} \right) }, \end{aligned}$$
(86c)
in which
$$\begin{aligned}&\rho = r\{ {( {\cos (\theta)+\xi \sin (\theta )} )^{2} + \eta ^{2}\sin ^{2}(\theta )} \}^{1/2},\end{aligned}$$
(87a)
$$\begin{aligned}&{\rho }^{\prime } =r\{ {( {\cos (\theta )-\xi \sin (\theta )} )^{2}+\eta ^{2}\sin ^{2}(\theta )} \}^{1/2},\end{aligned}$$
(87b)
$$\begin{aligned}&{\rho }^{\prime \prime } =r\{ {\cos ^{2}(\theta )+\zeta ^{2}\sin ^{2}(\theta )} \}^{1/2}, \end{aligned}$$
(87c)
and
$$\begin{aligned}&\cos ( {\psi (\theta )} )\!=\!\frac{\cos (\theta ) \!+\!\xi \sin (\theta )}{\{ {( {\cos (\theta )\!+\!\xi \sin (\theta )} )^{2}\!+\!\eta ^{2}\sin ^{2}(\theta )} \}^{1/2}},\end{aligned}$$
(88a)
$$\begin{aligned}&\sin ( {\psi (\theta )} )\!=\!\frac{\eta \sin (\theta )}{\{ {( {\cos (\theta )\!+\!\xi \sin (\theta )} )^{2}\!+\!\eta ^{2}\sin ^{2}(\theta )} \}^{1/2}},\end{aligned}$$
(88b)
$$\begin{aligned}&\cos ( {{\psi }^{\prime }(\theta )} ) \!=\!\frac{\cos (\theta )\!-\!\xi \sin (\theta )}{\{ {( {\cos (\theta )\!-\!\xi \sin (\theta )} )^{2}\!+\!\eta ^{2}\sin ^{2}(\theta )} \}^{1/2}},\end{aligned}$$
(88c)
$$\begin{aligned}&\sin ( {{\psi }^{\prime }(\theta )} ) \!=\!\frac{\eta \sin (\theta )}{\{ {( {\cos (\theta )\!-\!\xi \sin (\theta )} )^{2}\!+\!\eta ^{2}\sin ^{2}(\theta )} \}^{1/2}},\end{aligned}$$
(88d)
$$\begin{aligned}&\cos ( {{\psi }^{\prime \prime }(\theta )} )=\frac{\cos (\theta )}{\{ {\cos ^{2}(\theta )+\zeta ^{2}\sin ^{2}(\theta )} \}^{1/2}},\end{aligned}$$
(88e)
$$\begin{aligned}&\sin ( {{\psi }^{\prime \prime }(\theta )} )=\frac{\zeta \sin (\theta )}{\{ {\cos ^{2}(\theta )+\zeta ^{2}\sin ^{2}(\theta )} \}^{1/2}}, \end{aligned}$$
(88f)
the general asymptotic form for the displacement and stress fields can be written as follows:
$$\begin{aligned}&u(r,\theta ,z)=r^{s}D_b (z)(ik)^{s}[ \{ (\cos (\theta )+\xi \sin (\theta ))^{2}\nonumber \\&\quad +\eta ^{2}\sin ^{2}(\theta ) \}^{s/2}\{ A_1 \cos (s\psi )+A_2\sin (s\psi ) \}\nonumber \\&\quad + \{ ( {\cos (\theta )-\xi \sin (\theta )} )^{2}+ \eta ^{2}\sin ^{2}(\theta ) \}^{s/2}\nonumber \\&\quad \times \{ A_3 \cos ( {s{\psi }^{\prime }} ) + A_4 \sin ( {s{\psi }^{\prime }} ) \}\nonumber \\&\quad + \{ {\cos ^{2}(\theta ) + \zeta ^{2}\sin ^{2}(\theta )} \}^{s/2} \{ A_5 \cos ( {s{\psi }^{\prime \prime }} ) \nonumber \\&\quad + A_6 \sin ( {s{\psi }^{\prime \prime }} ) \} ] +O( {r^{s+2}}),\end{aligned}$$
(89a)
$$\begin{aligned}&v(r,\theta ,z)=r^{s}D_b ( z ) ( {ik} )^{s}[ \{ ( \cos (\theta )+\xi \sin (\theta ) )^{2}\nonumber \\&\quad +\eta ^{2}\sin ^{2}(\theta ) \}^{s/2}\{{( {H_1 A_1 } }+H_2 A_2 )\cos ( {s\psi } ) \nonumber \\&\quad +( {H_1 A_2 \!-\! H_2 A_1 } ) \sin ( {s\psi } ) \} \!+\! \{ {( {\cos (\theta )\!-\!\xi \sin (\theta )} )^{2}} \nonumber \\&\quad {+\eta ^{2}\sin ^{2}(\theta )} \} ^{s/2}\{ ( {H_3 A_3 + H_4 A_4 } ) \cos ( {s{\psi }^{\prime }} ) \nonumber \\&\quad +( {H_3 A_4 - H_4 A_3 } )\sin ( {s{\psi }^{\prime }} ) \}\nonumber \\&\quad +\{ \cos ^{2}(\theta ) {+\zeta ^{2}\sin ^{2}(\theta )} \} ^{s/2}\{ ( {H_5 A_5 + H_6 A_6 } ) \nonumber \\&\quad \times \cos ( {s{\psi }^{\prime \prime }} )+( {H_5 A_6 - H_6 A_5 } )\sin ( {s{\psi }^{\prime \prime }} )\} ]\nonumber \\&\quad +O( {r^{s+2}} ),\end{aligned}$$
(89b)
$$\begin{aligned}&w(r,\theta ,z)=r^{s}D_b ( z ) ( {ik} )^{s}[ \{ ( \cos (\theta )+\xi \sin (\theta ) )^{2}\nonumber \\&\quad +\eta ^{2}\sin ^{2}(\theta ) \}^{s/2}\{ {( {{H}^{\prime }_1 A_1 } } {+{H}^{\prime }_2 A_2 } )\cos ( {s\psi } )\nonumber \\&\quad + {( {{H}^{\prime }_1 A_2 \!-\! {H}^{\prime }_2 A_1 } ) \sin ( {s\psi } )} \} \!+\! \{ {( {\cos (\theta )\!-\!\xi \sin (\theta )} )^{2}} \nonumber \\&\quad {+\eta ^{2}\sin ^{2}(\theta )} \} ^{s/2}\{ ( {{H}^{\prime }_3 A_3 + {H}^{\prime }_4 A_4 } ) \cos ( {s{\psi }^{\prime }} ) \nonumber \\&\quad +( {{H}^{\prime }_3 A_4 - {H}^{\prime }_4 A_3 } )\sin ( {s{\psi }^{\prime }} ) \}\nonumber \\&\quad +\{ \cos ^{2}(\theta ) {+\zeta ^{2}\sin ^{2}(\theta )} \} ^{s/2}\{ ( {{H}^{\prime }_5 A_5 + {H}^{\prime }_6 A_6 } )\nonumber \\&\quad \times \cos ( {s{\psi }^{\prime \prime }} ) +( {{H}^{\prime }_5 A_6 - {H}^{\prime }_6 A_5 } )\sin ( {s{\psi }^{\prime \prime }} ) \} ]\nonumber \\&\quad +O( {r^{s+2}} ), \end{aligned}$$
(89c)
and
$$\begin{aligned}&\sigma _x ( {r,\theta ,z} )=r^{s-1}D_b ( z )_ ({ik})^{s}s \langle \{ ( {\cos (\theta )\!+\!\xi \sin (\theta )} )^{2} \nonumber \\&\quad + \eta ^{2}\sin ^{2}(\theta ) \}^{(s-1)/2}[ {( {A_1 } } \{ {{c}^{\prime }_{11} } +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{12}\nonumber \\&\quad +( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } ){c}^{\prime }_{14} \} +A_2 \{ ( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{12}\nonumber \\&\quad +( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } ){c}^{\prime }_{14} \} )\cos ( {( {s-1} )\psi } )\nonumber \\&\quad +( - A_1 \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{12} +( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } ){c}^{\prime }_{14} } \}\nonumber \\&\quad \!+\!A_2 \{ {{c}^{\prime }_{11} } \!+\!( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{12}+( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } ) { {{c}^{\prime }_{14} } \} } )\nonumber \\&\quad \times {\sin ( {( {s-1} )\psi } )} ]+ \{ {( {\cos (\theta )-\xi \sin (\theta )} )^{2} } \nonumber \\&\quad +\eta ^{2}\sin ^{2}(\theta ) \} ^{(s-1)/2}[ {( {A_3 } } \{ {{c}^{\prime }_{11} } -( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{12}\nonumber \\&\quad -( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ){c}^{\prime }_{14} \} +A_4 \{ ( {\eta H_3 -\xi H_4 } ){c}^{\prime }_{12} \nonumber \\&\quad +( \eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 ){c}^{\prime }_{14} \} )\cos ( {( {s-1} ){\psi }^{\prime }} )\nonumber \\&\quad +( - A_3 \{ ( {\eta H_3 -\xi H_4 } ){c}^{\prime }_{12} +( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } ){c}^{\prime }_{14} \}\nonumber \\&\quad +A_4 \{ {{c}^{\prime }_{11} } -( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{12}\nonumber \\&\quad { {-( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ) {{c}^{\prime }_{14} } \} } )\sin ( {( {s-1} ){\psi }^{\prime }} )} ]\nonumber \\&\quad +\{{\cos ^{2}(\theta )} {+\zeta ^{2}\sin ^{2}(\theta )}\} ^{(s-1)/2}[ {( {A_5 } } \{ {c}^{\prime }_{11}- \zeta H_6 {c}^{\prime }_{12}\nonumber \\&\quad {-\zeta {H}^{\prime }_6 {c}^{\prime }_{14} } \} +A_6 \{ \zeta H_5 {c}^{\prime }_{12} +\zeta {H}^{\prime }_5{c}^{\prime }_{14} \} )\nonumber \\&\quad \times \cos ( {( {s-1}){\psi }^{\prime \prime }} )+( - A_5 \{ {\zeta H_5 {c}^{\prime }_{12} +\zeta {H}^{\prime }_5 {c}^{\prime }_{14} } \}\nonumber \\&\quad +A_6 \{ {{c}^{\prime }_{11} } { { {-\zeta H_6 {c}^{\prime }_{12} -\zeta {H}^{\prime }_6 {{c}^{\prime }_{14} } \} } )\sin ( {( {s-1} ){\psi }^{\prime \prime }} )} ]} \rangle \nonumber \\&\quad + O( {r^{s+1}} ),\end{aligned}$$
(90a)
$$\begin{aligned}&\sigma _y ( {r,\theta ,z} )=r^{s-1}D_b ( z )({ik})^{s}s \langle \{ ( {\cos (\theta )+\xi \sin (\theta )} )^{2}\nonumber \\&\quad + \eta ^{2}\sin ^{2}(\theta ) \}^{(s-1)/2} [{({A_1 } } \{ {{c}^{\prime }_{12} } {+( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{22} } \} \nonumber \\&\quad +A_2 \{ ( \eta H_1+\xi H_2 ){c}^{\prime }_{22} \} )\cos ({( {s-1} )\psi } )\nonumber \\&\quad +( - A_1 \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22} } \}\nonumber \\&\quad +A_2 \{ {{c}^{\prime }_{12} } +( {\xi H_1 -\eta H_2 } ) { { {{c}^{\prime }_{22} } \} } )\sin ( {( {s-1} )\psi } )} ]\nonumber \\&\quad + \{ {( {\cos (\theta )-\xi \sin (\theta )} )^{2} } {+\eta ^{2}\sin ^{2}(\theta )} \} ^{(s-1)/2}\nonumber \\&\quad \times [ {( {A_3 } } \{ {{c}^{\prime }_{12} } {-( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{22} } \} \nonumber \\&\quad +A_4 ( {\eta H_3 -\xi H_4 } ){c}^{\prime }_{22} )\cos ( {( {s-1} ){\psi }^{\prime }} )\nonumber \\&\quad +( - A_3 \{ {( {\eta H_3 -\xi H_4 } ){c}^{\prime }_{22} } \}\nonumber \\&\quad +A_4 \{ {{c}^{\prime }_{12} -( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{22} \} )\sin ( {( {s-1} ){\psi }^{\prime }} ) ]} \nonumber \\&\quad +\{ {\cos ^{2}(\theta ) } {+\zeta ^{2}\sin ^{2}(\theta )} \} ^{(s-1)/2}\nonumber \\&\quad \!\times [ {( {A_5 } } \{ {c}^{\prime }_{12} \!-\!\zeta H_6 {c}^{\prime }_{22} \} \!+\!A_6 \zeta H_5 {c}^{\prime }_{22} ) \cos ( {( {s-1} ){\psi }^{\prime \prime }} )\nonumber \\&\quad +\{ -A_5 \zeta H_5 {c}^{\prime }_{22} + A_6 ( {c}^{\prime }_{12} -\zeta H_6 {c}^{\prime }_{22} ) \}\nonumber \\&\quad \times { {\sin ( {( {s-1} ){\psi }^{\prime \prime }} )} ]} \rangle + O( {r^{s+1}} ),\end{aligned}$$
(90b)
$$\begin{aligned}&\tau _{xy} ( {r,\theta ,z} )=r^{s-1}D_b ( z )( {ik} )^{s}s \langle \{ ( {\cos (\theta )+\xi \sin (\theta )} )^{2}\nonumber \\&\quad +\eta ^{2}\sin ^{2}(\theta ) \}^{(s-1)/2}[ {( {A_1 \{ {{c}^{\prime }_{56} } } } {H}^{\prime }_1+ {{c}^{\prime }_{66} ( {\xi +H_1 } )} \}\nonumber \\&\quad +A_2 \{ {c}^{\prime }_{56} {H}^{\prime }_2+{c}^{\prime }_{66} ( {\eta +H_2 } ) \} )\cos ( {( {s-1} )\psi } )\nonumber \\&\quad +( {-A_1 \{ {{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} } ( {\eta +H_2 } ) \} } \nonumber \\&\quad {+A_2 \{ {{c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} ( {\xi +H_1 } )} \}} ) {\sin ( {( {s-1} )\psi } )} ]\nonumber \\&\quad +\{ ( {\cos (\theta )-\xi \sin (\theta )} )^{2}+\eta ^{2}\sin ^{2}(\theta ) \}^{(s-1)/2}\nonumber \\&\quad \times [ {( {A_3 \{ {{c}^{\prime }_{56} } } } {H}^{\prime }_3+ {{c}^{\prime }_{66} ( {-\xi +H_3 } )} \}\nonumber \\&\quad +A_4 \{ {c}^{\prime }_{56} {H}^{\prime }_4 +{c}^{\prime }_{66} ( {\eta +H_4 } ) \} )\cos ( {( {s-1} ){\psi }^{\prime }} )\nonumber \\&\quad +( {-A_3 \{ {{c}^{\prime }_{56} {H}^{\prime }_4 +{c}^{\prime }_{66} } ( {\eta +H_4 } ) \} } \nonumber \\&+A_{4}\{c_{56}^{\prime } H_{3}^{\prime }+c_{66}^{\prime }(-\xi +H_{3})\})\nonumber \\&\times \sin ((s-1)\psi ^{\prime })]+\{\cos ^{2}(\theta )+\zeta ^{2}\sin ^{2}(\theta )\}^{(s-1)/2}\nonumber \\&\quad \times [(A_{5}\{c_{56}^{\prime }H_{5}^{\prime }+ {{c}^{\prime }_{66} H_5 } \} + A_6 \{ {c}^{\prime }_{56} {H}^{\prime }_6 +{c}^{\prime }_{66} ( {\zeta +H_6 } ) \} )\nonumber \\&\quad \times \cos ( {( {s-1} ){\psi }^{\prime \prime }} )+( -A_5 \{ {c}^{\prime }_{56} {H}^{\prime }_6 \nonumber \\&\quad +{c}^{\prime }_{66} ( {\zeta +H_6 } )\} {+A_6 \{ {{c}^{\prime }_{56} {H}^{\prime }_5 +{c}^{\prime }_{66} H_5 } \}} )\nonumber \\&\quad \times {\sin ( {( {s-1} ){\psi }^{\prime \prime }} )} ] \rangle + O( {r^{s+1}} ),\end{aligned}$$
(90c)
$$\begin{aligned}&\sigma _z ( {r,\theta ,z} )=r^{s-1}D_b ( z ) ( {ik} )^{s}s \langle \{ ( {\cos (\theta )+\xi \sin (\theta )} )^{2} \nonumber \\&\quad + \eta ^{2}\sin ^{2}(\theta ) \}^{(s-1)/2}[ {( {A_1 } } \{ {{c}^{\prime }_{13} } + ( \xi H_1 -\eta H_2 ){c}^{\prime }_{23} \nonumber \\&\quad +( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } ){c}^{\prime }_{34} \}+A_2 \{ ( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{23}\nonumber \\&\quad +( \eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 ){c}^{\prime }_{34} \} )\cos ( {({s-1} )\psi } )\nonumber \\&\quad +( - A_1 \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{23} +( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } ){c}^{\prime }_{34} } \}\nonumber \\&\quad +A_2 \{{{c}^{\prime }_{13} } +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{23}\nonumber \\&\quad +( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } ) { { {{c}^{\prime }_{34} } \} } )\sin ( {( {s-1} )\psi } )} ]\nonumber \\&\quad + \{ ( \cos (\theta )-\xi \sin (\theta ) )^{2} {+\eta ^{2}\sin ^{2}(\theta )} \} ^{(s-1)/2} \nonumber \\&\quad \times [ {( {A_3 } } \{ {{c}^{\prime }_{13} } {-( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{23} -( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ){c}^{\prime }_{34} } \} \nonumber \\&\quad +A_4 \{ {( {\eta H_3 -\xi H_4 } ){c}^{\prime }_{23} +( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } ){c}^{\prime }_{34} } \} )\nonumber \\&\quad \times \cos ( {( {s-1} ){\psi }^{\prime }} )+( - A_3 \{ ( {\eta H_3 -\xi H_4 } ){c}^{\prime }_{23} \nonumber \\&\quad +( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } ){c}^{\prime }_{34} \}_ +A_4 \{ {{c}^{\prime }_{13} } -( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{23}\nonumber \\&\quad { {-( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ) {{c}^{\prime }_{34} } \} } )\sin ( {( {s-1} ){\psi }^{\prime }} )} ]\nonumber \\&\quad +\{ {\cos ^{2}(\theta )} {+\zeta ^{2}\sin ^{2}(\theta )} \} ^{(s-1)/2}[ {( {A_5 } } \{ {{c}^{\prime }_{13} } -\zeta H_6 {c}^{\prime }_{23}\nonumber \\&\quad { {-\zeta {H}^{\prime }_6 {c}^{\prime }_{34} } \} +A_6 \zeta \{ {H_5 {c}^{\prime }_{23} +{H}^{\prime }_5 {c}^{\prime }_{34} } \}} )\nonumber \\&\quad \times \cos ( {( {s-1} ){\psi }^{\prime \prime }} )+( - A_5 \zeta \{ {H_5 {c}^{\prime }_{23} +{H}^{\prime }_5 {c}^{\prime }_{34} } \}\nonumber \\&\quad { { {+A_6 \{ {{c}^{\prime }_{13} } -\zeta H_6 {c}^{\prime }_{23} -\zeta {H}^{\prime }_6 {{c}^{\prime }_{34} } \} } )\sin ( {( {s-1} ){\psi }^{\prime \prime }} )} ]} \rangle \nonumber \\&\quad + O( {r^{s+1}} ),\end{aligned}$$
(90d)
$$\begin{aligned}&\tau _{xz} ( {r,\theta ,z} )=r^{s-1}D_b ( z )( {ik} )^{s}s \langle \{ ( {\cos (\theta )+\xi \sin (\theta )} )^{2}\nonumber \\&\quad +\eta ^{2}\sin ^{2}(\theta ) \}^{(s-1)/2}[ {( {A_1 \{ {{c}^{\prime }_{55} {H}^{\prime }_1 } } } + {{c}^{\prime }_{56} ( {\xi +H_1 } )} \}\nonumber \\&\quad +A_2 \{ {c}^{\prime }_{55} {H}^{\prime }_2+{c}^{\prime }_{56} ( {\eta +H_2 } ) \})\cos ( {( {s-1} )\psi } )\nonumber \\&\quad +( {-A_1\{ {{c}^{\prime }_{55} {H}^{\prime }_2 +{c}^{\prime }_{56} } ( {\eta +H_2 } ) \} } \nonumber \\&\quad {+A_2 \{ {{c}^{\prime }_{55} {H}^{\prime }_1 +{c}^{\prime }_{56} ( {\xi +H_1 } )} \}} ) {\sin ( {( {s-1} )\psi } )} ]\nonumber \\&\quad +\{ ( {\cos (\theta )-\xi \sin (\theta )} )^{2}+\eta ^{2}\sin ^{2}(\theta ) \}^{(s-1)/2}\nonumber \\&\quad \times [ {( {A_3 \{ {{c}^{\prime }_{55} } } } {H}^{\prime }_3+ {{c}^{\prime }_{56} ( {-\xi +H_3 } )} \} +A_4 \{ {c}^{\prime }_{55} {H}^{\prime }_4\nonumber \\&\quad +{c}^{\prime }_{56} ( {\eta +H_4 } ) \} )\cos ( {( {s-1} ){\psi }^{\prime }} )\nonumber \\&\quad +( {-A_3 \{ {{c}^{\prime }_{55} {H}^{\prime }_4 +{c}^{\prime }_{56} ( {\eta +H_4 } )} \}} \nonumber \\&\quad {+A_4 \{ {{c}^{\prime }_{55} {H}^{\prime }_3 +{c}^{\prime }_{56} ( {-\xi +H_3 } )} \}} ) {\sin ( {( {s-1} ){\psi }^{\prime }} )} ]\nonumber \\&\quad +\{ {\cos ^{2}(\theta )} {+\zeta ^{2}\sin ^{2}(\theta )} \} ^{(s-1)/2}[ {( {A_5 \{ {{c}^{\prime }_{55} } } } {H}^{\prime }_5\nonumber \\&\quad + {{c}^{\prime }_{56} H_5 } \} + {A_6 \{ {{c}^{\prime }_{55} {H}^{\prime }_6 +{c}^{\prime }_{56} ( {\zeta +H_6 } )} \}} )\nonumber \\&\quad \times \cos ( {( {s-1} ){\psi }^{\prime \prime }} )+( {-A_5 \{{{c}^{\prime }_{55} {H}^{\prime }_6 +{c}^{\prime }_{56} ( {\zeta +H_6 } )} \}} \nonumber \\&\quad {+A_6 \{ {{c}^{\prime }_{55} {H}^{\prime }_5 +{c}^{\prime }_{56} H_5 } \}} ) {\sin ( {( {s-1} ){\psi }^{\prime \prime }} )} ] \rangle \nonumber \\&\quad + O( {r^{s+1}} ),\end{aligned}$$
(90e)
$$\begin{aligned}&\tau _{yz} ( {r,\theta ,z} )=r^{s-1}D_b ( z ) ( {ik} )^{s}s \nonumber \\&\quad \times \langle \{ ( {\cos (\theta )+\xi \sin (\theta )} )^{2}+ \eta ^{2}\sin ^{2}(\theta ) \}^{(s-1)/2}\nonumber \\&\quad \times [ {( {A_1 } } \{ {{c}^{\prime }_{14} } {+( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } ){c}^{\prime }_{44} } \}\nonumber \\&\quad +A_2 \{ ( \eta {H}^{\prime }_1+\xi {H}^{\prime }_2 ){c}^{\prime }_{44} \} ) \cos ( {( {s-1} )\psi } )\nonumber \\&\quad +(- A_1 \{ {( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } ){c}^{\prime }_{44} } \}\nonumber \\&\quad +A_2 \{ {{c}^{\prime }_{14} } +( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } ) { { {{c}^{\prime }_{44} } \} } )\sin ( {( {s-1} )\psi } )} ]\nonumber \\&\quad + \{ {( {\cos (\theta )-\xi \sin (\theta )} )^{2}} {+\eta ^{2}\sin ^{2}(\theta )} \} ^{(s-1)/2}\nonumber \\&\quad \times {[ {( {A_3 } } \{ {{c}^{\prime }_{14} } -( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ){c}^{\prime }_{44} } \} \nonumber \\&\quad +A_4 \{ {( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } ){c}^{\prime }_{44} } \} )\cos ( {( {s-1} ){\psi }^{\prime }} )\nonumber \\&\quad +( - A_3 \{ {( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } ){c}^{\prime }_{44} } \}_ +A_4 \{ {{c}^{\prime }_{14} } \nonumber \\&\quad -(\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 ) {{c}^{\prime }_{44} } \} )\sin ( {( {s-1} ){\psi }^{\prime }} ) ]\nonumber \\&\quad +\{ {\cos ^{2}(\theta ) } {+\zeta ^{2}\sin ^{2}(\theta )} \} ^{(s-1)/2}[ ( {A_5 } \{ {c}^{\prime }_{14} \nonumber \\&\quad -\zeta {H}^{\prime }_6 {c}^{\prime }_{44} \} +A_6 \zeta {H}^{\prime }_5 {c}^{\prime }_{44} ) \cos ( {( {s-1} ){\psi }^{\prime \prime }} )\nonumber \\&\quad +( - A_5 \zeta {H}^{\prime }_5 {c}^{\prime }_{44} +A_6 \{ {{c}^{\prime }_{14} } {-\zeta {H}^{\prime }_6 {{c}^{\prime }_{44} } \} })\nonumber \\&\quad \times \sin ( {( {s-1} ){\psi }^{\prime \prime }} )]\rangle + O( {r^{s+1}} ), \end{aligned}$$
(90f)
in which
$$\begin{aligned}&A_1 = \overline{{A}}_1 + \overline{{A}}_2 , \quad A_2 = i \left( {\overline{{A}}_1- \overline{{A}}_2 } \right) ,\end{aligned}$$
(91a)
$$\begin{aligned}&A_3 = \overline{{A}}_3 + \overline{{A}}_4 , \quad A_4 = i \left( {\overline{{A}}_3 - \overline{{A}}_4 } \right) ,\end{aligned}$$
(91b)
$$\begin{aligned}&A_5 = \overline{{A}}_5 + \overline{{A}}_6 , \quad A_6 = i \left( {\overline{{A}}_5 - \overline{{A}}_6 } \right) , \end{aligned}$$
(91c)
and
$$\begin{aligned} D_b (z) = D_1 \sin \left( {kz} \right) +D_2 \cos \left( {kz} \right) , \end{aligned}$$
(92)
with
$$\begin{aligned} D_1&= i{\overline{\overline{{D}}}}_1,\end{aligned}$$
(93a)
$$\begin{aligned} D_2&= {\overline{\overline{D}}}_2 . \end{aligned}$$
(93b)
It may be noted that since s or Re s (when s is complex) is positive, all the higher order terms in Eqs. (89) and (90) vanish as r \(\rightarrow 0\). The components of displacement can now be expressed in the cylindrical polar coordinate system as follows:
$$\begin{aligned}&u_r (r,\theta ,z) = r^{s}D_b ( z ) ( {ik} )^{s} \langle \{ ( \cos (\theta ) \nonumber \\&\quad +\xi \sin (\theta ) )^{2} + \eta ^{2}\sin ^{2}(\theta ) \}^{^{s/2}} [ { \{ {A_1 \cos ( \theta ) } } \nonumber \\&\quad {+ ( {H_1 A_1 +H_2 A_2 } )\sin (\theta )} \} \cos ( {s\psi } ) \nonumber \\&\quad + { \{ {A_2 \cos ( \theta ) + ( {H_1 A_2 -H_2 A_1 } )\sin (\theta )} \} \sin ( {s\psi } )} ]\nonumber \\&\quad + \{ { ( {\cos (\theta )-\xi \sin (\theta )} )^{2}+\eta ^{2}\sin ^{2}(\theta )} \}^{s/2} [ \{ A_3 \cos ( \theta ) \nonumber \\&\quad + ( {H_3 A_3 -H_4 A_4 } )\sin (\theta ) \}\cos ( {s{\psi }^{\prime }} ) \nonumber \\&\quad + { \{ {A_4 \cos ( \theta ) + ( {H_3 A_4 -H_4 A_3 } )\sin (\theta )} \} \sin ( {s{\psi }^{\prime }} )} ]\nonumber \\&\quad + \{ {\cos ^{2}(\theta ) + \zeta ^{2}\sin ^{2}(\theta )} \}^{s/2} [ { \{ {A_5 \cos ( \theta ) } } \nonumber \\&\quad {+ ( {H_5 A_5 +H_6 A_6 } )\sin (\theta )} \} \cos ( {s{\psi }^{\prime \prime }} ) \nonumber \\&\quad + { \{ {A_6 \cos ( \theta ) + ( {H_5 A_6 -H_6 A_5 } )\sin (\theta )} \} \sin ( {s{\psi }^{\prime \prime }} )} ] \rangle \nonumber \\&\quad + O ( {r^{s+2}} ),\end{aligned}$$
(94a)
$$\begin{aligned}&u_\theta (r,\theta ,z) = r^{s}D_b ( z ) ( {ik} )^{s} \langle \{ ( {\cos (\theta )+\xi \sin (\theta )} )^{2} \nonumber \\&\quad + \eta ^{2}\sin ^{2}(\theta ) \}^{^{s/2}} [ { \{ {-A_1 \sin ( \theta ) } } \nonumber \\&\quad {+ ( {H_1 A_1 +H_2 A_2 } )\cos (\theta )} \} \cos ( {s\psi } ) \nonumber \\&\quad + { \{ {-A_2 \sin ( \theta ) + ( {H_1 A_2 -H_2 A_1 } )\cos (\theta )} \} \sin ( {s\psi } )} ]\nonumber \\&\quad + \{ { ( {\cos (\theta )\!-\!\xi \sin (\theta )} )^{2} \!+\! \eta ^{2}\sin ^{2}(\theta )} \}^{s/2} [- \{A_3 \sin ( \theta ) \nonumber \\&\quad + ( {H_3 A_3 +} { {H_4 A_4 } )\cos (\theta )} \} \cos ( {s{\psi }^{\prime }} )\nonumber \\&\quad + { \{ {-A_4 \sin ( \theta ) + ( {H_3 A_4 -H_4 A_3 } )\cos (\theta )} \} \sin ( {s{\psi }^{\prime }} )} ]\nonumber \\&\quad + \{ {\cos ^{2}(\theta ) + \zeta ^{2}\sin ^{2}(\theta )} \}^{s/2} [ { \{ {-A_5 \sin ( \theta )} } \nonumber \\&\quad + ( {H_5 A_5 +H_6 A_6 } )\cos (\theta ) \} \cos ( {s{\psi }^{\prime \prime }} ) + \{ -A_6 \sin ( \theta ) \nonumber \\&\quad + ( {H_5 A_6 -H_6 A_5 } )\cos (\theta ) \} \sin ( {s{\psi }^{\prime \prime }} ) ] \rangle \nonumber \\&\quad + O ( {r^{s+2}} ), \end{aligned}$$
(94b)
\(w(r,\theta ,z)\) is given as before by Eq. (89c).
Similarly, the components of the asymptotic stress field can be conveniently expressed by using standard transformation rule:
$$\begin{aligned} \left\{ {{\begin{array}{c} {\sigma _r } \\ {\sigma _\theta } \\ {\tau _{r\theta }} \\ \end{array} }}\right\} \!&= \!\left[ {{\begin{array}{ccc} {\cos ^{2}\theta }&{} {\sin ^{2}\theta }&{} {\sin \left( {2\theta } \right) } \\ {\sin ^{2}\theta }&{} {\cos ^{2}\theta }&{} {-\sin \left( {2\theta } \right) } \\ {-\frac{1}{2}\sin \left( {2\theta } \right) }&{} {\frac{1}{2}\sin \left( {2\theta } \right) }&{} {\cos \left( {2\theta } \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\sigma _x } \\ {\sigma _y } \\ {\tau _{xy} } \\ \end{array} }} \right\} ,\end{aligned}$$
(95a)
$$\begin{aligned} \left\{ {{\begin{array}{c} {\tau _{rz} } \\ {\tau _{\theta z} } \\ \end{array} }} \right\} \!&= \!\left[ {{\begin{array}{cc} {\cos \theta }&{} {\sin \theta } \\ {-\sin \theta }&{} {\cos \theta } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\tau _{xz} } \\ {\tau _{yz} } \\ \end{array} }} \right\} . \end{aligned}$$
(95b)
The stress component, \(\sigma _{z}\), is as given in Eq. (90d).
Appendix C: Definition of certain constants referred to in Sect. 4
The constants, \(T_{11} ,{\ldots }, T_{34} \), referred to in Eqs. (13) and (19) are given as follows:
$$\begin{aligned}&T_{11} =t_1 +{t}^{\prime \prime }_2 t_{21} +{t}^{\prime \prime }_1 t_{22},\quad T_{12} =t_2 -{t}^{\prime \prime }_1 t_{21} +{t}^{\prime \prime }_2 t_{22},\nonumber \\&T_{13} ={t}^{\prime }_1 +{t}^{\prime \prime }_2 t_{23} +{t}^{\prime \prime }_1 t_{24},\quad T_{14} ={t}^{\prime }_2 -{t}^{\prime \prime }_1 t_{23} +{t}^{\prime \prime }_2 t_{24},\nonumber \\&T_{21} =t_3 +t_7 t_{22} +t_8 t_{21},\quad T_{22} =-t_4 -t_7 t_{21} +t_8 t_{22} ,\nonumber \\&T_{23} =t_5 +t_7 t_{24} +t_8 t_{23},\quad T_{24} \!=\!-t_6 -t_7 t_{23} +t_8 t_{24}, \nonumber \\&T_{31} =t_9 +t_{13} t_{22} +t_{14} t_{21},\quad T_{32} \!=\!-t_{10} \!-\!t_{13} t_{21} \!+\!t_{14} t_{22},\nonumber \\&T_{33} =t_{11} \!+\!t_{13} t_{24} +t_{14} t_{23},\quad T_{34} =-t_{12} -t_{13} t_{23} +t_{14} t_{24}, \end{aligned}$$
(96)
in which
$$\begin{aligned}&t_1 ={c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} \xi , \quad t_2 ={c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} \eta ,\nonumber \\&{t}^{\prime }_1 ={c}^{\prime }_{56} {H}^{\prime }_3 -{c}^{\prime }_{66} \xi , \quad {t}^{\prime }_2 ={c}^{\prime }_{56} {H}^{\prime }_4 +{c}^{\prime }_{66} \eta ,\nonumber \\&{t}^{\prime \prime }_1 ={c}^{\prime }_{56} {H}^{\prime }_5 ,\quad {t}^{\prime \prime }_2 ={c}^{\prime }_{56} {H}^{\prime }_6 +{c}^{\prime }_{66} \zeta ,\nonumber \\&t_3 ={c}^{\prime }_{22} ( {\eta H_1 +\xi H_2 } ),\quad t_4 ={c}^{\prime }_{12} +{c}^{\prime }_{22} ( {\xi H_1 -\eta H_2 } ),\nonumber \\&t_5 ={c}^{\prime }_{22} ( {\eta H_3 -\xi H_4 } ),\quad t_6 ={c}^{\prime }_{12} -{c}^{\prime }_{22} ( {\xi H_3 +\eta H_4 } ), \nonumber \\&t_7 \!=\!{c}^{\prime }_{22} \zeta H_5,\quad t_8 \!=\!{c}^{\prime }_{12} \!-\!{c}^{\prime }_{22} \zeta H_6 ,\nonumber \\&t_9 \!=\!{c}^{\prime }_{56} {H}^{\prime }_2 \!+\!{c}^{\prime }_{66} ({\eta \!+\!H_2 } ),\,\, t_{10} \!=\!{c}^{\prime }_{56} {H}^{\prime }_1 \!+\!{c}^{\prime }_{66} ( {\xi \!+\!H_1 } ), \nonumber \\&t_{11} \!=\!{c}^{\prime }_{56} {H}^{\prime }_4 \!+\!{c}^{\prime }_{66} ( {\eta \!+\!H_4 } ),\,\,t_{12} \!=\!{c}^{\prime }_{56} {H}^{\prime }_3 \!-\!{c}^{\prime }_{66} ( {\xi \!-\!H_3 } ),\nonumber \\&t_{13} ={c}^{\prime }_{56} {H}^{\prime }_6 +{c}^{\prime }_{66} ( {\zeta +H_6 } ),\,\,t_{14} ={c}^{\prime }_{56} {H}^{\prime }_5 +{c}^{\prime }_{66} H_5 ,\nonumber \\&t_{15} \!=\!{c}^{\prime }_{14} \!+\!{c}^{\prime }_{44} ( {\xi {H}^{\prime }_1 \!-\!\eta {H}^{\prime }_2 } ),\,\, t_{16} \!=\!{c}^{\prime }_{44} ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } ),\nonumber \\&t_{17} ={c}^{\prime }_{14} -{c}^{\prime }_{44} ( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ),\,\, t_{18} ={c}^{\prime }_{44} ( {\eta {H}^{\prime }_3 \!-\!\xi {H}^{\prime }_4 } ), \nonumber \\&t_{19} ={c}^{\prime }_{14} -{c}^{\prime }_{44} \zeta {H}^{\prime }_6 ,\quad t_{20} ={c}^{\prime }_{44} \zeta {H}^{\prime }_5 ,\nonumber \\&t_{21} \!=\!-\frac{ ( {t_{15} t_{20} \!-\!t_{16} t_{19} } )}{ ( {t_{19}^2 \!+\!t_{20}^2 } )},\quad t_{22} \!=\!-\frac{ ( {t_{15} t_{19} +t_{16} t_{20} } )}{ ( {t_{19}^2 +t_{20}^2 } )},\nonumber \\&t_{23}\!=\!-\frac{ ( {t_{17} t_{20} \!-\!t_{18} t_{19} } )}{ ( {t_{19}^2 \!+\!t_{20}^2 } )},\quad t_{24} \!=\!-\frac{ ( {t_{17} t_{19} \!+\!t_{18} t_{20} } )}{ ( {t_{19}^2 +t_{20}^2 } )}.\qquad \end{aligned}$$
(97)
The constants, \({T}^{\prime }_{11} ,{\ldots }, {T}^{\prime }_{14} \), referred to in Eqs. (19) are written as follows:
$$\begin{aligned} {T}^{\prime }_{11} \!=\!1\!+\!t_{22},\quad {T}^{\prime }_{12} \!=\!-t_{21} , {T}^{\prime }_{13} \!=\!1\!+\!t_{24},\quad {T}^{\prime }_{14} \!=\!-t_{23}.\nonumber \\ \end{aligned}$$
(98)
The constants, \({T}^{\prime \prime }_{11},{\ldots },{T}^{\prime \prime }_{34}\), referred to in Eqs.(25) can be written as follows:
$$\begin{aligned}&{T}^{\prime \prime }_{11} \!=\!{H}^{\prime }_1 \!+\!{H}^{\prime }_3 t_{25} \!-\!{H}^{\prime }_4 t_{26},\quad {T}^{\prime \prime }_{12} \!=\!{H}^{\prime }_2 \!+\!{H}^{\prime }_3 t_{26} +{H}^{\prime }_4 t_{25} ,\nonumber \\&{T}^{\prime \prime }_{13} \!=\!{H}^{\prime }_5 \!+\!{H}^{\prime }_3 t_{27} \!-\!{H}^{\prime }_4 t_{28},\quad {T}^{\prime \prime }_{14} \!=\!{H}^{\prime }_6 \!+\!{H}^{\prime }_3 t_{28} +{H}^{\prime }_4 t_{27},\nonumber \\&{T}^{\prime \prime }_{21} \!=\!t_4 +t_6 t_{25} -t_5 t_{26},\quad {T}^{\prime \prime }_{22} =t_3 +t_6 t_{26} +t_5 t_{25} ,\nonumber \\&{T}^{\prime \prime }_{23} \!=\!t_8 +t_6 t_{27} -t_5 t_{28},\quad {T}^{\prime \prime }_{24} =t_7 +t_6 t_{28} +t_5 t_{27} ,\nonumber \\&{T}^{\prime \prime }_{31} \!=\!t_3 +t_5 t_{25} \!+\!t_6 t_{26},\quad {T}^{\prime \prime }_{32} =-t_4 +t_5 t_{26} -t_6 t_{25} ,\nonumber \\&{T}^{\prime \prime }_{33} =t_7 \!+\!t_5 t_{27} +t_6 t_{28},\quad {T}^{\prime \prime }_{34} \!=\!-t_8 \!+\!t_5 t_{28} \!-\!t_6 t_{27} , \end{aligned}$$
(99)
where
$$\begin{aligned}&t_{25} =-\frac{\left( {t_9 t_{11} +t_{10} t_{12} } \right) }{\left( {t_{11}^2 +t_{12}^2 } \right) },\quad t_{26} =-\frac{\left( {t_9 t_{12} -t_{10} t_{11} } \right) }{\left( {t_{11}^2 +t_{12}^2 } \right) },\nonumber \\&t_{27} =-\frac{\left( {t_{12} t_{14} +t_{11} t_{13} } \right) }{\left( {t_{11}^2 +t_{12}^2 } \right) },\quad t_{28} =-\frac{\left( {t_{12} t_{13} -t_{11} t_{14} } \right) }{\left( {t_{11}^2 +t_{12}^2 } \right) }.\nonumber \\ \end{aligned}$$
(100)
Finally, the constants, \(\Delta _1 , \Delta _2 , \Delta _3\), referred to in Eqs. (13), (19) and (25), respectively, are given as follows:
$$\begin{aligned} \Delta _1 \!&= \!T_{12} \left( {T_{23} T_{34} -T_{24} T_{33} } \right) -T_{13} \left( {T_{22} T_{34} -T_{24} T_{32} } \right) \nonumber \\&+T_{14} \left( {T_{22} T_{33} -T_{23} T_{32} } \right) ,\end{aligned}$$
(101a)
$$\begin{aligned} \Delta _2 \!&= \!{T}^{\prime }_{11} \left( {T_{23} T_{34} -T_{24} T_{33} } \right) -{T}^{\prime }_{13} \left( {T_{21} T_{34} -T_{24} T_{31} } \right) \nonumber \\&+{T}^{\prime }_{14} \left( {T_{21} T_{33} -T_{23} T_{31} } \right) ,\end{aligned}$$
(101b)
$$\begin{aligned} \Delta _3 \!&= \!{T}^{\prime \prime }_{11} \left( {{T}^{\prime \prime }_{22} {T}^{\prime \prime }_{33} -{T}^{\prime \prime }_{23} {T}^{\prime \prime }_{32} } \right) -{T}^{\prime \prime }_{12} \left( {{T}^{\prime \prime }_{21} {T}^{\prime \prime }_{33} -{T}^{\prime \prime }_{23} {T}^{\prime \prime }_{31} } \right) \nonumber \\&+{T}^{\prime \prime }_{13} \left( {{T}^{\prime \prime }_{21} {T}^{\prime \prime }_{32} -{T}^{\prime \prime }_{22} {T}^{\prime \prime }_{31} } \right) . \end{aligned}$$
(101c)
Appendix D: Definition of certain constants referred to in Sect. 7
The constants, \(\Gamma _{11} ,{\ldots }, \Gamma _{36}\), referred to in Eqs. (17), (23) and (29) are given as follows:
$$\begin{aligned} \Gamma _{11}&= \frac{1}{[ { {\{ {{c}^{\prime }_{12} } +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{22} } \} +Q_{11} \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22} } \}} ]}\nonumber \\&\times [{{c}^{\prime }_{11} +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{12} } +( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } ){c}^{\prime }_{14}\nonumber \\&+Q_{11} \{ ( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{12} +( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } ){c}^{\prime }_{14} \}\nonumber \\&+ Q_{12} \{ {{c}^{\prime }_{11} }\,\, {-( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{12} -( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ){c}^{\prime }_{14} } \}\nonumber \\&+Q_{13} \{ {( {\eta H_3 -\xi H_4 } ){c}^{\prime }_{12} +( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } ){c}^{\prime }_{14} } \}\nonumber \\&+Q_{14} \{ {{c}^{\prime }_{11} } {-{c}^{\prime }_{12} \zeta H_6 -{c}^{\prime }_{14} \zeta {H}^{\prime }_6 } \}\nonumber \\&{+Q_{15} \{ {{c}^{\prime }_{12} \zeta H_5 +{c}^{\prime }_{14} \zeta {H}^{\prime }_5 } \}} ], \end{aligned}$$
(102a)
$$\begin{aligned} \Gamma _{12}&= 1+\frac{Q_{12} \{ {{c}^{\prime }_{12} {-( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{22} } \} +Q_{13} \{ {( {\eta H_3 -\xi H_4 } ){c}^{\prime }_{22} } \}} }{ {\{ {{c}^{\prime }_{12} } +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{22} } \} +Q_{11} \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22} } \}}\nonumber \\&\!+\frac{Q_{14} \{ {{c}^{\prime }_{12} {\!-\!\zeta H_6 {c}^{\prime }_{22} } \} \!+\!Q_{15} \zeta H_5 {c}^{\prime }_{22} } }{ {\{ {{c}^{\prime }_{12} } \!+\!( {\xi H_1 \!-\!\eta H_2 } ){c}^{\prime }_{22} } \} \!+\!Q_{11} \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22} } \}}, \end{aligned}$$
(102b)
$$\begin{aligned} \Gamma _{13}&= \frac{1}{[ { {\{ {{c}^{\prime }_{12} } +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{22} } \} +Q_{11} \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22} } \}} ]}\nonumber \\&\times \, [{c}^{\prime }_{13} +{c}^{\prime }_{23} ( {\xi H_1 -\eta H_2 } )+{c}^{\prime }_{34} ( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 })\nonumber \\&+Q_{11} \{ {{c}^{\prime }_{23} ( {\eta H_1 } } {+\xi H_2 } )+{c}^{\prime }_{34} ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } ) \}\nonumber \\&+Q_{12} \{ {{c}^{\prime }_{13} } {-( {\xi H_3 +\eta H_4 } ){c}^{\prime }_{23} -( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ){c}^{\prime }_{34} } \} \nonumber \\&+Q_{13} \{ {{c}^{\prime }_{23} } ( {\eta H_3 -\xi H_4 } ) {+{c}^{\prime }_{34} ( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } )} \}\nonumber \\&{+Q_{14} \{ {{c}^{\prime }_{13} } -{c}^{\prime }_{23} \zeta H_6 -{c}^{\prime }_{34} \zeta {H}^{\prime }_6 } \}\nonumber \\&+Q_{15} \{ {{c}^{\prime }_{23} } \zeta H_5 +{c}^{\prime }_{34} { {\zeta {H}^{\prime }_5 } \} } ],\end{aligned}$$
(102c)
$$\begin{aligned} \Gamma _{14}&= \frac{1}{[ { {\{ {{c}^{\prime }_{12} } +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{22} } \} +Q_{11} \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22} } \}} ]}\nonumber \\&\times \,[ {c}^{\prime }_{14} +{c}^{\prime }_{44} ( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } )+Q_{11} {c}^{\prime }_{44} ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } )\nonumber \\&+ {Q_{12} \{ {{c}^{\prime }_{14} } -( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ){c}^{\prime }_{44} } \} +Q_{13} {c}^{\prime }_{44} ( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } )\nonumber \\&{+Q_{14} \{ {{c}^{\prime }_{14} {-{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \} } +Q_{15} {c}^{\prime }_{44} \zeta {H}^{\prime }_5 } ],\end{aligned}$$
(102d)
$$\begin{aligned} \Gamma _{15}&= \frac{1}{[ { {\{ {{c}^{\prime }_{12} } +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{22} } \} +Q_{11} \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22} } \}} ]}\nonumber \\&\times \,[ {{c}^{\prime }_{55} } +{c}^{\prime }_{56} ( {\xi +H_1 } )+Q_{11} \{ {{c}^{\prime }_{55} } +{c}^{\prime }_{56} {( {\eta +H_2 } )} \} \nonumber \\&+Q_{12} \{ {{c}^{\prime }_{55} } - {{c}^{\prime }_{56} ( {\xi -H_3 } )} \} +Q_{13} \{ {{c}^{\prime }_{55} } +{c}^{\prime }_{56} {( {\eta +H_4 } )} \}\nonumber \\&+Q_{14} \{ {{c}^{\prime }_{55} } + {{c}^{\prime }_{56} H_5 } \} +Q_{15} \{ {{c}^{\prime }_{55} +{c}^{\prime }_{56} ( {\zeta +H_6 } )} \},\end{aligned}$$
(102e)
$$\begin{aligned} \Gamma _{16}&= \frac{1}{[ { {\{ {{c}^{\prime }_{12} } +( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{22} } \} +Q_{11} \{ {( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22} } \}} ]}\nonumber \\&\times \, [ {\{ {{c}^{\prime }_{56} {H}^{\prime }_1 {+{c}^{\prime }_{66} ( {\xi +H_1 } )} \} } } +Q_{11} \{ {{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )} \}\nonumber \\&+Q_{12} \{ {{c}^{\prime }_{56} } {H}^{\prime }_3 - {{c}^{\prime }_{66} ( {\xi -H_3 } )} \} +Q_{13} \{ {{c}^{\prime }_{56} {H}^{\prime }_4 +{c}^{\prime }_{66} ( {\eta +H_4 } )} \}\nonumber \\&+Q_{14} \{ {{c}^{\prime }_{56} {H}^{\prime }_5 } + {{c}^{\prime }_{66} H_5 } \} +Q_{15} \{ {{c}^{\prime }_{56} {H}^{\prime }_6 +{c}^{\prime }_{66} ( {\zeta +H_6 } )} \} ],\nonumber \\ \end{aligned}$$
(102f)
$$\begin{aligned} \Gamma _{21}&= \frac{1}{[ {{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )+Q_{21} \{ {{c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} ( {\xi +H_1 } )} \}} ]}\nonumber \\&\times [ {( {Q_{21} } } \{ {{c}^{\prime }_{11} } + {{c}^{\prime }_{12} ( {\xi H_1 -\eta H_2 } )+{c}^{\prime }_{14} ( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } )} \}\nonumber \\&+{c}^{\prime }_{12} ( {\eta H_1 +\xi H_2 } )+{c}^{\prime }_{14} ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } )\nonumber \\&+Q_{22} \{ {{c}^{\prime }_{11} -{c}^{\prime }_{12} ( {\xi H_3 +\eta H_4 } )} {-{c}^{\prime }_{14} ( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } )} \}\nonumber \\&+Q_{23} \{ {{c}^{\prime }_{12} ( {\eta H_3 -\xi H_4 } )} {+{c}^{\prime }_{14} ( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } )} \}\nonumber \\&+Q_{24} \{ {{c}^{\prime }_{11} } \!-\!\zeta {( {{c}^{\prime }_{12} H_6 \!+\!{c}^{\prime }_{14} {H}^{\prime }_6 } )} \}\nonumber \\&+ Q_{25} \zeta \{ {( {{c}^{\prime }_{12} H_5 +{c}^{\prime }_{14} {H}^{\prime }_5 } )} \} ],\end{aligned}$$
(103a)
$$\begin{aligned} \Gamma _{22}&= \frac{1}{[ {{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )+Q_{21} \{ {{c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} ( {\xi +H_1 } )} \}} ]}\nonumber \\&\times [ {Q_{21} } \{ {{c}^{\prime }_{12} } {+( {\xi H_1 -\eta H_2 } ){c}^{\prime }_{22} } \}+( {\eta H_1 +\xi H_2 } ){c}^{\prime }_{22}\nonumber \\&+Q_{22} \{ {{c}^{\prime }_{12} } -{c}^{\prime }_{22} ( {\xi H_3 +\eta H_4 } ) \} +Q_{23} {c}^{\prime }_{22} ( {\eta H_3 -\xi H_4 } )\nonumber \\&+Q_{24} \{ {{c}^{\prime }_{12} } {-{c}^{\prime }_{22} \zeta H_6 } \} +Q_{25} {c}^{\prime }_{22} \zeta H_5 ],\end{aligned}$$
(103b)
$$\begin{aligned} \Gamma _{23}&= \frac{1}{[ {{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )+Q_{21} \{ {{c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} ( {\xi +H_1 } )} \}} ]}\nonumber \\&\times [ {Q_{21} } \{ {{c}^{\prime }_{13} } +{c}^{\prime }_{23} ( {\xi H_1 -\eta H_2 } ){+{c}^{\prime }_{34} ( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } )} \}\nonumber \\&+\{ {{c}^{\prime }_{23} } ( {\eta H_1 +\xi H_2 } )+ {{c}^{\prime }_{34} ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } )} \}\nonumber \\&+Q_{22} \{ {{c}^{\prime }_{13} } {-{c}^{\prime }_{23} ( {\xi H_3 +\eta H_4 } )-{c}^{\prime }_{34} ( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } )} \}\nonumber \\&+Q_{23} \{ {{c}^{\prime }_{23} ( {\eta H_3 -\xi H_4 } )+{c}^{\prime }_{34} ( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } )} \}\nonumber \\&+( {Q_{24} } \{ {{c}^{\prime }_{13} -} {\zeta ( {{c}^{\prime }_{23} H_6 +{c}^{\prime }_{34} {H}^{\prime }_6 } )} \}\nonumber \\&+Q_{25} \zeta \{ {{c}^{\prime }_{23} H_5 +{c}^{\prime }_{34} {H}^{\prime }_5 } \} ],\end{aligned}$$
(103c)
$$\begin{aligned} \Gamma _{24}&= \frac{1}{[ {{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )+Q_{21} \{ {{c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} ( {\xi +H_1 } )} \}} ]}\nonumber \\&\times [ {Q_{21} } \{ {{c}^{\prime }_{14} } + {{c}^{\prime }_{44} ( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } )} \} +{c}^{\prime }_{44} ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 })\nonumber \\&+ {Q_{22} \{ {{c}^{\prime }_{14} } -{c}^{\prime }_{44} ( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } )} \} +Q_{23} {c}^{\prime }_{44} ( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } )\nonumber \\&+Q_{24} \{ {{c}^{\prime }_{14} {-{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \} +Q_{25} {c}^{\prime }_{44} \zeta {H}^{\prime }_5 } ],\end{aligned}$$
(103d)
$$\begin{aligned} \Gamma _{25}&= \frac{1}{[ {{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )+Q_{21} \{ {{c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} ( {\xi +H_1 } )} \}} ]}\nonumber \\&\times [ {Q_{21} } \{ {{c}^{\prime }_{55} } {H}^{\prime }_1 + {{c}^{\prime }_{56} ( {\xi +H_1 } )} \}+{c}^{\prime }_{55} {H}^{\prime }_2 +{c}^{\prime }_{56} ( {\eta +H_2 } )\nonumber \\&+Q_{22} \{ {{c}^{\prime }_{55} {H}^{\prime }_3 } \!-\! {{c}^{\prime }_{56} ( {\xi \!-\!H_3 } )} \} \!+\!Q_{23} \{ {{c}^{\prime }_{55} {H}^{\prime }_4 } \!+\!{c}^{\prime }_{56} ( {\eta \!+\!H_4 } ) \}\nonumber \\&+Q_{24} \{ {{c}^{\prime }_{55} {H}^{\prime }_5 } + {{c}^{\prime }_{56} H_5 } \} {+Q_{25} \{ {{c}^{\prime }_{55} {H}^{\prime }_6 +{c}^{\prime }_{56} ( {\zeta +H_6 } )} \}} ], \end{aligned}$$
(103e)
$$\begin{aligned}&\Gamma _{26} =1\nonumber \\&\quad +\frac{Q_{22} \{ {{c}^{\prime }_{56} {H}^{\prime }_3 - {{c}^{\prime }_{66} ( {\xi -H_3 } )} \} +Q_{23} \{ {{c}^{\prime }_{56} {H}^{\prime }_4 +{c}^{\prime }_{66} ( {\eta +H_4 } )} \}} }{{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )+Q_{21} \{ {{c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} ( {\xi +H_1 } )} \}}\nonumber \\&\quad +\frac{Q_{24} \{ {{c}^{\prime }_{56} {H}^{\prime }_5 + {{c}^{\prime }_{66} H_5 } \} +Q_{25} \{ {{c}^{\prime }_{56} {H}^{\prime }_6 +{c}^{\prime }_{66} ( {\zeta +H_6 } )} \}} }{{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )+Q_{21} \{ {{c}^{\prime }_{56} {H}^{\prime }_1 +{c}^{\prime }_{66} ( {\xi +H_1 } )} \}}.\nonumber \\ \end{aligned}$$
(103f)
$$\begin{aligned} \Gamma _{31}&= \frac{1}{\sqrt{2\pi r} [ {Q_{35} \{ {{c}^{\prime }_{14} -{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \}+{c}^{\prime }_{44} \zeta {H}^{\prime }_5 } ]}\nonumber \\&\times [ {Q_{31} } \{ {{c}^{\prime }_{11} } +{c}^{\prime }_{12} ( {\xi H_1 -\eta H_2 } ) {+{c}^{\prime }_{14} ( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } )} \}\nonumber \\&+Q_{32} \{ {{c}^{\prime }_{12} ( {\eta H_1 +\xi H_2 } )+{c}^{\prime }_{14} ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } )} \}\nonumber \\&+Q_{33} \{ {{c}^{\prime }_{11} -{c}^{\prime }_{12} } ( {\xi H_3 +\eta H_4 } ) {-{c}^{\prime }_{14} ( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } )} \}\nonumber \\&+Q_{34} \{ {{c}^{\prime }_{12} ( {\eta H_3 -\xi H_4 } )+{c}^{\prime }_{14} ( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } )} \}\nonumber \\&+Q_{35} \{ {{c}^{\prime }_{11} } -{c}^{\prime }_{12} \zeta H_6 {-{c}^{\prime }_{14} \zeta {H}^{\prime }_6 } \}\nonumber \\&+ \{ {{c}^{\prime }_{12} \zeta H_5 +{c}^{\prime }_{14} \zeta {H}^{\prime }_5 } \} ],\end{aligned}$$
(104a)
$$\begin{aligned} \Gamma _{32}&= \frac{1}{ [ {Q_{35} \{ {{c}^{\prime }_{14} -{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \}+{c}^{\prime }_{44} \zeta {H}^{\prime }_5 } ]}\nonumber \\&\times [ {Q_{31} } \{{c}^{\prime }_{12} {+{c}^{\prime }_{22} ( {\xi H_1 -\eta H_2 } )} \}\nonumber \\&+Q_{32} {c}^{\prime }_{22} ( {\eta H_1 +\xi H_2 } ) \nonumber \\&+Q_{33} \{ {{c}^{\prime }_{12} } {-{c}^{\prime }_{22} ( {\xi H_3 +\eta H_4 } )} \}\nonumber \\&+Q_{34} {c}^{\prime }_{22} ( {\eta H_3 -\xi H_4 } )\nonumber \\&+Q_{35} \{ {{c}^{\prime }_{12} } { {-{c}^{\prime }_{22} \zeta H_6 } \} +{c}^{\prime }_{22} \zeta H_5 } ],\end{aligned}$$
(104b)
$$\begin{aligned} \Gamma _{33}&= \frac{1}{ [ {Q_{35} \{ {{c}^{\prime }_{14} -{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \}+{c}^{\prime }_{44} \zeta {H}^{\prime }_5 } ]}\nonumber \\&\times [ {Q_{31} } \{ {{c}^{\prime }_{13} +{c}^{\prime }_{23} { ( {\xi H_1 -\eta H_2 } )+{c}^{\prime }_{34} ( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } )} \} } \nonumber \\&+Q_{32} \{ {{c}^{\prime }_{23} } ( {\eta H_1 +\xi H_2 } )+{c}^{\prime }_{34} { ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } )} \} \nonumber \\&+Q_{33} \{ {{c}^{\prime }_{13} } -{c}^{\prime }_{23} ( {\xi H_3 +\eta H_4 } )-{c}^{\prime }_{34} ( {\xi {H}^{\prime }_3 +\eta {H}^{\prime }_4 } ) \}\nonumber \\&+Q_{34} \{ {{c}^{\prime }_{23} ( {\eta H_3 -\xi H_4 } )+{c}^{\prime }_{34} ( {\eta {H}^{\prime }_3 -\xi {H}^{\prime }_4 } )} \}\nonumber \\&+Q_{35} \{ {{c}^{\prime }_{13} -{c}^{\prime }_{23} \zeta H_6 } { {-{c}^{\prime }_{34} \zeta {H}^{\prime }_6 } \} +\zeta \{ {{c}^{\prime }_{23} H_5 +{c}^{\prime }_{34} {H}^{\prime }_5 } \}} ],\end{aligned}$$
(104c)
$$\begin{aligned} \Gamma _{34}&= \frac{Q_{31} \{ {{c}^{\prime }_{14} +{c}^{\prime }_{44} ( {\xi {H}^{\prime }_1 -\eta {H}^{\prime }_2 } )} \}+Q_{32} {c}^{\prime }_{44} ( {\eta {H}^{\prime }_1 +\xi {H}^{\prime }_2 } )}{Q_{35} \{ {{c}^{\prime }_{14} -{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \}+{c}^{\prime }_{44} \zeta {H}^{\prime }_5 }\nonumber \\&+\frac{Q_{33} \{ {{c}^{\prime }_{14} \!-\!{c}^{\prime }_{44} ( {\xi {H}^{\prime }_3 \!+\!\eta {H}^{\prime }_4 } )} \}\!+\!Q_{34} {c}^{\prime }_{44} ( {\eta {H}^{\prime }_3 \!-\!\xi {H}^{\prime }_4 } )}{Q_{35} \{ {{c}^{\prime }_{14} \!-\!{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \}\!+\!{c}^{\prime }_{44} \zeta {H}^{\prime }_5 }\!+\!1.\end{aligned}$$
(104d)
$$\begin{aligned} \Gamma _{35}&= \frac{1}{ [ {Q_{35} \{ {{c}^{\prime }_{14} -{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \}+{c}^{\prime }_{44} \zeta {H}^{\prime }_5 } ]}\nonumber \\&\times [ {Q_{31} \{ {{c}^{\prime }_{55} {H}^{\prime }_1 +{c}^{\prime }_{56} ( {\xi +H_1 } )} \}} \nonumber \\&+Q_{32} \{ {{c}^{\prime }_{55} {H}^{\prime }_2 } +{c}^{\prime }_{56} { ( {\eta +H_2 } )} \}\nonumber \\&+Q_{33} \{ {{c}^{\prime }_{55} } {H}^{\prime }_3 - {{c}^{\prime }_{56} ( {\xi -H_3 } )} \}\nonumber \\&+Q_{34} \{ {{c}^{\prime }_{55} } {H}^{\prime }_4 +{c}^{\prime }_{56} { ( {\eta +H_4 } )} \}\nonumber \\&+Q_{35} \{ {{c}^{\prime }_{55} {H}^{\prime }_5 } + {{c}^{\prime }_{56} H_5 } \}\nonumber \\&+ \{ {{c}^{\prime }_{55} {H}^{\prime }_6 +{c}^{\prime }_{56} ( {\eta +H_6 } )} \} ],\end{aligned}$$
(104e)
$$\begin{aligned} \Gamma _{36}&= \frac{1}{\sqrt{2\pi r} [ {Q_{35} \{ {{c}^{\prime }_{14} -{c}^{\prime }_{44} \zeta {H}^{\prime }_6 } \}+{c}^{\prime }_{44} \zeta {H}^{\prime }_5 } ]}\nonumber \\&\times [ {Q_{31} } \{ {{c}^{\prime }_{56} {H}^{\prime }_1 {+{c}^{\prime }_{66} ( {\xi +H_1 } )} \} } \nonumber \\&+Q_{32} \{ {{c}^{\prime }_{56} {H}^{\prime }_2 +{c}^{\prime }_{66} ( {\eta +H_2 } )} \}\nonumber \\&+Q_{33} \{ {{c}^{\prime }_{56} } {H}^{\prime }_3 - {{c}^{\prime }_{66} ( {\xi -H_3 } )} \}\nonumber \\&+Q_{34} \{ {{c}^{\prime }_{56} {H}^{\prime }_4 +{c}^{\prime }_{66} ( {\eta +H_4 } )} \}\nonumber \\&+Q_{35} \{ {{c}^{\prime }_{56} } {H}^{\prime }_5 + {{c}^{\prime }_{66} H_5 } \}\nonumber \\&+ \{ {{c}^{\prime }_{56} {H}^{\prime }_6 +{c}^{\prime }_{66} ( {\zeta +H_6 } )} \} ]. \end{aligned}$$
(104f)
Appendix E: Transformation of stress components
Transformation of stress components from \(x = [1\bar{{1}}0], y = [111], z = [\bar{{1}}\bar{{1}}2]\) to \({x}^{\prime }= [1\bar{{1}}0], {y}^{\prime } = [11\bar{{1}}], {z}^{\prime } = [112]\), referred to earlier in Sect. 7, can be written as follows:
$$\begin{aligned} \left\{ {{\begin{array}{c} {{\sigma }^{\prime }_x } \\ {{\sigma }^{\prime }_y } \\ {{\sigma }^{\prime }_z } \\ {{\tau }^{\prime }_{yz} } \\ {{\tau }^{\prime }_{xz} } \\ {{\tau }^{\prime }_{xy} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1&{} 0&{} 0&{} 0&{} 0&{} 0 \\ 0&{} {\cos ^{2}\left( \alpha \right) }&{} {\sin ^{2}\left( \alpha \right) }&{} {\sin \left( {2\alpha } \right) }&{} 0&{} 0 \\ 0&{} {\sin ^{2}\left( \alpha \right) }&{} {\cos ^{2}\left( \alpha \right) }&{} {-\sin \left( {2\alpha } \right) }&{} 0&{} 0 \\ 0&{} {-\frac{1}{2}\sin \left( {2\alpha } \right) }&{} {\frac{1}{2}\sin \left( {2\alpha } \right) }&{} {\cos \left( {2\alpha } \right) }&{} 0&{} 0\\ 0&{} 0&{} 0&{} 0&{} {\cos \left( \alpha \right) }&{} {-\sin \left( \alpha \right) } \\ 0&{} 0&{} 0&{} 0&{} {\sin \left( \alpha \right) }&{} {\cos \left( \alpha \right) } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\sigma _x } \\ {\sigma _y } \\ {\sigma _z } \\ {\tau _{yz} } \\ {\tau _{xz} } \\ {\tau _{xy} } \\ \end{array} }} \right\} . \end{aligned}$$
(105)
Next, transformation of stress components from \({x}^{\prime }= [1\bar{{1}}0], {y}^{\prime } = [11\bar{{1}}], {z}^{\prime } = [112]\) to \({x}^{\prime \prime } = [\bar{{1}}\bar{{1}}0], {y}^{\prime \prime } = [\bar{{1}}11], {z}^{\prime \prime } = [\bar{{1}}1\bar{{2}}]\), referred to in Sect. 7, can be written as follows:
$$\begin{aligned} \left\{ {{\begin{array}{c} {{\sigma }^{\prime \prime }_x } \\ {{\sigma }^{\prime \prime }_y } \\ {{\sigma }^{\prime \prime }_z } \\ {{\tau }^{\prime \prime }_{yz} } \\ {{\tau }^{\prime \prime }_{xz} } \\ {{\tau }^{\prime \prime }_{xy} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {a_{11}^2 }&{} {a_{12}^2 }&{} {a_{13}^2 }&{} {2a_{12} a_{13} }&{} {2a_{11} a_{13} }&{} {2a_{11} a_{12} } \\ {a_{21}^2 }&{} {a_{22}^2 }&{} {a_{23}^2 }&{} {2a_{22} a_{23} }&{} {2a_{21} a_{23} }&{} {2a_{21} a_{22} } \\ {a_{31}^2 }&{} {a_{32}^2 }&{} {a_{33}^2 }&{} {2a_{32} a_{33} }&{} {2a_{31} a_{33} }&{} {2a_{31} a_{32} } \\ {a_{21} a_{31} }&{} {a_{22} a_{32} }&{} {a_{23} a_{33} }&{} {a_{22} a_{33} +a_{23} a_{32} }&{} {a_{21} a_{33} +a_{23} a_{31} }&{} {a_{21} a_{32} +a_{22} a_{31} } \\ {a_{11} a_{31} }&{} {a_{12} a_{32} }&{} {a_{13} a_{33} }&{} {a_{12} a_{33} +a_{13} a_{32} }&{} {a_{11} a_{33} +a_{13} a_{31} }&{} {a_{11} a_{32} +a_{12} a_{31} } \\ {a_{11} a_{21} }&{} {a_{12} a_{22} }&{} {a_{13} a_{23} }&{} {a_{12} a_{23} +a_{13} a_{22} }&{} {a_{11} a_{23} +a_{13} a_{21} }&{} {a_{11} a_{22} +a_{12} a_{21} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {{\sigma }^{\prime }_x } \\ {{\sigma }^{\prime }_y } \\ {{\sigma }^{\prime }_z } \\ {{\tau }^{\prime }_{yz} } \\ {{\tau }^{\prime }_{xz} } \\ {{\tau }^{\prime }_{xy} } \\ \end{array} }} \right\} , \end{aligned}$$
(106)
in which
$$\begin{aligned} \begin{aligned}&a_{11} =\frac{1}{2}\left[ {\bar{{1}}\bar{{1}}0} \right] .\left[ {1\bar{{1}}0} \right] =0, \quad a_{12} =\frac{1}{\sqrt{6}}\left[ {\bar{{1}}\bar{{1}}0} \right] .\left[ {11\bar{{1}}} \right] =-\frac{\sqrt{2}}{\sqrt{3}},\quad a_{13} =\frac{1}{2\sqrt{3}}\left[ {\bar{{1}}\bar{{1}}0} \right] .\left[ {112} \right] =-\frac{1}{\sqrt{3}},\\&a_{21} =\frac{1}{\sqrt{6}}\left[ {\bar{{1}}11} \right] .\left[ {1\bar{{1}}0} \right] =-\frac{2}{\sqrt{6}},\quad a_{22} =\frac{1}{3}\left[ {\bar{{1}}11} \right] .\left[ {11\bar{{1}}} \right] =-\frac{1}{3},\quad a_{23} =\frac{1}{3\sqrt{2}}\left[ {\bar{{1}}11} \right] .\left[ {112} \right] =\frac{\sqrt{2}}{3},\\&a_{31} =\frac{1}{2\sqrt{3}}\left[ {\bar{{1}}1\bar{{2}}} \right] .\left[ {1\bar{{1}}0} \right] =-\frac{1}{\sqrt{3}},\quad a_{32} =\frac{1}{3\sqrt{2}}\left[ {\bar{{1}}1\bar{{2}}} \right] .\left[ {11\bar{{1}}} \right] =\frac{\sqrt{2}}{3},\quad a_{33} =\frac{1}{6}\left[ {\bar{{1}}1\bar{{2}}} \right] .\left[ {112} \right] =-\frac{2}{3}. \end{aligned} \end{aligned}$$
(107)
Finally, transformation of stress components from \({x}^{\prime \prime } = [\bar{{1}}\bar{{1}}0], {y}^{\prime \prime } = [\bar{{1}}11], {z}^{\prime \prime } = [\bar{{1}}1\bar{{2}}]\) back to \(x = [1\bar{{1}}0], y = [111], z = [\bar{{1}}\bar{{1}}2]\), referred to in Sect. 7, can be written as follows:
$$\begin{aligned}&\left\{ {{\begin{array}{c} {\sigma _x } \\ {\sigma _y } \\ {\sigma _z } \\ {\tau _{yz} } \\ {\tau _{xz} } \\ {\tau _{xy} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {{{a}^{\prime 2}_{11}}}&{} {{{a}^{\prime 2}_{12}}}&{} {{{a}^{\prime 2}_{13}} }&{} {2{a}^{\prime }_{12} {a}^{\prime }_{13} }&{} {2{a}^{\prime }_{11} {a}^{\prime }_{13} }&{} {2{a}^{\prime }_{11} {a}^{\prime }_{12} } \\ {{{a}^{\prime 2}_{21}} }&{} {{{a}^{\prime 2}_{22}} }&{} {{{a}^{\prime 2}_{23}} }&{} {2{a}^{\prime }_{22} {a}^{\prime }_{23} }&{} {2{a}^{\prime }_{21} {a}^{\prime }_{23} }&{} {2{a}^{\prime }_{21} {a}^{\prime }_{22} } \\ {{{a}^{\prime 2}_{31}} }&{} {{{a}^{\prime 2}_{32}} }&{} {{{a}^{\prime 2}_{33}} }&{} {2{a}^{\prime }_{32} {a}^{\prime }_{33} }&{} {2{a}^{\prime }_{31} {a}^{\prime }_{33} }&{} {2{a}^{\prime }_{31} {a}^{\prime }_{32} } \\ {{a}^{\prime }_{21} {a}^{\prime }_{31} }&{} {{a}^{\prime }_{22} {a}^{\prime }_{32} }&{} {{a}^{\prime }_{23} {a}^{\prime }_{33} }&{} {{a}^{\prime }_{22} {a}^{\prime }_{33} +{a}^{\prime }_{23} {a}^{\prime }_{32} }&{} {{a}^{\prime }_{21} {a}^{\prime }_{33} +{a}^{\prime }_{23} {a}^{\prime }_{31} }&{} {{a}^{\prime }_{21} {a}^{\prime }_{32} +{a}^{\prime }_{22} {a}^{\prime }_{31} } \\ {{a}^{\prime }_{11} {a}^{\prime }_{31} }&{} {{a}^{\prime }_{12} {a}^{\prime }_{32} }&{} {{a}^{\prime }_{13} {a}^{\prime }_{33} }&{} {{a}^{\prime }_{12} {a}^{\prime }_{33} +{a}^{\prime }_{13} {a}^{\prime }_{32} }&{} {{a}^{\prime }_{11} {a}^{\prime }_{33} +{a}^{\prime }_{13} {a}^{\prime }_{31} }&{} {{a}^{\prime }_{11} {a}^{\prime }_{32} +{a}^{\prime }_{12} {a}^{\prime }_{31} } \\ {{a}^{\prime }_{11} {a}^{\prime }_{21} }&{} {{a}^{\prime }_{12} {a}^{\prime }_{22} }&{} {{a}^{\prime }_{13} {a}^{\prime }_{23} }&{} {{a}^{\prime }_{12} {a}^{\prime }_{23} +{a}^{\prime }_{13} {a}^{\prime }_{22} }&{} {{a}^{\prime }_{11} {a}^{\prime }_{23} +{a}^{\prime }_{13} {a}^{\prime }_{21} }&{} {{a}^{\prime }_{11} {a}^{\prime }_{22} +{a}^{\prime }_{12} {a}^{\prime }_{21} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {{\sigma }^{\prime \prime }_x } \\ {{\sigma }^{\prime \prime }_y } \\ {{\sigma }^{\prime \prime }_z } \\ {{\tau }^{\prime \prime }_{yz} } \\ {{\tau }^{\prime \prime }_{xz} } \\ {{\tau }^{\prime \prime }_{xy} } \\ \end{array} }} \right\} ,&\end{aligned}$$
(108)
in which
$$\begin{aligned}&{a}^{\prime }_{11} =\frac{1}{2}\left[ {\bar{{1}}\bar{{1}}0} \right] .\left[ {\bar{{1}}\bar{{1}}0} \right] =0,\nonumber \nonumber \\&{a}^{\prime }_{12} =\frac{1}{\sqrt{6}}\left[ {1\bar{{1}}0} \right] .\left[ {\bar{{1}}11} \right] =-\frac{\sqrt{2}}{\sqrt{3}},\nonumber \\&{a}^{\prime }_{13} =\frac{1}{2\sqrt{3}}\left[ {1\bar{{1}}0} \right] .\left[ {\bar{{1}}1\bar{{2}}} \right] =-\frac{1}{\sqrt{3}},\nonumber \\&{a}^{\prime }_{21} =\frac{1}{\sqrt{6}}\left[ {111} \right] .\left[ {\bar{{1}}\bar{{1}}0} \right] =-\frac{\sqrt{2}}{\sqrt{3}},\nonumber \\&{a}^{\prime }_{22} =\frac{1}{3}\left[ {111} \right] .\left[ {\bar{{1}}11} \right] =\frac{1}{3},\nonumber \\&{a}^{\prime }_{23} =\frac{1}{3\sqrt{2}}\left[ {111} \right] .\left[ {\bar{{1}}1\bar{{2}}} \right] =-\frac{\sqrt{2}}{3},\nonumber \\&{a}^{\prime }_{31} =\frac{1}{2\sqrt{3}}\left[ {\bar{{1}}\bar{{1}}2} \right] .\left[ {\bar{{1}}\bar{{1}}0} \right] =\frac{1}{\sqrt{3}},\nonumber \\&{a}^{\prime }_{32} =\frac{1}{3\sqrt{2}}\left[ {\bar{{1}}\bar{{1}}2} \right] .\left[ {\bar{{1}}11} \right] =\frac{\sqrt{2}}{3},\nonumber \\&{a}^{\prime }_{33} =\frac{1}{6}\left[ {\bar{{1}}\bar{{1}}2} \right] .\left[ {\bar{{1}}1\bar{{2}}} \right] =-\frac{2}{3}. \end{aligned}$$
(109)