No Heading
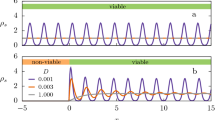
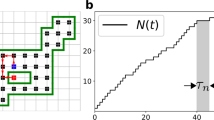
The dynamics of complex systems can be mapped onto trajectories on their energy landscape. The properties of such trajectories as a function of temperature, and thus the chances of the system to enter certain regions of the state space, can be understood in terms of such energy landscapes. Here we show that their kinetic features are of equal importance as the previously discussed energetic and entropic features. Especially for barrier-crossing movements on mountainous landscapes, we observe competing effects between these three aspects, which can lead to surprising inversions in the chances to find certain states such as local minima in the systems.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
1. C. M. Dobson, A. Sali, and M. Karplus, “Protein folding: A perspective from theory and experiment,” Angew. Chem. Int. Ed. 37, 868–893 (1998).
2. P. Salamon, P. Sibani, and R. Frost, “Facts, Conjectures, and Improvements for Simulated Annealing,” Vol. 7 of Monographs on Mathematical Modeling and Computation (SIAM, Philadelphia, 2002).
3. E. J. Corey, “The logic of chemical synthesis multi-step synthesis of complex carbogenic molecules,” Angew. Chem. Int. Ed. 30, 455–465 (1991).
4. D. J. Wales, J. P. K. Doye, M. A. Miller, P. N. Mortenson, and T. R. Walsh, “Energy landscapes: From clusters to biomolecules,” Adv. Chem. Phys. 115, 1–115 (2000).
5. J. C. Schön and M. Jansen, “A first step towards planning of syntheses in solid state chemistry: Determination of promising structure candidates using global optimization,” Angew. Chem. Int. Ed. 35, 1286–1304 (1996).
6. J. C. Schön and P. Sibani, “Properties of the energy landscape of network models for covalent glasses,” J. Phys. A: Math. Gen. 31, 8165–8178 (1998).
7. J. Bryngelson, J. Onuchic, N. Socci, and P. Wolynes, “Funnels, pathways, and the energy landscape of protein folding: A synthesis,” Proteins: Struct. Funcl. Genet. 21, 167–195 (1995).
8. S. Geman and D. Geman, “Stochastic relaxation, Gibbs distribution, and the Bayesian restoration of images,” in IEEE Transanctions on Pattern Analysis and Machine Intelligence PAMI 6 721–741, 1984.
9. J. Schön, “Preferential trapping on energy landscapes in regions containing deep-lying minima the reason for the success of simulated annealing?” J. Phys. A: Math. Gen. 30, 2367–2389 (1997).
10. P. Sibani, J. C. Schön, P. Salamon, and J.-O. Andersson, “Emergent hierarchical structures in complex system dynamics, a phase space analysis of the travelling salesman problem,” Europhys. Lett. 22, 479–485 (1993).
11. J. C. Schön, “Energy landscape of two-dimensional lattice polymers,” J. Phys. Chem. A 106, 10886–10892 (2002).
12. T. Klotz and S. Kobe, “Exact low-energy landscape and relaxation phenomena in Ising spin glasses,” Acta Physica Slovaca 44, 347 (1994).
13. O. Becker and M. Karplus, “The topology of multidimensional potential energy surfaces: Theory and application to peptide structure and kinetics,” J. Chem. Phys. 106, 1495–1517 (1997).
14. K. D. Ball and R. S. Berry, “Realistic master equation modeling of relaxation on complete potential energy surfaces: Partition function models and equilibrium results,” J. Chem. Phys. 109, 8541–8556 (1998).
15. K. D. Ball and R. S. Berry, “Realistic master equation modeling of relaxation on complete potential energy surfaces: Kinetic results,” J. Chem. Phys. 109, 8557–8572 (1998).
16. J. C. Schön, M. A. C. Wevers, and M. Jansen, “Entropically stabilized region on the energy landscape of an ionic solid,” J. Phys.: Condens. Matter 15, 5479–5486 (2003).
17. S. Kobe and J. Krawezyk, “Relationship between energy landscape and low-energy dynamics of |-J spin glasses,” J. Magn. Magn. Matter 272–276, 1284–1285 (2004).
18. K. H. Hoffmann, S. Schubert, and P. Sibani, “Age reinitialization in hierarchical relaxation models for spin-glass dynamics,” Europhys. Lett. 38, 613–618 (1997).
19. A. Heuer, “Properties of a glass-forming system as derived from its potential energy landscape,” Phys. Rev. Lett. 78, 4051–4054 (1997).
20. K. H. Hoffmann and P. Sibani, “Diffusion in hierarchies,” Phys. Rev. A 38, 4261–4270 (1988).
21. F. H. Stillinger and T. A. Weber, “Hidden structure in liquids,” Phys. Rev. A 25, 987–989 (1982).
22. T. Klotz, S. Schubert, and K. H. Hoffmann, “Coarse graining of a spin-glass state space,” J. Phys.: Condens. Matter 10, 6127–6134 (1998).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Hoffmann, K., Schön, J. Kinetic Features of Preferential Trapping on Energy Landscapes. Found Phys Lett 18, 171–182 (2005). https://doi.org/10.1007/s10702-005-3960-8
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10702-005-3960-8