Abstract
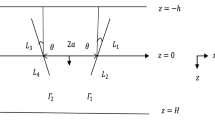
On the basis of linear water-wave theory, an explicit expression is presented for the reflection coefficient R ∞ when a plane wave is obliquely incident upon a semi-infinite porous plate in water of finite depth. The expression, which correctly models the singularity in velocity at the edge of the plate, does not rely on knowledge of any of the complex-valued eigenvalues or corresponding vertical eigenfunctions in the region occupied by the plate. The solution R ∞ is the asymptotic limit of the reflection coefficient R as a → ∞, for a plate of finite length a bounded by a rigid vertical wall, and forms the basis of a rapidly convergent expansion for R over a wide range of values of a. The special case of normal incidence is relevant to the design of submerged wave absorbers in a narrow wave tank. Modifications necessary to account for a finite submerged porous plate in a fluid extending to infinity in both horizontal directions are discussed.
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Wu J, Wan Z, Fang Y (1998) Wave reflection by a vertical wall with a horizontal submerged porous plate. Ocean Eng 25(9): 767–779
Chwang AT, Wu J (1994) Wave scattering by submerged porous disk. J Eng Mech 120(12): 2575–2587
Hassan M, Meylan MH, Peter MA (2009) Water-wave scattering by submerged elastic plates. Q J Mech Appl Math 62(3): 321–344
Porter R, Evans DV (1995) Complementary approximations to wave scattering by vertical barriers. J Fluid Mech 294: 155–180
Linton CM, McIver P (2001) Handbook of mathematical techniques for wave structure interactions. Chapman & Hall/CRC, Boca Raton
McIver P (1998) The dispersion relation and eigenfunction expansions for water waves in a porous structure. J Eng Math 34: 319–334
Heins AE (1950) Water waves over a channel of finite depth with a submerged plane barrier. Can J Math 2: 210–222
Linton CM, Evans DV (1991) Trapped modes above a submerged horizontal plate. Q J Mech Appl Math 44(3): 487–506
Evans DV, Davies TV (1968) Wave–ice interaction. Technical report 1313, Davidson Laboratory, Stevens Institute of Technology, New Jersey
Balmforth NJ (1999) Craster RV Ocean waves and ice sheets. J Fluid Mech 395: 89–124
Tkacheva LA (2004) The diffraction of surface waves by a floating elastic plate at oblique incidence. J Appl Math Mech 68(3): 425–436
Chung H, Fox C (2002) Calculation of wave–ice interaction using the Wiener–Hopf technique. N Z J Math 31: 1–18
Linton CM, Chung H (2003) Reflection and transmission at the ocean/sea-ice boundary. Wave Motion 38(1): 43–52
Evans DV, Peter MA (2009) Reflection of water waves by a submerged horizontal porous plate. In: Korobkin A, Plotnikov P (eds), Proceedings of 24th international workshop on water waves and floating bodies, Zelenogorsk, Russia, pp 82–85
Chwang AT (1983) A porous-wavemaker theory. J Fluid Mech 132: 395–406
Gradshteyn, IS, Ryzhik, IM, Jeffrey, A, Zwillinger, D (eds) (2000) Table of integrals, series, and products, 6 edn. Academic Press, New York
Cho IH, Kim MH (2008) Development of wave absorbing system using an inclined porous plate. In: Choi HS, Kim Y (eds) Proceedings of 23rd international workshop on water waves and floating bodies, Jeju, Korea, pp 25–28
Mittra R, Lee SW (1971) Analytical techniques in the theory of guided waves. Macmillan, New York
Evans DV (1992) Trapped acoustic modes. IMA J Appl Math 49: 45–60
Meylan MH, Gross L (2003) A parallel algorithm to find the zeros of a complex analytic function. ANZIAM J 44(E): E216–E234
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Evans, D.V., Peter, M.A. Asymptotic reflection of linear water waves by submerged horizontal porous plates. J Eng Math 69, 135–154 (2011). https://doi.org/10.1007/s10665-009-9355-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10665-009-9355-2