On the Effect of the Volumetric Deformation in Soft Dielectric Composites with High Phase Contrast

Abstract

Towards the accurate modelling of soft dielectric composites, this investigation aims at demonstrating that the incompressibility constraint customarily adopted in the literature may lead to largely inaccurate predictions. This claim is grounded on the premise that, even though in these composites each phase may individually be assumed to be incompressible, the volumetric deformation of the softest phase can provide a significant contribution to the effective behaviour if the phase contrast is high enough. To reach our goal, we determine the actuation response of two-phase dielectric laminated composites (DLCs) where the softest phase admits volumetric deformation. Our results, discussed in the light of the limit case in which the softest phase consists of vacuum, on the one hand, challenge the hypotheses usually assumed in the modelling of soft dielectric composites and, on the other hand, are expected to provide useful information for the design of high-performance hierarchical DLCs.

1 Introduction

Since the cornerstone contributions to finite deformation hyperelasticity of the fifties (see, e.g., Rivlin and Saunders [1] and references therein), the incompressibility constraint has been often adopted to obtain analytical solutions of relatively simple boundary-value problems, as it may lead to predictions accurately matching experimental data in problems involving homogeneous materials [2–4]. In fact, in typical elastomers the bulk modulus may be four orders of magnitude larger than the Young modulus [5].

After the earlier pivotal works of Toupin [6] and Eringen [7], the more recent efforts of Dorfmann and Ogden [8], McMeeking and Landis [9], Fosdick and Tang [10], and Suo et al. [11] have paved the way for the development of models for soft dielectric materials, where the assumption of isochoric deformation also conveniently applies (see, e.g., the review of Lu et al. [12]), although McMeeking and Landis [9] already provided evidence “that one must be careful when using an incompressible material model”.

Homogeneous soft dielectric materials are characterised by low permittivity, such that their actuation requires an inconvenient large electric field. As experimentally demonstrated (see, e.g, [13, 14]), a way to address this issue consists of designing composite materials that, through the optimisation of their microstructure, allow the enhancement of the electromechanical performance of soft dielectric transducers [15–20]. Certainly, even though incompressibility has been very often assumed for heterogeneous materials as well (in addition to previous references, see also [21] for a purely mechanical study and [22–25] about electroelasticity), in such a case one should be even more careful in evaluating its suitability for the problem at hand. In fact, although all the composite phases may be individually considered as incompressible (i.e., in most cases, they may be assumed to undergo isochoric deformation in boundary-value problems involving only a single homogeneous phase), for high phase contrast in terms of elastic moduli, the volumetric deformation of the softest phase can provide a contribution to the displacement field that is not negligible, being comparable to the contribution due to the deviatoric deformation of the stiffest phase.

Additionally, studying compressible nonlinear electroelasticity has also become important in relation to multiphysics theories for electroactive polymers referred to as ionomer membranes (e.g., Nafion^TM and Flemion^TM), whose actuation and sensing properties depend on the transport of mobile ions in a solvent. The redistribution of these species governs the macroscopic volumetric deformation of the ionomer membrane, which can be described by relying on hyper-electro-elastic models [26–28].

In this investigation, we focus on a two-phase dielectric laminated composite (DLC) actuator [15, 16, 22, 29] in order to demonstrate the enormous impact that considering compressibility may have on the effective response of soft dielectric composites. More specifically, we assume the stiffest dielectric phase to be incompressible, whereas we admit volumetric deformation in the softest dielectric phase. Even under this very specific configuration, we obtain an effective actuation response that is much richer than that predicted for the analogous incompressible DLC, as the compressible response displays a unique multi-branch behaviour featuring two distinct levels of electromechanical instability.

We demonstrate our findings by considering both uncoupled and coupled constitutive laws for the compressible phase [4], and also by analysing in great detail the limit case in which the compressible phase is vacuum. “Porous” dielectric composites have been investigated also by Lopez-Pamies and co-workers in [30] and [31] for microstructures encompassing a matrix phase. In particular, in [30] the dielectric elastomeric matrix contains spherical cavities, while [31] considers vacuum in the form of aligned fibres. Although both these studies are limited to moderate electric fields and small strains and rotations, they allow Lopez-Pamies and co-workers to conclude that vacuum, or extremely soft inclusions, can greatly enhance the electromechanical properties of soft dielectric composites. Our findings for DLCs under finite electric and deformation fields confirm that dielectric composites with high phase contrast are well worth thorough studies, for the understanding of their complex nonlinear behaviour is expected to open the door to interesting novel applications.

Outline In Sect. 2 we provide the equations governing the continuum microelectromechanics of the compressible two-phase DLC actuator under study. In particular, in Sect. 2.1 we provide the balance and compatibility equations to determine the effective response of general compressible two-phase DLCs, whereas in Sect. 2.2 we specify the peculiar constitutive laws here adopted to discuss the effect of compressibility on the actuator effective behaviour. Section 2.3 describes the macroscopic boundary conditions for the actuation problem here of interest and Sect. 2.4 contains analytical manipulations aiding an efficient computation of the effective response. In Sect. 3 we consider the DLC in which the compressible phase is vacuum, referred to as “porous DLC”. This limit case turns out to be very important to shed light on the results obtained for the compressible DLC, which we report in Sect. 4. Section 5 offers our concluding remarks, including some important open issues to address.

2 A Continuum Microelectromechanical Framework for a Compressible Two-Phase DLC Actuator

2.1 Balance and Compatibility for the Homogenisation of a Compressible Two-Phase DLC Actuator

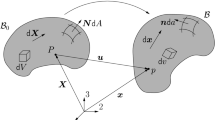
We investigate the DLC actuator whose undeformed configuration $\Omega ={\Omega }_{a}\cup {\Omega }_{b}$ is illustrated in Fig. 1, where ${\Omega }_{a}$ and ${\Omega }_{b}$ are the space regions occupied by the two phases $a$ and $b$, respectively. The DLC is built by filling the space along the longitudinal axis $X_{1}$ with a unit cell constituted by the two phases, both ideally unbounded along the out-of-plane axis $X_{3}$. With reference to hierarchical laminated composites, such a DLC is also denoted as a rank-one DLC [17, 24]. The geometry is characterised by the initial thickness $h_{0}$, the initial phase volume fractions ${c}_{a}$ and ${c}_{b}=1-{c}_{a}$, and the initial lamination angle $\theta _{0}\in [0,\pi /2]$ defining the unit vectors

$$\textbf{m}^{0}=\left [ { \textstyle\begin{array}{c} -\cos {\theta _{0}} \\ -\sin {\theta _{0}} \\ \end{array}\displaystyle } \right ] \quad \text{and}\quad \textbf{n}^{0}= \left [ { \textstyle\begin{array}{c} \sin {\theta _{0}} \\ -\cos {\theta _{0}} \\ \end{array}\displaystyle } \right ] $$

that identify, respectively, the tangential and normal directions to the interfaces between the two constituents.

Fig. 1

Reference configuration of the DLC actuator consisting of incompressible phase $a$ and compressible phase $b$, subjected to a voltage difference $\Delta \phi$ applied across perfectly compliant electrodes. The initial thickness is $h_{0}$ and, according to the positive direction of the out-of-plane axis $X_{3}$, the initial lamination angle $\theta _{0}$ is positive if anticlockwise. Although the boundary conditions refer to the macroscopic scale, where the actuator should appear homogeneous, for the sake of describing the whole problem in a single figure, in this schematic we represent also the microstructure

The crucial aspect of this investigation is that phase $b$ is compressible, while we assume that phase $a$, which is considerably stiffer, undergoes isochoric deformation.

In order to determine the macroscopic response of the composite subjected to an external electromechanical load, we follow a standard homogenisation procedure, initially developed by deBotton [21] for the purely mechanical problem and then extended to electroelasticity (see, e.g., [15–17, 29]). In particular, we study a voltage-driven actuation process and we adopt a Lagrangian formulation, in which all variables are referred to the undeformed configuration. Hence, as primal variables to describe the effective constitutive behaviour of the DLC, we select the nominal electric field $\textbf{E}$ and the deformation gradient

$$\textbf{F}={\frac{\partial \textbf{x}}{\partial \textbf{X}}}\, , $$

where $\textbf{x}(\textbf{X})$ is the current position of the macroscopic material point placed at $\textbf{X}$ in the reference configuration. We adopt the simplest possible electrostatic constitutive law such that the macroscopic field work-conjugate to $\textbf{E}$ is the nominal electric displacement $\textbf{D}$, while the field dual to F, which is the nominal (Piola) stress, is denoted as $\textbf{S}$.

We recall that the fields entering the problem can be referred to the current configuration, thus defining the true (or Eulerian) electric field, $\textbf{e}$, the true electric displacement, $\textbf{d}$, and the Cauchy stress, $\boldsymbol{\sigma }$. Their relations to the Lagrangian quantities read [8]

$$ \textbf{e}=\textbf{F}^{\mathrm{-T}}\textbf{E}\, , $$

(1a)

$$ \textbf{d}=J^{-1}\textbf{F}\textbf{D}\, , $$

(1b)

$$ \boldsymbol{\sigma }=J^{-1}\textbf{S}\textbf{F}^{\mathrm{T}}\, , $$

(1c)

in which

$$ J=\det {\textbf{F}}$$

is the volume ratio. The corresponding microscopic fields are indicated with subscripts $a$ and $b$, depending on the phase where they are evaluated.

We assume a spatially uniform response in each phase [21, 22, 24], such that the macroscopic fields can be expressed as the weighed sums of the corresponding microscopic quantities:

$$ \textbf{F}={c}_{a}{\textbf{F}}_{a}+{c}_{b}{\textbf{F}}_{b}\, , $$

(2a)

$$ \textbf{E}={c}_{a}{\textbf{E}}_{a}+{c}_{b}{\textbf{E}}_{b}\, , $$

(2b)

$$ \textbf{S}={c}_{a}{\textbf{S}}_{a}+{c}_{b}{\textbf{S}}_{b}\, , $$

(2c)

$$ \textbf{D}={c}_{a}{\textbf{D}}_{a}+{c}_{b}{\textbf{D}}_{b}\, . $$

(2d)

Moreover, the following continuity conditions hold at internal interfaces [8, 21]:

$$ ({\textbf{F}}_{a}-{\textbf{F}}_{b})\textbf{m}^{0}=\textbf{0}\, , $$

(3a)

$$ ({\textbf{S}}_{a}-{\textbf{S}}_{b})\textbf{n}^{0}=\textbf{0}\, , $$

(3b)

$$ ({\textbf{D}}_{a}-{\textbf{D}}_{b})\cdot \textbf{n}^{0}=0\, , $$

(3c)

$$ \textbf{n}^{0}\times ({\textbf{E}}_{a}-{\textbf{E}}_{b})=\textbf{0}\, , $$

(3d)

where ⋅ and × denote the inner and vector products, respectively. The continuity of the displacement field at the interfaces, which is expressed in Eq. (3a) in terms of the microscopic deformation gradient, may be rewritten as [21]

$$ {\textbf{F}}_{a}-{\textbf{F}}_{b}=\textbf{w}\otimes \textbf{n}^{0}\, , $$

(4)

where

$$ \textbf{w}=({\textbf{F}}_{a}-{\textbf{F}}_{b})\textbf{n}^{0}$$

is referred to as the amplitude vector and ⊗ denotes the tensor product. It is convenient to further manipulate Eq. (4) to obtain

$$ {\textbf{F}}_{a}-{\textbf{F}}_{b}=\textbf{F}\boldsymbol{\omega }\otimes \textbf{n}^{0} $$

(5)

in terms of the unknown vector

$$ \boldsymbol{\omega }=\textbf{F}^{-1}\textbf{w}\, . $$

Since only phase $a$ is constrained to undergo isochoric deformation, such as ${J}_{a}=1$, the macroscopic volume ratio reads

$$ J={c}_{a}+{c}_{b}{J}_{b}\, . $$

This noticeably implies that $\boldsymbol{\omega }$ is not necessarily coaxial with $\textbf{m}^{0}$, contrary to the case of incompressible laminates, where the possibility of enforcing isochoric micro- and macro-deformation allows the reduction of the vectorial unknown $\boldsymbol{\omega }$ to a single scalar unknown [21, 24, 29].

Combination of Eqs. (2a) and (5) leads to the following expressions for the microscopic deformation gradients:

$$ {\textbf{F}}_{a}=\textbf{F}(\textbf{I}+{c}_{b}\boldsymbol{\omega }\otimes \textbf{n}^{0})\, , $$

(6a)

$$ {\textbf{F}}_{b}=\textbf{F}(\textbf{I}-{c}_{a}\boldsymbol{\omega }\otimes \textbf{n}^{0})\, , $$

(6b)

where $\textbf{I}$ is the second-order identity tensor.

By using relation (2b), we rewrite condition (3d) in terms of the unknown scalar $\beta$ [21, 22, 24], thus obtaining

$$ {\textbf{E}}_{a}=\textbf{E}+{c}_{b}\beta \,\textbf{n}^{0}\, , $$

(7a)

$$ {\textbf{E}}_{b}=\textbf{E}-{c}_{a}\beta \,\textbf{n}^{0}\, . $$

(7b)

Finally, note that assuming spatially uniform microscopic fields implies that the interface remains planar during deformation and the current unit vectors defining its tangential and normal directions can be written in terms of the macroscopic deformation gradient:

$$ \textbf{m}={ \frac{\textbf{F}\textbf{m}^{0} }{|\textbf{F}\textbf{m}^{0}|}}=\left [ { \textstyle\begin{array}{c} -\cos {\theta } \\ -\sin {\theta } \\ \end{array}\displaystyle } \right ] \quad \text{and}\quad \textbf{n}= { \frac{\textbf{F}^{\mathrm{-T}}\textbf{n}^{0} }{|\textbf{F}^{\mathrm{-T}}\textbf{n}^{0}|}}= \left [ { \textstyle\begin{array}{c} \sin {\theta } \\ -\cos {\theta } \\ \end{array}\displaystyle } \right ]\, , $$

(8)

where $\theta$ is the current lamination angle, which determines the evolution of the DLC anisotropy.

2.2 Local Constitutive Prescriptions

We assume hyper-electro-elastic behaviour obtained by combining neo-Hookean hyperelasticity and ideal dielectricity, whereby the Helmholtz free-energy density depends on the invariants ${\mathrm{tr}}\textbf{C}\equiv \textbf{F}\cdot \textbf{F}$ and $|\textbf{F}^{\mathrm{-T}}\textbf{E}|$, along with $J$ for the compressible phase. Here and henceforth, ${\mathrm{tr}}$ is the operator providing the trace of a second-order tensor, $\textbf{C} =\textbf{F}^{\mathrm{T}}\textbf{F}$ indicates the right Cauchy-Green deformation tensor, and $|\textbf{A}|\equiv \sqrt{\textbf{A}\cdot \textbf{A}}$ denotes the modulus of $\textbf{A}$.

In particular, the following free-energy density governs the isotropic behaviour of the incompressible phase $a$:

$$ {W}_{a}({\textbf{F}}_{a},{\textbf{E}}_{a})= \textstyle\begin{cases} \displaystyle {\frac{{\mu }_{a}}{2}}\left ({\mathrm{tr}}{\textbf{C}}_{a}-3 \right )-\displaystyle {\frac{{\epsilon }_{a}}{2}}|{\textbf{F}}_{a}^{ \mathrm{-T}}{\textbf{E}}_{a}|^{2} & \text{if}\ \ \ {J}_{a}=1 \\ +\infty & \text{if}\ \ \ {J}_{a}\ne 1 \end{cases}\displaystyle \, , $$

(9)

where ${\mu }_{a}$ is the shear modulus and ${\epsilon }_{a}$ is the dielectric permittivity.

To reach our goal (that is, the discussion of the effect of accounting for the volumetric deformation in soft dielectric composites), it is crucial that for phase $b$ we select a free-energy density that admits to be written as the sum of two separate terms for its contributions due to the deviatoric and volumetric deformations. In the literature, this type of potential is briefly referred to as uncoupled energy.

Hence, in this investigation, we mainly make use of the following isotropic energy, in which the deviatoric and volumetric deformations are controlled by the shear modulus ${\mu }_{b}$ and the bulk modulus ${K}_{b}$, respectively (see Holzapfel [32] and Saccomandi [33]):

$$ {W}_{b}({\textbf{F}}_{b},{\textbf{E}}_{b})=\frac{{\mu }_{b}}{2}\left ( \frac{{\mathrm{tr}}{\textbf{C}}_{b}}{{J}_{b}^{2/3}}-3\right )+ \frac{{K}_{b}}{2}\left (\frac{{J}_{b}^{2}-1}{2}-\ln {{J}_{b}}\right )- \frac{{\epsilon }_{b}{J}_{b}}{2}|{\textbf{F}}_{b}^{\mathrm{-T}}{\textbf{E}}_{b}|^{2} \, , $$

(10)

where $J^{-2/3}\textbf{C}$ is the isochoric right Cauchy-Green deformation tensor and ${\epsilon }_{b}$ is the dielectric permittivity of phase $b$. However, our results will be discussed and validated by assuming that phase $b$ either is vacuum or obeys a coupled energy, the latter defined in Sect. 2.2.1.

Although the key parameter in our investigation is the phase contrast expressed in terms of the ratio between the shear modulus of the incompressible phase and the bulk modulus of the softest phase, denoted as

$$ \rho _{K}={\mu }_{a}/{K}_{b}\, , $$

(11)

we will show that the interplay between $\rho _{K}$ and the phase contrast in terms of the shear moduli, i.e.

$$ \rho _{\mu }={\mu }_{a}/{\mu }_{b}\, , $$

(12)

is also important in establishing the actuation response of the compressible DLC.

Additionally, definitions (11) and (12) are such that the ratio of the two parameters measuring the phase contrast provides the ratio between the bulk and shear moduli of phase $b$, in turn determining its Poisson’s ratio through the well-known relations for isotropic materials:

$$ {\nu }_{b} =\frac{3\rho _{\mu }/\rho _{K}-2}{6\rho _{\mu }/\rho _{K}+2}\, , $$

(13)

which can be used for a comparison with the typical quantitative difference between the initial bulk and shear moduli of elastomers (see, e.g., [5, 34]).

The microscopic constitutive relations read (see, e.g., [8, 32] and references therein):

$$ {\textbf{S}}_{a}=\frac{\partial {W}_{a}}{\partial {\textbf{F}}_{a}}-{p}_{a}{ \textbf{F}}_{a}^{\mathrm{-T}}\, , $$

(14a)

$$ {\textbf{S}}_{b}=\frac{\partial {W}_{b}}{\partial {\textbf{F}}_{b}}\, , $$

(14b)

$$ \textbf{D}_{k}=-\frac{\partial W_{k}}{\partial \textbf{E}_{k}} \quad \text{with} \quad k=a,b\, , $$

(14c)

where ${p}_{a}$ is a Lagrangian multiplier representing a hydrostatic pressure, to be determined by imposing equilibrium.

Through combination of Eqs. (9), (10), and (14a)–(14c) we obtain the microscopic stresses

$$ {\textbf{S}}_{a}={\mu }_{a}{\textbf{F}}_{a}-{p}_{a}{\textbf{F}}_{a}^{ \mathrm{-T}}+{\epsilon }_{a}{\textbf{F}}_{a}^{\mathrm{-T}}{\textbf{E}}_{a} \otimes {\textbf{C}}_{a}^{-1}{\textbf{E}}_{a}\, , $$

(15a)

$$\begin{array}{c}{\mathbf{\text{S}}}_b=\frac{{\mu }_b}{J_b^{2/3}}({\mathbf{\text{F}}}_b-\frac{\mathrm{tr}{\mathbf{\text{C}}}_b}{3}{\mathbf{\text{F}}}_b^{-\mathrm{T}})+\frac{K_b}{2}(J_b^2-1){\mathbf{\text{F}}}_b^{-\mathrm{T}}\hfill \\ \hfill +{ϵ}_b{J}_b{\mathbf{\text{F}}}_b^{-\mathrm{T}}{\mathbf{\text{E}}}_b\otimes {\mathbf{\text{C}}}_b^{-1}{\mathbf{\text{E}}}_b-\frac{{ϵ}_b{J}_b}{2}{|{\mathbf{\text{F}}}_b^{-\mathrm{T}}{\mathbf{\text{E}}}_b|}^2{\mathbf{\text{F}}}_b^{-\mathrm{T}}\end{array}$$

(15b)

and the microscopic electric displacements

$$ {\textbf{D}}_{a}={\epsilon }_{a}{\textbf{C}}_{a}^{-1}{\textbf{E}}_{a}\, , $$

(16a)

$$ {\textbf{D}}_{b}={\epsilon }_{b}{J}_{b}{\textbf{C}}_{b}^{-1}{\textbf{E}}_{b} \, . $$

(16b)

Substitution of Eq. (15b) into Eq. (1c) readily shows that the volume ratio dependence in the selected free energy (10) leads to a hydrostatic component of the mechanical contribution to the Cauchy stress that is proportional to ${J}_{b}-(1/{J}_{b})$.

2.2.1 A Coupled Free-Energy Density for the Compressible Phase

We will validate our findings based on the free energy (10) by also employing for the compressible phase $b$ a coupled potential, whose use has two purposes. First, obtaining similar results with two significantly different free-energy densities for the compressible phase will allow us to infer that, qualitatively, our findings are somewhat general. Second, it is known that uncoupled energies, such as that in Eq. (10), may be inaccurate in the description of the large volumetric deformation behaviour of elastomers (see, e.g., Boyce and Arruda [4]).

Hence, for phase $b$, we also consider the following potential, whose mechanical part corresponds to the proposal of Blatz and Ko [35] in which the dependence on the (second) invariant $[({\mathrm{tr}}\textbf{C})^{2}-{\mathrm{tr}}(\textbf{C}^{2})]/2$ is neglected [36]:

$$ {W}_{b}({\textbf{F}}_{b},{\textbf{E}}_{b})= \frac{{\mu }_{b}}{2}\left ({ \mathrm{tr}}{\textbf{C}}_{b}-3\right ) +\frac{{\mu }_{b}}{2{\gamma }_{b}} \left ({J}_{b}^{-2{\gamma }_{b}}-1\right ) - \frac{{\epsilon }_{b}{J}_{b}}{2}|{\textbf{F}}_{b}^{\mathrm{-T}}{\textbf{E}}_{b}|^{2} \, . $$

(17)

Here, by assuming isotropy, ${\gamma }_{b}$ is a material parameter that can be expressed in terms of the Poisson’s ratio (13) as

$$ {\gamma }_{b}=\frac{{\nu }_{b}}{1-2{\nu }_{b}}={ \frac{{K}_{b}}{2 {\mu }_{b}}}-{\frac{1}{3}}={ \frac{\rho _{\mu }}{2 \rho _{K}}}-{\frac{1}{3}}\, , $$

(18)

in which we have employed definitions (11) and (12) to express ${\gamma }_{b}$ in terms of the phase contrast.

Given the potential (17), the stress in phase $b$ reads

$$ {\textbf{S}}_{b}={\mu }_{b}\left ({\textbf{F}}_{b}-{J}_{b}^{-2{\gamma }_{b}}{ \textbf{F}}_{b}^{\mathrm{-T}}\right ) +{\epsilon }_{b}{J}_{b}{\textbf{F}}_{b}^{ \mathrm{-T}}{\textbf{E}}_{b}\otimes {\textbf{C}}_{b}^{-1}{\textbf{E}}_{b}- \frac{{\epsilon }_{b}{J}_{b}}{2}|{\textbf{F}}_{b}^{\mathrm{-T}}{\textbf{E}}_{b}|^{2}{ \textbf{F}}_{b}^{\mathrm{-T}}\, , $$

such that, through Eq. (1c), we obtain the mechanical contribution to the Cauchy stress as the sum of two terms both involving the volumetric deformation: ${\mu }_{b}({\textbf{F}}_{b}{\textbf{F}}_{b}^{\mathrm{T}} - {J}_{b}^{-2{ \gamma }_{b}}\textbf{I})/{J}_{b}$.

2.3 Macroscopic Boundary Conditions

We focus on plane-strain conditions and, due to the very small ratio between the thickness $h_{0}$ and the actuator length, we disregard edge effects at the actuator ends, thus assuming that the macroscopic electric field $\textbf{E}$ uniformly acts along the transverse direction $X_{2}$ (see Fig. 1). This implies

$$ {\mathrm{E}}_{1}=0\, , $$

(19)

whereas we apply

$$ {\mathrm{E}}_{2}=\frac{\Delta \phi }{h_{0}}\, , $$

(20)

in which $\Delta \phi$ is the voltage drop across the electrodes. It is however convenient to express the results in terms of the nondimensional electric field

$$ \bar{\mathrm{E}}_{2}={\mathrm{E}}_{2}\sqrt{{\epsilon }_{a}/{\mu }_{a}}\, . $$

We remark that the longitudinal component of the macroscopic electric displacement ${\mathrm{D}}_{1}$ is in general non-vanishing due to the effective dielectric anisotropy of the laminated composite.

In this first contribution towards assessing the role of compressibility in soft dielectric composites, we follow [22, 29, 37] and assume that macroscopic shear deformations are hampered such that the macroscopic deformation gradient depends on the macroscopic free stretches $\lambda _{1}$ and $\lambda _{2}$ only:

$$ \textbf{F}= \left [ { \textstyle\begin{array}{c@{\quad }c@{\quad }c} \lambda _{1} & 0 & 0 \\ 0 & \lambda _{2} & 0 \\ 0 & 0 & 1 \\ \end{array}\displaystyle } \right ]\, . $$

(21)

Correspondingly, the following effective direct stress components vanish

$$ {\mathrm{S}}_{11}=0\, , $$

(22a)

$$ {\mathrm{S}}_{22}=0\, , $$

(22b)

while, in general, ${\mathrm{S}}_{12}\neq 0$. In concluding the paper in Sect. 5 we will briefly discuss possible outcomes of more general boundary conditions.

By combining Eqs. (8) and (21), we obtain the current lamination angle as a function of the macroscopic principal stretches and the initial lamination angle:

$$ \theta = \arctan \left (\frac{\lambda _{2}}{\lambda _{1}}\tan \theta _{0} \right )\, . $$

(23)

Next, we find analytical expressions for the localisation parameters that turn out to be useful for the efficient numerical computation of the effective behaviour under investigation.

2.4 Analytical Simplification of the Solving System with Focus on the Localisation Parameters

Here, we analytically manipulate the foregoing governing equations to obtain convenient expressions for the localisation parameters $\boldsymbol{\omega }$ and $\beta$ entering the homogenisation problem through Eq. (6a)–(6b) for the deformation gradient and Eq. (7a)–(7b) for the nominal electric field, respectively. Note that under plane strain the relevant components of $\boldsymbol{\omega }$ are $\omega _{1}$ and $\omega _{2}$.

By substituting Eqs. (16a) and (16b) in condition (3c), $\beta$ assumes the following form:

$$ \beta = \frac{\left [{\epsilon }_{b}{J}_{b}B(\boldsymbol{\omega })-{\epsilon }_{a}C(\boldsymbol{\omega })\right ]B(\boldsymbol{\omega })C(\boldsymbol{\omega })}{{c}_{b}{\epsilon }_{a}C^{2}(\boldsymbol{\omega })+{c}_{a}\epsilon _{0}{J}_{b}B^{2}(\boldsymbol{\omega })} \ \frac{\textbf{F}^{\mathrm{-T}}\textbf{E}\cdot (\textbf{F}^{\mathrm{-T}}\textbf{n}^{0})}{|\textbf{F}^{\mathrm{-T}}\textbf{n}^{0}|^{2}}+ \textbf{E}\cdot \boldsymbol{\omega }\, , $$

(24)

where

$$ B(\boldsymbol{\omega })=1+{c}_{b}\boldsymbol{\omega }\cdot \textbf{n}^{0} \quad \text{and}\quad C(\boldsymbol{\omega })=1-{c}_{a}\boldsymbol{\omega }\cdot \textbf{n}^{0}\, . $$

We note that, by setting ${J}_{b}=1$ and $\boldsymbol{\omega }=\alpha \textbf{m}^{0}$, with $\alpha$ denoting an unknown scalar, Eq. (24) can be particularised to the analogous expression obtained in [29] for an incompressible DLC.

By focusing on the free energy (10) for the compressible phase, to determine $\omega _{1}$ and $\omega _{2}$, we substitute Eqs. (15a)–(15b) and (24) into Eq. (3b); then, we take the inner products between the left-hand side of the obtained relation and $\textbf{F}\textbf{m}^{0}$ and $\textbf{F}^{\mathrm{-T}}\textbf{n}^{0}$, which, respectively, leads to

$$ \textbf{F}\boldsymbol{\omega }\cdot (\textbf{F}\textbf{m}^{0})=- \frac{{\mu }_{a}{J}_{b}^{2/3}-{\mu }_{b}}{{c}_{b}{\mu }_{a}{J}_{b}^{2/3}+{c}_{a}{\mu }_{b}} \textbf{F}\textbf{n}^{0}\cdot (\textbf{F}\textbf{m}^{0}) $$

(25a)

and

$$\begin{array}{c}{\mu }_{a}B(\mathit{\omega })-\frac{{\mu }_b}{J_b^{2/3}}C(\mathit{\omega })+{[{\mathbf{\text{F}}}^{-\mathrm{T}}\mathbf{\text{E}}\cdot ({\mathbf{\text{F}}}^{-\mathrm{T}}{\mathbf{\text{n}}}^0)]}^2\frac{{ϵ}_a{ϵ}_b{J}_b[{ϵ}_b{J}_{b}B(\mathit{\omega })-{ϵ}_{a}C(\mathit{\omega })]}{{[c_b{ϵ}_a{C}^2(\mathit{\omega })+c_a{ϵ}_b{J}_b{B}^2(\mathit{\omega })]}^2}\hfill \\ \hfill +{|{\mathbf{\text{F}}}^{-\mathrm{T}}{\mathbf{\text{n}}}^0|}^2(\frac{{ϵ}_b{J}_b}{2C(\mathit{\omega })}{|{\mathbf{\text{F}}}_b^{-\mathrm{T}}{\mathbf{\text{E}}}_b|}^2-\frac{p_a}{B(\mathit{\omega })}-\frac{K_b(J_b^2-1)}{2C(\mathit{\omega })}+\frac{{\mu }_b\mathrm{tr}{\mathbf{\text{C}}}_b}{3J_b^{2/3}C(\mathit{\omega })})=0.\end{array}$$

(25b)

The unknown pressure ${p}_{a}$ in Eq. (25b) can be determined by imposing the macroscopic boundary condition (22b). Then, Eqs. (25a) and (25b) can be solved by coupling them with the constraint $\det {\textbf{F}_{a}} = 1$ and the macroscopic boundary condition (22a). This algebraic system allows us to compute the actuation stretches, $\lambda _{1}$ and $\lambda _{2}$, along with the localisation parameters, $\omega _{1}$ and $\omega _{2}$.

3 Effective Response of a “Porous DLC”

Here, we study the behaviour of the DLC actuator in which the compressible phase $b$ is just vacuum.

3.1 Influence of the Vacuum Phase on the Governing Equations

The (spatially uniform) deformation gradient ${\textbf{F}}_{b}$ of the vacuum phase is defined in terms of the displacement field at the interface between the solid phase $a$ and the vacuum, that is

$$ {\textbf{F}}_{b}=\frac{1}{|{\Omega }_{b}|}\int _{\partial {\Omega }_{b}} \textbf{x} \otimes \textbf{n}^{0}\text{d}A\, , $$

where $\partial {\Omega }_{b}$ and $|{\Omega }_{b}|$ respectively indicate the undeformed boundary and the initial volume of the space region occupied by the vacuum phase and, here, $\textbf{n}^{0}$ points outward ${\Omega }_{b}$.

In the “porous DLC”, the three mechanical stress components in the vacuum are zero, such that, on the one hand, we have three less unknowns. On the other hand, we have two less conditions, because Eq. (3a) on the continuity of the microscopic displacement at the interfaces does not play any role. Hence, this might seem to be an ill-posed problem, and this might be ascribed to the strong assumption of spatially uniform microscopic fields. This notwithstanding, we will demonstrate its usefulness in interpreting the results of the compressible DLC: this is the case because, as shown below, once the electric field is applied, the vacuum phase suddenly changes its volume in such a way that all the governing equations can be satisfied.

In the vacuum, only electrostatics contributes to the free-energy density, such that both Eqs. (10) and (17) particularise to

$$ {W}_{b}=-\frac{\epsilon _{0}{J}_{b}}{2}|{\textbf{F}}_{b}^{\mathrm{-T}}{ \textbf{E}}_{b}|^{2}\, , $$

(26)

where $\epsilon _{0}=8.85\times 10^{-12}$ F/m is the vacuum permittivity. When dealing with “porous DLCs”, we denote the relative permittivity of phase $a$ simply as

$$ \epsilon _{r}={\epsilon }_{a}/\epsilon _{0}\, . $$

(27)

By combining Eqs. (26), (14b), and (14c) we determine the stress and the electric displacement in the vacuum, which read

$$ {\textbf{S}}_{b}=\epsilon _{0}{J}_{b}({\textbf{F}}_{b}^{\mathrm{-T}}{ \textbf{E}}_{b}\otimes {\textbf{C}}_{b}^{-1}{\textbf{E}}_{b})- \frac{\epsilon _{0}{J}_{b}}{2}|{\textbf{F}}_{b}^{\mathrm{-T}}{\textbf{E}}_{b}|^{2}{ \textbf{F}}_{b}^{\mathrm{-T}} $$

(28a)

and

$$ {\textbf{D}}_{b}=\epsilon _{0}{J}_{b}{\textbf{C}}_{b}^{-1}{\textbf{E}}_{b} \, . $$

(28b)

By applying transformation (1c) to Eq. (28a), and accounting for Eq. (1a), we obtain the Cauchy stress tensor in the vacuum due to the Eulerian electric field in the absence of magnetism, that is the Maxwell stress

$$ {\boldsymbol{\sigma }}_{b}=\epsilon _{0}\Bigl({\textbf{e}}_{b}\otimes { \textbf{e}}_{b} -\frac{1}{2}|{\textbf{e}}_{b}|^{2}\textbf{I}\Bigr)\, . $$

(29)

By following Sect. 2.4, we determine the expressions of the localisation parameters. It turns out that $\beta$ reads as in Eq. (24), except that the permittivity ${\epsilon }_{b}$ is substituted by $\epsilon _{0}$, while relations (25a) and (25b) for $\boldsymbol{\omega }$ can be simplified into

$$ \textbf{F}\boldsymbol{\omega }\cdot (\textbf{F}\textbf{m}^{0})=-\frac{1}{{c}_{b}} \textbf{F}\textbf{n}^{0}\cdot (\textbf{F}\textbf{m}^{0})\quad \Rightarrow \quad \textbf{C}\boldsymbol{\omega }\cdot \textbf{m}^{0}=- \frac{1}{{c}_{b}}\textbf{C}\textbf{n}^{0}\cdot \textbf{m}^{0} $$

(30)

and

$$\begin{array}{c}{\mu }_{a}B(\mathit{\omega })+{|{\mathbf{\text{F}}}^{-\mathrm{T}}{\mathbf{\text{n}}}^0|}^2(\frac{{ϵ}_0{J}_b}{2C(\mathit{\omega })}{|{\mathbf{\text{F}}}_b^{-\mathrm{T}}{\mathbf{\text{E}}}_b|}^2-\frac{p_a}{B(\mathit{\omega })})\hfill \\ \hfill +{[{\mathbf{\text{F}}}^{-\mathrm{T}}\mathbf{\text{E}}\cdot ({\mathbf{\text{F}}}^{-\mathrm{T}}{\mathbf{\text{n}}}^0)]}^2\frac{{ϵ}_a{J}_b[J_{b}B(\mathit{\omega })-{ϵ}_{r}C(\mathit{\omega })]}{{[c_b{ϵ}_r{C}^2(\mathit{\omega })+c_a{J}_b{B}^2(\mathit{\omega })]}^2}=0.\end{array}$$

(30)

3.2 Effective Actuation Response of the “Porous DLC”: Results, Analysis, and Discussion

3.2.1 General Features of the “Porous DLC” Actuation

By referring to the macroscopic boundary conditions illustrated in Sect. 2.3, we apply an increasing voltage across the electrodes. We initially set the volume fraction of the vacuum phase ${c}_{b}=0.1$, the contrast on electric permittivities of the two phases $\epsilon _{r} =10$, and the lamination angle $\theta _{0}=3\pi /8$. We will clarify the reason for choosing such an angle in the analysis of Sect. 3.2.2 and will explore different values of $\theta _{0}$ and $\epsilon _{r}$ in Sect. 3.2.3. Here and henceforth, the numerical results are obtained by solving the equations presented in Sects. 2 and 3.1 through the commercial software Mathematica^® (Wolfram Research, Inc.).

Figure 2 displays the actuation response in terms of the longitudinal stretch $\lambda _{1}$ as a function of $\bar{\mathrm{E}}_{2}$, along with drawings of three relevant stages of deformation, labelled with capital letters B to D on the red curve, the letter A identifying the undeformed configuration. These drawings refer to a single unit cell of the laminate, where phases $a$ and $b$ are coloured in red and blue, respectively. The change of curve style from continuous to dashed indicates the switch from $\bar{\mathrm{E}}_{2}$-controlled to $\lambda _{1}$-controlled analysis, needed because of the presence of a maximum in the $\bar{\mathrm{E}}_{2}(\lambda _{1})$ function. ¹ As a reference, the dotted black curve in Fig. 2 provides the prediction computed by using the Spinelli and Lopez-Pamies [22] analytical form of the effective energy density for two-phase incompressible neo-Hookean DLCs, in which we numerically set ${\mu }_{b}\to 0$ to mimic the vacuum phase, although such phase may not admit volumetric deformation in the analytical solution presented in [22]. The fact that, within this layout, the incompressibility constraint leads to a larger actuation is counterintuitive and should be ascribed to the non-trivial deformation path followed by the unconstrained vacuum phase, as described below.

Fig. 2

Actuation response and relevant deformation stages of the “porous DLC”, for $\epsilon _{r}=10$, ${c}_{b}=0.1$, and $\theta _{0}=(3/8)\pi$. The change from continuous to dashed curve corresponds to the switch from $\bar{\mathrm{E}}_{2}$-controlled to $\lambda _{1}$-controlled analysis. The dotted curve refers to the analogous DLC where phase $b$ is constrained to be incompressible

The four stages A, B, C, and D subdivide the actuation response in the following three different branches:

• transient branch A-B (dotted line): except for the stages A and B, in this initial branch our algorithm cannot properly satisfy condition (3b) on the continuity of the traction vector at the interfaces, whereby the vacuum phase suddenly reduces its volume. Quasi-statics seems to be unable to properly describe the behaviour of the material until the configuration B is reached, $(\lambda _{1}, \bar{\mathrm{E}}_{2}) \approx (0.973, 0.00025)$, in which all governing equations are satisfied;

• branch B-C: by increasing the potential jump across the electrodes, the laminate elongates in the $X_{1}$ direction while shrinking along the $X_{2}$ axis, until $\bar{\mathrm{E}}_{2}$ reaches a maximum value at C, $(\lambda _{1}, \bar{\mathrm{E}}_{2}^{\mathrm{cr}}) \approx (1.155, 0.459)$, that we ascribe to the onset of a pull-in electromechanical instability. In our numerical simulation almost all of this branch is obtained by applying ${\mathrm{E}}_{2}$. We remark that the electromechanical instability is absent from the response of a homogeneous dielectric material under plane strain, at least for the neo-Hookean energy density (9), such that it represents a peculiar feature of the composite [29];

• ${\lambda }_{1}$-controlled branch C-D: once the critical value $\bar{\mathrm{E}}_{2}^{\mathrm{cr}}=0.459$ is reached, the longitudinal stretch $\lambda _{1}$ can increase up to the limit point D of coordinates $(\lambda _{1}^{\mathrm{max}}, \bar{\mathrm{E}}_{2}) \approx (1.289, 0.335)$, in which the vacuum phase vanishes (that is, ${J}_{b}\to 0$). In the absence of numerical issues preventing us from completing the analysis, the last point of the actuation curves presented in this work always corresponds to the collapse of the vacuum phase. Clearly, this may not happen in the particularisation to “porous DLCs” of the solution of Spinelli and Lopez-Pamies [22] for incompressible DLCs.

Moreover, the results of our numerical simulations, presented in Sect. 3.2.3 and obtained by varying the initial lamination angle and the relative permittivity, indicate that the actuation behaviour of the “porous DLC” is characterised by the two following important features, henceforth referred to as ${\mathcal{F}}_{\mathrm{A}}$ and ${\mathcal{F}}_{\mathrm{B}}$.

${\mathcal{F}}_{\mathrm{A}}$):

At stage B the two direct components of the microscopic Cauchy stress vanish:

$$ \sigma _{a11}=\sigma _{a22}=\sigma _{b11}=\sigma _{b22}=0\, . $$

(31a)

Noticeably, in order to satisfy Eq. (3b), this results in a microscopically uniform Cauchy stress, i.e.

$$ \sigma _{a12}=\sigma _{b12}\, , $$

(31b)

which is obviously identical to the effective Cauchy stress $\sigma _{12}$. The stress state is therefore pure shear throughout the actuator.

Moreover, by combining conditions (30a) with the general form (29) of the Maxwell stress, which is the sole contribution to the stress in phase $b$, we obtain the following condition among the components of the current electric field:

$$ {\mathrm{e}}_{\mathrm{b1}}=-{\mathrm{e}}_{\mathrm{b2}}\, . $$

(32)

Once conditions (30a) and (31) on the local fields are attained at stage B, they are maintained for the whole process (up to stage D), although after B the interface may undergo significant rotation for certain values of the initial lamination angle $\theta _{0}$.

${\mathcal{F}}_{\mathrm{B}}$):

In the transient branch the interface is subject to negligible rotations if $\theta _{0}$ is suitably larger than $\pi /4$, with $\theta _{0}\le \pi /2$.

Next, through a simplified analytical investigation, we focus on the explanation of the behaviour observed in the initial transient branch A-B.

3.2.2 A Simplified Analysis of the Initial Transient

The two foregoing observations ${\mathcal{F}}_{\mathrm{A}}$ and ${\mathcal{F}}_{\mathrm{B}}$ allow us to provide an interpretation of the response in the initial transient reported in Fig. 2 by resorting to the algebraic system constituted by the average condition on the electric field (2b) along with the interface continuity conditions (3c) and (3d) for the electric displacement and the electric field, respectively.

To this purpose, we rewrite such conditions in the current configuration, thus involving the Eulerian quantities $\textbf{d}$ and $\textbf{e}$ (as defined by transformations (1b) and (1a), respectively):

$$ ({\textbf{d}}_{a}-{\textbf{d}}_{b})\cdot \textbf{n}=0\, , $$

(33a)

$$ ({\textbf{e}}_{a}-{\textbf{e}}_{b})\cdot \textbf{m}=0\, , $$

(33b)

$$ {c}_{a}{\textbf{e}}_{a}+{c}_{b}{J}_{b}{\textbf{e}}_{b}=\textbf{e}({c}_{a}+{c}_{b}{J}_{b}) \, , $$

(33c)

where the unit vectors $\textbf{m}$ and $\textbf{n}$ are defined by Eq. (8) in terms of the current lamination angle $\theta$.

By substituting in Eq. (32a) the microscopic electrostatic constitutive laws ${\textbf{d}}_{a}={\epsilon }_{a}{\textbf{e}}_{a}$ and ${\textbf{d}}_{b}=\epsilon _{0}{\textbf{e}}_{b}$, where Eq. (27) holds, and by accounting for ${\mathrm{e}}_{1}=0$, which is due to the macroscopic conditions (19) and (21) and transformation (1a), we obtain the system

$$ \textstyle\begin{cases} \epsilon _{r}{\mathrm{e}}_{\mathrm{a2}}-{\mathrm{e}}_{\mathrm{b2}}+({\mathrm{e}}_{\mathrm{b1}}- \epsilon _{r}{\mathrm{e}}_{\mathrm{a1}})\tan {\theta }=0 \\ {\mathrm{e}}_{\mathrm{a1}}-{\mathrm{e}}_{\mathrm{b1}}+({\mathrm{e}}_{\mathrm{a2}}-{\mathrm{e}}_{\mathrm{b2}}) \tan {\theta }=0 \\ {c}_{a}{\mathrm{e}}_{\mathrm{a1}}+{c}_{b}{J}_{b}{\mathrm{e}}_{\mathrm{b1}}=0 \\ {c}_{a}{\mathrm{e}}_{\mathrm{a2}}+{c}_{b}{J}_{b}{\mathrm{e}}_{\mathrm{b2}}={\mathrm{e}}_{2}({c}_{a}+{c}_{b}{J}_{b}) \end{cases}\displaystyle \, . $$

(34)

We, first, consider feature ${\mathcal{F}}_{\mathrm{A}}$ by making use of Eq. (31). Thus, by substituting in the first two equations of system (33) its third equation along with condition (31), we obtain two homogeneous equations that are linear in the same two unknown components of the electric field. Hence, such two equations must be linearly dependent, and this turns out to be equivalent to the condition

$$ \frac{\epsilon _{r}}{\tan {\theta }}= \frac{1+\left (\epsilon _{r} \displaystyle {\frac{{c}_{b}{J}_{b}}{{c}_{a}}} +1\right )\tan {\theta }}{\tan {\theta }-1-\displaystyle {\frac{{c}_{b}{J}_{b}}{{c}_{a}}}} \, , $$

(35)

whose inspection shows that $\theta =\pi /2$ is impossible, and if $\theta \in [0,\pi /2)$, in order to avoid non-positive $\epsilon _{r}$, we have the further condition:

$$ \tan {\theta }>1+\frac{{c}_{b}{J}_{b}}{1-{c}_{b}}\quad \Rightarrow \quad \theta >\frac{\pi }{4}\, . $$

(36)

Hence, assumption (31) may hold for actual lamination angle belonging to the interval

$$ {\frac{\pi }{4}}< \theta < {\frac{\pi }{2}} $$

and this somehow well agrees with our numerical investigations on the fully nonlinear problem that we will present in Sect. 3.2.3, whereby it becomes actually harder to obtain solutions for the initial lamination angle $\theta _{0}$ approaching either $\pi /4$ from above or $\pi /2$ from below.

We now consider feature ${\mathcal{F}}_{\mathrm{B}}$, thus assuming $\theta =\theta _{0}$ in the transient branch A-B (recall that this should hold for $\theta _{0}$ suitably larger than $\pi /4$). This allows the use of Eq. (34) to estimate ${J}_{b}$ at stage B, denoted as ${J}_{b}^{\mathrm{B}}$, when all governing equations are satisfied:

$$ {J}_{b}^{\mathrm{B}} \approx [\epsilon _{r} \tan {\theta _{0}} - (\epsilon _{r}+ \tan {\theta _{0}}+ \tan ^{2}{\theta _{0}} )] { \frac{1-{c}_{b}}{{c}_{b}\epsilon _{r}(1+\tan ^{2}{\theta _{0}})}}\, . $$

(36)

This estimate, relying also on the conditions (30a), says that, in order to ensure ${J}_{b}>0$, one should have

$$ \epsilon _{r} > {\frac{1+ \tan {\theta _{0}}}{1-\cot {\theta _{0}}}}\, , $$

(37)

which provides an interesting constraint on the relative permittivity of phase $a$ as a function of the lamination angle only, given its independence from the vacuum volume fraction. In fact, Eq. (36) can be conveniently discussed by selecting a positive value of $\epsilon _{r}$, thus bringing to the conclusion that the lamination angle needs to be suitably larger than $\pi /4$ and suitably smaller than $\pi /2$. Violating constraint (36) would lead to the collapse of the vacuum phase within the transient branch A-B, thus hampering, in our model that disregards contact between interfaces initially separated by vacuum, the attainment of a configuration where all the governing equations are satisfied.

Moreover, from Eq. (35) we deduce that, for large enough $\epsilon _{r}$, the vacuum phase enlarges, instead of shrinking as for the case illustrated in Fig. 2. By imposing that the right-hand side of Eq. (35) is larger than 1, we estimate that this happens under the two following conditions: the lamination angle should be such that

$$ f(\theta _{0},{c}_{b})\equiv \tan {\theta _{0}}- 1-{ \frac{{c}_{b}(1+\tan ^{2}{\theta _{0}})}{1-{c}_{b}}}>0 $$

(38)

and the relative permittivity should satisfy

$$ \epsilon _{r} > (\tan {\theta _{0}}+ \tan ^{2}{\theta _{0}})/f(\theta _{0},{c}_{b}) \, . $$

(39)

Differently from constraint (36), conditions (37) and (38) depend on the vacuum volume fraction. In general, the larger ${c}_{b}$, the smaller the $\epsilon _{r}$ required to avoid transient shrinkage. However, for a given $\theta _{0}$, ${c}_{b}$ is limited by the constraint (37), providing

$${c}_{b} < {\frac{1-\cot {\theta _{0}}}{1+ \tan {\theta _{0}}}}\, , $$

(40)

which states that, to avoid transient shrinkage, there should be no vacuum phase (${c}_{b}=0$) for both $\theta _{0}=\pi /4$ and $\theta _{0}=\pi /2$, while the maximum allowed value of ${c}_{b}$ is $3-2\sqrt{2}\approx 0.1716$ (requiring, however, $\epsilon _{r}\to \infty$ because of Eq. (36)), being attained at

$$ \theta _{0} = \frac{3}{8}\pi \, . $$

Noticeably, this value of $\theta _{0}$ maximises ${J}_{b}^{\mathrm{B}}$ independently of both $\epsilon _{r}$ and ${c}_{b}$, also being the value where the function at the right-hand side of Eq. (36) attains its minimum, thus indicating that $\epsilon _{r}$ may not be lower than $3+2\sqrt{2}\approx 5.82843$.

Moreover, the right-hand side of Eq. (38) provides an estimate for the watershed between shrinkage and expansion within the transient. For ${c}_{b}=0.1$ and $\theta _{0} = 3\pi /8$, we obtain $\epsilon _{r}\approx 12.5746$.

By imposing the equality between the left-hand and right-hand sides of Eq. (38), we can compute the vacuum volume fraction to be interpreted as an estimate for the volume fraction that the vacuum assumes at the end of the initial transient (stage B in Fig. 2). For this quantity we adopt the symbol ${c}_{b}^{\mathrm{B}}$ and obtain

$$ {c}_{b}^{\mathrm{B}} = 1 + { \frac{\epsilon _{r}(1-\cot {\theta _{0}})}{(\epsilon _{r}-1)\cos {(2\theta _{0})}}} \, . $$

(40)

We observe that Eq. (39) can also be solved to obtain the range of admissible $\theta _{0}$, by imposing that $0<{c}_{b}^{\mathrm{B}}<1$. For instance, by selecting $\epsilon _{r}=10$, we obtain $52^{\circ}.4<\theta _{0}<82^{\circ}.6$.

Additionally, once ${c}_{b}^{\mathrm{B}}$ is known from Eq. (39), straightforward arguments lead to the estimate of the volume ratio of the vacuum phase at stage B, which reads

$$ {J}_{b}^{\mathrm{B}}={ \frac{{c}_{a}{c}_{b}^{\mathrm{B}}}{{c}_{b}(1-{c}_{b}^{\mathrm{B}})}}\, . $$

(41)

Of course, by substituting Eq. (39) into Eq. (40) one can exactly obtain the right-hand side of Eq. (35).

It is interesting to observe that the foregoing analysis, along with the fundamental feature ${\mathcal{F}}_{\mathrm{A}}$, is fully confirmed by the exact solution of the electroelastic actuation problem in the framework of small strains and rotations. In fact, in this framework there is only a one-way coupling between electrostatics and mechanics [17], whereby electrostatics can be solved first. System (33) particularises to

$$ \textstyle\begin{cases} \epsilon _{r}{\mathrm{E}}_{\mathrm{a2}}-{\mathrm{E}}_{\mathrm{b2}}+({\mathrm{E}}_{\mathrm{b1}}- \epsilon _{r}{\mathrm{E}}_{\mathrm{a1}})\tan {\theta _{0}}=0 \\ {\mathrm{E}}_{\mathrm{a1}}-{\mathrm{E}}_{\mathrm{b1}}+({\mathrm{E}}_{\mathrm{a2}}-{\mathrm{E}}_{\mathrm{b2}}) \tan {\theta _{0}}=0 \\ {c}_{a}{\mathrm{E}}_{\mathrm{a1}}+{c}_{b}{\mathrm{E}}_{\mathrm{b1}}=0 \\ {c}_{a}{\mathrm{E}}_{\mathrm{a2}}+{c}_{b}{\mathrm{E}}_{\mathrm{b2}}={\mathrm{E}}_{2} \end{cases} $$

and can be easily directly solved for the four components of the microscopic electric fields. In particular, by setting ${c}_{a}=1-{c}_{b}$, the components of the electric field in the vacuum read

$$ {\mathrm{E}}_{\mathrm{b1}} = -{ \frac{(1-{c}_{b})(\epsilon _{r}-1)\cos (2\theta _{0}) }{2[1+{c}_{b}(\epsilon _{r}-1)]}}{ \mathrm{E}}_{2}\, , $$

(42a)

$$ {\mathrm{E}}_{\mathrm{b2}} = \biggl({ \frac{\epsilon _{r} \cos ^{2}\theta _{0} }{1+{c}_{b}(\epsilon _{r}-1)}}+ \sin ^{2}\theta _{0}\biggr){\mathrm{E}}_{2}\, . $$

(42b)

Then, we can compute the microscopic electrostatic contribution to the stress through

$$ {\boldsymbol{\sigma }}_{a}-{\boldsymbol{\sigma }}_{a}^{\mathrm{mec}} ={\epsilon }_{a}\Bigl({ \textbf{E}}_{a}\otimes {\textbf{E}}_{a}-\frac{1}{2}|{\textbf{E}}_{a}|^{2} \textbf{I}\Bigr) \quad \text{and} \quad {\boldsymbol{\sigma }}_{b}=\epsilon _{0}\Bigl({\textbf{E}}_{b}\otimes { \textbf{E}}_{b}-\frac{1}{2}|{\textbf{E}}_{b}|^{2}\textbf{I}\Bigr)\, , $$

where ${\boldsymbol{\sigma }}_{a}^{\mathrm{mec}}$ is the mechanical stress in phase $a$.

Finally, the remaining unknowns are the three components of ${\boldsymbol{\sigma }}_{a}^{\mathrm{mec}}$. Once they are obtained, through the constitutive law one obtains the strain field in phase $a$, which governs the macroscopic deformation. However, as mentioned above, we have four equations to obtain these last three unknowns. Such equations consist of the continuity of the traction vector at the interfaces (3b) and conditions (22a)–(22b) on the two macroscopic direct stress components, which must vanish. It is however possible to solve this problem by assuming ${c}_{b}$ as a fourth unknown, becoming the volume fraction that the vacuum must assume in order to satisfy all the governing equations, which refers to the stage B in Fig. 2. For such a vacuum volume fraction we obtain exactly Eq. (39). Noticeably, if expression (39) is substituted for ${c}_{b}$ in Eqs. (41a)–(41b) one obtains relation (31), implying conditions (30a)–(30b) on the microscopic stress and confirming our observation, referred to as feature ${\mathcal{F}}_{\mathrm{A}}$, relying on the numerical results obtained by solving the original nonlinear problem.

Clearly, in the framework of small strains and rotations, once the configuration established by Eq. (39), in which the DLC is subject to uniform shear stress only, is “attained”, it remains fixed and one can determine the effective DLC deformation through the strain field in phase $a$. Conversely, in the geometrically nonlinear setting, after this configuration is attained, we can observe a non-trivial evolution of the DLC actuation. Incidentally, it is noteworthy that our implementation of the nonlinear problem can automatically attain this configuration in a relatively small amount of applied electric field.

Next, we further numerically assess the foregoing analysis with two purposes. First, we aim at understanding the behaviour reported in Fig. 2, which is crucial in order to tackle the problem of the compressible DLC dealt with in Sect. 4. Second, we want to establish at which extent the foregoing analysis may be adopted as a criterion to select the key parameters of a “porous DLC”, or even a compressible DLC with extremely high contrast in the elastic moduli.

3.2.3 Numerical Assessment and Discussion

We begin by assessing the estimate provided by the right-hand side of Eq. (38), which gives $\epsilon _{r}\approx 12.5746$ for ${c}_{b}=0.1$ and $\theta _{0} = 3\pi /8$. The complete analysis on the basis of the results of Sect. 3.1 agrees with this estimate as it provides no transient branch at all for $\epsilon _{r}= 12.5746$; more precisely, ${J}_{b}\approx 1.0$ remains almost constant up to $\bar{\mathrm{E}}_{2}\approx 0.03$ and then slightly decreases to ${J}_{b}\approx 0.999975$ at $\bar{\mathrm{E}}_{2}\approx 0.07$. In this case, the peak of the $\bar{\mathrm{E}}_{2}(\lambda _{1})$ curve (that is, the electromechanical instability) is reached at $(\lambda _{1}, \bar{\mathrm{E}}_{2}) \approx (1.183, 0.468)$.

Then, initially for the case $\epsilon _{r}=10$, we investigate the influence of the lamination angle in the actuation response of the composite, by properly selecting $\theta _{0}$ in the open interval $(\pi /4,\pi /2)$. In particular, in Fig. 3 we consider $\theta _{0}=${45^∘,50^∘,60^∘,70^∘,80^∘,81^∘}. We remark that, as displayed in the drawing of the deformation stage E in Fig. 3, for $\theta _{0}=45$^∘ the interface is subject to a significant rotation, so that feature ${\mathcal{F}}_{\mathrm{B}}$ of Sect. 3.2.1 does not hold, as well as the analysis leading to Eqs. (35)–(39). This notwithstanding, the sole non-vanishing Cauchy stress component is still the shear one, which is spatially uniform over the whole DLC. This important feature, referred to as ${\mathcal{F}}_{\mathrm{A}}$ in Sect. 3.2.1, is common to all the lamination angles, volume fractions, and permittivities, and is maintained up to the end of the analysis, always corresponding to collapse of the vacuum phase (${J}_{b}\to 0$). This happens at stage D in Fig. 2 or much earlier, even before reaching the electromechanical instability, for low $\theta _{0}$, as for instance for the cases $\theta _{0}=45^{\circ}$ and $\theta _{0}=50^{\circ}$ in Fig. 3.

Fig. 3

Actuation response of the “porous DLC” for $\epsilon _{r}=10$, ${c}_{b}=0.1$, and variable lamination angle $\theta _{0}$. The stages of deformation E and F correspond to the first equilibrium configuration after the transient branch for $\theta _{0}=$45^∘ and $\theta _{0}=$80^∘, respectively. The change from continuous to dashed curve corresponds to the switch from $\bar{\mathrm{E}}_{2}$-controlled to $\lambda _{1}$-controlled analysis. The red curve is the same as in Fig. 2

For $\theta _{0}=80^{\circ}$, the stage of deformation denoted with F in Fig. 3 shows that the unit cell exhibits negligible rotations, thus confirming feature ${\mathcal{F}}_{\mathrm{B}}$. This is actually common to all $\theta _{0}\ge 3\pi /8$ up to the maximum possible initial lamination angle, whose actual value can be estimated through Eq. (39). Our code cannot solve the problem for $\theta _{0}=82^{\circ} .5$, as in this case the transient ends up with a complete collapse of the vacuum phase, which, in fact, quite well agrees with Eq. (39), establishing that the maximum $\theta _{0}$ for the selected relative permittivity, $\epsilon _{r}=10$, is equal to $\approx 82^{\circ} .6$ (${c}_{b}^{ \mathrm{B}}$ would be negative at larger $\theta _{0}$). For the sake of graphical clarity, Fig. 3 does not display the complete actuation response for large $\theta _{0}$, which we will discuss in detail below for higher relative permittivity.

Back to the cases of “small” initial lamination angle, according to the foregoing observation, Eq. (39) would predict that, in order to avoid ${c}_{b}^{\mathrm{B}}\le 0$, the smallest possible $\theta _{0}$ for $\epsilon _{r}=10$ is $\theta _{0}\approx$ 52.4, which does not actually agree with the results of our fully nonlinear analyses. In fact, the interface rotation allows a different solution to be attained, which is anyway associated with a poor actuation, as is clear from Fig. 3. We obtain totally analogous solutions with initial lamination angle even smaller than $45^{\circ}$ (but, obviously, not significantly smaller than $45^{\circ}$).

Now, in discussing the case $\epsilon _{r}= 20$, we delve into further details. The results in terms of the actuation response for various $\theta _{0}$ are reported in Figs. 4 and 5. In particular, Fig. 4 provides results for both “small” and “large” initial lamination angles along with a comparison with the case $\epsilon _{r}= 10$, while Fig. 5 focuses on the whole actuation response for “large” initial lamination angles. Note that, in this case, Eq. (38) predicts that the possible range of the initial lamination angle approximately is $\theta _{0}\in (48^{\circ} .2,86^{\circ} .8)$.

Fig. 4

Actuation response of the “porous DLC” for $\epsilon _{r}=20$, ${c}_{b}=0.1$, and variable lamination angle $\theta _{0}$. The change from continuous to dashed curve corresponds to the switch from $\bar{\mathrm{E}}_{2}$-controlled to $\lambda _{1}$-controlled analysis. For comparison, the red curve represents the solution for $\epsilon _{r}=10$ and $\theta _{0}=(3/8)\pi \equiv 67^{\circ} .5$, already plotted in Figs. 2 and 3

Fig. 5

Actuation response of the “porous DLC” for $\epsilon _{r}=20$, ${c}_{b}=0.1$, and variable lamination angle $\theta _{0}$. The change from continuous to dashed curve corresponds to the switch from $\bar{\mathrm{E}}_{2}$-controlled to $\lambda _{1}$-controlled analysis

We begin by considering the predictions provided by Eqs. (39) and (40) (or, equivalently, Eq. (35)) for the volume ratio of the vacuum phase at the end of the initial transient. The results are reported in Table 1, where we compare them with our findings from the fully nonlinear analyses, by also reporting the percentage relative error.

Table 1 Volume ratio of the vacuum phase at the end of the initial transient: comparison between the results of the fully nonlinear analyses and the analytical estimate (35)

As expected, for $\theta _{0}=3\pi /8$, we observe an excellent agreement between the predictions, delivering ${c}_{b}^{\mathrm{B}}\approx 0.12797$ and ${J}_{b}^{\mathrm{B}}\approx 1.3208$, and the fully nonlinear analysis, providing ${J}_{b}^{\mathrm{B}}\approx 1.3176$. As $\theta _{0}$ either decreases towards $48^{\circ} .2$ or increases towards $86^{\circ} .8$ the agreement becomes much worse.

As for the case $\epsilon _{r}= 10$, we could not attain solutions up to the electromechanical instability for low initial lamination angle (see the case $\theta _{0}=50^{\circ}$), as the vacuum phase collapses earlier. In very good agreement with Eq. (38), which predicts a maximum possible initial lamination angle $\approx 86^{\circ} .8$, $\theta _{0}=86^{\circ} .4$ is the largest initial lamination angle that we can select in the fully nonlinear analysis in order to avoid that at stage B (that is, at the end of the initial transient) the vacuum phase collapses, thus ending the analysis. For such a large $\theta _{0}$, the actuation performance is noticeable, as the final longitudinal stretch $\lambda _{1}$ goes up to the value 3.577. In general, the actuation response, as expressed in terms of the obtained maximum $\lambda _{1}$, largely improves by increasing the lamination angle towards its maximum value as estimated by Eq. (38). Hence, the criterion adopted to choose $\theta _{0}=3\pi /8$ does not lead to the best actuation performance at all, that is, the best DLC actuation is not that of the actuator minimising the shrinkage (or even maximising the enlargement) of the vacuum phase in the initial transient branch.

Differently from the case $\epsilon _{r}= 10$, in the case $\epsilon _{r}= 20$ the maximum of the $\bar{\mathrm{E}}_{2}(\lambda _{1})$ curve is always attained exactly at the end of the $\bar{\mathrm{E}}_{2}$-controlled analysis. This is further evidenced by the square symbols in Fig. 6, where, for the sake of completeness, we provide the evolution of the (spatially uniform) Cauchy shear stress as a function of the longitudinal stretch.

Fig. 6

Nondimensional Cauchy shear stress in the actuation of the “porous DLC” for ${c}_{b}=0.1$ and variable lamination angle $\theta _{0}$ and relative permittivity $\epsilon _{r}$. The change from continuous to dashed curve corresponds to the switch from $\bar{\mathrm{E}}_{2}$-controlled to $\lambda _{1}$-controlled analysis, while the square symbol indicates the point where the $\bar{\mathrm{E}}_{2}(\lambda _{1})$ curve attains its maximum

4 Effective Response of a Compressible DLC: Results, Validation, and Discussion

On the basis of the analysis for the limit case of the “porous DLC” discussed in Sect. 3, here we finally illustrate the behaviour of the compressible DLC actuator. The results are obtained by implementing the governing equations presented in Sect. 2 in the commercial software Mathematica^® (Wolfram Research, Inc.).

Except when otherwise specified, we will focus on the contrast between the shear moduli (12) equal to

$$ \rho _{\mu }= 3\times 10^{3}\, . $$

(43)

Figures 7 and 8 display the actuator response for not-too-large longitudinal stretch. We provide the response as a function of the bulk modulus ${K}_{b}$ through the ratio (11) measuring the phase contrast. For the sake of understanding, we explore a wide range of this ratio, $\rho _{K}= 1 , 10 , 10^{2} , 10^{3} , 10^{6}$, which, by keeping the parameter (42) fixed, corresponds to Poisson’s ratio values ${\nu }_{b}\approx 0.4998 , 0.4983 , 0.4835 , 0.35 , -0.9866$, respectively.

Fig. 7

Actuation response of the compressible DLC as a function of the ratio (11), for $\rho _{\mu }=3\times 10^{3}$, ${\epsilon }_{a}/{\epsilon }_{b}=10$, ${c}_{b}=0.1$, and $\theta _{0}=3\pi /8$: behaviour for electric field limited to its first stationary value compared with the incompressible ($\rho _{K}=0$) and homogeneous cases, represented by the dotted and dashed black curves, respectively. The change from continuous to dashed style in the coloured curves corresponds to the switch from $\bar{\mathrm{E}}_{2}$-controlled to $\lambda _{1}$-controlled analysis. Coloured dotted curves represent the response predicted within the small strains and rotations framework

Fig. 8

Actuation response of the compressible DLC as a function of the phase contrast: behaviour for monotonically increasing electric field up to its second stationary value and comparison with the response of the “porous DLC”, plotted in thick red as in Fig. 2. As indicated, $\rho _{K}\in [1,10^{6}]$, while $\rho _{\mu }=3\times 10^{3}$ except for the gray and yellow curves, where $\rho _{\mu }=3\times 10^{4}$ and $\rho _{\mu }=3\times 10^{5}$, respectively. Note that a response almost superposed to the gray curve has been obtained with $\rho _{\mu }=3\times 10^{5}$. Other material parameters are ${\epsilon }_{a}/{\epsilon }_{b}=10$, ${c}_{b}=0.1$, and $\theta _{0}=3\pi /8$. The dashed style for coloured curves indicates the transient response

In Fig. 7 we also consider the incompressible case ($\rho _{K}=0$), which is obtained through the Spinelli and Lopez-Pamies [22] analytical form of the effective energy density. The closeness of this exact solution with the response obtained for $\rho _{K}=1$ (which is the smallest value of $\rho _{K}$ here investigated) provides a further confirmation on the accuracy of our algorithm, implemented as described in Sect. 2.4, for the solution of the fully nonlinear problem of DLC actuation.

Figure 7 shows the performance enhancement of the DLC with respect to both the analogous incompressible actuator and the homogeneous actuator constituted by the incompressible phase only. Each of the responses reaches a maximum indicating the onset of pull-in electromechanical instability beyond which the electrostatic stress cannot be equilibrated by the elastic stress. Analogously to Sect. 3, this critical value of the electric field approximately corresponds with the end of the $\bar{\mathrm{E}}_{2}$-controlled branch of the simulation, which is followed by a $\lambda _{1}$-controlled analysis, whose results are represented with dashed curves in our figures. We note that the value of $\lambda _{1}$ at the onset of the pull-in instability increases by augmenting the parameter $\rho _{K}$ (that is, by diminishing ${K}_{b}$ for a given ${\mu }_{a}$). As a reference, Fig. 7 also reports, in coloured dotted curves, the responses predicted within the framework of small strains and rotations.

The most interesting feature of the obtained actuation response for the compressible DLC is reported in Fig. 8, which shows that, for large enough phase contrast in terms of elastic moduli, by increasing $\bar{\mathrm{E}}_{2}$ beyond the critical value highlighted in Fig. 7, the solution switches to a distinct branch, exhibiting similarities with the initial transient branch of the actuation response obtained for the “porous DLC” (see Sect. 3). In fact, the lower and upper branches of the responses of the compressible DLC exhibiting a middle transient branch feature direct stress components of the total Cauchy stress that are numerically completely negligible with respect to the shear component. This is not the case, of course, in the transient branch itself, where the algorithm cannot satisfy all the governing equations. We remark that the almost-pure shear stress state holds for longitudinal stretch limited as in Figs. 7 and 8; in fact, as shown below, the picture significantly changes for larger $\lambda _{1}$.

Before delving into further details of the response illustrated in Fig. 8, which constitutes one of the main outcomes of this investigation, it is important to further characterise the actuation response of Fig. 7. This is accomplished through Figs. 9 and 10, where we focus on the case $\rho _{K}= 10^{3}$.

Fig. 9

Actuation response with some relevant deformation stages of the compressible DLC, for nondimensional electric field (20) limited to its first stationary value. The main model parameters are: $\rho _{K}=10^{3}$, $\rho _{\mu }=3\times 10^{3}$, ${\epsilon }_{a}/{\epsilon }_{b}=10$, ${c}_{b}=0.1$, and $\theta _{0}=3\pi /8$

Fig. 10

Actuation response of the compressible DLC for $\rho _{K}=10^{3}$, $\rho _{\mu }=3\times 10^{3}$, ${\epsilon }_{a}/{\epsilon }_{b}=10$, ${c}_{b}=0.1$, and $\theta _{0}=3\pi /8$: first branch up to very large longitudinal stretches. The black dotted curve represents the behaviour of the incompressible DLC

Figure 9 displays drawings of the unit cell at three significant stages of deformation, labelled with capital letters A to C, which identify the following branches:

• ${\mathrm{E}}_{2}$-controlled branch A-B: the input potential jump triggers an immediate elongation in the longitudinal direction, along with a considerably large increase of the volume of the softer phase $b$, which almost doubles its initial volume at point B, $(\lambda _{1}, \bar{\mathrm{E}}_{2}) \approx (1.261,0.117)$, corresponding to the onset of the instability;

• $\lambda _{1}$-controlled branch B-C: by increasing the longitudinal stretch $\lambda _{1}$ up to the limit value $\lambda _{1}=2$, we observe a monotonic decrease of the electric field, whereas the DLC further shrinks along the transverse direction $X_{2}$. Along this branch, the softer phase $b$ highly deforms by incrementing its volume.

However, the analysis does not end at stage C, as reported in Fig. 10. In fact, after the minimum in the $\bar{\mathrm{E}}_{2}(\lambda _{1})$ curve, at $\lambda _{1}\approx 2$, the stress state in the DLC changes completely: it does not consist of homogeneous Cauchy shear stress only, as the direct stress components are not negligible anymore and, in particular, $\sigma _{11}$ definitely becomes the largest Cauchy stress component with the increase of $\lambda _{1}$. In more detail, this regime is characterised by the volume of the compressible phase almost vanishing while the current lamination angle tends to zero: this, on the one hand, leads to a very large Cauchy pressure and, on the other hand, allows the compressible phase to largely elongate along the longitudinal direction. Actually, our model can obtain solutions even for far larger values of the longitudinal stretch than the value $\lambda _{1}=5.5$ limiting Fig. 10, with $\bar{\mathrm{E}}_{2}$ monotonically increasing, although very slightly. However, a deeper investigation on this behaviour is out of the scope of this work, as it would first of all require a critical assessment of the constitutive electromechanical models to adopt, to be carefully selected for these very large deformations [1, 2, 4, 33, 35, 38–40], possibly involving inelasticity and requiring a deformation-dependent apparent permittivity (see, e.g., [25, 41] and references therein). These would certainly be crucial issues to address for the softest phase, given the huge volumetric contraction that is just predicted with the hyper-electro-elastic models here adopted, and should be first of all ascertained to some extent with respect to the actual employed material.

Back to Fig. 8, by increasing $\bar{\mathrm{E}}_{2}$ beyond the onset of the (first) pull-in instability, for large enough phase contrast, we obtain the interesting results therein illustrated. After attaining the critical stage with quite good numerical accuracy, the further increase of $\bar{\mathrm{E}}_{2}$ leads to a transient branch, displayed with dashed lines, where, analogously to the A-B transient observed in the “porous DLC”, the stress continuity condition at the interface (3b) cannot be properly satisfied. Correspondingly, as $\bar{\mathrm{E}}_{2}$ increases, the fields in the actuator largely modify, with the longitudinal stretch suddenly decreasing up to overall shortening ($\lambda _{1}<1$), to reach a new configuration in which all the governing equations are fulfilled. In Fig. 8 this configuration corresponds to the first point of the continuous curves to the left of the red curve describing the response of the “porous DLC”, playing the role of a master curve. In fact, the response of the “porous DLC” is approached, when further increasing $\bar{\mathrm{E}}_{2}$, by all the responses for $\rho _{K}\ge 10^{2}$ by setting $\rho _{\mu }$ as in (42). We observe that, for this contrast in terms of shear moduli and $\rho _{K}= 10^{2}$, the Poisson’s ratio of the compressible phase is ${\nu }_{b}\approx 0.4835$. In order to obtain such a behaviour for a larger Poisson’s ratio, one has to leverage on $\rho _{\mu }$. This is for instance the case of the gray and yellow curves in Fig. 8, where we have set $\rho _{\mu }= 3\times 10^{4}$, $\rho _{K}= 10^{2}$ and $\rho _{\mu }= 3\times 10^{5}$, $\rho _{K}= 10^{3}$, respectively, corresponding to ${\nu }_{b}\approx 0.4983$. Additionally, by setting $\rho _{\mu }= 3\times 10^{5}$, $\rho _{K}= 10^{2}$ (that implies ${\nu }_{b}\approx 0.49983$), we have obtained an actuation response, undisplayed in Fig. 8 for the sake of clarity, that is basically superposed to the prediction for $\rho _{\mu }= 3\times 10^{4}$, $\rho _{K}= 10^{2}$. This is quite important because this value of ${\nu }_{b}$ is comparable to that obtained from measurements of initial moduli of elastomers [5]. For instance, for the infinitesimal deformation of vulcanised natural rubber at temperature of 25^∘, Wood and Martin [34] measured a bulk modulus ≈1984.1 MPa which, in conjunction with a Young modulus of ≈1.2748 MPa, determines a Poisson’s ratio $\approx 0.49989$. We must remark, however, that these results suggest that an extremely large phase contrast is required for such a low compressibility to lead to the new multi-branch response. As a rule, the larger the phase contrast, the smaller the required compressibility of phase $b$. Let us finally observe that by increasing $\rho _{K}$ the switch of branch occurs at smaller values of $\bar{\mathrm{E}}_{2}$ and the master curve is approached earlier.

On the basis of the foregoing arguments, we can further infer that the whole first branch of the actuation response for the compressible DLC, as displayed in Fig. 8, collapses in the single origin point, $(\lambda _{1}, \bar{\mathrm{E}}_{2}) = (1,0)$, for $(\rho _{\mu }\to \infty , \rho _{K}\to \infty )$, that is, for the “porous DLC”. More importantly, we expect that the analysis of Sect. 3 for the “porous DLC” will be beneficial for the characterisation of the first electromechanical instability experienced by the compressible DLC, occurring at stage B in Fig. 9, which surely deserves an ad hoc future investigation.

Let us remark that in the boundary-value problem for the compressible DLC the number of equations to solve corresponds to the number of unknowns, while the lack of this algebraic condition has been detected in Sect. 3 as the main motivation for the existence of the initial transient branch in the “porous DLC”. Here, in the case of the compressible DLC, the fact that a similar transient shows up because of the nonlinearity of the problem gives ground to the hypothesis that it should be possible to properly describe this transient by extending the model to some appropriate physical aspects, such as dynamics.

For the sake of clarity, the responses in Fig. 8 are cut at the (second) occurrence of electromechanical instability. We fill this gap in Fig. 11, where, after this maximum of the $\bar{\mathrm{E}}_{2}(\lambda _{1})$ curve, we continue the analysis by applying monotonically increasing longitudinal stretch. It is interesting to observe that the response initially follows the post-critical behaviour of the “porous DLC” and, then, when this branch is abandoned our algorithm cannot obtain a solution satisfying all the governing equations (situation represented in Fig. 11 with a thin dashed line) until we obtain solutions by jumping on the lower $\lambda _{1}$-controlled branch following the very first electromechanical instability.

Fig. 11

Actuation response of the compressible DLC, for $\rho _{K}=10^{3}$, $\rho _{\mu }=3\times 10^{3}$, ${\epsilon }_{a}/{\epsilon }_{b}=10$, ${c}_{b}=0.1$, and $\theta _{0}=3\pi /8$. The red curve refers to the “porous DLC”, while the orange dashed curve reports the response obtained by switching to $\lambda _{1}$-controlled analysis after occurrence of the first electromechanical instability

Now, in Figs. 12 and 13, we give a further insight on the important role of the DLC anisotropy by providing results for variable initial lamination angle $\theta _{0}$. In the case ${\epsilon }_{a}/{\epsilon }_{b}=10$ (see Fig. 12), as expected, the curves for $\theta _{0}\ge 67^{\circ} .5$, towards their maximum electric field, approach their respective master curves (displayed with thin-dashed lines) referred to the corresponding “porous DLCs” (see Fig. 3). In agreement with the issues faced in Sect. 3.2 for the “porous DLC”, this is not exactly the case when setting $\theta _{0}=60^{\circ}$, for which the presence of a compressible phase instead of vacuum allows the application of a slightly larger maximum electric field, although the maximum that our code can reach is not yet a stationary value of the $\lambda _{1}(\bar{\mathrm{E}}_{2})$ function.

Fig. 12

Actuation response of the compressible DLC as a function of the initial lamination angle $\theta _{0}$: behaviour for monotonically increasing electric field beyond the transient response, indicated with thick-dashed style. Thin-dashed master curves, taken from Fig. 3, refer to the “porous DLCs”. The model parameters are $\rho _{\mu }=3\times 10^{3}$, $\rho _{K}=10^{2}$, ${\epsilon }_{a}/{\epsilon }_{b}=10$, and ${c}_{b}=0.1$

Fig. 13

Actuation response of the compressible DLC as a function of the initial lamination angle $\theta _{0}$: behaviour for monotonically increasing electric field beyond the transient response, indicated with thick-dashed style. Thin-dashed master curves, taken from Fig. 3, refer to the “porous DLCs”. The model parameters are $\rho _{\mu }=3\times 10^{3}$, $\rho _{K}=10^{2}$, ${\epsilon }_{a}/{\epsilon }_{b}=20$, and ${c}_{b}=0.1$

In the case ${\epsilon }_{a}/{\epsilon }_{b}=20$, the results displayed in Fig. 13 for $\theta _{0}\le 67^{\circ} .5$ unveil a further different behaviour, which is characterised by a single branch where all the equations governing the nonlinear problem are always satisfied. Note that in these responses, initially, the longitudinal stretch very slightly increases and the master curves of the corresponding “porous DLCs” are never approached. Moreover, in spite of the stark contrast between this type of response and that multi-branch mainly documented in this study, observation ${\mathcal{F}}_{\mathrm{A}}$ of Sect. 3.2.1 still holds, that is, also in this single branch behaviour the sole non-vanishing Cauchy stress component is the shear one. Finally, and again as expected from the analysis of Sect. 3.2 on the “porous DLC”, the actuation performance is poor for low initial lamination angles, such that we leave a deeper study of this type of response for future investigations.

Table 2 provides the values of the current lamination angle, obtained through Eq. (23), corresponding to the occurrence of the two electromechanical instabilities characterising each $\lambda _{1}(\bar{\mathrm{E}}_{2})$ curve under monotonically increasing applied voltage. In particular, $\theta _{1}$ refers to the first instability and $\theta _{\mathrm{max}}$ refers to the second instability or, if a maximum in the $\lambda _{1}(\bar{\mathrm{E}}_{2})$ curve cannot be reached, to the largest obtained value of $\bar{\mathrm{E}}_{2}$. Remarkably, in all cases in which we can identify both $\theta _{1}$ and $\theta _{\mathrm{max}}$ they turn out to be quite close to each other. This phenomenon might be ascribed to the dependence of the macroscopic DLC anisotropy on the microstructure evolution, possibly encompassing an overall stiffness which is a non-monotonic function of the current lamination angle (on the same line of the purely mechanical studies on fibre-reinforced elastomers [42]).

Table 2 Current lamination angle at occurrence of instabilities for $\rho _{\mu }=3\times 10^{3}$, $\rho _{K}=10^{2}$, and ${c}_{b}=0.1$

Finally, it is important to demonstrate that, qualitatively, the behaviour illustrated in Fig. 8 is due to the allowed volumetric deformation in the compressible DLC, while it does not ensue from the specific choice (10) for the free-energy density of the compressible phase $b$. This is accomplished in Fig. 14, where we observe similar responses if we model phase $b$ through either the coupled free energy (17) or the decoupled potential (10). Note that in the coupled energy (17) we have set ${\gamma }_{b}=1/6$, which would imply, through Eq. (18), ${K}_{b}={\mu }_{b}$, that is $\rho _{K}=3\times 10^{3}$, according to the choice in Eq. (42). In fact, setting relatively large values of ${\gamma }_{b}$ leads to inaccurate numerical results in our code, and the results that we have obtained for ${\gamma }_{b}=7/6$, which would be consistent with $\rho _{K}=10^{3}$, are already unreliable. ² We emphasise that the DLC whose compressible phase is described by the coupled potential (17) not only exhibits a multi-branch response totally similar to that described so far by adopting the uncoupled energy (10), but, after the transient branch, it also approaches the response of the “porous DLC”.

Fig. 14

Actuation response, limited to the maximum value reached by the applied electric field, of the compressible DLC obtained by adopting either the decoupled free energy density (10) (cyan curve) or the coupled free energy density (17) (blue curve). The significant material parameters are $\rho _{\mu }=3\times 10^{3}$, $\rho _{K}=3\times 10^{3}$ (which is consistent with ${\gamma }_{b}=1/6$ in the energy (17)), ${\epsilon }_{a}/{\epsilon }_{b}=10$, ${c}_{b}=0.1$, and $\theta _{0}=3\pi /8$. For comparison, we also display the response of the “porous DLC” (red curve) and that of the compressible DLC with free energy density (10) and $\rho _{K}=10^{3}$ (orange curve), which appears in all the figures since Fig. 8

5 Concluding Remarks

In the context of soft dielectric composites with high phase contrast in terms of elastic moduli, up to the limit of a phase consisting of vacuum, our investigation has unveiled a quite complex electromechanical response due to the volumetric deformation, within the framework of finite deformations.

By referring to the actuation of two-phase dielectric laminated composites (DLCs), where only the stiffest phase is assumed to be incompressible, we have discovered a surprisingly rich set of possible responses, depending on model parameters such as the initial lamination angle $\theta _{0}$ and the phase contrast in terms of both elastic moduli and permittivities. In particular, we have focused on a behaviour characterised by a multi-branch response and two levels of electromechanical instability. Such a rich behaviour has been obtained for a DLC under plane strain and free to deform axially along its thickness and longitudinal directions, while being constrained to experience vanishing effective shear deformation. The DLC actuation performance is evaluated by measuring its longitudinal elongation under the application of an electric field along its thickness.

We have followed a well-known ad hoc homogenisation procedure for DLCs [17, 21, 29], which takes advantage of periodicity and assumes that the microscopic fields are spatially uniform within each phase. In the case of the “porous DLC”, that is the DLC in which a phase is vacuum, such homogenisation procedure leads to an initially ill-posed algebraic problem, having one extra equation to be satisfied with respect to the number of unknowns. We have demonstrated, by comparing analytical estimates and numerical results obtained for the fully nonlinear problem, that this mathematical impasse is overcome after a sudden transient branch in which the vacuum phase changes configuration until attaining a DLC arrangement in which all the governing equations are fulfilled. In general, this configuration change mostly involves a large variation of the vacuum volume, but it may also encompass variations of the lamination angle for a certain range of values of $\theta _{0}$ (see Fig. 1). The transient may correspond to either shrinkage or elongation along the longitudinal direction depending on $\theta _{0}$, the initial vacuum volume fraction ${c}_{b}$, and relative permittivity of the solid phase $\epsilon _{r}$. We have demonstrated that our analytical estimate for the configuration attained by the “porous DLC” just after the transient is accurate for $\theta _{0}$ not-too-far from $3\pi /8$, which is the value that maximises the volume of the vacuum phase at the end of the transient. Additionally, through the detailed analysis of the “porous DLC”, we have obtained estimates establishing that $\theta _{0}$ must range between $\pi /4$ and $\pi /2$, with better actuation performance for larger angles, and that ${c}_{b}$ may not exceed $3-2\sqrt{2}\approx 0.1716$, independently of $\theta _{0}$ and $\epsilon _{r}$.

The most noticeable result of our investigation is that a very similar transient branch is observed also for the general compressible DLC, in spite of the absence of the algebraic problem affecting the “porous DLC”. More specifically, the actuation response of the compressible DLC displays an initial branch exhibiting “usual” DLC elongation up to a first electromechanical instability. At this stage, upon increasing the applied electric field, the above mentioned transient branch appears and leads to a decrease of the effective longitudinal stretch up to an overall DLC shortening. After the transient, the actuation response suddenly approaches that of the “porous DLC” and, then, accurately follows it significantly beyond its electromechanical instability, which is the second level of instability for the compressible DLC. Although the occurrence of this behaviour depends on both $\theta _{0}$ and the phase contrast, it more easily holds for $\theta _{0}\ge 3\pi /8$, which, interestingly, leads to the best actuation performance, whereby the latter can be related to the evolution with the applied voltage of the current lamination angle and the corresponding overall DLC anisotropy.

Moreover, our results strongly confirm that by leveraging both on the phase contrast and on other microstructural parameters one can, in principle, greatly enhance the electromechanical performance of soft dielectric composites.

5.1 Open Issues

In our opinion, the rich response of compressible DLCs deserves to be further investigated, by first of all focusing on the characterisation of the two observed levels of electromechanical instability. Moreover, exploring the outcome of assuming an electric breakdown limit for the involved materials would certainly be worthwhile.

The high phase contrast in terms of elastic moduli that we have explored calls for a critical assessment of the assumption of spatially uniform microscopic fields on each phase, mostly in relation to the adopted boundary conditions. To this purpose, the comparison against the results of full-field simulations, for instance performed by resorting to the finite element method, would be extremely useful. As an additional detail, we note that the finite element method would allow the implementation of a contact law to perform analyses beyond the collapse of the vacuum phase, while, in the present investigation, this is the condition that typically ends the analysis.

In spite of the very simple composite layout that we have considered, a significant amount of work would still be needed in order to thoroughly explore the influence of all the geometrical and constitutive parameters involved. About geometry, although we have limited our analysis to initial volume fraction of the compressible phase, ${c}_{b}$, equal to 0.1, we think that it would be interesting to investigate on the effect of varying it. Moreover, on the basis of our detailed analysis of the influence of $\theta _{0}$ on the “porous DLC”, we have mostly focused on $\theta _{0}=3\pi /8$ for the compressible DLC, even though the effect of this important parameter would deserve further studies, also in the light of its influence on the overall DLC anisotropy. About constitutive parameters, a key point would be establishing a relationship for the combinations of phase contrast and soft phase compressibility (expressible in terms of the ratios defined in Eqs. (11) and (12), plus the permittivity contrast) able to trigger the multi-branch actuation response here unveiled. In this regard, an interesting option could consist of analytically approaching the DLC homogenisation in the limit of nearly incompressible [3] soft phase.

Regarding the mechanical boundary conditions, the macroscopic assumption of vanishing shear deformation might be relaxed by adopting a more general boundary condition elastically linking ${\mathrm{S}}_{12}$ and ${\mathrm{F}}_{12}$. A preliminary study involving this condition has shown the potential to provide further insight on the behaviour of compressible DLCs. However, the extra parameter involved in such a problem would turn out in a much more complex presentation of the results, without adding much to the message that we aim to convey. Moreover, note that in the case of free shear deformation (that is, if one imposes ${\mathrm{S}}_{12} = 0$, as investigated by Gei et al. [29] for incompressible DLCs and by Tian [17], further limiting the attention to small strains and rotations) it is impossible to obtain any solution for the actuation problem on the “porous DLC”, where, in such a case, the vacuum phase immediately collapses because of the possibility of the solid phase to rotate. Correspondingly, one faces difficulties, at least of numerical nature, in solving the actuation problem for the compressible DLC with high phase contrast.

Accounting for a more realistic boundary condition than vanishing macroscopic shear deformation is however beyond the goals of the present investigation. In fact, in a realistic simulation of a DLC actuator with very high phase contrast, such condition should be accompanied with a careful modelling of the boundary effects ensuing from the way the two phases are actually connected with the exterior, by for instance accounting for a finite electrode compliance in a rank-one DLC, or for the stiffness of the surrounding material in a hierarchical DLC. Unfortunately, this problem, which is at least fully two-dimensional and involves heterogeneous microscopic fields, would require a challenging computational effort that we leave for future investigations. Given that richer benchmarks will lead to even more complex behaviours than that unveiled in this contribution, we infer that the simple benchmark here adopted is enough for us both to warn against the indiscriminate use of the incompressibility assumption in soft dielectric composites and to claim that there is room for improvements in the design of DLC actuators.

Micro- and macro-scopic instabilities leading to non-homogeneous deformations can also be investigated in DLCs. In this case, the methodology presented in, e.g., [16, 22, 37] can be applied. In particular, microscopic instability corresponds to onset of non-homogeneous diffuse modes whose wavelengths are in the order of phase thicknesses, whereas a macroscopic instability is a large wavelength mode that can be analysed by determining the loss of ellipticity threshold of the homogenised constitutive response. It is expected that, along the paths described in Sect. 4, the first mode to occur among the two will depend in a complicated way on all the parameters involved (volume fractions, initial lamination angle, contrast between phases). Therefore, establishing reliable estimates of the critical mode surely deserves an ad hoc investigation.

About the electrostatic boundary condition, it might be worth to study the charge-controlled actuation process, where, instead of a voltage drop across the electrodes, one applies charges on the electrodes. This suggests a further line of research that would consist in selecting the nominal electric displacement $\textbf{D}$, instead of the nominal electric field $\textbf{E}$, as primal variable for the Helmholtz free-energy density.

The extension of our model to other physical aspects might be important in order to gain a better understanding of the observed transient branch in the actuation response. Additionally, the study of the response for very large deformations would also require a dedicated investigation towards employing suitable constitutive models for the adopted materials. Among several aspects disregarded in our study, without even mentioning inelasticity, let us recall the possibility of introducing a deformation-dependent apparent permittivity, at least for the softest phase.

We note that the study of the two-phase “porous DLC” might have an impact on nonlinear high-performance hierarchical DLCs, recently studied by limiting the attention to the incompressible case [15, 24]. More generally, it would be certainly important to carry out similar studies for soft dielectric composites with different microstructures, for instance encompassing randomness and the presence of a matrix (that is, a continuous phase, missing in laminated composites).