Abstract
In the framework of generalized extreme value (GEV) distribution, the frequentist and Bayesian methods have been used to analyse the extremes of annual maxima wind speed recorded by automatic weather stations in Cape Town, Western Cape, South Africa. In the frequentist approach, the GEV distribution parameters were estimated using maximum likelihood, whereas in the Bayesian method the Markov Chain Monte Carlo technique with the Metropolis–Hastings algorithm was used. The results show that the GEV model with trend in the location parameter appears to be a better model for annual maxima data. The paper also discusses a method to construct informative priors empirically using historical data of the underlying process from other weather stations. The results from the Bayesian analysis show that posterior inference might be affected by the choice of priors and hence by the distance between a weather station used to formulate the priors and the point of interest.




Similar content being viewed by others
Notes
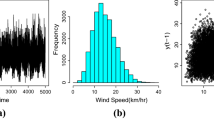
For example, the maximum wind speed at Cape Town station for years 2014 and 2015 was about 25.90 and this value is slightly greater than the annual maxima recorded in the previous 3 years.
References
An Y, Pandey MD (2005) A comparison of methods of extreme wind speed estimation. J Wind Eng Ind Aerodyn 93:535–545
Azzalini A (1996) Statistical inference: based on the likelihood. Chapman and Hall, London
Beirlant J, Goegebeur Y, Segeres J, Teugels J (2004) Statistics of extremes, 1st edn. Wiley, Chichester
Bronaugh D, Werner A (2013) zyp: Zhang & Yue-Pilon trends package. R package version 0.10-1. http://www.r-project.org/
Chikobvu D, Sigauke C (2013) Modelling inuence of temperature on daily peak electricity demand in South Africa. J Energy S Afr 24(4):63–70
Coles SG (2001) An introduction to statistical modeling of extreme values. Springer-Verlag, London
Coles SG, Tawn JA (1996) A Bayesian analysis of extreme rainfall data. Appl Stat 45:463–478
Coles SG, Tawn JA (2005) Bayesian modelling of extreme surges on the UK East Coast. Philos Trans R Soc A 363:1387–1406
Davison AC, Smith RL (1990) Models for exceedances over high thresholds (with discussion). J R Stat Soc B 52:393–442
Diriba TA, Debusho LK, Botai J (2015) Modeling extreme daily temperature using generalized pareto distribution at port Elizabeth, South Africa, peer-reviewed. In: Proceedings of the 57th annual conference of the South African statistical association, University of Pretoria, Pretoria, South Africa, 41–48 2015
Diriba TA, Debusho LK, Botai J, Hassen A (2014) Analysis of extreme rainfall at East London, South Africa, peer-reviewed. In: Proceedings of the annual conference of the South African statistical association, Rhodes University, Grahamstown, South Africa, 25–32 2014
Eastoe EF, Tawn JA (2012) Modelling the distribution of the cluster maxima of exceedances of sub-asymptotic thresholds. Biometrika 99:43–55
Eyewitness News (2015) Fires rage in Cape Town’s deep South. http://ewn.co.za/2015/03/02/Fires-rage-in-Cape-Towns-deep-south. Accessed 01 Feb 2016
Furrer EM, Katz RW (2008) Improving the simulation of extreme precipitation events by stochastic weather generators. Water Resour Res W12439(44):1–13
Gilleland E, Katz RW (2011) New software to analyze how extremes change over time. Eos Trans Am Geophys J 92(2):13–14
Harris I (2005) Generalised pareto methods for wind extremes useful tool or mathematical mirage. J Wind Eng Ind Aerodyn. doi:10.1016/j.jweia.2005.02.004
Jonathan P, Ewans KC (2013) Statistical modelling of extreme ocean environments with implications for marine design: a review. Ocean Eng 62:91–109
McLeod AI (2011) Kendall: Kendall rank correlation and Mann-Kendall trend test. R package version 2.2. http://www.stats.uwo.co/faculty/aim
Pickands J (1975) Statistical inference using extreme order statistics. Ann Stat 3:119–131
Rao CR (1973) Linear statistical inference and its applications, 2nd edn. Wiley, New York
R Development Core Team (2015) A language and environment for statistical computing, R foundation for statistical computing. http://cran.r-project.org/
Sen PK (1968) Estimates of the regression coefficient based on Kendall’s tau. J Am Stat Assoc 63(324):1379–1389
Smith RL (1989) Extreme value analysis of environmental time series: an application to trend detection in ground-level ozone. Stat Sci 4(4):367–393
Stephenson AG (2015) evd: Functions for extreme value distributions. R package version 2.3-2. http://cran.r-project.org/
Stephenson AG (2016) ismev: An introduction to statistical modeling of extreme values. R package version 1.41. http://www.ral.ucar.edu/~ericg/softextreme.php
Stephenson AG, Ribatet M (2015) evdbayes: Bayesian analysis in extreme value theory. R package version 1.1-1. http://cran.r-project.org/
Acknowledgements
The first author is indebted to the National Research Foundation (NRF), University of Pretoria and Department of Science and Technology for their financial support towards his study. The second, third and fourth authors acknowledge the support they had from the University of South Africa, South African Weather Service and University of Pretoria, respectively. They also thank the South African Weather Service for providing the data.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
No potential conflict of interest was reported by the authors.
Additional information
Handling Editor: Pierre Dutilleul.
Appendices
Appendix 1: The profile likelihood confidence intervals
Let \({\varvec{\theta }}\) = (\(\mu \), \(\sigma \), \(\xi \)) be a vector of GEV model parameters and \(\ell ({\varvec{\theta }})\) be the log-likelihood for \({\varvec{\theta }}\), given in Eq. (5). Then the profile likelihood intervals for return levels are constructed as follows.
Re-parameterize the GEV model parameters \({\varvec{\theta }}\) = (\(\mu \), \(\sigma \), \(\xi \)) so that \(y_p\) becomes one of the GEV model parameters. Using Eq. (6), for example, the location parameter \(\mu \) can be expressed as
for \(\xi \ne 0\). Let \(\ell (y_p, \sigma , \xi )\) be the log-likelihood for \({\varvec{\theta }}\) = (\(y_p\), \(\sigma \), \(\xi \)).
Now partition \({\varvec{\theta }}\) = (\(y_p\), \(\sigma \), \(\xi \)) into two components (\({\varvec{\theta }}_{(1)}\), \({\varvec{\theta }}_{(2)}\)) where \({\varvec{\theta }}_{(1)} = y_p\) and \({\varvec{\theta }}_{(2)}\) = (\(\sigma \), \(\xi \)). The profile log-likelihood for \({\varvec{\theta }}_{(1)} = y_p\) is defined as
That is, for a given value of \(y_p\), the profile log-likelihood is the maximized log-likelihood with respect to \({\varvec{\theta }}_{(2)}\) = (\(\sigma \), \(\xi \)).
Let \(\hat{{\varvec{\theta }}}\) be the MLE of \({\varvec{\theta }}\). Then under suitable regularity conditions, for large m
Thus, the set of values, say \(C_{\alpha }\), for which \(\{y_p: D_p(y_p) \le c_{\alpha } \}\) provides a (\(1 - \alpha \)) confidence interval for \(y_p\), where \(c_{\alpha }\) is the (\(1-\alpha \)) quantile of the \(\chi _1^2\) distribution. The (\(1 - \alpha \))100% profile likelihood confidence interval for \(y_p\) is the set of values \(C_{\alpha }\) given by the points of intersection between the line \(\frac{1}{2} \times \chi ^2_1(\alpha )\) and the profile log-likelihood for \(y_p\).
Appendix 2: R codes used for analysis






Rights and permissions
About this article
Cite this article
Diriba, T.A., Debusho, L.K., Botai, J. et al. Bayesian modelling of extreme wind speed at Cape Town, South Africa. Environ Ecol Stat 24, 243–267 (2017). https://doi.org/10.1007/s10651-017-0369-z
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10651-017-0369-z