Abstract
Discrete-time stochastic models of management of groundwater resources have been extensively used for understanding a number of issues in groundwater management. Most models used suffer from two drawbacks: relatively simplistic treatment of the cost of water extraction, and a lack of important structural results (such as monotonicity of extraction in stock and concavity of the value function), even in simple models. Lack of structural properties impede both practical policy simulation and clarity of understanding of the resulting models and the underlying economics. This paper provides a unifying framework for these models in two directions; first, the usual cost function is extended to encompass cases where marginal cost of pumping depends on the stock and second, the analysis dispenses with assumptions of concavity of the objective function and compactness of the state space, using instead lattice-theoretic methods. With these modifications, a comprehensive investigation of which structural properties can be proved in each of the resulting cases is carried out. It is shown that for some of the richer models more structural properties may be proved than for the simpler model used in the literature. This paper also introduces to the resource economics literature an important method of proving convergence to a stationary distribution which does not require monotonicity in stock of resource. This method is of interest in a variety of renewable resource model settings.
Similar content being viewed by others
Notes
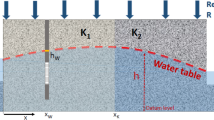
As is common in the literature, we work with the total stock of water instead of the ‘lift’, which is commonly used in the engineering literature. However, since both are related monotonically (lift increases as groundwater decreases) one may work with either without loss of generality.
The use of such a simplified balance equation, as remarked in Worthington et al. (1985, pp. 232–233) is a gross over simplification. Taken literally, this equation implies an instantaneous capture of all recharge by any pumping activity. However, this oversimplification can be remedied by either introducing relevant coefficients on recharge such that only a fraction of the recharge is captured or by using more detailed and accurate equations of motion for the stock. Note that in the case of many developing nations where discharge due to pumping is much larger than recharge, such an assumption is less of an oversimplification, since a large part of recharge is very likely captured within the region of pumping.
It is made explicit only in Worthington et al. (1985), wherein (Table 1, p. 236) they estimate an annual incremental drawdown given only the level of water table at the beginning of the season, independent of the quantity of water pumped.
An intuitive property of this cost function is that extraction of the nth unit of water is less costly than extraction of the \((n+m)\)th, \(\forall m,n>0\), and for all stock levels. For the particular functional form used, the marginal cost of extraction is \(\gamma (x-w)\), a function of both \(x \text { and } w\), with \(\dfrac{\partial ^2C}{\partial x \partial w}=\gamma ^{\prime } < 0\) and \(\dfrac{\partial ^2C}{\partial w^2}=-\gamma ^{\prime } > 0\).
We note the intimate relationship between model time-step and model formulation. In the context considered here, a time period is a full growing season, approximately of six-month duration, and in some part of the growing season, groundwater is the only source of water available. Given the length of the season, it is not clear that cost of extraction ought to depend upon beginning-of-period stock of water, especially if extraction is likely a large part of the stock (as is the case for the Telangana region in southern India, see Fishman et al. 2011).
Note that the latter interpretation can be justified by an appeal to the discussion accompanying figure 1.2 in Brozović et al. (2006), which makes clear that for many aquifers, if two pumping wells are only a small distance apart (certainly true for the context considered here) only pumping in the immediate past is of any relevance. Given the definition of a season, and the relatively small distance separating pumping wells in the context considered, our modeling of ‘path dependence’ in pumping as being restricted to a season, and affecting cost but not stock, is quite natural.
This issue, even with the confined aquifer assumption, has been remarked on before. For instance, Provencher and Burt (1994, p. 882) point out that groundwater levels do not adjust immediately after a local perturbation caused by pumping from the well, due to the fact that the equilibrating flows are both slow and subject to great variability. In particular, with heterogeneous aquifers and unequal pumping rates by farmers, they clearly recognized a not insubstantial lateral flow of groundwater, leading to uncertainty regarding future water availability. While their discussion was in the context of a common property problem, it is clearly applicable in the context of our modification to the cost function.
The finite difference approach is the standard approach to two- and three-dimensional groundwater flow modeling; e.g. the USGS’s MODFLOW (Harbaugh et al. 2000).
The precise correction is given by the formula \(0.3665 \dfrac{q_{i,j}(t)}{m_{i,j} T_{i,j}} \log \left( \dfrac{\Delta x}{4.81 r_{BH}}\right) \), where i, j refer to the finite difference cell index, m is the number of pumping wells in the cell with uniform pumping, T is the transmissivity, \(\Delta x\) and \(r_{BH}\) are respectively the cell size and radius of the well. See e.g. Siegfried (2004, pp. 52–53) for a description and Prickett and Lonnquist (1971) for a derivation.
This framework [cost in Eq. (8) and transition in Eq. (1)] is an uneasy combination of a particular form for stock-dependent cost with an infinite depth aquifer. See Remark 5 for a generalization. The use of the simplified transition Eq. (1) here is for the sake of unification, since our results with the cost function in Eq. (7) do not extend to the more realistic transition in Eq. (2).
To see this, note that \(C_{x}=-c\), \(C_{xx}=0\), thus \(\Pi _{xw}=-c\), \(\Pi _{xx}=-C_{xx}=0\), \(\Pi _{ww}=-B^{\prime \prime }\) . For \(\Pi \) to be jointly concave in (x, w), the Hessian is required to be negative semi-definite, implying \(B^{\prime \prime }C_{xx}\ge \left( C_{x}\right) ^{2}\) which in this case is equivalent to \(c^{2}\le 0\), evidently false.
To be more explicit, properties (a) and (e) are proved via assumptions on the objective function \(\Pi \)—which is recursive—rather than by considering a recursive utility function U operating on the profit function \(\Pi \), the latter being defined as in Knapp and Olson (1995). Thus, it is not possible to trace a direct link between the analysis in Knapp and Olson (1995) and Knapp and Olson (1996).
Consider first the function \(\log (w+D)\), \(D=1\). For \(B>B^{\prime }w\) for this function, it is required that \(\log (1+w)\ge \dfrac{w}{1+w}\). That this holds is evident from the logarithmic inequality \(\dfrac{w}{1+w}\le \log (1+w)\le w\). For the function \(B(w)=1-\exp (-aw)\), it is seen that \(B-wB^{\prime }=1-\exp (-aw)\left( 1+aw\right) \). That this is non-negative is evident from the following inequality: \(e^{-x}(1+x)<1\), with \(x=aw\).
A function f is locally Lipschitz if, for \(\forall x_{0}\in X\), \(\exists r>0\) such that f is Lipschitz continuous on \(B_{r}\left( x_{0}\right) \), an open ball centered at \(x_{0}\), with constant \(\Lambda \left( x_{0}\right) \) i.e. if \(|f\left( z\right) -f\left( x_{0}\right) |\le \Lambda \left( x_{0}\right) \) \(\forall z \in B_r \left( x_0\right) \). If \(\exists \)r for which the same Lipschitz constant \(\Lambda \) applies \(\forall x_{0}\in X\) then f is said to be globally Lipschitz.
The underlying assumption of Knapp and Olson (1995) is the supermodularity of \(B(x-y)-C(x, x-y)\) in (x, y), where B(w) is the benefit of withdrawing w units of water, but this condition sometimes fails for the model in Eq. (6); however, for Eq. (7), this supermodularity condition always holds, thereby enabling Property (c) to hold.
We have not been able to establish, for the cost function in Eq. (7), that question 2b can be answered in the affirmative. This is due to the fact that existing sufficient conditions are inapplicable to our case, and a direct proof is non-trivial. We leave this task for future work.
While powerful, the method used here suffers from a drawback, in the need for finding a function v which allows a verification of the condition of ‘drift to a small set’ (in Definition 2). The function v depends on the functional form of F(.) in Eq. (16); it is therefore not possible to provide generic conditions for convergence for arbitrary functional forms of F. Nonetheless, for commonly used functions for stock growth in renewable resource economics (e.g. linear, as here, or power functions), it is possible to find a function v for which convergence holds.
It is not difficult to see that it is not sufficient: observe that what is required is \(w(x)\ge x(1-\alpha )\), which is not guaranteed by \(w(x)>0, \forall x>0\).
Imposing constraints on controls, instead of on stocks, is rather unusual. However, conceptually at least, one may think of this constraint as representing a ‘penalty’ on lack of water. For instance, if in the absence of extracted groundwater, an alternative source of water has to be found, then the cost of extraction has to be unrealistically high for zero extraction to occur.
An alternate proof exists when the kernel P has a density, \(\phi \) [which exists in this case, see Stachurski (2009, Theorem 8.1.3)], of the form \(P(x,y)=\phi (y-a(x))>0\). Using \(Mv(x)=\int v(s)P(x,ds)\), and change of variable, \(z=y-a(x)\), \(v=y\), we have \(\int y\phi (y-a(x))dy=\int \left( a(x)+z\right) \phi (z)dz\le \alpha x+\beta \), where \(\beta :=\int z\phi (z)dz<\infty \).
Note that Propositions 1–4 do not depend upon the S.R.S, except insofar as Assumptions 3 and 11 are satisfied (which they are; the former since L is increasing, the latter a maintained assumption through out). For the cost functions in Eq. (6) and Eq. (8), Theorem 2 follows if Theorem 1 holds under the assumed conditions (which it does). We note that an extension of the results in HKW to the case of the stock-dependent recharge in Eq. (18), appears infeasible.
Possible values for \(\tilde{\alpha }\) are: (i) \(\tilde{\alpha }=1-\tilde{\beta }\), with \(0<\tilde{\beta }:=\inf \left\{ \dfrac{\partial w\left( x\right) }{\partial x}-\dfrac{\partial v\left( x\right) }{\partial x};x>0\right\} <1\), a more demanding condition than for a (e.g., if w and v are dominated by linear functions with slopes \(\eta _{w}\) and \(\eta _{\gamma }\), then it is necessary and sufficient that \(\eta _{w}>\eta _{\gamma }\)); (ii) if \(0\le \tilde{K}:=\sup \left\{ x+\gamma \left( x\right) -w\left( x\right) ;x>0\right\} <1\), then \(\tilde{\alpha }=\tilde{K}\); and (iii) if \(0<\tilde{\kappa }:=\inf \left\{ \dfrac{w\left( x\right) -\gamma \left( x\right) }{x};x>0\right\} <1\), then \(\tilde{\alpha }=1-\tilde{\kappa }\).
To illustrate, in the single-user case, different policies are easily evaluated and intuitively interpreted using only data on average depth to water and some measure of porosity, following Fishman et al. (2011). To extend the analysis in Athanassoglou et al. (2012), carried out for the case of two hypothetical users in the Telangana region (now state) in Southern India, to real-world aquifer systems with many users and with complex hydro-geology is likely challenging.
A partially ordered set \(\mathcal {X}\) is a lattice if, \(\forall x,y\in \mathcal {X}\), it is the case that \(x\wedge y\) and \(x \vee y\) \(\in \mathcal {X}\). When, as here, \(\mathcal {X} \subset \mathbb {R}\), with the usual order, then \(x \wedge y=\min \{x,y \}\) and \(x \vee y=\max \{x,y \}\).
Intuitively, a set \(\Gamma \) is a sub-lattice of \(\mathcal {X}\) if, \(\forall x,y \in \Gamma \), it is the case that \(x\wedge y\) and \(x \vee y\) \(\in \Gamma \).
References
Aggarwal RM, Narayan TA (2004) Does inequality lead to greater efficiency in the use of local commons? The role of strategic investments in capacity. J Environ Econ Manag 47(1):163–182
Athanassoglou S, Sheriff G, Siegfried T, Huh WT (2012) Optimal mechanisms for heterogeneous multi-cell aquifers. Environ Resour Econ 52:265–291
Brown G Jr, Deacon R (1972) Economic optimization of a single-cell aquifer. Water Resour Res 8:557–564
Brozović N, Sunding DL, Zilberman D (2010) On the spatial nature of the groundwater pumping externality. Resour Energy Econ 32:154–164
Brozović N, Sunding DL, Zilberman D (2006) Optimal management of groundwater over space and time. Front Water Resour Econ 29:109–135
Burness H, Brill T (2001) The role for policy in common pool groundwater use. Resour Energy Econ 23:19–40
Burt OR (1966) Economic control of groundwater reserves. J Farm Econ 48:632–647
Burt OR (1970) Groundwater storage control under institutional restriction. Water Resour Res 6:45–56
Burt OR (1964) Optimal resource use over time with an application to ground water. Manag Sci 11:80–93
Burt OR (1967) Temporal allocation of groundwater. Water Resour Res 3:45–56
Chakravorty U, Umetsu C (2003) Basinwide water management: a spatial model. J Environ Econ Manag 45:1–23
Fishman RM, Siegfried T, Raj P, Modi V, Lall U (2011) Over-extraction from shallow bedrock versus deep alluvial aquifers: Reliability versus sustainability considerations for India’s groundwater irrigation. Water Resour Res. doi:10.1029/2011WR010617
Gisser M, Sanchez DA (1980) Competition versus optimal control in groundwater pumping. Water Resour Res 16:638–642
Harbaugh AW, Banta ER, Hill MC, McDonald MG (2000) MODFLOW-2000, the US Geological Survey modular ground-water model: user guide to modularization concepts and the ground-water flow process. US Geological Survey, Reston
Hellegers P, Zilberman D, van Ierland E (2001) Dynamics of agricultural groundwater extraction. Ecol Econ 37:303–311
Heyman D, Sobel M (2003) Stochastic models in operations research: stochastic optimization, vol 2. Dover Pubns, Mineola
Hopenhayn H, Prescott E (1992) Stochastic monotonicity and stationary distributions for dynamic economies. Econometrica 60:1387–1406
Huh WT, Krishnamurthy CK, Weber R (2011) Concavity and monotonicity properties in a groundwater management model. Nav Res Logist (NRL) 58:670–675
Kennedy J, Hardaker J, Quiggin J (1994) Incorporating risk aversion into dynamic programming models: comment. Am J Agric Econ 76:960–964
Knapp K, Olson L (1996) Dynamic resource management: intertemporal substitution and risk aversion. Am J Agric Econ 78:1004–1014
Knapp K, Olson L (1995) The economics of conjunctive groundwater management with stochastic surface supplies. J Environ Econ Manag 28(3):340–356
Krautkraemer J, Van Kooten G, Young D (1992) Incorporating risk aversion into dynamic programming models. Am J Agric Econ 74:870–878
Krishnamurthy C (2012) Optimal management of groundwater under uncertainty: a unified approach. Working Paper No. 2012:19 (Revised June 2015), Center for Environmental and Resource Economics, Umeå
Madani K, Dinar A (2012) Non-cooperative institutions for sustainable common pool resource management: application to groundwater. Ecol Econ 74:34–45
Mendelssohn R, Sobel MJ (1980) Capital accumulation and the optimization of renewable resource models. J Econ Theory 23:243–260
Olson L, Roy S (2000) Dynamic efficiency of conservation of renewable resources under uncertainty. J Econ Theory 95:186–214
Prickett TA, Lonnquist CG (1971) Selected digital computer techniques for groundwater resource evaluation. Ill State Water Surv Bull 55:62
Provencher B, Burt O (1993) The externalities associated with the common property exploitation of groundwater. J Environ Econ Manag 24(2):139–158
Provencher B, Burt O (1994) A private property rights regime for the commons: the case for groundwater. Am J Agric Econ 76:875–888
Roseta-Palma C, Xepapadeas A (2004) Robust control in water management. J Risk Uncertain 29:21–34
Rubio S, Casino B (2001) Competitive versus efficient extraction of a common property resource: the groundwater case. J Econ Dyn Control 25:1117–1137
Rubio SJ, Castro JP (1996) Long run groundwater reserves under uncertainty. Investigaciones económicas 20:71–88
Sethi G, Costello C, Fisher A, Hanemann M, Karp L (2005) Fishery management under multiple uncertainty. J Environ Econ Manag 50(2):300–318
Shah T (2007) The groundwater economy of South Asia: an assessment of size, significance and socio-ecological impacts. In: Giordano M, Villholth KG (eds) The agricultural groundwater revolution: opportunities and threats to development. CABI, Wallingford, pp 7–36
Shah T (2010) Taming the anarchy: groundwater governance in South Asia. Routledge, London
Shah T, Bhatt S, Shah R, Talati J (2008) Groundwater governance through electricity supply management: assessing an innovative intervention in Gujarat, western India. Agric Water Manag 95:1233–1242
Siegfried T (2004) Optimal utilization of a non-renewable transboundary groundwater resource—Methodology, case study and policy implications, pp. 52–53. http://e-collection.library.ethz.ch/eserv/eth:27559/eth-27559-02.pdf
Stachurski J (2009) Economic dynamics: theory and computation. The MIT Press, Cambridge
Topkis D (1998) Supermodularity and complementarity. Princeton University Press, Princeton
Tsur Y, Graham-Tomasi T (1991) The buffer value of groundwater with stochastic water supplies. J Environ Econ Manag 21(3):201–224
Tsur Y, Zemel A (2004) Endangered aquifers: groundwater management under threats of catastrophic events. Water Resour Res 40:06S20. doi:10.1029/2003WR002168
Worthington VE, Burt OR, Brustkern RL (1985) Optimal management of a confined groundwater system. J Environ Econ Manag 12(3):229–245
Zeitouni N (2004) Optimal extraction from a renewable groundwater aquifer with stochastic recharge. Water Resour Res 40:W06S19
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper is extracted from Chapter 4 of my doctoral dissertation at Columbia University. I am very grateful to Bernard Salanié for a careful and critical reading of an early draft, to Tim Huh for key inputs, suggestions and general encouragement, to John Stachurski and Tobias Siegfried for helpful suggestions, and to my dissertation advisors Geoffrey Heal and Upmanu Lall. Thanks are also due to participants in the “Water Management II” session at the EAERE 2013, Toulouse, and to seminar participants at Columbia University. Finally, I wish to acknowledge very helpful suggestions and comments from an anonymous referee and the Editor that helped improve the quality of the paper. I alone am responsible for any errors and omissions.
Appendix: Definitions and Notations
Appendix: Definitions and Notations
1.1 Lattice Theory
We provide a few basic definitions of lattice theory, along with the needed notation, and direct the reader to Heyman and Sobel (2003) or Topkis (1998) for details. Let \(\mathcal {X}\subset \mathbb {R}_{+}\)be the state space (a lattice),Footnote 26 \(W:\mathcal {X}\rightarrow L\left( \mathcal {X}\right) \), with \(L(\mathcal {X})\) the set of all sub-lattices of \(\mathcal {X}\),Footnote 27 \(\mathcal {C}=\left\{ (x,w);x\in \mathcal {X},w\in W(x)\right\} \) be a sub-lattice of \(\mathbb {R}_{+}^{2}\).
Definition 4
(Ascending functions) The set-valued function W is called ascending in x on \(\mathcal {X}\) (or simply ‘ascending’) if it is increasing on \(\mathcal {X}\). Thus, if \(x_{1}, x_{2} \in \mathcal {X}\), then \(W(x_{1})\) and \(W(x_{2})\) are in \(L(\mathcal {X})\). Therefore, if \(x_{1}<x_{2}\), \(a\in W(x_{1})\) and \(b\in W(x_{2})\) and W is ascending on \(\mathcal {X}\), then necessarily \(a\wedge b\in W(x_{1})\) and \(a\vee b\in W(x_{2})\).
Definition 5
(Expanding Sets) The set W(x) is called “expanding” if \(x'<x\implies W(x)\subset W\left( x'\right) \).
Definition 6
(Stochastically supermodular) \(\tilde{X}(x,w)\), a random variable parametrized by (x, w), defined on a lattice \(\mathcal {X}\times \mathcal {X}\), \(F_{x,w}\) its distribution function, is said to be “stochastically supermodular” in (x, w) if either of the following conditions hold:
-
1.
\(\int _{S}dF_{x,w}(s)\) is supermodular in (x, w).
-
2.
\(\int h(s)dF_{x,w}(s)\) (as a deterministic function of (x, w)) is supermodular in (x, w), for all increasing and bounded functions h.
1.2 Convergence of Markov Processes
We provide here a very brief outline of key notions and definitions and refer the readers to Stachurski (2009, §8, §9.2, §11) for details. Denote by \(\mathcal {X}\) the state space, \(\mathcal {P}(\mathcal {X})\) the set of all (Borel-) probability measures on the state space, by \(\mathcal {B}(\mathcal {X})\) the set of Borel subsets of \(\mathcal {X}\), and by \(\mathcal {P}\left( \mathcal {R}\right) \) the set of all (Borel-) probability measures on the shock space, \(\mathcal {R}\). For ease of identification, we distinguish two sets of random variables, the initial state \(X_0\) and the Markov chain \(\left\{ X_t,t\ge 0 \right\} \), and the random recharge \(\left\{ R_t \right\} \), with respective densities (distributions) denoted by \(\psi \left( \Psi \right) \) and \(\phi \left( \Phi \right) \).
Definition 7
(Stochastic Kernel) P is a stochastic kernel for the S.R.S in Eq. (15), defined for \(B\in \mathcal {B}(\mathcal {X})\), \(x\in \mathcal {X}\), and \(\Phi \in \mathcal {P}\left( \mathcal {R}\right) \) as
with \(\mathbb {I}_{B}(.)\) an indicator function. To understand this definition, observe that \(P(x_t,B)=\mathbb {P}\left( F(x_t,R_{t+1}) \in B \right) =\mathbb {E}\left( \mathbb {I}_B \left[ F(x_t,R_{t+1})\right] \right) \).
Definition 8
(Markov Operator) Given a stochastic kernel P, an associated linear operator, the Markov operator \(M, M:\mathcal {P}(X)\rightarrow \mathcal {P}(X)\), maybe defined as
Let \(X_{0}\sim \Psi \in \mathcal {P}(\mathcal {X})\), and denote the distribution of \(\left( X_{t}\right) _{t\ge 0}\) as \(\Psi _{t}\). Then it is the case that the recursion \(\Psi _{t+1}=\Psi _{t}M\) holds, which yields, by an inductive argument, the infinite-dimensional version of the usual Markov chain identity: \(\Psi _{t+1}=\Psi M^{t}\).
Definition 9
(Feller Property) A Markov operator M is said to possess the ‘Feller Property’ if it maps bounded, continuous functions into bounded continuous functions.
Remark 12
(Sufficient condition for Feller Property) It can be shown that if the map F(x, R) is continuous in x for each R, then M satisfies the Feller Property. In fact, for F linear (affine) in x, as in the S.R.S in Eq. (16), it is sufficient that F is bounded. Considering instead the S.R.S corresponding to the transition equation for a finite aquifer in Eq. (2), it is evident that due to the continuity of \(\min (a(x),\overline{x})\) in x, F(x, R) is continuous and therefore, satisfies the Feller property. Similar is the case for the S.R.S in Eq. (18).
Definition 10
(Iterates of M) We illustrate the connection between the tth iterate of M applied to a function, h, and the same iterate applied to a distribution, \(\Psi \). Note first that since \(P^t(x,dy)\) may be interpreted as the distribution of \(X_t\) given \(X_0=x\), it is immediate that \(M^th(x)\), defined as
may be interpreted as a conditional expectation. Then, it can be shown (Stachurski 2009, Theorem 9.2.15) that \(\Psi (Mh)=(\Psi M)(h)=\int \left[ \int h(y) P(x,dy) \right] \Psi (dx)\), and by induction, \(\Psi (M^t h)=(\Psi M^t)(h)=\int \left[ \int h(y) P^t(x,dy) \right] \Psi (dx)\).
Definition 11
(Aperiodic kernel) A kernel P is said to be aperiodic if it has a \((\nu ,\epsilon )\)—small set C with \(\nu (C)>0\).
Definition 12
(Irreducible kernel) A kernel P is said to be \(\mu \)—irreducible, with \(\mu \in \mathcal {P}(\mathcal {X})\), if \( \forall x\in \mathcal {X} \& B \in \mathcal {B}(\mathcal {X})\) with \(\mu (B)>0\), \(\exists t\in \mathbb {N}\) s.t. \(P^{t}(x,B)>0\). If P is irreducible for an arbitrary \(\mu \in \mathcal {P}(\mathcal {X})\), then it is called irreducible.
Definitions 11 and 12 are the infinite state analogues of the classical definitions for finite state Markov Chains.
Definition 13
(Stability) Let \(\Psi ^{*}\) be an invariant distribution. Denoting by \(ib(\mathcal {X})\) \(\left( ibc(\mathcal {X})\right) \) the set of increasing and bounded (continuous) functions on \(\mathcal {X}\), stability of \(\Psi ^{*}\) is taken to mean
Definition 14
(Small set) Let \(\nu \in \mathcal {P}(\mathcal {X})\), \(\epsilon >0\). A set \(C\subset B(\mathcal {X})\) is called \((\nu ,\epsilon )\)—small for P if \(\forall x\in C\), it is the case that for \(A\in \mathcal {B}(\mathcal {X})\), \(P(x,A)\ge \epsilon \nu (A)\). If this condition holds for some \(\nu \) and \(\epsilon >0\), then the set C is called ‘small’.
Rights and permissions
About this article
Cite this article
Krishnamurthy, C.K.B. Optimal Management of Groundwater Under Uncertainty: A Unified Approach. Environ Resource Econ 67, 351–377 (2017). https://doi.org/10.1007/s10640-015-9989-7
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10640-015-9989-7