A Fitted L-Multi-Point Flux Approximation Method for Pricing Options

Abstract

In this paper, we introduce a special kind of finite volume method called Multi-Point Flux Approximation method (MPFA) to price European and American options in two dimensional domain. We focus on the L-MPFA method for space discretization of the diffusion term of Black–Scholes operator. The degeneracy of the Black-Scholes operator is tackled using the fitted finite volume method. This combination of fitted finite volume method and L-MPFA method coupled to upwind methods gives us a novel scheme, called the fitted L-MPFA method. Numerical experiments show the accuracy of the novel fitted L-MPFA method comparing to well known schemes for pricing options.

1 Introduction

In finance, an option is a contract which gives to the holder the right but not the obligation to buy (call) or to sell (put) an asset at a specific price (strike) at a certain date in the future (expiry date). We have two main types of options which are European and American options. European options are options that can be exercised only at expiry date while American options can be exercised anytime before the expiry date. This flexibility of exercising American options leads to solve an optimal stopping time problem in the Black–Scholes framework which incorporates the early exercise. Many studies focused on the pricing problem of American options were conducted and the linear complementary problem approach was quite popular for pricing American options (see Kovalov et al. 2007; Zhang et al. 2009; Wang et al. 2006; Topper 2005). This approach brings us to solve linear complementary problem stated as follows (see Topper 2005):

$$\begin{aligned} \left\{ \begin{array}{l} {{\cal L}}V \ge 0,\\ V-V^{\star } \ge 0,\\ {{\cal L}}V \cdot \big (V-V^{\star }\big ) = 0, \end{array} \right. \end{aligned}$$

(1)

where ${{\cal L}}$ is the following Black–Scholes operator

$$\begin{aligned} {{\cal L}}:=\dfrac{\partial V}{\partial \tau }-\frac{1}{2}\sum _{i,j=1}^n \sigma _i\sigma _j\rho _{ij}S_iS_j\frac{\partial ^2V}{\partial S_i \partial S_j}-r\sum _{i=1}^nS_i\frac{\partial V}{\partial S_i}+rV, \end{aligned}$$

(2)

with r is the risk free interest, V is the option value at time $\tau$, $V^{\star }$ is the payoff, $\tau =T-t$ with t and T respectively the instantaneous and maturity time. For $i,j=1,\ldots ,n,\,S_i$ represents the asset i price, $\sigma _i$ represents the volatility of asset i, $\rho _{ij}$ represents the correlation between the assets i and j.

Furthermore, (Wang et al. 2006) proposed a power penalty method to solve the linear complementary problem for pricing American options. The power penalty problem is formulated as follows:

$$\begin{aligned} {{\cal L}}V+\beta \big [V^{\star }-V\big ]_{+}^{1/k}=0, \end{aligned}$$

(3)

where $\beta$ is the penalty parameter and k is the power of the method. Let us notice that, when we take the penalty parameter $\beta =0$ in (3), we get the Black–Scholes Equation for pricing European options, with the operator ${{\cal L}}$ defined in (2). However, the power penalty problem (3) can not be solved analytically, therefore numerical methods are required for its resolution. Nevertheless, the Black–Scholes operator (2) is degenerated when the stock price approaches zero. This degeneracy can affect the accuracy of the numerical method used for the resolution. To tackle this problem, several methods have been proposed. The fitted finite volume method, proposed by S.Wang in Wang (2004) whereby a rigorous proof of convergence is provided, appears to be more attractive. Moreover, the fitted finite volume method has been used for the resolution of the two dimensional second order Black-Scholes PDE followed by the convergence proof in Huang et al. (2006). In spite of the fact that the fitted finite volume methods perform well for the resolution of the Black-Scholes PDE, they are only of order 1 with respect to asset price variable. Besides, the fitted O-Multi-Point Flux Approximation (O-MPFA) method has been proposed in Koffi and Tambue (2019a) to overcome the degeneracy problem of the Black–Scholes PDE. It has been shown that the O-MPFA is more accurate than the classical fitted finite volume method by Wang (2004). However, the O-MPFA is heavy (9 points stencil method) and for more general grids, the convergence rate of the O-MPFA method may decrease (see Aavatsmark 2007).

In this paper, we focus on the L-MPFA method which is based on the approximation of a linear function gradient defined over a given triangle and the continuity of flux through the edges of this triangle.

Indeed, the L-MPFA method is a 7 points stencil method while the O-MPFA is a 9 points stencil method. This shows that the O-MPFA method can be computationally more expensive than the L-MPFA method. Moreover, for more general grids, the order reduction in convergence rate is larger for the O-MPFA than the L-MPFA (see Aavatsmark 2002). Thereby, to approximate the solution of the second order Black-Scholes operator, we couple the L-MPFA method with the upwind methods (first and second order). Besides, the degeneracy of the Black-Scholes operator (2) is handled by the fitted finite volume,(Wang 2004), when the stock price is approaching zero. The L-MPFA method coupled with the upwind methods ($1{st}$ and $2{nd}$ order) is used to approximate the solution of (3) when the Black-Scholes operator is not degenerated. We call fitted L-MPFA method that combination of the L-MPFA method and the fitted finite volume method. Numerical simulations show that the new fitted L-MPFA method is more accurate than the fitted O-MPFA method developed in Koffi and Tambue (2019a) and the standard fitted finite volume method developed in Huang et al. (2006). Note that in dimension one, the L-MPFA method and the O-MPFA method are identical and are well known as Two Point Flux Approximation (TPFA). The rigorous convergence proof of the fitted TPFA for pricing options is provided in Koffi and Tambue (2019b). Note that the standard extension in high dimension of TPFA while keeping the two point flux approximation is very complicated on general grid and can only converge on M-orthogonal grids for simple diffusion problems (see Tambue 2016). Note that L-MPFA schemes are very different to O-MPFA schemes and the current paper is not a simple extension of the work in Koffi and Tambue (2019a). The key differences can be summarized in the following points:

• Here, we have considered American and Europeans options rather than Europeans options in Koffi and Tambue (2019a). Note that pricing American put options is very complicated as the exact solution does not exist even for constant coefficients. The American options pricing here is modeled by the nonlinear degenerated parabolic PDEs (4). We can observe that the current novel fitted L-MPFA is very robust for such degenerated nonlinear parabolic PDEs, where we have coupled with implicit time stepping methods. The corresponding nonlinear algebraic equations have been solved using a modified Newton method as the corresponding functions are not differentiable.

• The L-MPFA schemes presented here in two dimensional domain only have one additional cell added to the TPFA schemes, while still being able to handle general grids.

• For more general grids, the order reduction in convergence rate will be lower for the L-MPFA schemes than the O-MPFA schemes and few oscillations are expected here in the non-monotone parameter regions.

The paper is structured as follows. In Sect. 2, we present the power penalty problem with the corresponding initial and boundary conditions.

The spatial discretization of the linear operator is developed in the Sect. 3. Details on the L-MPFA method of the diffusion term discretization are provided. The convection term is discretized using the upwind methods ($1{st}$ and $2{nd}$ method). At the end of the Sect. 3, the novel fitted MPFA method is provided. The $\theta -$ Euler method is used for the time discretization method in the Sect. 4. Numerical experiments are presented for the different numerical methods in Sect. 5. The conclusions of our study are drawn in the last Section.

2 Formulation of the Problem

2.1 Option with Two Underlying Assets

Pricing an American option with 2 underlying assets leads to solve the following power penalty problem:

$$\begin{aligned} {{\cal L}}V+\beta \big [V^{\star }-V\big ]_{+}^{1/k}=0, \end{aligned}$$

(4)

where the Black–Scholes operator is defined as:

$$\begin{aligned} {{\cal L}}:=\frac{\partial V}{\partial \tau }-\frac{1}{2} \sigma ^2_1 x^2 \frac{\partial ^2 V}{\partial x^2} -\rho \sigma _1 \sigma _2 xy\frac{\partial ^2 V}{\partial x \partial y} - \frac{1}{2} \sigma _2^2 y^2 \frac{\partial ^2 V}{\partial y^2}-rx\frac{\partial V}{\partial x} -ry\frac{\partial V}{\partial y}+rV, \end{aligned}$$

(5)

with the following initial and boundary conditions

$$\begin{aligned} \left\{ \begin{array}{l} V(x,y,0) = V^*(x,y) = \max \left( K-\alpha _1 x-\alpha _2 y,0\right) ,\\ V(0,y,\tau ,)=V(x,0,\tau ,) = K,\\ \lim _{x,y\longrightarrow + \infty } V(x,y,\tau ) = 0 . \end{array} \right. \end{aligned}$$

(6)

K is the strike price, $V^*$ is the payoff for basket options and $\alpha _i, i=1,2$, are weights such that $\alpha _1+\alpha _2=1$.

In equation (4), when the penalty parameter $\beta =0$, we get the Black–Scholes Partial Differential Equation for pricing European options with the corresponding initial and boundary conditions

$$\begin{aligned} \left\{ \begin{array}{l} V(x,y,0)=V^*(x,y)=\max \left( K-\alpha _1 x-\alpha _2 y,0\right) ,\\ V(0,y,\tau )=V(x,0,\tau )=0,\\ \lim _{x\longrightarrow \infty }V(x,y,\tau )=x-Ke^{-r\tau },\\ \lim _{y\longrightarrow \infty }V(x,y,\tau )=y-Ke^{-r\tau }. \end{array}\right. \end{aligned}$$

(7)

In order to apply the finite volume method, it is convenient to re-write the Black–Scholes operator (5) in the following divergence form

$$\begin{aligned} \frac{\partial V}{\partial \tau }-\nabla \cdot (\mathbf {M}\nabla V)-\nabla (f V)-\lambda V+\beta \big [V^{\star }-V\big ]_{+}^{1/k}=0, \end{aligned}$$

(8)

where

$$\begin{aligned}&\mathbf {M}=\frac{1}{2}\left( \begin{array}{lr} \sigma _1^2 x^2 &{} \rho \sigma _1\sigma _2xy \\ &{} \\ \rho \sigma _1\sigma _2xy &{} \sigma _2^2 y^2 \end{array}\right) ,\quad f=\left( \begin{array}{c} (r-\sigma _1^2-\frac{1}{2}\rho \sigma _1\sigma _2)x \\ \\ (r-\sigma _2^2-\frac{1}{2}\rho \sigma _1\sigma _2)y \end{array}\right) ,\\&\\&\\& \lambda = -3r+\sigma _1^2+\sigma ^2_2+\rho \sigma _1\sigma _2. \end{aligned}$$

2.2 Finite Volume Method

Let us consider the new domain $\varOmega$ of study by truncating D such that $\varOmega =I_x\times I_y\times [0,T]$ where $I_x=[0,x_{\max }]$ and $I_y=[0,y_{\max }]$. In the sequel of this work, the Black–Scholes operator (5) is considered over the truncated domain $\varOmega$.

At $x=x_{\max }$ and $y=y_{\max }$, the linear boundary condition will be applied (Huang et al. 2006). The intervals $I_x$ and $I_y$ will be subdivided into $N+1$ subintervals in the following way:

$$\begin{aligned} I_{x_i}=[x_{i-1};x_i], \,\,I_{y_j}=[y_{j-1};y_j]\quad i,j =1,...,N+1. \end{aligned}$$

(9)

Let us set the mid-points $x_{i-\frac{1}{2}}$ and $y_{j-\frac{1}{2}}$ as follows

$$\begin{aligned} x_{i-\frac{1}{2}}=\frac{x_{i-1}+x_i}{2}, \,\,\, y_{j-\frac{1}{2}}=\frac{y_{j-1}+y_j}{2}, \qquad i,j =1,...,N, \end{aligned}$$

(10)

with $h_i=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}, l_j=y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}$, and

$$\begin{aligned} x_{-\frac{1}{2}}=x_0=0, \qquad x_{N+\frac{3}{2}}=x_{N+1}=x_{\max },\, y_{-\frac{1}{2}}=y_0=0 \,, \;\,y_{N+\frac{3}{2}}=y_{N+1}=y_{\max }. \end{aligned}$$

For $i,j=1,\ldots ,N$, we denote by $\mathcal {C}_{ij}=[x_{i-\frac{1}{2}};x_{i+\frac{1}{2}}]\times [y_{j-\frac{1}{2}};y_{j+\frac{1}{2}}]$ a control volume associated our subdivision. (Fig. 1)

Fig. 1

Control volume

Note that for $i,j=1,\ldots ,N$ the control volume $\mathcal {C}_{ij}$ is the area surrounding the grid point $(x_i,y_j)$.

Our goal is to approximate the option function V at $(x_i,y_j)$¹

by a function denoted $\mathcal {V}.$

The matrix $\mathbf {M}$ in (8) will be replaced by its average value in each control volume

$$\begin{aligned} \mathbf {M}^{ij}=\frac{1}{\mathrm {meas}(\mathcal {C}_{ij})}\int _{\mathcal {C}_{ij}}\mathbf {M}dxdy,\,\,\, i,j=1,...,N, \end{aligned}$$

(11)

where $\mathrm {meas}(\mathcal {C}_{ij})$ is the measure of $\mathcal {C}_{ij}$. Thereby,

$$\begin{aligned} M^{ij}= \left[ \begin{array}{lcr} \frac{\sigma _1^2}{6}\frac{x_{i+\frac{1}{2}}^3-x_{i-\frac{1}{2}}^3}{x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}}&{} &{}\frac{\rho \sigma _1\sigma _2}{8}(x_{i+\frac{1}{2}}+x_{i-\frac{1}{2}})(y_{j+\frac{1}{2}}+y_{j-\frac{1}{2}}) \\ &{} &{} \\ \frac{\rho \sigma _1\sigma _2}{8}(x_{i+\frac{1}{2}}+x_{i-\frac{1}{2}})(y_{j+\frac{1}{2}}+y_{j-\frac{1}{2}}) &{} &{} \frac{\sigma _2^2}{6}\frac{y_{j+\frac{1}{2}}^3 -y_{j-\frac{1}{2}}^3}{y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}} \end{array}\right] . \end{aligned}$$

Now let us consider the divergence form given in (8). According to the finite volume method, we integrate the partial differential equation (8) over each control volume $\mathcal {C}_{ij}$. For $i,j=1,...,N$,

$$\begin{aligned} \int _{\mathcal {C}_{ij}}\frac{\partial {\mathcal {V}}}{\partial {\tau }}d\mathcal {C}-\int _{\mathcal {C}_{ij}}\nabla \cdot (\mathbf {M}\nabla \mathcal {V}) d\mathcal {C}-\int _{\mathcal {C}_{ij}}\nabla (f \mathcal {V})d\mathcal {C}-\int _{\mathcal {C}_{ij}}\lambda \mathcal {V}d\mathcal {C}+\int _{\mathcal {C}_{ij}}\beta \big [V^{\star }-\mathcal {V}\big ]_{+}^{1/k}d\mathcal {C}=0. \end{aligned}$$

(12)

The next section will be dedicated to spatial discretization of equation (12). For the first and the last two terms on the left hand side of the equality sign, we use the mid-point quadrature rule for their approximation as follows:

$$\begin{aligned}&\int _{{\mathcal {C}}_{ij}}\frac{\partial {\mathcal {V}}}{\partial {\tau }}d\mathcal {C}\approx meas(\mathcal {C}_{ij})\frac{d{\mathcal {V}}}{d{\tau }}(x_i,y_j,\tau ) \approx h_il_j\frac{d{\mathcal {V}_{ij}}}{d{\tau }}, \end{aligned}$$

(13)

$$\begin{aligned}&\int _{{\mathcal {C}}_{ij}}\lambda \mathcal {V}d\mathcal {C}\approx meas(\mathcal {C}_{ij})\lambda \mathcal {V}(x_i,y_j,\tau ) \approx h_il_j\lambda \mathcal {V}_{ij}, \end{aligned}$$

(14)

$$\begin{aligned}&\int _{{\mathcal {C}}_{ij}}\beta \big [V^{\star }-\mathcal {V}\big ]_{+}^{1/k} d\mathcal {C}\approx meas(\mathcal {C}_{ij})\beta \big [V^{\star }-\mathcal {V}\big ]_{+}^{1/k} \approx h_il_j\beta \big [V_i^{\star }-\mathcal {V}_{ij}\big ]_{+}^{1/k}. \end{aligned}$$

(15)

The convection term

$$\begin{aligned} \int _{\mathcal {C}_{ij}}\nabla (f \mathcal {V})d\mathcal {C}\end{aligned}$$

(16)

of (12) will be approximated using the upwind methods (first or second order).

The diffusion term

$$\begin{aligned} \int _{\mathcal {C}_{ij}}\nabla \cdot (\mathbf {M}\nabla \mathcal {V}) d\mathcal {C}\end{aligned}$$

(17)

of (12) will be approximated using the L-Multi-Point Flux Approximation method (L-MPFA) or the fitted L- Multi-Point Flux Approximation method. More details about these methods will be given in the next section.

3 Space Discretization

The spatial discretization of (8) consists in approximating all terms in (12) over the control volumes of the study domain.

3.1 Discretization of the Diffusion Term

Let us start by applying the divergence theorem to the diffusion term (17) as follows, for $i,j=1,...,N$:

$$\begin{aligned} \mathcal {F}^{ij}=\int _{\mathcal {C}_{ij}}\nabla \cdot (\mathbf {M}^{ij}\nabla \mathcal {V}) d\mathcal {C}=\int _{\partial \mathcal {C}_{ij}}(\mathbf {M}^{ij}\nabla \mathcal {V})\cdot \mathbf {n}d\mathcal {C}, \end{aligned}$$

(18)

where $\mathbf {n}$ is the outward vector from the control volume.

Now, we can apply the so-called L-Multi-Point Flux Approximation (L-MPFA) method to approximate the integral defined in (18).

3.1.1 L -Multi-Point Flux Approximation (L-MPFA) Method

The L-MPFA method takes its name from the fact that the curve connecting the three control volume centres considered for the application of the method, constitutes a stylized “L”. Here, we follow the description of the L-method given in Aavatsmark (2002).

• Let us consider the triangle $x_1x_2x_3$ (see Fig. 2), and a linear function g defined over this triangle. We define

  $$\begin{aligned} \mathbf {X}\nabla g =\begin{bmatrix} g(x_2)-g(x_1) \\ g(x_3)-g(x_1) \end{bmatrix}, \end{aligned}$$

  (19)

  where

  $$\begin{aligned} \mathbf {X}=\begin{bmatrix} \big (x_2-x_1\big )^T\\ \big (x_3-x_1\big )^T \end{bmatrix}, \end{aligned}$$

  (20)

  Thereby, the gradient of the linear function g may be expressed as follows:

  $$\begin{aligned} \nabla g = \frac{1}{T} \Bigg (\nu _2\Big (g(x_2)-g(x_1)\Big )+\nu _3\Big (g(x_3)-g(x_1)\Big )\Bigg ), \end{aligned}$$

  (21)

  where $\nu _2,\nu _3$ are respectively the normal vector to $x_2-x_1$ and $x_3-x_1$ and defined by

  $$\begin{aligned} \nu _2=\mathbf {R}\big (x_2-x_1\big ),\,\,\nu _3=-\mathbf {R}\big (x_3-x_1\big ), \end{aligned}$$

  with

  $$ {\mathbf{R}} = \left[ {\begin{array}{*{20}l} 0 \hfill & 1 \hfill \\ { - 1} \hfill & 0 \hfill \\ \end{array} } \right] $$

  and

  $$\begin{aligned} T=\nu _2^T\mathbf {R}\nu _3. \end{aligned}$$

  Let’s notice that the matrix $\mathbf {R}$ is a rotation of angle $-\frac{\pi }{2}$. Thereby the vector $\nu _2$ and $\nu _3$ have same length with the vectors $x_2-x_1$ and $x_3-x_1$.

Fig. 2

Triangle $x_1x_2x_3$

Let us called interaction volume $\mathcal {R}_{ij}$, a cell grid defined as follows:

$$\begin{aligned} for\,i,j=1,\ldots ,N+1\quad \mathcal {R}_{ij}=[x_{i-1};x_i]\times [y_{j-1};y_j]. \end{aligned}$$

(22)

We denote respectively by $x_1(x_{i-1},y_{j-1}),x_2(x_{i},y_{j-1}),x_3(x_{i},y_{j})$  and $x_4(x_{i-1},y_{j})$ the centre of the control volumes $\mathcal {C}_{i-1, j-1},\mathcal {C}_{i, j-1},\mathcal {C}_{i-1,j}$ and $\mathcal {C}_{i,j}$. We denote also by $\bar{x}_1,\bar{x}_2,\bar{x}_3\,\,and\,\,\bar{x}_4$ the midpoints of the segment $x_1x_2$, $x_3x_4,x_1x_3\,\,and\,\,x_2x_4$. We may notice that an interaction volume $\mathcal {R}_{ij}$, for $i,j=1,\ldots ,N+1$, is covering an area in the intersection of the control volumes $\mathcal {C}_{{i-1},{j-1}},\mathcal {C}_{i,j-1},\mathcal {C}_{i-1,j}$ and $\mathcal {C}_{ij}$. An interaction volume can be divided into 2 triangles such that the half edges 1, 2 are in the triangle $T_1=x_1x_2x_3$ and the half edges 3, 4 are in the triangle $T_2=x_1x_3x_4$ (see Fig. 3).

Here, we follow the procedure in Aavatsmark (2007).

Fig. 3

Interaction volume

In an interaction volume, we aim to compute the flux through the half edges 1, 2, 3 and 4 (See Fig. 3).

Thereby, using (18), the flux $f_p^{ij}$ through the half edge p seen from the centre of the control volume $\mathcal {C}_{ij}$ is expressed as follows:

$$\begin{aligned} f_p^{ij}=n_p^T\mathbf {M}^{ij}\nabla \mathcal {V}_{ij}, \end{aligned}$$

(23)

where $n_p$ is the vector normal to the half edge p with the same length.

Fig. 4

Triangle $T_1$

Let us consider the triangle $T_1=x_1x_2x_3$ from the interaction volume $\mathcal {R}_{ij}$

• In the triangle $T_{12}=\bar{x}_1x_2\bar{x}_2$, using the flux expression (23) and the gradient expression (21), it follows that

  $$\begin{aligned} f_1^{i,j-1}= & {} \omega _{12}^{i,j-1}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\omega _{11}^{i,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1}\Big ), \nonumber \\ f_2^{i,j-1}= & {} \omega _{22}^{i,j-1}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\omega _{21}^{i,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1}\Big ), \end{aligned}$$

  (24)

  where

  $$\begin{aligned} \omega _{11}^{i,j-1}&= \frac{1}{T_1^{i,j-1}}\times n_1^T \mathbf {M}^{i,j-1} \nu _1,\quad\omega _{12}^{i,j-1}= \frac{1}{T_1^{i,j-1}}\times n_1^T \mathbf {M}^{i,j-1} \nu _2, \\ \omega _{21}^{i,j-1}&= \frac{1}{T_1^{i,j-1}}\times n_2^T \mathbf {M}^{i,j-1} \nu _1,\quad \omega _{22}^{i,j-1}= \frac{1}{T_1^{i,j-1}}\times n_2^T \mathbf {M}^{i,j-1} \nu _2, \end{aligned}$$

  with

  $$\begin{aligned} T_1^{i,j-1}=-\nu _2^T\mathbf {R}\nu _1. \end{aligned}$$

• Besides, using the property of the matrix $\mathbf {R}$, we have

  $$\begin{aligned} \nu _4=\mathbf {R}(\bar{x}_5-x_2). \end{aligned}$$

  (25)

  Moreover, using equation (19) and the expression of gradient (21) in the triangle $T_{12}$ leads to

  $$\begin{aligned} \bar{\mathcal {V}}_5 = \mathcal {V}_{i,j-1}+\chi _{42}^{i,j-1}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\chi _{41}^{i,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1}\Big ), \end{aligned}$$

  (26)

  where

  $$\begin{aligned} \chi _{41}^{i,j-1}=\frac{1}{T_1^{i,j-1}}\nu _4^T\mathbf {R}\nu _1 \\ \\ \chi _{42}^{i,j-1}=\frac{1}{T_1^{i,j-1}}\nu _4^T\mathbf {R}\nu _2, \end{aligned}$$

• In the triangle $T_{11}=x_1\bar{x}_1\bar{x}_5$,

  $$\begin{aligned} f_1^{i-1,j-1} = \omega _{13}^{i-1,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i-1,j-1}\Big )+\omega _{12}^{i-1,j-1}\Big (\bar{\mathcal {V}}_5-\mathcal {V}_{i-1,j-1}\Big ). \end{aligned}$$

  (27)

  Replacing $\bar{\mathcal {V}}_5$ by its expression (26) in (27), it reads

  $$\begin{aligned} f_1^{i-1,j-1}&= \omega _{13}^{i-1,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i-1,j-1}\Big ) \nonumber \\&\quad+\,\omega _{12}^{i-1,j-1}\Bigg (\mathcal {V}_{i,j-1}-\mathcal {V}_{i-1,j-1}+\chi _{42}^{i,j-1} \Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\chi _{41}^{i,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1}\Big )\Bigg ), \end{aligned}$$

  (28)

  where

  $$\begin{aligned} \omega _{13}^{i-1,j-1}= \frac{1}{T_1^{i-1,j-1}}\times n_1^T \mathbf {M}^{i-1,j-1} \nu _3,\quad \omega _{12}^{i-1,j-1}= \frac{1}{T_1^{i-1,j-1}}\times n_1^T \mathbf {M}^{i-1,j-1} \nu _2, \\ \end{aligned}$$

  with

  $$\begin{aligned} T_1^{i-1,j-1}=\nu _3^T\mathbf {R}\nu _2. \end{aligned}$$

• Similarly, in the triangle $T_{13}=\bar{x}_5\bar{x}_2x_3$,

  $$\begin{aligned} f_2^{ij} = -\omega _{21}^{ij}\Big (\bar{\mathcal {V}}_5-\mathcal {V}_{ij}\Big )+\omega _{23}^{ij}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{ij}\Big ). \end{aligned}$$

  (29)

  Replacing $\bar{\mathcal {V}}_5$ by its expression (26) in (29), it reads

  $$\begin{aligned} f_2^{ij}&= -\omega _{21}^{ij}\Bigg (\mathcal {V}_{i,j-1}-\mathcal {V}_{ij}+\chi _{42}^{i,j-1}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\chi _{41}^{i,j-1} \Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1}\Big )\Bigg ) \nonumber \\&\quad +\omega _{23}^{ij}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{ij}\Big ), \end{aligned}$$

  (30)

  where

  $$\begin{aligned} \omega _{21}^{ij}= \frac{1}{T_1^{ij}}\times n_2^T \mathbf {M}^{ij} \nu _1,\quad \omega _{23}^{ij}= \frac{1}{T_1^{ij}}\times n_2^T \mathbf {M}^{ij} \nu _3, \\ \end{aligned}$$

  with

  $$\begin{aligned} T_1^{ij}=-\nu _3^T\mathbf {R}\nu _3. \end{aligned}$$

• Since the flux is continuous through edges, then using (24), (28) and (30) leads to

  $$\begin{aligned}\left\{\begin{array}{l} f_1 = \omega _{12}^{i,j-1}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\omega _{11}^{i,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1}\Big ) \\ \quad = \omega _{13}^{i-1,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i-1,j-1}\Big )+\omega _{12}^{i-1,j-1}\Bigg (\mathcal {V}_{i,j-1}-\mathcal {V}_{i-1,j-1} +\chi _{42}^{i,j-1}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\chi _{41}^{i,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1}\Big )\Bigg ),\\ f_2 = \omega _{22}^{i,j-1}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\omega _{21}^{i,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1}\Big ) \\ \quad = -\omega _{21}^{ij}\Bigg (\mathcal {V}_{i,j-1}-\mathcal {V}_{ij}+\chi _{42}^{i,j-1}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{i,j-1}\Big )-\chi _{41}^{i,j-1}\Big (\bar{\mathcal {V}}_1-\mathcal {V}_{i,j-1} \Big )\Bigg )+\omega _{23}^{ij}\Big (\bar{\mathcal {V}}_2-\mathcal {V}_{ij}\Big ).\end{array}\right. \end{aligned}$$

  (31)

By setting

$$\begin{aligned} g=\left[ \begin{array}{c} f_1 \\ f_2\end{array}\right] , W=\left[ \begin{array}{c} \mathcal {V}_{i-1,j-1} \\ \mathcal {V}_{i,j-1} \\ \mathcal {V}_{ij}\end{array}\right] , \mathcal {V}=\left[ \begin{array}{c} \bar{\mathcal {V}}_1 \\ \bar{\mathcal {V}}_2 \\ \end{array}\right] , \end{aligned}$$

(32)

the system of equations (31) can be written as

$$\begin{aligned} g=C^{ij} \mathcal {V}+D^{ij}W, \end{aligned}$$

(33)

where

$$\begin{aligned} C^{ij}= & {} \left[ \begin{array}{cc} -\omega _{11}^{i,j-1} &{} \omega _{12}^{i,j-1} \\ &{} \\ -\omega _{21}^{i,j-1} &{} \omega _{22}^{i,j-1}\\ \end{array}\right] , D^{ij}=\left[ \begin{array}{ccc} 0 &{} \omega _{11}^{i,j-1}-\omega _{12}^{i,j-1} &{} 0 \\ &{} &{} \\ 0 &{} \omega _{21}^{i,j-1}-\omega _{22}^{i,j-1} &{} 0 \\ \end{array}\right] . \end{aligned}$$

Using the expressions at both sides of the second equalities of system equations (31) gives

$$\begin{aligned} A^{ij}\mathcal {V}=B^{ij}W, \end{aligned}$$

(34)

where

$$\begin{aligned} A^{ij}= & {} \left[ \begin{array}{cc} \omega _{11}^{i,j-1}+\omega _{13}^{i-1,j-1}-\omega _{12}^{i-1,j-1}\chi _{41}^{i,j-1} &{} -\omega _{12}^{i,j-1}+\omega _{12}^{i-1,j-1}\chi _{42}^{i,j-1} \\ &{} \\ \omega _{21}^{i,j-1}+\omega _{21}^{ij}\chi _{41}^{i,j-1} &{} -\omega _{22}^{i,j-1}+\omega _{23}^{ij}-\omega _{21}^{ij}\chi _{42}^{i,j-1}\\ \end{array}\right] , \\ B^{ij}= & {} \left[ \begin{array}{cccc} \omega _{13}^{i-1,j-1}+\omega _{12}^{i-1,j-1} &{} &{} -\omega _{12}^{i,j-1}+\omega _{11}^{i,j-1}-\omega _{12}^{i-1,j-1}\big (1+\chi _{41}^{i,j-1}-\chi _{42}^{i,j-1}\big ) &{} 0 \\ &{} &{} &{} \\ 0 &{} &{} -\omega _{22}^{i,j-1}+\omega _{21}^{i,j-1}+\omega _{21}^{ij}\big (1+\chi _{41}^{i,j-1}-\chi _{42}^{i,j-1}\big ) &{} -\omega _{21}^{ij}+\omega _{23}^{ij}\\ \end{array}\right] . \end{aligned}$$

Thereby, by solving (34) with respect to $\mathcal {V}$ and replacing in (33) we get

$$\begin{aligned} g=R^{ij}\mathcal {V}, \end{aligned}$$

(35)

where

$$\begin{aligned} R^{ij}=C^{ij}[A^{ij}]^{-1}B^{ij}+D^{ij}. \end{aligned}$$

Now considering the triangle $T_2$ (see Fig. 3) and applying the above procedure used in the triangle $T_1$, we are able to calculate the fluxes through the half edges 3 and 4 as follows:

$$\begin{aligned} h=S^{ij}V, \end{aligned}$$

(36)

where

$$\begin{aligned} h=\left[ \begin{array}{c} f_3 \\ f_4\end{array}\right] , V=\left[ \begin{array}{c} \mathcal {V}_{i,j-1} \\ \mathcal {V}_{ij} \\ \mathcal {V}_{ij}\end{array}\right] . \end{aligned}$$

For simplicity, in an interaction volume $\mathcal {R}_{ij}$, the flux through the half edges 1, 2, 3 and 4 are given by

$$\begin{aligned} f=T^{ij}\mathcal {V}\end{aligned}$$

(37)

where

$$\begin{aligned} f=\left[ \begin{array}{c} f_1 \\ f_2 \\ f_3 \\ f_4 \end{array}\right] , \mathcal {V}=\left[ \begin{array}{c} \mathcal {V}_{i-1,j-1} \\ \mathcal {V}_{i,j-1} \\ \mathcal {V}_{ij} \\ \mathcal {V}_{i-1,j} \end{array}\right] , \end{aligned}$$

(38)

and $T^{ij}$ is $4\times 4$ matrix coming from $R^{ij}$ and $S^{ij}$ defined in (35),(36). $T^{ij}$ is called the transmissibility matrix of the interaction volume $\mathcal {R}_{ij}$.

Let us notice that the flux through a full edge will be the addition of the fluxes through its 2 half edges. (Fig. 5)

Let us recall that, from (18), our aim is to compute the flux through the edges of the control volume $\mathcal {C}_{ij}$. In order to cover the boundary of a control volume, we need four interaction volumes

Fig. 5

Flux through eastern edge of control volume C_ij

Let us denote, for the volume control $\mathcal {C}_{ij}$, by ${}_{\mathcal {E}}f_{l}^{ij}$ the flux through lower half eastern edge, by ${}_{\mathcal {E}}f_{u}^{ij}$ the flux through the upper half eastern edge. The flux ${}_{\mathcal {E}}f^{ij}$ through the east edge of the control volume $\mathcal {C}_{ij}$ is calculated as follows:

The lower half eastern edge is in position 3 in the triangle $T_2$ of the interaction volume $\mathcal {R}_{i+1,j}$ (see Fig. 4). So by using (37), the flux is given by

$$\begin{aligned} {}_{\mathcal {E}}f_{l}^{ij}=T_{31}^{i+1,j}\mathcal {V}_{i,j-1}+T_{33}^{i+1,j}\mathcal {V}_{i+1,j}+T_{34}^{i+1,j}\mathcal {V}_{ij}. \end{aligned}$$

Similarly, the upper half eastern edge is in position 1 in the triangle $T_1$ of the interaction volume $\mathcal {R}_{i+1,j+1}$ and it is in position 1 in the interaction volume. Thereby using (37), the flux is given by

$$\begin{aligned} {}_{\mathcal {E}}f_u^{ij}=T_{11}^{i+1,j+1}\mathcal {V}_{ij}+T_{12}^{i+1,j+1}\mathcal {V}_{i+1,j}+T_{13}^{i+1,j+1}\mathcal {V}_{i+1,j+1}. \end{aligned}$$

Finally the flux through the eastern edge of the control volume $\mathcal {C}_{ij}$ will be the addition of ${}_{\mathcal {E}}f_{l}^{ij}$ and ${}_{\mathcal {E}}f_u^{ij}$. Thus,

$$\begin{aligned} {}_{\mathcal {E}}f^{ij}&= {}_{\mathcal {E}}f_d^{ij}+{}_{\mathcal {E}}f_u^{ij} \nonumber \\ {}_{\mathcal {E}}f^{ij}&= T_{31}^{i+1,j}\mathcal {V}_{i,j-1}+\Big (T_{33}^{i+1,j}+T^{i+1,j+1}_{12}\Big )\mathcal {V}_{i+1,j}+\Big (T_{11}^{i+1,j+1}+T_{34}^{i+1,j}\Big )\mathcal {V}_{ij} \nonumber \\&\quad +T_{13}^{i+1,j+1}\mathcal {V}_{i+1,j+1}, \end{aligned}$$

(39)

The same method is applied to calculate the flux through the northern, western and southern edges of the control volume $\mathcal {C}_{ij}$. The flux through the edges of the control volume $\mathcal {C}_{ij}$ is obtained by summing up the flux through the 4 edges. This gives :

$$\begin{aligned} \mathcal {F}_{ij} = a_{ij}\mathcal {V}_{ij}+b_{ij}\mathcal {V}_{i+1,j}+c_{ij}\mathcal {V}_{i+1,j+1}+d_{ij}\mathcal {V}_{i,j+1}+e_{ij}\mathcal {V}_{i-1,j}+\alpha _{ij}\mathcal {V}_{i-1,j-1}+\beta _{ij}\mathcal {V}_{i,j-1} , \end{aligned}$$

(40)

where

$$\begin{aligned}&a_{ij}=T_{11}^{i+1,j+1}+T_{34}^{i+1,j}+T_{41}^{i+1,j+1}+T_{22}^{i,j+1}-T_{12}^{i,j+1}-T_{33}^{ij}-T_{23}^{ij}-T_{44}^{i+1,j},\\&b_{ij}=T_{33}^{i+1,j}+T^{i+1,j+1}_{12}-T_{43}^{i+1,j}, c_{ij}=T_{13}^{i+1,j+1}+T^{i+1,j+1}_{43}, d_{ij}=T_{23}^{i,j+1}+T_{44}^{i+1,j+1}-T_{13}^{i,j+1},\\&e_{ij}=T_{21}^{i,j+1}-T_{11}^{i,j+1}-T_{34}^{ij}, \alpha _{ij}=-T_{31}^{ij}-T_{21}^{ij}, \beta _{ij}=T_{31}^{i+1,j}-T_{22}^{ij}-T_{41}^{i+1,j}. \end{aligned}$$

This leads to a system of equations which can be written as follows:

$$\begin{aligned} \mathcal {F}=A_{mp}\mathcal {V}+F_{mp}, \end{aligned}$$

(41)

where

$$\begin{aligned} \mathcal {F}=\begin{bmatrix} \mathcal {F}_{11}\\ \mathcal {F}_{12}\\ \vdots \\ \mathcal {F}_{1N}\\ \mathcal {F}_{21}\\ \mathcal {F}_{22}\\ \vdots \\ \vdots \\ \mathcal {F}_{NN} \end{bmatrix}, \mathcal {V}=\begin{bmatrix} \mathcal {V}_{11}\\ \mathcal {V}_{12}\\ \vdots \\ \mathcal {V}_{1N}\\ \mathcal {V}_{21}\\ \mathcal {V}_{22}\\ \vdots \\ \vdots \\ \mathcal {V}_{NN} \end{bmatrix}, A_{mp}=\begin{bmatrix} W_1 &{} X_1 &{} 0_N &{} \ldots &{} \ldots &{} \ldots &{} \ldots &{} 0_N\\ Y_2 &{} W_2 &{} X_2 &{} \ddots &{} &{} &{} &{} \vdots \\ 0_N &{} Y_3 &{} W_3 &{} X_3 &{} \ddots &{} &{} &{} \vdots \\ \vdots &{} \ddots &{} Y_4 &{} W_4 &{} X_4 &{} \ddots &{} &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} 0_N&{} \\ \vdots &{} &{} &{} &{} \ddots &{} Y_{N-1} &{} W_{N-1} &{} X_{N-1} \\ 0_N &{} \ldots &{} \ldots &{} \ldots &{} \ldots &{} 0_N &{} Y_N &{} W_N \end{bmatrix}, \end{aligned}$$

with $0_N$ is $N\times N$ zeros matrix, $W_i,X_i,Z_i$ are tridiagonal matrix and $F_{mp}$ is a $N^2$ vector coming from the boundary conditions.

As we can see on Fig. 6, the L-MPFA method is a 7 points stencil method, unlike the O-MPFA method (see Koffi and Tambue 2019a ) which is a 9 points stencil method.

Fig. 6

A structure of the diffusion matrix using L-MPFA method

3.2 Discretisation of the Convection Term

The integral of convection term

$$\begin{aligned} \int _{\mathcal {C}_{ij}}\nabla (f \mathcal {V})d\mathcal {C}, \end{aligned}$$

where

$$\begin{aligned} f=\left( \begin{array}{c} (r-\sigma _1^2-\frac{1}{2}\rho \sigma _1\sigma _2)x \\ (r-\sigma _2^2-\frac{1}{2}\rho \sigma _1\sigma _2)y \end{array}\right) , \end{aligned}$$

will be approximated using the upwind methods ($1{st}$ and $2{nd}$ order ). We start by applying the divergence theorem, and we have for $i,j=1,...,N$:

$$\begin{aligned} I^{ij}=\int _{\mathcal {C}_{ij}}\nabla (f \mathcal {V}) d \mathcal {C}_{ij}=\int _{\partial \mathcal {C}_{ij}}(f\cdot \mathcal {V})\cdot \mathbf {n}d\mathcal {C}_{i,j}, \end{aligned}$$

(42)

with n an outward unit normal vector.

3.2.1 First Order Upwind Method

The first order upwind method discussed in (LeVeque 2004, chapter 4.8) will be applied to evaluate the second term of (12).

$I^{ij}$ is calculated by summing up the flux through the edges of the control volume $\mathcal {C}_{ij}$.

The flux through an edge using the first order upwind will depend on the sign of $f\cdot \mathbf {n}$ on this edge. If the sign of $f\cdot \mathbf {n}$ is positive, $\mathcal {V}_{ij}$ will be used to approximate $(f\cdot \mathbf {n} \mathcal {V})$ otherwise we will use the value of $\mathcal {V}$ in other side of the edge.

By doing so, we get for $i,j=1,...,N,$

$$\begin{aligned} I^{ij}=& {} \epsilon _{ij}\mathcal {V}_{i-1,j}+\mu _{ij}\mathcal {V}_{i,j-1}+\varOmega _{ij}\mathcal {V}_{ij}+ \phi _{ij}\mathcal {V}_{i,j+1}+\varPsi _{ij}\mathcal {V}_{i+1,j}, \end{aligned}$$

(43)

where

$$\begin{aligned}&\epsilon _{ij}=-l_jf_x^{i-1}\max (f_x^{i-1},0), \mu _{ij}=-h_if_y^{j-1}\max (f_y^{j-1},0),\\&\varOmega _{ij}=l_j\Bigg (f_x^{i}\max (f_x^{i},0)- f_x^{i-1}\min (f_x^{i-1},0)\Bigg ) +h_i\Bigg (f_y^j\max (f_y^j,0)-f_y^{j-1}\min (f_y^{j-1},0)\Bigg ),\\&\phi _{ij}=h_if_y^j\min (f_y^j,0), \varPsi _{ij}=l_jf_x^{i}\min (f_x^{i},0). \end{aligned}$$

Equation (43) will lead to a system of equations which be written as follows:

$$\begin{aligned} I=A_{up} \mathcal {V}+F_{up}, \end{aligned}$$

(44)

$A_{up}$ is a ${N^2} \times {N^2}$ matrix

$$\begin{aligned} I=\begin{bmatrix} I^{11}\\ I^{12}\\ \vdots \\ I^{1N}\\ I^{21}\\ I^{22}\\ \vdots \\ \vdots \\ I^{NN}\\ \end{bmatrix}, \mathcal {V}=\begin{bmatrix} \mathcal {V}_{11}\\ \mathcal {V}_{12}\\ \vdots \\ \mathcal {V}_{1N}\\ \mathcal {V}_{21}\\ \mathcal {V}_{22}\\ \vdots \\ \vdots \\ \mathcal {V}_{NN}\\ \end{bmatrix}, A_{up}=\begin{bmatrix} H_1 &{} P_1 &{} 0_N &{} \ldots &{} \ldots &{} \ldots &{} 0_N \\ Q_2 &{} H_2 &{} P_2&{} \ddots &{} &{} &{} \vdots \\ 0_N &{} Q_3 &{} H_3 &{} P_3 &{} \ddots &{} &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} \ddots &{} Q_{N-2} &{} H_{N-2} &{} P_{N-2} &{} 0_N \\ \vdots &{} &{} &{} \ddots &{} Q_{N-1} &{} H_{N-1} &{} P_{N-1}\\ 0_N &{} \dots &{} \ldots &{} \ldots &{} 0_N &{} Q_N &{} H_N \end{bmatrix}, \end{aligned}$$

with $0_{N}$ is $N\times N$ zeros matrix, $H_i$ is a tridiagonal matrix, $P_i,Q_i$ are diagonal matrices and $F_{up}$ is a vector coming from the boundary conditions.

Therefore, combining the L-MPFA method (41) and the first order upwind (44), we get

$$\begin{aligned} \frac{d\mathcal {V}}{d\tau }=A\mathcal {V}+G(\mathcal {V})+F, \end{aligned}$$

(45)

with

$$\begin{aligned} A=L^{-1}\Bigg (A_{mp}+A_{up}+A_L\Bigg ), G(\mathcal {V})=\beta \Big [\max \Big (\mathcal {V}^*-\mathcal {V},0\Big )\Big ]^{1/k}, F=L^{-1}\Bigg (F_{mp}+F_{up}\Bigg ), \end{aligned}$$

where $A_L$ is a diagonal matrix of size ${N^2}\times {N^2}$ coming from the discretisation of (14). The diagonal elements of $A_L$ are $(A_L)_{ii}=h_il_i\lambda,$ for $i=1,...,N^2$ with $\lambda$ given in (8). The matrix L is also a diagonal matrix of size $N^2 \times N^2$ whose diagonal elements are $L_{ii}=h_il_i,$ for $i=1,\ldots ,N^2.$

3.2.2 Second Order Upwind Method

A second order approximation is used to calculated the flux defined in (42). For instance, the flux ${}_{\mathcal {E}}J^{ij}$ through the eastern edge of the control volume $\mathcal {C}_{ij}$ is approximated as follows: We will start by giving an approximation of the gradient in the integral expression (18)

$$\begin{aligned} {}_{\mathcal {E}}J^{ij}=\int _{\mathcal {E}_{ij}} (f\cdot \mathcal {V})\cdot n_{\mathcal {E}}, \end{aligned}$$

(46)

where

$$\begin{aligned} \mathbf {n}_{\mathcal {E}}=\begin{bmatrix} 1\\ \\ 0 \end{bmatrix}, \end{aligned}$$

is the outward unit normal vector to the eastern edge $\mathcal {E}_{ij}$ of the control volume $\mathcal {C}_{ij}$. We set $f_x=f\cdot n_{\mathcal {E}}$ and we have

$$\begin{aligned} \mathcal {V}\approx \left\{ \begin{array}{ll} \frac{3\mathcal {V}_{ij}-\mathcal {V}_{i-1,j}}{2}& \quad if\,\,f_x\ge 0, \\ \frac{3\mathcal {V}_{i+1,j}-\mathcal {V}_{i+2,j}}{2} & \quad if\,\,f_x<0. \end{array} \right. \end{aligned}$$

(47)

Then we get

$$\begin{aligned} {}_{\mathcal {E}}J^{ij}=l_j\Bigg [\frac{3}{2}\max (f_x^{i+1},0)\mathcal {V}_{ij}-\frac{1}{2}\max (f_x^{i+1},0)\mathcal {V}_{i-1,j} +\frac{3}{2}\min (f_x^{i+1},0)\mathcal {V}_{i+1,j}-\frac{1}{2}\min (f_x^{i+1},0)\mathcal {V}_{i+2,j}\Bigg ], \end{aligned}$$

(48)

with

$$\begin{aligned} f_x^{i+1}=(r-\sigma _x^2 - \frac{1}{2}\rho \sigma _x \sigma _y)x_{i+\frac{1}{2}}. \end{aligned}$$

We use the same argument to calculate the flux ${}_{{N}}J^{ij},{}_{\mathcal {W}}J^{ij},{}_{S}J^{ij}$ through the northern, western and southern edges of the control volume $\mathcal {C}_{ij}$ and after sum them up. We get then

$$\begin{aligned} J^{ij}&= \epsilon _{ij}\mathcal {V}_{i-2,j}+\eta _{ij}\mathcal {V}{i-1,j}+\kappa _{ij}\mathcal {V}_{i,j-2}+\mu _{ij}\mathcal {V}_{i,j-1}+\varOmega _{ij}\mathcal {V}_{ij} \nonumber \\&\quad +\phi _{ij}\mathcal {V}_{i,j+1}+\varPsi _{ij}\mathcal {V}_{i,j+2}+\varDelta _{ij}\mathcal {V}_{i+1,j} \nonumber \\&\quad +\Pi _{ij}\mathcal {V}_{i+2,j}, \end{aligned}$$

(49)

where

$$\begin{aligned}&\epsilon _{ij}=\frac{1}{2}l_j\max (f_x^i,0), \eta _{ij}=-\frac{1}{2}l_j\max (f_x^{i+1},0)-\frac{3}{2}l_j\max (f_x^{i},0),\\&\kappa _{ij}=\frac{1}{2}h_i\max (f_y^j,0), \mu _{ij}=-\frac{1}{2}h_i\max (f_y^{j+1},0)-\frac{3}{2}h_i\max (f_y^{j},0),\\&\varOmega _{ij}=\frac{3}{2}l_j\max (f_x^{i+1},0)+\frac{3}{2}h_i\max (f_y^{j+1},0)-\frac{3}{2}l_j\min (f_x^{i},0)-\frac{3}{2}h_i\min (f_y^{j},0),\\&\phi _{ij}=\frac{3}{2}h_i\min (f_y^{j+1},0)+\frac{1}{2}h_i\min (f_y^j,0), \varPsi _{ij}=-\frac{1}{2}h_i\min (f_y^{j+1},0),\\&\varDelta _{ij}=\frac{3}{2}l_j\min (f_x^{i+1},0)+\frac{1}{2}l_j\min (f_x^i,0), \Pi _{ij}=-\frac{1}{2}l_j\min (f_x^{i+1},0). \end{aligned}$$

For the control volumes near the boundary of the study domain, the first order upwind method is used for the approximation of the flux through edges directly connected to the boundary.

Equation (49) leads to a system of equations which can be written as:

$$\begin{aligned} J=A_{2up} \mathcal {V}+F_{2up}, \end{aligned}$$

(50)

where

$$\begin{aligned} J=\begin{bmatrix} J^{11}\\ J^{12}\\ \vdots \\ J^{1N}\\ J^{21}\\ J^{22}\\ \vdots \\ J^{NN} \end{bmatrix}, \mathcal {V}=\begin{bmatrix} \mathcal {V}_{11}\\ \mathcal {V}_{12}\\ \vdots \\ \mathcal {V}_{1N}\\ \mathcal {V}_{21}\\ \mathcal {V}_{22}\\ \vdots \\ \mathcal {V}_{NN}\\ \end{bmatrix}, A_{2up}=\begin{bmatrix} K_1 &{} R_1 &{} G_1 &{} 0_N &{} \ldots &{} \ldots &{} 0_N \\ S_2 &{} K_2 &{} R_2&{} G_2 &{} \ddots &{} &{} \vdots \\ H_3 &{} S_3 &{} K_3 &{} R_3 &{} G_3 &{} \ddots &{} \vdots \\ 0_N &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} 0_N\\ \vdots &{} &{} H_{N-2} &{} S_{N-2} &{} K_{N-2} &{} R_{N-2} &{} G_{N-2} \\ \vdots &{} &{} &{} H_{N-1} &{} S_{N-1} &{} K_{N-1} &{} R_{N-1}&{} \\ 0_N &{} \dots &{} \ldots &{} 0_N &{} H_N &{} S_N &{} K_N \\ \end{bmatrix}, \end{aligned}$$

where for $i=1,\ldots ,N, K_i$ is penta-diagonal matrice and $R_i,G_i,S_i,H_i$ are diagonal matrices. $F_{2up}$ is a vector coming from the boundary conditions.

Therefore, combining the L-MPFA method (41) and the second order upwind method (50), we have

$$\begin{aligned} \frac{d\mathcal {V}}{d\tau }=A\mathcal {V}+G(\mathcal {V})+F, \end{aligned}$$

(51)

with

$$\begin{aligned} A=L^{-1}\Bigg (A_{mp}+A_{2up}+A_L\Bigg ), G(\mathcal {V})=\beta \Big [\max \Big (\mathcal {V}^*-\mathcal {V},0\Big )\Big ]^{1/k}, F=L^{-1}\Bigg (F_{mp}+F_{2up}\Bigg ), \end{aligned}$$

where $A_L$ is a diagonal matrix of size ${N^2}\times {N^2}$ coming from the discretisation of (14). The diagonal elements of $A_L$ are $(A_L)_{ii}=h_il_i\lambda,$ for $i=1,...,N^2$ with $\lambda$ given in (8). The matrix L is also a diagonal matrix of size $N^2 \times N^2$ whose diagonal elements are $L_{ii}=h_il_i,$ for $i=1,\ldots ,N^2$.

Besides, the ellipticity condition for the PDE (2) is not satisfied when the stocks price ($x\rightarrow 0$ and/or $y\rightarrow 0$) is near to zero. This may cause some oscillations of the numerical solution when the PDE is degenerate.

Nevertheless, (Wang 2004) suggested a fitted finite volume method to deal with the degeneracy of the PDE. Thereby, the fitted finite volume method will be applied in the degeneracy region ($x\rightarrow 0$ and/or $y\rightarrow 0$) in the next section.

3.2.3 Fitted Finite Volume

The fitted finite volume method is used to approximated the flux through edges which are (fully) in the degeneracy region i.e the western edge of the control volume $\mathcal {C}_{1,j},\,j=1,..,N$ and the southern edge of the control volume $\mathcal {C}_{i,1},\,i=1,\ldots ,N$.

For the western edge of the control volume $\mathcal {C}_{1,j} j=1,\ldots ,N$, using the mid-quadrature rule, the flux is given by

$$\begin{aligned} \int _{(x_{\frac{1}{2}},y_{j-\frac{1}{2}})}^{(x_{\frac{1}{2}},y_{j+\frac{1}{2}})}\Bigg (m_{11}\frac{\partial \mathcal {V}}{\partial x}+m_{12}\frac{\partial \mathcal {V}}{\partial y}+p\mathcal {V}\Bigg )dy \approx \Bigg (m_{11}\frac{\partial \mathcal {V}}{\partial x}+m_{12}\frac{\partial \mathcal {V}}{\partial y}+p\mathcal {V}\Bigg )_{(x_{\frac{1}{2}},y_j)} \cdot l_j, \end{aligned}$$

(52)

Besides,

$$\begin{aligned} m_{11}\frac{\partial \mathcal {V}}{\partial x}+m_{12}\frac{\partial \mathcal {V}}{\partial y}+p\mathcal {V}= & {} x\Bigg (ax\frac{\partial \mathcal {V}}{\partial x}+d\frac{\partial \mathcal {V}}{\partial y}+b\mathcal {V}\Bigg ), \end{aligned}$$

(53)

with $a=\frac{1}{2}\sigma _1^2$ , $b=r-\sigma _1^2-\frac{1}{2}\rho \sigma _1\sigma _2$ and $d=\frac{1}{2}\rho \sigma _1\sigma _2y$.

We want to approximate

$$\begin{aligned} g(\mathcal {V})=ax\frac{\partial \mathcal {V}}{\partial x}+b\mathcal {V}, \end{aligned}$$

by a constant over $I_{x_1}=(0,x_1)$ satisfying the following two-point boundary value problem

$$\begin{aligned} \left\{ \begin{array}{l} g'(v) =\Bigg (ax\frac{\partial v}{\partial x}+bv\Bigg )'=K_1,\\ v(0,y_j) =\mathcal {V}_{0,j}, v(x_1,y_j)=\mathcal {V}_{1,j}. \end{array}\right. \end{aligned}$$

(54)

By solving this problem, it yields to

$$\begin{aligned} \mathcal {V}=\mathcal {V}_{0,j}+(\mathcal {V}_{1,j}-\mathcal {V}_{0,j})\frac{x}{x_{1}}. \end{aligned}$$

(55)

Thereby, by using (52),(53), (54), (55) and the forward difference to approximate the first partial derivative $\frac{\partial \mathcal {V}}{\partial y}$ we get

$$\begin{aligned}&\int _{(x_{\frac{1}{2}},y_{j-\frac{1}{2}})}^{(x_{\frac{1}{2}},y_{j+\frac{1}{2}})}\Bigg (m_{11}\frac{\partial \mathcal {V}}{\partial x}+m_{12}\frac{\partial \mathcal {V}}{\partial y}+p\mathcal {V}\Bigg )dy \approx \frac{1}{2}x_1\Big [\frac{1}{2}l_j(a+b)-d_j\Big ]\mathcal {V}_{i,1} \nonumber \\&\quad +\frac{1}{2}d_jx_1\mathcal {V}_{1,j+1}-\frac{1}{4}x_1l_j(a-b)\mathcal {V}_{0,j}, \end{aligned}$$

(56)

where

$$\begin{aligned} a=\frac{1}{2}\sigma _1^2, b=r-\sigma _1^2-\frac{1}{2}\rho \sigma _1\sigma _2, d_j=\frac{1}{2}\rho \sigma _1\sigma _2y_j, l_j=y_{j+\frac{1}{2}}-y_{j-\frac{1}{2}}. \end{aligned}$$

Similarly, for the flux through the southern edge of the control volume $\mathcal {C}_{i,1} i=1,...,N$, it is given by

$$\begin{aligned}&\int _{(x_{i-\frac{1}{2}},y_{\frac{1}{2}})}^{(x_{i+\frac{1}{2}},y_{\frac{1}{2}})}\Bigg (m_{21}\frac{\partial \mathcal {V}}{\partial x}+m_{22}\frac{\partial \mathcal {V}}{\partial y}+q\mathcal {V}\Bigg )dx \approx \frac{1}{2}y_1\Big [\frac{1}{2}h_i(e+k)-h_i'\Big ]\mathcal {V}_{i,1} \nonumber \\&\quad +\frac{1}{2}h_i'y_1\mathcal {V}_{i+1,1}-\frac{1}{4}y_1h_i(e-k)\mathcal {V}_{i,0}, \end{aligned}$$

(57)

where

$$\begin{aligned} e=\frac{1}{2}\sigma _2^2, k=r-\sigma _2^2-\frac{1}{2}\rho \sigma _1\sigma _2, h_i'=\frac{1}{2}\rho \sigma _1\sigma _2x_i, h_i=x_{i+\frac{1}{2}}-x_{i-\frac{1}{2}}. \end{aligned}$$

3.2.4 The Fitted L-Multi-Point Flux Approximation Method ( with the $1{st}$ Order Upwind method )

• 1. Fitted L-MPFA method (with $1{st}$ order upwind method)

  Here the fitted finite volume method is combined with the first order upwind method . Thereby we have:

  • For the control volume $\mathcal {C}_{11}$, the western and southern edges are (fully) in the degeneracy region. The integrals over the western and southern edges of the control volume $\mathcal {C}_{11}$ are then approximated using the fitted finite volume (56) and (57). The integrals over the eastern and northern edges of the control $\mathcal {C}_{11}$, which are not in the degeneracy region, are approximated using the L-MPFA method coupled to the upwind methods ($1{st}$ and $2{nd}$ order).

    $$\begin{aligned} \int _{{\mathcal {C}}_{11}}\nabla k(\mathcal {V}) d \mathcal {C}_{11}&\approx aa_{11}\mathcal {V}_{11}+bb_{11}\mathcal {V}_{21}+cc_{11}\mathcal {V}_{22}+dd_{11}\mathcal {V}_{12}+ee_{11}\mathcal {V}_{01}+\beta \beta _{11}\mathcal {V}_{10}, \end{aligned}$$

    where

    $$\begin{aligned}&aa_{11}= T_{11}^{22}+T_{34}^{21}+T_{41}^{22}+T_{22}^{12}+l_1\max (f_x^2,0)+h_1\max (f_y^{2},0)-\frac{1}{2}x_1\Big (\frac{1}{2}l_1(a+b)-d_1\Big ),\\& -\frac{1}{2}y_1\Big (\frac{1}{2}h_1(e+k)-h_1'\Big ),\\&bb_{11}=T_{33}^{21}+T^{22}_{12}+l_1\min (f_x^2,0)-\frac{1}{2}h_1'y_1, cc_{11}=T_{13}^{22}+T_{43}^{22},\\&dd_{11}=T_{23}^{12}+T_{44}^{22}+h_1\min (f_y^{2},0)-\frac{1}{2}d_1x_1, ee_{11}=T_{21}^{12}+\frac{1}{4}l_1x_1(a-b),\\&\beta \beta _{11}=T_{31}^{21}+\frac{1}{4}y_1h_1(e-k). \end{aligned}$$

  • Similarly, for the control volume $\mathcal {C}_{1,j},\,j=1,\ldots ,N$, only the southern edge is (fully) in the degeneracy region. Then, the integral over the southern edge is approximated using the fitted finite volume method (57). The integrals over the eastern, northern and western edges are approximated using the L-MPFA method coupled to the upwind methods($1{st}$ and $2{nd}$ order)

    $$\begin{aligned} \int _{C_{1,j}} \nabla \mathbf {k}\mathcal {V}d \mathcal {C} &= aa_{1,j}\mathcal {V}_{1,j}+bb_{1,j}\mathcal {V}_{2,j}+cc_{1,j}\mathcal {V}_{2,j+1}+dd_{1,j}\mathcal {V}_{1,j+1}+\beta \beta _{1,j}\mathcal {V}_{1,j-1} \nonumber \\&\quad +\, \alpha \alpha _{1,j}\mathcal {V}_{0,j-1}+ee_{1,j}\mathcal {V}_{0,j}, \end{aligned}$$

    (58)

    where

    $$\begin{aligned} aa_{1,j}&=T_{11}^{2,j+1}+T_{34}^{2,j}+T_{41}^{2,j+1}+T_{22}^{1,j+1}-T_{23}^{1,j}-T_{44}^{2,j}+l_j\max (f_x^2,0) \\&\quad +h_1\max (f_y^{j+1},0)-h_1\min (f_y^{j},0), -\frac{1}{2}x_1\Big (\frac{1}{2}l_j(a+b) -d_j\Big ),\\ bb_{1,j}&=T_{33}^{2,j}+T^{2,j+1}_{12}-T_{43}^{2,j}+l_j\min (f_x^2,0), \\ cc_{1,j}&=T_{13}^{2,j+1}+T_{43}^{2,j+1},\\ dd_{1,j}&=T_{23}^{1,j+1}+T_{44}^{2,j+1} +h_1\min (f_y^{j+1},0)-\frac{1}{2}d_jx_1, \\ \beta \beta _{1,j}&=T_{31}^{2,j}-T_{22}^{1,j}-T_{41}^{2,j}-h_1\max (f_y^{j},0),\\ \alpha \alpha _{1,j}&=-T_{21}^{1,j}, \\ ee_{1,j}&=T_{21}^{1,j+1}+\frac{1}{4}l_jx_1(a-b). \end{aligned}$$

  • Using the same argument as above, for the control volume $\mathcal {C}_{i,1} i=2,..,N$, the integral over the southern edge is approximated using the fitted finite volume (57). The integrals over the eastern, northern and western edges are approximated using the L-MPFA method combined with the upwind methods ($1{st}$ and $2{nd}$ order)

    $$\begin{aligned} \int _{{\mathcal {C}}_{i,1}}\nabla (\mathbf {k}\mathcal {V}) d \mathcal {C}&= aa_{i,1}\mathcal {V}_{i,1}+bb_{i,1}\mathcal {V}_{i+1,1}+cc_{i,1}\mathcal {V}_{i+1,2}+dd_{i,1}\mathcal {V}_{i,2} \nonumber \\&\quad +ee_{i,1}\mathcal {V}_{i-1,1}+\alpha \alpha _{i,1}\mathcal {V}_{i-1,0} \nonumber \\&\quad +\beta \beta _{i,1}\mathcal {V}_{i,0}, \end{aligned}$$

    (59)

    where

    $$\begin{aligned} aa_{i,1}&=T_{11}^{i+1,2}+T_{34}^{i+1,1}+T_{41}^{i+1,2}+T_{22}^{i,2}-T_{12}^{i,2}-T_{33}^{i,1}+l_1\max (f_x^{i+1},0) \\&\quad +h_i\max (f_y^2,0)-l_1\min (f_x^{i},0) -\frac{1}{2}y_1\Big (\frac{1}{2}h_i(e+k)-h_i'\Big ), \\ bb_{i,1}&=T_{33}^{i+1,1}+T^{i+1,2}_{12}+l_1\min (f_x^{i+1},0)-\frac{1}{2}h_i'y_1, \\ cc_{i,1}&=T_{13}^{i+1,2}+T_{43}^{i+1,2},\\ dd_{i,1}&=T_{23}^{i,2}+T_{44}^{i+1,2}-T_{13}^{i,2}+h_i\min (f_y^2,0), \\ ee_{i,1}&=T_{21}^{i,2}-T_{11}^{i,2}-T_{34}^{i,1}-l_1\max (f_x^{i},0),\\ \alpha \alpha _{i,1}&=-T_{31}^{i,1}, \\ \beta \beta _{i,1}&=T_{31}^{i+1,1}+\frac{1}{4}y_1h_i(e-k). \end{aligned}$$

  Besides, for the control volume $\mathcal {C}_{ij}, i,j=2,...,N$, the L-MPFA method is used to approximate the diffusion term and the upwind to approximate the advection term. This leads to the following semi-discrete equation

  $$\begin{aligned} \frac{d\mathcal {V}}{d\tau }=A\mathcal {V}+G(\mathcal {V})+F, \end{aligned}$$

  (60)

  where

  $$\begin{aligned} \mathcal {V}=\begin{bmatrix} \mathcal {V}_{11}\\ \mathcal {V}_{12}\\ \vdots \\ \mathcal {V}_{1N}\\ \mathcal {V}_{21}\\ \mathcal {V}_{22}\\ \vdots \\ \mathcal {V}_{NN} \end{bmatrix} A=L^{-1}\Bigg (Z+A_L\Bigg ), G(\mathcal {V})=\beta \Big [\max \Big (\mathcal {V}^*-\mathcal {V},0\Big )\Big ]^{1/k}, \end{aligned}$$

  with F the vector of boundary conditions and $A_L$ a diagonal matrix of size ${N^2}\times {N^2}$ coming from the discretisation of (14). The diagonal elements of $A_L$ are $(A_L)_{ii}=h_il_i\lambda,$ for $i=1,...,N^2$ with $\lambda$ given in (8). The matrix L is also a diagonal matrix of size $N^2 \times N^2$ whose diagonal elements are $L_{ii}=h_il_i,$ for $i=1,\ldots ,N^2$ and

  $$\begin{aligned} Z=\begin{bmatrix} D_1 &{} K_1 &{} 0_N &{} \ldots &{} \ldots &{} \ldots &{} \ldots &{} 0_N\\ L_2 &{} D_2 &{} K_2 &{} \ddots &{} &{} &{} &{} \vdots \\ 0_N &{} L_3 &{} D_3 &{} K_3 &{} \ddots &{} &{} &{} \vdots \\ \vdots &{} \ddots &{} L_4 &{} D_4 &{} K_4 &{} \ddots &{} &{} \vdots \\ \vdots &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} 0_N&{} \\ \vdots &{} &{} &{} &{} \ddots &{} L_{N-1} &{} D_{N-1} &{} K_{N-1} \\ 0_N &{} \ldots &{} \ldots &{} \ldots &{} \ldots &{} 0_N &{} L_N &{} D_N \end{bmatrix}. \end{aligned}$$

  The elements of matrix Z are matrices. $0_N$ is a zeros matrix of size $N \times N$. The matrices $D_i,K_i,L_i$ are tri-diagonal matrices defined as follows:

  $$\begin{aligned} for\,\, i&= {} 1\, or \,i=N, \\ k&= {} 1,\ldots ,N (D_i)_{kk}=aa_{1,k}, k=1,\ldots ,N-1 (D_i)_{k,k+1}=dd_{1,k}, k=2,\ldots ,N (D_i)_{k,k-1}=\beta \beta _{1,k};\\ for\,\, i&= {} 1, \, k=1,\ldots ,N (K_1)_{kk}=bb_{1,k}, k=1,\ldots ,N-1 (K_1)_{k,k+1}=cc_{1,k};\\ for\, \,i&= {} N, \, (L_N)_{11}=ee_{N1}, k=2,\ldots ,N (L_N)_{kk}=e_{N,k}+\eta _{N,k}, k=2,\ldots ,N (L_N)_{k,k+1}=\alpha _{N,k}; \\& \quad for\, i=2,\ldots ,N-1, \\ (D_i)_{11}&= {} aa_{i,1}, (D_i)_{12}=dd_{i,1}, (K_i)_{11}=bb_{i,1}, (K_i)_{12}=cc_{i,1}, (L_i)_{11}=ee_{i,1},\\ k&= {} 2,\ldots ,N, (D_i)_{kk}=a_{i,k}+\varOmega _{i,k}, (K_i)_{kk}=b_{i,k}+\varDelta _{i,k}, (L_i)_{kk}=e_{i,k}+\eta _{i,k},\\ k&= {} 2,\ldots ,N-1, (D_i)_{k,k+1}=d_{i,k}+\phi _{i,k}, (K_i)_{k,k+1}=c_{i,k},\\ k&= {} 2,\ldots ,N, (D_i)_{k,k-1}=\beta _{i,k}+\mu _{i,k}, (L_i)_{k,k-1}=\alpha _{i,k}. \end{aligned}$$

  where the elements $aa_{ij},bb_{ij},cc_{ij},dd_{ij},ee_{ij},\beta \beta _{ij}$ are defined in (58),(58),(59), and the elements $a_{ij},b_{ij},c_{ij},d_{ij},e_{ij},\varOmega _{ij}$ $\varDelta _{ij},\beta _{ij},\phi _{ij},\alpha _{ij},\mu _{ij},\eta _{ij}$ are defined in (40) and (43).

• 2. Fitted Multi-Point Flux Approximation ($2{nd}$ order upwind)

  Similarly, the fitted MPFA-L method deriving from the combination of the L-MPFA method and the $2{nd}$ order upwind method leads to the following equation :

  $$\begin{aligned} \frac{d\mathcal {V}}{d\tau }=A\mathcal {V}+G(\mathcal {V})+F, \end{aligned}$$

  (61)

  where

  $$\begin{aligned} \mathcal {V}=\begin{bmatrix} \mathcal {V}_{11}\\ \mathcal {V}_{12}\\ \vdots \\ \mathcal {V}_{1N}\\ \mathcal {V}_{21}\\ \mathcal {V}_{22}\\ \vdots \\ \mathcal {V}_{NN} \end{bmatrix}, A=L^{-1}\Bigg (Y+A_L\Bigg ), G(\mathcal {V})=\beta \Big [\max \Big (\mathcal {V}^*-\mathcal {V},0\Big )\Big ]^{1/k}, \end{aligned}$$

  with F the vector of boundary conditions. $A_L$ is a diagonal matrix of size ${N^2}\times {N^2}$ coming from the discretisation of (14). The diagonal elements of $A_L$ are $(A_L)_{ii}=h_il_i\lambda,$ for $i=1,...,N^2$ with $\lambda$ given in (8). The matrix L is also a diagonal matrix of size $N^2 \times N^2$ whose diagonal elements are $L_{ii}=h_il_i,$ for $i=1,\ldots ,N^2$

  and

  $$\begin{aligned} Y=\begin{bmatrix} H_1 &{} P_1 &{} R_1 &{} 0_N &{} \ldots &{} \ldots &{} \ldots &{} &{} 0_N &{} 0_N\\ Q_2 &{} H_2 &{} P_2&{} R_2 &{} 0_N &{} &{} &{} &{} &{} 0_N \\ W_3&{} Q_3 &{} H_3 &{} P_3 &{} R_3 &{} 0_N &{} &{} &{} &{} \vdots \\ 0_N &{} W_4 &{} Q_4 &{} H_4 &{} P_4 &{} R_4 &{} \ddots \\ 0_N &{} 0_N &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots \\ \vdots &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots \\ \vdots &{} &{} &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} 0_N \\ &{} &{} &{} &{} \ddots &{} W_{N-2} &{} Q_{N-2} &{} H_{N-2} &{} P_{N-2} &{} R_{N-2} \\ \vdots &{} &{} &{} &{} &{} \ddots &{} W_{N-1} &{} Q_{N-1} &{} H_{N-1} &{} P_{i,N-1}\\ 0_N &{} \dots &{} \ldots &{} \ldots &{} &{} \ldots &{} 0_N &{} W_N &{} Q_{N} &{} H_{N} \\ \end{bmatrix}. \end{aligned}$$

  The elements of matrix Y are matrices. $0_N$ is a zeros matrix of size $N \times N$. The matrices $H_i, \, i=1,..,N$ are a penta-diagonal matrices and the matrices $P_i,R_i,Q_i,W_i$ are diagonal matrices.

  Furthermore, The $\theta$-Euler method will be applied on the semi-discrete equations (45), (51), (60) and (61) for the spatial discretisation.

4 Time Discretization

Let us consider the ODE stemming from the spatial discretization and given by (45), (51), (60) and (61)

$$\begin{aligned} \frac{d\mathcal {V}}{d\tau }=A\mathcal {V}+G(\mathcal {V})+F. \end{aligned}$$

By using the $\theta$-Euler method for the time discretization, it follows

$$\begin{aligned} \frac{\mathcal {V}^{m+1}-\mathcal {V}^m}{\varDelta \tau }=\theta \Big (A\mathcal {V}^{m+1}+G(\mathcal {V}^{m+1})+F(t_{m+1})\Big )\nonumber \\+(1-\theta )\Big (A\mathcal {V}^m+G(\mathcal {V}^m)+F(t_m)\Big ), \, m&=0,\ldots ,M, \end{aligned}$$

(62)

At every time iteration, the nonlinear system where $\mathcal {V}^{m+1}$ is the solution using the Newton method. Note that

$$\begin{aligned}&\mathcal {V}^m=\begin{bmatrix} \mathcal {V}_{11}(\tau _m), \mathcal {V}_{12}(\tau _m), \ldots, \mathcal {V}_{1N}(\tau _m), \mathcal {V}_{21},(\tau _m) \mathcal {V}_{22}(\tau _m), \ldots, \mathcal {V}_{2N}(\tau _m), \ldots, \mathcal {V}_{N,1}(\tau _m), \mathcal {V}_{N,2}(\tau _m), \ldots, \ldots, \mathcal {V}_{NN}(\tau _m) \end{bmatrix}^T,\\&\\& \tau _m=m\varDelta \tau . \end{aligned}$$

where the time step is $\varDelta \tau =\frac{T}{M}$, T being the maturity time.

5 Numerical Experiments

In this section, we perform some numerical simulations for the L-MPFA method combined to the upwind methods (first and second order) and for the fitted L-MPFA method combined to the upwind methods (first and second order).

5.1 Errors for European Call Options

The computational domain of the problem is $\varOmega =[0;300]\times [0;300]\times [0;T]$ with T=1/12. The numerical experiments are performed with the strike price $E=100$, the volatilities $\sigma _1=\sigma _2=0.3$, the correlation coefficient $\rho =0.3$ and the risk free interest $r=0.08$.

Here, by taking $\beta =0$ in (4), the L-MPFA method illustrated in the previous sections will be compared to the fitted finite volume method, (Wang 2004), and the fitted O-MPFA methods for pricing multi-asset options introduced in Koffi and Tambue (2019a). The relative error will be computed with respect to the analytical solution of the Black–Scholes PDE defined in Haug (2007) as follows

$$\begin{aligned} C(S_1,S_2,K,T) &= {} S_1e^{-rT}M(y_1,d;\rho _1)+S_2e^{-rT}M(y_2,-d+\sigma \sqrt{T};\rho _2) \nonumber \\&\quad -\, Ke^{-rT}\times \left( 1-M(-y_1+\sigma _1\sqrt{T},-y_2+\sigma _2\sqrt{T};\rho )\right) , \end{aligned}$$

(63)

where

$$\begin{aligned}&d=\frac{ln(S_1/S_2)+(b_1-b_2+\sigma _1^2/2)T}{\sigma \sqrt{T}},\\&y_1 = \frac{ln(S_1/K)+(b_1+\sigma _1^2/2)T}{\sigma _1\sqrt{T}}, y_2=\frac{ln(S_2/K)+(b_1+\sigma _2^2/2)T}{\sigma _2\sqrt{T}},\\&\sigma =\sqrt{\sigma _1^2+\sigma _2^2-2\rho \sigma _1\sigma _2}, \rho _1=\frac{\sigma _1-\rho \sigma _2}{\sigma }, \rho _2=\frac{\sigma _2-\rho \sigma _1}{\sigma }, \end{aligned}$$

and

$$\begin{aligned} M(a,b;\rho )=\frac{1}{2\pi \sqrt{1-\rho ^2}}\int _{-\infty }^a\int _{-\infty }^bexp\left( -\frac{x^2-2\rho xy+y^2}{2(1-\rho ^2)}\right) dxdy. \end{aligned}$$

Fig. 7

Analytical solution

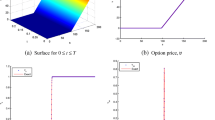
The solution using the L-MPFA coupled to the $2{nd}$ order upwind method is illustrated as below

Fig. 8

L-MPFA-upwind $2{nd}$ order

The $L^2$-norm used to compute the error is given by

$$\begin{aligned} err=\frac{\sqrt{\sum _{i,j=1}^N meas(\mathcal {C}_{ij}) \big (\mathcal {V}_{ij}-V_{ij}^{ana}\big )^2}}{\sqrt{\sum _{i=1}^n meas(\mathcal {C}_{ij}) \big (V_{ij}^{ana}\big )^2}}, \end{aligned}$$

(64)

where $\mathcal {V}$ is the numerical solution, $V^{ana}$ the analytical solution and $meas(\mathcal {C}_{ij})$ is the measure of the control volume $\mathcal {C}_{ij}$. This gives the following tables:

Table 1 Table of errors

Table 2 Table of errors

As we can observe in Tables 1 and 2, the new fitted L-MPFA method is more accurate than the fitted O-MPFA method developed in Koffi and Tambue (2019a) and the standard fitted finite volume method developed in Huang et al. (2006). (Figs. 7 and 8)

5.2 Errors for American Put Options

Since there is no analytical solution for the power penalty problem (4) for pricing American put options, and the numerical solution given by the fitted L-MPFA coupled to $2{nd}$ order upwind method is more accurate when pricing European options (see Tables 1 and 2), we have chosen for reference solution or ”exact solution” the numerical solution given by the fitted L-MPFA coupled to $2{nd}$ order upwind method with $dt=T/256$. The relative error of all the numerical methods used in this study will be performed with respect to this reference solution. Note that the penalty term is not differentiable, so we have used a modified Newton method with the following approximation $[ \mathcal {V}^{*m}- \mathcal {V}^{m}]^{1/k}_{+}=\max \left\{ [ \mathcal {V}^{*m}- \mathcal {V}^{m}]^{1/k},0\right\}$,

$$\begin{aligned} {[} \mathcal {V}^{*m}- \mathcal {V}^{m}]^{1/k}_{+} \approx \left\{ \begin{array}{ll} {[} \mathcal {V}^{*m}- \mathcal {V}^{m}]^{1/k}, \,\,\, &\mathrm {if} \, \mathcal {V}^{*m} - \mathcal {V}^{m}\ge \epsilon\\ 0,& \mathrm {otherwise}. \end{array}\right. \end{aligned}$$

(65)

that is for $\epsilon >0$. In our simulation we take $\epsilon =10^{-6}$.

Fig. 9

Reference solution

For the numerical simulations below, the computational domain of the problem is $\varOmega = [0; 300] \times [0; 300] \times [0; T ]$ with $T = 1/6, K = 100$, the volatilities $\sigma _1 = \sigma _2 = 0.3$. The correlation coefficient is $\rho = 0.3$ , the risk free interest r = 0.08. The penalty parameter $\beta =256$ and the power penalty $k=1/2$. (Fig. 9)

Table 3 Table of errors for $\varDelta \tau = T/64$

Table 4 Table of errors for $\varDelta \tau = T/128$

Again we can observe in Tables 3 and 4, the novel fitted L-MPFA coupled to the $2{nd}$ order upwind method is more accurate than the standard fitted finite volume by Huang et al. (2006).

6 Conclusion

In this paper, the L-MPFA methods have been introduced to approximate the diffusion term of the Black–Scholes PDE. The upwind methods ($1{st}$ and $2{nd}$ order) are used for space discretization of the convection term appearing in the two dimensional Black–Scholes PDE. We have provided a novel scheme called the fitted L-MPFA method to handle the degeneracy of the Black-Scholes PDE by combining the fitted finite volume and the L-MPFA method coupled to the upwind methods. Numerical experiments are performed and comparison between the L-MPFA methods, the O-MPFA methods by Koffi and Tambue (2019a) and the fitted finite methods by Huang et al. (2006) are performed. The results have shown that the fitted L-MPFA method coupled to the $2{nd}$ order upwind method is more accurate than the fitted finite volume by Huang et al. (2006) and the O-MPFA method by Koffi and Tambue (2019a) for pricing Europeans and American options.