Abstract
In this work, we decompose a time series into trend and cycle by introducing a novel de-trending approach based on a family of semi-parametric artificial neural networks. Based on this powerful approach, we propose a relevant filter and show that the proposed trend specification is a global approximation to any arbitrary trend. Furthermore, we prove formally a famous claim by Kydland and Prescott (1981, 1997) that over long time periods, the average value of the cycles is zero. A simple procedure for the econometric estimation of the model is developed as a seven-step algorithm, which relies on standard techniques, where all relevant measures may be computed routinely. Next, using relevant DGPs, we compare and show by means of Monte Carlo simulations that our approach is superior to Hodrick–Prescott (HP) and Baxter and King (BK) regarding the generated distortionary effects and the ability to operate in various frequencies, including changes in volatility, amplitudes and phase. In fact, while keeping the structure of the model relatively simple, our approach is perfectly capable of addressing the case of stochastic trend, in the sense that the generated distortionary effects in the near unit root case are minimal and, by all means, considerably fewer than those generated by HP and BK. Application to EU15 business cycles clustering is presented and the empirical results are consistent with the rigorous theoretical framework developed in this work.



Similar content being viewed by others
Notes
Other popular approaches include the Kalman filter. For an enlightening survey see Kim and Nelson (1999) and for a rigorous analysis of the theory regarding models with non-stationary time series see Chang et al. (2009). Also, several non-linear models have been estimated on real output growth (e.g. Terasvirta 1994). This strand of the literature assumes that output growth is measured accurately, which is quite unlikely to happen since the data contain measurement errors (e.g. Zellner 1992). Hence, sampling all the states conditional on the parameters is relevant (Giordani et al. 2007) but it is not true of threshold models (Pitt et al. 2010). Pitt et al. (2012) used the particle filter to integrate out the states. Also, Malik and Pitt (2011), using particle filtering theory, approximated the likelihood of the unobserved components.
For the standard approaches, the trend of a time series is usually regarded as the component, which comprises its non-cyclical elements together with the cyclical elements of lowest frequency (Kozicki 1999). In particular, according to Pollock (2000) popular filters such as the HP, allow powerful low-frequency components to pass through into the de-trended series when they ought to be impeded by the filter and this deficiency is liable to induce spurious cycles in de-trended data series. This is one of the drawbacks of the HP filter. Of course, there exist other model-based approaches that constitute important alternatives (e.g. Harvey and Todd 1983; Hillmer and Tiao 1982; Koopman et al. 1995) which, however, impose features that are often regarded as being undesirable (Pollock 2000).
In this section, for reasons of notation, when we consider fixed (instead of free) parameters, then the respective parameter is denoted by an upper bar.
However, in general, the empirical results are robust, regardless of the activation function used because of the typical properties they posses (Haykin 1999).
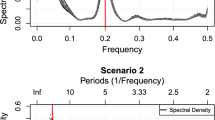
This selection of the cyclical component was made so that the peak of the spectrum in our cycle could be either at zero frequency or at business cycle frequencies.
Despite the difference in the number of iterations between the two procedures, in an econometric perspective, the average correlation coefficient in both procedures is robust, and the only difference lies in the range intervals of their estimates. To this end, without loss of generality, 10,000 iterations are considered to be an asymptotic estimate. Nevertheless, our analysis is based on the average estimates.
The smoothing parameters used for the HP and BK are again set equal to 1600 and 6–32 respectively, as the relevant literature suggests (e.g. Baum et al. 2006), contrarily to the NNF which is data driven.
We would like to thank an anonymous referee for this suggestion.
In order to avoid biased inferences due to differences in the size of each economy, the cyclical components were standardized by their standard deviation.
We should note of course that the filters of BK and HP do not presuppose the use of stationary time series, i.e. Sowell MLE estimations. Despite the fact that in the case of NNF this is also true, we examined the stationarity characteristics of the cyclical components extracted for reasons of robustness. We would like to thank an anonymous referee for this comment.
References
Adya, M., & Collopy, F. (1998). How effective are neural networks at forecasting and prediction? A review and evaluation. Journal of Forecasting, 17, 481–495.
Agresti, A., & Mojon, B. (2001). Some stylised facts on the euro area business cycle. ECB Working Paper 95.
Aminian, F., Suarez, E. D., Aminian, M., & Waltz, D. T. (2006). Forecasting economic data with neural networks. Computational Economics, 28(1), 71–88.
Anderson, H. M., & Ramsey, J. B. (2002). U.S. and Canadian industrial production indices as coupled oscillators. Journal of Economic Dynamics and Control, 26(1), 33–67.
Andreano, M. S., & Savio, G. (2002). Further evidence on business cycle asymmetries in G7 countries. Applied Economics, 34(7), 895–904.
Andreasen, M. M. (2011). Non-linear DSGE models and the optimized central difference particle filter. Journal of Economic Dynamics and Control, 35(10), 1671–1695.
Andreasen, M. M. (2013). Non linear DSGE models and the central difference Kalman filter. Journal of Applied Econometrics, 28(6), 929–955.
Artis, M., & Zhang, W. (1997). International business cycle and the ERM: Is there a European business cycle? International Journal of Finance and Economics, 2, 1–16.
Artis, M., & Zhang, W. (1998a). Core and periphery in EMU: A cluster analysis, EUI working paper RSC No. 98/37.
Artis, M., & Zhang, W. (1998b). Membership of EMU: A fuzzy clustering analysis of alternative criteria, EUI working paper RSC no. 98/52.
Balke, N. S., & Fomby, T. B. (1994). Large shocks, small shocks, and economic fluctuations: outliers in macroeconomic time series. Journal of Applied Econometrics, 9(2), 181–200.
Baxter, M., & King, R. G. (1999). Measuring business cycles: Approximate band-pass filters for economic time series. Review of Economic and Statistics, 81(4), 575–593.
Baum F.C. (2006). Introduction to modern eonometrics using Stata. Texas: Stata Press.
Bayoumi, T., & Eichengreen, B. (1993). Shocking aspects of European monetary integration. In F. Torres & F. Giavazzi (Eds.), Adjustment and growth in the European Monetary Union. Cambridge: Cambridge University Press.
Bayoumi, T., & Eichengreen, B. (1997a). Ever closer to heaven? An optimum-currency-area index for European countries. European Economic Review, 41, 761–770.
Bayoumi, T., & Eichengreen, B. (1997b). Optimum currency areas and exchange rate volatility; theory and evidence compared. In B. Cohen (Ed.), International trade and finance: New frontiers for research: Essays in honour of Peter Kenen. Cambridge: Cambridge University Press.
Beaudry, P., & Koop, G. (1993). Do recessions permanently change output? Journal of Monetary Economics, 31(2), 149–163.
Bezdec, J. C. (1981). Pattern recognition with fuzzy objective function algorithms. New York: Plenum Press.
Bidarkota, P. V. (1999). Sectoral investigation of asymmetries in the conditional mean dynamics of the real US GDP. Studies in onlinear Dynamics and Econometrics, 3, 191–200.
Binner, J. M., Gazely, A. M., & Chen, S. (2002). Financial innovation and Divisia money in Taiwan: A neural network approach. The European Journal of Finance, 8, 238–247.
Binner, J. M., Gazely, A. M., Chen, S., & Chie, B. (2004). Financial innovation and Divisia money in Taiwan: Comparative evidence from neural network and vector error-correction forecasting models. Contemporary Economic Policy, 22(2), 213–224.
Binner, J. M., Bissoondeeal, R. K., Elger, T., Gazely, A. M., & Mullineux, A. W. (2005). A comparison of linear forecasting models and neural networks: An application to Euro inflation and Euro Divisia. Applied Economics, 37(6), 665–680.
Bishop, C. M. (1995). Neural networks for pattern recognition. New York: Oxford University Press.
Brockett, P., Cooper, W., Golden, L., & Pitaktong, U. (1994). A neural network method for obtaining an early warning of insurer insolvency. The Journal of Risk and Insurance, 61(3), 402–424.
Bock, H. H. (1974). AutomatischeKlassifikation (Clusteranalyse). Goettingen: Vandenhoek&Ruprecht.
Bozdogan, H. (1993). Choosing the number of component clusters in the mixture model using a new informational complexity criterion of the inverse Fisher information matrix. In O. Opitz, B. Lausen, & R. Klar (Eds.), Information and classification (pp. 40–54). Berlin: Springer.
Brazili, A., & Siltzia, B. (2003). Risk related non-linearities is exchange rates: Evidence from a panel of Central and Eastern European Countries. Open Economies Review, 14, 135–155.
Brunner, A. D. (1997). On the dynamic properties of asymmetric models of real GNP. The Review of Economics and Statistics, 79(2), 321–352.
Burns, A. F., & Mitchell, W. C. (1946). Measuring business cycles. New York: National Bureau of Economic Research.
Camacho, M., Perez-Quiros, G., & Saiz, L. (2006). Are European business cycle close enough to be just one?CEPR discussion papers, No. 4824.
Campbell, J. Y. & Perron, P. (1991). Pitfalls and opportunities: What macroeconomists should know about unit roots. In O. Blanchard, & S. Fischer (Eds.), NBER Macroeconomics Annual 1991, Vol. 6.
Canova, F. (1998). Detrending and business cycle facts. Journal of Monetary Economics, 41, 475–512.
Canzoneri, M., Valles, J., & Vinals, J. (1996). Do exchange rates move to address international macroeconomic imbalances? CERP discussion papers, No. 1948. London Venter of Economic Policy Research.
Chan, N. H., & Genovese, R. C. (2001). A comparison of linear and nonlinear statistical techniques in performance attribution. IEEE Transactions on Neural Networks, 12(4), 922–928.
Chang, Y., Miller, I. J., & Park, J. Y. (2009). Extracting a common stochastic trend: Theory with some applications. Journal of Econometrics, 150, 231–247.
Clements, M. P., & Krolzig, H.-M. (2004). Can regime-switching models reproduce the business cycle features of US aggregate consumption, investment and output? International Journal of Finance & Economics, 9(1), 1–14.
Concaria, L. A., & Soares, M. J. (2009). Business cycle synchronization across the Euro area: A wavelet analysis, NIPE working papers.
Creal, D., Koopman, S. J., & Zivot, E. (2010). Extracting a robust US business cycle using a time-varying multivariate model-based bandpass filter. Journal of Applied Econometrics, 25(4), 695–719.
Crowley P., & Christi, C. (2003). European Union Studies Association (EUSA), Biennial Conference, (8th), March 27–29.
Dickerson, A., Gibson, H., & Tsakalotos, E. (1998). Business cycle correspondence in the European Union. Economica, 25, 51–77.
Diebold, F. X., & Rudebusch, G. D. (1989). Long memory and persistence in aggregate output. Journal of Monetary Economics, 24(2), 189–209.
Engelman, L., & Hartigan, J. A. (1969). Percentage points of a test for clusters. Journal of American Statistical Association, 64, 1647.
Falk, B. (1986). Further evidence on the asymmetric behavior of economic time series over the business cycle. Journal of Political Economy, 94(5), 1096–1109.
Faraway, J., & Chatfield, C. (1998). Time series forecasting with neural networks: A comparative study using the airline data. Applied Statistics, 47(2), 231–250.
Gencay, R. (1999). Linear, non-linear and essential foreign exchange rate prediction with simple technical trading rules. Journal of International Economics, 47(1), 91–107.
Giordani, P., Kohn, R., & van Dijk, D. (2007). A unified approach to nonlinearity, structural change, and outliers. Journal of Econometrics, 137, 112–133.
Guarin A., Liu, X., & Ng, W. L. (2013). Recovering default risk from CDS spreads with a nonlinear filter. Journal of Economic Dynamics and Control (forthcoming October 2013).
Guay, A., & Saint-Amant, P. (2005). Do the Hodrick-Prescott and Baxter-King filters provide a good approximation of business cycles? Annalesd’Economieet de Statistique. ENSAE, issue, 77, 133–155.
Hamilton, J. D. (1990). Analysis of time series subject to changes in regime. Journal of Econometrics, 45(1–2), 39–70.
Hanke, M. (1999). Neural networks versus Black-Scholes: An empirical comparison of the pricing accuracy of two fundamentally different option pricing methods. Journal of Computational Intelligence in Finance, 5, 26–34.
Hartigan, J. A., & Wong, M. A. (1978). Algorithm AS 136: A K-means clustering algorithm. Applied Statistics, 28, 100–108.
Harvey, A. C., & Todd, P. H. (1983). Forecasting economic time series with structural and BoxJenkins models: A case study. Journal of Business and Economic Forecasting, 1, 299–307.
Harvey, A. C., & Jaeger, A. (1993). Detrending: Stylized facts and the business cycle. Journal of Applied Econometrics, 8, 231–247.
Haykin, S. (1999). Neural Networks. New Jersey: Prentice-Hall.
Hess, G. D., & Iwata, S. (1997). Asymmetric persistence in GDP? A deeper look at depth. Journal of Monetary Economics, 40(3), 535–554.
Hillmer, S. C., & Tiao, G. C. (1982). An ARIMA-model-based approach to seasonal adjustment. Journal of the American Statistical Association, 77, 63–70.
Hodrick, R. J., & Prescott, E. C. (1981). Postwar U.S. business cycles: An empirical investigation. Carnegie Mellon University, discussion paper no. 451.
Hodrick, R. J., & Prescott, E. C. (1997). Postwar U.S. business cycles: An empirical investigation. Journal of Money, Credit, and Banking, 29(1), 1–16.
Hornik, K. (1991). Approximation capabilities of multilayer feedforward networks. Neural Networks, 4(2), 251–257.
Hornik, K., Stinchcombe, M., & White, H. (1989). Multilayer feedforward networks are universal approximators. Neural Networks, 2, 359–366.
Hornik, K., Stinchcombe, M., & White, H. (1990). Universal approximation of an unknown mapping and its derivatives using multilayer feedforward networks. Neural Networks, 3, 551–560.
Hutchinson, J. M., Lo, A. W., & Poggio, T. (1994). A nonparametric approach to pricing and hedging derivative securities via learning networks. Journal of Finance, 49, 851–889.
Jacquemin, A., & Sapir, A. (1995). Is a European hard core credible? (p. 1242). CEPR discussion paper: A statistical analysis.
Kauermann, G., Teuber, T., & Flaschel, P. (2012). Exploring US business cycles with bivariate loops using penalized spline regression. Computational Economics, 39(4), 409–427.
Kiani, K. M. (2005). Detecting business cycle asymmetries using artificial neural networks and time series models. Computational Economics, 26(1), 65–85.
Kiani, K. M. (2007). Asymmetric business cycle fluctuations and contagion effects in G7 countries. International Journal of Business and Economics, 6(3), 237–253.
Kiani, K. M. (2009a). Asymmetries in macroeconomic time series in eleven Asian economies. International Journal of Business and Economics, 8(1), 37–54.
Kiani, K. M. (2009b). Neural networks to detect nonlinearities in time series: Analysis of business cycle in France and the United Kingdom. Applied Econometrics and International Development, 9(1), 67–76.
Kiani, M. K. (2011). Fluctuations in economic and activity and stabilization policies in the CIS. Computational Economics, 37(2), 193–220.
Kiani, K. M., & Bidarkota, P. V. (2004). On business cycle asymmetries in G7 countries. Oxford Bulletin of Economics and Statistics, 66(3), 333–351.
Kiani, K., & Kastens, T. L. (2006). Using macro-financial variables to forecast recessions: An analysis of Canada, 1957–2002. Applied Econometrics and International Development 2005, 6(3), 97–106.
Kiani, K. M., Bidarkota, P. V., & Kastens, T. L. (2005). Forecast performance of neural networks and business cycle asymmetries. Applied Financial Economics Letters, 1(4), 205–210.
Koopman, S. J., Harvey, A. C., Doornick, J. A., & Shephard, N. (1995). STAMP 5.0: Structural time series analyser modeller and predictor: The manual. London: Chapman & Hall.
Konishi, S., & Kitagawa, G. (1996). Generalized information criteria for model selection. Biometrika, 83(4), 875–890.
Kozicki, S. (1999). Multivariate detrending under common trend restrictions: Implications for business cycles research. Journal of Economic Dynamics and Control, 23, 997–1028.
Kuan, C. M., & White, H. (1994). Artificial neural networks: An econometric perspective. Econometric Reviews, 13, 1–91.
Kim, C.-J., & Nelson, C. R. (1999). Friedman’s plucking model of business fluctuations: Tests and estimates of permanent and transitory components. Journal of Money, Credit and Banking, 31(3), 317–334.
Lee, T., White, H., & Granger, C. W. J. (1993). Testing for neglected nonlinearity in time series models. Journal of Econometrics, 56, 269–290.
Ljung, G., & Box, G. E. P. (1978). On a measure of lack of fit in time series models. Biometrika, 65, 297–303.
Lucas, R. E, Jr. (1977). Understanding business cycles. In K. Karl Brunner & A. Meltzer (Eds.), Stabilization of the domestic and international economy. Amsterdam: North Holland.
MacQueen, J. B. (1967). Some methods for classification and analysis of multivariate observations. In Proceedings of 5th Berkeley symposium on mathematical statistics and probability (Vol. 1, pp. 281–297). Berkeley: University of California Press.
Malik, S., & Pitt, M. K. (2011). Particle filters for continuous likelihood evaluation and maximazation. Journal of Econometrics, 165, 190–209.
Massmann, M., & Mitchell, J. (2004). Reconsidering the evidence: Are Eurozone business cycles converging? Journal of Business Cycle Measurement and Analysis, 1, 275–307.
Mise, E., Kim, T.-H., & Newbold, P. (2005). On suboptimality of the Hodrick–Prescott filter at time series endpoints. Journal of Macroeconomics, 27(1), 53–67.
Michaelides, P. G., Vouldis, A. T., & Tsionas, E. G. (2010). Globally flexible functional forms: The neural distance function. European Journal Of Operational Research, 206, 456–469.
Neftci, S. N. (1984). Are economic time series asymmetric over the business cycle? Journal of Political Economy, 92(2), 307–328.
Nelson, C. R., & Plosser, C. I. (1982). Trends and random walks in macroeconomics time series: Some evidence and implications. Journal of Monetary Economics, 10, 139–167.
Oh, K., Zivot, E., & Creal, D. (2008). The relationship between the Beveridge-Nelson decomposition and other permanent transitory decompositions that are popular in economics. Journal of Econometrics, 146, 207–219.
Owners, R., & Sarte, P. D. (2005). How well do diffusion indexes capture business cycles? A spectral analysis. Federal Reserve Bank of Richmond Economic Quarterly, 91(Fall (4)), 23–42.
Ozbek, L., & Ozlale, U. (2005). Employing the extended Kalman filter in measuring the output gap. Journal of Economic Dynamics and Control, 29(9), 1611–1622.
Papageorgiou, T., Michaelides, P. G., & Milios, J. G. (2010). Business cycles synchronization and clustering in Europe (1960–2009). Journal of Economics and Business, 62(5), 419–470.
Pedersen, T. M. (2001). The Hodrick-Prescott filter, the Slutsky effect, and the distortionary effects of filters. Journal of Economic Dynamics and Control, 25, 1081–1101.
Pesaran, M. H., & Potter, S. M. (1997). A floor and ceiling model of US output. Journal of Economic Dynamics and Control, 21(4–5), 661–695.
Phillips, P. C. B., & Magdalinos, T. (2008). Limit theory for explosively cointegrated systems. Econometric Theory, 24, 865–887.
Pitt, M., Giordani, P., & Kohn, R. (2010). Bayesian inference for time series state space models. In J. Geweke, G. Koop, & H. van Dijk (Eds.), Handbook of Bayesian econometric. Oxford: Oxford University Pres.
Pitt, M., dos Santos Silva, R., Giordani, P., & Kohn, R. (2012). On some properties of Markov chain Monte Carlo simulation methods based on the particle filter. Journal of Econometrics, 171, 134–151.
Pollock, D. S. G. (2000). Trend estimation and de-trending via rational square-wave filters. Journal of Econometrics, 99, 317–334.
Psaradakis, Z., & Sola, M. (2003). On detreding and cyclical assymetry. Journal of Applied Econometrics, 18, 271–289.
Qi, M., & Maddala, C. S. (1999). Economic factors and the stock market: A new perspective. Journal of Forecasting, 18, 151–166.
Qi, M. (2001). Predicting U.S. recessions with leading indicators via neural network models. International Journal of Forecasting, 17, 383–401.
Ramsey, J. B., & Rothman, P. (1996). Time irreversibility and business cycle asymmetry. Journal of Money, Credit and Banking, 28(1), 1–21.
Rudin, W. (1976). Principles of mathematical analysis. New York: McGraw-Hill International Edition.
Santin, D., Delgado, F., & Valino, A. (2004). The measurement of technical efficiency: A neural network approach. Applied Economics, 36, 627–635.
Scheinkman, J. A., & LeBaron, B. (1989). Nonlinear dynamics and stock returns. The Journal of Business, 62(3), 311–337.
Schumpeter, J. A. (1939). Business cycles: A theoretical, historical and statistical analysis of the capitalist process. New York: McGraw Hill.
Serrano-Cinca, C. (1997). Feedforward neural networks in the classification of financial information. The European Journal of Finance, 3, 183–202.
Sheela G. K., & Deepa S. N. (2013). Review on methods to fix number of hidden neurons in neural networks. Mathematical Problems in Engineering, Vol. 2013, Article ID 425740. doi:10.1155/2013/425740.
Stock, J. H., & Watson, M. W. (1999). Forecasting inflation. Journal of Monetary Economics, 44(2), 293–335.
Swanson, N. R., & White, H. (1995). A model-selection approach to assessing the information in the term structure using linear models and artificial neural networks. Journal of Business & Economic Statistics, 13(3), 265–275.
Swanson, N. R., & White, H. (1997a). A model selection approach to real-time macroeconomic forecasting using linear models and artificial neural networks. The Review of Economics and Statistics, 79(4), 540–550.
Swanson, N. R., & White, H. (1997b). Forecasting economic time series using flexible versus fixed specification and linear versus nonlinear econometric models. International Journal of Forecasting, 13(4), 439–461.
Tanizaki, H., & Mariano, R. S. (1994). Prediction, filtering and smoothing in non-linear and non-normal cases using Monte Carlo integration. Journal of Applied Econometrics, 9, 163–179.
Taylor, C. (1995). EMU 2000? Prospects for European Monetary Union. London: Chatham House Papers, The Royal Institute of International Affairs.
Terasvirta, T. (1994). Specification, estimation, and evaluation of smooth transition autoregressive models. Journal of the American Statistical Association, 89, 208–218.
Tsay, R. S. (1988). Outliers, level shifts, and variance changes in time series. Journal of Forecasting, 7, 1–20.
Vishwakarma, K. P. (1994). Reckognizing business cycles turning points by means of neural networks. Journal of Computational Economics, 7, 175–185.
Watanabe, T. (1999). A non-linear filtering approach to stochastic volatility models with application to daily stock returns. Journal of Applied Econometrics, 14, 101–121.
Whittaker, E. T. (1923). On a new method of graduations. Proceedings of the Edinburgh Mathematical Society, 41, 63–75.
Wingrove, C. R., & Davis, E. R. (2012). Classical linear-control analysis applied to business-cycle dynamics and stability. Journal of Computational Economics, 39(1), 77–98.
Woitek, U. (1998). Note on the Baxter–King filter. Working Papers 9813, Business School, Economics, University of Glasgow.
Zellner, A. (1992). Commentary. In Belagia, M. & Garfinkel, M. (Eds.), The business cycle: Theories and evidence: Proceedings of the sixteenth annual economic policy conference of the Reserve Bank of St Louis.
Zhang, G. P., & Berardi, V. L. (2001). Time series forecasting with neural network ensembles: An application for exchange rate prediction. Journal of the Operational Research Society, 52, 652–664.
Acknowledgments
We are indebted to three anonymous Referees and the Editor-in-Chief, Hans Amman, for their diligent reading of the manuscript and for the constructive feedback. The first author (P.G.M.) would also like to thank Alexandros Eskenazis for a fruitful discussion on a previous version of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
This paper should not be reported as representing the views of the European Central Bank (ECB). The views expressed are those of the author and do not necessarily reflect those of the ECB.
Appendix
Appendix
Definition 1
(Trend set) Consider \(g_{t_j } ,t\in T\subseteq {\mathbb {R}}^{+},j\in J\subseteq {\mathbb {R}}\) representing the trend of a time series \(x_{t_j } \forall j\in J\), such that \(g_{t_j } \in {\mathbb {R}}\), \(\forall j\in J\). Without loss of generality, let \(\mathop \bigcup \nolimits _{t_j } g_{t_j } =\{g_{t_j } :g_{t_j } is~the~trend~of~x_{t_j } \forall j\in J\}\subseteq {\mathbb {R}}\) be the trend set which is assumed to be closed and bounded.
Definition 2
(Time series as random variable) A time series model for the observed data \(x_{t_j } ,j\in J\) is a specification of the joint distributions, or only the means and covariances, of a sequence of random variables \(\left\{ {X_t } \right\} _{t\in T} \) of which {\(x_{t_j } \}_{t\in T} \) is postulated to be a realization.
Definition 3
(Time series set) Consider \(x_{t_j } ,j\in J\) an arbitrary macroeconomic time series, such that \(x_{t_j } \in {\mathbb {R}}\forall t\in T\subseteq {\mathbb {R}}^{+}\). Without loss of generality, let \(\bigcup _{j\in J} x_{t_j } \subseteq {\mathbb {R}}\) be the time series set.
Theorem 2
Proof
From Lemma 1 the trend set is compact. From Lemma 2 any function of the form \(:\hbox {F}\left( \hbox {t} \right) \equiv \hbox {d}+\hbox {ct}+\mathop \sum \nolimits _{\mathrm{i=1}}^{\mathrm{N}} \hbox {a}_{\mathrm{i}} \upvarphi \left( {\hbox {b}_{\mathrm{i}} \hbox {t}} \right) ,\upvarphi _{\mathrm{i}} ,\hbox {b}_{\mathrm{i}} ,\hbox {d}\in {\mathbb {R}}, \hbox {c}\in {\mathbb {R}}-\left\{ 0 \right\} \}\) is non-constant, bounded and continuous. Then, from Theorem 1, the family: \(\mathcal{F}=\{\hbox {F}\left( \hbox {t} \right) \in \hbox {C}\left( {\mathop \bigcup \nolimits _{j\in J} g_{t_i } } \right) :\hbox {F}\left( \hbox {t} \right) \equiv \hbox {d}+\hbox {ct}+\mathop \sum \nolimits _{\mathrm{i=1}}^{\mathrm{N}} \hbox {a}_{\mathrm{i}} {\upvarphi }\left( {\hbox {b}_{\mathrm{i}} \hbox {t}} \right) ,\upvarphi _{\mathrm{i}} ,\hbox {b}_{\mathrm{i}} ,\hbox {d},\hbox {c}\in {\mathbb {R}}\}\) is dense in \(\hbox {C}\left( {\mathop \bigcup \nolimits _{j\in J} g_{t_j } } \right) \). \(\square \)
Theorem 3 (Linear time trend as degenerate form of NNF)
Proof
Let \(x_{t_i } ,i\in I \) be a time series and let \(\bar{m} \in \left\{ {1,..M} \right\} \). Then, \(\exists \overline{\beta _{\bar{m}_i}} \in {\mathbb {R}}^{\bar{m}}\), \(\overline{a_{\bar{m}_i}}\in {\mathbb {R}}^{\bar{m}}+ , \overline{a_{0 \bar{m}_i }}\in {\mathbb {R}}\) and \(\overline{\delta _{\bar{m}_i }} \in {\mathbb {R}}\) such that the trend of the macroeconomic time series be given by the following expression:
Now, since I is a compact subset of \({\mathbb {R}}\) then it is closed and bounded and there exists \(i_0 \in I\) such that \(\overline{\beta _{\bar{m}_{i_0}}}=\hbox {max}\{\overline{\beta _{\bar{m}_i}}\in {\mathbb {R}}^{\bar{m}}\)}. For, this \(\overline{\beta _{\bar{m}_{i_0}}}\) we have that \(\overline{\delta _{\bar{m}_{i_0}}} =\hbox {max}\left\{ {\overline{\delta _{\bar{m}_i}} ,\bar{m}_i \in \left\{ {1,\ldots M} \right\} } \right\} \), while the trend of this macroeconomic time series is given by the expression:
But, since: \(\overline{\beta _{\bar{m}_{i_0}} }=\hbox {max}\left\{ {\overline{\beta _{\bar{m} _i}},\overline{\beta _{\bar{m}_i}}\in {\mathbb {R}}^{\bar{m}}} \right\} \), then: \(\mathop \sum \nolimits _{\mathrm{k=1}}^{\bar{m}_{i_0}} \overline{\alpha _k } \varphi \left( {\overline{\beta _k }}t \right) =\mathop \sum \nolimits _{\mathrm{k=1}}^{\bar{m}_{i_0 } } \overline{\alpha _k }\) . In view of \(\varphi \) being increasing monotonic and \(\varphi :{\mathbb {R}}\rightarrow \left[ {0,1} \right] \), we have that: \(g_t =\overline{a_0 }+ \overline{\delta _{\bar{m}_{i_0}}} t+\mathop \sum \nolimits _{\mathrm{k=1}}^{\bar{m}_{i_0}}\overline{\alpha _k }\).
Hence, the trend approximation is equal to the linear trend, i.e. \(g_t =\gamma +\delta t\), where: \(\gamma =\overline{a_0} +\mathop \sum \nolimits _{\mathrm{k=1}}^{\bar{m}_{i_0}} \overline{\alpha _k }\). \(\square \)
Theorem 4 (Mean value of the cycle is zero)
Proof
Let \({x_{{t_j}}}\), \(j \in J\) be a time series whose cyclical component is given by the expression:
Let \(\{{p_{{t_j}}}\}_{j \in J}\) be the respective probability measure assigned on each cyclical times series \({c_{{t_j}}} \forall t \in T\).
Now, provided that:\(\sum \nolimits _{{\mathrm{t}\in {\mathrm{T}}}}({\hbox {x}_{{\hbox {t}_{\mathrm{j}}}}}-{\hbox {g}_{{\hbox {t}_{\mathrm{j}}}}}),{\hbox {p}_{{\hbox {t}_\mathrm{j}}}} \) converges absolutely, i.e. \(\sum \nolimits _{t\in T}|({x_{{t_j}}}-{g_{{t_j}}}), {p_{{t_j}}}|< \infty \), the expected value of our cyclical component is given by the following expression:
But, since \(\bigcup _{t_{i}}g_{t_{i}}\) is a dense subset on \(\bigcup _{t_{j}}x_{t_{j}}\), then by the definition of density we have that \(\forall \varepsilon >0 \) and \(\forall x_{t_{j} }, j \in J\) there exists \(g_{t_{i}}\), \(i \in I\) such that \(\left| {x_{t_j } -g_{t_i }} \right| <\varepsilon \forall j\in J~and~ \forall i\in I\). Thus, \(\forall \left\{ {\hbox {p}_{\mathrm{t}_{\mathrm{j}}}} \right\} _{\mathrm{j}\in \hbox {J}} \) in a relevant probability space, we have that: \(|(x_{t_j }-g_{t_j })p_{t_j }|< \varepsilon p _{tj}< \varepsilon \, \forall j \in J \) and \(\forall p_{t_j } \in \left[ {0,1} \right] .\)
But, without loss of generality, for \(\varepsilon _t =1-\frac{1}{2^{t}}\), \(\forall t\in T\) we have that: \(\sum \nolimits _{t \in T}({1}-\frac{1}{2^{t}})< \infty \).
Hence: \(\mathop \sum \nolimits _{t\in T} \left| {(x_{t_j } -g_{t_j ,} )p_{t_j } } \right| <\infty \) (A.14) and, therefore, Eq. (29) defines the expected value of the cyclical component of the time series.
Thus:
But: \(\mathop \sum \nolimits _{t\in T} (x_{t_j } -g_{t_j ,} )p_{t_j } =(x_{1_j } -g_{1_j ,} )p_{1_j } +\cdots +(x_{t_j } -g_{t_j ,} )p_{t_j } +\ldots \) and \((x_{1_j } -g_{1_j ,} )p_{1_j } +\cdots +(x_{t_j } -g_{t_j ,} )p_{t_j } <\varepsilon _1 p_{1_j } +\cdots +\varepsilon _T p_{T_j } +\ldots \), \(\forall j\in J\), \(t\in T\) because of the density of \(\bigcup _{t_i } g_{t_i } \) on \(\bigcup _{t_j } x_{t_j } \) which implies: \(\left| {x_{t_j } -g_{t_i } } \right| <\varepsilon \forall j\in J~and~\forall i\in I\).
However:\(\left| {x_{t_j } -g_{t_i } } \right|<\varepsilon _t \Leftrightarrow -\varepsilon _t<x_{t_j } -g_{t_i } <\varepsilon _t \), \(\forall j\in J\),\(\forall t\in T\) and \(\forall i\in I\)
Now, without loss of generality, for \(\varepsilon _t =1-\frac{1}{2^{t}}\),\(\forall t\in T\) we have that:
But, given that \(1-\frac{1}{2^{t}}>0\) and \(p_{tj}\in [0,1] \), we have that:
Similarly: \(-\mathop \sum \nolimits _{t\in T} \left( {1-\frac{1}{2^{t}}} \right) p_{t_j } \rightarrow 0\)
Hence, given that: \(-\mathop \sum \nolimits _{t\in T} \varepsilon _t p_{t_j } \le \mathop \sum \nolimits _{t\in T} \left( {x_{t_j } -g_{t_j } } \right) p_{t_j } \le \mathop \sum \nolimits _{t\in T} \varepsilon _t p_{t_j } \forall j\in J\), \(\forall p_{t_j } \in \left[ {0,1} \right] \) and that: \(-\mathop \sum \nolimits _{t\in T} \left( {1-\frac{1}{2^{t}}} \right) p_{t_j } \rightarrow 0\) and \(\mathop \sum \nolimits _{t\in T} \left( {1-\frac{1}{2^{t}}} \right) p_{t_k } \rightarrow 0\) we get:
\(\square \)
Theorem 5 (Mean value of the NNF cycle is zero)
Proof
Based on Theorem 2, \(\mathcal{F}=\{F\left( t \right) \in C\left( X \right) :F\left( t \right) \equiv d+ct+\mathop \sum \nolimits _{i=1}^N a_i \varphi \, \left( {\beta _i t} \right) ,\alpha _i ,\beta _i ,d,c\in {\mathbb {R}}\}\) is dense in \(\bigcup _{t_i } g_{t_i } \). Hence, in view of Theorem 4, we have that: \(\left( {c_{t_j } } \right) =0\forall j\in J\). \(\square \)
Rights and permissions
About this article
Cite this article
Michaelides, P.G., Tsionas, E.G., Vouldis, A.T. et al. A Semi-Parametric Non-linear Neural Network Filter: Theory and Empirical Evidence. Comput Econ 51, 637–675 (2018). https://doi.org/10.1007/s10614-016-9628-6
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-016-9628-6