Abstract
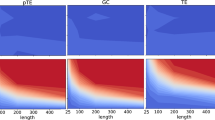
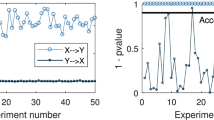
In this paper, a framework is developed for the identification of causal effects from non-stationary time series. Focusing on causality measures that make use of delay vectors from time series, the idea is to account for non-stationarity by considering the ranks of the components of the delay vectors rather than the components themselves. As an exemplary measure, we introduce the partial symbolic transfer entropy (PSTE), which is an extension of the bivariate symbolic transfer entropy quantifying only the direct causal effects among the variables of a multivariate system. Through Monte Carlo simulations it is shown that the PSTE is directly applicable to non-stationary in mean and variance time series and it is not affected by the existence of outliers and VAR filtering. For stationary time series, the PSTE is also compared to the linear conditional Granger causality index (CGCI). Finally, the causal effects among three financial variables are investigated. Computations of the PSTE and the CGCI on both the initial returns and the VAR filtered returns, and the PSTE on the original non-stationary time series, show consistency of the PSTE in estimating the causal effects.





Similar content being viewed by others
Notes
The interdependence measure in Chicharro and Andrzejak (2009) uses ranks but on the basis of the distances calculated on the embedding vectors.
References
Alexander, C. (2008). Practical Financial Econometrics. New York: Wiley.
Alper Emre, C. & Forni, L. (2011). Public debt in advanced economies and its spillover effects on long-term yields. IMF working paper, no. 11/210 (Washington: International Monetary Fund).
Ardagna, S., Caselli, F., & Lane, T. (2007). Fiscal discipline and the cost of public debt service: Some estimates for OECD countries. The BE Journal of Macroeconomics, 7(1), 1–35.
Arnhold, J., Grassberger, P., Lehnertz, K., & Elger, C. (1999). A robust method for detecting interdependences: Application to intracranially recorded EEG. Physica D, 134, 419–430.
Baccala, L., & Sameshima, K. (2001). Partial directed coherence: A new concept in neural structure determination. Biological Cybernetics, 84, 463–474.
Baghli, M. (2006). A model-free characterization of causality. Economics Letters, 91, 380–388.
Barnett, L., & Seth, A. (2011). Behaviour of Granger causality under filtering: Theoretical invariance and practical application. Journal of Neuroscience Methods, 201, 404–419.
Bekaert, G., Hoerova, M. & Lo Duca, M. (2011). Risk, uncertainty and monetary policy. Netspar discussion papers, DP 05/2011-102.
Bossomaier, T., Barnett, L. & Harre, M. (2013). Information and phase transitions in socio-economic systems. Complex Adaptive Systems Modeling, 1–9.
Brandt, P. T., & Williams, J. T. (2007). Multiple time series models, ch. 2. Oxford: Sage Publications.
Chen, Y., Bressler, M., & Ding, S. L. (2006). Frequency decomposition of conditional Granger causality and application to multivariate neural field potential data. Journal of Neuroscience Methods, 150(2), 228–237.
Chen, Y., Rangarajan, G., Feng, J., & Ding, M. (2004). Analyzing multiple nonlinear time series with extended Granger causality. Physics Letters A, 324, 26–35.
Cheng, J., Taylor, L., & Weng, W. (2010). The links between international parity conditions and Granger causality: A study of exchange rates and prices. Applied Economics, 42, 3491–3501.
Chicharro, D., & Andrzejak, R. (2009). Reliable detection of directional couplings using rank statistics. Physical Review E, 80, 026217.
Cover, T., & Thomas, J. (1991). Elements of Information Theory. New York: Wiley.
Diks, C., & Panchenko, V. (2006). A new statistic and practical guidelines for nonparametric Granger causality testing. Journal of Economic Dynamics and Control, 30(9–10), 1647–1669.
Engle, R., & Granger, C. (1987). Cointegration and error correction: Representation, estimation and testing. Econometrica, 5, 251–276.
Fadlallah, B., Seth, S., Keil, A., & Príncipe, J. (2012). Quantifying cognitive state from EEG using dependence measures. IEEE Transactions on Biomedical Engineering, 59(10), 2773–2781.
Favero, C., Pagano, M., & Von Thadden, E. L. (2010). How does liquidity affect bond yields? Journal of Financial and Quantitative Analysis, 45(1), 107–134.
Geweke, J. (1982). Measurement of linear dependence and feedback between multiple time series. Journal of the American Statistical Association, 77(378), 304–313.
Geweke, J. (1984). Measures of conditional dependence and deedback between time series. Journal of the American Statistical Association, 79(388), 907–915.
Gomez-Herrero, G. (2010). Brain connectivity analysis with EEG. Ph.D. Thesis, Tampere University of Technology, Finland.
Gourévitch, B., Le Bouquin-Jeannés, R., & Faucon, G. (2006). Linear and nonlinear causality between signals: Methods, examples and neurophysiological applications. Biological Cybernetics, 95, 349–369.
Granger, J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica, 37, 424–438.
Hiemstra, C., & Jones, J. D. (1994). Testing for linear and nonlinear Granger causality in the stock pricevolume relation. Journal of Finance, 49, 1639–1664.
Karagianni, S., & Kyrtsou, C. (2011). Analysing the dynamics between US inflation and Dow Jones index using nonlinear methods. Studies in Nonlinear Dynamics and Econometrics, 15(2), 1–25.
Kendall, M. (1938). A new measure of rank correlation. Biometrika, 30(1–2), 81–89.
Kim, C., & Park, J. (2010). Cointegrating regressions with time heterogeneity. Econometric Reviews, 29, 397–438.
Kowalski, A. M., Martin, M. T., Plastino, A., & Zunino, L. (2010). Information flow during the quantum-classical transition. Physics Letters A, 374(17–18), 1819–1826.
Kraskov, A., Stögbauer, H., & Grassberger, P. (2004). Estimating mutual information. Physical Review E, 69(6), 066138.
Ku, S. W., Lee, U., Noh, G. J., Jun, I. G., & Mashour, G. A. (2011). Preferential inhibition of frontal-to-parietal feedback connectivity is a neurophysiologic correlate of general anesthesia in surgical patients. PLoS ONE, 6(10), e25155.
Kugiumtzis, D. (2012). Transfer entropy on rank vectors. Journal of Nonlinear Systems and Applications, 3(2), 73–81.
Kugiumtzis, D. (2013). Partial transfer entropy on rank vectors. The European Physical Journal Special Topics, 222(2), 401–420.
Kyrtsou, C. (2005). Don’t bleach highly complex data: A multivariate study. Thessaloniki: Mimeo, University of Macedonia.
Kyrtsou, C., & Malliaris, A. (2009). The impact of information signals on market prices when agents have non-linear trading rules. Economic Modelling, 26(1), 167–176.
Kyrtsou, C., & Vorlow, C. (2009). Modelling nonlinear comovements between time series. Journal of Macroeconomics, 30(2), 200–211.
Laubach, T. (2009). New evidence on the interest rate effects of budget deficits and debt. Journal of the European Economic Association, 7–4, 858–885.
Lee, H., Lin, K., & Wu, J. L. (2002). Pitfalls in using Granger causality tests to find an engine of growth. Applied Economics Letters, 9, 411–414.
Martini, M., Kranz, T. A., Wagner, T., & Lehnertz, K. (2011). Inferring directional interactions from transient signals with symbolic transfer entropy. Physical Review E, 83(1), 011919.
Paluš, M., Komárek, V., Hrnčíř, Z., & Štěrbová, K. (2001). Synchronization as adjustment of information rates: Detection from bivariate time series. Physical Review E, 63, 046211.
Papana, A., Kyrtsou, C., Kugiumtzis, D., & Diks, C. (2013). Simulation study of direct causality measures in multivariate time series. Entropy, 15(7), 2635–2661.
Papana, A., Kyrtsou, C., Kugiumtzis, D. & Diks, C. (2014). Identifying causal relationships in case of non-stationary time series. Working Paper 14–09, Center for nonlinear dynamics in economics and finance (CeNDEF) (http://www1.fee.uva.nl/cendef/publications/)
Quian Quiroga, R., Kraskov, A., Kreuz, T., & Grassberger, P. (2002). Performance of different synchronization measures in real data: A case study on electroencephalographic signals. Physical Review E, 65, 041903.
Roley, V., & Sellon, G. (1995). Monetary policy actions and long-term interest rates, federal reserve bank of kansas city. Economic Review, Fourth quarter, 73–89
Romano, M. C., Thiel, M., Kurths, J., & Grebogi, C. (2007). Estimation of the direction of the coupling by conditional probabilities of recurrence. Physical Review E, 76(3), 036211.
Schreiber, T. (2000). Measuring information transfer. Physical Review Letters, 85(2), 461–464.
Schwartz, G. (1978). Estimating the dimension of a model. The Annals of Statistics, 5(2), 461–464.
Sharp, G.D. (2010). Lag length selection for vector error correction models. PhD thesis, Rhodes University.
Silverman, B. (1986). Density estimation for statistics and data analysis. London: Chapman and Hall.
Spearman, C. (1904). The proof and measurement of association between two things. American Journal of Psychology, 15, 72–101.
Staniek, M., & Lehnertz, K. (2008). Symbolic transfer entropy. Physical Review Letters, 100(15), 158101.
Vejmelka, M., & Paluš, M. (2008). Inferring the directionality of coupling with conditional mutual information. Physical Review E, 77, 026214.
Wei, W. W. S. (2006). Time Series Analysis. Univariate & Multivariate Methods (2nd ed.). Reading: Addison-Wesley.
Xu, K., & Phillips, P. (2008). Adaptive estimation of autoregressive models with time-varying variances. Journal of Econometrics, 142, 265–280.
Yu, G. H., & Huang, C. C. (2001). A distribution free plotting position. Stochastic Environmental Research And Risk Assessment, 15(6), 462–476.
Acknowledgments
The research project is implemented within the framework of the Action ’Supporting Postdoctoral Researchers’ of the Operational Program ’Education and Lifelong Learning’ (Action’s Beneficiary: General Secretariat for Research and Technology), and is co-financed by the European Social Fund (ESF) and the Greek State.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Papana, A., Kyrtsou, C., Kugiumtzis, D. et al. Detecting Causality in Non-stationary Time Series Using Partial Symbolic Transfer Entropy: Evidence in Financial Data. Comput Econ 47, 341–365 (2016). https://doi.org/10.1007/s10614-015-9491-x
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10614-015-9491-x