Abstract
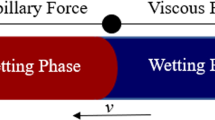
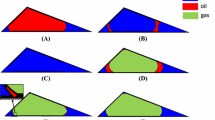
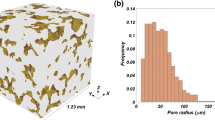
Imbibition is an important process encountered in many porous media applications. At the pore scale, pore network models (PNM) are computationally efficient and can model drainage accurately. However, using PNM to model imbibition still remains a challenge due to the complexities encountered in understanding pore-scale flow phenomena related to pore body filling (PBF) and snap-off along with the relative competition between these events. In this work, we use direct numerical simulations (DNS) to revisit the basic principles of PBF in a two-dimensional synthetic pore geometry. We notice that PBF during spontaneous imbibition is dependent on several parameters such as shape of the transition zone, contact angle and the fluid properties like density. The interactions between these parameters are investigated in a quantitative manner. We demonstrate the existence of a critical contact angle 𝜃c and a barrier contact angle 𝜃b. 𝜃c depends on the shape of the pore geometry, whereas 𝜃b depends on the pore geometry, contact angle and fluid properties. For a system comprising of light fluids, 𝜃b is only slightly larger than 𝜃c; whereas for a system occupied by dense fluids, 𝜃b is notably larger than 𝜃c. The contact angle of the wetting phase 𝜃 in relation to 𝜃c and 𝜃b decides if the wetting phase can imbibe a pore body. Imbibition always occurs if 𝜃 < 𝜃c. For 𝜃 > 𝜃c, we observe capillary barrier zones in which capillary forces accompany viscous forces to resist spontaneous imbibition. For this case, we observe smooth transition of the meniscus curvature while the meniscus enters and exits capillary barrier zones. For 𝜃c ≤ 𝜃 ≤ 𝜃b, inertia assists the wetting phase to overcome resisting forces and imbibe the pore space. For 𝜃 > 𝜃b, the resisting forces dominate over inertia so that the wetting phase cannot imbibe the pore space. For the synthetic pore geometries investigated, we provide analytical and semi-analytical expressions to determine 𝜃c and the position of capillary barrier zones respectively. The barrier contact angle 𝜃b is computed numerically for several inertial systems and for various shapes of the synthetic pore geometry. The results of this quantitative analysis can be utilised to improve the existing pore filling rules and predictive capabilities of PNM used for two-phase flows.
Article PDF
Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.Avoid common mistakes on your manuscript.
References
Afkhami, S., Zaleski, S., Bussmann, M.: A mesh-dependent model for applying dynamic contact angles to vof simulations. J. Comput. Phys. 228(15), 5370–5389 (2009)
Batchelor, G.K.: An introduction to fluid dynamics. Cambridge University Press, Cambridge (2000)
Berthier, J., Brakke, K.A.: The physics of microdroplets. Wiley, New York (2012)
Blunt, M.J.: Multiphase flow in permeable media: A pore-scale perspective. Cambridge University Press, Cambridge (2017)
Brackbill, J., Kothe, D.B., Zemach, C.: A continuum method for modeling surface tension. J. Comput. Phys. 100(2), 335–354 (1992)
Denner, F., Wachem, B.G.: Numerical time-step restrictions as a result of capillary waves. J. Comput. Phys. 285, 24–40 (2015)
Dong, H., Blunt, M.J.: Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E 80(3), 036307 (2009)
Ferrari, A., Lunati, I.: Inertial effects during irreversible meniscus reconfiguration in angular pores. Adv. Water Resour. 74, 1–13 (2014)
Graue, A., Viksund, B.G., Eilertsen, T., Moe, R.: Systematic wettability alteration by aging sandstone and carbonate rock in crude oil. J. Pet. Sci. Eng. 24(2-4), 85–97 (1999)
Hirt, C.W., Nichols, B.D.: Volume of fluid (vof) method for the dynamics of free boundaries. J. Comput. Phys. 39(1), 201–225 (1981)
Huh, C., Scriven, L.: Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interface Sci. 35(1), 85–101 (1971)
Issa, R.I.: Solution of the implicitly discretised fluid flow equations by operator-splitting. J. Comput. Phys. 62(1), 40–65 (1986)
Lenormand, R., Zarcone, C., Sarr, A.: Mechanisms of the displacement of one fluid by another in a network of capillary ducts. J. Fluid Mech. 135, 337–353 (1983)
Lenormand, R., Zarcone, C., et al.: Role of Roughness and Edges during Imbibition in Square Capillaries. In: SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers (1984)
Mathematica, W.: Wolfram Research. Illinois, Inc., Champaign (2018)
Méheust, Y., Løvoll, G., Måløy, K.J., Schmittbuhl, J.: Interface scaling in a two-dimensional porous medium under combined viscous, gravity, and capillary effects. Phys. Rev. E 66(5), 051603 (2002)
Navier, C.: Mémoire sur les lois du mouvement des fluides. Mem. Acad. Sci. Inst. Fr 6(1823), 389–416 (1823)
Pavuluri, S., Maes, J., Doster, F.: Spontaneous imbibition in a microchannel: analytical solution and assessment of volume of fluid formulations. Microfluid. Nanofluid. 22(8), 90 (2018)
Raeini, A.Q., Blunt, M.J., Bijeljic, B.: Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 231(17), 5653–5668 (2012)
Raeini, A.Q., Blunt, M.J., Bijeljic, B.: Direct simulations of two-phase flow on micro-ct images of porous media and upscaling of pore-scale forces. Adv. Water Resour. 74, 116–126 (2014)
Rusche, H.: Computational fluid dynamics of dispersed two-phase flows at high phase fractions. Ph.D. thesis, Imperial College London (University of London) (2003)
Singh, K., Bijeljic, B., Blunt, M.J.: Imaging of oil layers, curvature and contact angle in a mixed-wet and a water-wet carbonate rock. Water Resour. Res. 52(3), 1716–1728 (2016)
Singh, K., Menke, H., Andrew, M., Lin, Q., Rau, C., Blunt, M.J., Bijeljic, B.: Dynamics of snap-off and pore-filling events during two-phase fluid flow in permeable media. Sci. Rep. 7(1), 5192 (2017)
Sinha, P.K., Wang, C.Y.: Pore-network modeling of liquid water transport in gas diffusion layer of a polymer electrolyte fuel cell. Electrochim. Acta 52(28), 7936–7945 (2007)
Zacharoudiou, I., Chapman, E.M., Boek, E.S., Crawshaw, J.P.: Pore-filling events in single junction micro-models with corresponding lattice boltzmann simulations. Journal of Fluid Mechanics (2017)
Zhao, B., MacMinn, C.W., Juanes, R.: Wettability control on multiphase flow in patterned microfluidics. Proc. Natl. Acad. Sci. 113(37), 10251–10256 (2016)
Zhou, X., Morrow, N.R., Ma, S., et al.: Interrelationship of wettability, initial water saturation, aging time, and oil recovery by spontaneous imbibition and waterflooding. SPE J. 5(02), 199–207 (2000)
Acknowledgements
The authors would like to thank TOTAL management for the authorisation to publish this work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Pavuluri, S., Maes, J., Yang, J. et al. Towards pore network modelling of spontaneous imbibition: contact angle dependent invasion patterns and the occurrence of dynamic capillary barriers. Comput Geosci 24, 951–969 (2020). https://doi.org/10.1007/s10596-019-09842-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10596-019-09842-7