Skip to main content
Springer Nature Link
Log in

A coupling of mixed and continuous Galerkin finite element methods for poroelasticity I: the continuous in time case

  • Original Paper
  • Published:
Computational Geosciences Aims and scope Submit manuscript

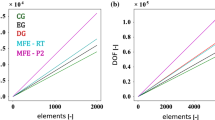
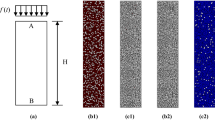
Abstract

In this paper, we formulate a finite element procedure for approximating the coupled fluid and mechanics in Biot’s consolidation model of poroelasticity. Here, we approximate the pressure by a mixed finite element method and the displacements by a Galerkin method. Theoretical convergence error estimates are derived in a continuous in-time setting for a strictly positive constrained specific storage coefficient. Of particular interest is the case when the lowest-order Raviart–Thomas approximating space or cell-centered finite differences are used in the mixed formulation, and continuous piecewise linear approximations are used for displacements. This approach appears to be the one most frequently applied to existing reservoir engineering simulators.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  1. Abousleiman, Y., Cheng, A.-D., Cui, L., Detournay, E., Roegiers, J.: Mandel’s problem revisited. Géotechnique 46, 187–195 (1996)

    Article  Google Scholar 

  2. Biot, M.: General theory of three-dimensional consolidation. J. Appl. Phys. 2, 155–164 (1941)

    Article  Google Scholar 

  3. Biot, M.: Theory of elasticity and consolidation for a porous anisotropic media. J. Appl. Phys. 26(2), 182–185 (1955)

    Article  MathSciNet  MATH  Google Scholar 

  4. Boyce, W., DiPrima, R.: Elementary Differential Equations, 7th edn. Wiley, New York (2001)

    Google Scholar 

  5. Brenner, S., Scott, L.: The Mathematical Theory of Finite Element Methods. Springer, Berlin Heidelberg New York (1994)

    MATH  Google Scholar 

  6. Coussy, O.: Poromechanics. Wiley, New York (2004)

    Google Scholar 

  7. Detournay, E., Cheng, A.-D.: Poroelastic response of a borehole in non-hydrostatic stress field. Int. J. Rock Mech. Mining Sci. 25, 171–182 (1988)

    Article  Google Scholar 

  8. Evans, L.: Partial Differential Equations. American Mathematical Society, Providence (1998)

    MATH  Google Scholar 

  9. Gai, X.: A Coupled Geomechanics and Reservoir Flow Model on Parallel Computers. Ph.D. thesis, University of Texas at Austin (2004)

  10. Garagash, D., Detournay, E.: An analysis of the influence of the pressurization rate on the borehole breakdown pressure. J. Solids Struct. 34(2), 3099–3118 (1997)

    Article  MATH  Google Scholar 

  11. Gibson, R., Knight, K., Taylor, P.: A critical experiment to examine theories of three-dimensional consolidation. Eur. Conf. Soil Mech. 1, 69–73 (1963)

    Google Scholar 

  12. Hudson, J., Stephansson, O., Andersson, J., Tsang, C.-F., Ling, L.: Coupled T-H-M issues related to radioactive waste repository design and performance. Int. J. Rock Mech. Mining Sci. 38, 143–161 (2001)

    Article  Google Scholar 

  13. Kim, J.-M., Parizek, R.: Numerical simulation of the noordbergum effect resulting from groundwater pumping in a layered aquifer system. J. Hydrol. 202, 231–243 (1997)

    Article  Google Scholar 

  14. Langford, T.: Northwest Houston Sinking Faster than Coastal Areas. http://www.Reporter-News.com (1997)

  15. Lewis, R.W., Schrefler, B.A.: The Finite Element Method in the Deformation and Consolidation of Porous Media. Wiley & Sons, Chichester (1987)

    Google Scholar 

  16. Lin, J.: An Interview with Jian Lin, Ph.D. http://www.esi-topics.com/earthquakes/interviews/JianLin.html (2003)

  17. Liu, R.: Discontinuous Galerkin finite element solution for poromechanics. Ph.D. thesis, University of Texas at Austin (2004)

  18. Lubick, N.: Modeling complex, multiphase porous media systems. SIAM News 5(3) (2002)

  19. Mandel, J.: Consolidation des sols (étude mathématique). Géotechnique 30, 287–299 (1953)

    Google Scholar 

  20. Nedelec, J.: Mixed finite elements in ℝ3. Numer. Math. 35, 315–341 (1980)

    Article  MATH  MathSciNet  Google Scholar 

  21. Phillips, P.J.: Finite element methods for linear poroelasticity: theoretical and computational results. Ph.D. thesis, University of Texas at Austin (2005)

  22. Phillips, P.J., Wheeler, M.F. : A coupling of mixed and continuous Galerkin finite element methods for poroelasticity II: the discrete-in-time case. Comput. Geosci. doi:10.1007/s10596-007-9044-z

  23. Rajapakse, R.: Stress analysis of borehole in poroelastic medium. J. Eng. Mech. 119(6), 1205–1227 (1993)

    Article  Google Scholar 

  24. Raviart, R.A, Thomas, J.W.: A mixed finite element method for 2nd order elliptic problems. In: Mathematical Aspects of the Finite Element Method. Lecture Notes in Mathematics, vol. 606, pp. 292–315. Springer, Berlin Heidelberg New York (1977)

    Chapter  Google Scholar 

  25. Rivière, B., Wheeler, M.: Optimal error estimates applied to linear elasticity. Technical report, ICES Report. ICES, Austin (2000)

  26. Roose, T., Netti, P., Munn, L., Boucher, Y., Jain, R.: Solid stress generated by spheroid growth estimated using a linear poroelastic model. Microvasc. Res. 66, 204–212 (2003)

    Article  Google Scholar 

  27. Rutqvist, J., Tsang, C.-F.: Analysis of thermal–hydrologic–mechanical behavior near an emplacement drift at Yucca mountain. J. Contam. Hydrol. 62–63, 637–652 (2003)

    Article  Google Scholar 

  28. Showalter, R.E.: Diffusion in poro-elastic media. J. Math. Anal. Appl. 251, 310–340 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  29. Smillie, A., Sobey, I., Molnar, Z.: A hydro-elastic model of hydrocephalus. Technical report, Oxford University Computing Laboratory: Numerical Analysis Group, Oxford (2004)

  30. Swan, C., Lakes, R., Brand, R., Stewart, K.: Micromechanically based poroelastic modeling of fluid flow in Haversian bone. J. Biomech. Eng. 125(1), 25–37 (2003)

    Article  Google Scholar 

  31. Terzaghi, K.: Principle of Soil Mechanics. A Series of Articles. McGraw-Hill, New York (1926)

    Google Scholar 

  32. Verruijt, A.: Discussion. Proc. 6th Int. Conf. Soil Mech. 3, 401–402 (1965)

    Google Scholar 

  33. Wang, H.F.: Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology. Princeton University Press, Princeton (2000)

    Google Scholar 

  34. Wang, Y., Dusseault, M.: A coupled conductive-convective thermo-poroelastic solution and implications for wellbore stability. J. Petrol. Sci. Eng. 38, 187–198 (2003)

    Article  Google Scholar 

  35. Weiser, A., Wheeler, M.: On convergence of block-centered finite differences and elliptic equations. SIAM J. Numer. Anal. 251(2), 351–375 (1988)

    Article  MathSciNet  Google Scholar 

  36. Wheeler, M.F.: A priori L 2 error estimates for Galerkin approximations to parabolic partial differential equations. SIAM J. Numer. Anal. 10, 723–759 (1973)

    Article  MATH  MathSciNet  Google Scholar 

  37. Wheeler, M.F., Phillips, P.J.: A coupling of mixed and Galerkin methods for poro-elasticity. In: Proceedings of the Second MIT Conference on Computational Fluid and Solid Mechanics, MIT, Cambridge, 17–20 June 2003

    Google Scholar 

  38. Zenisek, A.: The existence and uniqueness theorem in Biot’s consolidation theory. Aplik. Matem. 29, 194–210 (1984)

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Center for Subsurface Modeling (CSM), Institute for Computational Engineering and Sciences (ICES), University of Texas at Austin, Austin, TX, USA

    Phillip Joseph Phillips

  2. CSM, ICES, Department of Aerospace Engineering and Engineering Mechanics, University of Texas at Austin, Austin, TX, USA

    Mary F. Wheeler

  3. Department of Petroleum Engineering and Geosystems Engineering, University of Texas at Austin, Austin, TX, USA

    Mary F. Wheeler

  4. Institute for Computational Engineering and Sciences, University of Texas at Austin, Austin, TX, USA

    Mary F. Wheeler

Authors
  1. Phillip Joseph Phillips
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Mary F. Wheeler
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Mary F. Wheeler.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Phillips, P.J., Wheeler, M.F. A coupling of mixed and continuous Galerkin finite element methods for poroelasticity I: the continuous in time case. Comput Geosci 11, 131–144 (2007). https://doi.org/10.1007/s10596-007-9045-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10596-007-9045-y

Keywords