Abstract
This paper contains equations for the motion of linear viscoelastic bodies interacting under gravity. The equations are fully three dimensional and allow for the integration of the spin, the orbit, and the deformation of each body. The goal is to present good models for the tidal forces that take into account the possibly different rheology of each body. The equations are obtained within a finite dimension Lagrangian framework with dissipation function. The main contribution is a procedure to associate to each spring–dashpot model, which defines the rheology of a body, a potential and a dissipation function for the body deformation variables. The theory is applied to the Earth (solid part plus oceans) and a comparison between model and observation of the following quantities is made: norm of the Love numbers, rate of tidal energy dissipation, Chandler period, and Earth–Moon distance increase.






Similar content being viewed by others
Notes
The moment of inertia of a thin ellipsoidal shell about a principal axis is \(I_a=M(b^2+c^2)/3\), where M is the mass of the shell and b and c are semi axis. Hypothesis (b) implies that \(b=R(1+\varepsilon _b)\) and \(c=R(1+\varepsilon _c)\) where \(\varepsilon _b\ll 1\) and \(\varepsilon _c\ll 1\). Therefore \(I_a=2MR^2(1+\varepsilon _b+\varepsilon _c+\cdots )/3\) and after integration over the radius we obtain that hypothesis (b) is equivalent to \(|\mathbf {B}|\ll 1\).
If \(\varDelta I_{ij}(spin)\) denotes the change of the inertia tensor due to the planet spin \(\varOmega \), a is the planet volumetric radius, and \(\mathrm {k}_\circ \) is the planet secular Love number, then \(\varDelta I_{ij}(spin)=-{\mathrm{I}_\circ }B_{ij}(spin)= \mathrm {k}_\circ \frac{a^5}{3G}\left\{ \varOmega _i\varOmega _j- \frac{1}{3}|\varOmega |^2\delta _{ij}\right\} \) [see, for instance, Williams et al. (2001), Eqs. (11)]. Therefore the moment of inertia strain \(\varDelta I_{ij}/{\mathrm{I}_\circ }\) is related to the moment of inertia stress \(\sigma _{ij}=\left\{ \varOmega _i\varOmega _j- \frac{1}{3}|\varOmega |^2\delta _{ij}\right\} \) as \(\gamma \varDelta I_{ij}/{\mathrm{I}_\circ }=\sigma _{ij}\). This explains the unusual dimension \(\hbox {s}^{-2}\) of the stiffness coefficient \(\gamma \). The same reasoning explains the unusual dimensions of the other rheological constants.
The term \({\mathbf {F}}\) (and also \({\varvec{\varLambda }}_j\)) is being called “force” although it has dimension \(\hbox {s}^{-2}\). It could be more appropriate to call it by “moment of inertia stress” as in the footnote 2 as well as to call \(\mathbf {B}\) by “moment of inertia strain”. For simplicity we will keep using the words force and deformation for \({\mathbf {F}}\) and \(\mathbf {B}\), respectively.
Notice that the Love numbers \(k_o\) in Table 1 have negative real part. This and Eq. (47) imply that \(J<0\) for the ocean tides. Since J gives the time-average balance of kinetic and potential energy, see footnote in the Sect. 1, we conclude that for the oceans the inertia cannot be neglected (kinetic energy only exists when there is inertia). We remark that the presence of an inertial term proportional to \(\mu \) in our model changes completely the behavior of the Love numbers at high frequencies. So, if we compare the imaginary part of the Love number in Eq. (51) with that for the Burgers model in Table 1 of Henning et al. (2009), we conclude that they are not the same, though the Burgers model and the Wiechert model are equivalent. The difference is the inertia. If we make \(\mu =0\) in Eq. (51), then our expression coincides with that in Henning et al. (2009) after redefinition of parameters.
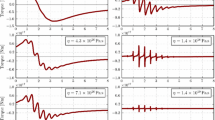
The eigenvalues of free oscillations of our model are (\(\hbox {s}^{-1}\)): \(-1.15\times 10^{-4}\), \(-9.17\times 10^{-6} \pm 5.54\times 10^{-4}i\), and \(-2.96\times 10^{-9}\). The relaxation times corresponding to these eigenvalues are 2.41 h, 30.3 h, and 10.7 years, respectively.
The deformation variables used in Boué et al. (2016), \( Z_{2,m}\), \(m=0,1,2\), are proportional to the \(b_m\) we defined in Sec. 5.1, namely \(\overline{Z}_{2,0}=\varepsilon _1b_0\), \(\overline{Z}_{2,m}=\varepsilon _1b_m/2\), \(m=1,2\), where: \(\overline{Z}\) denotes the complex conjugate of Z and \(\varepsilon _1=\sqrt{45/(16\pi )}{\mathrm{I}_\circ }/(m_1 a^2)\) with \(m_1,a,{\mathrm{I}_\circ }\) being the mass, radius, and moment of inertia of the planet, respectively. Using the decomposition \(-({\varvec{\varOmega }}^{i})^2+\frac{1}{3}\ \mathrm{Tr}\ (({\varvec{\varOmega }}^i))\mathbb {I} \rightarrow (p_0,p_1,p_2)\) given in Eqs. (39) and (40), we obtain that the tidal force coefficients in Boué et al. (2016), denoted as \(Z^e_{2,m}\), \(m=0,1,2\), are given in terms of our coefficients \(a_m\) given in Sec. 5.1 by means of \(\overline{Z}_{2,0}^e=\varepsilon _2(p_0+a_0)\), \(\overline{Z}^e_{2,m}=\varepsilon _2(p_m+a_m)/2\), \(m=1,2\), where \(\varepsilon _2=\sqrt{5/(16\pi )}a^3k_2^0/(m_1 G)\) with \(k^0_2\) being the fluid Love number of the planet. Their parameters \((k^2_0,\tau _2,\tau _e)\) are related to ours \((\mu ,\gamma ,\alpha _1,\alpha _2,\eta _1,\eta _2)\) as: \(\mu =\alpha _2=\eta _2=0\), \(\gamma =\varepsilon _1/\varepsilon _2\), \(\tau _e=\eta _1/\alpha _1\), and \(\tau _2=\eta _1(\alpha _1^{-1}+\gamma ^{-1})\). With these identifications their tidal response equation in the body frame \(Z_{2,m}+\tau _2\dot{Z}_{2,m}=Z^e_{2,m}+\tau _e{\dot{Z}}^e_{2,m}\), \(m=0,1,2\), coincides with our Eq. (49) with the term \(p_m\) added to the left-hand side.
The origin of the name is the following. Consider the harmonic oscillator \(\mu {\ddot{x}}+\eta {\dot{x}}+\gamma x=F(t)\). Multiplying both sides of the equation by \({\dot{x}}\) and time-averaging gives \(\lim _{T\rightarrow \infty }\frac{1}{T}\int _0^TF(t){\dot{x}}(t)dt=\)Footnote 9 continued
\(\lim _{T\rightarrow \infty }\frac{1}{T}\int _0^T\eta {\dot{x}}^2(t)dt=W\) that is the time-average dissipation rate. Multiplying both sides of the equation by x and time-averaging gives \(\lim _{T\rightarrow \infty }\frac{1}{T}\int _0^T F(t) x(t)dt =\lim _{T\rightarrow \infty }\frac{1}{T}\int _0^T [-\mu {\dot{x}}^2(t)+\gamma x^2(t)]dt= J\) that is the time-average balance of kinetic and potential energy.
References
Agnew, D.C.: Treatise on geophysics and geodesy. Earth Tides, pp. 163–195. Elsevier, New York (2007)
Antognini, F., Biasco, L., Chierchia, L.: The spin–orbit resonances of the Solar System: a mathematical treatment matching physical data. J. Nonlinear Sci. 24, 473–492 (2014)
Bambusi, D., Haus, E.: Asymptotic behavior of an elastic satellite with internal friction. Math. Phys. Anal. Geom. 18(1), 1–18 (2015)
Bills, B.G., Ray, R.D.: Lunar orbital evolution: a synthesis of recent results. Geophys. Res. Lett. 26, 3045–3048 (1999)
Bland, D.: Linear Viscoelasticity. Pergamon Press, Oxford (1960)
Boué, G., Correia, A.C., Laskar, J.: Complete spin and orbital evolution of close-in bodies using a Maxwell viscoelastic rheology. Celest. Mech. Dyn. Astron. 126(1–3), 31–60 (2016)
Bryan, G.H.: The waves on a rotating liquid spheroid of finite ellipticity. Philos. Trans. R. Soc. Lond. A 180, 187–219 (1889)
Carr, J.: Applications of Centre Manifold Theory. Springer, New York (1981)
Celletti, A.: Analysis of resonances in the spin–orbit problem in Celestial Mechanics: The synchronous resonance (Part I). J. Appl. Math. Phys. (ZAMP) 41, 174–204 (1990)
Correia, A.C.M., Boué, G., Laskar, J., Rodríguez, A.: Deformation and tidal evolution of close-in planets and satellites using a Maxwell viscoelastic rheology. Astron. Astrophys. 571, A50 (2014)
Dickey, J., Shelus, P., Veillet, C., Whipple, A., Wiant, J., Williams, J., et al.: Lunar laser ranging: a continuing legacy of the Apollo program. Science 265, 482 (1994)
Efroimsky, M.: Tidal dissipation compared to seismic dissipation: in small bodies, earths, and super-earths. Astrophys. J. 746(2), 150 (2012)
Efroimsky, M., Williams, J.G.: Tidal torques: a critical review of some techniques. Celest. Mech. Dyn. Astron. 104, 257–289 (2009)
Egbert, G.D., Ray, R.D.: Estimates of \({M}_2\) tidal energy dissipation from TOPEX/Poseidon altimeter data. J. Geophys. Res. 106, 475–502 (2001)
Ferraz-Mello, S.: Tidal synchronization of close-in satellites and exoplanets. A rheophysical approach. Celest. Mech. Dyn. Astron. 116, 109–140 (2013)
Goldreich, P.: On the eccentricity of satellite orbits in the Solar System. Mon. Not. R. Astron. Soc. 126(3), 257–268 (1963)
Henning, W.G., O’Connell, R.J., Sasselov, D.D.: Tidally heated terrestrial exoplanets: viscoelastic response models. Astrophys. J. 707(2), 1000–1015 (2009)
Hut, P.: Stability of tidal equilibrium. Astron. Astrophys. 92, 167–170 (1980)
Kearsley, E.A., Fong, J.: Linearly independent sets of isotropic Cartesian tensors of ranks up to eight. J. Res. Natl. Bureau Stand. Part B: Math. Sci. B 79, 49–58 (1975)
Lamb, H.: Hydrodynamics, 6th edn. Cambridge Mathematical Library, Cambridge (1932)
Lambeck, K.: The Earth’s Variable Rotation: Geophysical Causes and Consequences. Cambridge University Press, Cambridge (1980)
Mignard, F.: The evolution of the lunar orbit revisited I. Moon Planets 20, 301–315 (1979)
Munk, W.: Once again: once again-tidal friction. Progr. Oceanogr. 40, 7–35 (1997)
Munk, W.H., MacDonald, G.J.F.: The Rotation of the Earth. Cambridge University Press, New York (1961)
Peskin, C.S.: Wave Momentum. Courant Institute of Mathematical Sciences. http://silverdialogues.fas.nyu.edu/docs/IO/24452/peskin.pdf (2010)
Petit, G., Luzum, B.: IERS conventions (2010). Technical report, DTIC Document (2010)
Platzman, G.W.: Planetary energy balance for tidal dissipation. Rev. Geophys. Space Phys. 22, 73–84 (1984)
Ragazzo, C., Ruiz, L.S.: Dynamics of an isolated, viscoelastic, self-gravitating body. Celest. Mech. Dyn. Astron. 122, 303–332 (2015)
Ray, R.D., Erofeeva, S.Y.: Long-period tidal variations in the length of day. J. Geophys. Res.: Solid Earth 119(2), 1498–1509 (2014)
Rochester, M.G., Smylie, D.E.: On changes in the trace of the Earth’s inertia tensor. J. Geophys. Res. 79, 4948–4951 (1974)
Wahr, J.M.: Body tides on an elliptical, rotating, elastic and oceanless earth. Geophys. J. Int. 64, 677–703 (1981)
Wahr, J.M.: Earth tides. In: Ahrens, T.J. (ed.) Global Earth Physics: A Handbook of Physical Constants, vol. 1, pp. 40–46. American Geophysical Union, Washington (1995)
Williams, J.G., Boggs, D.H., Yoder, C.F., Todd Ratcliff, J., Dickey, J.O.: Lunar rotational dissipation in solid body and molten core. J. Geophys. Res. 106, 933–968 (2001)
Wisdom, J., Meyer, J.: Dynamic elastic tides. Celest. Mech. Dyn. Astron. 126, 1–30 (2016)
Yoder, C.: Astrometric and geodetic properties of Earth and the Solar System. In: Ahrens, T.J. (ed.) Global Earth Physics: A Handbook of Physical Constants, vol. 1, pp. 1–31. American Geophysical Union, Washington (1995)
Yoder, C.F., Williams, J.G., Parke, M.E.: Tidal variations of Earth rotation. J. Geophys. Res.: Solid Earth 86, 881–891 (1981)
Zlenko, A.A.: A celestial-mechanical model for the tidal evolution of the Earth–Moon system treated as a double planet. Astron. Rep. 59, 72–87 (2014)
Acknowledgements
We are very grateful to Sylvio Ferraz Mello for all discussions and advices. We also thank Alexandre Correia for the discussions about his work. This paper is part of a project supported by FAPESP 2011/16265-8. C. Ragazzo is partially supported by FAPESP 2011/16265-8.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: The kinetic energy when the angular momentum of tidal waves is relevant
The following analysis of a particular set of solutions to Eq. (12) shows that the Lagrangian function (11) sometimes misses important physical features of the dynamics.
Equation (12) have an interesting set of “tidal wave” (or “quadrupole wave”) solutions:
where \({\hat{a}}>0\) is the wave amplitude,
is the wave angular velocity,
Since \({\varvec{\varOmega }}=0\), the body frame \(\mathrm {K}\) is an inertial frame (if \(\mathbf {Y}(0)=\mathbb {I} \) then \(\mathrm {K}=\kappa \) for all t) and the angular momentum \({\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B})\in \mathrm {K}\) is null in both \(\mathrm {K}\) and \(\kappa \). This seems to be not physically correct since waves do usually have an associated momentum, as explained by the following interesting remarks taking from Peskin (2010). “The phenomenon of wave momentum is remarkable in several respects. First, it is not clear a priori that waves ought to have associated momentum. Waves are commonly divided into two types: transverse and longitudinal waves. In the transverse case, since nothing is moving in the direction of propagation, how can there be associated momentum in that direction? Even in the longitudinal case, since the wave motion is typically oscillatory, one would think that the average momentum density would be zero. How can there be net momentum in the direction of the wave?”. The same type of question applies to the tidal wave above, which is transverse to the radial direction. The answer is essentially the same as that given in Peskin (2010) for water waves, which are also transverse waves: “The motion of fluid particles in water waves is circular, and one might think that the net momentum in the direction of propagation would be zero. This reasoning is incorrect, however, because of the correlation between the height of the water and the direction of horizontal motion. As any swimmer knows, the water is moving forward (i.e., in the direction of the wave) at the crest of the wave, and backward in the trough. This asymmetry is the fundamental source of net momentum in the direction of wave propagation\(\ldots \)”
The arguments in the previous paragraph shows that a term must be added to the Lagrangian function (12) in order to a tidal wave solution to have an associated angular momentum even when \(\varOmega =0\) (or even when there is no mass net rotation). The term we add is motivated by an “\(\varepsilon \)-expansion” of the pseudo-rigid body Lagrangian function in Ragazzo and Ruiz (2015) (it is the only term of order \(\varepsilon ^{5/2}\) in that expansion). The new Lagrangian function is
where \(\beta \) is a dimensionless constant. The Lagrangian function (86) is invariant under the action \(\text {SO(3)}\times \text {SO(3)}\rightarrow \text {SO(3)}\) given by \((U,Y)\rightarrow UY\). As in the case of the rigid body the angular momentum \({\varvec{\ell }}\) defined in Eq. (10) is a conserved quantity. Again a computation gives that \({\varvec{\ell }}=\mathbf {Y}\,\mathbf {L}\,\mathbf {Y}^T\) but in this case the angular momentum \(\mathbf {L}\) in the body frame \(\mathrm {K}\) is given by \( \mathbf {L}={\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B})+{\mathrm{I}_\circ }\beta \mu [{\dot{\mathbf {B}}},\mathbf {B}]. \) In this expression, the first term \({\mathrm{I}_\circ }({\varvec{\varOmega }}+\mathbf {B}{\varvec{\varOmega }}+{\varvec{\varOmega }}\mathbf {B}):\mathrm {K}\rightarrow \mathrm {K}\) represents the angular momentum of the body relative to the inertial frame \(\kappa \) as if it had no motion relative to \(\mathrm {K}\). The second term \({\mathrm{I}_\circ }\beta \mu [{\dot{\mathbf {B}}},\mathbf {B}]\) represents the angular momentum of the body relative to the frame \(\mathrm {K}\). The value of \(\beta \) is directly connected to the choice of the body frame \(\mathrm {K}\). In particular, unless \(\beta \mu [{\dot{\mathbf {B}}},\mathbf {B}]=0\), the frame \(\mathrm {K}\) is not a Tisserand frame (see Munk and MacDonald 1961).
As before, the equation for \({\varvec{\varOmega }}\) derived from the Lagrangian function (86) is
The equations of motion for \(\mathbf {B}\) can be obtained in the following way. The set of matrices \(\mathbf {B}\) can be considered as the subset of all \(3\times 3\) matrices that satisfy the constraints \(f_{km}(\mathbf {B})=B_{km}-B_{mk}=0\) and \(f_0(\mathbf {B})=\ \mathrm{Tr}\ \mathbf {B}=0\). Let \(\chi _{mk}\) and \(\chi _0\) denote the Lagrange multipliers associated to these constraints. The equations of motion are obtained from the extended Lagrangian function
in the usual way:
Using the expressions for \({\widehat{\mathscr {L}}}\) we obtain
In order to eliminate the Lagrange multipliers \(\chi _{ij}\) we add this equation to its transpose and divide by two to obtain
In order to determine \(\chi _0\) we take the trace of this expression to get
So, the differential equation for \(\mathbf {B}\) is
Equations (87) and (88) have the same tidal wave solution as that in Eq. (83). The angular momentum associated to this wave is
which implies that the angular momentum vector have components \(\ell _1=0\), \(\ell _2=0\), and \(\ell _3={\mathrm{I}_\circ }\beta \mu 4\omega _\circ {\hat{a}}^2\). The energy associated to this wave is
As in Sect. 2, consider a mass m of homogeneous inviscid liquid under self-gravity. At rest the liquid has a spherical shape and moment of inertia \({\mathrm{I}_\circ }=0.4\,ma^2\), where a is the radius of equilibrium. In this case \(\mu =\mu _f=1\) and \(\gamma =\gamma _f=2{\mathrm{I}_\circ }G\left( \frac{5}{2}\frac{{\mathrm{I}_\circ }}{m}\right) ^{-5/2}\) as given in Eqs. (16) and (15), respectively. Suppose that the liquid is rotating uniformly with constant angular velocity \(\varOmega =\varOmega _3\mathrm{e}_3\). The equation for the small free oscillations of \(\mathbf {B}\) about the equilibrium shape is
The decomposition of matrix \(\mathbf {B}\rightarrow (b_0,b_1,b_2)\) given in Eqs. (39) and (40) can be used to rewrite this equation as:
The frequency of small oscillations \(\sigma \) obtained from this equation is
Comparing this expression to that in Eq. (87) in Bryan (1889) we obtain that for a mass of perfect liquid
For several types of waves (electromagnetic waves, sound waves, water waves, and certain kinds of traveling waves on strings under tension) the following simple relation holds (Peskin 2010)
For a wave moving along a circular path, like the tidal wave above, this relation could be changed as
where \(R>0\) is some reference radius. If we assumed that the previous relation would hold for the tidal wave solution then, using the expressions for \(\ell _3\) and E above, we would obtain \(\beta =1\). Therefore, it seems that \(\beta \ge 0\) can vary depending on the rheological nature of the body.
To finish, consider the tide response equations [compare to Eq. (37)]:
where \({\dot{{\varvec{\varOmega }}}}=0\) and \(\varOmega =\varOmega _3\mathrm{e}_3\). If we apply the decomposition \(\mathbf {B}\rightarrow (b_0,b_1,b_2)\), \({\mathbf {A}}\rightarrow (a_1,a_2,a_3)\), and \({\varvec{\varLambda }}\rightarrow (\lambda _0,\lambda _1,\lambda _2)\) given in Eqs. (39) and (40) we rewrite Eq. (91) as [compare to Eq. (49)]:
As before \(a_j(t)\) can be Fourier expanded. For a term of the form \(a_j(t)={\hat{a}}\mathrm{e}^{i(\omega t+\varphi )}\), there corresponds a solution of the form \(b_j(t)={\hat{b}}\mathrm{e}^{i(\omega t+\varphi )}\), \(\lambda _j(t)={\hat{\lambda }}\mathrm{e}^{i(\omega t+\varphi )}\), such that \({\hat{a}}\), \({\hat{b}}\), and \({\hat{\lambda }}\) are related as
For the diurnal and the semi-diurnal frequencies \(\omega =j\varOmega _3\), \(j=1,2\), the first of these equations becomes
that is an equation equal to that obtained in Sect. 5.1 for the same frequencies except for the change \(\mu \rightarrow \mu (1-2\beta )\). This is very convenient in the fit of the parameters \(c_1,c_2,c_3,c_4\) as we did in Sect. 6.2. Essentially, the same procedure used in that section can be used in this case and since \(\mu (1-2\beta )\) can be either positive or negative this relaxes the positivity condition we had on the parameter \(\mu \).
Appendix 2: The planetary dissipation of tidal energy and the average work done by the tidal force: relations to the dissipation function and to the Lagrangian function, respectively
In this appendix we present a classical formula of Zschau and Platzman for the time-average planetary dissipation rate of tide energy W. We apply this formula to our model and show that it gives the time average of the dissipation function of the model, which shows that our choice of dissipation function is consistent with results obtained from continuum mechanics. The clear and elegant deduction of the formula of Zschau and Platzman in Platzman (1984) lead us to an analogous, apparently new, formula for the time-average of the work done by the primary tidal force in deforming the planet. This new formula, deduced in Appendix “The average work done by the tidal force and the Lagrangian function” section, gives the “time-average planetary tidal balance of potential and kinetic energy”Footnote 9 J. This new formula is related to the Lagrangian function of our model in the same way as the Zschau and Platzman formula is related to the dissipation function.
1.1 Appendix 2.1: A formula of Zschau and Platzman for the planetary dissipation function and the Rayleigh dissipation function
Following Platzman (1984), let \(\overline{\varPsi }\) be the primary astronomical potential (due to the satellite), \(\varPsi ^\prime \) be the secondary potential due to the tidal redistribution of the mass of the planet, and \(\varPsi =\overline{\varPsi }+\varPsi ^\prime \) be the complete tide potential. Let
be the solid harmonic decomposition of \(\varPsi \), where: \(\overline{\varPsi }_n\) and \( \varPsi _n^\prime \) are spherical surface harmonics of degree n, \((r,\theta ,\phi )\) are spherical coordinates in the rotating reference frame \(\mathrm {K}\), and a is the radius of a spherical surface \(S_a\) that contains the planet inside and does not contain the satellite. In Platzman (1984, Eq. (6)), it is shown that the time-average of the planetary dissipation of tidal energy is given by
where dS is the surface element and \(\langle \cdot \rangle \) denotes the average over a period tide. Since \(\overline{\varPsi }\) is dominated by \(\overline{\varPsi }_2\), all terms in this formula but those of second-degree can be neglected
The energy dissipation rate W is related to the Rayleigh dissipation function \(\mathscr {D}\) in Eq. (23) as follows.
In our model, the primary potential has only the the second-degree harmonic
where \(x=|x|{\hat{x}}\). The secondary potential is
Using that \(dS=a^2\sin \theta d\theta d\phi =a^2d{\hat{x}}\) on \(S_a\), where \((\theta , \phi )\) are polar coordinates on the unit sphere, Eq. (95) can be written as
Now, the same argument as that given at the end of Sect. 3 implies that \(\varGamma _{ijkl}\) is a linear combination of the three tensors \(\delta _{ij}\delta _{kl}\), \(\delta _{ik}\delta _{jl}\), and \(\delta _{il}\delta _{jk}\). An easy computation using polar coordinates shows that
and
In principle the time average must be taken over a period tide. It happens that the tide is not exactly periodic but only almost periodic usually with a dominance of the semi-diurnal mode, so the average is still well defined as \(T\rightarrow \infty \). For the computations, T must be taken as a large multiple of the semi-diurnal period.
Finally, multiplying both sides of the first equation in (36) by \({\dot{\mathbf {B}}}\), taking the trace and the averaging of both sides, and using that the average of a time derivative is zero \(\langle \frac{df}{dt}\rangle =0\), we obtain
Multiplying both sides of the second and third equations in (36) by \({\varvec{\varLambda }}_1\) and \({\varvec{\varLambda }}_2\), respectively, taking the trace and the averaging of both sides, we obtain
where we used that \({\varvec{\varLambda }}_1=\eta _1\dot{{\tilde{\mathbf {B}}}}_1\) and \({\varvec{\varLambda }}_2=\eta _2\dot{{\tilde{\mathbf {B}}}}_2\), similarly to \(\eta _1{\dot{{\tilde{x}}}}_1=\lambda _1\) and \(\eta _2{\dot{{\tilde{x}}}}_2=\lambda _2\) in Eq. (20). This last equation and Eqs. (98) and (23) imply that
This equation shows that the planetary dissipation of tidal energy as given in Eq. (95) coincides with the average power dissipated by the planet in our model.
1.2 Appendix 2.2: The average work done by the tidal force and the Lagrangian function
There are two fundamental functions in our theory of tide response: the Lagrangian \(\mathscr {L}_{\mathbf {B}}\) and the dissipation \(\mathscr {D}\) functions both given in Eq. (23). After we showed the relation between the formula of Zschau and Platzman in Eq. (95) and the dissipation function \(\mathscr {D}\), we wandered whether there would exist a similar relation for \(\mathscr {L}_{\mathbf {B}}\). Indeed there is, \(\mathscr {L}_{\mathbf {B}}\) is equal to the time-average of the work done by the tidal force to deform the planet or equivalently to the “time-average planetary tidal balance of energy”(see footnote at the first page).
Let \({\tilde{J}}\) be the work done by the primary tidal force to deform the planet
where: \(B_a\) is a solid ball that contains the planet and does not contain the satellite, d is the displacement vector, \(\rho \) is the density of the deformed state, and \(-\rho \nabla \overline{\varPsi }\) is the primary tidal force [see Lambeck (1980), p. 7 for details]. It is convenient to suppose that the density is a smooth function that vanishes outside the planet, so the nontrivial part of the integral is restricted to the planet interior. The result we obtain below is the same as that obtained supposing that \(\rho \) varies discontinuously at some interfaces [see Platzman (1984) for the treatment of discontinuities]. Partial integration, the use of \(\nabla ^2\varPsi ^\prime =-4\pi G\nabla (\rho d)\) [see Lambeck (1980), p. 7], and that \(\rho =0\) over the spherical surface \(S_a\) leads to
Partial integration twice and the use of \(\nabla ^2\overline{\varPsi }=0\) in \(B_a\) implies that
Then, by using the solid harmonic decomposition of \(\varPsi ^\prime \) and \(\overline{\varPsi }\) in Eq. (93) the integral becomes
Finally, taking the time average of this equation we obtain
that is similar to Eq. (94) of Zschau and Platzman. Since \(\overline{\varPsi }\) is dominated by \(\overline{\varPsi }_2\), all terms but those of second-degree can be neglected in the above formula, so
that is similar to Eq. (95).
The same reasoning that lead to Eq. (98) shows that the average planetary tidal balance of energy can be written as
Finally, multiplying both sides of the equation of motion (36) by \(\frac{{\mathrm{I}_\circ }}{2} \mathbf {B}\), using the constraints \(\mathbf {B}=\mathbf {B}_1+{\tilde{\mathbf {B}}}_1\) and \(\mathbf {B}=\mathbf {B}_2+{\tilde{\mathbf {B}}}_2\), using the relations \({\varvec{\varLambda }}_1=\alpha _1\mathbf {B}=\eta _1\dot{{\tilde{\mathbf {B}}}}_1\) and \({\varvec{\varLambda }}_2=\alpha _2\mathbf {B}=\eta _2\dot{{\tilde{\mathbf {B}}}}_2\), which are similar to those in Eq. (20), and using Eq. (102) we obtain
that is similar to Eq. (99). Therefore, J is related to the Lagrangian function \(\mathscr {L}_{\mathbf {B}}\) given in Eq. (23) in the same way as the rate of dissipation of tidal energy W is related to the dissipation function \(\mathscr {D}\) given in Eq. (23).
Rights and permissions
About this article
Cite this article
Ragazzo, C., Ruiz, L.S. Viscoelastic tides: models for use in Celestial Mechanics. Celest Mech Dyn Astr 128, 19–59 (2017). https://doi.org/10.1007/s10569-016-9741-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10569-016-9741-9