Wind-Tunnel Simulation of Stable Atmospheric Boundary Layers with an Overlying Inversion

Abstract

Four cases of an overlying inversion imposed on a stable boundary layer are investigated, extending the earlier work of Hancock and Hayden (Boundary-Layer Meteorol 168:29–57, 2018), where no inversion was imposed. The inversion is imposed to one or other of two depths within the layer: midway or deep. Four cases of changed surface condition are also investigated, and it is seen that the surface and imposed conditions behave independently. A change of imposed inversion condition leaves the bottom 1/3 of the layer almost completely unaffected; a change of the surface condition leaves the top 2/3 unaffected. Comparisons are made against two sets of local-scaling systems over the full height of the boundary layer. Both show some influence of the inversion condition. The surface heat flux and the reduction in surface shear stress, and hence the ratio of the boundary-layer height to surface Obukhov length, are determined by the temperature difference across the surface layer (not the whole layer), bringing all cases together in single correlations as functions of a surface-layer bulk Richardson number.

1 Introduction

A stable atmospheric boundary is a naturally occurring phenomenon, for example, arising after the cessation of daytime convective motions. In a previous paper, Hancock and Hayden (2018) investigated a technique for generating an artificially deepened boundary layer in a wind tunnel that had characteristics typical of weakly and moderately stable, horizontally-homogeneous atmospheric boundary layers, drawing on wind-engineering techniques employed extensively for studies in neutral flow. These well-established techniques use a system of tall flow generators and surface roughness in order to create profiles of mean velocity and turbulence quantities that have characteristics of the atmospheric boundary layer, where the term ‘tall’ is used to mean a height comparable with the boundary layer that is generated downstream (and in contrast to a transition trip that is much smaller). A deep boundary layer (say, about 1 m deep) makes simulation conditions—principally the necessary change of temperature for a given freestream speed and bulk Richardson number—more achievable, as well as giving the benefit of a higher Reynolds number than would otherwise occur. It is also generally advantageous in terms of instrumentation and the airflow model in question. This paper is an extension of Hancock and Hayden (2018).

Here, we use the term inversion to mean a temperature profile that is increasing with height above the top of the boundary layer, and created or ‘imposed’ in practice by means of a system of heaters in the upstream flow. Hancock and Hayden (2018) deliberately did not impose an inversion. However, they found that the temperature profile at the wind-tunnel working-section inlet must be non-uniform, i.e. increasing with height, over the depth of the boundary layer if the whole depth of the layer is to be stably stratified. A uniform inlet temperature (above that of the surface) led to about the top third of the layer remaining neutral,¹ the bottom third being stable, and the middle third being an adjustment region. Turbulence quantities such as Reynolds stresses could then vary non-monotonically with height. The non-uniformity of the inlet temperature profile needs to be carefully specified if Reynolds stresses and other quantities are to vary monotonically and smoothly with height. They also found that the initial part of the surface must not be cooled, for the same reason. The influence of stability means that conditions set up in the initial part of the flow tend to be longer-lasting as stability increases. Further details, and a broader background to relevant wind-tunnel experiments, are given in Hancock and Hayden (2018); it is not necessary to repeat them here except to refer to Ohya and Uchida (2003) and Hancock and Pascheke (2014).

Ohya and Uchida (2003) imposed a non-uniform inlet temperature profile in their experiment. The profile was piecewise linear in two stages, with a decrease of gradient at a point above the top of the boundary layer, at $z/h$ = 1.3, where h is the height of the boundary layer based on the mean velocity profile. The degree of stability was altered by a change in freestream speed. Their weakest case (S1) had a bulk Richardson number comparable with one case here (case 6), though their aerodynamic roughness length was larger by a factor of 3.3. Hancock and Pascheke (2014) also used a linear increase in temperature at the working section inlet. The physical set-up was similar to that used in the present experiments, except that the flow generators were too tall to allow a region of uniform, low-turbulence flow above the nominal top of the boundary layer. Moreover, only one stable case was investigated (and is approximately equivalent to case 8 here).

Here, we present an investigation of the effect of imposing an inversion on a stable boundary layer, where the temperature gradient of the inversion is of the same order of magnitude as the average temperature gradient across the boundary layer and comparable with 0.01 K m⁻¹, taken as typical of an inversion strength (see, for example, Beare et al. 2006). Assuming a linear rise of temperature, there are two parameters that describe the imposed inversion: the magnitude of the gradient and the height at which the gradient commences. In all, eight inversion cases are given, with two baseline cases: those of no-inversion and neutral flow. As will be seen, it has been possible, (i) to impose an inversion over the bulk of the boundary layer, but with little effect on the behaviour in the lowest part of the layer, and (ii) for a given imposed inversion, to change the temperature difference across the lowest part of the layer, but without affecting the behaviour above. Thus the surface condition and the imposed condition are, in effect, treated independently. Indeed, for the cases considered, the two conditions are independent.

The overall objective is the extension of the simulation technique presented in Hancock and Hayden (2018) to the case where there is an overlying inversion, and such that the Reynolds stresses also decrease smoothly to a low turbulence level above the top of the boundary layer. As in that study, validation is based primarily on the local scaling frameworks of Nieuwstadt (1984) and Sorbjan (2010). The particular application to which both that and the present work is directed is that of wakes of wind turbines in offshore wind farms, and is the reason for the low aerodynamic roughness length. However, Hancock and Hayden (2018) has also been extended to that of rougher surfaces for studies of the urban environment (Marucci et al. 2018) in stable boundary layers.

2 Wind Tunnel and Instrumentation

The wind-tunnel set-up and the instrumentation were essentially identical to that employed by Hancock and Hayden (2018). Therefore, only key summary features are given here. The EnFlo wind tunnel has a working section that is 20 m in length, 3.5 m in width and 1.5 m in height. Stratification is achieved by means of 15 sets of working-section inlet heating elements, combined with cooled floor panels for stable stratification. The deep boundary layer was generated by means of 13 flat-plate spires mounted 0.5 m from the working-section inlet, together with sharp-edged roughness elements mounted on the floor. The spires were slightly truncated triangles with a base width of 60 mm, tip width of 4 mm, and height of 600 mm, spaced laterally at intervals of 266 mm. The roughness elements were blocks 50 mm wide, 16 mm high, and 5 mm thick, standing on the 50 mm × 5 mm face. They were placed in a staggered arrangement with streamwise and lateral pitches of 360 mm and 510 mm, respectively. Figure 1 of Hancock and Hayden (2018) shows the spires and roughness elements.

Measurements of the mean velocity and Reynolds stresses were made using a two-component, frequency-shifted laser-Doppler anemometry (LDA) system (FibreFlow, Dantec, Denmark) with the probe head held by a traversing system that hung from rails mounted beneath the wind tunnel roof. Only the streamwise and vertical velocity components were measured, u and w denoting the fluctuating parts, respectively, and U the streamwise mean velocity component. Mean temperatures were measured using thermistor probes and the fluctuating temperature by means of a cold-wire, fast-response probe held 4 mm behind the LDA measurement volume in order to measure the turbulent heat fluxes, where the advection time was calculated using the instantaneous velocity component $\left( {U + u} \right)$ in order to correct for the displacement. The cold wire was calibrated against a thermistor, itself used against a standard calibration; differences between thermistors were < 0.1 °C. Sample times were 3 min at a data rate of typically 100 Hz. As in Hancock and Hayden (2018), statistical errors were within about ± 0.5% for mean velocity and within ± 5% for the second-order momentum and thermal moments, to a 95% confidence level. Surface values of shear stress and heat flux were determined from linear extrapolation of the corresponding profiles, over about the inner third of the boundary layer, with extrapolation expected to be within about ± 6% for both. The viscous and thermal conduction contributions over the measured profiles did not exceed about 3.5% and 7%, respectively. The wind-tunnel reference velocity, $U_{\text{Ref}}$, was measured using an ultrasonic anemometer mounted in a upstream position, at X = 5 m, Y = 1 m, z = 1 m, where X is the distance from the working-section inlet, Y is the lateral distance from the working-section centreline, and z is the vertical distance from the wind-tunnel floor; $U_{\text{Ref}}$ was 1.5 m s⁻¹. (It is not the local freestream velocity at the station where the measurements were made.)

The gradient of mean temperature imposed by the inlet heaters needs to be much larger than is the case in the full-scale atmosphere. If H and h are the heights of the full-scale and wind-tunnel-scale boundary layers, respectively, and suffixes H and h denote full- and wind-tunnel scale, then

$$ \frac{{\left( {d\Theta /dz} \right)_{h} }}{{\left( {d\Theta /dz} \right)_{H} }} = \left( {\frac{H}{h}\frac{{\left( {U_{R} } \right)_{h} }}{{\left( {U_{R} } \right)_{H} }}} \right)^{2} , $$

where U_R denotes a reference speed at geometrically equivalent heights. Supposing a full-scale stable boundary-layer height of 200 m and a full-scale reference speed of 10 m s⁻¹ then, for the present boundary layers, the temperature gradient must be about a factor 3600 larger than that at full scale. Based on a full-scale gradient of 0.01 K m⁻¹ (e.g. Beare et al. 2006) the laboratory gradient must be about 40 K m⁻¹.

3 Results and Discussion

As mentioned in the Introduction, eight inversion cases in all were investigated, falling into two categories, cases 3–6 and cases 7–10, controlled by the working-section inlet temperature profile. In the first category, the imposed inversion was varied while the near-surface temperature difference was kept (approximately) constant, by virtue of the way in which the flow was found to behave. In the second, the imposed inversion was kept constant while the near-surface temperature difference was varied. That is, in essence, the surface and overlying conditions were varied independently.

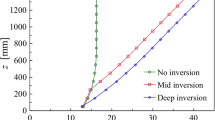
The working-section inlet temperature, $\Theta_{\text{IN}} \left( z \right)$, for cases 3–6 is shown in the profiles of Fig. 1a, together with the profile for no inversion, case 2, this latter case corresponding to the ‘final case’ example given in Hancock and Hayden (2018); $\Theta_{0}$ is the surface temperature. Case 1 is for an isothermal flow, and details for all cases are given in Table 1. The inversion cases 3–6 were defined by an increment, $\Delta \Theta_{\text{IN}}$, above that of the no-inversion profile, as follows: $\Delta \Theta_{\text{IN}} = 2\, {\text{K and}} \Delta \Theta_{\text{IN}} = 4\, {\text{K}}$ for an interval, $\Delta z$ = 100 mm, between the centres of the heater units. These increments were started from origins at z = 250 mm and z = 50 mm, and are denoted as ‘mid’ and ‘deep’ inversions, respectively.

Fig. 1

Working-section inlet temperature profiles. a Cases 2–6; b cases 7–10

Table 1 Cases investigated and salient parameters. $Re_{h} = U_{h} h/\nu$, where ν is the kinematic viscosity evaluated at the surface. Other symbols defined in the text

The working-section inlet temperature profiles for cases 7–10 are shown in Fig. 1b, along with the no-inversion case 2. These were achieved by reducing all of the inlet- heater temperatures for a deep inversion with respect to the surface temperature, by a fixed amount. (The slight kink in the bottom of the profile of case 10 occurred because the laboratory room temperature was not quite low enough; the input power to the lowest heater was zero.) In these cases the gradient of the inversion was $\Delta \Theta_{\text{IN}} /\Delta z$ = 3/100 K mm⁻¹. Guided by the earlier work of Hancock and Hayden (2018) measurements were made at a single streamwise station, X = 11.2 m.

3.1 Cases 3–6

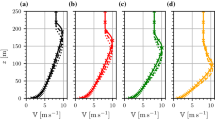
Profiles of mean velocity, mean temperature, Reynolds stresses and second-moment thermal quantities are shown in Fig. 2. The mean velocity and the Reynolds stresses are shown normalized with respect to the reference velocity, but the thermal quantities are shown in dimensional terms as it is advantageous to do so. There is no more than a slight change in the mean velocity profile, Fig. 2a, with inversion condition. For the mid-inversion cases (3 and 4), the mean temperature in Fig. 2e clearly follows closely the no-inversion profile below about z = 300 mm, independent of inversion strength, while this is not the case for the deep inversion examples. It will be noticed that each of the inversion-case temperature profiles shows a distinct kink in the profile between about z = 600 and 700 mm, but not when there is no inversion. The kink is attributed to the formation of the boundary layer just above the top of the spires, and is only visible when a temperature gradient is present. The average straight-line gradient spanning beyond the kink is close to that prescribed at the inlet (Fig. 1).

Fig. 2

Profiles of mean velocity, Reynolds stresses, mean temperature, heat fluxes, and mean-square temperature fluctuation. Symbols as in (a)

The Reynolds stresses, Fig. 2b–d, are all lower than in the neutral case, as is to be anticipated from the influence of stability. Compared with the no-inversion case, the mid-inversion cases are distinct in that the stresses are quite unaffected below about z = 300 mm. Above this height they are clearly lower, consistent with the rising mean temperature above this height. Thus, the effect on the Reynolds stresses of imposing a mid-height inversion is limited to the upper part of the flow, where the mean temperature profile differs from that of the no-inversion profile, there being no discernable influence below. However, with the deep inversion, the Reynolds stresses are reduced over the whole depth of the flow, though only slightly near the surface.

The heat-flux profiles, Fig. 2f, g, exhibit a quite unexpected feature, namely, that there is no discernable change below a height of about z = 150 mm, and only a small change in $\overline{{\theta^{2} }}$ (Fig. 2h). Clearly, for the deep-inversion cases, the mean temperature (above the surface temperature) in this part of the flow is higher, but this has not been met with an increase in the vertical heat flux in particular. Above the height of z = 150 mm the heat-flux profiles show a more complex oscillatory-like behaviour, falling above and below the no-inversion profile.

The second-order moments of Fig. 2 are shown again in Fig. 3 but normalized on the friction velocity, $u_{*}$, and the surface-layer temperature scale, $\theta_{*}$, where $\theta_{*} = - \left( {\overline{w\theta } } \right)_{0} /u_{*}$, and z is normalized by the boundary-layer height, h. Here, $\left( {\overline{w\theta } } \right)_{0}$ denotes the kinematic heat flux at the surface, obtained by linear extrapolation of $\overline{w\theta }$, and $u_{*}$ was obtained from linear extrapolation of $- \overline{uw}$, denoted by ${-}\left( {\overline{uw} } \right)_{0}$. Figure 3 also shows profiles of the local Obukhov length, L, defined below, and the gradient Richardson number, $Ri$, but presented as $Ri/\left( {1 + Ri} \right)$.

$$ L = - \frac{1}{\kappa }\frac{\Theta }{g}\frac{{\left( { - \overline{uw} } \right)^{3/2} }}{{\overline{w\theta } }}, $$

where $\kappa = 0.4$ is the von Kármán constant, $\Theta$ is the absolute temperature, and $g$ is the acceleration due to gravity; $Ri = (g/\Theta )\left( {{\text{d}}\Theta /{\text{d}}z} \right)/\left( {{\text{d}}U/{\text{d}}z} \right)^{2}$. Near the surface, the Reynolds-stress profiles come close to those for neutral flow, most noticeably for $\overline{{w^{2} }}$, though with a visible distinction between the deep- and mid-inversion cases. The thermal quantities show a high degree of concurrence with each other near the surface.

Fig. 3

Profiles of second-order moments, normalized by surface scales, local Obukhov length and gradient Richardson number, as functions of $z/h$. Symbols as in (a)

In the upper part of the flow, the shear stress for the no-inversion case falls to zero at a height a little below that for the neutral case. The effect of the inversions is to reduce the shear stress to zero at a substantially lower height, though $\overline{{u^{2} }}$ and $\overline{{w^{2} }}$ are still decreasing to the respective freestream levels. A similar feature was seen by Hancock and Pascheke (2014). The behaviour of $\overline{{\theta^{2} }}$ is qualitatively as expected in that a peak is caused by the imposed mean temperature gradient and the presence of vertical fluctuations. The peak is larger for the larger gradient and occurs at a lower height for the deeper penetration. The local Obukhov length displays a consistent behaviour of first decreasing with height before rising to a peak in the middle of the layer, except for the deep inversion cases where this characteristic has almost ceased. Overall, the flow near the surface, and hence the surface condition, is almost completely independent of the imposed inversions.

3.2 Cases 7–10

Figure 4 shows the same quantities as in Fig. 2, but where the inversion imposed is a deep inversion (Fig. 1b). The mean velocity profiles of these cases are even closer than in Fig. 2, though there is a small but distinct difference from the neutral profile. The Reynolds-stress profiles are almost entirely unchanged in the upper part of the layer (though there is a slight discrepancy seen in $\overline{{w^{2} }}$ near the top of the layer for case 7); the picture is quite different from that seen in Fig. 2. The primary changes in the second-order moments seen in Fig. 4 all occur below about z = 200 mm. The heat fluxes and the level of the temperature fluctuations all decrease as the near-surface mean temperature difference decreases (Fig. 4e), and the Reynolds stresses increase, as would be expected from a reduced effect of stability. The height of 200 mm is roughly 1/3 of the boundary-layer height, and the influence of the surface condition to this height is consistent with observations by Hancock and Hayden (2018). In the light of the behaviour seen in cases 3–6, this independence between the flow near the surface and that higher up is not unexpected. It does, though, underline the independence observed earlier.

Fig. 4

Profiles of mean velocity, Reynolds stresses, mean temperature, heat fluxes, and mean-square temperature fluctuation. Symbols as in (a)

Figure 5, like Fig. 3, shows the results in terms of surface-layer variables and z/h. Again, near the surface, the Reynolds stresses come close to those of the neutral flow, and the profiles of heat flux and $\overline{{\theta^{2} }}$ all show very close, though not precise, concurrence. That is, the independence between surface and imposed conditions might not be complete. It is supposed that near-independence might cease as the strength of stability increases (though independence would be, in practice, a useful feature). Figure 6 shows the local Obukhov length normalized by its surface value, evaluated in terms of $u_{*}$ and $\left( {\overline{w\theta } } \right)_{0}$, and denoted by $L_{0}$. For all cases these profiles fall close to each other in the lower part of the layer, below about z/h = 0.2. The differences in the profiles above this height for cases 3–6 reflect the influences of the different inversion conditions.

Fig. 5

Profiles of second-order moments, normalized by surface scales, local Obukhov length and gradient Richardson number, as functions of $z/h$. Symbols as in (a)

Fig. 6

Local Obukhov length normalized by the surface Obukhov length, as functions of z/h. a Cases 2–6; b cases 7–10, and case 2

3.3 Surface-Layer Similarity

Profiles of mean velocity and mean temperature are shown in Fig. 7, in semi-logarithmic axes, fitted to surface-layer functions given by

$$ U = \frac{{u_{*} }}{\kappa }\left[ {\ln \left( {\frac{z}{{z_{0} }}} \right) + \beta_{m} \frac{{z - z_{0} }}{{L_{0} }}} \right] $$

(1)

and

$$ \Theta - \Theta_{0} = \frac{{\theta_{*} }}{\kappa }\left[ {0.95 \ln \left( {\frac{z}{{z_{0\theta } }}} \right) + \beta_{\theta } \frac{{z - z_{0\theta } }}{{L_{0} }}} \right], $$

(2)

where $\beta_{m}$ and $\beta_{\theta }$ have been taken as 8 and 16, respectively, as discussed and employed by Hancock and Hayden (2018). The aerodynamic and thermal roughness lengths, respectively $z_{0}$ and $z_{0\theta }$, are given in Table 2, as are $u_{*} /U_{h}$ and $\theta_{*}$, where $U_{h}$ is $U$ at z = h. As found by Hancock and Hayden (2018) and Hancock and Pascheke (2014), and earlier by Beljaars and Holtslag (1991) and Duynkerke (1999), the thermal roughness length is orders of magnitude smaller than the aerodynamic roughness length. Figure 7a, b shows the profiles for cases 3–6, and Fig. 7c, d, the profiles for cases 7–10, along with the no-inversion profiles, and also the neutral profiles of velocity.

Fig. 7

Mean velocity and mean temperature profiles, normalized by $u_{*}$ and $\theta_{*}$ respectively, and comparisons with surface-layer functions, Eqs. 1 and 2, shown by full lines, no symbols. a, b cases 3–6; c, d cases 7–10; cases 1 and 2 also shown. Symbols for (b) as in (a), for (d) as in (c)

Table 2 Surface-layer quantities

The measured mean velocity profiles, Fig. 7a, show reasonably good concurrence with Eq. 1 near the surface, and there is no particular trend with imposed inversion. The no-inversion case (case 2) falls close to all, except the profile for case 4. It is not known why this case does not fall within the trend of the other cases of this group. On the other hand, while there is reasonable concurrence of velocity profiles, the temperature profiles in Fig. 7b show a clear trend with the inversion case; the deeper the inversion and the stronger the inversion the further the profile is from the no-inversion case. There is, though, reasonable agreement with Eq. 2.

Cases 7–10 show different trends. For the mean velocity, Fig. 7c, cases 7 and 8 are close to each other, close to the no-inversion case, and close to cases 3–6 (Fig. 7a). However, cases 9 and 10 follow distinctly different shapes. Curiously, they fall close to the analytical form to a greater height. In contrast, the mean temperature profiles, Fig. 7d, show the four inversion cases to fall fairly close to each other (below about z = 200 mm) but clearly separate from the no-inversion case; there is no trend as seen in Fig. 7b. What is more, while two cases (7 and 8) follow Eq. 2 reasonably well, the other two cases do not. (The thermal roughness length quoted in Table 2 for these cases has been obtained from the lowest few measurement points, even though Fig. 7d shows Eq. 2 not to be valid.) All that has changed in cases 7–10 is the near-surface temperature difference (successively decreasing), but a very marked change has taken place in both the velocity and the temperature profiles at some point between case 8 and case 9. In the earlier experiment reported in Hancock and Pascheke (2014) good concurrence was obtained with Eq. 2, where their case is fairly close to case 8, as mentioned earlier.

Figure 8 shows the surface-layer similarity functions for momentum and temperature, respectively $\phi_{m}$ and $\phi_{\theta }$, where these are defined by

$$ \phi_{m} = \frac{\kappa z}{{u_{*} }}\frac{\partial U}{\partial z}, $$

$$ \phi_{\theta } = \frac{\kappa z}{{\theta_{*} }}\frac{\partial \Theta }{\partial z}. $$

Fig. 8

Surface-layer similarity functions, $\phi_{m}$ and $\phi_{\theta }$. a, b Cases 3–6; c, d cases 7–10; case 2 also shown in each. Symbols for (b) as in (a), for (d) as in (c). Full lines: Eqs. 3 and 4

The figure also shows the surface-layer forms given by

$$ \phi_{m} = 1 + \beta_{m} \frac{z}{{L_{0} }}, $$

(3)

$$ \phi_{\theta } = 0.95 + \beta_{\theta } \frac{z}{{L_{0} }}. $$

(4)

Note, z is normalized by $L_{0}$ in this figure. Figure 8a, b gives the profiles for cases 3–6, and Fig. 8c, d the profiles for 7–10. Starting with cases 3–6, the respective profiles near the surface fall fairly close to each other as is to be expected on the basis of surface similarity, although $\phi_{m}$ and $\phi_{\theta }$ are larger than given by Eqs. 3 and 4. The same features were seen by Hancock and Hayden (2018). Further from the surface, the presence of the inversion leads to large values of $\phi_{\theta }$ compared with the no-inversion case. The picture near the surface for cases 7 and 8 is that they are close to the cases just discussed, but for 9 and 10 there is a further departure from Eqs. 3 and 4. It is supposed that this departure is linked to that seen in Fig. 7c, d, for the mean velocity and mean temperature profiles. It is also supposed that if the gradient of the imposed inversion were reduced such that the near-surface temperature difference was unchanged, then the distinctly different behaviour seen in cases 9 and 10 would cease. If so, then the conformity to forms (1) and (2) is contingent on the flow above the surface layer meeting certain (yet to be determined) conditions. Indeed, as a general point not pursued further here, this is well established for neutral turbulent boundary layers (see, for example, Townsend 1976).

3.4 Comparisons with the Local-Scaling Analyses of Nieuwstadt and Sorbjan

As in Hancock and Hayden (2018), we compare the present measurements with the local-scaling analyses of Nieuwstadt (1984) and Sorbjan (2010). All stable cases (2–10) are shown together, and the measurements presented in Hancock and Hayden (2018) are shown as single trend lines. Nieuwstadt’s (1984) analysis gives predictions for non-dimensional groups as functions of z/L. Figure 9 shows the following six quantities:

$$ Ri,\quad \frac{{\overline{{w^{2} }}^{1/2} }}{{\left( { - \overline{uw} } \right)^{1/2} }},\quad \frac{{\left( {\overline{{\theta^{2} }} \left( { - \overline{uw} } \right)} \right)^{1/2} }}{{\overline{w\theta } }},\quad \frac{{ - \overline{u\theta } }}{{\overline{w\theta } }},\quad \frac{{K_{m} }}{{L\left( { - \overline{uw} } \right)^{1/2} }},\quad \frac{{K_{\theta } }}{{L\left( { - \overline{uw} } \right)^{1/2} }}, $$

where

$$ K_{m} = - \overline{uw} /\frac{\partial U}{\partial z}, $$

and

$$ K_{\theta } = - \overline{w\theta } /\frac{\partial \Theta }{\partial z}, $$

and Nieuwstadt’s (1984) predictions along with his trend lines through the Cabauw field data. These groups are ill-conditioned near the top of the boundary layer and so the measurements have not been plotted when either $\left| {{-}\overline{uw} } \right|$ or $\left| {\overline{w\theta } } \right|$ is less than 0.1 of the respective surface value.² Although there is some scatter in the measurements, which increases with increasing $z/L$, they follow similar trends, if not falling close to a single trend line in each set. There are some differences in trend for cases 3 and 4 in particular, seen in Fig. 9a, c, d and f, all of which refer to thermal quantities. These features are linked to the change in mean temperature gradient that arises in the middle of the layer. In Fig. 9f, for example, there is not a commensurate increase in heat transfer, leading this quantity to fall below the trend of the other cases. That there is less scatter between cases 7–10 than there is between cases 3–6 arises because the outer flow is not affected by the change of the surface condition, as already noted. These trends broadly coincide with those of Hancock and Hayden (2018), differing mostly in the thermal quantities, and departing from some of the trends of Nieuwstadt (1984) in much the same way. Only in some quantities is their behaviour approximately ‘z-less’, i.e. constant, at larger $z/L.$

Fig. 9

Parameters according to Nieuwstadt’s (1984) local scaling. Symbols as in (b). Full lines show Nieuwstadt’s analytical results; broken lines, the field measurement trend lines. Dotted lines show Hancock and Hayden (2018) trend lines

Nieuwstadt (1985) gives further theoretical analysis with a closure model based on constant gradient- and flux-Richardson numbers (each of 0.2), which allows prediction of quantities as functions of $z/h$. The temperature varies as $- { \ln }\left( {1 - z/h} \right)$, and so has an infinite gradient at $z = h$. (For further discussion of the singularity see Derbyshire 1990.) Its curvature below this height loosely resembles the curves of positive $d^{2} \Theta /dz^{2}$ for the inversion cases (Figs. 2e, 4e) but not, of course, for the no-inversion case. Other quantities generally do not follow the predicted forms, for instance, a linear decrease of $- \overline{w\theta }$. Clearly, too, the gradient Richardson number (Figs. 2h, 4h) does not exhibit the assumed value. While an implicit assumption of this study is that the inlet temperature profile can be ‘fine tuned’ to give desired characteristics it remains to be seen quite what can be achieved, not forgetting that neither the time-dependent nature of a stable boundary layer nor the Earth’s angular acceleration can be represented.

Figure 10 gives the measurements in terms of Sorbjan’s (2010) ‘master’ scaling, employing a length scale $\kappa z$, a velocity scale, $U_{S} = \kappa zN$, and a temperature scale, $\Theta_{S} = \kappa z{\text{d}}\Theta /{\text{d}}z$, where $N^{2} = \left( {g/\Theta } \right)\left( {{\text{d}}\Theta /{\text{d}}z} \right)$. Four of the non-dimensional groups that follow are

$$ \frac{{ - \overline{uw} }}{{U_{S}^{2} }},\quad \frac{{ - \overline{w\theta } }}{{U_{S} \Theta_{S} }},\quad \frac{{ - \left( {\overline{{w^{2} }} } \right)^{1/2} }}{{U_{S} }},\quad \frac{{ - \left( {\overline{{\theta^{2} }} } \right)^{1/2} }}{{\Theta_{S} }}, $$

and are shown in Fig. 10, where this figure also gives Sorbjan’s (2010) empirical forms for these functions, based on the data from the SHEBA field programme. In addition, as in Hancock and Hayden (2018), Fig. 10 gives the functions based on the data of Caughey et al. (1979). The same constraint has been applied to these measurements as those given in Fig. 9. (Relaxing the constraint leads to the trends extending to higher Ri, though with no increase in scatter.) For each group, the cases broadly follow a single trend line, though there is some difference seen in Fig. 10a, c, between cases 3–6 and 7–10, where this difference occurs in the middle of the range covered, rather than at one end or the other. Primarily because of the presence of an inversion, the parameter range is greater than that covered by the measurements of Hancock and Hayden (2018). Though not included for the sake of clarity in Fig. 10, their measurements exhibit good general agreement with those here. The measurement trends show similar variations to those found by Sorbjan (2010), except that the trend slopes are clearly less negative. Hancock and Hayden (2018) found that $\left( {\overline{{\theta^{2} }} } \right)^{1/2} /\Theta_{S}$ differed most from the full-scale empirical curve, though here, at higher Ri, it is $- \overline{uw} /U_{S}^{2}$ that differs the most. Nevertheless, Fig. 10 as a whole is taken as further confirmation that the present simulation is representative of a full-scale stable atmospheric boundary layer.

Fig. 10

Parameters according to Sorbjan’s (2010) local scaling. Symbols as in (a). Lines with no symbols show Sorbjan’s fitted curves. For Caughey et al. (1979) average values for $u_{*}$ and $\theta_{*}$: 0.16 m s⁻¹, 0.065 K

3.5 Surface Heat Flux

Hancock and Hayden (2018) found that the surface heat flux, expressed in terms of the surface Obukhov length as the ratio $h/L_{0}$, to be a function alone of a bulk Richardson number $Ri_{h} = g \Delta \Theta_{h} h/\left( {\Theta_{0} U_{h}^{2} } \right)$, where $\Delta \Theta_{h}$ is the mean temperature difference $\Theta_{h} - \Theta_{0}$, and $\Theta_{h}$ is the mean temperature at the boundary-layer edge ($z = h$). The surface shear stress was also found to be a function of $Ri_{h}$. Figure 11a, b shows $h/L_{0}$ and $- \left( {\overline{uw} } \right)_{0} /U_{h}^{2}$ for cases 3–6 and cases 7–10, together with the trend lines given by Hancock and Hayden (2018). Not surprisingly, the inversion cases do not fall close to these lines. As was seen earlier (Fig. 2g), the surface heat flux of cases 3–6 was unaffected by the imposition of an inversion, while imposing an inversion clearly increases the difference $\Delta \Theta_{h}$ and increases $Ri_{h}$. Similar comments apply to $- \left( {\overline{uw} } \right)_{0} /U_{h}^{2}$ in Fig. 11b. For cases 7–10 the changes in the temperature profiles (Fig. 4e) lead primarily to changes in the temperature gradient near the surface, the decrease in gradient corresponding to the decrease in surface heat flux, and also an increase in surface shear stress as the local effect of stability decreases.

Fig. 11

Length ratio $h/L_{0}$ and surface shear stress as functions of Richardson number. a, b Bulk Richardson number, $Ri_{h}$; c, d hybrid Richardson number, $Ri'_{h}$, and surface-layer Richardson number, $Ri_{SL}$. Symbols in (b) as in (a), in (d) as in (c). × denotes shear stress in neutral flow (case 1). Full lines in (a) and (b), repeated in (c) and (d), are from Hancock and Hayden (2018). Broken lines in (c) and (d) are given by Eqs. 5 and 6

Given the insensitivity of the surface heat flux to the inversion strength seen in Fig. 2f, and the change seen in Fig. 4f, it looks as though the heat flux is determined primarily by the temperature near the surface (with respect to $\Theta_{0}$), rather than that at the top of the boundary layer. Two Richardson numbers are therefore defined in terms of a nominal surface layer, denoted by SL: $Ri'_{h} = g \Delta \Theta_{SL} h/\left( {\Theta_{0} U_{h}^{2} } \right)$ and $Ri_{SL} = g \Delta \Theta_{SL} h_{SL} /\left( {\Theta_{0} U_{SL}^{2} } \right),$ where $\Delta \Theta_{SL}$ is the mean temperature difference across a supposed surface layer of height, $h_{SL}$, and $U_{SL}$ is the flow speed at the height $h_{SL}$. Here, $h_{SL}$ has been taken as a measurement point at z = 79 mm, corresponding to about 0.14 h. Figure 11c shows $h/L_{0}$ against $Ri'_{h}$ and against $Ri_{SL}$. When plotted against $Ri'_{h}$ the measurements in all cases (2, 3–6 and 7–10) fall close to the trend line from Hancock and Hayden (2018), underlining the conclusion that the heat flux is not determined by the temperature difference across the flow above the surface layer. Again, similar comments apply to $- \left( {\overline{uw} } \right)_{0} /U_{h}^{2}$, shown in Fig. 11d. When plotted against $Ri_{SL}$ we also see the measurements falling close to single trend lines. (That these also fall close to single trend lines is expected to follow in that $U_{SL} /U_{h}$ varies by only about ± 2%, and $h_{SL}$ is a fixed fraction of h.) These lines are given by

$$ h/L_{0} = 20 Ri_{SL} $$

(5)

and

$$ - \left( {\overline{uw} } \right)_{0} /U_{h}^{2} = 0.0020\left( {1 - 7.5 Ri_{SL} } \right), $$

(6)

for $Ri_{SL} \,{ \lesssim }\,0.04$, the limit of the present experiment. As noted by Hancock and Hayden (2018), the constant term on the right-hand side of Eq. 6 pertains to the state of the neutral layer, which would be different in other circumstances, and so this equation cannot be regarded as general as Eq. 5, though the functional form may be. The measurements of Hancock and Pascheke (2014) imply a factor of 22 in Eq. 5. Overall, all the cases show that the surface heat flux and the change in the surface shear stress are determined by the temperature difference across the surface layer, and not by the temperature difference above the surface layer. The definition of the surface layer—or near-surface layer—height is not critical to the argument. Supposing its edge to be at 0.2 h, that is at 110 mm, leads to the same conclusions, though the lines have gradients that are 17% less steep.³ Of course, Eq. 5 could be expressed in terms of the surface layer alone, $h_{SL} /L_{0} \approx 3Ri_{SL}$, but the principal interest here is the whole layer.

Although all the cases fall close to the lines given by Eqs. 5 and 6 it is clear that $\phi_{m}$ and $\phi_{h}$ in Fig. 8c, d do not conform to surface-layer scaling, namely that these quantities should be functions only of $z/L_{0}$. The progressive weakening of the near-surface temperature gradient in cases 7–10, and the unchanging gradient in the flow above the surface layer, means that the effect of stratification in the surface layer, relative to that above, is also progressively weaker, as was noted earlier. Nevertheless, the departure from the surface-layer forms of Eqs. 1–4 is not seen in terms of bulk parameters applied to a nominal surface layer, as presented here.

4 Further and Concluding Comments

A surprising and quite remarkable feature in this investigation is the almost complete independence between (approximately) the lower 1/3 and upper 2/3 of the boundary layer; a change of inversion condition having little or no influence in the lower 1/3, and change in near-surface condition (in terms of near-surface temperature difference) having no influence in the upper 2/3. This behaviour, however, is not like that of an internal boundary layer because a change in the outer flow would lead to a change in the internal boundary layer (though not vice versa, by definition of an internal layer). Rather, it is seen as the effect of stability in reducing vertical influence. As a summary characteristic this demarcation has been inferred from a variety of upstream conditions: no-inversion, two inversion depths, a range of inversion gradients, a range of near-surface temperature difference. But these various upstream conditions lead to some different, finer features that do not fall within this one-third to two-thirds demarcation (e.g. Fig. 3a compared with the other figures of Fig. 3).

Imposing an inversion reduces the levels of the Reynolds stresses, but only above about $z/h$ = 0.6 for the ‘mid’ inversion cases (3 and 4), while the heat fluxes and the mean square temperature fluctuation show no significant change in the lower 1/3 of the boundary layer for either ‘mid’ or ‘deep’ inversion (cases 3–6). Whereas the Reynolds stresses generally decrease smoothly and monotonically over the full depth of the layer, the heat fluxes and mean square temperature fluctuation do not. Non-monotonic behaviour of the latter (seen in the upper 2/3) is to be expected, and associated with the gradient of mean temperature and the vertical fluctuations, which in turn qualitatively accounts for the behaviour seen in the vertical heat flux, and in the horizontal heat flux (from the correlation between vertical and horizontal velocity fluctuations, manifest in the Reynolds shear stress). It is assumed that different shapes of imposed temperature profile would lead to different profile shapes for these thermal quantities, as well as different shapes for the Reynolds stresses. Reducing the near-surface temperature difference, while maintaining the same imposed inversion profile, affected the second-order moments in only the lower 1/3 of the layer, increasing the Reynolds stresses and reducing the heat fluxes and the temperature fluctuations.

Surface-layer similarity is exhibited for the second-order moments, except for $\overline{{u^{2} }}$ falling below that of the level in neutral flow. The higher level of $\overline{{u^{2} }}$ in the surface layer of the neutral case, but the concurrence of $\overline{{w^{2} }}$, is not unlike that seen by Hancock and Bradshaw (1989) where the longitudinal fluctuations can be lower when freestream turbulence is present, assuming the higher level of turbulence in the flow above the surface layer is qualitatively like freestream turbulence. Surface-layer similarity fails for the mean velocity and mean temperature when the near-surface temperature difference is weakened sufficiently (cases 9 and 10), all else constant. In that a ‘smaller’ temperature difference across the surface layer is closer to neutral flow (including the case of passive heat transfer), where conformity would be expected, it is inferred that a change in the flow structure above the surface layer has, somehow, become dominant in affecting the surface layer.

Examining the various cases in the local-scaling framework of Nieuwstadt (1984) showed concurrence of all cases for some parameters, but not completely for groups involving mean or fluctuating thermal quantities. The theory presented by Nieuwstadt (1984) does not include the influence of an inversion as imposed here, though an outcome of the theory is that there is an infinite temperature gradient at the top of the layer, where all the turbulence quantities have reduced to zero. Preliminary measurements not presented here showed no significant effect of an inversion imposed at the top of the boundary layer. In the local-scaling framework of Sorbjan (2010) the various cases show close though not complete agreement with each other, the differences occurring in the middle of the layer but neither in the upper part nor near the surface. Cases 7–10 fall closer together than do cases 3–6, the variations amongst the latter corresponding to differences between these cases seen in the upper 2/3 of the layer. In overall terms, as seen in Hancock and Hayden (2018), each of the general trends has a lower slope than the consensus of the field data used by Sorbjan (2010).

The near independence between the lower 1/3 and the upper 2/3 of the boundary layer means that the relationship between surface heat flux, expressed in terms of $h/L_{0}$, and a bulk Richardson number can be generalized from that given by Hancock and Hayden (2018). The ratio $h/L_{0}$ and the reduction in surface shear stress are closely linked solely to a bulk Richardson number for the surface layer for all the cases investigated. The temperature difference across the remainder of the boundary layer plays no significant part.

Both the concurrence with and the departures from the frameworks of Nieuwstadt (1984) and Sorbjan (2010) suggest that the present results could also be of use in gaining a better understanding of the full-scale atmospheric boundary layer.