Skip to main content
SpringerLink
Log in

Water-Tank Studies of Separating Flow Over Rough Hills

  • Original Paper
  • Published:
Boundary-Layer Meteorology Aims and scope Submit manuscript

Abstract

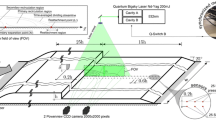
The present work investigates the lower boundary condition for flows over a steep, rough hill. Simple asymptotic arguments together with the mixing-length hypothesis are used to derive a local analytical solution that is tested against three different flow conditions. In all, 36 velocity profiles are compared with the proposed expression. The experiments were carried out in a water channel and velocity measurements were made through laser Doppler anemometry. The extent of separated flow was made to vary as a function of the roughness and the Reynolds number. The analysis includes regions of attached as well as separated flow. In particular, the solution of Stratford is studied at the points of separation and re-attachment and found to apply equally well in rough walls.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Allen B, Brown AR (2002) Large-eddy simulation of turbulent separated flow over rough hills. Boundary-Layer Meteorol 102: 177–198

    Article  Google Scholar 

  • Andreopoulos J, Durst F, Zaric Z, Jovanovic J (1984) Influence of Reynolds number on characteristics of turbulent wall boundary layers. Exp Fluids 2: 7–16

    Article  Google Scholar 

  • Bevington PR (1969) Data reduction and error analysis for the physical sciences. McGraw-Hill, New York, 351 pp

    Google Scholar 

  • Brown AR, Hobson JM, Wood N (2001) Large-eddy simulation of neutral turbulent flow over rough sinusoidal ridges. Boundary-Layer Meteorol 98: 411–441

    Article  Google Scholar 

  • Castro IP (2007) Rough-wall boundary layers: mean flow universality. J Fluid Mech 585: 469–485

    Article  Google Scholar 

  • Castro IP, Apsley DD (1997) Flow and dispersion over topography: a comparison between numerical and laboratory data for two-dimensional flows. Atmos Environ 31: 839–850

    Article  Google Scholar 

  • Cheng H, Castro IP (2002) Near-wall flow development after a step change in surface roughness. Boundary-Layer Meteorol 105: 411–432

    Article  Google Scholar 

  • Clauser FH (1954) Turbulent boundary layers in adverse pressure gradients. J Aeronaut Sci 21: 91–108

    Google Scholar 

  • Cruz DOA, Silva Freire AP (1998) On single limits and the asymptotic behaviour of separating turbulent boundary layers. Int J Heat Mass Transfer 41: 2097–2111

    Article  Google Scholar 

  • Cruz DOA, Silva Freire AP (2002) Note on a thermal law of the wall for separating and recirculating flows. Int J Heat Mass Transfer 45: 1459–1465

    Article  Google Scholar 

  • Fernholz HH, Krause E, Nockemann M, Schober M (1995) Comparative measurements in the canonical boundary layer at Re δ2 ≤ 6 × 104 on the wall of the DNW. Phys Fluids A 7: 1275–1281

    Article  Google Scholar 

  • Finnigan JJ (1983) A streamlined coordinate system for distorted turbulent shear flows. J Fluid Mech 130: 241–258

    Article  Google Scholar 

  • Flack KA, Schultz MP, Connely JS (2007) Examination of a critical roughness height for outer layer. Phys Fluids 19: 95–104

    Article  Google Scholar 

  • Gad-el-Hak M, Bandyopadhyay PR (1994) Reynolds number effects in wall-bounded turbulent flows. Appl Mech Review 47: 307–365

    Article  Google Scholar 

  • Garratt JR (1992) The atmospheric boundary layer. Cambridge University Press, Cambridge, 316 pp

    Google Scholar 

  • Goldstein S (1948) On laminar boundary layer flow near a position of separation. Quart J Mech Appl Maths 1: 43–69

    Article  Google Scholar 

  • Hewer FE (1998) Non-linear numerical model predictions of flow over an isolated hill of moderate slope. Boundary-Layer Meteorol 87: 381–408

    Article  Google Scholar 

  • Hunt JCR, Leibovich S, Richards KJ (1988) Turbulent shear flow over low hills. Quart J Roy Meteorol Soc 114: 1435–1470

    Article  Google Scholar 

  • Iizuka S, Kondo H (2004) Performance of various sub-grid scale models in large-eddy simulations of turbulent flow over complex. Atmos Environ 38: 7083–7091

    Article  Google Scholar 

  • Jackson PS, Hunt JCR (1975) Turbulent wind flow over a low hill. Quart J Roy Meteorol Soc 101: 929–955

    Article  Google Scholar 

  • Kaplun S (1967) Fluid mechanics and singular perturbations. Academic Press, 369 pp

  • Kim HG, Patel VC (2000) Test of turbulence models for wind flow over terrain with separation and recirculation. Boundary-Layer Meteorol 94: 5–21

    Article  Google Scholar 

  • Krogstad PA, Antonia RA (1999) Surface roughness effects in turbulent boundary layers. Exp Fluids 27: 450–460

    Article  Google Scholar 

  • Lagerstrom PA, Casten RG (1972) Basic concepts underlying singular perturbation techniques. SIAM Rev 14: 63–120

    Article  Google Scholar 

  • Loureiro JBR, Soares DV, Fontoura Rodrigues JLA, Pinho FT, Silva Freire AP (2007a) Water tank and numerical model studies of flow over steep smooth two-dimensional hills. Boundary-Layer Meteorol 122: 343–365

    Article  Google Scholar 

  • Loureiro JBR, Pinho FT, Silva Freire AP (2007b) Near wall characterization of the flow over a two-dimensional steep smooth hill. Exp Fluids 42: 441–457

    Article  Google Scholar 

  • Mellor GL (1966) The effects of pressure gradients on turbulent flow near a smooth wall. J Fluid Mech 24: 255–274

    Article  Google Scholar 

  • Mellor GL (1972) The large Reynolds number, asymptotic theory of turbulent boundary layers. Int J Eng Sci 10: 851–873

    Article  Google Scholar 

  • Nakayama A, Koyama H (1984) A wall law for turbulent boundary layers in adverse pressure gradients. AIAA J 22: 1386–1389

    Article  Google Scholar 

  • Oke TR (1987) Boundary layer climates. Routledge, London, 435 pp

    Google Scholar 

  • Perry AE, Joubert PN (1963) Rough-wall boundary layers in adverse pressure gradients. J Fluid Mech 17: 193–211

    Article  Google Scholar 

  • Perry AE, Schofield WH, Joubert PN (1969) Rough-wall turbulent boundary layers. J Fluid Mech 37: 383–413

    Article  Google Scholar 

  • Prandtl L (1925) Über die ausgebildete Turbulenz. ZAMM 5: 136–139

    Google Scholar 

  • Ross AN, Arnold S, Vosper SB, Mobbs SD, Nixon N, Robins AG (2004) A comparison of wind-tunnel experiments and numerical simulations of neutral and stratified flow over a hill. Boundary-Layer Meteorol 113: 427–459

    Article  Google Scholar 

  • Schlichting H (1979) Boundary layer theory. McGraw Hill, New York, 817 pp

    Google Scholar 

  • Snyder WH, Castro IP (2002) The critical Reynolds number for rough-wall boundary layers. J Wind Eng Ind Aerodyn 90: 41–54

    Article  Google Scholar 

  • Stratford BS (1959) The prediction of separation of the turbulent boundary layer. J Fluid Mech 5: 1–16

    Article  Google Scholar 

  • Sychev VV, Sychev VV (1987) On turbulent boundary layer structure. PMM USSR 51: 462–467

    Google Scholar 

  • Sykes RI (1980) An asymptotic theory of incompressible turbulent boundary-layer flow over a small hump. J Fluid Mech 101: 647–670

    Article  Google Scholar 

  • von Kármán Th (1930) Mechanische ahnlichkeit und turbulenz. Proc Third Intern Congress for Appl Mech, Stockholm

  • Yajnik KS (1970) Asymptotic theory of turbulent shear flow. J Fluid Mech 42: 411–427

    Article  Google Scholar 

  • Ying R, Canuto VM (1997) Numerical simulation of the flow over two-dimensional hills using a second-order turbulence closure model. Boundary-Layer Meteorol 85: 447–474

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Programa de Engenharia Mecânica (COPPE/UFRJ), Universidade Federal do Rio de Janeiro, C.P. 68503, 21945-970, Rio de Janeiro, Brazil

    J. B. R. Loureiro, A. S. Monteiro & A. P. Silva Freire

  2. Divisão de Metrologia Científica e Industrial, Instituto Nacional de Metrologia (INMETRO), 22050-050, Rio de Janeiro, Brazil

    J. B. R. Loureiro

  3. Centro de Estudos de Fenómenos de Transporte, Faculdade de Engenharia da Universidade do Porto, Rua Dr. Roberto Frias s/n, 4200-465, Porto, Portugal

    F. T. Pinho

  4. Universidade do Minho, Largo do Paço, 4704-553, Braga, Portugal

    F. T. Pinho

Authors
  1. J. B. R. Loureiro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. S. Monteiro
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. F. T. Pinho
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. P. Silva Freire
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. B. R. Loureiro.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Loureiro, J.B.R., Monteiro, A.S., Pinho, F.T. et al. Water-Tank Studies of Separating Flow Over Rough Hills. Boundary-Layer Meteorol 129, 289–308 (2008). https://doi.org/10.1007/s10546-008-9314-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10546-008-9314-x

Keywords

Search

Navigation