Skip to main content
SpringerLink
Log in

Geometric integration of Hamiltonian systems perturbed by Rayleigh damping

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

Abstract

Explicit and semi-explicit geometric integration schemes for dissipative perturbations of Hamiltonian systems are analyzed. The dissipation is characterized by a small parameter ε, and the schemes under study preserve the symplectic structure in the case ε=0. In the case 0<ε≪1 the energy dissipation rate is shown to be asymptotically correct by backward error analysis. Theoretical results on monotone decrease of the modified Hamiltonian function for small enough step sizes are given. Further, an analysis proving near conservation of relative equilibria for small enough step sizes is conducted.

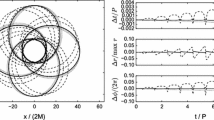
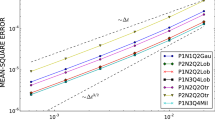
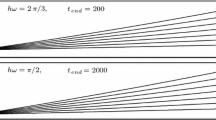
Numerical examples, verifying the analyses, are given for a planar pendulum and an elastic 3D pendulum. The results are superior in comparison with a conventional explicit Runge-Kutta method of the same order.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Abraham, R., Marsden, J.E.: Foundations of Mechanics, 2nd edn. Benjamin/Cummings, Reading (1978)

    MATH  Google Scholar 

  2. Armero, F., Romero, I.: On the formulation of high-frequency dissipative time-stepping algorithms for nonlinear dynamics. I. Low-order methods for two model problems and nonlinear elastodynamics. Comput. Methods Appl. Mech. Eng. 190(20–21), 2603–2649 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  3. Armero, F., Romero, I.: On the formulation of high-frequency dissipative time-stepping algorithms for nonlinear dynamics. II. Second-order methods. Comput. Methods Appl. Mech. Eng. 190(51–52), 6783–6824 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  4. Gonzalez, O.: Time integration and discrete Hamiltonian systems. J. Nonlinear Sci. 6(5), 449–467 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  5. Gonzalez, O., Simo, J.C.: On the stability of symplectic and energy-momentum algorithms for non-linear Hamiltonian systems with symmetry. Comput. Methods Appl. Mech. Eng. 134(3–4), 197–222 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  6. Grabowski, J.: Free subgroups of diffeomorphism groups. Fundam. Math. 131(2), 103–121 (1988)

    MathSciNet  MATH  Google Scholar 

  7. Hairer, E., Lubich, C., Wanner, G.: Geometric numerical integration illustrated by the Störmer-Verlet method. Acta Numer. 12, 399–450 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration, 2nd edn. Springer Series in Computational Mathematics, vol. 31. Springer, Berlin (2006)

    MATH  Google Scholar 

  9. Hansen, A.C.: A theoretical framework for backward error analysis on manifolds. J. Geom. Mech. 3(1), 81–111 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hochbruck, M., Ostermann, A.: Exponential integrators. Acta Numer. 19, 209–286 (2010)

    Article  MathSciNet  Google Scholar 

  11. Holm, D.D.: Geometric Mechanics. Part I. Imperial College Press, London (2008)

    MATH  Google Scholar 

  12. Kane, C., Marsden, J.E., Ortiz, M., West, M.: Variational integrators and the Newmark algorithm for conservative and dissipative mechanical systems. Int. J. Numer. Methods Eng. 49(10), 1295–1325 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kriegl, A., Michor, P.W.: The Convenient Setting of Global Analysis. Mathematical Surveys and Monographs, vol. 53. Am. Math. Soc., Providence (1997)

    MATH  Google Scholar 

  14. Lubich, C., Walther, B., Brügmann, B.: Symplectic integration of post-Newtonian equations of motion with spin. Phys. Rev. D 81(10), 104025 (2010)

    Article  Google Scholar 

  15. Marsden, J.E.: Lectures on Mechanics. London Mathematical Society Lecture Note Series, vol. 174. Cambridge University Press, Cambridge (1992)

    MATH  Google Scholar 

  16. Marsden, J.E., Misiołek, G., Ortega, J.P., Perlmutter, M., Ratiu, T.S.: Hamiltonian Reduction by Stages. Lecture Notes in Mathematics, vol. 1913. Springer, Berlin (2007)

    MATH  Google Scholar 

  17. Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry, 2nd edn. Texts in Applied Mathematics, vol. 17. Springer, New York (1999)

    MATH  Google Scholar 

  18. McLachlan, R., Perlmutter, M.: Conformal Hamiltonian systems. J. Geom. Phys. 39(4), 276–300 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  19. McLachlan, R.I., Quispel, G.R.W.: Splitting methods. Acta Numer. 11, 341–434 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  20. McLachlan, R.I., Quispel, G.R.W.: Geometric integrators for ODEs. J. Phys. A 39(19), 5251–5285 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  21. Modin, K.: Adaptive geometric numerical integration of mechanical systems. Ph.D. thesis, Lund University (2009)

  22. Modin, K., Perlmutter, M., Marsland, S., McLachlan, R.I.: On Euler-Arnold equations and totally geodesic subgroups. J. Geom. Phys. 61(8), 1446–1461 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  23. Reich, S.: Backward error analysis for numerical integrators. SIAM J. Numer. Anal. 36(5), 1549–1570 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  24. Smale, S.: Topology and mechanics. I. Invent. Math. 10, 305–331 (1970)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Engineering and Advanced Technology, Massey University, Private Bag 11 222, Palmerston North, 4442, New Zealand

    Klas Modin

  2. Centre for Mathematical Sciences, Lund University, Box 118, 221 00, Lund, Sweden

    Gustaf Söderlind

Authors
  1. Klas Modin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Gustaf Söderlind
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Klas Modin.

Additional information

Communicated by Christian Lubich.

Presented at the BIT50 conference in Lund, Sweden, 17–20 June 2010.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Modin, K., Söderlind, G. Geometric integration of Hamiltonian systems perturbed by Rayleigh damping. Bit Numer Math 51, 977–1007 (2011). https://doi.org/10.1007/s10543-011-0345-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10543-011-0345-1

Keywords

Mathematics Subject Classification (2000)

Search

Navigation