Skip to main content
SpringerLink
Log in

Rational approximation to trigonometric operators

  • Published:
BIT Numerical Mathematics Aims and scope Submit manuscript

Abstract

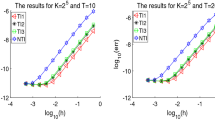
We consider the approximation of trigonometric operator functions that arise in the numerical solution of wave equations by trigonometric integrators. It is well known that Krylov subspace methods for matrix functions without exponential decay show superlinear convergence behavior if the number of steps is larger than the norm of the operator. Thus, Krylov approximations may fail to converge for unbounded operators. In this paper, we propose and analyze a rational Krylov subspace method which converges not only for finite element or finite difference approximations to differential operators but even for abstract, unbounded operators. In contrast to standard Krylov methods, the convergence will be independent of the norm of the operator and thus of its spatial discretization. We will discuss efficient implementations for finite element discretizations and illustrate our analysis with numerical experiments.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. L. Bergamaschi and M. Vianello, Efficient computation of the exponential operator for large, sparse, symmetric matrices, Numer. Linear Algebra Appl., 7 (2000), pp. 27–45.

    Article  MATH  MathSciNet  Google Scholar 

  2. D. Cohen, E. Hairer, and C. Lubich, Long-time analysis of nonlinearly perturbed wave equations via modulated Fourier expansions, Arch. Ration. Mech. Anal., 187 (2008), pp. 341–368.

    Article  MATH  MathSciNet  Google Scholar 

  3. D. Cohen, E. Hairer, and C. Lubich, Conservation of energy, momentum and actions in numerical discretizations of nonlinear wave equations, to appear in Numer. Math. (2008).

  4. D. Cohen, E. Hairer, and C. Lubich, Energy conservation over long times of numerical discretizations for nonlinear wave equations, to appear in Proceedings of Equadiff07, (2008).

  5. V. A. Dougalis and S. M. Serbin, Remarks on a class of rational approximations to the cosine, BIT, 20 (1980), pp. 204–211.

    Article  MATH  MathSciNet  Google Scholar 

  6. V. L. Druskin and L. A. Knizhnerman, Extended Krylov subspaces: approximation of the matrix square root and related functions, SIAM J. Matrix Anal. Appl., 19 (1998), pp. 755–771.

    Article  MATH  MathSciNet  Google Scholar 

  7. M. Eiermann and O. Ernst, A restarted Krylov subspace method for the evaluation of matrix functions, SIAM J. Numer. Anal., 44 (2006), pp. 2481–2504.

    Article  MATH  MathSciNet  Google Scholar 

  8. A. Frommer and V. Simoncini, Stopping criteria for rational matrix functions of Hermitian and symmetric matrices, SIAM J. Sci. Comput., 30 (2008), pp. 1387–1412.

    Article  MathSciNet  Google Scholar 

  9. B. García-Archilla, J. Sanz-Serna, and R. Skeel, Long-time-step methods for oscillatory differential equations, SIAM J. Sci. Comput., 30(3) (1998), pp. 930–963.

    Article  Google Scholar 

  10. G. H. Golub and C. F. van Loan, Matrix Computations, 2nd edn., Johns Hopkins University Press, Baltimore, MD, 1989.

    MATH  Google Scholar 

  11. V. Grimm, A note on the Gautschi-type method for oscillatory second-order differential equations, Numer. Math., 102 (2005), pp. 61–66.

    Article  MATH  MathSciNet  Google Scholar 

  12. V. Grimm, On error bounds for the Gautschi-type exponential integrator applied to oscillatory second-order differential equations, Numer. Math., 100 (2005), pp. 71–89.

    Article  MATH  MathSciNet  Google Scholar 

  13. V. Grimm, On the use of the Gautschi-type exponential integrator for wave equations, in Numerical Mathematics and Advanced Applications, ENUMATH 2005, A. Bermúdez de Castro, D. Gómez, P. Quintela, and P. Salgado, eds., Springer, Berlin, Heidelberg, 2006, pp. 557–563.

    Chapter  Google Scholar 

  14. V. Grimm and M. Hochbruck, Error analysis of exponential integrators for oscillatory second-order differential equations, J. Phys. A, Math. Gen., 39 (2006), pp. 5495–5507.

    Article  MATH  MathSciNet  Google Scholar 

  15. E. Hairer and C. Lubich, Long-time energy conservation of numerical methods for oscillatory differential equations, SIAM J. Numer. Anal., 38 (2000), pp. 414–441.

    Article  MATH  MathSciNet  Google Scholar 

  16. E. Hairer and C. Lubich, Spectral semi-discretisations of weakly nonlinear wave equations over long times, Found. Comput. Math., 8 (2008), pp. 319–334.

    Article  Google Scholar 

  17. E. Hairer and C. Lubich, Oscillations over long times in numerical Hamiltonian systems, to appear in Proceedings of the HOP programme, Isaac Newton Institute, 2008.

  18. M. Hochbruck and C. Lubich, On Krylov subspace approximations to the matrix exponential operator, SIAM J. Numer. Anal., 34 (1997), pp. 1911–1925.

    Article  MATH  MathSciNet  Google Scholar 

  19. M. Hochbruck and C. Lubich, A Gautschi-type method for oscillatory second-order differential equations, Numer. Math., 83 (1999), pp. 403–426.

    Article  MATH  MathSciNet  Google Scholar 

  20. L. Lopez and V. Simoncini, Analysis of projection methods for rational function approximation to the matrix exponential, SIAM J. Numer. Anal., 44(2) (2006), pp. 613–635.

    Article  MATH  MathSciNet  Google Scholar 

  21. I. Moret and P. Novati, RD-rational approximations of the matrix exponential, BIT, 44 (2004), pp. 595–615.

    Article  MATH  MathSciNet  Google Scholar 

  22. I. Moret and P. Novati, Interpolating functions of matrices on zeros of quasi-kernel polynomials, Numer. Linear Algebra Appl., 11 (2005), pp. 337–353.

    Article  MathSciNet  Google Scholar 

  23. O. Nevanlinna, Convergence of Iterations for Linear Equations, Birkhäuser, Basel, 1993.

    MATH  Google Scholar 

  24. P. P. Petrushev and V. A. Popov, Rational Approximation of Real Functions, Cambridge University Press, Cambridge, 1987.

    MATH  Google Scholar 

  25. M. Popolizio and V. Simoncini, Accerleration techniques for approximating the matrix exponential operator, SIAM J. Matrix Anal. Appl., 30 (2008), pp. 657–683.

    Article  Google Scholar 

  26. A. Ruhe, Rational Krylov sequence methods for eigenvalue computation, Linear Algebra Appl., 58 (1984), pp. 391–405.

    Article  MATH  MathSciNet  Google Scholar 

  27. Y. Saad, Analysis of some Krylov subspace approximations to the matrix exponential operator, SIAM J. Numer. Anal., 29 (1992), pp. 209–228.

    Article  MATH  MathSciNet  Google Scholar 

  28. J. M. Sanz-Serna, Mollified impulse methods for highly-oscillatory differential equations, SIAM J. Numer. Anal., 46 (2008), pp. 1040–1059.

    Article  MathSciNet  Google Scholar 

  29. G. R. Sell and Y. You, Dynamics of Evolutionary Equations, Springer, New York, Berlin, Heidelberg, 2002.

    MATH  Google Scholar 

  30. A. F. Timan, Theory of Approximation of Functions of a Real Variable, Pergamon Press, Oxford, 1963.

    MATH  Google Scholar 

  31. J. van den Eshof and M. Hochbruck, Preconditioning Lanczos approximations to the matrix exponential, SIAM J. Sci. Comput., 24(4) (2006), pp. 1438–1457.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mathematisches Institut, Heinrich-Heine-Universität Düsseldorf, Universitätsstr. 1, D-40225, Düsseldorf, Germany

    V. Grimm & M. Hochbruck

Authors
  1. V. Grimm
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Hochbruck
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Hochbruck.

Additional information

AMS subject classification (2000)

65F10, 65L60, 65M60, 65N22

Rights and permissions

Reprints and permissions

About this article

Cite this article

Grimm, V., Hochbruck, M. Rational approximation to trigonometric operators . Bit Numer Math 48, 215–229 (2008). https://doi.org/10.1007/s10543-008-0185-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10543-008-0185-9

Key words

Search

Navigation