Seismic hazard for the Trans Adriatic Pipeline (TAP). Part 1: probabilistic seismic hazard analysis along the pipeline

Abstract

The design of critical facilities needs a targeted computation of the expected ground motion levels. The Trans Adriatic Pipeline (TAP) is the pipeline that transports natural gas from the Greek-Turkish border, through Greece and Albania, to Italy. We present here the probabilistic seismic hazard analysis (PSHA) that we performed for this facility, and the deaggregation of the results, aiming to identify the dominant seismic sources for a selected site along the Albanian coast, where one of the two main compressor stations is located. PSHA is based on an articulated logic tree of twenty branches, consisting of two models for source, seismicity, estimation of the maximum magnitude, and ground motion. The area with the highest hazard occurs along the Adriatic coast of Albania (PGA between 0.8 and 0.9 g on rock for a return period of 2475 years), while strong ground motions are also expected to the north of Thessaloniki, Kavala, in the southern Alexandroupolis area, as well as at the border between Greece and Turkey. The earthquakes contributing most to the hazard of the test site at high and low frequencies (1 and 5 Hz) and the corresponding design events for the TAP infrastructure have been identified as local quakes with M_W 6.6 and 6.0, respectively.

1 Introduction

The Trans Adriatic Pipeline (TAP) is the pipeline that transports natural gas from the Greek-Turkish border, through Greece and Albania, to Italy (TAP AG 2020). The TAP, together with the Trans Anatolian Pipeline (TANAP) and the South Caucasus Pipeline (SCPX), is one of the transport infrastructures of the so-called Southern Gas Corridor, allowing access to the European market for natural gas reserves in the Caspian Sea area (Shah Deniz II Consortium, offshore field south of Baku). By enabling diversification of supply sources, TAP has been one of the projects of most interest to the European Union with a total investment of over €40 billion.

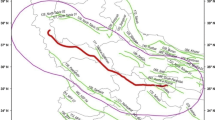
The pipeline starts at Kipoi in Greece, near the border with Turkey, where it is connected with the TANAP. The total length of the pipeline is about 878 km, most of which in Greece (550 km), 215 km in Albania, 105 km offshore in the Adriatic Sea, and about 8 km in Italy (Fig. 1). The TAP maximum elevation is about 2100 m above sea level, along the mountain ranges of Albania, while its maximum depth is about 810 m below sea level in the Adriatic Sea. Along the route, there are four compression stations (two for the initial phase). The pipe diameter is 1.22 m on the stretch of land with a pressure of 95 bar and 1.07 m on the stretch of sea with a pressure of 145 bar (TAP AG 2020).

Fig. 1

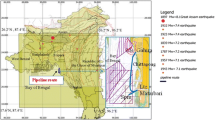
Basic information about the study region crossed by the TAP: a simplified sketch map showing the plate-tectonic framework of the eastern Mediterranean Sea and surrounding area. The main faults (modified from Aksu et al. 2005) are reported; the blue arrows indicate the relative motions of plates with respect to Eurasia (McClusky et al. 2003); b horizontal GNSS velocities (red arrows) and corresponding error ellipses (red ellipses) modified from Rossi et al. (2020). The TAP route is plotted in green; c fault plane solutions of earthquakes with M_W > 5 from the global CMT catalogue (www.globalcmt.org) in the 400-km wide buffer zone around the TAP route (in green). For M_W > 6.0 events is reported the date

The safety aspects of the pipelines are not covered by specific European regulations (Eurocode 8–Part 4; CEN 2006), mainly focusing on major accident prevention for industrial plants. However, piping systems are not excluded from the same disaster scenarios, in terms of incidence and severity, as those observed for fixed industrial installations. Also, damage to pipelines can cause serious cascading crashes, such as fires and explosions, which pose a significant threat to people and infrastructure near the place of failure. Pipelines buried in earthquake-prone areas may leak or break following a seismic event, especially if the pipeline is affected by permanent ground displacement or strong transient ground jolts (Pyrras and Sextos 2018). Most of the damage reported to date is attributed to peak ground displacement (PGD; O'Rourke and Palmer 1996; Chen et al. 2002), with possible failures triggered by active fault movements (Melissianos et al. 2017), landslides, and liquefaction phenomena (De Risi et al. 2018). Wave propagation effects can also contribute to pipe damage (Sakurai and Takanashi 1969; Esposito et al. 2009; O’Rourke 2009), though to a lesser extent. In fact, ground shaking is not considered a major threat for buried pipelines, except for those sites characterised by the transition between very stiff and very soft soils, locations of pump stations or other critical facilities. For earthquake ground motion assessment, in terms of peak ground acceleration (PGA), peak ground velocity (PGV), and spectral acceleration (SA), a probabilistic seismic hazard analysis (PSHA) is usually adopted (e.g., Mousavi et al. 2014). The more problematic aspect of PGD has been approached in two different ways, either following a deterministic approach based on empirical relationships between the maximum fault displacement and the surface-wave magnitude (Liu et al. 2010) or performing a probabilistic fault displacement hazard analysis (Melissianos et al. 2017).

In this context, to assure the long-term safety of the pipeline, it is critical to conduct a study of seismic hazard along the entire route and lifetime of the pipeline. In this paper, we summarise the PSHA done for the TAP. The novelty of this study, with respect to the previously cited studies, is the deep examination of all existing data and the detailed evaluation of the uncertainties involved in the computation. Therefore, a wide range of experts from different disciplines (geology, seismology, geophysics, physics, engineering) was involved in the present study. To account for uncertainties, we applied two approaches for PSHA based on fault characteristics, in addition to the standard approach based on large seismogenic zones (SZs). Seismic hazard based on linear seismic sources (faults) is an innovative approach, although already applied within the European SHARE project (Giardini et al. 2014). It is based on the characterisation of the fault activity, a consolidated topic if well supported by tectonic information. The results based on the fault activity (Sandron et al. 2019) will be of great importance compared to those obtained by the well-known approach based on large SZs, which is here employed as a benchmark for any PSHA.

This study was carried out a few years ago, and some of the ingredients, such as the ground motion models (GMMs), may appear to be outdated. However, we believe this is a case study of broader interest as it is complemented with the results of the deterministic approach (see Moratto et al. 2020 preliminary accepted), and because of its multidisciplinary approach (including geodetic, geophysical, geological surveys).

2 Geological context

The geological investigation along the TAP route has been carried out at a regional scale (1:200,000 scale) within a 400-km wide (200 km on both sides) buffer zone along the 878 km of its extent. The overall aim was to: (1) identify and map the seismogenic sources that could affect the pipeline, (2) provide their seismotectonic parameters. We provide an updated tectonic model of the study area that includes the Italian, Greek, Albanian, and South Adriatic sectors, as well as north-western Turkey, southern Bulgaria, and North Macedonia (Fig. 1). In particular, 163 seismogenic sources have been identified along the pipeline route: 61 in Greece, 30 in Albania, 27 in Bulgaria, 13 in North Macedonia, 1 in Serbia, 2 in Montenegro, 23 in Turkey, and 6 in Italy (Fig. 2).

Fig. 2

Simplified fault model representing the top margin of the composite seismogenic sources identified in the 400-km wide buffer zone (cyan line) around the TAP route (double blue line). The labels are the codes of the faults reported in the electronic supplements ES 1 and ES 2. Legend: solid line = active fault, dashed line = silent fault, green line = normal fault, red line = reverse fault, yellow line = strike-slip fault. The inset is an enlargement of the Fier area with the dominant faults

The TAP route crosses different structural/geodynamic domains, resulting in a strongly variable geotectonic setting that needs to be considered along the main pipeline route. The present-day geological framework of the Mediterranean region results from a series of connected fold-and-thrust belts, associated foreland and back-arc basins of different age, deformation, and internal architecture (e.g., Gueguen et al. 1998; Cavazza and Wezel 2003; Perouse et al. 2012). This configuration is the result of the complex interaction between the Eurasian and African-Arabian continental plates that produced consumption and partial obduction of the oceanic lithosphere of the Tethys region, except for the Ionian basin and the south-eastern Mediterranean. In particular, the tectonic evolution of the eastern Mediterranean has been mainly controlled by (Fig. 1a): (i) the northward subduction (Hellenic subduction) of the African plate along the Hellenic arc beneath western Turkey and the Aegean region, started from at least 100 Myr (e.g., Jolivet and Brun 2010); (ii) the continental collision in eastern Turkey (e.g., Taymaz et al. 2007). The Hellenic subduction produced back-arc extension and volcanism, thinning the continental crust of the overlying Aegean-west Anatolia region (Van Hinsbergen and Schmid 2012; Faccenna et al. 2014; Menant et al. 2016; Papazachos 2019) after the Paleocene compressional phase that formed the Dinarides and Hellenides chains (Faccenna et al. 2014). Eastern Turkey suffered crustal shortening and thickening due to the northward motion of the Arabian plate relative to Eurasia (e.g., Taymaz et al. 1990; McClusky et al. 2003; Dilek and Pavlides 2006). GNSS (Global Navigation Satellite System) data show the counter-clockwise rotation of the Aegean-Anatolian plate (Fig. 1b) probably generated by the combination of the slab pull force related to the subduction to the west, and of the pushing from the convergent zone to the east (Taymaz et al. 2007), facilitated by strike-slip movements (Fig. 1c) along the North Anatolian Fault Zone (NAFZ), to the north, and the East Anatolian Fault Zone (EAFZ), to the south (Le Pichon and Kreemer 2010; Nocquet 2012). Presently, African subduction and trench retreat are still active, in particular, the African plate converges at about 0.6 cm/yr with Eurasia (Nocquet 2012).

The complexity of the geodynamic framework of the eastern Mediterranean region, including western Turkey and Greece, is reflected in its seismicity. This area is one of the most seismically active and rapidly deforming regions of the world. The seismicity is mostly concentrated along the Hellenic subduction, not included in the study area. Even if the subduction process has no direct influence on the TAP route hazard, part of the tectonics of Greece and Turkey affecting the study area is related to the above mentioned subduction.

2.1 Italy and the Adriatic sector

The receiving terminal of the TAP is located in the Salento Peninsula (Apulia) in southern Italy. The Salento Peninsula, together with offshore so-called Apulia swell, constitute the southern tip of the Adria microplate, a carbonate platform sitting on a Mesozoic basement (the Apulian foreland) characterised by two opposite-verging Neogene-Quaternary chains: the NE-verging southern Apennines to the west, and the SW-verging Albanides-External Hellenides to the east (Moretti and Royden 1988; Argnani et al. 2001). The Apulian foreland is considered the peripheral bulge produced by the flexural bending due to the loading of the two opposing chains. The southern Apennines are mainly the result of a Neogene deformation that affected the passive Mesozoic palaeomargin of Adria, and consist of a pile of thrust sheets derived from the deformation of Mesozoic-Cenozoic carbonate platform and basin successions detached from their basement (e.g., D’Argenio et al. 1973; Mostardini and Merlini 1986; Casero et al. 1988; Patacca and Scandone 2001) and overthrusted on the Apulian platform during the early Pliocene. Later, the inner part of the Apulian platform was involved in a contractional deformation (buried duplex system) (e.g., Shiner et al. 2004; Patacca and Scandone 2007).

2.2 Albania

Albania hosts the Albanides fold-and-thrust belt, which, with the Dinarides to the north and the Hellenides to the south, form a branch of the Alpine orogenic belt. The Albanides are a mainly Neogene chain composed of magmatic and sedimentary rocks from the Ordovician to the Quaternary age that can be subdivided into an eastern internal zone and a western external zone (Robertson and Shallo 2000; Nieuwland et al. 2001; Frasheri et al. 2009; Lacombe et al. 2009). The inner Albanides consist of thick-skinned thrust sheets composed in the Mirdita Zone of Triassic-Jurassic ophiolites and sedimentary deposits, which were involved in the Middle Jurassic to Tertiary tectonism and intense metamorphism. At present, this internal domain is affected by the extension, with direction varying from E-W to N-S (Jouanne et al. 2012). The external Albanides, developed off the passive eastern margin of the Adria plate, are composed by NNW-SSE to NW–SE thrusts, back-thrusts, and folds affected by transfer zones with a NE-SW to nearly E-W orientation (Caputo and Pavlides 2013), such as the Vlora-Elbasani-Dibra (VED) fault zone (Roure et al. 2004) that continues in Macedonia (Dumurdzanov et al. 2005). The external Albanides consist of Mesozoic carbonates and evaporites, and Oligocene to Pliocene–Quaternary clastic deposits.

2.3 Greece

The Hellenic orogeny results from the closure of a series of interconnected neo-Tethyan basins and the subsequent collision between Gondwana-derived continental fragments and Eurasia from the Cretaceous to the Oligocene time (e.g., Mountrakis et al. 1983; Mountrakis 2010). Post-Oligocene tectonics was governed by the subduction of Africa beneath the Aegean microplate. The most prominent geodynamic feature of the Aegean region is the Hellenic Arc, consisting of an outer sedimentary arc and an inner volcanic arc (Fig. 1a). The Hellenides are composed of two structural provinces, the external and internal Hellenides, affected by the ophiolitic suture zones of Vardar and Pindos (e.g., Papanikolaou 1997, 2009; Mountrakis 2010; Kilias et al. 2016). The internal Hellenides were characterised by a flyschoid deposition from the Triassic to the Paleogene-Neogene, becoming progressively younger from east to west due to the orogeny migration. A Cenozoic thin-skinned tectonics, characterised by the development of NW-trending thrusts, marks the structural evolution of the external Hellenides (Kilias et al. 2016). The mainland eastern part of the internal Hellenides, which includes southern Bulgaria, mainly consists of a Palaeozoic continental crust affected by Alpine metamorphism (Meinhold and Kostopoulos 2013; Kilias et al. 2016). The western portion of the internal Hellenides mainly consists of polymetamorphic imbricated nappes emplaced during the Oligocene, composed of a Palaeozoic or older basement overlain by a Triassic-Jurassic clastic and carbonate succession (Kilias et al. 2016).

3 Seismogenic sources

The new seismogenic fault database for the entire TAP, containing all identified active and potentially active composite seismogenic sources (CSSs) in the 400-km wide buffer zone (Fig. 2), was obtained by integrating:

• onshore and offshore geological investigations conducted both on re-elaborated existing geological and geophysical data and new field surveys. In particular, structural data have been collected in some areas of Italy (pipeline receiving terminal zone), Albania, and Greece, while high resolution seismic profiles were acquired by the Statoil (now Equinor) in 2012 along the Adriatic route of TAP and made available for the aim of the project;

• data collected from the databases of seismogenic faults [EDSF-European Database of Seismogenic Faults (Basili et al. 2013), DISS-Database of Individual Seismogenic Sources for Italy (Basili et al. 2008); GreDaSS-Greek Database of Seismogenic Sources (Caputo et al. 2012)]. The sources identified in the cited databases are not actual faults but CSSs (i.e., inferred structures based on regional surface and subsurface geological data that are exploited well beyond the simple identification of active faults or youthful tectonic features) that may contain one or more fault segments and, hence, one or more actual seismogenic sources (Basili et al. 2008, 2013). In the following, the terms fault and CSS are used as equivalents for our purposes;

• literature information.

Following Slejko et al. (2011), we call hereafter “silent faults” the potentially active faults, i.e., the tectonic structures with no clear association with seismicity but showing geological evidence of activity during Late Quaternary and can be, therefore, expected to move within a future time span of concern to society (Wallace 1986). The silent faults (dashed lines in Fig. 2) are applied here for the PSHA because they cannot be neglected, when dealing with a strategic facility [see the safety standards for nuclear installations (IAEA 2010) and Slejko et al. (2011)] and constitute a conservative estimate of the hazard representing the extreme shaking scenarios.

To identify the seismogenic sources (silent faults included) along the pipeline transect in the Adriatic offshore, a combined interpretation of high-resolution swath bathymetric data, high-resolution sub-bottom, and deep seismic profiles were carried out. For the tectonic characterisation of the Italian Adriatic sector, we used the 2D seismic reflection profiles and borehole data made available by the Italian Ministry of Economic Development in the framework of the project “Visibility of Petroleum Exploration Data in Italy” (ViDEPI: www.videpi.com). Consistent geophysical data were unavailable along the Albanian and Greek Adriatic margins, except for part of multichannel seismic lines for the Albania offshore (M-38) and the Greek continental margin (M-34), acquired in 1995 in the framework of the Italian Deep Crust Project (CROP: Finetti 2005). Literature information was used to define this sector better (e.g., Finetti and Del Ben 2005; Aliaj 2006; Argnani 2013; Caputo and Pavlides 2013).

The new seismogenic fault database (Fig. 2) has been populated digitally using a GIS database (MapInfo^®), and it includes all the offshore and onshore CSSs identified along the TAP route in the 400-km wide buffer zone around it, and their main seismotectonic parameters. All data referring to the geometry and the activity of the faults illustrated in Fig. 2 are reported in the electronic supplement ES1. The values of the slip rates for the CSSs and their dimensions were computed from geodetic strain-rates (Hollenstein et al. 2006; Pérouse et al. 2012). We interpolated the horizontal strain-rate data considering the region as a continuum and considering individual blocks characterised by a specific tectonic setting, or deformation style (Rossi et al. 2020). The approach considers the fault settings (strike and dip) and the horizontal strain tensor affecting the area containing the seismogenic source. By applying simple trigonometric formulae, the rake is easily calculated. Considering that most of the seismically related deformation occurs within a limited volume surrounding the fault plane, the slip vector can also be obtained by assuming a buffer zone. If the time is included in the calculations (i.e. strain rate values), the slip rates are finally inferred for each fault. Values are reported in the electronic supplement ES2.

4 PSHA computation

The seismic hazard of a site is defined as the probability of exceeding a certain level of ground shaking y in a fixed time period. In the probabilistic approach, its calculation is based on the Total Probability Theorem that, in the case of seismic hazard, can be written as:

$$\lambda_{y} = \sum\limits_{1}^{{N_{s} }} {\nu_{i} \int_{{m_{0} }}^{{m_{\max } }} {\int_{{r_{\min } }}^{{r_{\max } }} {P[Y > y|M = m,R = r]f_{M} (m)f_{R} (r)dmdr} } }$$

(1)

where $\lambda_{y}$ is the mean annual rate of exceedance of the ground motion y; $\nu_{i}$ is the mean annual rate of occurrence of earthquakes with magnitude larger than, or equal to, m₀ in the seismogenic source i; f_M(m) and f_R(r) are the probability density functions of the magnitude m and distance r, respectively; and N_S is the number of the seismogenic sources considered in the hazard computation. The above equation represents the seismic hazard curve, in terms of the annual rate (almost equivalent to probability) of exceeding a threshold shaking (McGuire 1995, 2004). The conditional probability P[Y>y|M=m, R=r] is simply given by the GMM.

Any distribution can be chosen for both magnitude and distance, as well as for earthquake occurrence. Details about the computation of seismic hazard according to the probabilistic approach can be found in the seminal paper by Cornell (1968), considerations on the pros and cons of application of different distributions and PSHA are extensively described by McGuire (2001, 2004). The quantification of the uncertainties (McGuire 1977) is a well-recognised important point in modern PSHA. Both aleatory variability and epistemic uncertainty (McGuire and Shedlock 1981; Toro et al. 1997) conditionate strongly the hazard estimates, and need proper consideration (Kulkarni et al. 1984; Coppersmith and Youngs 1986).

In the present study, a logic tree (Fig. 3) with twenty branches has been constructed for capturing the epistemic uncertainties. It consists of two source models (faults and wide SZs); two models of faults (only active and active plus silent); two zonations for the model with wide SZs; two seismicity models for the source model based on faults [characteristic earthquake (CE) model and Gutenberg-Richter (GR) model based on slip rates and tectonic features] and only one based on SZs (GR based on earthquakes); two different models (statistical for the SZs and tectonic for the faults) for the computation of the maximum magnitude (M_max); and two GMMs for the ground motion parameters [Akkar and Bommer (2010; hereafter A&B) and Danciu and Tselentis (2007; hereafter D&T)]. For the source model with faults and the CE seismicity model, two rupture areas have been considered: the whole rupture of the fault length, and the rupture according to a possible segmentation. The ground motion parameters considered are PGA, SA for the two spectral ordinates of 0.2 s (SA0.2) and 1.0 s (SA1.0), and PGV. Notice that though PSHA is usually performed for bedrock site geology [class A according to CEN (2005)], we have also performed computations for stiff and soft soil conditions, corresponding roughly to B and C soil classes according to CEN (2005).

Fig. 3

The logic tree consisting of the two source models: faults and wide SZs. There are two models of faults, the active (AF) and active plus silent (AF + SF) faults; two zonations (Z100 and Z200) for the model with wide SZs, two seismicity models for the source model based on faults [CE and GR based on slip rates and tectonic features (GR-G)] and only one for that based on SZs [GR based on earthquakes (GR-E)]. In the case of the source model with faults and the CE seismicity model, two rupture areas have been considered: the whole rupture of the fault length (absolute scenario: Abs) and the rupture of only a part of the total length according to a possible segmentation (most credible scenario: Cred). There are two different models [i.e. statistical (STAT) for the SZs and tectonic (TECT) for the faults] for the computation of the maximum magnitude (M_max), and two GMMs for the ground motion parameters [Akkar and Bommer (2010; A&B) and Danciu and Tselentis (2007; D&T)]. Numbers identify the weight of each branch

We decided to apply a large suite of models within the TAP project, to take into account all opinions available in the literature, after their detailed evaluation. As we had no way to prefer one choice in the logic tree to another, all branches have been weighted evenly, and the total weight of each branch is reported in Fig. 3.

4.1 Earthquake catalogue

The geographical window adopted for the construction of the catalogue is from 38.4° N to 43.5° N and from 16.0° E to 28.5° E. It is assumed that all the earthquakes that could contribute to the ground shaking along the pipeline corridor have been taken into account.

The compilation of the catalogue followed two phases: the preparation of a data set for the Balkan area (Greece and Albania) and another for Italy and the Ionian Sea. The primary data sources are reported in Table 1. All the data have been checked (257 events modified) for the period preceding the year 1900 using the SHEEC catalogue (Stucchi et al. 2012), developed in the framework of the European project SHARE (Giardini et al. 2014) and released to the scientific community during the TAP project. Moreover, all Italian entries have been checked (187 events modified) with those of the most recent version of the Italian earthquake catalogue available at that time: i.e., CPT11 (Rovida et al. 2011). Double events have been eliminated following a quality criterion, giving preference to the local information.

Table 1 List of original catalogues used to construct the TAP earthquake catalogue

The type of magnitude adopted uniformly for the catalogue built for the TAP project (hereafter TAP catalogue) is the moment magnitude (M_W). For several, mainly large magnitude events, original M_W estimates were available and published from well-known and calibrated sources (e.g., Pacheco and Sykes 1992, GCMT, USGS, etc.). However, in most cases, the originally reported magnitudes were various local magnitude (M_L) versions, not necessarily computed from Wood-Anderson (WA) instruments but from other short-period sensors (Teledyne S13 for most Balkan networks), calibrated against WA M_L by each reporting Balkan network. Moreover, for a large number of events other magnitudes (e.g., M_S, m_b, etc.) reported by various sources (e.g., ISC, NEIC, etc.) were available. For all previous magnitudes we have employed appropriate scaling laws converting the original magnitudes to M_W (e.g., Papazachos et al. 1997; Baba et al. 2000; Scordilis 2005, 2006; Tsampas 2006; Duni et al. 2010). This “equivalent” M_W was estimated as the weighted mean of all available converted M_W estimates from other magnitudes, using the inverse standard deviations (SDs) of the conversion relations as weights. Notice that a magnitude conversion was applied only for the range for which each original conversion relation was reported as valid. Using this approach, we also computed a weighted SD for the final M_W estimate. While these errors vary, the average SD associated with the final M_W of the catalogue (original or “equivalent”) is of the order of 0.3 for instrumental locations. For historical events (typically before 1900), when only an estimate of the macroseismic intensity was available, M_W has been evaluated using the Papazachos and Papaioannou (1997) macroseismic attenuation relationship proposed for the Balkan region, which also accounts for differences in attenuation among the various Balkan countries. Notice that in this case the typical magnitude SD increases to 0.5 for these historical events.

The TAP catalogue consists of 49,852 earthquakes (49,149 of which refer to the Balkan sub-catalogue) with magnitude M_W ≥ 3 from 510 B.C. to 2012. There is a consistent and continuous flow of information for earthquakes with M_W ≥ 6 for the entire historical period, even before 0 A.D. (Fig. 4a); the information is good for events with an M_W ≥ 5 and above since 1500 (Fig. 4b) and for M_W ≥ 4 since 1900, and increases since 1970, with the appearance of M_W ≤ 3.5 events (see Fig. 4c). Most earthquakes (87%) have a focal depth within 20 km and the maximum depth is 60 km.

Fig. 4

Distribution of magnitude versus time of the TAP earthquake catalogue for three time periods: a whole catalogue span 500 B.C. to 2012; b period 1500 to 2012; c period 1850 to 2012

The seismicity influencing the TAP route is shown in Fig. 5; the buffer region of 200 km around the pipeline corridor, for which we consider that earthquakes can contribute to the seismic hazard, is also drawn. The TAP crosses the most seismically active area in Albania and only a few earthquakes are reported along the eastern Greek segment of the TAP route, as well as in the Ionian Sea.

Fig. 5

Epicentres of the earthquakes in the TAP catalogue. The green symbols indicate events with M_W 4.0 to 4.9, the yellow symbols M_W 5.0 to 5.9, the orange symbols M_W 6.0 to 6.9, and the red symbols M_W 7.0 to 7.6. In double blue line the corridor of the TAP. The cyan line indicates the 400-km wide buffer zone around the TAP corridor

According to the Poisson process, we considered only independent events. Consequently, we removed the aftershocks from the TAP earthquake catalogue; more problematic is the removal of foreshocks because no indication is available in the literature, and they are very limited in number, if any. The exclusion of the dependent events was done according to the Gardner and Knopoff (1974) approach: i.e., by applying a space–time window calibrated on the Greek seismic sequences (Latoussakis and Stavrakakis 1992). In such a way, 25,685 dependent events were eliminated from the complete TAP catalogue and the final data file used for hazard estimates (hereafter TAP-DEC catalogue) includes 24,367 events with M_W ≥ 3.0. The declustering algorithm eliminated six earthquakes with an M_W ≥ 6; they are 8 June 1638 (M_W 6.9), 12 February 1743 (M_W 6.6), 17 October 1851 (M_W 6.6), 13 September 1912 (M_W 6.7), 18 January 1982 (M_W 7.0), and 6 August 1983 (M_W 6.8).

An additional assumption requested by the Poisson process is stationarity. Due to the variable population density and reporting, the rates of earthquake activity decrease going back with time. This is a problem due to the catalogue completeness. Only during the last few decades, when regional networks came into operation, the catalogue magnitude of completeness (M_c) has decreased below 3. Therefore, the catalogue completeness for each magnitude class needs to be evaluated on a regional basis. This has been done separately for Greece and the rest of the Balkan region using the Stepp (1972) graphs (Table 2). Such analysis points out the stationarity of the seismicity by showing the annual rate of earthquake occurrences in time. For Italy and the Adriatic offshore, the M_c computed for the whole TAP region has been applied to guarantee a robust regression and the TAP-DEC earthquake catalogue results complete in a quite long period for large magnitudes (M_W > 6), i.e., about four centuries.

Table 2 Completeness periods for the magnitude classes. Route means the whole TAP-DEC catalogue, applied for the offshore sector and Italy

4.2 Source models

In addition to the linear sources (Fig. 2), identified by the previous geological description, merging the information of the TAP earthquake catalogue (Fig. 5) and the tectonic model, with all available literature about focal mechanisms and stress field, enabled us to define the seismogenic sources, in terms of wide areal SZs (see the complete description in chapter 4.2.2).

For the PSHA along the TAP route, we considered two different approaches in defining the seismogenic sources. The first refers to individual faults, more precisely, CSSs that may contain one or more fault segments, and, hence, one or more actual seismogenic sources (Basili et al. 2008, 2013); the second relates to wide SZs. Silent faults have also been considered in the elaborations related to the model based on faults (see Fig. 2).

4.2.1 The fault model

The first source model is linked to the tectonic structures represented by their upper tip in Fig. 2 showing active and potentially active seismogenic sources within the 400-km wide buffer zone along the TAP route. In the present work, we took a precautionary approach considering as active faults the structures showing evidence of displacements during Late Quaternary.

Faults have been classified (and colour coded in Fig. 2) according to kinematics (rake) based on literature information, databases of seismogenic sources as GreDaSS (Caputo et al. 2012), DISS (Basili et al. 2008), and EDSF (Basili et al. 2013), geological and neotectonic maps (see Caputo and Pavlides 2013 and references therein), or it was inferred from the regional stress field obtained from focal mechanisms. Moreover, field studies have carried out collection of structural data where needed in some areas of Italy, Albania, and Greece. In addition, the interpretation of geophysical data was performed to characterise the faults of the offshore part of the TAP route (Adriatic and Ionian seas). The interpreted data set includes 2D multichannel seismic lines, well data, and technical reports related to the hydrocarbon exploration made available in the framework of the ViDEPI project, MS-29 and CROP M-34 seismic lines, high-resolution profiles of the Statoil TAP survey data set acquired in 2012 along the Adriatic route of the pipeline.

Special mention deserves the source of the M_W 7.1 20 February 1743 earthquake, which was widely felt, with damages, in the Salento peninsula (Apulia) and Ionian islands. The earthquake was perceived by the majority of the witnesses as a sequence of three violent shocks and this may be the result of the activation of different fault segments. The epicentre of this event is quite uncertain, and its location reported in Italian [offshore the Salento peninsula (Rovida et al. 2011)] and Greek [south of Corfu island (Papazachos and Papazachou 2003)] catalogues differ notably. Although different faults have been proposed for this earthquake (Argnani et al. 2001; Galli and Naso 2008; Milia et al. 2017; Maesano et al. 2020), the source remains poorly constrained: we considered the source proposed in the DISS (Basili et al. 2008) and the AHEAD (European Archive of Historical Earthquake Data, www.emidius.eu/AHEAD) databases, also supported by additional considerations by Argnani et al. (2001), in the Otranto channel, where some small magnitude events were located instrumentally (D’Ingeo et al. 1980; Gasparini et al. 1985; Favali et al. 1990). As we are not able to model a 3D geometry for this source, we represented it as a horizontal 20-km deep polygon, whose top does not intersect the surface, in agreement with the Argnani et al. (2001) interpretation confirmed also by the recent data and interpretation of Maesano et al. (2020). This geometry could also justify the wide perceptibility area of the 1743 earthquake.

4.2.2 The wide SZ model

The choice to consider SZs, wide or narrow according to the available seismotectonic information, is motivated by the difficulty of associating specific earthquakes with individual faults, due to the uncertainties in the earthquake location and the poor knowledge of the geometry of the faults at depths. To delineate seismogenic sources, an adequate kinematic model is essential, capable of explaining the Quaternary evolution of the whole area and describing the current movements linked to the seismicity. The seismotectonic model of the TAP offshore region was approached by extending the kinematic and seismotectonic analyses of the Adria microplate (Slejko et al. 1999). The Adriatic region is interpreted as a rigid microplate bordered on the eastern, northern, and western margins by deforming mountain belts, including the Albanides, the Dinarides, the Southern Alps, and the Apennines. The southern margin of the plate, i.e., the Africa-Adria boundary, is still undefined. Transversal tectonic structures to the chains, which interrupt the continuity of the mountain belts, are interpreted as shear zones. They separate sectors of the chain affected by different deformation age, distinct structural trend and tectonic evolution. The Cephalonia transform fault zone represents the most evident shear zone. Other regional structures are the VED transversal fault zone, which affects the central part of the Ionian-Adriatic thrust fault zone (Albanides), and the Scutari-Pec (SP) fault that marks the boundary between the external Dinarides and Albanides (Aliaj 1998).

The seismogenic model proposed for the TAP route (400-km wide from the TAP route itself) is, then, based on all available geological literature (Aliaj 1998, 1999, 2000; Velaj et al. 1999; Robertson and Shallo 2000; Nieuwland et al. 2001; Zelilidis et al.; 2003; Roure et al. 2004; Frasheri et al. 2009; Lacombe et al. 2009; Vilasi et al. 2009; Silo et al. 2010; Jardin et al. 2011; Jouanne et al. 2012), on earthquakes distribution (Fig. 5), and previous proposed seismogenic zonation for Albania (Aliaj et al. 2000, 2004; Aliaj 2002; Sulstarova and Aliaj 2001), for Greece (Papaioannou and Papazachos 2000; SEAHELLARC Working Group 2010, 2014; Vamvakaris et al. 2016), for Bulgaria (Orozova-Stanishkova and Slejko 1994; Simeonova et al. 2006), for North Macedonia (Salic et al. 2010), and Italy (Meletti et al. 2008).

The model based on wide SZs has two variants (zonations): with transfer zones along the Albanian coast (hereafter Z100, see Fig. 6a) and without them (hereafter Z200, see Fig. 6b). According to the logic tree approach, the different branches should be mutually exclusive and collectively exhaustive, although this requirement is often not formally satisfied in the literature. In our case, the kinematic model for the coastal area (Slejko et al. 1999), which is the most important sector for the TAP route due to its high seismic activity, suggests two alternative kinds of activity for some tectonic structures. Then, our two zonations reflect this primary aspect, whereas for the SZS in the remaining study area we did not identify relevant differences (Slejko et al. 2014).

Fig. 6

Seismogenic zonations for the TAP route: a Z100 that considers the transfer zones in Albania (nos. 173, 176, 179); b Z200 without them. The cyan line indicates the 400-km wide buffer around the pipeline route (double blue line). The colour indicates the kinematic character of the zone: green = normal, red = reverse, yellow = strike-slip

More precisely, Z100 (Fig. 6a) takes into account three shear zones as actual seismogenic sources: the SP (modelled as SZ 173 in Fig. 6a) in the north, the VED (modelled as SZs 176 and 177) in the central part of Albania, and the Othoni Island-Dhermi Pass (modelled as SZ 179) in southernmost Albania. The subdivision of the VED transversal zone into two parts is motivated by the different kinematics that it exhibits: pure strike-slip movement in the south-western sector, and transtensive kinematics in the north-eastern one. Also, geodetic information supports the adopted separation (Rossi et al. 2020). Another important tectonic structure affecting the external Albanides is the ENE-trending Othoni Island-Dhërmi Pass (OD) right-lateral strike-slip fault (SZ 179), located to the south of the Karaburun Peninsula, which is characterised by earthquakes with an M_W greater than 6. This lineament is considered the most active fault of Albania (Jouanne et al. 2012). The VED transversal zone and the OD fault divide the Ionian-Adriatic thrust fault zone into three segments (SZs 174, 178, and 128). In particular, the northern (SZ 174) and southern (SZ 128, including the offshore Corfu thrust and the contractional structures of the Saranda area) zones comprise both onshore and offshore contractional structures, characterised by earthquakes with an M_W greater than 7. SZ 153 corresponds to the northern part of the Cephalonia seismogenic tectonic lineament: only this sector has been considered because the southern part is too far away from the TAP route and does not contribute to the expected ground motion.

The seismogenic model for broader Greece (Pavlides et al. 2010; Caputo et al. 2012; Vamvakaris et al. 2016) has been fully adopted with very minor changes along its peripheral margins to take into proper consideration also the national seismogenic models proposed for Bulgaria (Simeonova et al. 2006). In particular, as these areas are quite far from the TAP route and can contribute very marginally to the expected ground motion, fewer details have been incorporated to allow a conservative distribution of the seismicity.

The SZs defined in Italy are taken from the seismogenic zonation used to compute the Italian seismic hazard map (Stucchi et al. 2011) with some modifications. More specifically, SZ 102 has been enlarged towards the sea, according to recent literature (Zecchin et al. 2018; Mangano et al. 2020). SZ 103 has been introduced because a few earthquakes close to magnitude 6 affected the tectonic structure of Pollino, in southern Italy.

The second zonation (Z200, see Fig. 6b) considers the transversal shear zones only as borders of the seismogenic zones affected by thrust tectonics.

The SZs in the peri-Adriatic region, shaped according to seismicity data too, represent the surface projection of the active fault systems capable of producing earthquakes characterised by similar mechanisms. Considering the fault type inside each SZ as previously described (Fig. 2), it was possible to define a dominating character (normal, reverse, transcurrent) for each SZ of Z100 (Fig. 6a) and Z200 (Fig. 6b).

All the SZs of the two zonations have been modelled as flat surficial planes.

4.3 Seismicity models

For the wide SZs the seismicity is generally characterised using the GR model (GR-E in Fig. 3). For individual faults the related seismicity model is difficult to define and questionable (e.g., Wesnousky 1994), because of the hypocentre location errors and because of the poor knowledge of the fault deep geometry. Therefore, we decided to consider two possible seismicity models for the faults: the GR model fed by geodetic data (GR-G in Fig. 3) and the CE model fed by tectonic evidence (CE in Fig. 3). According to a geodetic model, the seismicity of the faults is derived from the geometric characteristics of the fault ruptures (see the electronic supplement ES1) and the regional/areal strain rates calculated from GNSS information (see the electronic supplement ES2). Instead, the tectonic model considers the CE with related recurrence intervals (see ES2) associated with each fault; all details are given in the following chapters.

4.3.1 GR seismicity rates from observed seismicity on wide SZs

The individual seismicity rates for each SZ, i.e., the number of events in each 0.3 magnitude bin, have been calculated from the TAP-DEC earthquake catalogue by the “higher-not-highest “ approach, developed for the seismic hazard map of the Italian territory (Slejko et al. 1998) in terms of M_W. In this approach, the seismicity rates are computed for all magnitude classes and several time intervals (among which those indicated by the analysis of completeness), all ending at the end of the catalogue. For each magnitude, the highest seismicity rate related to a time period not shorter than the complete one is selected as the rate of that magnitude. Additionally, if the selected rate corresponds to a recurrence interval (1/rate) shorter than the interval on which this selected rate is calculated, any rate referred to an interval richer of earthquakes but longer than that of the selected rate is finally chosen as seismicity rate of that magnitude class [more information and examples can be found in Slejko et al. (1998)]. This method is conservative: the seismicity rates are computed considering the completeness and the level of seismicity in different time periods.

There are different methodologies for assessing the b-value of the GR relation. The least squares method is often used, although not formally appropriate, since magnitude is not error free, cumulative event counts are not independent, and the error distribution of the number of earthquake occurrences does not follow a Gaussian distribution. In this study, we applied the maximum likelihood method, introduced by Aki (1965) and Utsu (1965), for which Weichert (1980) proposed a general routine suitable for different completeness periods of the earthquake catalogue. In the few cases (SZs  x18,  x19,  x26,  x34, where x stands both for 1 and 2, see Fig. 6) where the regression line overestimates notably the observed seismicity rates, this fact has been associated with a lack of low magnitude events, possibly due to an incompleteness in the earthquake catalogue, caused by unsatisfactory seismological monitoring in the region. For the sources where a low number of seismicity rates or a disagreement between the regression line and the observed seismicity rates have been identified (SZs  x16,  x17,  x18,  x19,  x26,  x29,  x34,  x35,  x36,  x37,  x50,  x51,  x54,  x58,  x59), a merging of neighbouring SZs has been applied [( x16 +   x17), ( x18 +   x19), ( x26 +   x34), ( x29 +   x54), ( x35 +   x36 + x37) see Fig. 7, ( x50 +  x51 +   x58  + x59)]. The minimum magnitude value is fixed at 4.0, except for few cases (SZs  x02,  x03,  x04,  x17,  x35) according to the range of the available seismicity rates. Electronic supplements ES3 and ES4 contain the a- and b-values calculated for the SZs of Z100 and Z200 zonations.

Fig. 7

Seismicity rates and GR fit for three SZs which have been merged because of few earthquakes: a SZ 135; b SZ 136; c SZ 137; d cumulated rates

Figures 8a to d show the a- and b-values obtained for the zonations Z100 and Z200, respectively. The little differences relate only to Albania, where transverse SZs have been introduced in Z100. It can be seen that a high a-value (> 5) is found in Italy and in the Adriatic Sea, where the b-value is also quite high (> 1.1). Conversely, Albania is characterised by average a- (> 3.5) and b- (> 0.9) values. Greece shows average a-values and b-values moderately high. This situation implies that the number of large events is proportionally low in Italy and the Adriatic Sea, whereas it is large in Albania.

Fig. 8

GR parameters for the proposed SZs: a a-values for Z100; b b-values for Z100; c a-values for Z200; d b-values for Z200; e a-value for the CSSs; f b-value for the CSSs. In double blue line the TAP corridor

4.3.2 GR seismicity rates from fault activity evidence

This approach has been applied in the European SHARE project (Giardini et al. 2014), and it is based on information about the 3D geometry of the active fault surface and the slip rate. The original idea was formulated by Anderson and Luco (1983), who proposed three categories of models for defining a magnitude recurrence distribution from the geological slip. In the first model, the recurrence is related to the entire fault (or fault segment) rupture, while the second and third models relate the recurrence to the rupture area of the maximum earthquake, and this magnitude could be associated with the geometry of the (entire or segmented) fault.

The estimation of the activity rates (N(M), e.g., the annual number of earthquakes with a magnitude larger than, or equal to, M), involves parameters that come from the definition of the seismic moment (M₀) for a particular event (Aki and Richards 2002), as the rigidity or shear modulus, the average displacement across the fault, the rupture area, and the geological (annual) slip rate, assuming conservatively that all the fault slip occurs seismically and ignoring possible aseismic creep. For the TAP calculations, we used the first Anderson and Luco (1983) formulation, as proposed by Bungum (2007):

$$N(M) = \left( {\frac{{\overline{d} - \overline{b}}}{{\overline{d}}}} \right)\left( {\frac{S}{\beta }} \right){\text{e}}^{{\overline{b}(M_{\max } - M)}} {\text{e}}^{{ - \left[ {\left( {{\raise0.7ex\hbox{${\overline{d}}$} \!\mathord{\left/ {\vphantom {{\overline{d}} 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)M_{\max } } \right]}}$$

with:

$$\begin{aligned} \overline{b} & = b[\ln (10)] \\ \overline{d} & = d[\ln (10)] \\ \beta & = \sqrt {[\alpha M_{0} (0)]/(\mu W)} \\ \alpha & = D/L \\ \end{aligned}$$

where M₀(0) is the seismic moment for M = 0, b is the b-value of the GR relation, d is the magnitude scaling coefficient of the moment – magnitude scaling law (Kanamori and Anderson 1975) and the value of the maximum magnitude M_max can be calculated by scaling laws between magnitude and fault dimensions (e.g., Wells and Coppersmith 1994).

The GR distributions are limited at the upper end by M_max, assuming a sharp cut-off, and at the lower one by a threshold magnitude, usually around 4 to 5. In our case, the threshold magnitude was fixed at 4, the b-values (Fig. 8f) were obtained from the recorded seismicity in six wide background zones (see Fig. 9), M_max was computed from the fault dimensions (i.e., area, from Wells and Coppersmith 1994) taking into account the fault type (N = normal, R = reverse, S = strike-slip, see Fig. 2), and the rigidity or shear modulus was computed using the European crustal model EPcrust (Molinari and Morelli 2011).

Fig. 9

Background zones and their kinematic character: cyan (Bg_IT) = reverse and transcurrent for Italy offshore, pink (Bg_R_AL) = Albania reverse, pale green (Bg_N_AL) = Albania normal; medium green (Bg_N_BL) = Bulgaria normal; dark green (Bg_N_GR) = Greece normal; yellow (Bg_S_GR) = Greece strike-slip. Red lines are active faults, blue lines are silent faults. Bg stands for background zone, R for reverse, N for normal, S for strike-slip. In double blue line the TAP corridor

The GR parameters (a-value, b-value, M_max) and their uncertainties are reported in the electronic supplements ES5 and ES6 for the two fault models considered (with and without segmentation) and are depicted in Figs. 8e, f and 10. A general agreement between the a-values computed for SZs and CSSs can be identified for some areas (see Fig. 8), with low a-values in Montenegro (less than 3.5) and Italy (less than 4.0), and with average values in North Macedonia (between 3.5 and 4.5). In Greece and Bulgaria, the a-values for the CSSs are lower than those of the SZs. It should be noted that the data sources (seismicity and slip rates), the approach, and the spatial attribution (wide SZs and CSSs) are completely different. A general agreement can also be found for the b-values in Italy, along the Balkan coast (both with values lower than 1.0), and in Bulgaria (values between 1.0 and 1.2).

Fig. 10

M_max: a for Z100; b for Z200; c for the faults. In double blue line the TAP corridor

4.3.3 Characteristic earthquake model

The CE model was introduced by Schwartz and Coppersmith (1984) for the seismicity of the Wasatch and San Andreas faults in California and states that each fault can produce events of a specific narrow range of magnitude, in agreement with the geometric dimensions of the possible ruptures along the fault. A similar model (maximum magnitude model) was also suggested by Wesnousky (1986) for the seismicity associated with the faults in California. Meanwhile, Youngs and Coppersmith (1985) defined the probabilistic distribution for a model with a GR distribution for weak and moderate earthquakes and a CE (uniform) distribution for the high magnitudes: the authors called also this CE model. According to this model, Wells and Coppersmith (1994) developed scaling laws between the fault-rupture dimensions and the related characteristic magnitude. The difficulty of associating earthquakes to faults does not allow the seismologists to ultimately decide whether this model is valid worldwide, only for some faults or never. In any case, its likelihood is quite good and both DISS (Basili et al. 2008) and GreDaSS (Caputo and Pavlides 2013) are based on this model. Without entering into the scientific debate on the validity of the CE model, supported by observational data (Swan et al. 1980; Papageorgiou and Aki 1983) but also challenged (Grant 1996; Bakun et al. 2005), the estimation of the maximum expected magnitude for a fault is based on the expected rupture geometries, in terms of rupture length or rupture area, available from direct observations only for some recent events.

The fault databases report the parameters for the geometric definition (length, width, etc.) and the information on the activity, from paleoseismological surveys, or geodetic measurements, of all CSSs of Fig. 2 (see ES1 and ES2), that are associated with the actual faults, whenever their possible segmentation is suggested. From those parameters, the characteristic magnitude can be estimated. The recurrence interval, i.e., the mean time period of repetition of the CE, has been taken directly from the fault database (see ES2). It is assessed in different ways: inferred from slip rate and average displacement, based on paleoseismology (4000 years preferred), on geological constraints, derived from slip rate and slip per event, or modelling of marine terraces. It is well known (e.g., Nicol et al. 2005) that recurrence intervals and average displacements obtained in such a way are affected by large uncertainties and, consequently, the related hazard results should be considered our best estimates.

Two scenarios have been considered for the active faults (solid lines in Fig. 2) and the silent faults (dashed lines in Fig. 2): the absolute scenario, where the rupture length corresponds to the whole fault length, originating the largest possible magnitude for those fault dimensions; and the segmented scenario, where only a part of the fault ruptures, according to a segmentation scheme based on geologic/geodetic considerations (Caputo and Pavlides 2013).

Also, six background zones have been introduced: they collect the low seismicity not linked to any CSS (Fig. 9). More precisely, the events in each background zone with a magnitude lower than the minimum characteristic magnitude of the faults of the zone were fitted according to the GR model, and this seismicity has been treated in the PSHA elaboration in a zone-source fashion.

4.4 M_max

To estimate M_max, we applied a statistical approach (Kijko and Graham 1998) for the wide SZs, and a tectonic approach for the model based on faults.

The approach by Kjiko and Graham (1998) computes M_max for a source on a statistical basis using as input data: the maximum observed magnitude (M_maxobs); the threshold magnitude considered complete in the catalogue; the average error in the magnitude estimates (fixed in our case arbitrarily at 0.2); the b-value of the GR relation and its SD; the annual rate (i.e., the number of earthquakes with magnitude greater than, or equal to, the threshold magnitude); and the catalogue time span which is considered complete. This last parameter was set equal to the completeness period of M_maxobs. Four formulations for M_max computation are implemented in the method; we applied here the Bayesian formula of Kijko and Sellevoll (1989). The M_max values estimated for each SZ are reported in the electronic supplements ES3 and ES4 and mapped in Figs. 10a and b for the two zonations Z100 and Z200. The highest values of M_max (larger than 7.0) are found along the Montenegro coast, in the easternmost sector of the TAP route in Greece and eastwards (Figs. 10a and b), where the North Anatolian Fault and its continuation along the North Aegean Trough dominate the tectonic framework. The highest expected M_max, i.e., even larger than 7.5 is in the area north of Thessaloniki and the border area with Turkey (Figs. 10a and b) crossed by the TAP. Z200 determines that the whole of Albania shows an expected M_max between 6.5 and 7.0 (Fig. 10b) instead of only the sector affecting the TAP route (Fig. 10a). In a few SZs, M_max results were extremely low (see grey and pale blue SZs in Figs. 10a and b), mainly because of the poorly documented seismicity and, consequently, the limited range of magnitude classes. A check has been done by increasing M_max to 5.5, but no difference was observed in the computed seismic hazard.

For the models based on faults, we estimated M_max according to the dimensions of the fault and the fault type (N, R, S) using the Wells and Coppersmith (1994) scaling laws. However, since the Wells and Coppersmith (1994) scaling laws consider the rupture length, we made some considerations about the possible fault segmentation. Thus, we have an M_max based on the full rupture along the fault length, and a credible M_max based on the rupture length derived by the expected segmentation of the fault. These two values of M_max are reported in the electronic supplements ES5 and ES6. The values of M_max for the CSSs are almost all between 6.5 and 7.0 (Fig. 10c), in agreement with those of the SZs along the Balkan coast.

4.5 GMMs

The choice of the GMMs suitable for the PSHA is an important issue, and some guidelines should be followed (Cotton et al. 2006). The selected GMMs should be exhaustive and mutually exclusive in the logic tree approach, and their number should be the smallest needed to capture the range of future ground motions. The main criteria for the selection are: compatibility of the tectonic regime, international appreciation, robustness of calibration data, and parameter suitability. We explored the GMM list collected by Douglas (2011) and, according to the above cited criteria, selected one global GMM and one regional GMM, suitable for the study region: the A&B and the D&T GMMs. The A&B GMM is calibrated on 532 strong motion data from Europe and Middle East in the 5.0–7.6 M_W range, uses the Joyner and Boore (1981) metrics for distance and parameters for fault style and site conditions are available. The D&T GMM is calibrated on 335 Greek strong motion data in the 4.5–6.9 M_W range, uses the epicentral distance and parameters for fault style and site conditions are available. The two GMMs are calibrated almost on different data (mutually exclusive) and represent the minimum number of models representing the ground motion of the study region (exhaustive). Both GMMs treat M_W and have parameters for fault style and site conditions without asking additional unknown parameters. The difference in the distance metrics is not crucial in the case of wide SZs, while it could introduce some differences in the case of fault; in our case, the CSSs represent something wider than actual faults.

In the magnitude range 4.0 to 5.4, where the A&B GMM is not, or poorly, constrained, we adopted the Bragato and Slejko (2005, hereafter B&S) GMM calibrated on weak motions. Considering the role of the Adriatic Moho in the attenuation, we extrapolated the ground motion at a 70-km distance as far as a 200-km distance following Bragato et al. (2011) in both GMMs.

All the cited GMMs were defined for PGA, SA, and PGV: SA at 0.2 s (SA0.2) and 1.0 s (SA1.0) are the spectral ordinates considered in the elaborations provided for the TAP route. Both A&B and D&T GMMs are defined for different tectonic styles and they have been applied in agreement with the tectonic style associated with the faults of Fig. 2.

The extrapolation of GMMs both in magnitude and distance is a delicate operation and needs a robust control, although in the standard PSHA it does not play a strategic role, because the contribution of very large magnitude events is limited. As a few events exceed the magnitude range where the A&B and D&T GMMs are defined (7.6 and 6.9, respectively), we have checked if the cited GMMs can be extrapolated outside their upper magnitude range, an operation always considered acceptable by Ambraseys (1995).

The two chosen GMMs, in terms of median values of PGA, are quite similar in the range of M_W 5.5 to 6.5 outside the near field (Fig. 11). At M_W 4.5 the A&B GMM, corrected according to the B&S one, produces lower shakings than the D&T GMM for distances larger than 10 km, but in both cases, the values are very low (less than 0.01 g). A quite large shaking is modelled by the D&T model for M_W 7.5, where the data do not constrain the cited GMM. A comparison between the two GMMs at 6.9, where both are valid, has shown, however, that the D&T model gives a PGA larger of about 0.3 g in the near field. Similar considerations also hold for the spectral acceleration. To avoid the problematic extrapolation of the D&T GMM, a correction in agreement with the behaviour of the A&B model has been applied. More precisely, the D&T model has been considered valid for M_W 7.0 (actually the maximum M_W where the relation is calibrated is 6.9). Considering that A&B GMM is calibrated for M_W 7.6, the percentage of increment in the A&B GMM between M_W 7.0 and 7.5 has been applied to the D&T model. In such a way, the high values given by the D&T model are limited, although a difference of about 0.2 g remains as it is motivated by the values of the two GMMs at M_W 6.5, where both are validated. This last version of modified GMMs has been applied in the PSHA (Fig. 11).

Fig. 11

Comparison between the D&T and A&B GMMs for reverse faulting and four magnitudes (4.5, 5.5, 6.5, 7.5). The PGA value is fixed from a 70- to a 200-km distance (see the text for the explanation). For M_W less than 5.5, the A&B GMM is substituted by the B&S GMM

5 Results and discussion

An updated 2012 version of the computer code Crisis (Ordaz et al. 2013) was applied for all the elaborations: it considers as sources both wide zones, and 3D faults, and for the seismicity both a GR model and a CE model. The results refer to the computations performed considering the different source and seismicity models. The following return periods (RPs) have been chosen, and they correspond to specific levels of exceedance probability in 50 years (T50, considered as the standard lifetime for a residential building): 475 years (corresponding to probability 0.10 in T50), 975 years (corresponding to 0.05 T50), 2475 years (corresponding to 0.02 T50), 4975 years (corresponding to 0.01 T50), and 9975 years (corresponding to 0.005 T50). The final results are aggregated by a proper weighting of the different branches of the logic tree (Fig. 3).

Before presenting the final estimated ground motions along the TAP route, we show the results obtained by the individual branches, to highlight the differences produced by the different choices in the input data.

The ground motions of the 20 branches of the logic tree (Fig. 3) for a 2475-year RP are plotted on a 50-km wide (25 km on both sides) strip around the TAP route (Figs. 12 and 13): the 2475-year RP is considered the adequate RP for ground shaking hazard along a pipeline (Golara 2014) and the choice of the 50-km wide corridor is motivated by the possibility to show the pattern of the shaking. The results are displayed in maps, in terms of PGA values, for different combinations of the model parameters. No value interpolation was applied and the computed results are mapped simply as data posting. Figure 12 corresponds to the ten branches that consider the A&B GMM, while Fig. 13 refers to the corresponding results for the D&T GMM. The first evidence is that the A&B GMM produces higher values with respect to the D&T GMM, regardless of the models selected, except in two cases, where the CE model is associated with a fault segmentation (compare Figs. 12c with 13c and 12g with 13g). In these cases, this is due to the combined effect of the D&T GMM associated with the high magnitude of the fault segments. The influence of the two source models depends on the other models considered and the model with wide SZs gives high PGA values in large regions (Figs. 12a, b, 13a, b), while the model based on faults produces high values only in limited areas. The introduction of transversal SZs (zonation Z100) has a more significant effect on the PSHA results when the D&T GMM is employed (compare Figs. 13a and b) than with the A&B GMM (compare Figs. 12a and b). The contribution of the silent faults, when added to the active fault database, is not marginal, and locally increases the expected PGA values by 0.2 g (e.g., along the Albanian coast; compare Figs. 12g to l with Figs. 12c to f, and Figs. 13g to l with Figs. 13c to f). The seismicity model [CE (Figs. 12c, d, 13c, and d) versus GR (Figs. 12e, f, 13e, and f)] applied to the fault source model, does not produce a systematic influence (increase or decrease) of the computed ground motions, but depends on the other models. In general, the model that considers fault segmentation (Figs. 12c, e, 13c, and e) results in slightly higher PGA levels than that without segmentation, again due to the high magnitude associated with the different fault segments.

Fig. 12

PGA with a 2475-year return period with the A&B GMM. The ten maps refer to the odd ten branches (BR in the figure) of the logic tree (Fig. 3), identified by the number in each panel

Fig. 13

PGA with a 2475-year RP with the D&T GMM. The ten maps refer to the even ten branches (BR in the figure) of the logic tree (Fig. 3), identified by the number in each panel

The results from the twenty branches previously described have been aggregated according to the weights assigned to the branches (see the numbers at the nodes of the logic tree in Fig. 3). Here, we show the complete suite of PSHA maps only for the 2475-year RP for all considered parameters (PGA, SA0.2, SA1.0, PGV) for rock (Figs. 14a to d), stiff soil (Figs. 14e to h), and soft soil (Figs. 14i to l).

Fig. 14

Ground motions along the TAP route for RP = 2475 years and rock: a PGA; b SA0.2; c SA1.0; d PGV; stiff soil: e PGA; f SA0.2; g SA1.0; h PGV; and soft soil: i PGA; j SA0.2; k SA1.0; l PGV

The largest PGA values for rock site geology are observed along the Albanian coast, west of Fier, with values ranging from 0.8 to 0.9 g (Fig. 14a). A secondary maximum is identified in a rather large area around Thessaloniki and at the Turkish border (SW of Alexandroupolis), with both sites showing much lower PGA levels (0.5 to 0.6 g, see Fig. 14a). A similar pattern is shown by the SA0.2 map with values exceeding 2.0 g along the Albanian coast (Fig. 14b). The SA1.0 map (Fig. 14c) identifies also the Alexandroupolis area, at the Turkish border, at similar levels with the Albanian coast and values exceeding 0.7 g, while the Greek sector north of Thessaloniki displays values slightly lower (between 0.6 and 0.7 g). Moreover, the PGV map identifies the same sector of the Albanian coast as the most seismically active with values exceeding 50 cm/s (Fig. 14d).

A similar pattern is also revealed by the maps referring to stiff (Fig. 14e to h) and soft (Fig. 14i to l) soil local geology with the maximum values increasing roughly by one class (0.2 g) in the case of stiff soil and two classes (0.4 g) in the case of soft soil with respect to the rock maps.

From the different seismic hazard curves related to the individual branches, all statistical percentiles have been calculated. A study test site was considered west of Fier, along the Albanian coast, where the main compressor station will be placed (see its location in Fig. 2). The seismic hazard curves for PGA, SA0.2, SA1.0, and PGV, obtained as weighted mean from the individual branches, are displayed in Fig. 15: each panel shows the mean seismic hazard curve for rock, stiff, and soft soil local geology conditions, together with the related uncertainties, represented by the SD obtained from the 20 branches of the logic tree (Fig. 3). In such a way, it is possible to evaluate the differences in the expected shaking caused by the various choices made at the nodes of the logic tree and quantify the total uncertainty in the final results. We adopt here the standard approach to present mean value plus 1 SD results, though this (more conservative) is rarely adopted in seismic design practice. However, when the dispersion in the results of the different branches of the logic tree is relatively large, adopting a + 1 SD limit for the PSHA results is a reasonable safety measure: this is the main case for SA1.0 (Fig. 15c) and PGV (Fig. 15d). The curves related to rock and stiff soil local geology conditions are very similar for all considered quantities, while those for soft soil exceed the corresponding rock ones by roughly 20% to 40% for the different quantities examined.

Fig. 15

Seismic hazard curves (in terms of exceedance probability in 50 years) for the Fier site (see its location in Fig. 2) for rock, stiff, and soft soils: a PGA, b SA0.2, c SA1.0, d PGV. The coloured (yellow = rock, red = stiff, blue = soft) solid lines indicate the mean values and the coloured areas the related uncertainties

Figure 16 shows the uniform hazard spectra (UHSs) calculated for the Albanian coast compressor test site. Figure 16a displays the results for the twenty branches and the corresponding mean value plus 1 SD for a 2475-year RP considering a rock site, while the other three panels show the UHSs for all investigated RPs (475, 975, 2475, 4975, and 9975 years) respectively for rock (Fig. 16b), stiff soil (Fig. 16c), and soft soil (Fig. 16d) local geology conditions. The weighted mean UHS is derived from two main families of spectra: those computed with the A&B GMM and those calculated with the D&T one. The corresponding results from the two families are notably different. In fact, the A&B GMM emphasises the low periods (peak at 0.1 s) while the D&T one exhibits a maximum at 0.4–0.5 s, hence, the resulting spectra are characterised by the presence of a quite large peak. The amount of the SD gives a clear idea about the uncertainty of the average spectrum. The reasons discussed above explain why the obtained UHSs are generally characterised by a large dispersion among the different branches of the logic tree (Fig. 16a), justifying the use of the mean value plus one SD.

Fig. 16

UHSs for the Fier site (see its location in Fig. 2): a for a 2475-year RP (mean and 20 branches), rock conditions; b for different RPs, rock; c for different RPs, stiff soil; d for different RPs, soft soil

Considering the details of the obtained results, we see that the high dispersion is mainly caused by branch 14, based on the CE model for seismicity with segmented rupture on active and silent faults, roughly 50% higher than the other spectra. This observation can be explained by the specific recurrence interval of the earthquakes associated with faults in the proximity of the site, and the large acceleration modelled by the D&T GMM for 0.5 s. The addition of one SD to the mean spectrum would be consistent with all the individual spectra except for three, with only one of them exhibiting a remarkably higher acceleration. The mean UHSs show a high hazard for all RPs with the dominant period of 0.15 s. Also, the 0.4-s period becomes important at long RPs, causing an almost flat top for the 9975-year RP: this testifies the increasing contribution of distant seismicity with increasing RP. The maximum acceleration for a 2475-year RP is reached at 0.15 s with a value of 1.9 g (Fig. 16b). The acceleration at 0.4-s period dominates instead in the UHS for stiff (Fig. 16c) and soft (Fig. 16d) soils.

The PSHA procedure also allows the computation of the mean annual rate of exceedance at a particular site, based on the aggregate hazard from potential earthquakes of many different magnitudes occurring at many different source-to-site distances. Therefore, the rate of exceedance computed in a PSHA is not associated with any particular earthquake magnitude or source-to-site distance. In some cases, however, it may be useful to estimate the earthquake magnitude and/or the source-site distance contributing most to hazard. These quantities may be used, for example, to construct ground shaking and risk scenarios, as well as to select existing ground motion records (recorded in earthquakes of similar magnitude at a similar source-site distance) for response analyses. The methodology to identify the largest contributor, in the set of all earthquakes constructing the hazard at a site, is called deaggregation, and was introduced by McGuire (1995). The deaggregation requires that the mean annual rate of exceedance be expressed as a function of magnitude and distance. The full analysis can be conducted simply by appropriately discretising the range of allowable magnitudes and distances (the reference binning values in our case were Δm = 0.3 and Δr≈10 km). As the summation runs over all sources, in the case of many sources, placed at similar distances, it could be not trivial to identify the one hosting the dominant earthquake for the hazard at the site. The various sources must be, then, analysed individually.

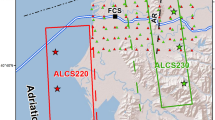
The compressor station along the Albanian coast (see location in the inset of Fig. 2) has been considered for the PSHA deaggregation, i.e., for the identification of the dominant earthquake. The deaggregation has been performed on the source model based on faults, because when wide SZs are used the dominant quake results almost always in an event located under the site, if the site is contained into an SZ with activity similar to, or larger than, the surrounding ones, as in the present case. Two ground motions have been considered: SA0.2, which represents the high-frequency vibration, and SA1.0, representing the low-frequency vibration. In general, SA0.2 should be produced mainly by local earthquakes, while SA1.0 should be generated by more distant, strong quakes. The results suggest that the main contribution to hazard for the considered test site is given by local earthquakes respectively of M_W 6.0 and 6.6 for SA0.2 (Fig. 17a) and SA1.0 (Fig. 17b), respectively. This is not surprising if we consider the presence of the Vlore backthrust (A220 in Fig. 2) and the Fier thrust (A230 in Fig. 2) that have generated strong earthquakes in the past. On the basis of these results, we deemed that further investigation and detailed ground motion scenarios could provide a valuable contribution to the estimate of the seismic hazard of the test site area. Therefore, we performed a deterministic seismic hazard assessment study, as reported in the companion paper by Moratto et al. (2020, this issue).

Fig. 17

Deaggregation for the Fier site (see its location in Fig. 2) and RP = 2475 years: a SA0.2; b SA1.0

6 Conclusions

A comprehensive PSHA has been performed for the TAP route. This analysis consisted of the compilation of an earthquake catalogue suitable for the study and the definition of the (active and possibly active) faults that can contribute to the ground motion along the corridor.

With the aid of an appropriate logic tree (Fig. 3), where different options have been considered for the main parameters involved in PSHA, the ground motion along the TAP route has been estimated in terms of PGA, SA0.2, SA1.0, and PGV (Fig. 14) for different RPs (475, 975, 2475, 4975, and 9975 years) and different local geology conditions (rock, stiff soil, and soft soil). The area with the highest hazard occurs west of Fier, along the Adriatic coast of Albania (PGA between 0.8 and 0.9 g, SA0.2 between 2.0 and 2.25 g, SA1.0 between 0.7 and 0.8 g, and PGV between 50 and 60 cm/s, for an RP of 2475 years on rock), while strong ground motions are also expected for the area north of Thessaloniki, to the north of Kavala, in the southern Alexandroupolis area, as well as the border of Greece with Turkey (Fig. 14).

Moreover, a selected site along the TAP route with the highest expected ground motion (west of Fier) has been investigated in detail in terms of hazard curves (Fig. 15) and UHSs (Fig. 16). The earthquakes contributing most to the hazard of the test site at low and high frequencies (1 and 5 Hz) have been identified by deaggregating the hazard results referred to the 2475-year RP (Fig. 17), and the corresponding design events for the TAP infrastructure have been identified as local quakes with M_W 6.6 and 6.0, respectively. For this site, detailed ground motion scenarios are needed to provide additional information and to better constrain the seismic hazard of the area.

The shaking values obtained in this study agree with the most recent large-scale investigations conducted in this area. Focusing on the Albanian coastal sector near the test site, the values according to the present study (Fig. 15) for a 475-year RP on rock are 0.42, 0.31, and 1.1 g, respectively for PGA, SA1.0, and SA0.2 while those on stiff soil are 0.45, 0.40, and 1.2 g. For the same RP, the estimates of the SHARE project (Giardini et al. 2014) on rock are between 0.4 and 0.425 g, around 0.25–0.275 g, and 0.8 g for PGA, SA1.0, and SA0.3, respectively. A previous similar study (Jimenez et al. 2001) gives values around 0.5 g for PGA, 0.3 g for SA1.0, and 1.0 g for SA0.3, respectively, for the same RP, but for stiff soil.