A-Priori Assessment of Interfacial Sub-grid Scale Closures in the Two-Phase Flow LES Context

Abstract

Due to the continuous increase in available computing power, the Large Eddy Simulation (LES) of two-phase flows started to receive more attention in recent years. Well-established models from single-phase flows are often used to close the sub-grid scale convective momentum transport and recently some modifications have been suggested to account for the jump of density and viscosity at the interface of multi-phase flows. However, additional unclosed terms in multi-phase flows, which are absent in single-phase flows, often remain ignored. This paper focuses on the crucial gaps in literature, namely the modeling of volume fraction advection and surface tension effects on sub-grid level. An a-priori analysis has been conducted for this purpose, i.e. the Direct Numerical Simulation of an academic two-phase flow configuration (single wobbling bubble in a turbulent background flow) has been explicitly filtered (corresponding to implicit filtering in actual LES) for varying filter width and the corresponding sub-grid terms have been compared to potentially suitable model expressions. Besides other approaches, adequately formulated models based on the scale similarity principle emerged to be promising candidates for both sub-grid volume fraction advection as well as sub-grid surface tension effects. In this context, special attention has to be paid to the secondary filter. Owing to the nature of the quasi-singular surface tension term, surface-weighted filtering may be more appropriate and robust than standard volume filtering.

1 Introduction

Turbulent bubbly flows play an essential role in a large number of technical applications, e.g. for chemical reactors in the process industry. Since Direct Numerical Simulation (DNS) is usually too expensive for technically relevant Reynolds numbers, sub-grid closures for the computationally more efficient Large Eddy Simulation (LES) are urgently needed. Compared to the LES of single-phase flows, LES of turbulent two-phase flows involves additional unclosed terms as can be seen in Sect. 2. Appropriate sub-grid models for momentum advection have been developed for variable density single-phase flows, e.g. by Vreman et al. (1995). Ketterl and Klein (2018) investigated a large variety of sub-grid models for the LES of primary breakup. At least in the context of a-priori analysis, structural models (mostly of scale similarity type) performed clearly better than functional models (mostly of eddy viscosity type) and a regularization of the first kind has been suggested to ensure their numerical stability in the context of a-posteriori LES (Klein et al. 2020). An overview of different LES modeling strategies for multi-fluid flows has recently been presented by Lakehal (2018). From the existing literature, it appears that sub-grid contributions arising due to the jump of fluid properties at the interface or due to the singular surface tension force are often neglected whilst only the closure of momentum advection is accounted for. Consequently, this work focuses on those closure terms that appear exclusively due to the two-phase nature of the flow, i.e. in the vicinity of the phase interface. One of a few exceptions is the work of Aniszewski et al. (2012) who applied the approximate deconvolution technique to sub-grid surface tension as it has originally been applied to turbulent stresses (Stolz and Adams 1999). Saeedipour et al. (2019) later applied the approximate deconvolution technique to all unclosed terms in the a-posteriori calculation of the two-dimensional phase inversion benchmark. For all models based on the eddy viscosity concept (not only related to the closure of momentum advection), another interesting approach (Saeedipour and Schneiderbauer 2019) accounts for unresolved interfacial work done by surface tension by adding a correction term to increase the turbulent viscosity at the interface. Using the concept of a critical grid-based Weber number, Ketterl et al. (2019) recently introduced a sub-grid model which increases the surface tension coefficient depending on the local flow conditions and the local curvature of the interface to ensure a solution that can be well represented by the grid.

A limited complexity test case (a single rising bubble in a turbulent background flow) is chosen here to allow for straight-forward plausibility checks (e.g. bubble shape oscillations) and to avoid additional complex phenomena in two-phase flows like coalescence, breakup etc. which complicate the interpretation of the results. For the popular phase inversion benchmark (Vincent et al. 2008) or similarly atomization problems, involving highly fragmented interfaces, it is extremely expensive, if not impossible, to compute a fully resolved three-dimensional DNS solution as a reference. The process of ligament stretching and rupture, or generally regions of high interface curvature, usually remain under-resolved in such cases. In this work, both promising existing models as well as novel models are tested by means of a-priori analysis.

2 LES Formalism

Using the usual notation (density $\rho$, velocity $u_i$, pressure p, dynamic viscosity $\mu$, gravitational acceleration $g_i$, surface tension coefficient $\sigma$, interface normal $n_i$, interface curvature $\kappa$, volume fraction $\alpha$), the filtered LES equations (Toutant et al. 2009) based on the one-fluid formulation read

$$\begin{aligned}&\frac{\partial \, \overline{u}_i}{\partial x_i} = \,\,0 \end{aligned}$$

(1)

$$\begin{aligned}&\frac{\partial \, \overline{\rho }\,\overline{u}_i}{\partial t} + \frac{\partial \,\overline{\rho }\,\overline{u}_i \overline{u}_j}{\partial x_j} = - \frac{\partial \, \overline{p}}{\partial x_i} + \frac{\partial }{\partial x_j} \left[ \overline{\mu }\,\left( \frac{\partial \, \overline{u}_i}{\partial x_j} + \frac{\partial \, \overline{u}_j}{\partial x_i}\right) \right] + \overline{\rho } g_i + \sigma \,\overline{n}_i^s\,\overline{\kappa }^s\,\overline{\delta }_S \nonumber \\&\quad - \frac{\partial }{\partial x_j}\,\tau _{\rho uu,ij} + \frac{\partial }{\partial x_j}\,\tau _{\mu S,ij} + \tau _{nn,i} - \frac{\partial }{\partial t}\,\tau _{tt,i} \end{aligned}$$

(2)

$$\begin{aligned}&\frac{\partial \, \overline{\alpha }}{\partial t}+\frac{\partial }{\partial x_i}(\overline{\alpha }\, \overline{u}_i) = - \frac{\partial }{\partial x_i}\tau _{\alpha u,i} \end{aligned}$$

(3)

with the corresponding sub-grid closure terms

$$\begin{aligned} \tau _{\rho uu,ij}&=\overline{\rho \, u_i u_j}-\overline{\rho }\,\overline{u}_i \,\overline{u}_j \end{aligned}$$

(4)

$$\begin{aligned} \tau _{tt,i}&= \overline{\rho \, u_i}-\overline{\rho }\,\overline{u}_i \end{aligned}$$

(5)

$$\begin{aligned} \tau _{\mu S,ij}&= \overline{\mu \,\left( \frac{\partial \, u_i}{\partial x_j} +\frac{\partial \, u_j}{\partial x_i}\right) } - \overline{\mu }\,\left( \frac{\partial \, \overline{u}_i}{\partial x_j} +\frac{\partial \, \overline{u}_j}{\partial x_i}\right) \end{aligned}$$

(6)

$$\begin{aligned} \tau _{nn,i}&= \sigma \, \overline{n_i\,\kappa }^s\,\overline{\delta }_S- \sigma \,\overline{n}^s_i\,\overline{\kappa }^s\,\overline{\delta }_S \end{aligned}$$

(7)

$$\begin{aligned} \tau _{\alpha u,i}&= \overline{\alpha \, u_i}-\overline{\alpha }\,\overline{u}_i \end{aligned}$$

(8)

In addition to volume filtering

$$\begin{aligned} \overline{\phi }(x_i)=\int \phi (y_i) G(x_i-y_i) dy_i \end{aligned}$$

(9)

with a Gaussian filter kernel

$$\begin{aligned} G(x,y,z)= G(x)G(y)G(z); \ G(x_i) = \left( 6 \over \pi \varDelta ^2 \right) ^{1/2} \exp \left( - {6 x_i^2 \over \varDelta ^2} \right) , \end{aligned}$$

(10)

surface filtering is defined by

$$\begin{aligned} \overline{\phi }^s=\overline{\phi \delta _S}/\overline{\delta }_S, \end{aligned}$$

(11)

which is used to reformulate the filtered surface tension term in this work:

$$\begin{aligned} \sigma \, \overline{n_i\,\kappa \,\delta _S} = \sigma \, \overline{n_i\,\kappa }^s\,\overline{\delta }_S. \end{aligned}$$

(12)

Although the surface tension force is singular in theory, the interface indicator function $\delta _S$ has to be approximated in numerical practice, usually by $\delta _S=|\nabla \alpha |$. It is known from literature (Klein et al. 2019) that the diffusive term closure (Eq. 6) is of inferior importance. The closure of momentum advection (Eq. 4) is of significant importance but a large variety of models is already available from single-phase flows that can be reasonably well modified for two-phase flows (Ketterl and Klein 2018). Thus, the present study focuses on the crucial gaps, namely the closures of volume fraction advection (Eq. 8) and the quasi-singular surface tension force (Eq. 7), which contribute only in the vicinity of the interface of both phases. Since Eqs. 5 and 8 are of the same mathematical nature, similar models may be used.

It is worth noting that a different set of two-phase flow governing equations can be obtained when the filtering operation is replaced by a density-weighted, i.e. Favre-filtering operation (Labourasse et al. 2007) or by a phase-conditional averaging operation (Sabisch et al. 2001). The properties and commonalities of these approaches are discussed by Klein et al. (2019).

3 DNS Database

Fig. 1

The red surface represents the bubble interface in the turbulent flow and the semi-transparent grey $Q=10^4/s^2$ iso-contour indicates dominant vortical structures in four consecutive snapshots. The a-priori analysis presented in this paper is based on the first snapshot shown here. The gravitational acceleration is acting in vertical direction

The DNS database has been generated by the state-of-the-art two-phase flow solver PARIS (main features: unsteady incompressible Navier–Stokes equations; finite-volume discretization on staggered grid; third-order QUICK scheme for momentum advection; second-order central differencing scheme for diffusive fluxes; second-order Runge-Kutta scheme for time integration; piecewise-linear geometrical interface reconstruction; curvature calculation by height function method; pressure projection method implemented by a multi-grid Poisson solver provided by the HYPRE library; parallelization by domain decomposition with MPI communication) (Ling et al. 2015), and explicitly filtered (Eq. 9) with a Gaussian filter kernel (Eq. 10) for varying filter width $\varDelta$.

The DNS setup consists of a single air bubble in a water-filled rectangular box with periodic boundary conditions on all sides. As can be seen in four consecutive snapshots in Fig. 1, a wobbling ellipsoidal bubble is observed due to the imposed fluid properties ($\rho _l/\rho _g=831.8$, $\mu _l/\mu _g=54.96$) and a spherical bubble diameter of $d_b = 5$ mm. Considering the bubble Reynolds number

$$\begin{aligned} Re_b = {u_{x,rel} \ d_b \over \nu _l} \approx 996, \end{aligned}$$

(13)

it is clear that the observed behavior is in agreement with the regime diagram of Clift et al. (2005). For that matter, the relative vertical velocity of both phases is calculated as $u_{x,rel}=\langle u_x \rangle _l - \langle u_x \rangle _g \approx 0.2$ m/s using a phase-conditional spatial averaging $\langle \cdot \rangle _{l,g}$, where x represents the direction in which gravitational acceleration is acting. The time span between the snapshots is approximately 0.15 s, i.e. around 6 bubble overflow times $t_b=d_b/u_{x,rel} \approx 0.025$ s. The a-priori analysis presented in this paper is based on the first snapshot in Fig. 1, for which the bubble does not extend across the periodic boundaries. The size of the cubic domain, $(0.01~\hbox {m})^3$, is chosen such that the overall gas void fraction lies in the technically relevant range ($V_g/(V_g+V_l)=6.6\%$ here). Since the turbulence is induced by the buoyant bubble itself, the simulation has to be continued at least until a converged state is reached in terms of first-order statistics like the relative bubble rise velocity $u_{x,rel}$ (Fig. 2, left) or the conditionally averaged enstrophy in the matrix phase $E_l = \langle \omega _i \omega _i /2 \rangle _l$ (Fig. 2, right) where $\omega _i$ is the vorticity. The chaotic flow structure does not exactly resemble the behavior in a dense bubble swarm consisting of independent bubbles, but a similar level of turbulence-interface interaction events is achieved, which is of prior importance for this study. Moreover, it may be more appropriate to speak of pseudo-turbulence instead of fully developed turbulence in this context.

Fig. 2

Temporal evolution of the relative bubble rise velocity $u_{x,rel}$ (left) and the conditionally averaged enstrophy in the liquid phase $E_l$ (right)

Hence, a numerically clean setup without the influence of simplified boundary conditions is investigated. Meshing by a uniform Cartesian grid $\varDelta x = \varDelta y = \varDelta z = 78.125~\upmu$m yields $d_b/\varDelta x = 64$. This resolution of 64 cells per spherical bubble diameter is considerably higher than in most DNS studies on bubbly flows available in the literature. According to Cifani et al. (2018), accurately capturing the interface dynamics requires at least 15 cells per diameter for nearly spherical bubbles in the framework of the geometrical Volume-of-Fluid method. For wobbling ellipsoidal bubbles, it is assumed that at least 25–30 cells per equivalent spherical bubble diameter are required. In terms of the relative rise velocity of the bubble, there is hardly any difference between 16 and 32 cells per bubble diameter according to Koebe et al. (2003). Following Kolmogorov’s universal equilibrium theory, the smallest turbulent flow structures that have to be resolved in a DNS can be estimated by $\eta \approx L_t Re_t^{-3/4}$ using the integral turbulent length scale $L_t$ and the turbulent Reynolds number $Re_t=u' L_t / \nu _l$ (Batchelor 1953). Assuming, in a conservative manner, that $Re_t=Re_b$ and $L_t=d_b$ yields $\eta \approx 28.2~\upmu$m. One may alternatively estimate $\varepsilon \approx u_{x,rel} \; g_x$ (Koebe et al. 2003) and use $\nu =\nu _l$ to obtain the Kolmogorov length scale $\eta =(\nu ^3/\varepsilon )^{1/4} \approx 26.8~\upmu$m. The achieved grid spacing is of the same order of magnitude as $\eta$ and can thus be considered sufficient for the evaluation of first- and second-order statistics (Grötzbach 2011). In a closely related setup (bubble Reynolds number $\approx 10^3$, identical fluid properties), a similar grid resolution ($d_b/\varDelta x = 40$) has also been used in earlier DNS studies (Hasslberger et al. 2018) on bubbly flows. However, it may be questioned whether the resolution is fine enough to fully resolve the boundary layers on both sides of the interface. The thickness of the viscous boundary layer $\delta$ at the surface of a bubble can be estimated (Levich 1962) as

$$\begin{aligned} \delta \approx {d_b \over \sqrt{2 Re_b}}. \end{aligned}$$

(14)

If we require to resolve the boundary layer by at least two uniform cells, the number of cells per bubble diameter is given by

$$\begin{aligned} d_b / \varDelta x \ge 2 \sqrt{2 Re_b} \approx 89 \end{aligned}$$

(15)

for $Re_b=996$. Consequently, the sensitivity of the a-priori results of this paper have been double-checked for a higher resolution of $d_b/\varDelta x = 128$ which fulfills the above boundary layer resolution criterion. It is exemplified in the “Appendix” (Fig. 10) that no major differences in terms of model performance occur between 64 and 128 cells per bubble diameter.

4 Models and Results

4.1 Volume Fraction Advection

Besides potentially suitable existing models for $\tau _{\alpha u,i}$, i.e. the widespread gradient flux model (based on the eddy viscosity $\nu _t$, e.g. provided by Smagorinsky’s model (Smagorinsky 1963), and a turbulent Schmidt number, $Sc_t=1.0$ here)

$$\begin{aligned} \tau _{\alpha u,i}^{GFM} = -{ \nu _t \over Sc_t}{ \partial \overline{\alpha } \over \partial x_i} = -{ (0.18 \varDelta )^2 \over Sc_t} \sqrt{2 \overline{S}_{ij}\overline{S}_{ij}} { \partial \overline{\alpha } \over \partial x_i}, \end{aligned}$$

(16)

Clark’s tensor diffusivity model (Clark et al. 1979) applied to scalar flux modeling (Klein et al. 2016)

$$\begin{aligned} \tau _{\alpha u,i}^{CTM} = { \varDelta ^2 \over 12}{ \partial \overline{u}_i \over \partial x_k}{ \partial \overline{\alpha } \over \partial x_k}, \end{aligned}$$

(17)

and Bardina’s scale similarity model (discussed below), several new models are tested. Depending on the model variant, the filter-scale velocity gradient tensor $\overline{A}_{ij}=\partial \overline{u}_i / \partial x_j$ in the model (Ketterl and Klein 2018) inspired by Bray-Moss-Libby (BML) theory (i.e. flamelet theory of turbulent combustion (Bray et al. 1985)) given by

$$\begin{aligned} \tau _{\alpha u,i}^{BML} = \overline{\alpha }(1-\overline{\alpha }) \varDelta \overline{A}_{ij} \overline{n}_j \end{aligned}$$

(18)

is either replaced by a blending such that

$$\begin{aligned} \tau _{\alpha u,i}^{BML-F} = \overline{\alpha }(1-\overline{\alpha }) \varDelta \left( (1-F_{CS}) \overline{S}_{ij} + (1+F_{CS}) \overline{W}_{ij} \right) \overline{n}_j , \end{aligned}$$

(19)

or by an alternative blending such that

$$\begin{aligned} \tau _{\alpha u,i}^{BML-SW} = \overline{\alpha }(1-\overline{\alpha }) \varDelta \left( (1-\overline{\alpha }) \overline{S}_{ij} + \overline{\alpha } \ \overline{W}_{ij} \right) \overline{n}_j , \end{aligned}$$

(20)

where $\overline{S}_{ij}$ and $\overline{W}_{ij}$ are the symmetric and anti-symmetric part of $\overline{A}_{ij} = \overline{S}_{ij} +\overline{W}_{ij}$, respectively. In the first formulation BML-F, the coherent structure function is defined as

$$\begin{aligned} F_{CS} = {2Q \over (\overline{A}_{ij})^2}, \end{aligned}$$

(21)

where $Q=(\text {trace}(\overline{A}_{ij})^2-\text {trace}(\overline{A}_{ij}^2))/2$ is the second invariant of $\overline{A}_{ij}$. The blending by means of $-1\le F_{CS}\le 1$ takes into account whether the flow is locally strain- or vorticity-dominated on the resolved level. The same dominant flow behavior can then be assumed on sub-grid level because in LES, other than in (U)RANS, there is usually a sufficiently high correlation between the strain-vorticity relationship in the DNS and the resolved level (Kobayashi 2005). It has been found in literature (Hasslberger et al. 2018) that especially the regions of high interface curvature in bubbly flows are dominated by vortices. In regions characterized by $F_{CS}=0$ (strain-vorticity equilibrium), the original formulation (Eq. 18) is locally recovered. The simplified second formulation BML-SW utilizes the fact that the bubble interior and exterior close to the interface are usually vorticity- and strain-dominated, respectively (Hasslberger et al. 2018). Here, $\alpha$ is taken to be the volume fraction of the lighter phase, in which the vorticity tends to accumulate in unsteady turbulent flows (Tripathi et al. 2014; Hasslberger et al. 2018, 2019). Finally, the scale similarity (SS) ansatz for this term (Chesnel et al. 2011) reads

$$\begin{aligned} \tau _{\alpha u,i}^{SS} = \widehat{\overline{\alpha } \, \overline{u}_i} - \widehat{\overline{\alpha }}\,\widehat{\overline{u}}_i, \end{aligned}$$

(22)

where the secondary test filter for any field quantity $\phi _{i,j,k}$ at the discrete location given by the index triple (i, j, k) is implemented according to Anderson and Domaradzki (2012):

$$\begin{aligned} \widehat{\phi }_{i,j,k} = \sum _{l=-1}^{+1} \sum _{m=-1}^{+1} \sum _{n=-1}^{+1} b_l \cdot b_m \cdot b_n \cdot \phi _{i+l,j+m,k+n}. \end{aligned}$$

(23)

This three-dimensional filter is the product of the convolution of three one-dimensional filters with coefficients $(b_{-1},b_{0},b_{+1})=(C,1-2C,C)$ where $C=1/12$. Hence, the considered cell itself and direct neighbor cells $(l,m,n \in \{-1,0,+1 \})$ are taken into account by different weights for secondary filtering. Same as for differentiation, the secondary filtering operation is based on filtered quantities available on the coarse LES grid. It is worth noting that the gradient-based CTM model is basically a low-order approximation of the SS model which can be shown by a Taylor-series-development and truncating higher-order terms of the secondary filtering operation. A pragmatic approach (without stringent derivation) accounting for both the scale similarity principle as well as the bi-modal distribution of the unresolved discontinuous phase indicator function can be constructed as

$$\begin{aligned} \tau _{\alpha u,i}^{SS-BML} = 4 \, \overline{\alpha }(1-\overline{\alpha }) \left( \widehat{\overline{\alpha } \, \overline{u}_i} - \widehat{\overline{\alpha }}\,\widehat{\overline{u}}_i \right) , \end{aligned}$$

(24)

which reduces to Eq. 22 at $\overline{\alpha }=0.5$. Note that all model-related derivatives are discretized by second-order central differences on the coarse LES grid.

Fig. 3

Correlation of $\tau _{\alpha u,i}$ in vertical direction (top left), in lateral direction (top right) and $\partial \tau _{\alpha u,i} / \partial x_i$ (bottom) with the corresponding models, depending on the normalized filter width $\varDelta /\varDelta _{DNS}$

Fig. 4

$L_2$-norm of $\tau _{\alpha u,i}$ in vertical direction (top left), in lateral direction (top right) and $\partial \tau _{\alpha u,i} / \partial x_i$ (bottom) of the corresponding models compared with DNS, depending on the normalized filter width $\varDelta /\varDelta _{DNS}$

Pearson’s correlation coefficient is defined as

$$\begin{aligned} P={Cov(\tau ,\tau ^{m}) \over \sqrt{Var(\tau )} \sqrt{Var(\tau ^{m})}} = {\sum _{k = 1}^{N}(\tau _{k} - \langle \tau \rangle ) \ \sum _{k = 1}^{N}(\tau _{k}^{m} - \langle \tau ^{m} \rangle ) \over \sqrt{ \sum _{k = 1}^{N}(\tau _{k} - \langle \tau \rangle )^{2} \ \sum _{k = 1}^{N}(\tau _{k}^{m} - \langle \tau ^{m} \rangle )^{2}}} \end{aligned}$$

(25)

where Cov denotes the covariance, Var the variance and $\sqrt{Var}$ the standard deviation. $\tau$ and $\tau ^m$ represent the ‘exact’ values from the explicitly filtered DNS (Eqs. 7 and 8) and the values predicted by the corresponding model, respectively. The mean of N samples is calculated as

$$\begin{aligned} \langle \tau \rangle ={1\over N} \sum _{k =1}^{N} \tau _k. \end{aligned}$$

(26)

According to the Cauchy–Schwarz inequality, P assumes values between $-1$ and $+1$, where $+1$ is a total positive linear correlation, 0 is no linear correlation, and $-1$ is a total negative linear correlation. Particularly to test the mathematical structure (or alignment) of the models, those correlation coefficients, before and after taking the divergence of $\tau _{\alpha u,i}$, are presented in Fig. 3. Since the flow behavior in vertical (the direction subject to gravitational acceleration, i.e. the main flow direction) and lateral directions is rather different as shown by Hasslberger et al. (2018) who analyzed the flow structure in turbulent bubbly flows in detail by means of a local flow topology analysis, correlation coefficients in both directions are evaluated separately. All models, except the GFM model, show increasing correlation values for decreasing filter width ($\varDelta /\varDelta _{DNS} \rightarrow 1$) which is an important consistency check. The bad performance of the GFM model is attributed to the fact that this model is the only one which cannot switch between gradient and counter-gradient transport depending on local conditions. Even with an advanced calculation of $\nu _t$ accounting for sub-grid surface tension effects (Saeedipour and Schneiderbauer 2019), this deficit persists. It is interesting to note that Clark’s model CTM is obtained when $\overline{\alpha }(1-\overline{\alpha })$ in the BML model (Eq. 18) is replaced by $|\nabla \overline{\alpha }|\, \varDelta$. Whereas Clark’s model is likely to perform better for passive scalar mixing, the $\overline{\alpha }(1-\overline{\alpha })$-proportionality accounts for the discontinuous two-phase interface prohibiting intermediate states in terms of the unresolved discontinuous phase indicator function $\alpha$ (not $\overline{\alpha }$) with a bi-modal distribution, i.e. either liquid or gas without mixing. It then follows from probability theory that the highest probability for unresolved interface modulations occurs at $\overline{\alpha }=0.5$ where also the interface area in the cell reaches its statistical maximum. For $\overline{\alpha }=0$ and $\overline{\alpha }=1$, no interface is contained in the computational cell, and consequently the model accounting for unresolved interface modulations should be zero as well. This property is assumed to be the main reason for the superior performance of the BML-type models before taking the divergence. After taking the divergence, the correlation values are generally lower than before taking the divergence due to additional differentiation errors. The SS-type models show the highest correlation results after taking the divergence. As Fig. 4 demonstrates, the order of magnitude and general increasing/decreasing trend of $L_2$-norms of $\tau _{\alpha u,i}$ and $\partial \tau _{\alpha u,i} / \partial x_i$ agree reasonably well with the DNS. Due to the unacceptable correlation results, the norms of the GFM model are omitted in Fig. 4. The results of the a-priori analysis are fairly insensitive to the specific two-phase flow configuration as the comparison with the performance of some of the above models in the context of primary breakup (Ketterl and Klein 2018) reveals. In general, all models selected for this paper (except GFM) show comparable results and can be assessed as potential candidates for further a-posteriori analysis. Additional requirements like numerical stability may rule out some of the above models in actual LES calculations. Particularly, models proportional to $\overline{\alpha }(1-\overline{\alpha })$ may behave differently in terms of stability than models proportional to $|\nabla \overline{\alpha }|\, \varDelta$ since the discrete version of the latter formulation leads to a wider region around the interface where the sub-grid term is unequal to zero. It is also important to mention that incorporating explicit models for $\tau _{\alpha u,i}$ in a-posteriori analysis with Volume-of-Fluid solvers potentially produces boundedness violation errors ($\overline{\alpha }<0$ or $\overline{\alpha }>1$) which necessitate countermeasures like a redistribution algorithm to guarantee acceptable volume conservation. Having a right-hand side in Eq. 3 acts like a source or sink in terms of the conserved volume which is potentially problematic.

4.2 Surface Tension

The magnitude of $\tau _{nn,i}$ can be of the same order of magnitude as the momentum advection sub-grid term (Klein et al. 2019) and it is potentially important for topological changes, as well as vorticity production at the interface, cf. Hasslberger et al. (2018). Its importance is also underlined by Aniszewski et al. (2012). To the best of the authors’ knowledge, no well-established model exists in literature for sub-grid surface tension effects in the context of surface filtering which is the focus of this work. Corresponding results for volume filtering are reported in Ketterl and Klein (2018). Multiplication of Shirani’s model (Shirani et al. 2011), originally developed in the context of volume filtering,

$$\begin{aligned} \tau _{nn,i}^{SHIR} = C_{st}\, \sqrt{|\overline{S}_{ij}|}\, {\varDelta \over \sqrt{\nu }}\, \sigma \,\overline{n}^s_i\,\overline{\kappa }^s \,\overline{\delta }_S \end{aligned}$$

(27)

by the correction $(1-2 \overline{\alpha })$ makes the model potentially applicable in the surface filtering context (as demonstrated subsequently):

$$\begin{aligned} \tau _{nn,i}^{SHIR-Corr} = C_{st}\, (1-2 \overline{\alpha })\, \sqrt{|\overline{S}_{ij}|}\, {\varDelta \over \sqrt{\nu }}\, \sigma \,\overline{n}^s_i\,\overline{\kappa }^s\,\overline{\delta }_S. \end{aligned}$$

(28)

$C_{st}$ is an empirically determined constant and the model scales with the filter width, i.e. it vanishes when $\varDelta \rightarrow 0$. $|\overline{S}_{ij}|$ can be interpreted as a measure of unresolved turbulence (and therefore unresolved interface modulation), which also appears in the famous Smagorinsky sub-grid model (Smagorinsky 1963), for instance. Using the concept of eddy viscosity $v_t \propto \varDelta ^2 |\overline{S}_{ij}|$, the latter model can be reformulated to

$$\begin{aligned} \tau _{nn,i}^{SHIR-Corr} \propto (1-2 \overline{\alpha })\, \sqrt{\nu _t \over \nu }\, \sigma \,\overline{n}^s_i\,\overline{\kappa }^s\,\overline{\delta }_S, \end{aligned}$$

(29)

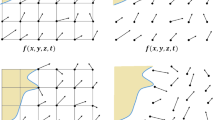
showing its relation with classical turbulence modeling ideas. According to the schematic in Fig. 5, it seems reasonable that the sub-grid surface tension force changes its sign on both sides of the resolved/filtered interface because it is the nature of (sub-grid) surface tension to minimize the interface surface area. The linear correction $(1-2 \overline{\alpha })$ within the interface region (varies from $+1$ at $\overline{\alpha }=0$ to $-1$ at $\overline{\alpha }=1$) may be assumed as a first approximation. On average, the lowest sub-grid curvature occurs at $\overline{\alpha }=0.5$ and, hence, the sub-grid surface tension force is assumed to vanish in this region. Such behavior can indeed be seen in Fig. 6 which shows the vertical component of the evaluated sub-grid surface tension term $\tau _{nn,i}$ for two different filter widths. Even with increasing filter width, this idealized behavior persists in a large share of the visualized interface region in Fig. 6. Deviations from this idealized behavior can be observed in the regions of high interface curvature and these deviations become stronger for increasing filter width.

Fig. 5

Relationship between the real interface (continuous line) and the resolved/filtered interface (dashed lines). Red arrows indicate sub-grid surface tension forces

Fig. 6

Vertical-lateral slice through the ellipsoidal bubble, showing the vertical component of the sub-grid surface tension term $\tau _{nn,i}$ for a normalized filter width of $\varDelta /\varDelta _{DNS}=4$ (left) and $\varDelta /\varDelta _{DNS}=8$ (right). Gravitational acceleration is acting in vertical direction

Modeling the singular surface tension force as a distributed volume force (as suggested by Brackbill et al. (1992)), the profile of the total filtered surface tension

$$\begin{aligned} \sigma \, \overline{n_i\,\kappa \,\delta _S} = \sigma \, \overline{n_i\,\kappa }^s\,\overline{\delta }_S = \sigma \,\overline{n}^s_i\,\overline{\kappa }^s\,\overline{\delta }_S + \tau _{nn,i} \end{aligned}$$

(30)

in interface-normal direction becomes increasingly asymmetric with increasing impact of the sub-grid model $\tau _{nn,i}$, as qualitatively sketched in Fig. 7. In an ideal LES, the sum of the resolved part $\sigma \,\overline{n}^s_i\,\overline{\kappa }^s\,\overline{\delta }_S$ (assumed to be symmetric in the sketch because it is proportional to $\overline{\delta }_S=\overline{| \nabla \alpha |}$) and the sub-grid model part $\tau _{nn,i}$ would be identical to the filtered DNS $\sigma \, \overline{n_i\,\kappa }^s\,\overline{\delta }_S$. The universal validity of the above models is also limited due to the influence of the model coefficient $C_{st}$. Shirani et al. (2011) set $C_{st}=0.15$ to obtain optimal agreement with the phase inversion benchmark, i.e. involving a highly fragmented interface, which is in contrast to the compact wobbling bubble investigated here, i.e. involving relatively mild interface modulations. However, the a-priori correlation analysis (not the $L_2$-norm analysis) performed here is independent of a constant multiplied to the model, cf. Eq. 25.

Fig. 7

Qualitative volume force profiles in interface-normal direction of the resolved ($\sigma \,\overline{n}^s_i\,\overline{\kappa }^s\,\overline{\delta }_S$, blue), sub-grid ($\tau _{nn,i}$, red) and total filtered surface tension ($\sigma \,\overline{n}^s_i\,\overline{\kappa }^s\,\overline{\delta }_S + \tau _{nn,i}$, yellow). The impact of the sub-grid model $\tau _{nn,i}$ is assumed to rise from left to right

An alternative, parameter-free, approach is again given by the scale similarity ansatz for the sub-grid surface tension term:

$$\begin{aligned} \tau _{nn,i}^{SS-vol} = \sigma \left( \widehat{\overline{n}^s_i\,\overline{\kappa }^s} - \widehat{\overline{n}^s_i}\,\widehat{\overline{\kappa }^s} \right) \overline{\delta }_S. \end{aligned}$$

(31)

It can also be formulated with a surface test filter

$$\begin{aligned} \widehat{\phi }^s=\widehat{\phi \delta _S}/\widehat{\delta }_S, \end{aligned}$$

(32)

instead of a volume test filter $\widehat{\phi }$, which seems to be more consistent in the surface-filtering context:

$$\begin{aligned} \tau _{nn,i}^{SS-surf} = \sigma \left( \widehat{\overline{n}^s_i\,\overline{\kappa }^s}^s - \widehat{\overline{n}^s_i}^s\,\widehat{\overline{\kappa }^s}^s \right) \overline{\delta }_S. \end{aligned}$$

(33)

An additional model variant SS-vol-trim is based on the same formulation as SS-vol. However, $\overline{n}^s_i$ and $\overline{\kappa }^s$ are trimmed to the region $0<\overline{\alpha }<1$, i.e. where reasonable values (particularly of curvature which involves second-order derivatives) can be expected in actual LES calculations. Beyond this region, these quantities are set to a value of zero which is likely to be the default in a-posteriori analysis. After this trimming process, the secondary filtering operation is executed. It has to be emphasized that the ‘trim’ variants of models SS-vol and SS-surf are not supposed to be independent new models which shall explicitly be implemented like this in an LES solver. The trimming process is rather supposed to mimic what could happen in real a-posteriori LES calculations when implementing either the SS-vol or the SS-surf model in the form as specified by Eqs. 31 and 33, respectively.

Fig. 8

Correlation of $\tau _{nn,i}$ and the corresponding models in vertical (left) and lateral (right) direction, depending on the normalized filter width $\varDelta /\varDelta _{DNS}$

Fig. 9

$L_2$-norm of $\tau _{nn,i}$ in vertical (left) and lateral (right) direction of the corresponding models compared with DNS, depending on the normalized filter width $\varDelta /\varDelta _{DNS}$

Correlation coefficients and $L_2$-norms of $\tau _{nn,i}$ are shown in Figs. 8 and 9, respectively. When comparing a fixed filter width, unacceptable changes of the correlation sign depending on the spatial direction occur for both the uncorrected SHIR model as well as the SS-vol-trim model. Since the correlation behavior of these models is also very similar for changes of the filter width, they seem to suffer from the same shortcomings. The proposed correction factor $(1-2 \overline{\alpha })$ leads to a significant correlation improvement of existing models being directly proportional to the resolved/surface-filtered curvature and normal vector, which is here demonstrated by the SHIR-Corr model. At least for small and medium filter width, consistently high positive correlation values can be observed for the SHIR-Corr model. The norms of the SHIR and SHIR-Corr model are far off (and thus not included here) which is probably due to the fact that the model coefficient $C_{st}=0.15$ was tuned for a different regime of interface modulation—compact bubble vs. strong fragmentation in the phase inversion case. A convincing performance can be attributed to the SS-vol and SS-surf model considering the high sensitivity of this sub-grid term. Besides correlations, also the norms capture well the trends with increasing filter width as compared to DNS. By means of the secondary filtering operation, the latter models are able to account for changes in interface-normal direction, particularly the change of sign of the sub-grid term on both sides of the interface as sketched in Fig. 5, in a natural manner without additional corrections. In contrast to the unacceptable results of the SS-vol-trim model, the model variant SS-surf-trim yields practically identical results as SS-surf (thus no independent line in the figures), i.e. this formulation with a secondary surface filter instead of a secondary volume filter is perfectly robust against the trimming process (which mimics what could happen in a-posteriori LES calculations). Hence, it is likely that the SS-vol model performs worse in a-posteriori analysis than in a-priori analysis. The SS-surf model has a higher chance of performing equally well in both a-priori and a-posteriori analysis.

Another issue is related to the special numerical treatment of the volume fraction advection equation, Eq. 3. Either a geometric reconstruction of the interface or a compression term in the volume fraction advection equation is usually implemented to counteract numerical dissipation which would continuously smoothen the interface in an unphysical manner. Hence, the thickness of the interface region from the filtered DNS field ($0<\overline{\alpha }<1$) is not perfectly transferable to the situation in actual LES calculations. Consequently, the strong correlation decrease of the SHIR-Corr model with increasing filter width may be less problematic in a-posteriori analysis than it is suggested by the a-priori analysis discussed here.

5 Concluding Remarks

Using a-priori analysis, several suitable model candidates for closing the volume fraction advection equation have been identified and the impact of different model contributions has been discussed. It seems to be important to account for the bi-modal character of the unresolved discontinuous phase indicator function as well as the fact that both gradient and counter-gradient transport can be represented by the sub-grid model. Mainly because it fails with respect to this last property, the frequently used gradient flux model showed the worst performance and cannot be recommended. All other models, either gradient-based or based on secondary filtering, were successful in reproducing the generally correct behavior. Further model variants accounting for the local character of the flow by means of a blending between vorticity- and strain-dominated regions also showed promising results. Similar blending ideas may be applied to the closure of momentum advection.

Regarding the closure of sub-grid surface tension, a linear correction has been proposed to make available models, which are directly proportional to the resolved/surface-filtered curvature and normal vector, applicable in the surface filtering context as investigated here. However, that modeling idea might be limited to wrinkled/corrugated interfaces and not be valid for highly fragmented interfaces. In addition, the scale similarity ansatz with a secondary surface-weighted filter showed a convincing behavior. Depending on the regime of interface modulation, a blending of these different approaches could be worthwhile to investigate in future studies.

As a next step, the robustness of the tested/proposed models has to be checked in a-posteriori analysis—including additional challenges like the interaction with numerical schemes and sub-grid models of other terms, particularly the closure of momentum advection.

Appendix

In the subsequent comparison on the sensitivity of the a-priori analysis findings in reply to the resolution of the DNS database (Fig. 10), the values presented in the lower resolution case ($d_b/\varDelta x = 64$) correspond to twice the normalized filter width $\varDelta /\varDelta _{DNS}$ in the higher resolution case ($d_b/\varDelta x = 128$). For example, a normalized filter width of $\varDelta /\varDelta _{DNS} = 8$ in the higher resolution case has to be compared to $\varDelta /\varDelta _{DNS} = 4$ in the lower resolution case. It has to be mentioned that the instantaneous flow and the bubble shape evolve differently in the DNS simulations depending on the grid resolution due to the chaotic nature of turbulence. Hence, it has been assured that a quasi steady-state has been reached in terms of the turbulent flow field in both cases. Due to the very similar correlation values of $\tau _{\alpha u,i}$ in vertical direction as exemplified here, it is expected that also all the other a-priori evaluations do not show significant differences depending on the resolution of the DNS database.

Fig. 10

Correlation of $\tau _{\alpha u,i}$ in vertical direction with the corresponding models compared for different grid resolution ($d_b/\varDelta x = 64$ on the left and $d_b/\varDelta x = 128$ on the right), depending on the normalized filter width $\varDelta /\varDelta _{DNS}$