Skip to main content
SpringerLink
Log in

Coupled flapwise-chordwise-axial-torsional dynamic responses of rotating pre-twisted and inclined cantilever beams subject to the base excitation

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

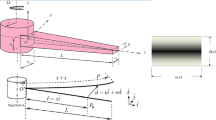
A rotating pre-twisted and inclined cantilever beam model (RPICBM) with the flapwise-chordwise-axial-torsional coupling is established with the Hamilton principle and the finite element (FE) method. The effectiveness of the model is verified via comparisons with the literatures and the FE models in ANSYS. The effects of the setting and pre-twisted angles on the dynamic responses of the RPICBM are analyzed. The results show that: (i) the increase in the setting or pre-twisted angle results in the increases in the first-order flapwise and torsional frequencies while the decrease in the first-order chordwise frequency under rotating conditions; (ii) a positive/negative setting angle leads to a positive/negative constant component, while a positive/negative pre-twisted angle leads to a negative/positive constant component; (iii) when the rotation speed is non-zero, the pre-twisted angle or non-zero setting angle will result in the coupled flapwise-chordwise-axial-torsional vibration of the RPICBM under axial base excitation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

A :

cross-sectional area

A 0 :

amplitude of the base excitation

OXYZ :

global coordinate system

OX r Y r Z r :

rotating coordinate system

o b x b y b z b :

local coordinate system

o e x e y e z e :

element coordinate system

A i :

coordinate-transformation matrix

b :

beam width at the arbitrary section

b 0 :

beam width at the root section

c :

a constant

C :

the Rayleigh damping

E :

Young’s modulus

F b :

base excitation force in the x-direction

F c :

centrifugal force

F e :

element nodal force vector in oexeyeze

\(F_{\rm{r}}^{\rm{e}}\) :

element nodal force vector in OXrYrZr

F :

global nodal force vector

f e :

excitation frequency

G :

shear modulus

f i :

concerned end frequency

G e :

element Coriolis matrix in oexeyeze

\(G_{\rm{r}}^{\rm{e}}\) :

element Coriolis matrix in OXrYrZr

G :

global Coriolis matrix

h :

beam thickness at the arbitrary section

h 0 :

beam thickness at the root section

I x :

area moment of the cross-section inertia about ox3

I y :

area moment of the cross-section inertia about oy3

I z :

area moment of the cross-section inertia about oz3

J :

torsional moment of the inertia of a pre-twisted rectangular beam

J s :

torsional moment of the inertia of a straight rectangular beam

J a :

additional torsional moment of the inertia caused by γ(L)

\(K_{\rm{e}}^{\rm{e}}\) :

element structural stiffness matrix in oexeyeze

\(K_{\rm{c}}^{\rm{e}}\) :

element centrifugal stiffening matrix in oexeyeze when \(\dot{\alpha}=1 \rm{rad}\cdot{s}^-1\)

\(K_{\rm{s}}^{\rm{e}}\) :

spin softening matrix in oexeyeze when \(\dot{\alpha}=1 \rm{rad}\cdot{s}^-1\)

\(K_{\rm{e,r}}^{\rm{e}}\) :

element structural stiffness matrix in OXrYrZr

\(K_{\rm{c,r}}^{\rm{e}}\) :

element centrifugal stiffening matrix in OXrYrZr when \(\dot{\alpha}=1 \rm{rad}\cdot{s}^-1\)

\(K_{\rm{s,r}}^{\rm{e}}\) :

element spin softening matrix in OXrYrZr when \(\dot \alpha=1\;{\rm{rad}}\cdot{{\rm{s}}^{ - 1}}\)

K e :

global structural stiffness matrix

K c :

global centrifugal stiffening matrix

K s :

global spin softening matrix

\(K_{\rm{acc}}^{\rm{e}}\) :

stiffness matrix related to \(\ddot{\alpha}\) in oexeyeze

\(K_{\rm{acc,r}}^{\rm{e}}\) :

stiffness matrix related to \(\ddot{\alpha}\) in OXrYrZr

K acc :

global stiffness matrix related to \(\ddot \alpha \)

L :

beam length

l k :

kth element length

M e :

element mass matrix in oexeyeze

\(M_{\rm{r}}^{\rm{e}}\) :

element mass matrix in OXrYrZr

M :

global mass matrix

N :

total number of the beam elements

n :

rotation speed

R d :

disk radius

R k :

x coordinate of oe in OXrYrZr

r P :

coordinate vector of the arbitrary point P in OXYZ

ṙ P :

velocity vector of the arbitrary point P in OXYZ

T k :

kinetic energy of the kth rotating Timoshenko beam element

T :

transformation matrix from OXrYrZr to oexeyeze

t 1 :

starting moment of the variation

t 2 :

ending moment of the variation

U k :

potential energy of the fcth rotating Timoshenko beam element; linear displacements of the centroid of an arbitrary beam cross-section along the positive xe-, ye-, and ze-axes

\(\dot{u}, \dot{v}, \dot{w}\) :

velocities of the centroid of an arbitrary beam cross-section along the positive xe-, ye-, and ze-axes

\(\ddot{u}, \ddot{v}, \ddot{w}\) :

accelerations of the centroid of an arbitrary beam cross-section along the positive xe-, ye- and ze-axes

u′, v′, w′:

the derivative of u, v, and w versus the coordinate x

\(X_u^{\rm{r}}\) :

base excitation along the Xr-direction

x k :

x coordinate of oe in obxbybzb

(X P, Y P, Z P):

coordinate components of Point P along the X-, Y-, and Z-directions

(x, y, z):

coordinate components of Point P along the x3-, y3-, and z3-directions

Y I :

first-order flapwise frequency

Y II :

second-order flapwise frequency

Z I :

first-order chordwise frequency

Z II :

second-order chordwise frequency

α :

rotating angle

\(\dot \alpha \) :

angular velocity

\(\ddot \alpha \) :

angular acceleration

α 1, β 1 :

Rayleigh damping coefficients

β 0 :

initial setting angle

β k :

setting angle of the kth Timoshenko beam element

γ k :

pre-twisted angle of the fcth Timoshenko beam element

γ(L):

pre-twisted angle at L

δ :

variational symbol

δ e :

element nodal displacement vector in oexeyeze

\(\delta_{\rm{r}}^{\rm{e}}\) :

element nodal displacement vector in OXrYrZr

ζ :

correction factor

θ :

angular displacement with respect to the xe-axis

\(\dot\theta\) :

velocity with respect to the xe-axis

\(\ddot\theta\) :

acceleration with respect to the xe-axis

θ′:

the derivative of θ versus the coordinate x

θ I :

the first-order torsional frequency

κ y :

shear coefficient in the y-direction

κ z :

shear coefficient in the z-direction

ξ 1, ξ 2 :

modal damping ratios

ρ :

density

τ b :

breadth taper

T h :

thickness taper

υ :

Poisson’s ratio

φ :

angular displacement with respect to the ze-axis

\(\dot\varphi\) :

velocity with respect to the ze-axis

\(\ddot\varphi\) :

acceleration with respect to the ze axis

φ′:

the derivative of φ versus the coordinate x

χ :

a symbol representing global matrices

\(\chi_k^{\rm{e}}\) :

a symbol representing element matrices

ϕ :

angular displacement with respect to the ye-axis

\(\dot\phi\) :

velocity with respect to the ye-axis

\(\ddot\phi\) :

acceleration with respect to the ye-axis

ϕ′:

derivative of ϕ versus the coordinate x

References

  1. YARDIMOGLU, B. and YILDIRIM, T. Finite element model for vibration analysis of pre-twisted Timoshenko beam. Journal of Sound and Vibration, 273, 741–754 (2004)

    Article  Google Scholar 

  2. YANG, X. D., WANG, S. W., ZHANG, W., QIN, Z. H., and YANG, T. Z. Dynamic analysis of a rotating tapered cantilever Timoshenko beam based on the power series method. Applied Mathematics and Mechanics (English Edition), 38(10), 1425–1438 (2017) https://doi.org/10.1007/s10483-017-2249-6

    Article  MathSciNet  MATH  Google Scholar 

  3. RAO, J. S. and CARNEGIE, W. Solution of the equations of motion of coupled-bending bending torsion vibrations of turbine blades by the method of Ritz-Galerkin. International Journal of Mechanical Sciences, 12, 875–882 (1970)

    Article  MATH  Google Scholar 

  4. HOUBOLT, J. C. and BROOKS, G. W. Differential equations of motion for combined flapwise bending, chordwise bending, and torsion of twisted nonuniform rotor blades. NACA Report, TN 3905, NASA Langley Research Center, Hampton (1958)

    Google Scholar 

  5. SKAR, G. and SABUNCU, M. Dynamic stability of a rotating asymmetric cross-section blade subjected to an axial periodic force. International Journal of Mechanical Sciences, 45, 1467–1482 (2003)

    Article  MATH  Google Scholar 

  6. YANG, X. D., WANG, S. W., ZHANG, W., YANG, T. Z., and LIM, C. W. Model formulation and modal analysis of a rotating elastic uniform Timoshenko beam with setting angle. European Journal of Mechanics-A/Solids, 72, 209–222 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  7. RAFIEE, M., NITZSCHE, F., and LABROSSE, M. Dynamics, vibration and control of rotating composite beams and blades: a critical review. Thin-Walled Structures, 119, 795–819 (2017)

    Article  Google Scholar 

  8. QIN, Y., LI, X., YANG, E. C., and LI, Y. H. Flapwise free vibration characteristics of a rotating composite thin-walled beam under aerodynamic force and hygrothermal environment. Composite Structures, 153, 490–503 (2016)

    Article  Google Scholar 

  9. TIAN, J. J., SU, J. P., ZHOU, K., and HUA, H. X. A modified variational method for nonlinear vibration analysis of rotating beams including Coriolis effects. Journal of Sound and Vibration, 426, 258–277 (2018)

    Article  Google Scholar 

  10. LIN, S. C. and HSIAO, K. M.4 Vibration analysis of a rotating Timoshenko beam. Journal of Sound and Vibration, 240, 303–322 (2001)

    Article  MATH  Google Scholar 

  11. YOUNG, T. H. Dynamic response of a pretwisted, tapered beam with non-constant rotating speed. Journal of Sound and Vibration, 150, 435–446 (1991)

    Article  Google Scholar 

  12. QIN, Y., WANG, L., and LI, Y. H. Coupled vibration characteristics of a rotating composite thin-walled beam subjected to aerodynamic force in hygrothermal environment. International Journal of Mechanical Sciences, 140, 260–270 (2018)

    Article  Google Scholar 

  13. MA, H., XIE, F. T., NAI, H. Q., and WEN, B. C. Vibration characteristics analysis of rotating shrouded blades with impacts. Journal of Sound and Vibration, 378, 92–108 (2016)

    Article  Google Scholar 

  14. XIE, F. T., MA, H., CUI, C., and WEN, B. C. Vibration response comparison of twisted shrouded blades using different impact models. Journal of Sound and Vibration, 397, 171–191 (2017)

    Article  Google Scholar 

  15. ŞKAR, G. and SABUNCU, M. Buckling and dynamic stability of a rotating pretwisted asymmetric cross-section blade subjected to an axial periodic force. Finite Elements in Analysis and Design, 40, 1399–1415 (2004)

    Article  Google Scholar 

  16. SABUNCU, M. and EVRAN, K. Dynamic stability of a rotating pre-twisted asymmetric cross-section Timoshenko beam subjected to an axial periodic force. International Journal of Mechanical Sciences, 48, 579–590 (2006)

    Article  MATH  Google Scholar 

  17. OZGUMUS, O. O. and KAYA, M. O. Energy expressions and free vibration analysis of a rotating Timoshenko beam featuring bending-bending-torsion coupling. Archive of Applied Mechanics, 83, 97–108 (2013)

    Article  MATH  Google Scholar 

  18. SINHA, S. K. Combined Torsional-bending-axial dynamics of a twisted rotating cantilever Timoshenko beam with contact-impact loads at the free end. Journal of Applied Mechanics, 74, 505–522 (2006)

    Article  MATH  Google Scholar 

  19. GEORGIADES, F., LATALSKI, J., and WARMINSKI, J. Equations of motion of rotating composite beam with a nonconstant rotation speed and an arbitrary preset angle. Meccanica, 49, 1833–1858 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  20. BANERJEE, S. and RAO, J. S. Coupled bending-torsion vibrations of rotating blades. Gas Turbine and Fluids Engineering Conference, American Society of Mechanical Engineers, New Orleans (1976)

    Google Scholar 

  21. BANERJEE, J. R. Development of an exact dynamic stiffness matrix for free vibration analysis of a twisted Timoshenko beam. Journal of Sound and Vibration, 270, 379–401 (2004)

    Article  MATH  Google Scholar 

  22. BANERJEE, J. R., SU, H., and JACKSON, D. R. Free vibration of rotating tapered beams using the dynamic stiffness method. Journal of Sound and Vibration, 298, 1034–1054 (2006)

    Article  Google Scholar 

  23. BANERJEE, J. R. and JACKSON, D. R. Free vibration of a rotating tapered Rayleigh beam: a dynamic stiffness method of solution. Computers and Structures, 124, 11–20 (2013)

    Article  Google Scholar 

  24. STAFFORD, R. O. and GIURGIUTIU, V. Semi-analytic methods for rotating Timoshenko beams. International Journal of Mechanical Sciences, 17, 719–727 (1975)

    Article  MATH  Google Scholar 

  25. KAYA, M. O. Free vibration analysis of a rotating Timoshenko beam by differential transform method. Aircraft Engineering and Aerospace Technology, 78, 194–203 (2006)

    Article  Google Scholar 

  26. QIN, Y. and LI, Y. H. Influences of hygrothermal environment and installation mode on vibration characteristics ofa rotating laminated composite beam. Mechanical Systems and Signal Processing, 91, 23–40 (2017)

    Article  Google Scholar 

  27. DU, H., LIM, M. K., and LIEW, K. M. A power series solution for vibration of a rotating Timoshenko beam. Journal of Sound and Vibration, 175, 505–523 (1994)

    Article  MATH  Google Scholar 

  28. FANG, J. S. and ZHOU, D. Free vibration analysis of rotating axially functionally graded tapered Timoshenko beams. International Journal of Structural Stability and Dynamics, 16, 1–9 (2015)

    MathSciNet  Google Scholar 

  29. RAO, S. S. and GUPTA, R. S. Finite element vibration analysis of rotating Timoshenko beams. Journal of Sound and Vibration, 242, 103–124 (2001)

    Article  MATH  Google Scholar 

  30. BAZOUNE, A. Effect of tapering on natural frequencies of rotating beams. Shock and Vibration, 14, 169–179 (2007)

    Article  Google Scholar 

  31. REDDY, J. N. Energy Principles and Variational Methods in Applied Mechanics, John Wiley and Sons, New York, 475–483 (2002)

    Google Scholar 

  32. SUN, Q., MA, H., ZHU, Y. P., HAN, Q. K., and WEN, B. C. Comparison of rubbing induced vibration responses using varying-thickness-twisted shell and solid-element blade models. Mechanical Systems and Signal Processing, 108, 1–20 (2018)

    Article  Google Scholar 

  33. HE, Q., XUAN, H. J., LIU, L. L., HONG, W. R., and WU, R. R. Perforation of aero-engine fan casing by a single rotating blade. Aerospace Science and Technology, 25, 234–241 (2013)

    Article  Google Scholar 

  34. HAMMOND, C. E. An application of Floquet theory to prediction of mechanical instability. Journal of the American Helicopter Society, 19, 14–23 (1974)

    Article  Google Scholar 

  35. TAN, T. H., LEE, H. P., and LENG, G. S. B. Dynamic stability of a radially rotating beam subjected to base excitation. Computer Methods in Applied Mechanics and Engineering, 146, 265–279 (1997)

    Article  MATH  Google Scholar 

  36. OZGUMUS, O. O. and KAYA, M. O. Energy expressions and free vibration analysis of a rotating double tapered Timoshenko beam featuring bending-torsion coupling. International Journal of Engineering Science, 45, 562–586 (2007)

    Article  MATH  Google Scholar 

  37. HODGES, D. H. Torsion of pretwisted beams due to axial loading. Journal of Applied Mechanics, 47, 393–397 (1980)

    Article  MATH  Google Scholar 

  38. BAZOUNE, A., KHULIEF, Y. A., and STEPHEN, N. G. Shape functions of three-dimensional Timoshenko beam element. Journal of Sound and Vibration, 259, 473–480 (2003)

    Article  Google Scholar 

  39. WANG, M. Z., WANG, W., and WU, J. K. Course of Elastic Mechanics (in Chinese), Beijing University Press, Beijing, 146–150 (2002)

    Google Scholar 

  40. WILLIAM, C. Vibrations of pre-twisted cantilever blading. Proceedings of the Institution of Mechanical Engineers, 173, 343–374 (1959)

    Article  Google Scholar 

  41. RAO, J. S. Flexural vibration of pretwisted tapered cantilever blades. Journal of Engineering for Industry, 94, 343–346 (1972)

    Article  Google Scholar 

  42. ZENG, J., CHEN, K. K., MA, H., DUAN, T. T., and WEN, B. C. Vibration response analysis of a cracked rotating compressor blade during run-up process. Mechanical Systems and Signal Processing, 118, 568–583 (2019)

    Article  Google Scholar 

  43. ANSYS Inc. ANSYS Mechanical APDL and Mechanical Applications Theory Reference, ANSYS Release 13.0, ANSYS Inc., Lincoln (2010)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, China

    Jin Zeng, Hui Ma, Kun Yu, Zhitao Xu & Bangchun Wen

  2. Key Laboratory of Vibration and Control of Aero-Propulsion System Ministry of Education, Northeastern University, Shenyang, 110819, China

    Hui Ma

Authors
  1. Jin Zeng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hui Ma
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Kun Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhitao Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Bangchun Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Hui Ma.

Additional information

Citation: ZENG, J., MA, H., YU, K., XU, Z. T., and WEN, B. C. Coupled flapwise-chordwiseaxial-torsional dynamic responses of rotating pre-twisted and inclined cantilever beams subject to the base excitation. Applied Mathematics and Mechanics (English Edition) 40(8), 1053–1082 (2019) https://doi.org/10.1007/s10483-019-2506-6

Project supported by the National Natural Science Foundation of China (No. 11772089), the Fundamental Research Funds for the Central Universities of China (Nos. N170308028 and N170306004), the Program for the Innovative Talents of Higher Learning Institutions of Liaoning of China (No. LR2017035), and the LiaoNing Revitalization Talents Program of China (No. XLYC1807008)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zeng, J., Ma, H., Yu, K. et al. Coupled flapwise-chordwise-axial-torsional dynamic responses of rotating pre-twisted and inclined cantilever beams subject to the base excitation. Appl. Math. Mech.-Engl. Ed. 40, 1053–1082 (2019). https://doi.org/10.1007/s10483-019-2506-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10483-019-2506-6

Key words

Chinese Library Classification

2010 Mathematics Subject Classification

Search

Navigation