Abstract
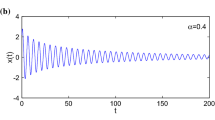
This paper investigates the stochastic P-bifurcation (SPB) of a fractionally damped oscillator subjected to additive and multiplicative Gaussian white noise. Variable transformation and the stochastic averaging technique are applied to derive the expression of probability density function (PDF) of the system response. Critical conditions of the stochastic bifurcation induced by system parameters are presented based on the change in the number of extreme points of the probability density function. Numerical results are given to show the effectiveness of the proposed approach. Stochastic P-bifurcations for additive and multiplicative noise are studied in detail according to the critical conditions.
Graphic abstract
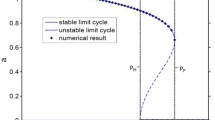
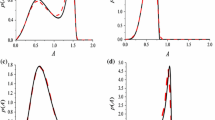
Stochastic P-bifurcation (SPB) for additive noise can be investigated by the critical conditions. SPB induced by the fractional order is described in the bifurcation plane, see Fig. a. Figure b shows that the probability density function (PDF) for (0.1, 0.005) ∈ R2 has one peak, while the PDF for (0.8, 0.005) ∈ R2 has two peaks. It implies that the change of the fractional order leads to the variation of the structure of the PDF, which indicates the occurrence of the SPB.











Similar content being viewed by others
References
Podlubny, I.: Fractional Differential Equations: an Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Elsevier, New York (1998)
Chen, Y., Petras, I, Xue, D.: Fractional order control-a tutorial. In: Proceedings of the 2009 American Control Conference, IEEE, pp. 1397–1411 (2009)
Li, C., Cai, M.: Theory and Numerical Approximations of Fractional Integrals and Derivatives. SIAM, Bangkok (2019)
Wang, Y., Li, X., Shen, Y.: Cluster oscillation and bifurcation of fractional-order Duffing system with two time scales. Acta Mech. Sin. 36, 926–932 (2020)
Rossikhin, Y.A., Shitikova, M.V.: Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl. Mech. Rev. 63, 010801 (2010)
Mei, R., Xu, Y., Kurths, J.: Transport and escape in a deformable channel driven by fractional Gaussian noise. Phys. Rev. E 100, 022114 (2019)
Diethelm, K., Ford, N.J., Freed, A.D.: A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dynam. 29, 3–22 (2002)
Li, C., Wang, Z.: The local discontinuous Galerkin finite element methods for Caputo-type partial differential equations: mathematical analysis. Appl. Numer. Math. 150, 587–606 (2020)
Spanos, P., Di Matteo, A., Pirrotta, A.: Steady-state dynamic response of various hysteretic systems endowed with fractional derivative elements. Nonlinear Dynam. 98, 3113–3124 (2019)
Huang, Z.L., Jin, X.L.: Response and stability of a SDOF strongly nonlinear stochastic system with light damping modeled by a fractional derivative. J. Sound Vib. 319, 1121–1135 (2009)
Chen, L., Zhao, T., Li, W., et al.: Bifurcation control of bounded noise excited Duffing oscillator by a weakly fractional-order PIλDλ feedback controller. Nonlinear Dynam. 83, 529–539 (2016)
Niu, J., Hou, J., Shen, Y., et al.: Dynamic analysis and vibration control of nonlinear boring bar with fractional-order model of magnetorheological fluid. Int. J. Nonlinear Mech. 121, 103459 (2020)
Fragkoulis, V.C., Kougioumtzoglou, I.A., Pantelous, A.A., et al.: Non-stationary response statistics of nonlinear oscillators with fractional derivative elements under evolutionary stochastic excitation. Nonlinear Dynam. 97, 2291–2303 (2019)
Lü, Q.F., Zhu, W.Q., Deng, M.L.: Reliability of quasi integrable and non-resonant Hamiltonian systems under fractional Gaussian noise excitation. Acta Mech. Sin. 36, 902–909 (2020)
Huang, D., Zhou, S., Litak, G.: Analytical analysis of the vibrational tristable energy harvester with a RL resonant circuit. Nonlinear Dynam. 97, 663–677 (2019)
Wang, J., Zhou, S., Zhang, Z., et al.: High-performance piezoelectric wind energy harvester with Y-shaped attachments. Energ. Convers. Manage. 181, 645–652 (2019)
Rounak, A., Gupta, S.: Stochastic P-bifurcation in a nonlinear impact oscillator with soft barrier under Ornstein–Uhlenbeck process. Nonlinear Dynam. 99, 2657–2674 (2020)
Li, W., Huang, D., Zhang, M., et al.: Bifurcation control of a generalized VDP system driven by color-noise excitation via FOPID controller. Chaos Soliton. Fract. 121, 30–38 (2019)
Chen, L., Liang, X., Zhu, W., et al.: Stochastic averaging technique for SDOF strongly nonlinear systems with delayed feedback fractional-order PD controller. Sci. China Technol. Sci. 62, 287–297 (2019)
Yue, X., Wang, Y., Han, Q., et al.: Probabilistic response and stochastic bifurcation in a turbulent swirling flow. J. Comput. Nonlin. Dyn. 14, 111005 (2019)
Fokou, I.S.M., Buckjohn, C.N.D., Siewe, M.S., et al.: Probabilistic distribution and stochastic P-bifurcation of a hybrid energy harvester under colored noise. Commun. Nonlinear Sci. 56, 177–197 (2018)
Qian, J., Chen, L.: Random vibration of SDOF vibro-impact oscillators with restitution factor related to velocity under wide-band noise excitations. Mech. Syst. Signal Pr. 147, 107082 (2021)
Liu, W., Guo, Z., Yin, X.: Stochastic averaging for SDOF strongly nonlinear system under combined harmonic and Poisson white noise excitations. Int. J. Nonlinear Mech. 126, 103574 (2020)
Zhang, Y., Jin, Y., Xu, P., et al.: Stochastic bifurcations in a nonlinear tri-stable energy harvester under colored noise. Nonlinear Dynam. 99, 879–897 (2020)
Zhang, J., Sun, Z., Yang, X., et al.: Controlling bifurcations in fractional-delay systems with colored Noise. Int. J. Bifurcat. Chaos 28, 1850137 (2018)
Li, W., Zhang, M.T., Zhao, J.F.: Stochastic bifurcations of generalized Duffing–van der Pol system with fractional derivative under colored noise. Chin. Phys. B 26, 090501 (2017)
Di Matteo, A., Spanos, P.D., Pirrotta, A.: Approximate survival probability determination of hysteretic systems with fractional derivative elements. Prob. Eng. Mech. 54, 138–146 (2018)
Sun, Y., Yang, Y.: Stochastic averaging for the piezoelectric energy harvesting system with fractional derivative element. IEEE Access 8, 59883–59890 (2020)
Yang, Y., Xu, W., Gu, X., et al.: Stochastic response of a class of self-excited systems with Caputo-type fractional derivative driven by Gaussian white noise. Chaos Soliton. Fract. 77, 190–204 (2015)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grants 12002089, 11902081 and 11872305).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Executive Editor: Jian Xu
Rights and permissions
About this article
Cite this article
Sun, YH., Yang, YG. & Xu, W. Stochastic P-bifurcations of a noisy nonlinear system with fractional derivative element. Acta Mech. Sin. 37, 507–515 (2021). https://doi.org/10.1007/s10409-020-01020-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10409-020-01020-8