1 Introduction

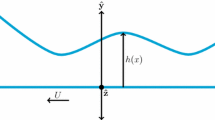
Lubrication flows are ubiquitous in both natural and technological settings. These flows involve one physical dimension that is much smaller than the others, which allows for a reduction in the dimensionality of the flow and a simplified fluid dynamics treatment (Szeri 2010). There are several industries that require the accurate modeling of lubrication-type flows at low pressures, such as vacuum pumping (Kwon and Hwang 2004; Huck et al. 2018; Naris et al. 2014) and processor chip manufacturing (Wright et al. 1995; Goodman 2008; Qin and McTeer 2007), where accurate prediction of gas motion and heat transfer is valuable in the chuck design process, or with very small spatial dimensions, such as in MEMS devices (Gupta et al. 2012; Alfeeli and Agah 2009; Parkos et al. 2013) and dry gas seals (Peng et al. 2007) that are a critical component of devices like compressors. These conditions pose two main challenges when solving a time-dependent lubrication problem. First, the Knudsen number (a measure of the deviation from local thermodynamic equilibrium) is relatively high, typically \(\textrm{Kn} \gtrsim 0.1\), where \(\textrm{Kn} = \lambda /H\), \(\lambda\) is the mean free path and H is the smallest length-scale. This means that the continuum assumption of quasi-local thermodynamic equilibrium breaks down, requiring a kinetic-theory approach based on the Boltzmann equation. Second, the computational cost of solving the Boltzmann equation using brute-force, fully kinetic numerical schemes, such as the direct simulation Monte Carlo (DSMC), is often prohibitively high, as it is proportional to both the length-scale of the geometry and the time-scale of the flow problem. For example, in a low-pressure device with a lubrication dimension of H in micrometers and lateral flow dimensions in millimeters, operating at a few pascals with a transient time-scale in seconds, the Kn value remains consistently high and varies with time and space, requiring the use of DSMC over the entire geometry. To simulate this, DSMC would involve trillions of particles and billions of time steps, limited by an integration time step of the mean time between collisions. Consequently, this gas flow would take millennia to solve with DSMC, even on the most powerful supercomputer, and new methods are clearly needed to solve this class of problems.

Several modifications have been made to classical lubrication theory to extend it to non-equilibrium flows. These include the use of slip boundary conditions based on the Navier–Stokes (NS) equations (Alexander et al. 1994; Wu and Bogy 2003), the incorporation of an effective viscosity in addition to the slip boundary conditions using NS (Sun et al. 2003), the development of new moment methods to include higher-order terms in extended NS equations (Gu et al. 2016), and the use of concurrent hybrid methods that combine conservation equations with DSMC (John et al. 2018; Patronis et al. 2013) or first-principles kinetic equations (Cercignani et al. 2007; Fukui and Kaneko 1988, 1990). These approaches have been applied to a wide range of rarefied lubrication problems, such as flows of bouncing droplets under low pressure (Chubynsky et al. 2020), the miniaturized reading head in hard-disk drives (Chen and Bogy 2010; John et al. 2018), thermal transpiration flows in Knudsen pumps (Aoki et al. 2007; Lockerby et al. 2015; Tatsios et al. 2017) and force-balanced piston gauges (Sharipov et al. 2016; Naris et al. 2018).

However, most of the studies in this area have focused on analyzing steady, quasi-2D gas flows (i.e. flows along one lateral dimension), which may not be sufficient for the design of engineering systems. In this work, we propose a new lubrication modeling approach for time-dependent, non-equilibrium, low-speed, isothermal, quasi-3D gas flows. The proposed approach is made possible by the large length- and time-scale separation present in these types of problems and uses a local descriptor of the flow response from DSMC or kinetic simulations between parallel plates.

The rest of this paper is organized as follows. The mathematical formulation of the problem and our numerical method of the solution are presented in Sect. 2. The results on benchmark configurations are discussed and the computational savings are analyzed in Sect. 3. Finally, concluding remarks and future research directions are provided in Sect. 4.

2 Multiscale method

This section presents a multiscale method for accurately simulating low-speed, time-dependent, non-equilibrium gas flows in quasi-3D geometries. The key modeling idea is to describe the gas flow by the balance of mass using a simplified expression of the local mean velocity. The direction of the local mean velocity is given by the pressure gradient, while the values for the magnitude, which depend on the local Knudsen number, can be found tabulated in literature (Sharipov and Seleznev 1998) and are stored in a look-up table for efficient use. The method therefore has a computational cost similar to a 2D computational fluid dynamics (CFD) finite-volume method, but with accuracy comparable to the DSMC method, making it useful for engineering problems that are beyond the capabilities of existing tools.

Our multiscale method is built upon four assumptions that are usually valid for lubrication flows due to the large separation in length and time scales.

  • Assumption 1: The density is constant in the direction perpendicular to the gas flow, i.e.,

    $$\begin{aligned} \frac{\partial \rho }{\partial z}=0, \end{aligned}$$
    (1a)

    where the gas is assumed to flow parallel to the xy-plane.

  • Assumption 2: The local normalized pressure gradient is small, i.e.,

    $$\begin{aligned} X_P =\left|\frac{H}{P}\frac{\partial P}{\partial s} \right|\ll 1, \end{aligned}$$
    (1b)

    where H is the lubrication dimension perpendicular to the gas flow (in the z-direction) and s is a lateral flow direction (e.g. x or y).

  • Assumption 3: The kinetic time-scale is negligible compared to the macroscopic time-scale, i.e.,

    $$\begin{aligned} X_{\tau }= \left|\frac{\tau _c}{P}\frac{\partial P}{\partial t} \right|\ll 1, \end{aligned}$$
    (1c)

    where \(\tau _c\) is the mean time between gas collisions.

  • Assumption 4: The flow is fully developed and locally one-dimensional (Sharipov 1999), i.e.,

    $$\begin{aligned} L/H \gg 1, \end{aligned}$$
    (1d)

    where L is some characteristic distance between geometric features in the xy-plane (e.g., between a gas filling hole and a flow obstacle).

In practice, we find that a ratio of \(L/H>20\) and \(X_P, X_\tau <0.1\) is typically sufficient to ensure the validity of the method. Note that other criteria for the validity of the linearized approaches have also been formulated in the literature (Titarev and Shakhov 2013; Valougeorgis et al. 2017). We choose the ones above as it allows us to untangle the scale separation arising in the geometry and fluid dynamics separately, which aids in understanding the sources of errors when using this method.

2.1 Mathematical formulation

Suppose the gas flows through the three-dimensional domain shown in Fig. 1, seen from the top view. The domain includes internal/external solid boundaries \((\partial \Omega _S)\) defined by the impermeability condition, external open boundaries \((\partial \Omega _O)\), where gas can flow in and out in the xy-plane, and internal open regions \((\Omega _O)\), where gas can flow in and out of the domain. The three-dimensional mass balance is the key equation that forms the basis of our approach

$$\begin{aligned} \frac{\partial \rho }{\partial t} +\nabla \cdot (\rho {\varvec{v}})=\rho ^{\pm }\chi , \end{aligned}$$
(2)

where \(\rho\) is the gas density, \({\varvec{v}}\) is the local flow velocity, \(\rho ^{\pm }\) is a sink/source term that accounts for the gas flowing in and out in the z-direction, and \(\chi\) is the indicator function

$$\begin{aligned} \chi = {\left\{ \begin{array}{ll} 1, &{} \text {if } {\varvec{x}} \in \Omega _O, \\ 0, &{} \text {if } {\varvec{x}} \notin \Omega _O. \end{array}\right. } \end{aligned}$$
(3)

By integrating Eq. (2) over the z-axis and accounting for the constant density in that direction (assumption 1), we find the following two-dimensional mass balance equation

$$\begin{aligned} \frac{2H}{\upsilon _0^2}\frac{\partial P}{\partial t} +\nabla \cdot {\varvec{\mathcal {M}}}={\mathcal S}\chi , \end{aligned}$$
(4)

where the pressure is given by the ideal equation of state \(P=1/2\rho \upsilon _0^2\), with \(\upsilon _0=\sqrt{2R_gT}\) being the most probable molecular speed at temperature T for a gas with specific gas constant \(R_g\). Note that the height of the points of the open regions is assumed to be equal to that of the corresponding boundaries.

In Eq. (4), \({\varvec{\mathcal {M}}}\) and \(\mathcal S\) represent the mass flow rate per unit length and the rate of change of the mass per unit area due to the movement of molecules through open regions, respectively. The mass flow rate per unit length is directly proportional to the local gradient of pressure as determined by the momentum equation, given that the gas flow is low-speed (assumption 2) and it is possible to adopt a quasi-steady approach (assumption 3). This relationship can be expressed as

$$\begin{aligned} {\varvec{\mathcal {M}}} = \int _0^H \rho {\varvec{v}} \ \textrm{dz} \approx -\frac{H^2 G}{\upsilon _0} \nabla P, \end{aligned}$$
(5)

where G is the reduced mass flow rate, which in this work is assumed to depend solely on the local Knudsen number, such that \(G \equiv G(\mathrm Kn)\). The values of G can be obtained from kinetic or molecular simulations using the appropriate molecular model and gas–surface interaction, or from experimental measurements of pressure driven flow between infinite parallel plates (assumption 4).

The rate of change of mass per unit area, due to the movement of molecules through open regions is estimated based on the assumption that the molecules are distributed according to undrifted Maxwellian distributions at a constant temperature T, with densities determined by the fixed pressure outside the domain \(P_O\), and the local pressure inside the domain P, giving

$$\begin{aligned} \mathcal{S}= H\left( \frac{\partial \rho }{\partial t}\right) _O = \frac{1}{\upsilon _0} \frac{P_O-P}{\sqrt{\pi }}. \end{aligned}$$
(6)

By substituting Eqs. (5) and (6) into Eq. (4), we obtain

$$\begin{aligned} \frac{\partial P}{\partial t} - \nabla \cdot (\Gamma \nabla P) =\frac{\upsilon _0}{2 H} \frac{P_O-P}{\sqrt{\pi }} \chi , \end{aligned}$$
(7)

where \(\Gamma = GH\upsilon _0/2\) is a space-dependent diffusion-like coefficient.

Fig. 1
figure 1

Generic computational domain \(\Omega\)

Full size image

At internal/external solid boundaries (\(\partial \Omega _S\)), the normal mass flow rate is set to zero, and the boundary condition is given by:

$$\begin{aligned} \nabla P \cdot \varvec{n} = 0, \hspace{10pt} \forall \varvec{x}\in \partial \Omega _S. \end{aligned}$$
(8)

Here, \(\varvec{n}\) is the unit vector in the xy-plane that is normal to the boundary and points outward from the simulation domain.

At the open boundaries, a known pressure \(P_B\) is imposed by specifying the mass flow rate normal to the boundary in a similar way to the mass flux in the z-direction boundaries, resulting in the mixed (Robin) boundary condition:

$$\begin{aligned} \nabla P \cdot \varvec{n}=\frac{(P_B-P)\upsilon _0}{2\Gamma \sqrt{\pi }}, \hspace{10pt} \forall \varvec{x}\in \partial \Omega _O. \end{aligned}$$
(9)

The above boundary condition is able to capture the transient behavior of the system more accurately, especially for relatively small systems, than the more straightforward specification of the pressure through a Dirichlet boundary condition, i.e., \(P=P_B, \forall \varvec{x}\in \partial \Omega _O\), as the latter assumes an instantaneous response of the gas to the external pressure at initial time steps.

2.2 Implementation

The numerical solution of Eq. (7) under the boundary conditions given by Eqs. (8) and (9) is based on the finite-volume method (Mazumder 2015), using an unstructured triangular 2D mesh for space discretization. The SALOME platform is used to design the CAD model of the system under investigation and generate the computational mesh, which includes the relevant information for the initialization, height and boundary condition zones. The developed multiscale approach is implemented in Fortran and the mesh is imported using an I-deas universal (UNV) file. Backwards (implicit) time discretization with an adaptive time step is used, leading to an unconditionally stable scheme, and the tangential fluxes are treated explicitly. Due to the implicit nature of the scheme in time, the solution of a system of linear algebraic equations is required to propagate the solution to the next time step. This system is solved using the Successive Over-Relaxation (SOR) method. Note that at each time step, the values of G and \(\Gamma\) are calculated from the local height and the pressure values of the previous time step. The visualization of the simulation results can be performed using Paraview. The implementation described above allows the simulation of systems of arbitrary geometric complexity, which may include an arbitrary number of features, such as internal boundaries and inlet/outlet holes.

3 Results and discussion

Fig. 2
figure 2

Benchmark geometrical configurations

Full size image
Fig. 3
figure 3

Reduced flow rate G in terms of Kn

Full size image

The developed multiscale approach is used to study the time- and space variation of pressure in a quasi-2D and a quasi-3D flow cases, in Sects. 3.1 and 3.2, respectively. These cases are shown in Fig. 2. Validation is performed by comparing the multiscale results with DSMC results obtained using the dsmcFoam+ code (White et al. 2018). The working gas is assumed to be a monatomic hard sphere gas. The reduced flow rate, in terms of the Knudsen number, which we use in this work, is obtained from the solution of the linearized Shakhov model equation for a hard sphere gas assuming purely diffusive boundary conditions at the solid boundaries (Titarev 2012). A dense database of the reduced flow rate in terms of the Knudsen number is constructed and the values along with reference data given in (Sharipov and Seleznev 1998) are shown in Fig. 3. The first test case involves a simple flow in a long channel, while the second test case includes the complexity of more general problems, such as having different inflow/outflow boundaries in all three dimensions and internal obstacles, but with overall case dimensions small enough for comparison with a DSMC benchmark solution.

For convenience, the following dimensionless quantities are introduced

$$\begin{aligned} x^*=\frac{x}{H}, y^*=\frac{y}{H}, L^*=\frac{L}{H}, W^*=\frac{W}{H}, R^*=\frac{R}{H}, t^*=\frac{t}{H/\upsilon _0}, \tau ^*=\frac{\tau }{H/\upsilon _0}, P^*=\frac{P}{P_0}, \end{aligned}$$
(10)

where the reference pressure \(P_0\) is defined as the lowest pressure in each case. In the rest of the section, the superscripts \((^*)\) are dropped, and all the quantities are presented in dimensionless units.

3.1 Quasi-2D test case: long channel

Fig. 4
figure 4

Quasi-2D test case: filling (left) and venting (right) scenarios. The top panels display the average pressure and the lower panels the maximum value of \(X_P\) and \(X_{\tau }\) during the simulation

Full size image

The flow geometry of the first test case is shown in Fig. 2a. It is a long channel of length L = 500 and infinite width, although a small width W = 0.5 is selected with symmetric boundary conditions in the y-direction for purposes of running the DSMC benchmark simulation. The simulation starts at time \(t=0\) with a constant initial internal pressure in the channel, one closed end (\(x = L\)) and one open end (\(x=0\)) set to a target pressure, larger/smaller than the internal pressure. The simulation will then consider the time response to the change in this initial step pressure variation in the channel. The upper, lower, and closed-end boundaries are assumed to be diffusive.

Filling and venting scenarios are both evaluated. In the filling scenario, the open end is set as an inlet at a pressure \(P = 10\), higher than the initial internal pressure (the reference pressure \(P_0\)). In the venting scenario, the initial internal pressure is at \(P=10\), and the open end is set as an outlet with a lower pressure (the reference pressure \(P_0\)).

Figure 4 shows the comparison of the average pressure inside the channel between our multiscale approach and the DSMC benchmark solution. The multiscale method is in excellent agreement with the DSMC solution, with the maximum relative difference being less than \(2\%\) for the filling case and less than \(5\%\) for the venting case. The maximum values of \(X_P\) and \(X_{\tau }\) are also shown in Fig. 4. The core assumptions of the method are briefly breached in the early time steps when large flow gradients are present. However, the values of \(X_P\) and \(X_{\tau }\) quickly fall below the 0.1 limit, and the effect on the accuracy of the simulation is minimal.

In both filling and venting cases, the Knudsen number varies between Kn = 10.9 when the pressure is lowest at \(P_0\) and Kn = 1.09 at the highest pressure \(P=10\), covering a large part of the transition regime. This regime is selected because neither the standard no-slip Navier Stokes (NS) or its modification with slip (NS slip) can be used to accurately describe the non-equilibrium transport, as shown in Fig. 4. It is apparent that the no-slip NS approach is not suitable for this flow configuration, while the slip solution remains inaccurate, as it overestimates the time to reach steady state by 37% in the filling scenario and 90% in the venting scenario.

In terms of computational speed-up, the multiscale method is \({\sim }\)100,000 times faster than the DSMC simulation for the filling process and \({\sim }\)30,000 times for the venting process. A more thorough analysis of the computational savings is presented in the next section for the quasi-3D case, which is the scope of our paper.

3.2 Quasi-3D test case: parallel circular plates

The flow geometry of the second test case is shown in Fig. 2b. It consists of two circular plates of radius R separated by a height H, with a few arbitrary features placed between the two plates, to test the limitations of our method. The system is simplified to an axisymmetric wedge, with a coordinate system centered on the axis of the wedge. In the filling scenario, the initial internal pressure of the system is taken as before as the reference pressure \(P_0\) and the open perimeter of the wedge is set as an inlet to a pressure of \(P_\mathrm{{fill}}=10\). In the venting scenario, the open perimeter is set to a lower reference pressure than the initial internal pressure \(P_\mathrm{{init}}=10\).

Two pillars of radius R/20 are located at \(\left( \pm R/(2\sqrt{3}), R/2\right)\) to create obstacles to the flow, and an inlet/outlet hole of radius R/20 is located between the two pillars at (0, R/2) with the pressure outside the hole set to the perimeter pressure. The circular plates, as well as the gas entering from the perimeter and the inlet hole, are kept at a constant temperature.

In both filling/venting scenarios, the Knudsen number varies from a value of \(\textrm{Kn}=10.9\) at the reference pressure to a value of \(\textrm{Kn}=1.09\) at the high pressure, covering a large part of the transition regime.

In the dsmcFoam+ benchmark simulation, the cell size used was about \(\Delta r\approx H\), smaller than the mean free path (\(\Delta r/\lambda \lesssim 1\)), and the time step was set to \(\Delta t=0.016\), smaller than the mean time between collisions (\(\Delta t/\tau _c\lesssim 0.015\)), to provide a sufficient number of samples per time bin and properly resolve the transient dynamics. The number of particles per cell increased from about 10 at low pressure to about 100 at high pressure.

Fig. 5
figure 5

Quasi-3D test case: Average pressure given by the multiscale method and DSMC (left) and maximum value of \(X_P\) and \(X_\tau\) (right) in terms of time for various values of R for the filling scenario. The relative error is calculated by taking the percentage difference between the average pressure values obtained using the multiscale method and DSMC at different time instances (\(\tau _{ss}\): time to reach steady state)

Full size image
Fig. 6
figure 6

Pressure distribution along \(x=0\) at various time instances for different values of R for the filling scenario

Full size image
Fig. 7
figure 7

Pressure contours at various time instances for \(R=80\), DSMC (left) and multiscale (right) simulation results for the filling scenario

Full size image

3.2.1 Filling scenario

In Fig. 5a, the average pressure in the domain \((P_\mathrm{{ave}})\) calculated using our multiscale method is compared with the prediction provided by DSMC. The two methods are in excellent agreement, with the relative error being larger than 1% only for the smaller cases (\(R=20\) and \(R=40\)) at the initial time steps. These deviations in the pressure field can be attributed to the fact that the ratio R/H is relatively small, violating the assumption of a fully developed and locally one-dimensional flow (assumption 4).

During the simulation, the values of \(X_P\) and \(X_\tau\) are monitored to ensure that the assumptions of the method are met. These quantities are shown in Fig. 5b. It is observed that for all cases, both \(X_P\) and \(X_\tau\) are initially greater than 0.1, but they decrease rapidly without affecting the accuracy of the simulation.

As shown in Fig. 6, the pressure distributions along the \(x=0\) axis at different times given by the multiscale method are generally in close agreement with the DSMC benchmark solutions. However, there are some noticeable deviations in the vicinity of the inlet hole, especially for smaller radii. These discrepancies decrease with increasing system size. As the system’s lateral size increases, so does the distance between the various flow elements. For instance, the distance between the pillars and the inlet hole only approaches the threshold value of \(L/H \sim\) 20 (assumption 4) for \(R=100\).

Figure 7 shows a side-by-side comparison of the pressure contours between the multiscale method (right part) and the DSMC method (left part) for the case with \(R=80\) at different times. The contour lines show excellent agreement between the two methods. Moreover, the multiscale method does not suffer from statistical noise which is inherent in DSMC. This is an added benefit in cases where a low noise solution is needed, since ensemble averaging of multiple DSMC realizations can dramatically increase the computational cost.

Fig. 8
figure 8

Average pressure given by the multiscale method and DSMC (left) and maximum value of \(X_P\) and \(X_\tau\) (right) in terms of time for various values of R for the venting scenario. The relative error is calculated by taking the percentage difference between the average pressure values obtained using the multiscale method and DSMC at different time instances

Full size image
Fig. 9
figure 9

Pressure distribution along \(x=0\) at various time instances for different values of R for the venting scenario

Full size image
Fig. 10
figure 10

Pressure contours at various time instances for \(R=80\), DSMC (left) and multiscale (right) simulation results for the venting scenario

Full size image

3.2.2 Venting scenario

For the venting scenario, a comparison of the average pressure between the multiscale method and DSMC is shown in Fig. 8a. The two methods are generally in good agreement, however the comparison is certainly not as good as for the filling case, with the relative difference taking values close to 6% for all values of R. The reason for this disagreement can be seen in Fig. 8b, where the maximum value of the dimensionless pressure gradient is higher than 0.1 \((X_{P,\textrm{max}}>0.1)\) for 40% of the simulation time, in contrast to the filling scenario where it quickly falls below the threshold value of 0.1 within 10% of the simulation time. The location of the maximum value is close to the outlet hole. The characteristic time ratio \(X_{\tau }\), also shown in Fig. 8b, is initially larger than 0.1, and rapidly decreases to small values.

A more detailed comparison is presented in Fig. 9 where the pressure distribution along the \(x=0\) axis at various time instances is shown. The multiscale method is generally in good agreement with DSMC. Large deviations appear in the vicinity of the outlet hole for small values of R, which decrease as R increases as before, due to the L/H ratio approaching 20. A comparison based on the pressure contours is presented for the case of \(R=80\) in Fig. 10, demonstrating the good agreement between the two methods.

Fig. 11
figure 11

Computational speed-up of the multiscale method compared to DSMC in terms of the radius R for the filling and venting scenarios. The fit indicates that the speed-up increases with \(R^3\) for filling and with \(R^2\) for venting

Full size image

3.2.3 Computational efficiency

The proposed multiscale method has the significant advantage of being computationally more efficient than the DSMC method. This is demonstrated in Fig. 11, which shows the speed-up, defined as the ratio of the computational time required by the DSMC method to the computational time required by the multiscale method, when both methods are run on 10 CPU cores. It can be observed that the multiscale simulation runs faster than DSMC by a factor that increases with \(R^3\) for the filling scenario and with \(R^2\) for the venting scenario. In the filling scenario, for the domain with radius \(R=100\), the DSMC simulation takes about 50 h, while the multiscale method is more than 1000 times faster. For the venting case in the same geometry, DSMC takes about 12 h and the multiscale method is 190 times faster. The difference in speed-up between the two cases is due to the fact that DSMC is more efficient for the venting case. In the filling scenario, a large number of DSMC particles need to be simulated for most of the simulation, whereas in the venting case the number of particles decreases rapidly. However, even for the venting case, DSMC can become extremely expensive as the problem size increases (as it may in practical applications), and this is where we expect the multiscale method to really be useful.

4 Conclusions

A multiscale method is proposed to solve low-speed, time-dependent, non-equilibrium gas flows in quasi-3D lubrication geometries. The method is developed under the assumption of large length and time scales separation leading to a quasi-steady simulation where the gas dynamic response to the pressure gradients is locally one dimensional. Geometries of arbitrary complexity can be simulated and the flow domain can contain an arbitrary number of internal boundaries and inlet/outlet holes.

Special attention is required to make sure that the assumptions of the method are valid. The geometric restriction of large lateral distance of flow elements to height ratios \((L/H>20)\) should be checked prior to the simulation. During the simulation, the values of \(X_P\) and \(X_\tau\) should be monitored to ensure the validity of the results. When all the conditions are satisfied, the proposed multiscale method is in good agreement with DSMC, with a maximum relative difference less than 1%.

The computational cost of the multiscale method applied to this problem is found to be around 2–3 orders of magnitude faster than DSMC, with the speed-up increasing at least quadratically as the problem size increases. This highlights the ability of the proposed multiscale method to handle large-scale engineering problems that would be infeasible to simulate using the DSMC method due to the high computational cost.

The method can become more flexible and handle an even wider range of configurations. Possible extensions of the method include a more robust treatment of the initial transient period where large gradients exist and the inclusion of additional physics. More general boundary conditions, such as different gas–surface scattering models, and molecular models as well as additional driving forces, such as shear and squeezing motion of the boundaries, can be incorporated using the appropriate values of the reduced flow rate.