Skip to main content

Advertisement

Springer Nature Link
Log in

Capillary contributions to the dynamics of discrete slugs in microchannels

  • Research Paper
  • Published:
Microfluidics and Nanofluidics Aims and scope Submit manuscript

Abstract

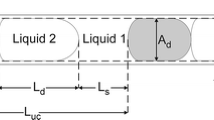
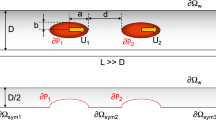
The dynamics of discrete slugs made of perfectly or partially wetting liquids is studied experimentally in microchannels with rectangular cross-sections. Two contributions to the applied pressure drop govern the observed steady motions during which the length and the speed of a slug remain constant. The first contribution is the viscous dissipation in the liquid column between the menisci of the slug and is approximated by the Hagen–Poiseuille’s law. The second contribution arises at the vicinity of the menisci and is deduced from the experimental data. Distinct regimes are observed for this contribution depending on the wetting properties of the liquid and on the capillary number Ca. In the dynamic regime, a typical visco-capillary scaling in Ca 2/3 is found for the wetting liquid whereas the contribution of the menisci in partial wetting tends towards the previous scaling as the capillary number increases. A quasi-static regime is observed in partial wetting at low driving pressures and the capillary number increases exponentially. This observation suggests the influence of friction on the motion of the contact line and leads us to discuss its effects in the dynamic regime. In particular, experimental results are compared to an empirical prediction involving the previous mechanism as well as dynamic contact angles.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  • Adzima BJ, Velankar SS (2006) Pressure drops for droplet flows in microfluidic channels. J Micromech Microeng 16(8):1504–1510

    Article  Google Scholar 

  • Ajaev V, Homsy G (2006) Modeling shapes and dynamics of confined bubbles. Annu Rev Fluid Mech 38(1):277–307

    Article  MathSciNet  Google Scholar 

  • Bico J, Quéré D (2001) Falling slugs. J Colloid Interface Sci 243:262–264

    Article  Google Scholar 

  • Bico J, Quéré D (2002) Rise of liquids and bubbles in angular capillary tubes. J Colloid Interface Sci 247:162–166

    Article  Google Scholar 

  • Blake TD (2006) The physics of moving wetting lines. J Colloid Interface Sci 299(1):1–13

    Article  Google Scholar 

  • Blake TD, Shikhmurzaev Y (2002) Dynamic wetting by liquids of different viscosity. J Colloid Interface Sci 253(1):196–202

    Article  Google Scholar 

  • Bowden N, Andreas T, Carbeck J, Whitesides G (1997) Self-assembly of mesoscale objects into ordered two-dimensional arrays. Science 276:233–235

    Article  Google Scholar 

  • Bretherton F (1961) The motion of long bubbles in tubes. J Fluid Mech 10:166–188

    Article  MATH  MathSciNet  Google Scholar 

  • Brody J, Yager P, Goldstein R, Austin R (1996) Biotechnology at low Reynolds numbers. Biophys J 71:3430–3441

    Article  Google Scholar 

  • Caço A, Dias A, Marrucho IM, Piñeiro M, Santos L, Coutinho J (2003) Thermophysical properties of perfluorocompounds. In: 15th symposium on thermophysical properties, Boulder, CO, USA

  • Concus P, Finn R (1974) On the capillary free surfaces in the absence of gravity. Acta Math 132:177–198

    Article  MATH  MathSciNet  Google Scholar 

  • Cox R (1986) The dynamics of spreading of liquids on a solid surface. J Fluid Mech 168:169–220

    Article  MATH  Google Scholar 

  • Cubaud T, Ho CM (2004) Transport of bubbles in square microchannels. Phys Fluids 16(12):4575–4585

    Article  Google Scholar 

  • Cubaud T, Ulmanella U, Ho CM (2004) Multiphase flow in microchannels with surface modifications. In: 5th international conference on multiphase flow, Yokohama, Japan

  • de Gennes P (1985) Wetting: statics and dynamics. Rev Mod Phys 57(3):827–863

    Article  Google Scholar 

  • Dong M, Chatzis I (1995) The imbibition and flow of a wetting liquid along the corners of a square capillary tube. J Colloid Interface Sci 172:278–288

    Article  Google Scholar 

  • Dreyfus R, Tabeling P, Willaime H (2003) Ordered and disordered patterns in two-phase flows in microchannels. Phys Rev Lett 90(14):144505/1–4

    Google Scholar 

  • Dussan EB (1979) On the spreading of liquids on solid surfaces: static and dynamic contact lines. Annu Rev Fluid Mech 11(1):371–400

    Article  MathSciNet  Google Scholar 

  • Eggers J (2005) Contact line motion for partially wetting fluids. Phys Rev E 72:061605

    Article  Google Scholar 

  • Fermigier M, Jenfer P (1991) An experimental investigation of the dynamic contact angle in liquid-liquid systems. J Colloid Interface Sci 146(1):226–241

    Article  Google Scholar 

  • Finn R (1986) Equilibrium capillary surfaces. Springer-Velag, New York

  • Finn R (1999) Capillary surface interfaces. Notices AMS 46(7):770–781

    MathSciNet  Google Scholar 

  • Freire M, Ferreira A, Fonseca I, Marrucho I, Coutinho J (2008) Viscosities of liquid fluorocompounds. J Chem Eng Data 53(2):538–542

    Article  Google Scholar 

  • Fuerstman MJ, Lai A, Thurlow ME, Shevkoplyas SS, Stone HA, Whitesides GM (2007) The pressure drop along rectangular microchannels containing bubbles. Lab Chip 7:1479–1489

    Article  Google Scholar 

  • Garstecki P, Gitlin I, DiLuzio W, Whitesides G, Kumacheva E, Stone HA (2004) Formation of monodisperse bubbles in a microfluidic flow-focusing device. Appl Phys Lett 85(13):2649–2651

    Article  Google Scholar 

  • Günther A, Jensen K (2006) Multiphase microfluidics: from flow characteristics to chemical and materials synthesis. Lab Chip 6:1487–1503

    Article  Google Scholar 

  • Günther A, Jhunjhunwala M, Thalmann M, Schmidt M, Jensen K (2005) Micromixing of miscible liquids in segmented gas-liquid flow. Langmuir 21(4):1547–55

    Article  Google Scholar 

  • Handique K, Burke D, Mastrangelo C, Burns M (2001) On-chip thermopneumatic pressure for discrete drop pumping. Anal Chem 73(8):1831–1838

    Article  Google Scholar 

  • Hazel A, Heil M (2002) The steady propagation of a semi-infinite bubble onto a tube of elliptical or rectangular cross-section. J Fluid Mech 470:91–114

    Article  MATH  Google Scholar 

  • He B, Patankar N, Lee J (2003) Multiple equilibrium droplet shapes and design criterion for rough hydrophobic surfaces. Langmuir 19:4999–5003

    Article  Google Scholar 

  • He M, Szuchmacher Blum A, Overney G, Overney RM (2002) Effect of interfacial liquid structuring on the coherence length in nanolubrication. Phys Rev Lett 88(15):154–302

    Article  Google Scholar 

  • Ichikawa N, Hosokawa K, Maeda R (2004) Interface motion of capillary-driven flow in rectangular microchannel. J Colloid Interface Sci 280:155–164

    Article  Google Scholar 

  • Joanny J, Robbins M (1990) Motion of a contact line on a heterogeneous surface. J Chem Phys 92(5):3206–3212

    Article  Google Scholar 

  • Jousse F, Lian G, Janes R, Melrose J (2005) Compact model for multi-phase liquid-liquid flows in micro-fluidic devices. Lab Chip 5:646–656

    Article  Google Scholar 

  • Kawahara A, Chung PY, Kawaji M (2002) Investigation of two-phase flow pattern, void fraction and pressure drop in a microchannel. Int J Mult Flow 28(9):1411–1435

    Article  MATH  Google Scholar 

  • Lee C, Homma H, Izumi K (2002) Surface properties of polydimethylsiloxane/poly(trifluoropropylmethylvinylsiloxane) blend for outdoor insulator. Trans Inst El Eng Jap 122-A(1):112–117

    Google Scholar 

  • Lee J, Park C, Whitesides G (2003) Solvent compatibility of poly(dimethylsiloxane)-based microfluidic devices. Anal Chem 75:6544–54

    Article  Google Scholar 

  • Lenormand R, Zarcone C, Sarr A (1983) Mechanisms of the displacement of one fluid by another in a network of capillary ducts. J Fluid Mech 135:337–353

    Article  Google Scholar 

  • Li W, Nie Z, Zhang H, Paquet C, Seo M, Garstecki P, Kumacheva E (2007) Screening of the effect of surface energy of microchannels on microfluidic emulsification. Langmuir 23:8010–8014

    Article  Google Scholar 

  • Marsh J, Garoff S, Dussan V E (1993) Dynamic contact angles and hydrodynamics near a moving contact line. Phys Rev Lett 70(18):2778–2781

    Article  Google Scholar 

  • Morra M, Occhiello E, Marola R, Garbasi F, Humphrey P, Johnson D (1990) On the aging of oxygen plasma-treated polydimethylsiloxane. J Colloid Interface Sci 137(1):11–24

    Article  Google Scholar 

  • Mumley TE, Radke CJ, Williams MC (1986) Kinetics of liquid/liquid capillary rise. I—experimental observations. J Colloid Interface Sci 109(2):413–425

    Article  Google Scholar 

  • Ody C, Baroud C, de Langre E (2007) Transport of wetting liquid plugs in bifurcating microfluidic channels. J Colloid Interface Sci 308(1):231–238

    Article  Google Scholar 

  • Quake S, Scherer A (2000) From micro- to nano-fabrication with soft materials. Science 290(5496):1536–1540

    Article  Google Scholar 

  • Quéré D (1991) Sur la vitesse minimale d’étalement en mouillage partiel. CR Acad Sc Paris, Série II 313:313–318

    Google Scholar 

  • Raphael E, de Gennes P (1989) Dynamics of wetting with nonideal surfaces. The single defect problem. J Chem Phys 90(12):7577–7584

    Article  Google Scholar 

  • Ratulowski J, Chang HC (1989) Transport of gas bubbles in capillaries. Phys Fluids A 1(10):1642–1655

    Article  MathSciNet  Google Scholar 

  • Song H, Tice J, Ismagilov R (2003) A microfluidic system for controlling reaction networks in time. Angew Chem Int Ed 42(7):768–772

    Article  Google Scholar 

  • Squires T, Quake S (2005) Microfluidics: fluid physics at the nanoliter scale. Rev Mod Phys 77:977–1026

    Article  Google Scholar 

  • Stark J, Manga M (2000) The motion of long bubbles in a network of tubes. Transp Porous Media 40:201–218

    Article  Google Scholar 

  • Stokes J, Higgins M, Kushnick A, Bhattacharya S (1990) Harmonic generation as a probe of dissipation at a moving contact line. Phys Rev Lett 65(15):1885–1888

    Article  Google Scholar 

  • Stone H, Stroock A, Ajdari A (2004) Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu Rev Fluid Mech 36:381–411

    Article  Google Scholar 

  • Thulasidas T, Abraham M, Cerro R (1995) Bubble-train flow in capillaries of circular and square cross section. Chem Eng Sci 50(2):183–199

    Article  Google Scholar 

  • van Steijn V, Kreutzer MT, Kleijn CR (2008) Velocity fluctuations of segmented flow in microchannels. Chem Eng J 135(1):159–165

    Google Scholar 

  • Wong H, Radke C, Morris S (1995) The motion of long bubbles in polygonal capillaries. Part II. Drag, fluid pressure and fluid flow. J Fluid Mech 292:95–110

    Article  Google Scholar 

  • Xia Y, Whitesides G (1998) Soft lithography. Angew Chem Int Ed 37(5):550–575

    Article  Google Scholar 

  • Zheng Y, Anderson J, Suresh V, Grotberg J (2005) Effect of gravity on liquid plug transport through an airway bifurcation model. J Biomech Eng 127:798–806

    Article  Google Scholar 

  • Zhou MY, Sheng P (1990) Dynamics of immiscible-fluid displacement in a capillary tube. Phys Rev Lett 64(8):882–885

    Article  Google Scholar 

Download references

Acknowledgements

I am grateful to José Bico who suggested the method of calculation of the capillary contributions and to Pascal Hémon for his help with the second camera. I also would like to thank Charles Baroud, Emmanuel de Langre, Matthias Heil and Élise Lorenceau.

Author information

Authors and Affiliations

  1. Laboratoire d’Hydrodynamique, École Polytechnique – CNRS, 91128, Palaiseau Cedex, France

    Cédric P. Ody

  2. Université of Rennes 1, Rennes Cedex, France

    Cédric P. Ody

Authors
  1. Cédric P. Ody
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Cédric P. Ody.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ody, C.P. Capillary contributions to the dynamics of discrete slugs in microchannels. Microfluid Nanofluid 9, 397–410 (2010). https://doi.org/10.1007/s10404-009-0557-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10404-009-0557-8

Keywords