A dynamic model for viscoelastic materials with prescribed growing cracks

Abstract

In this paper, we prove the existence of solutions for a class of viscoelastic dynamic systems on time-dependent cracked domains, with possibly degenerate viscosity coefficients. Under stronger regularity assumptions, we also show a uniqueness result. Finally, we exhibit an example where the energy-dissipation balance is not satisfied, showing there is an additional dissipation due to the crack growth.

1 Introduction

In the theory of dynamic fracture, the deformation of an elastic material evolves according to the elastodynamics system, while the evolution of the crack follows Griffith’s dynamic criterion, see [13]. This principle, originally formulated in [11] for the quasi-static setting, states that there is an exact balance between the energy released during the evolution and the energy used to increase the crack, which is postulated to be proportional to the area increment of the crack itself.

For an antiplane displacement, the elastodynamics system leads to the following wave equation

$$\begin{aligned} {\ddot{u}}(t,x)-\Delta u(t,x)=f(t,x)\quad t\in [0,T],\ x\in \Omega {\setminus }\Gamma _{t}, \end{aligned}$$

(1.1)

with some prescribed boundary and initial conditions. Here, $\Omega \subset {\mathbb {R}}^d$ is an open bounded set with Lipschitz boundary, which represents the cross section of the material, the closed set $\Gamma _t\subset {{\overline{\Omega }}}$ models the crack at time t in the reference configuration, $u(t):\Omega {\setminus }\Gamma _{t}\rightarrow {\mathbb {R}}$ is the antiplane displacement, and f is a forcing term. In this case, Griffith’s dynamic criterion reads

$$\begin{aligned} {\mathcal {E}}(t)+{\mathcal {H}}^{d-1}(\Gamma _t{\setminus }\Gamma _0)=\mathcal E(0)+\text {work of external forces}, \end{aligned}$$

where ${\mathcal {E}}(t)$ is the total energy at time t, given by the sum of kinetic and elastic energy, and ${\mathcal {H}}^{d-1}$ is the $(d-1)$-dimensional Hausdorff measure.

From the mathematical point of view, the first step to study the evolution of the fracture is to solve the wave equation (1.1) when the evolution of the crack is assigned, see, for example, [2, 3, 7, 14, 18] (we refer also to [6, 10, 16] for the case of a one-dimensional model). When we want to take into account the viscoelastic properties of the material, Kelvin–Voigt’s model is the most common one. If no crack is present, this leads to the damped wave equation

$$\begin{aligned} {\ddot{u}}(t,x)-\Delta u(t,x)-\Delta {\dot{u}}(t,x)=f(t,x)\quad (t,x)\in (0,T)\times \Omega . \end{aligned}$$

(1.2)

As it is well known, the solutions to (1.2) satisfy the energy-dissipation balance

$$\begin{aligned} {\mathcal {E}}(t)+\int _0^t\int _\Omega |\nabla {\dot{u}}|^2\,\mathrm {d}x\,\mathrm {d}s={\mathcal {E}}(0)+\text {work of external forces}. \end{aligned}$$

(1.3)

When we consider a crack in a viscoelastic material, Griffith’s dynamic criterion becomes

$$\begin{aligned} {\mathcal {E}}(t)+\mathcal H^{d-1}(\Gamma _t{\setminus }\Gamma _0)+\int _0^t\int _{\Omega \setminus \Gamma _s}|\nabla {\dot{u}}|^2\,\mathrm {d}x\,\mathrm {d}s={\mathcal {E}}(0)+\text {work of external forces}. \end{aligned}$$

(1.4)

For a prescribed crack evolution, this model was already considered by Dal Maso and Larsen [3] in the antiplane case and more in general by Tasso [18] for the vector-valued case. As proved in the quoted papers, the solutions to (1.2) on a domain with a prescribed time-dependent crack, i.e., with $\Omega$ replaced by $\Omega {\setminus }\Gamma _t$, satisfy (1.3) for every time. This equality implies that (1.4) cannot be satisfied unless $\Gamma _t=\Gamma _0$ for every t. This phenomenon was already well known in mechanics as the viscoelastic paradox, see, for instance, [17, Chapter 7].

To overcome this problem, we modify Kelvin–Voigt’s model by considering a possibly degenerate viscosity term depending on t and x. More precisely, we study the following equation

$$\begin{aligned} {\ddot{u}}(t,x)-\Delta u(t,x)-\mathrm{div}(\Psi ^2(t,x)\nabla {\dot{u}}(t,x))=f(t,x)\quad t\in [0,T],\, x\in \Omega {\setminus }\Gamma _t. \end{aligned}$$

(1.5)

On the function $\Psi :(0,T)\times \Omega \rightarrow {\mathbb {R}}$, we only require some regularity assumptions (see (2.7)); a particularly interesting case is when $\Psi$ assumes the value zero on some points of $\Omega$, which means that the material has no longer viscoelastic properties in such a zone.

The main result of this paper is Theorem 3.1, in which we show the existence of a weak solution to (1.5). This is done in the more general case of linear elasticity, that is, when the displacement is vector-valued and the elastic energy depends only on the symmetric part of its gradient. To this aim, we first perform a time discretization in the same spirit of [3], and then we pass to the limit as the time step goes to zero by relying on energy estimates; as a byproduct, we obtain the energy-dissipation inequality (4.4). By using the change of variables method implemented in [7, 14], we also prove a uniqueness result, but only in dimension $d=2$ and when $\Psi (t)$ vanishes on a neighborhood of the tip of $\Gamma _t$.

We complete our work by providing an example in $d=2$ of a weak solution to (1.5) for which the fracture can grow while balancing the energy. More precisely, when the cracks $\Gamma _t$ move with constant speed along the $x_1$-axis and $\Psi (t)$ is zero in a neighborhood of the crack tip, we construct a function u which solves (1.5) and satisfies

$$\begin{aligned} {\mathcal {E}}(t)+\int _0^t\int _{\Omega \setminus \Gamma _s}|\Psi \nabla {\dot{u}}|^2\,\mathrm {d}x\,\mathrm {d}s+{\mathcal {H}}^1(\Gamma _t{\setminus }\Gamma _0)={\mathcal {E}}(0)+\text {work of external forces}. \end{aligned}$$

(1.6)

Notice that this is the natural extension of Griffith’s dynamic criterion (1.4) to this setting.

The paper is organized as follows. In Sect. 2, we fix the notation adopted throughout the paper, we list the standard assumptions on the family of cracks $\{\Gamma _t\}_{t\in [0,T]}$ and on the function $\Psi$, and we specify the notion of weak solution to problem (1.5). In Sect. 3, we state our main existence result (Theorem 3.1) and we implement the time discretization method. We conclude the proof of Theorem 3.1 in Sect. 4, where we show the validity of the initial conditions and the energy-dissipation inequality (4.4). Section 5 deals with uniqueness: under stronger regularity assumptions on the cracks sets, in Theorem 5.5 we prove the uniqueness of a weak solution, but only when the space dimension is $d=2$. To this aim, we assume also that the function $\Psi$ is zero in a neighborhood of the crack tip. We conclude with Sect. 6, where in dimension $d=2$, we show an example of a moving crack that satisfies Griffith’s dynamic energy-dissipation balance (1.6).

2 Notation and preliminary results

The space of $m\times d$ matrices with real entries is denoted by ${\mathbb {R}}^{m\times d}$; in case $m=d$, the subspace of symmetric matrices is denoted by ${\mathbb {R}}^{d\times d}_\mathrm{{sym}}$. Given two vectors $v_1,v_2\in {\mathbb {R}}^d$, their Euclidean scalar product is denoted by $v_1\cdot v_2\in {\mathbb {R}}$ and their tensor product is denoted by $v_1\otimes v_2\in {\mathbb {R}}^{d\times d}$; we use $v_1\odot v_2\in {\mathbb {R}}^{d\times d}_\mathrm{{sym}}$ to denote the symmetric part of $v_1\otimes v_2$, namely $v_1\odot v_2:=\frac{1}{2}(v_1\otimes v_2+v_2\otimes v_1)$. Given $A\in {\mathbb {R}}^{m\times d}$, we use $A^T$ to denote its transpose; we use $A_1\cdot A_2\in {\mathbb {R}}$ to denote the Euclidean scalar product of two matrices $A_1,A_2\in {\mathbb {R}}^{d\times d}$.

The partial derivatives with respect to the variable $x_i$ are denoted by $\partial _i$. Given a function $f:{\mathbb {R}}^d\rightarrow {\mathbb {R}}^m$, we denote its Jacobian matrix by $\nabla f$, whose components are $(\nabla f)_{ij}:=\partial _j f_i$, $i=1,\dots ,m$, $j=1,\dots ,d$. For a tensor field $F:{\mathbb {R}}^d\rightarrow {\mathbb {R}}^{m\times d}$, by $\mathrm{div}F$, we mean the divergence of F with respect to rows, namely $(\mathrm{div}F)_i:=\sum _{j=1}^d\partial _jF_{ij}$, for $i=1,\dots ,m$.

The d-dimensional Lebesgue measure is denoted by ${\mathcal {L}}^d$ and the $(d-1)$-dimensional Hausdorff measure by $\mathcal H^{d-1}$. We adopted standard notations for Lebesgue and Sobolev spaces on open subsets of ${\mathbb {R}}^d$; given an open set $\Omega \subseteq {\mathbb {R}}^d$, we use $||\cdot ||_\infty$ to denote the norm of $L^\infty (\Omega ;{\mathbb {R}}^m)$. The boundary values of a Sobolev function are always intended in the sense of traces. Given an open bounded set $\Omega$ with Lipschitz boundary, we denote by $\nu$ the outer unit normal vector to $\partial \Omega$, which is defined ${\mathcal {H}}^{d-1}$-a.e. on the boundary.

Given a Banach space X, its norm is denoted by $\Vert \cdot \Vert _X$; if X is an Hilbert space, we use $(\cdot ,\cdot )_X$ to denote its scalar product. The dual space of X is denoted by $X'$, and we use $\langle \cdot , \cdot \rangle _{X'}$ to denote the duality product between $X'$ and X. Given two Banach spaces $X_1$ and $X_2$, the space of linear and continuous maps from $X_1$ to $X_2$ is denoted by ${\mathscr {L}}(X_1;X_2)$; given $\mathbb A\in {\mathscr {L}}(X_1;X_2)$ and $u\in X_1$, we write ${\mathbb {A}} u\in X_2$ to denote the image of u under ${\mathbb {A}}$.

Given an open interval $(a,b)\subseteq {\mathbb {R}}$, $L^p(a,b;X)$ is the space of $L^p$ functions from (a, b) to X. Given $u\in L^p(a,b;X)$, we denote by ${\dot{u}}\in {\mathcal {D}}'(a,b;X)$ its distributional derivative. The set of continuous functions from [a, b] to X is denoted by $C^0([a,b];X)$. Given a reflexive Banach space X, $C_w^0([a,b];X)$ is the set of weakly continuous functions from [a, b] to X, namely, it is the collection of maps $u:[a,b]\rightarrow X$ such that $t\mapsto \langle x',u(t)\rangle _{X'}$ is continuous from [a, b] to $\mathbb {R}$ for every $x'\in X'$.

Let T be a positive real number and let $\Omega \subset {\mathbb {R}}^d$ be an open bounded set with Lipschitz boundary. Let $\partial _D\Omega$ be a (possibly empty) Borel subset of $\partial \Omega$ and let $\partial _N\Omega$ be its complement. We assume the following hypotheses on the geometry of the cracks:

• (E1) $\Gamma \subset {{\overline{\Omega }}}$ is a closed set with ${\mathcal {L}}^d(\Gamma )=0$ and $\mathcal H^{d-1}(\Gamma \cap \partial \Omega )=0$;

• (E2) for every $x\in \Gamma$, there exists an open neighborhood U of x in ${\mathbb {R}}^d$ such that $(U\cap \Omega ){\setminus }\Gamma$ is the union of two disjoint open sets $U^+$ and $U^-$ with Lipschitz boundary;

• (E3) $\{\Gamma _t\}_{t\in [0,T]}$ is a family of closed subsets of $\Gamma$ satisfying $\Gamma _s\subset \Gamma _t$ for $0\le s\le t\le T$.

Thanks to (E1)–(E3), the space $L^2(\Omega {\setminus }\Gamma _t;{\mathbb {R}}^m)$ coincides with $L^2(\Omega ;{\mathbb {R}}^m)$ for every $t\in [0,T]$ and $m\in {\mathbb {N}}$. In particular, we can extend a function $u\in L^2(\Omega {\setminus }\Gamma _t;{\mathbb {R}}^m)$ to a function in $L^2(\Omega ;{\mathbb {R}}^m)$ by setting $u=0$ on $\Gamma _t$. Moreover, the trace of $u\in H^1(\Omega {\setminus }\Gamma )$ is well defined on $\partial \Omega$. Indeed, we may find a finite number of open sets with Lipschitz boundary $U_j\subset \Omega {\setminus }\Gamma$, $j=1,\dots m$, such that $\partial \Omega {\setminus }(\Gamma \cap \partial \Omega )\subset \cup _{j=1}^m\partial U_j$. Since ${\mathcal {H}}^{d-1}(\Gamma \cap \partial \Omega )=0$, there exists a constant $C>0$, depending only on $\Omega$ and $\Gamma$, such that

$$\begin{aligned} ||u ||_{L^2(\partial \Omega )}\le C||u ||_{H^1(\Omega {\setminus }\Gamma )}\quad \text {for every }u\in H^1(\Omega {\setminus }\Gamma ;{\mathbb {R}}^d). \end{aligned}$$

(2.1)

Similarly, we can find a finite number of open sets $U_j\subset \Omega {\setminus }\Gamma$, $j=1,\dots m$, with Lipschitz boundary, such that $\Omega {\setminus }\Gamma =\cup _{j=1}^m U_j$. By using second Korn’s inequality in each $U_j$ (see, e.g., [15, Theorem 2.4]) and taking the sum over j, we can find a constant $C_K$, depending only on $\Omega$ and $\Gamma$, such that

$$\begin{aligned} ||\nabla u ||_{L^2(\Omega ;{\mathbb {R}}^{d\times d})}^2\le C_K\left( ||u ||_{L^2(\Omega ;{\mathbb {R}}^d)}^2+||Eu ||_{L^2(\Omega ;{\mathbb {R}}^{d\times d}_\mathrm{{sym}})}^2\right) \end{aligned}$$

(2.2)

for every $u\in H^1(\Omega {\setminus }\Gamma ;{\mathbb {R}}^d),$ where $Eu$ is the symmetric part of $\nabla u$, i.e., $Eu:=\frac{1}{2}( \nabla u+ \nabla u^T)$.

For every $t\in [0,T]$, we define

$$\begin{aligned} V_t:=\{u\in L^2(\Omega {\setminus }\Gamma _t;{\mathbb {R}}^d):Eu\in L^2(\Omega {\setminus }\Gamma _t;{\mathbb {R}}^{d\times d}_\mathrm{{sym}})\}. \end{aligned}$$

Notice that in the definition of $V_t$, we are considering only the distributional gradient of u in $\Omega {\setminus }\Gamma _t$ and not the one in $\Omega$. The set $V_t$ is a Hilbert space with respect to the following norm:

$$\begin{aligned} ||u ||_{V_t}:=(||u ||_{H}^2+||Eu ||_{H}^2)^{\frac{1}{2}}\quad \text {for every }u\in V_t. \end{aligned}$$

To simplify our exposition, we set $H:=L^2(\Omega ;{\mathbb {R}}^m)$ and $H_N:=L^2(\partial _N\Omega ;{\mathbb {R}}^m)$; for every $m\in {\mathbb {N}}$, we always identify the dual of H by H itself and $L^2(0,T;L^2(\Omega ;{\mathbb {R}}^m))$ by $L^2((0,T)\times \Omega ;{\mathbb {R}}^m)$.

Thanks to (2.2), the space $V_t$ coincides with the usual Sobolev space $H^1(\Omega {\setminus }\Gamma _t;{\mathbb {R}}^d)$. Therefore, by (2.1), it makes sense to consider for every $t\in [0,T]$ the set

$$\begin{aligned} V_t^D:=\{u\in V_t\,:u=0\text { on }\partial _D\Omega \}, \end{aligned}$$

which is a Hilbert space with respect to $||\cdot ||_{V_t}$. Moreover, by combining (2.2) with (2.1), we derive also the existence of a constant $C_{tr}>0$ such that

$$\begin{aligned} ||u ||_{H_N}\le C_{tr}||u ||_{V_T}\quad \text {for every }u\in V_T. \end{aligned}$$

(2.3)

Let ${\mathbb {C}},{\mathbb {B}}:\Omega \rightarrow {\mathscr {L}}({\mathbb {R}}^{d\times d}_\mathrm{{sym}};{\mathbb {R}}^{d\times d}_\mathrm{{sym}})$ be two fourth-order tensors satisfying

$$\begin{aligned}&{\mathbb {C}}_{ijhk},{\mathbb {B}}_{ijhk}\in L^\infty (\Omega )\quad \text {for every } i,j,h,k=1,\dots ,d, \end{aligned}$$

(2.4)

$$\begin{aligned}&\mathbb {C}(x)\eta _1\cdot \eta _2=\eta _1\cdot \mathbb {C}(x)\eta _2\quad \text {for a.e. }x\in \Omega \text { and for every }\eta _1,\eta _2\in \mathbb {R}^d_{\mathrm {sym}}, \nonumber \\&\mathbb {B}(x)\eta _1\cdot \eta _2=\eta _1\cdot \mathbb {B}(x)\eta _2\quad \text {for a.e. }x\in \Omega \text { and for every }\eta _1,\eta _2\in \mathbb {R}^d_{\mathrm {sym}}, \end{aligned}$$

(2.5)

$$\begin{aligned}&{\mathbb {C}}(x)\eta \cdot \eta \ge \lambda _1|\eta |^2,\quad \mathbb B(x)\eta \cdot \eta \ge \lambda _2|\eta |^2\quad \text {for a.e. } x\in \Omega \text { and for every } \eta \in {\mathbb {R}}_\mathrm{{sym}}^{d\times d}, \end{aligned}$$

(2.6)

for two positive constants $\lambda _1,\lambda _2$ independent of x. Consider a function $\Psi :(0,T)\times \Omega \rightarrow {\mathbb {R}}$ satisfying

$$\begin{aligned} \Psi \in L^\infty ((0,T)\times \Omega ),\quad \nabla \Psi \in L^\infty ((0,T)\times \Omega ;{\mathbb {R}}^d). \end{aligned}$$

(2.7)

Given $f\in L^2(0,T;H)$, $w\in H^2(0,T;H)\cap H^1(0,T;V_0)$, $g\in H^1(0,T;H_N)$, $u^0\in V_0$ with $u^0-w(0)\in V_0^D$, and $u^1\in H$, we want to find a solution to the viscoelastic dynamic system

$$\begin{aligned} {\ddot{u}}(t)-\mathrm{div}({\mathbb {C}}Eu(t))-\mathrm{div}(\Psi ^2(t){\mathbb {B}} E{\dot{u}}(t))=f(t)\quad \text {in } \Omega {\setminus }\Gamma _t, t\in (0,T), \end{aligned}$$

(2.8)

satisfying the following boundary and initial conditions

$$\begin{aligned}&u(t)=w(t)&\qquad \qquad \qquad \qquad \qquad \qquad \text {on } \partial _D\Omega , t\in (0,T),&\end{aligned}$$

(2.9)

$$\begin{aligned}&({\mathbb {C}}Eu(t)+\Psi ^2(t){\mathbb {B}} E{\dot{u}}(t))\nu =g(t)&\qquad \qquad \qquad \quad \text {on } \partial _N\Omega , t\in (0,T),&\end{aligned}$$

(2.10)

$$\begin{aligned}&({\mathbb {C}}Eu(t)+\Psi ^2(t){\mathbb {B}} E{\dot{u}}(t))\nu =0&\qquad \qquad \qquad \quad \text {on } \Gamma _t, \quad ~ t\in (0,T),&\end{aligned}$$

(2.11)

$$\begin{aligned}&u(0)=u^0,\;\quad {\dot{u}}(0)=u^1. \end{aligned}$$

(2.12)

As usual, the Neumann boundary conditions are only formal, and their meaning will be specified in Definition 2.4.

Throughout the paper, we always assume that the family $\{\Gamma _t\}_{t\in [0,T]}$ satisfies (E1)–(E3), as well as ${\mathbb {C}}$, ${\mathbb {B}}$, $\Psi$, f, w, g, $u^0$, and $u^1$ the previous hypotheses. Let us define the following functional spaces:

$$\begin{aligned}&{\mathcal {V}}:=\{\varphi \in L^2(0,T;V_T):{\dot{\varphi }}\in L^2(0,T;H),\,\varphi (t)\in V_t\text { for a.e. } t\in (0,T)\},\\&{\mathcal {V}}^D:=\{\varphi \in {\mathcal {V}}:\varphi (t)\in V_t^D\text { for a.e. } t\in (0,T)\},\\&{\mathcal {W}}:=\{u\in {\mathcal {V}}:\Psi {\dot{u}}\in L^2(0,T;V_T),\,\Psi (t){\dot{u}}(t)\in V_t\text { for a.e. } t\in (0,T) \}. \end{aligned}$$

Remark 2.1

In the classical viscoelastic case, namely when $\Psi$ is identically equal to 1, the solution u to system (2.8) has derivative ${\dot{u}}(t)\in V_t$ for a.e. $t\in (0,T)$ with $E{\dot{u}}\in L^2(0,T;H)$. For a generic $\Psi$, we expect to have $\Psi E{\dot{u}}\in L^2(0,T;H)$. Therefore, ${\mathcal {W}}$ is the natural setting when looking for a solution to (2.8). Indeed, from a distributional point of view, we have

$$\begin{aligned} \Psi (t)E{\dot{u}}(t)=E(\Psi (t) {\dot{u}}(t))-\nabla \Psi (t)\odot {\dot{u}}(t)\quad \text {in }{\mathcal {D}}'(\Omega {\setminus }\Gamma _t;{\mathbb {R}}^{d\times d}_\mathrm{{sym}})\text { for a.e. }t\in (0,T), \end{aligned}$$

and $E(\Psi \dot{u}),\nabla \Psi \odot \dot{u}\in L^2(0,T;H)$ if $u\in {\mathcal {W}}$, thanks to (2.7).

Remark 2.2

The set ${\mathcal {W}}$ coincides with the space of functions $u\in H^1(0,T;H)$ such that $u(t)\in V_t$ and $\Psi (t){\dot{u}}(t)\in V_t$ for a.e. $t\in (0,T)$, and satisfying

$$\begin{aligned} \int _0^T ||u(t) ||^2_{V_t}+||\Psi (t){\dot{u}}(t) ||_{V_t}^2 \,\mathrm {d}t<\infty . \end{aligned}$$

(2.13)

This is a consequence of the strong measurability of the maps $t\mapsto u(t)$ and $t\mapsto \Psi (t){\dot{u}}(t)$ from (0, T) into $V_T$, which gives that (2.13) is well defined and $u,\Psi \dot{u}\in L^2(0,T;V_T)$. To prove the strong measurability of these two maps, it is enough to observe that $V_T$ is a separable Hilbert space and that the maps $t\mapsto {\dot{u}}(t)$ and $t\mapsto \Psi (t){\dot{u}}(t)$ from (0, T) into $V_T$ are weakly measurable. Indeed, for every $\varphi \in C^\infty _c(\Omega {\setminus }\Gamma _T)$, the maps

$$\begin{aligned}&t\mapsto \int _{\Omega {\setminus }\Gamma _T}Eu(t,x) \varphi (x)\,\mathrm {d}x=-\int _{\Omega {\setminus }\Gamma _T} u(t,x)\odot \nabla \varphi (x)\,\mathrm {d}x,\\&t\mapsto \int _{\Omega {\setminus }\Gamma _T}E(\Psi (t,x)\dot{u}(t,x))\varphi (x)\,\mathrm {d}x=-\int _{\Omega {\setminus }\Gamma _T}\Psi (t,x)\dot{u}(t,x)\odot \nabla \varphi (x)\,\mathrm {d}x \end{aligned}$$

are measurable from (0, T) into ${\mathbb {R}}$, and $C^\infty _c(\Omega {\setminus }\Gamma _T)$ is dense in $L^2(\Omega )$.

Lemma 2.3

The spaces ${\mathcal {V}}$ and ${\mathcal {W}}$ are Hilbert spaces with respect to the following norms:

$$\begin{aligned}&||\varphi ||_{\mathcal V}:=(||\varphi ||^2_{L^2(0,T;V_T)}+||\dot{\varphi } ||^2_{L^2(0,T;H)})^{\frac{1}{2}}\quad \text {for every }\varphi \in {\mathcal {V}},\\&||u ||^2_{{\mathcal {W}}}:=(||u ||_{{\mathcal {V}}}+||\Psi \dot{u} ||^2_{L^2(0,T;V_T)})^{\frac{1}{2}}\quad \text {for every }u\in \mathcal W. \end{aligned}$$

Moreover, ${\mathcal {V}}^D$ is a closed subspace of ${\mathcal {V}}$.

Proof

It is clear that $||\cdot ||_{{\mathcal {V}}}$ and $||\cdot ||_{{\mathcal {W}}}$ are norms on ${\mathcal {V}}$ and $\mathcal W$ induced by scalar products. We just have to check the completeness of such spaces with respect to these norms.

Let $\{\varphi _k\}_k\subset {\mathcal {V}}$ be a Cauchy sequence. Then, $\{\varphi _k\}_k$ and $\{{\dot{\varphi }}_k\}_k$ are Cauchy sequences, respectively, in $L^2(0,T;V_T)$ and $L^2(0,T;H)$, which are complete Hilbert spaces. Thus, there exists $\varphi \in L^2(0,T;V_T)$ with ${\dot{\varphi }}\in L^2(0,T;H)$ such that $\varphi _k\rightarrow \varphi$ in $L^2(0,T;V_T)$ and ${\dot{\varphi }}_k\rightarrow {\dot{\varphi }}$ in $L^2(0,T;H)$. In particular, there exists a subsequence $\{\varphi _{k_j}\}_j$ such that $\varphi _{k_j}(t)\rightarrow \varphi (t)$ in $V_T$ for a.e. $t\in (0,T)$. Since $\varphi _{k_j}(t)\in V_t$ for a.e. $t\in (0,T)$, we deduce that $\varphi (t)\in V_t$ for a.e. $t\in (0,T)$. Hence, $\varphi \in \mathcal V$ and $\varphi _k\rightarrow \varphi$ in ${\mathcal {V}}$. With a similar argument, we can prove that ${\mathcal {V}}^D\subset {\mathcal {V}}$ is a closed subspace.

Let us now consider a Cauchy sequence $\{u_k\}_k\subset {\mathcal {W}}$. We have that $\{u_k\}_k$ and $\{\Psi \dot{u}_k\}_k$ are Cauchy sequences, respectively, in ${\mathcal {V}}$ and $L^2(0,T;V_T)$, which are complete Hilbert spaces. Thus, there exist two functions $u\in {\mathcal {V}}$ and $z\in L^2(0,T;V_T)$ such that $u_k\rightarrow u$ in ${\mathcal {V}}$ and $\Psi \dot{u}_k\rightarrow z$ in $L^2(0,T;V_T)$. Since $\dot{u}_k\rightarrow \dot{u}$ in $L^2(0,T;H)$ and $\Psi \in L^\infty ((0,T)\times \Omega )$, we also have that $\Psi \dot{u}_k\rightarrow \Psi \dot{u}$ in $L^2(0,T;H)$, which gives that $z=\Psi \dot{u}$. Finally, let us prove that $\Psi (t){\dot{u}}(t)\in V_t$ for a.e. $t\in (0,T)$. By the fact that $\Psi \dot{u}_k\rightarrow \Psi \dot{u}$ in $L^2(0,T;V_T)$, there exists a subsequence $\{\Psi \dot{u}_{k_j}\}_j$ such that $\Psi (t)\dot{u}_{k_j}(t)\rightarrow \Psi (t){\dot{u}}(t)$ in $V_T$ for a.e. $t\in (0,T)$. Since $\Psi (t)\dot{u}_{k_j}(t)\in V_t$ for a.e. $t\in (0,T)$, we deduce that $\Psi (t){\dot{u}}(t)\in V_t$ for a.e. $t\in (0,T)$. Hence, $u\in {\mathcal {W}}$ and $u_k\rightarrow u$ in ${\mathcal {W}}$. $\square$

We are now in position to define a weak solution to (2.8)–(2.11).

Definition 2.4

(Weak solution) We say that $u\in {\mathcal {W}}$ is a weak solution to system (2.8) with boundary conditions (2.9)–(2.11) if $u-w\in \mathcal V^D$ and

$$\begin{aligned} \begin{aligned}&-\int _0^T({\dot{u}}(t),{\dot{\varphi }}(t))_H \,\mathrm {d}t+\int _0^T({\mathbb {C}}Eu(t),E\varphi (t))_{H} \,\mathrm {d}t+\int _0^T({\mathbb {B}}E(\Psi (t){\dot{u}}(t)),\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t\\&\quad -\int _0^T({\mathbb {B}}\nabla \Psi (t)\odot {\dot{u}}(t),\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t =\int _0^T(f(t),\varphi (t))_H \,\mathrm {d}t+\int _0^T(g(t),\varphi (t))_{H_N} \,\mathrm {d}t \end{aligned} \end{aligned}$$

(2.14)

for every $\varphi \in {\mathcal {V}}^D$ such that $\varphi (0)=\varphi (T)=0$.

Notice that the Neumann boundary conditions (2.10) and (2.11) can be obtained from (2.14), by using integration by parts in space, only when u(t) and $\Gamma _t$ are sufficiently regular.

Remark 2.5

If $\dot{u}$ is regular enough (for example, $\dot{u}\in L^2(0,T;V_T)$ with ${\dot{u}}(t)\in V_t$ for a.e. $t\in (0,T)$), then we have $\Psi E\dot{u}=E(\Psi \dot{u})-\nabla \Psi \odot \dot{u}$. Therefore, (2.14) is coherent with the strong formulation (2.8). In particular, for a function $u\in {\mathcal {W}}$, we can define

$$\begin{aligned} \Psi E\dot{u}:=E(\Psi \dot{u})-\nabla \Psi \odot \dot{u}\in L^2(0,T;H), \end{aligned}$$

(2.15)

so that Eq. (2.14) can be rephrased as

$$\begin{aligned} \begin{aligned}&-\int _0^T({\dot{u}}(t),{\dot{\varphi }}(t))_H \,\mathrm {d}t+\int _0^T({\mathbb {C}}Eu(t),E\varphi (t))_{H} \,\mathrm {d}t +\int _0^T({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t\\&\quad =\int _0^T(f(t),\varphi (t))_H \,\mathrm {d}t+\int _0^T(g(t),\varphi (t))_{H_N} \,\mathrm {d}t \end{aligned} \end{aligned}$$

for every $\varphi \in {\mathcal {V}}^D$ such that $\varphi (0)=\varphi (T)=0$.

Definition 2.6

(Initial conditions) We say that $u\in {\mathcal {W}}$ satisfies the initial conditions (2.12) if

$$\begin{aligned} \lim _{h\rightarrow 0^+}\frac{1}{h}\int _0^h(||u(t)-u^0 ||_{V_t}^2+||{\dot{u}}(t)-u^1 ||_H^2) \,\mathrm {d}t=0. \end{aligned}$$

(2.16)

3 Existence

We now state our main existence result, whose proof will be given at the end of Sect. 4.

Theorem 3.1

There exists a weak solution $u\in {\mathcal {W}}$ to (2.8)–(2.11) satisfying the initial conditions $u(0)=u^0$ and $\dot{u}(0)=u^1$ in the sense of (2.16). Moreover $u\in C_w([0,T];V_T)$, $\dot{u}\in C_w([0,T];H)\cap H^1(0,T;(V_0^D)')$, and

$$\begin{aligned} \lim _{t\rightarrow 0^+}u(t)= u^0\hbox { in}\ V_T,\quad \lim _{t\rightarrow 0^+}{\dot{u}}(t)=u^1\hbox { in}\ H. \end{aligned}$$

To prove the existence of a weak solution to (2.8)–(2.11), we use a time discretization scheme in the same spirit of [3]. Let us fix $n\in {\mathbb {N}}$ and set

$$\begin{aligned} \tau _n:=\frac{T}{n},\quad u_n^0:=u^0,\quad u_n^{-1}:=u^0-\tau _nu^1. \end{aligned}$$

We define

$$\begin{aligned}&V_n^k:=V_{k\tau _n}^D,\quad g_n^k:=g(k\tau _n),\quad w_n^k:=w(k\tau _n)\quad \text {for }k=0,\dots ,n,\\&f_n^k:=\frac{1}{\tau _n}\int _{(k-1)\tau _n}^{k\tau _n} f(s)\,\mathrm {d}s,\quad \Psi _n^k:=\frac{1}{\tau _n}\int _{(k-1)\tau _n}^{k\tau _n}\Psi (s)\,\mathrm {d}s,\quad \delta g_n^k:=\frac{g_n^k-g_n^{k-1}}{\tau _n}\quad \text {for }k=1,\dots ,n,\\&\delta w_n^0:=\dot{w}(0),\quad \delta w_n^k:=\frac{w_n^k- w_n^{k-1}}{\tau _n},\quad \delta ^2 w_n^k:=\frac{\delta w_n^k-\delta w_n^{k-1}}{\tau _n}\quad \text {for }k=1,\dots ,n. \end{aligned}$$

For every $k=1,\dots ,n$, let $u_n^k\in V_T$, with $u_n^k-w_n^k\in V_n^k$, be the solution to

$$\begin{aligned} (\delta ^2u_n^k,v)_H+({\mathbb {C}}Eu_n^k,Ev)_{H}+({\mathbb {B}}\Psi _n^k E\delta u_n^k,\Psi _n^k Ev)_{H}=(f_n^k,v)_H+(g_n^k,v)_{H_N} \end{aligned}$$

(3.1)

for every $v\in V_n^k,$ where

$$\begin{aligned}&\delta u_n^k:=\frac{u_n^k- u_n^{k-1}}{\tau _n}\quad \text {for }k=0,\dots ,n,\quad \delta ^2u_n^k:=\frac{\delta u_n^k-\delta u_n^{k-1}}{\tau _n}\quad \text {for }k=1,\dots ,n. \end{aligned}$$

The existence of a unique solution $u_n^k$ to (3.1) is an easy application of Lax–Milgram’s theorem.

Remark 3.2

Since $\delta u_n^k\in V_{(k-1)\tau _n}$, then $\Psi _n^kE\delta u_n^k=E(\Psi _n^ku_n^k)-\nabla \Psi _n^k\odot u_n^k$, so that the discrete equation (3.1) is coherent with the weak formulation given in (2.14).

In the next lemma, we show a uniform estimate for the family $\{u_n^k\}_{k=1}^n$ with respect to $n\in {\mathbb {N}}$ that will be used later to pass to the limit in the discrete equation (3.1).

Lemma 3.3

There exists a constant $C>0$, independent of $n\in {\mathbb {N}}$, such that

$$\begin{aligned} \max _{i=1,..,n}\Vert \delta u_n^i\Vert _H+\max _{i=1,..,n}||Eu_n^i ||_H+\sum _{i=1}^n \tau _n ||\Psi _n^i E\delta u_n^i ||_H^2\le C. \end{aligned}$$

(3.2)

Proof

We fix $n\in {\mathbb {N}}$. To simplify the notation, we set

$$\begin{aligned} a(u,v):=({\mathbb {C}}Eu,Ev)_{H},\quad b_n^k(u,v):=(\mathbb B\Psi _n^k Eu,\Psi _n^k Ev)_{H}\quad \hbox { for every}\ u,v\in V_T. \end{aligned}$$

By taking as test function $v=\tau _n(\delta u_n^k-\delta w_n^k)\in V_n^k$ in (3.1), for $k=1,\dots ,n$, we obtain

$$\begin{aligned}&\Vert \delta u_n^k\Vert ^2_H-(\delta u_n^{k-1},\delta u_n^{k})_H+a(u_n^k,u_n^k)-a(u_n^k,u_n^{k-1})+\tau _n b_n^k(\delta u_n^k,\delta u_n^k)=\tau _n L_n^k, \end{aligned}$$

where

$$\begin{aligned} L_n^k:=(f_n^k,\delta u_n^k-\delta w_n^k)_H+(g_n^k,\delta u_n^k-\delta w_n^k)_{H_N}+(\delta ^2 u_n^{k},\delta w_n^{k})_H+a(u_n^k,\delta w_n^k)+b_n^k(\delta u_n^k,\delta w_n^k). \end{aligned}$$

Thanks to the following identities

$$\begin{aligned}&||\delta u_n^k ||_H^2-(\delta u_n^{k-1},\delta u_n^k)_H=\frac{1}{2}||\delta u_n^k ||_H^2-\frac{1}{2}||\delta u_n^{k-1} ||_H^2+\frac{\tau _n^2}{2}||\delta ^2 u_n^k ||_H^2,\\&a(u_n^k,u_n^k)-a(u_n^k,u_n^{k-1})=\frac{1}{2}a(u_n^k,u_n^k)-\frac{1}{2}a(u_n^{k-1},u_n^{k-1})+\frac{\tau _n^2}{2}a(\delta u_n^k,\delta u_n^k), \end{aligned}$$

and by omitting the terms with $\tau _n^2$, which are non-negative, we derive

$$\begin{aligned} \frac{1}{2}\Vert \delta u_n^k\Vert ^2_H-\frac{1}{2}\Vert \delta u_n^{k-1}\Vert ^2_H+\frac{1}{2}a(u_n^k,u_n^k)-\frac{1}{2}a(u_n^{k-1},u_n^{k-1})+\tau _n b_n^k(\delta u_n^{k},\delta u_n^{k})\le \tau _n L_n^k. \end{aligned}$$

We fix $i\in \{1,\dots ,n\}$ and sum over $k=1,\dots , i$ to obtain the following discrete energy inequality

$$\begin{aligned} \frac{1}{2}\Vert \delta u_n^i\Vert ^2_H+\frac{1}{2}a(u_n^i,u_n^i)+\sum _{k=1}^i\tau _n b_n^k(\delta u_n^{k},\delta u_n^{k})\le {\mathcal {E}}_0+\sum _{k=1}^i\tau _n L_n^k, \end{aligned}$$

(3.3)

where ${\mathcal {E}}_0:=\frac{1}{2}||u^1 ||_H^2+\frac{1}{2}(\mathbb CEu^0,Eu^0)_{H}$. Let us now estimate the right-hand side in (3.3) from above. By (2.3) and (2.4), we have

$$\begin{aligned}&\left| \sum _{k=1}^i \tau _n(f_n^k,\delta u_n^k-\delta w_n^k)_H\right| \le \Vert f\Vert ^2_{L^2(0,T;H)}+\frac{1}{2}\Vert {\dot{w}}\Vert ^2_{L^2(0,T;H)}+\frac{1}{2}\sum _{k=1}^i \tau _n\Vert \delta u_n^k\Vert ^2_H, \end{aligned}$$

(3.4)

$$\begin{aligned}&\left| \sum _{k=1}^i \tau _n a(u_n^k,\delta w_n^k)\right| \le \frac{\Vert {\mathbb {C}} \Vert _\infty }{2}\Vert \dot{ w}\Vert ^2_{L^2(0,T;V_0)}+\frac{\Vert {\mathbb {C}} \Vert _\infty }{2}\sum _{k=1}^i \tau _n\Vert Eu_n^k\Vert ^2_H, \end{aligned}$$

(3.5)

$$\begin{aligned}&\left| \sum _{k=1}^i \tau _n(g_n^k,\delta w_n^k)_{H_N}\right| \le \frac{1}{2}\Vert g\Vert ^2_{L^2(0,T;H_N)}+\frac{C_{tr}^2}{2}\Vert {\dot{w}}\Vert ^2_{L^2(0,T;V_0)}. \end{aligned}$$

(3.6)

For the other term involving $g_n^k$, we perform the following discrete integration by parts

$$\begin{aligned} \sum _{k=1}^i \tau _n (g_n^k, \delta u_n^k)_{H_N}&=(g_n^i,u_n^i)_{H_N}-(g(0),u^0)_{H_N}-\sum _{k=1}^{i}\tau _n (\delta g_n^{k}, u_n^{k-1})_{H_N}. \end{aligned}$$

(3.7)

Hence, for every $\epsilon \in (0,1)$, by using (2.3) and Young’s inequality, we get

$$\begin{aligned} \begin{aligned} \left| \sum _{k=1}^i \tau _n (g_n^k, \delta u_n^k)_{H_N}\right|&\le \frac{\epsilon }{2}\Vert u_n^i\Vert ^2_{H_N}+\frac{1}{2\epsilon }\Vert g\Vert ^2_{L^{\infty }(0,T;H_N)}+||g(0) ||_{H_N}||u^0 ||_{H_N}\\&\quad +\sum _{k=1}^i \tau _n \Vert \delta g_n^k\Vert _{H_N} \Vert u_n^{k-1}\Vert ^2_{H_N}\\&\le C_\epsilon +\frac{\epsilon C_{tr}^2}{2}\Vert u_n^i\Vert ^2_{V_T}+\frac{C_{tr}^2}{2}\sum _{k=1}^{i} \tau _n \Vert u_n^{k}\Vert ^2_{V_T}, \end{aligned} \end{aligned}$$

(3.8)

where $C_\epsilon$ is a positive constant depending on $\epsilon$. Thanks to Jensen’s inequality, we can write

$$\begin{aligned} \Vert u_n^l\Vert ^2_{V_T}\le \Vert Eu_n^l\Vert ^2_H+\left( ||u_0 ||_H+\sum _{j=1}^l\tau _n||\delta u_n^j ||_H\right) ^2\le \Vert Eu_n^l\Vert ^2_H+ 2||u^0 ||_H^2+2T\sum _{j=1}^l\tau _n||\delta u_n^j ||_H^2, \end{aligned}$$

so that (3.8) can be further estimated as

$$\begin{aligned} \begin{aligned} \left| \sum _{k=1}^i \tau _n (g_n^k, \delta u_n^k)_{H_N}\right|&\le C_\epsilon +\frac{\epsilon C_{tr}^2}{2}\left( \Vert Eu_n^i\Vert ^2_H+ 2||u^0 ||_H^2+2T\sum _{j=1}^i\tau _n||\delta u_n^j ||_H^2\right) \\&\quad +\frac{C_{tr}^2}{2}\sum _{k=1}^{i} \tau _n \left( \Vert Eu_n^k\Vert ^2_H+ 2||u^0 ||_H^2+2T\sum _{j=1}^k\tau _n||\delta u_n^j ||_H^2\right) \\&\le {\tilde{C}}_\epsilon +\frac{\epsilon C_{tr}^2}{2}\Vert Eu_n^i\Vert ^2_H+\tilde{C}\sum _{k=1}^{i} \tau _n \left( ||\delta u_n^k ||_H^2+\Vert Eu_n^k\Vert ^2_H\right) , \end{aligned} \end{aligned}$$

(3.9)

for some positive constants $\tilde{C}_\epsilon$ and $\tilde{C}$, with $\tilde{C}_\epsilon$ depending on $\epsilon$. Similarly to (3.7), we can say

$$\begin{aligned} \sum _{k=1}^i \tau _n (\delta ^2 u_n^k, \delta w_n^k)_{H} =(\delta u_n^i,\delta w_n^i)_{H}-(\delta u_n^0,\delta w_n^0)_{H}-\sum _{k=1}^{i}\tau _n (\delta u_n^{k-1},\delta ^2 w_n^{k})_{H}, \end{aligned}$$

(3.10)

from which we deduce that for every $\epsilon >0$

$$\begin{aligned} \left| \sum _{k=1}^i \tau _n (\delta ^2 u_n^k, \delta w_n^k)_{H}\right|&\le \Vert \delta u_n^i\Vert _H\Vert \delta w_n^i\Vert _H+\Vert u^1\Vert _H\Vert \dot{w}(0)\Vert _H+\sum _{k=1}^i \tau _n\Vert \delta u_n^{k-1}\Vert _H\Vert \delta ^2 w_n^k\Vert _H\nonumber \\&\le \frac{1}{2\epsilon }\Vert \delta w_n^i\Vert ^2_H+\frac{\epsilon }{2}\Vert \delta u_n^i\Vert ^2_H+\Vert u^1\Vert _H\Vert \dot{w}(0)\Vert _H+\frac{1}{2}\sum _{k=1}^i \tau _n\Vert \delta u_n^{k-1}\Vert _H^2\nonumber \\&\quad +\frac{1}{2}\sum _{k=1}^i \tau _n\Vert \delta ^2 w_n^k\Vert _H^2 \le {\bar{C}}_\epsilon +\frac{\epsilon }{2}\Vert \delta u_n^i\Vert ^2_H+\frac{1}{2}\sum _{k=1}^i \tau _n\Vert \delta u_n^{k}\Vert ^2_H, \end{aligned}$$

(3.11)

where ${\bar{C}}_\epsilon$ is a positive constant depending on $\epsilon$. We estimate from above the last term in the right-hand side of (3.3) in the following way

$$\begin{aligned} \begin{aligned} \sum _{k=1}^i \tau _n b_n^k(\delta u_n^k,\delta w_n^k)&\le \sum _{k=1}^i \tau _n(b_n^k(\delta u_n^k,\delta u_n^k))^{\frac{1}{2}}(b_n^k(\delta w_n^k,\delta w_n^k))^{\frac{1}{2}} \\&\le \frac{1}{2}\sum _{k=1}^i \tau _n b_n^k(\delta u_n^k,\delta u_n^k)+\frac{1}{2}||\mathbb B ||_\infty ||\Psi ||_\infty ^2||\dot{w} ||_{L^2(0,T;V_0)}^2. \end{aligned} \end{aligned}$$

(3.12)

By considering (3.3)–(3.12) and using (2.6), we obtain

$$\begin{aligned}&\left( \frac{1-\epsilon }{2}\right) \Vert \delta u_n^i\Vert ^2_H+\frac{\lambda _1-\epsilon C_{tr}^2}{2}||Eu_n^i ||_H^2+\frac{1}{2}\sum _{k=1}^i\tau _n b^k_n(\delta u_n^k,\delta u_n^k)\nonumber \\&\quad \le {\hat{C}}_\epsilon +{\hat{C}}\sum _{k=1}^i\tau _n\left( \Vert \delta u_n^k\Vert ^2_H+ \Vert Eu_n^k\Vert ^2_H\right) \end{aligned}$$

for two positive constants ${\hat{C}}_\epsilon$ and ${\hat{C}}$, with ${\hat{C}}_\epsilon$ depending on $\epsilon$. We choose $\epsilon <\frac{1}{2}\min \left\{ 1,\frac{\lambda _1}{C_{tr}^2}\right\}$ to derive the following estimate

$$\begin{aligned} \frac{1}{4}\Vert \delta u_n^i\Vert ^2_H+\frac{1}{4}||Eu_n^i ||_H^2+\frac{1}{2}\sum _{k=1}^i \tau _n b^k_n(\delta u_n^k,\delta u_n^k) \le C_1+C_2\sum _{k=1}^i\tau _n\left( \Vert \delta u_n^k\Vert ^2_H+ \Vert Eu_n^k\Vert ^2_H\right) , \end{aligned}$$

(3.13)

where $C_1$ and $C_2$ are two positive constants depending only on $u^0$, $u^1$, f, g, and w. Thanks to a discrete version of Gronwall’s lemma (see, e.g., [1, Lemma 3.2.4]), we deduce the existence of a constant $C_3>0$, independent of i and n, such that

$$\begin{aligned} \Vert \delta u_n^i\Vert _H+||Eu_n^i ||_H\le C_3 \quad \text {for every } i=1,\dots ,n \text { and for every } n\in {\mathbb {N}}. \end{aligned}$$

By combining this last estimate with (3.13) and (2.6), we finally get (3.2) and we conclude. $\square$

We now want to pass to the limit into the discrete equation (3.1) to obtain a weak solution to (2.8)–(2.11). We start by defining the following approximating sequences of our limit solution

Notice that $u_n\in H^1(0,T;H)$ with $\dot{u}_n(t)=\delta u_n^k=\tilde{u}^+_n(t)$ for $t\in ((k-1)\tau _n,k\tau _n)$ and $k=1,\dots ,n$. Let us approximate $\Psi$ and w by

Lemma 3.4

There exists a function $u\in {\mathcal {W}}$, with $u-w\in {\mathcal {V}}^D$, such that, up to a not relabeled subsequence

(3.14)

(3.15)

Proof

Thanks to Lemma 3.3, the sequences $\{u_n\}_n\subset H^1(0,T;H)\cap L^\infty (0,T;V_T)$, $\{u_n^\pm \}_n\subset L^\infty (0,T;V_T)$, and $\{{\tilde{u}}_n^\pm \}_n\subset L^\infty (0,T;H)$ are uniformly bounded. By Banach–Alaoglu’s theorem, there exist $u\in H^1(0,T;H)$ and $v\in L^2(0,T;V_T)$ such that, up to a not relabeled subsequence

Since there exists a constant $C>0$ such that

$$\begin{aligned} \Vert u_n-u^+_n\Vert _{L^\infty (0,T;H)}\le C \tau _n\xrightarrow [n\rightarrow \infty ]{}0, \end{aligned}$$

we can conclude that $u=v$. Moreover, given that $u^-_n(t)=u^+_n(t-\tau _n)$ for $t\in (\tau _n,T)$, $\tilde{u}^+_n(t)={\dot{u}}_n(t)$ for a.e. $t\in (0,T)$, and $\tilde{u}^-_n(t)={\tilde{u}}^+_n(t-\tau _n)$ for $t\in (\tau _n,T)$, we deduce

By (3.2), we derive that the sequences $\{E(\Psi ^+_n\tilde{u}^+_n)\}_n\subset L^2(0,T;H)$ and $\{\nabla \Psi ^+_n\odot \tilde{u}^+_n\}_n\subset L^2(0,T;H)$ are uniformly bounded. Indeed, there exists a constant $C>0$ independent of n such that

$$\begin{aligned} \Vert \nabla \Psi ^+_n\odot \tilde{u}^+_n\Vert ^2_{L^2(0,T;H)}&=\sum _{k=1}^n\int _{(k-1)\tau _n}^{k\tau _n}\Vert \nabla \Psi ^k_n\odot \delta u^k_n\Vert ^2_H \,\mathrm {d}t \le \Vert \nabla \Psi \Vert ^2_\infty \sum _{k=1}^n \tau _n \Vert \delta u^k_n\Vert ^2_{H}\le C,\\ \Vert E(\Psi ^+_n\tilde{u}^+_n)\Vert ^2_{L^2(0,T;H)}&=\sum _{k=1}^n\int _{(k-1)\tau _n}^{k\tau _n}\Vert E(\Psi ^k_n\delta u^k_n)\Vert ^2_H \,\mathrm {d}t =\sum _{k=1}^n\tau _n \Vert \Psi ^k_n E\delta u^k_n+\nabla \Psi ^k_n\odot \delta u^k_n\Vert ^2_H\\&\le 2\sum _{k=1}^n\tau _n\Vert \Psi ^k_n E\delta u^k_n\Vert ^2_H+ 2\sum _{k=1}^n\tau _n\Vert \nabla \Psi ^k_n\odot \delta u^k_n\Vert ^2_H\le C. \end{aligned}$$

Therefore, there exist $w_1,w_2\in L^2(0,T;H)$ such that, up to a further not relabeled subsequence

We want to identify the limit functions $w_1$ and $w_2$. Consider $\varphi \in L^2(0,T;H)$, then

$$\begin{aligned} \int _0^T(\nabla \Psi ^+_n\odot \tilde{u}^+_n,\varphi )_{H} \,\mathrm {d}t= & {} \frac{1}{2}\int _0^T(\tilde{u}^+_n,\varphi \nabla \Psi ^+_n)_{H} \,\mathrm {d}t+\frac{1}{2}\int _0^T(\tilde{u}^+_n,\varphi ^T\nabla \Psi ^+_n)_{H} \,\mathrm {d}t\\= & {} \int _0^T(\tilde{u}^+_n,\varphi ^\mathrm{{sym}}\nabla \Psi ^+_n)_{H} \,\mathrm {d}t, \end{aligned}$$

where $\varphi ^\mathrm{{sym}}:=\frac{\varphi +\varphi ^T}{2}$. Since and $\varphi ^\mathrm{{sym}}\nabla \Psi ^+_n \xrightarrow [n\rightarrow \infty ]{L^2(0,T;H)}\varphi ^\mathrm{{sym}}\nabla \Psi$ by dominated convergence theorem, we obtain

$$\begin{aligned} \int _0^T(\nabla \Psi ^+_n\odot \tilde{u}^+_n,\varphi )_{H} \,\mathrm {d}t\xrightarrow [n\rightarrow \infty ]{}\int _0^T({\dot{u}},\varphi ^\mathrm{{sym}}\nabla \Psi )_{H} \,\mathrm {d}t=\int _0^T(\nabla \Psi \odot {\dot{u}},\varphi )_{H} \,\mathrm {d}t, \end{aligned}$$

and so $w_1=\nabla \Psi \odot {\dot{u}}$. Moreover, for $\phi \in L^2(0,T;H)$, we have

$$\begin{aligned} \int _0^T(\Psi ^+_n\tilde{u}^+_n,\phi )_{H} \,\mathrm {d}t=\int _0^T(\tilde{u}^+_n,\phi \Psi ^+_n)_{H} \,\mathrm {d}t\xrightarrow [n\rightarrow \infty ]{}\int _0^T({\dot{u}},\Psi \phi )_{H} \,\mathrm {d}t=\int _0^T(\Psi {\dot{u}},\phi )_{H} \,\mathrm {d}t, \end{aligned}$$

thanks to and $\Psi ^+_n\phi \xrightarrow [n\rightarrow \infty ]{L^2(0,T;H)}\Psi \phi$, again implied by dominated convergence theorem. Therefore, , from which $E(\Psi ^+_n\tilde{u}^+_n)\xrightarrow [n\rightarrow \infty ]{{\mathcal {D}}'(0,T;H)}E(\Psi {\dot{u}})$, that gives $w_2=E(\Psi {\dot{u}})$. In particular, we have $\Psi \dot{u}\in L^2(0,T;V_T)$. By arguing in a similar way, we also obtain

Let us check that $u\in {\mathcal {W}}$. To this aim, let us consider the following set

$$\begin{aligned} F:=\{v\in L^2(0,T;V_T): v(t)\in V_t\text { for a.e. } t\in (0,T)\}\subset L^2(0,T;V_T). \end{aligned}$$

We have that F is a (strong) closed convex subset of $L^2(0,T;V_T)$, and so by Hahn–Banach’s theorem, the set F is weakly closed. Notice that $\{u^-_n\}_n,\{\Psi ^-_n\tilde{u}^-_n\}_n\subset F$, indeed

$$\begin{aligned}&u^-_n(t)=u^{k-1}_n\in V_{(k-1)\tau _n}\subset V_t\quad \text {for } t\in [(k-1)\tau _n,k\tau _n), k=1,\dots ,n,\\&\Psi _n^-(t){\tilde{u}}^-_n(t)=\Psi _n^{k-1}\delta u^{k-1}_n\in V_{(k-1)\tau _n}\subseteq V_t\quad \text {for } t\in [(k-1)\tau _n,k\tau _n), k=1,\dots ,n. \end{aligned}$$

Since and , we conclude that $u,\Psi \dot{u}\in F$. Finally, to show that $u-w\in {\mathcal {V}}^D$, we observe

$$\begin{aligned} u_n^-(t)-w_n^-(t)=u^{k-1}_n-w^{k-1}_n\in V_n^{k-1}\subseteq V_t^D\quad \text { for } t\in [(k-1)\tau _n,k\tau _n), k=1,\dots ,n. \end{aligned}$$

Therefore, $\{u_n^-w_n^-\}_n\subset \{v\in L^2(0,T;V_T): v(t)\in V_t^D\hbox { for a.e.}\ t\in (0,T)\}$, which is a (strong) closed convex subset of $L^2(0,T;V_T)$, and so it is weakly closed. Since and $w_n^-\xrightarrow [n\rightarrow \infty ]{L^2(0,T;V_0)}w$, we get that $u(t)-w(t)\in V_t^D$ for a.e. $t\in (0,T)$, which implies $u-w\in {\mathcal {V}}^D$. $\square$

We now use Lemma 3.4 to pass to the limit in the discrete equation (3.1).

Lemma 3.5

The limit function $u\in {\mathcal {W}}$ of Lemma 3.4 is a weak solution to (2.8)–(2.11).

Proof

We only need to prove that $u\in {\mathcal {W}}$ satisfies (2.14). We fix $n\in {\mathbb {N}}$, $\varphi \in C_c^1(0,T;V_T)$ such that $\varphi (t)\in V_t^D$ for every $t\in (0,T)$, and we consider

$$\begin{aligned}&\varphi _n^k:=\varphi (k\tau _n)\quad \text {for } k=0,\dots ,n,\quad \delta \varphi _n^k:=\frac{\varphi _n^k-\varphi _n^{k-1}}{\tau _n}\quad \text {for }k=1,\dots ,n, \end{aligned}$$

and the approximating sequences

$$\begin{aligned}&\varphi ^+_n(t):=\varphi _n^k,&\tilde{\varphi }^+_n(t):=\delta \varphi _n^k&t\in ((k-1)\tau _n,k\tau _n],\, k=1,\dots ,n. \end{aligned}$$

If we use $\tau _n\varphi _n^k\in V_n^k$ as test function in (3.1), after summing over $k=1,\ldots ,n$, we get

$$\begin{aligned} \begin{aligned}&\sum _{k=1}^n\tau _n(\delta ^2u_n^k,\varphi ^k_n)_H+\sum _{k=1}^n\tau _n(\mathbb CEu_n^k,E\varphi ^k_n)_{H}+\sum _{k=1}^n\tau _n(\mathbb B\Psi _n^kE\delta u_n^k,\Psi _n^k E\varphi ^k_n)_{H}\\&\quad =\sum _{k=1}^n\tau _n(f_n^k,\varphi ^k_n)_H+\sum _{k=1}^n\tau _n(g_n^k,\varphi ^k_n)_{H_N}. \end{aligned} \end{aligned}$$

(3.16)

By these identities

$$\begin{aligned} \sum _{k=1}^n \tau _n(\delta ^2 u^k_n,\varphi ^k_n)_H&= -\sum _{k=1}^n\tau _n(\delta u^{k-1}_n,\delta \varphi ^k_n)_H=-\int _0^T(\tilde{u}^-_n(t),\tilde{\varphi }^+_n(t))_H \,\mathrm {d}t, \end{aligned}$$

from (3.16), we deduce

$$\begin{aligned} \begin{aligned}&-\int _0^T(\tilde{u}^-_n,\tilde{\varphi }^+_n)_H \,\mathrm {d}t+\int _0^T({\mathbb {C}}Eu^+_n,E\varphi ^+_n)_{H} \,\mathrm {d}t-\int _0^T ({\mathbb {B}}\nabla \Psi ^+_n\odot \tilde{u}^+_n,E\varphi ^+_n)_{H} \,\mathrm {d}t\\&\quad +\int _0^T ({\mathbb {B}}E(\Psi ^+_n\tilde{u}^+_n),E\varphi ^+_n)_{H} \,\mathrm {d}t=\int _0^T(f^+_n,\varphi ^+_n)_H \,\mathrm {d}t+\int _0^T(g^+_n,\varphi ^+_n)_{H_N} \,\mathrm {d}t. \end{aligned} \end{aligned}$$

(3.17)

Thanks to (3.14), (3.15), and the following convergences

$$\begin{aligned} \varphi ^+_n\xrightarrow [n\rightarrow \infty ]{L^2(0,T;V_T)}\varphi , \quad \tilde{\varphi }^+_n\xrightarrow [n\rightarrow \infty ]{L^2(0,T;H)}\dot{\varphi },\quad f^+_n\xrightarrow [n\rightarrow \infty ]{L^2(0,T;H)}f ,\quad g^+_n\xrightarrow [n\rightarrow \infty ]{L^2(0,T;H_N)}g, \end{aligned}$$

we can pass to the limit in (3.17), and we get that the function $u\in {\mathcal {W}}$ satisfies (2.14) for every $\varphi \in C_c^1(0,T;V_T)$ such that $\varphi (t)\in V_t^D$ for every $t\in (0,T)$. Finally, by using a density argument (see [8, Remark 2.9]), we conclude that $u\in {\mathcal {W}}$ is a weak solution to (2.8)–(2.11). $\square$

4 Initial conditions and energy-dissipation inequality

To complete our existence result, it remains to prove that the function $u\in {\mathcal {W}}$ given by Lemma 3.5 satisfies the initial conditions (2.12) in the sense of (2.16). Let us start by showing that the second distributional derivative $\ddot{u}$ belongs to $L^2(0,T;(V_0^D)')$. If we consider the discrete equation (3.1), for every $v\in V_0^D\subseteq V_n^k$, with $\Vert v\Vert _{V_0}\le 1$, we have

$$\begin{aligned} |(\delta ^2 u^k_n,v)_H|&\le \Vert {\mathbb {C}}\Vert _\infty \Vert Eu^k_n\Vert _H+\Vert {\mathbb {B}}\Vert _\infty \Vert \Psi \Vert _\infty \Vert \Psi ^k_n E\delta u^k_n\Vert _H+\Vert f^k_n\Vert _H+C_{tr}\Vert g^k_n\Vert _{H_N}. \end{aligned}$$

Therefore, taking the supremum over $v\in V_0^D$ with $||v ||_{V_0}\le 1$, we obtain the existence of a positive constant C such that

$$\begin{aligned} \Vert \delta ^2 u^k_n\Vert _{(V_0^D)'}^2\le C(\Vert Eu^k_n\Vert _H^2+\Vert \Psi ^k_n E\delta u^k_n\Vert _H^2+\Vert f^k_n\Vert _H^2+\Vert g^k_n\Vert _{H_N}^2). \end{aligned}$$

If we multiply this inequality by $\tau _n$ and we sum over $k=1,\dots ,n$, we get

$$\begin{aligned}&\sum _{k=1}^n\tau _n\Vert \delta ^2 u^k_n\Vert ^2_{(V^D_0)'}\nonumber \\&\quad \le C\left( \sum _{k=1}^n\tau _n\Vert Eu^k_n\Vert _H^2+\sum _{k=1}^n\tau _n\Vert \Psi ^k_n E\delta u^k_n\Vert _H^2+\Vert f\Vert _{L^2(0,T;H)}^2+\Vert g\Vert _{L^2(0,T;H_N)}^2\right) . \end{aligned}$$

(4.1)

Thanks to (4.1) and Lemma 3.3, we conclude that $\sum _{k=1}^n\tau _n\Vert \delta ^2 u^k_n\Vert ^2_{(V_0^D)'}\le {\tilde{C}}$ for every $n\in {\mathbb {N}}$ for a positive constant ${\tilde{C}}$ independent on $n\in {\mathbb {N}}$. In particular, the sequence $\{\tilde{u}_n\}_n\subset H^1(0,T;(V_0^D)')$ is uniformly bounded (notice that $\dot{{\tilde{u}}}_n(t)=\delta ^2 u_n^k$ for $t\in ((k-1)\tau _n,k\tau _n)$ and $k=1,\dots ,n$). Hence, up to extract a further (not relabeled) subsequence from the one of Lemma 3.4, we get

(4.2)

and by using the following estimate

$$\begin{aligned} \Vert \tilde{u}_n-\tilde{u}^+_n\Vert _{L^2(0,T;(V^D_0)')}\le \tau _n\Vert \dot{\tilde{u}}_n\Vert _{L^2(0,T;(V^D_0)')}\le \tilde{C}\tau _n\xrightarrow [n\rightarrow \infty ]{}0 \end{aligned}$$

we conclude that $w_3={\dot{u}}$.

Let us recall the following result, whose proof can be found, for example, in [9].

Lemma 4.1

Let X, Y be two reflexive Banach spaces such that $X\hookrightarrow Y$ continuously. Then

$$\begin{aligned} L^{\infty }(0,T;X)\cap C^0_w([0,T];Y)= C^0_w([0,T];X). \end{aligned}$$

Since $H^1(0,T;(V^D_0)')\hookrightarrow C^0([0,T],(V^D_0)')$, by using Lemmas 3.4 and 4.1, we get that our weak solution $u\in {\mathcal {W}}$ satisfies

$$\begin{aligned} u\in C^0_w([0,T];V_T),\quad {\dot{u}}\in C^0_w([0,T];H),\quad \ddot{u} \in L^2(0,T;(V^D_0)'). \end{aligned}$$

By (3.14) and (4.2), we hence obtain

(4.3)

so that $u(0)=u^0$ and $\dot{u}(0)=u^1$, since $u_n(0)=u^0$ and $\tilde{u}_n(0)=u^1$.

To prove that

$$\begin{aligned} \lim _{h\rightarrow 0^+}\frac{1}{h}\int _0^h\left( \Vert u(t)-u^0\Vert ^2_{V_t}+\Vert {\dot{u}}(t)-u^1\Vert ^2_{H}\right) \,\mathrm {d}t=0, \end{aligned}$$

we will actually show

$$\begin{aligned} \lim _{t\rightarrow 0^+}u(t)= u^0\hbox { in}\ V_T,\quad \lim _{t\rightarrow 0^+}{\dot{u}}(t)=u^1\hbox { in}\ H. \end{aligned}$$

This is a consequence of the following energy-dissipation inequality which holds for the weak solution $u\in {\mathcal {W}}$ of Lemma 3.5. Let us define the total energy as

$$\begin{aligned} {\mathcal {E}}(t):=\frac{1}{2}||{\dot{u}}(t) ||_H^2+\frac{1}{2}(\mathbb CEu(t),Eu(t))_H\quad t\in [0,T]. \end{aligned}$$

Notice that the total energy ${\mathcal {E}}(t)$ is well defined for every $t\in [0,T]$ since $u\in C_w^0([0,T];V_T)$ and $\dot{u}\in C_w^0([0,T];H)$, and that ${\mathcal {E}}(0)=\frac{1}{2}|| u^1 ||_H^2+\frac{1}{2}(\mathbb CEu^0,Eu^0)_H$.

Theorem 4.2

The weak solution $u\in {\mathcal {W}}$ to (2.8)–(2.11), given by Lemma 3.5, satisfies for every $t\in [0,T]$ the following energy-dissipation inequality

$$\begin{aligned} {\mathcal {E}}(t)+\int _0^{t} ({\mathbb {B}}\Psi E{\dot{u}},\Psi E{\dot{u}} )_H\,\mathrm {d}s \le {\mathcal {E}}(0)+{\mathcal {W}}_\mathrm{{tot}}(t), \end{aligned}$$

(4.4)

where $\Psi E\dot{u}$ is the function defined in (2.15) and ${\mathcal {W}}_\mathrm{{tot}}(t)$ is the total work on the solution u at time $t\in [0,T]$, which is given by

$$\begin{aligned} \begin{aligned} {\mathcal {W}}_\mathrm{{tot}}(t):&=\int _0^{t}\left[ (f,{\dot{u}}-\dot{w})_H +({\mathbb {C}}Eu,E{\dot{w}})_H +({\mathbb {B}}\Psi E{\dot{u}},\Psi E{\dot{w}})_H \right] \,\mathrm {d}s\\&\quad -\int _0^t[(\dot{u},\ddot{w})_H+(\dot{g},u-w)_{H_N}]\,\mathrm {d}s+({\dot{u}}(t),{\dot{w}}(t))_H\\&\quad +(g(t),u(t)-w(t))_{H_N} -(u^1,{\dot{w}}(0))_H -(g(0),u^0-w(0))_{H_N}. \end{aligned} \end{aligned}$$

(4.5)

Remark 4.3

From the classical point of view, the total work on the solution u at time $t\in [0,T]$ is given by

$$\begin{aligned} {\mathcal {W}}_\mathrm{{tot}}(t):={\mathcal {W}}_\mathrm{{load}}(t)+{\mathcal {W}}_\mathrm{{bdry}}(t), \end{aligned}$$

(4.6)

where ${\mathcal {W}}_\mathrm{{load}}(t)$ is the work on the solution u at time $t\in [0,T]$ due to the loading term, which is defined as

$$\begin{aligned} {\mathcal {W}}_\mathrm{{load}}(t):=\int _0^t(f(s), \dot{u}(s))_H\,\mathrm {d}s, \end{aligned}$$

and ${\mathcal {W}}_\mathrm{{bdry}}(t)$ is the work on the solution u at time $t\in [0,T]$ due to the varying boundary conditions, which one expects to be equal to

$$\begin{aligned} {\mathcal {W}}_\mathrm{{bdry}}(t):=\int _0^t(g(s),\dot{u}(s))_{H_N}\,\mathrm {d}s+\int _0^t(({\mathbb {C}}Eu(s)+\Psi ^2(s){\mathbb {B}}E\dot{u}(s))\nu ,\dot{w}(s))_{H_D}\,\mathrm {d}s, \end{aligned}$$

being $H_D:=L^2(\partial _D\Omega ;{\mathbb {R}}^d)$. Unfortunately, $\mathcal W_\mathrm{{bdry}}(t)$ is not well defined under our assumptions on u. Notice that when $\Psi \equiv 1$ on a neighborhood U of the closure of $\partial _N\Omega$, then every weak solution u to (2.8)–(2.11) satisfies $u\in H^1(0,T;H^1((\Omega \cap U){\setminus }\Gamma ;{\mathbb {R}}^d))$, which gives that $u\in H^1(0,T;H_N)$ by our assumptions on $\Gamma$. Hence, the first term of ${\mathcal {W}}_\mathrm{{bdry}}(t)$ makes sense and satisfies

$$\begin{aligned} \int _0^t(g(s),\dot{u}(s))_{H_N}\,\mathrm {d}s=(g(t), u(t))_{H_N}-(g(0), u(0))_{H_N}- \int _0^t(\dot{g}(s), u(s))_{H_N}\,\mathrm {d}s. \end{aligned}$$

The term involving the Dirichlet datum w is more difficult to handle since the trace of $({\mathbb {C}}Eu+\Psi ^2{\mathbb {B}}E\dot{u})\nu$ on $\partial _D\Omega$ is not well defined even when $\Psi \equiv 1$ on a neighborhood of the closure of $\partial _D\Omega$. If we assume that $u\in H^1(0,T;H^2(\Omega {\setminus }\Gamma ;{\mathbb {R}}^d))\cap H^2(0,T;L^2(\Omega ;{\mathbb {R}}^d))$ and that $\Gamma$ is a smooth manifold, then we can integrate by part Eq. (2.14) to deduce that u satisfies (2.8). In this case, $({\mathbb {C}}Eu+\Psi ^2{\mathbb {B}}E\dot{u})\nu \in L^2(0,T;H_D)$ and by using (2.8), together with the divergence theorem and the integration by parts formula, we deduce

$$\begin{aligned}&\int _0^t(({\mathbb {C}}Eu(s)+\Psi ^2(s){\mathbb {B}}E\dot{u}(s))\nu ,\dot{w}(s))_{H_D}\,\mathrm {d}s\\&\quad =\int _0^t\left[ (\mathrm{div}({\mathbb {C}}Eu(s)+\Psi ^2(s){\mathbb {B}}E\dot{u}(s)),\dot{w}(s))_H+({\mathbb {C}}Eu(s), E\dot{w}(s))_H\right] \,\mathrm {d}s\\&\qquad \int _0^t\left[ (+\Psi ^2(s){\mathbb {B}}E\dot{u}(s),E\dot{w}(s))_H-(g(s),\dot{w}(s))_{H_N}\right] \mathrm {d}s\\&\quad =\int _0^t\left[ ({\ddot{u}}(s),\dot{w}(s))_H-(f(s),\dot{w}(s))_H+(\mathbb CEu(s), E\dot{w}(s))_H\right] \,\mathrm {d}s\\&\qquad \int _0^t[(+\Psi ^2(s){\mathbb {B}}E\dot{u}(s),E\dot{w}(s))_H-(g(s),\dot{w}(s))_{H_N}\big ]\mathrm {d}s\\&\quad =\int _0^{t}\left[ ({\mathbb {C}}Eu(s),E{\dot{w}}(s))_H+({\mathbb {B}}\Psi (s)E{\dot{u}}(s),\Psi (s) E\dot{ w}(s))_H-(f(s),\dot{w}(s))_H\right] \mathrm {d}s\\&\qquad +\int _0^t\left[ (\dot{g}(s),w(s))_{H_N}-({\dot{u}}(s),\ddot{ w}(s))_H\right] \mathrm {d}s-(g(t),w(t))_{H_N}+({\dot{u}}(t),{\dot{w}}(t))_H\\&\qquad +(g(0),w(0))_{H_N}-(u^1,{\dot{w}}(0))_H . \end{aligned}$$

Hence, the definition of total work given in (4.5) is coherent with the classical one (4.6). Notice that if u is the solution to (2.8)–(2.11) given by Lemma 3.5, then (4.5) is well defined for every $t\in [0,T]$, since $g\in C^0([0,T];H_N)$, $\dot{w}\in C^0([0,T];H)$, $u\in C_w^0([0,T];V_T)$, and $\dot{u}\in C_w^0([0,T];H)$. In particular, the function $t\mapsto \mathcal W_\mathrm{{tot}}(t)$ from [0, T] to ${\mathbb {R}}$ is continuous.

Proof

Fixed $t\in (0,T]$, for every $n\in {\mathbb {N}}$, there exists a unique $j\in \{1,\dots ,n\}$ such that $t\in ((j-1)\tau _n,j\tau _n]$. After setting $t_n:=j\tau _n$, we can rewrite (3.3) as

$$\begin{aligned} \frac{1}{2}\Vert \tilde{u}_n^+(t)\Vert ^2_H+\frac{1}{2}({\mathbb {C}}Eu_n^+(t),Eu_n^+(t))_H+\int _0^{t_n} ({\mathbb {B}}\Psi _n^+E\tilde{u}_n^{+},\Psi _n^+E\tilde{ u}_n^{+})_H\,\mathrm {d}s\le {\mathcal {E}}(0)+{\mathcal {W}}^+_n(t), \end{aligned}$$

(4.7)

where

$$\begin{aligned} {\mathcal {W}}^+_n(t)&:=\int _0^{t_n}\left[ (f^+_n,{\tilde{u}}_n^+-\tilde{ w}^+_n)_H+({\mathbb {C}} Eu^+_n,E\tilde{ w}^+_n)_H+({\mathbb {B}}\Psi _n^+ E{\tilde{u}}_n^+,\Psi _n^+ E\tilde{w}_n^+)_H\right] \mathrm {d}s\\&\quad +\int _0^{t_n}\left[ ({{\tilde{u}}}^+_n,\tilde{w}_n^+)_H+(g^+_n,{\tilde{u}}_n^+-\tilde{ w}^+_n)_{H_N}\right] \mathrm {d}s. \end{aligned}$$

Thanks to (3.2), we have

$$\begin{aligned}&\Vert u_n(t)-u_n^+(t)\Vert _H=\Vert u_n^j+(t-j\tau _n)\delta u_n^j-u_n^j\Vert _H\le \tau _n\Vert \delta u_n^j\Vert _H\le C\tau _n\xrightarrow [n\rightarrow \infty ]{}0,\\&\Vert \tilde{u}_n(t)-\tilde{u}_n^+(t)\Vert ^2_{(V_0^D)'}=\Vert \delta u_n^j+(t-j\tau _n)\delta ^2 u_n^j-\delta u_n^j\Vert ^2_{(V_0^D)'}\le \tau ^2_n\Vert \delta ^2 u_n^j\Vert ^2_{(V_0^D)'}\le C\tau _n\xrightarrow [n\rightarrow \infty ]{}0. \end{aligned}$$

The last convergences and (4.3) imply

and since $\Vert u_n^+(t)\Vert _{V_T}+\Vert \tilde{u}_n^+(t)\Vert _H\le C$ for every $n\in {\mathbb {N}}$, we get

(4.8)

By the lower semicontinuity properties of $v\mapsto ||v ||_H^2$ and $v\mapsto ({\mathbb {C}}Ev,Ev)_H$, we conclude

$$\begin{aligned}&\Vert {\dot{u}}(t)\Vert ^2_H\le \liminf _{n\rightarrow \infty }\Vert \tilde{u}_n^+(t)\Vert ^2_H, \end{aligned}$$

(4.9)

$$\begin{aligned}&({\mathbb {C}}Eu(t),Eu(t))_H \le \liminf _{n\rightarrow \infty }({\mathbb {C}}Eu_n^+(t),Eu_n^+(t))_H. \end{aligned}$$

(4.10)

Thanks to Lemma 3.4 and (2.15), we obtain

so that

$$\begin{aligned} \int _0^t ({\mathbb {B}}\Psi E{\dot{u}},\Psi E{\dot{u}})_H\,\mathrm {d}s\le & {} \liminf _{n\rightarrow \infty }\int _0^t ({\mathbb {B}}\Psi _n^+E\tilde{u}_n^{+},\Psi _n^+E\tilde{ u}_n^{+})_H\,\mathrm {d}s\nonumber \\\le & {} \liminf _{n\rightarrow \infty }\int _0^{t_n} ({\mathbb {B}}\Psi _n^+E\tilde{u}_n^{+},\Psi _n^+E\tilde{ u}_n^{+})_H\,\mathrm {d}s, \end{aligned}$$

(4.11)

since $t\le t_n$ and $v\mapsto \int _0^t(\mathbb {B}v,v)_H\,\mathrm {d}s$ is a non-negative quadratic form on $L^2(0,T;H)$. Let us study the right-hand side of (4.7). Given that we have

we can deduce

$$\begin{aligned} \int _0^{t_n}(f^+_n,\tilde{u}^+_n-\tilde{w}^+_n)_H\,\mathrm {d}s\xrightarrow [n\rightarrow \infty ]{}\int _0^t(f,{\dot{u}}-\dot{w})_H\,\mathrm {d}s. \end{aligned}$$

(4.12)

In a similar way, we can prove

$$\begin{aligned}&\int _0^{t_n}({\mathbb {C}}Eu^+_n,E\tilde{ w}^+_n)_H\,\mathrm {d}s \xrightarrow [n\rightarrow \infty ]{}\int _0^{t}({\mathbb {C}}Eu,E\dot{ w})_H\,\mathrm {d}s, \end{aligned}$$

(4.13)

$$\begin{aligned}&\int _0^{t_n}({\mathbb {B}}\Psi ^+_n E\tilde{u}^+_n,\Psi ^+_n E\tilde{ w}^+_n)_H\,\mathrm {d}s\xrightarrow [n\rightarrow \infty ]{}\int _0^{t}({\mathbb {B}}\Psi E\dot{u},\Psi E{\dot{w}})_H\,\mathrm {d}s, \end{aligned}$$

(4.14)

since the following convergences hold

It remains to study the behavior as $n\rightarrow \infty$ of the terms

$$\begin{aligned} \int _0^{t_n}(\dot{{\tilde{u}}}_n,{\tilde{w}}_n^+)_H\,\mathrm {d}s,\qquad \int _0^{t_n}(g^+_n,{\tilde{u}}_n^+-\tilde{ w}^+_n)_{H_N}\,\mathrm {d}s. \end{aligned}$$

Thanks to formula (3.10), we have

$$\begin{aligned} \int _0^{t_n}(\dot{{\tilde{u}}}_n,{\tilde{w}}_n^+)_H\,\mathrm {d}s=(\tilde{u}_n^+(t),{\tilde{w}}_n^+(t))_H-(u^1,\dot{w}(0))_H-\int _0^{t_n}(\tilde{u}_n^-,\dot{{\tilde{w}}}_n)_H\,\mathrm {d}s. \end{aligned}$$

By arguing as before, we hence deduce

$$\begin{aligned} \int _0^{t_n}(\dot{{\tilde{u}}}_n,{\tilde{w}}_n^+)_H\,\mathrm {d}s\xrightarrow [n\rightarrow \infty ]{}({\dot{u}}(t),\dot{w}(t))_H-(u^1,\dot{w}(0))_H-\int _0^{t}(\dot{u},{\ddot{w}})_H\,\mathrm {d}s, \end{aligned}$$

(4.15)

thanks to (4.8) and by these convergences

Notice that in the last convergence, we used the continuity of w from [0, T] in H. Similarly, we have

$$\begin{aligned} \int _0^{t_n}(g_n^+,{\tilde{u}}_n^+-{\tilde{w}}_n^+)_{H_N}\,\mathrm {d}s= & {} (g_n^+(t),u_n^+(t)- w_n^+(t))_{H_N}-(g(0),u^0- w(0))_{H_N}\\&-\int _0^{t_n}(\dot{g}_n,u_n^{-} -w_n^-)_{H_N}\,\mathrm {d}s \end{aligned}$$

so that we get

(4.16)

thanks to (4.8), the continuity of $s\mapsto g(s)$ in $H_N$, and the fact that

By combining (4.9)–(4.16), we deduce the validity of the energy-dissipation inequality (4.4) for every $t\in (0,T]$. Finally, for $t=0$, the inequality trivially holds since $u(0)=u^0$ and $\dot{u}(0)=u^1$. $\square$

We now are in position to prove the validity of the initial conditions.

Lemma 4.4

The weak solution $u\in {\mathcal {W}}$ to (2.8)–(2.11) of Lemma 3.5 satisfies

$$\begin{aligned} \lim _{t\rightarrow 0^+}u(t)= u^0\hbox { in}\ V_T,\quad \lim _{t\rightarrow 0^+}{\dot{u}}(t)=u^1\hbox { in}\ H. \end{aligned}$$

(4.17)

In particular, u satisfies the initial conditions (2.12) in the sense of (2.16).

Proof

By sending $t\rightarrow 0^+$ into the energy-dissipation inequality  (4.4) and using that the functions $u\in C_w^0([0,T];V_T)$ and $\dot{u}\in C_w^0([0,T];H)$, we deduce

$$\begin{aligned} {\mathcal {E}}(0)\le \liminf _{t\rightarrow 0^+}{\mathcal {E}}(t)\le \limsup _{t\rightarrow 0^+}{\mathcal {E}}(t)\le {\mathcal {E}}(0), \end{aligned}$$

since the right-hand side of (4.4) is continuous in t, $u(0)=u^0$, and $\dot{u}(0)=u^1$. Therefore, there exists $\lim _{t\rightarrow 0^+}{\mathcal {E}}(t)={\mathcal {E}}(0)$. By using the lower semicontinuity of $t\mapsto ||{\dot{u}}(t) ||^2_H$ and $t\mapsto ({\mathbb {C}}Eu(t),Eu(t))_H$, we derive

$$\begin{aligned} \lim _{t\rightarrow 0^+}||{\dot{u}}(t) ||_H^2=||u^1 ||_H^2,\quad \lim _{t\rightarrow 0^+}({\mathbb {C}}Eu(t),Eu(t))_H=({\mathbb {C}}Eu^0,Eu^0)_H. \end{aligned}$$

Finally, since we have

we deduce (4.17). In particular, the functions $u:[0,T]\rightarrow V_T$ and $\dot{u}:[0,T]\rightarrow H$ are continuous at $t=0$, which implies (2.16). $\square$

We can finally prove Theorem 3.1.

Proof of Theorem 3.1

It is enough to combine Lemmas 3.5 and 4.4. $\square$

Remark 4.5

We have proved Theorem 3.1 for the d-dimensional linear elastic case, namely when the displacement u is a vector-valued function. The same result is true with identical proofs in the antiplane case, that is, when the displacement u is a scalar function and satisfies (1.5).

5 Uniqueness

In this section, we investigate the uniqueness properties of system (2.8) with boundary and initial conditions (2.9)–(2.12). To this aim, we need to assume stronger regularity assumptions on the crack sets $\{\Gamma _t\}_{t\in [0,T]}$ and on the function $\Psi$. Moreover, we have to restrict our problem to the dimensional case $d=2$, since in our proof, we need to construct a suitable family of diffeomorphisms which maps the time-dependent crack $\Gamma _t$ into a fixed set, and this can be explicitly done only for $d=2$ (see [7, Example 2.14]).

We proceed in two steps; first, in Lemma 5.2, we prove a uniqueness result in every dimension d, but when the cracks are not increasing, that is, $\Gamma _T=\Gamma _0$. Next, in Theorem 5.5, we combine Lemma 5.2 with the finite speed of propagation theorem of [5] and the uniqueness result of [8] to derive the uniqueness of a weak solution to (2.8)–(2.12) in the case $d=2$.

Let us start with the following lemma, whose proof is similar to that one of [8, Proposition 2.10].

Lemma 5.1

Let $u\in {\mathcal {W}}$ be a weak solution to (2.8)–(2.11) satisfying the initial condition $\dot{u}(0)=0$ in the following sense

$$\begin{aligned} \lim _{h\rightarrow 0^+}\frac{1}{h}\int _0^h||{\dot{u}}(t) ||_H^2 =0. \end{aligned}$$

Then u satisfies

$$\begin{aligned} \begin{aligned}&-\int _0^T({\dot{u}}(t),{\dot{\varphi }}(t))_H \,\mathrm {d}t+\int _0^T({\mathbb {C}}Eu(t),E\varphi (t))_{H} \,\mathrm {d}t +\int _0^T({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t\\&\quad =\int _0^T(f(t),\varphi (t))_H \,\mathrm {d}t+\int _0^T(g(t),\varphi (t))_{H_N} \,\mathrm {d}t \end{aligned} \end{aligned}$$

for every $\varphi \in {\mathcal {V}}^D$ such that $\varphi (T)=0$, where $\Psi E\dot{u}$ is the function defined in (2.15).

Proof

We fix $\varphi \in {\mathcal {V}}^D$ with $\varphi (T)=0$ and for every $\epsilon >0$, we define the following function

$$\begin{aligned} \varphi _{\epsilon }(t):= {\left\{ \begin{array}{ll} \frac{t}{\epsilon }\varphi (t) &{}t\in [0,\epsilon ],\\ \varphi (t)&{}t\in [\epsilon ,T]. \end{array}\right. } \end{aligned}$$

We have that $\varphi _{\epsilon }\in {\mathcal {V}}^D$ and $\varphi _{\epsilon }(0)=\varphi _{\epsilon }(T)=0$, so we can use $\varphi _{\epsilon }$ as test function in (2.14). By proceeding as in [8, Proposition 2.10], we obtain

$$\begin{aligned}&\lim _{\epsilon \rightarrow 0^+}\int _0^T({\dot{u}}(t),{\dot{\varphi }}_{\epsilon }(t))_H \,\mathrm {d}t=\int _0^T({\dot{u}}(t),{\dot{\varphi }}(t))_H \,\mathrm {d}t,\\&\lim _{\epsilon \rightarrow 0^+}\int _0^T({\mathbb {C}} Eu(t),E\varphi _{\epsilon }(t))_H \,\mathrm {d}t= \int _0^T({\mathbb {C}} Eu(t),E\varphi (t))_H \,\mathrm {d}t,\\&\lim _{\epsilon \rightarrow 0^+}\int _0^T(f(t),\varphi _{\epsilon }(t))_H \,\mathrm {d}t= \int _0^T(f(t),\varphi (t))_H \,\mathrm {d}t. \end{aligned}$$

It remains to consider the terms involving ${\mathbb {B}}$ and g.

We have

$$\begin{aligned}&\int _0^T({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi _{\epsilon }(t))_{H} \,\mathrm {d}t=\int _0^{\epsilon }(\mathbb B\Psi (t)E{\dot{u}}(t),\frac{t}{\epsilon }\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t\\&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\quad +\int _{\epsilon }^{T}({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t,\\&\int _0^T(g(t),\varphi _{\epsilon }(t))_{H_N} \,\mathrm {d}t =\int _0^{\epsilon }(g(t),\frac{t}{\epsilon }\varphi (t))_{H_N} \,\mathrm {d}t+\int _{\epsilon }^{T}(g(t),\varphi (t))_{H_N} \,\mathrm {d}t, \end{aligned}$$

hence, by the dominated convergence theorem, we get

$$\begin{aligned}&\int _{\epsilon }^{T}({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t\xrightarrow [\epsilon \rightarrow 0^+]{}\int _{0}^{T}({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t,\\&\left| \int _0^{\epsilon }({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\frac{t}{\epsilon }\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t\right| \le ||\mathbb B ||_\infty ||\Psi ||_\infty \int _0^{\epsilon }||\Psi (t)E{\dot{u}}(t) ||_H||E\varphi (t) ||_{H} \,\mathrm {d}t\xrightarrow [\epsilon \rightarrow 0^+]{}0,\\&\int _{\epsilon }^{T}(g(t),\varphi (t))_{H_N} \,\mathrm {d}t\xrightarrow [\epsilon \rightarrow 0^+]{}\int _{0}^{T}(g(t),\varphi (t))_{H_N} \,\mathrm {d}t,\\&\left| \int _0^{\epsilon }(g(t),\frac{t}{\epsilon }\varphi (t))_{H_N} \,\mathrm {d}t\right| \le \int _0^{\epsilon }||g(t) ||_{H_N}||\varphi (t) ||_{H_N} \,\mathrm {d}t\xrightarrow [\epsilon \rightarrow 0^+]{}0. \end{aligned}$$

By combining together all the previous convergences, we get the thesis. $\square$

We now state the uniqueness result in the case of a fixed domain, that is, $\Gamma _T=\Gamma _0$. We follow the same ideas of [12], and we need to assume

$$\begin{aligned} \Psi \in \mathrm{Lip}([0,T]\times {{\overline{\Omega }}}),\quad \nabla {\dot{\Psi }}\in L^\infty ((0,T)\times \Omega ;{\mathbb {R}}^d), \end{aligned}$$

(5.1)

while on $\Gamma _0$, we do not require any further hypotheses.

Lemma 5.2

(Uniqueness in a fixed domain) Assume (5.1) and $\Gamma _T=\Gamma _0$. Then the viscoelastic dynamic system (2.8) with boundary and initial conditions (2.9)–(2.12) (the latter in the sense of (2.16)) has a unique weak solution.

Proof

Let $u_1,u_2\in {\mathcal {W}}$ be two weak solutions to (2.8)–(2.11) with initial conditions (2.12). The function $u:=u_1-u_2$ satisfies

$$\begin{aligned} \frac{1}{h}\int _0^h(||u(t) ||_{V_t}^2+||{\dot{u}}(t) ||_H^2) \,\mathrm {d}t\xrightarrow [h\rightarrow 0^+]{} 0, \end{aligned}$$

(5.2)

hence, by Lemma 5.1, it solves

$$\begin{aligned} -\int _0^T({\dot{u}}(t),{\dot{\varphi }}(t))_H \,\mathrm {d}t+\int _0^T({\mathbb {C}}Eu(t),E\varphi (t))_{H} \,\mathrm {d}t +\int _0^T({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi (t))_{H} \,\mathrm {d}t=0 \end{aligned}$$

(5.3)

for every $\varphi \in {\mathcal {V}}^D$ such that $\varphi (T)=0$. We fix $s\in (0,T]$ and consider the function

$$\begin{aligned} \varphi _{s}(t):= {\left\{ \begin{array}{ll} -\int _t^s u(\tau )\mathrm {d}\tau \quad &{}t\in [0,s],\\ 0\quad &{}t\in [s,T]. \end{array}\right. } \end{aligned}$$

Since $\varphi _s\in {\mathcal {V}}^D$ and $\varphi _s(T)=0$, we can use it as test function in (5.3) to obtain

$$\begin{aligned} -\int _0^s({\dot{u}}(t),u(t))_H \,\mathrm {d}t+\int _0^s({\mathbb {C}}E\dot{\varphi _s}(t),E\varphi _s(t))_{H} \,\mathrm {d}t +\int _0^s(\mathbb B\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi _s(t))_{H} \,\mathrm {d}t=0. \end{aligned}$$

In particular, we deduce

$$\begin{aligned}&-\frac{1}{2}\int _0^s\frac{\mathrm {d}}{\mathrm {d}t}\Vert u(t)\Vert ^2_H \,\mathrm {d}t+\frac{1}{2}\int _0^s\frac{\mathrm {d}}{\mathrm {d}t}({\mathbb {C}}E\varphi _s(t),E\varphi _s(t))_{H} \,\mathrm {d}t \\&\quad +\int _0^s({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi _s(t))_{H} \,\mathrm {d}t=0, \end{aligned}$$

which implies

$$\begin{aligned} \frac{1}{2}\Vert u(s)\Vert ^2_H+\frac{1}{2}({\mathbb {C}}E\varphi _s(0),E\varphi _s(0))_{H}=\int _0^s({\mathbb {B}}\Psi (t)E{\dot{u}}(t) ,\Psi (t) E\varphi _s(t) )_{H} \,\mathrm {d}t, \end{aligned}$$

(5.4)

since $u(0)=0=\varphi _s(s)$. From the distributional point of view, the following equality holds

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}(\Psi Eu)=\dot{\Psi }Eu+\Psi E{\dot{u}}\in L^2(0,T;H), \end{aligned}$$

(5.5)

indeed, for all $v\in C^{\infty }_c(0,T;H)$, we have

$$\begin{aligned}&\int _0^T\left( \frac{\mathrm {d}}{\mathrm {d}t}(\Psi (t) Eu(t)),v(t)\right) _H\mathrm {d}t=-\int _0^T\left( \Psi (t) Eu(t),{\dot{v}}(t)\right) _H\,\mathrm {d}t\\&\quad =-\int _0^T\left( E(\Psi (t) u(t))-\nabla \Psi (t)\odot u(t),{\dot{v}}(t)\right) _H\,\mathrm {d}t\\&\quad =\int _0^T (E(\dot{\Psi }(t)u(t))+E(\Psi (t) {\dot{u}}(t)),v(t))_H\,\mathrm {d}t\\&\qquad -\int _0^T (\nabla \dot{\Psi }(t)\odot u(t)+\nabla \Psi (t)\odot {\dot{u}}(t),v(t))_H\,\mathrm {d}t\\&\quad =\int _0^T(\dot{\Psi }(t) Eu(t),v(t))_H\,\mathrm {d}t+\int _0^T(\Psi (t) E{\dot{u}}(t),v(t))_H\,\mathrm {d}t. \end{aligned}$$

In particular, $\Psi Eu\in H^1(0,T;H)\subset C^0([0,T],H)$, so that by (5.2)

$$\begin{aligned} \Vert \Psi (0)Eu(0)\Vert ^2_H=\lim _{h\rightarrow 0}\frac{1}{h}\int _0^h \Vert \Psi (t)Eu(t)\Vert ^2_H \mathrm {d}t\le C\lim _{h\rightarrow 0}\frac{1}{h}\int _0^h \Vert u(t)\Vert ^2_{V_t} \mathrm {d}t=0 \end{aligned}$$

which yields $\Psi (0)Eu(0)=0$. Thanks to (5.5) and to property $\Psi u\in H^1(0,T;H)$, we deduce

$$\begin{aligned} \begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t}\left( {\mathbb {B}}\Psi Eu ,\Psi E\varphi _s \right) _H&=({\mathbb {B}}\dot{\Psi } Eu ,\Psi E\varphi _s )_H+({\mathbb {B}}\Psi E{\dot{u}} ,\Psi E\varphi _s )_H+({\mathbb {B}}\Psi Eu ,\dot{\Psi } E\varphi _s )_H\\&\quad +({\mathbb {B}}\Psi Eu ,\Psi E\dot{\varphi }_s )_H\\&=2({\mathbb {B}}\Psi Eu ,{\dot{\Psi }} E\varphi _s )_H+({\mathbb {B}}\Psi E{\dot{u}} ,\Psi E\varphi _s )_H+({\mathbb {B}}\Psi Eu ,\Psi E\dot{\varphi }_s )_H, \end{aligned} \end{aligned}$$

and by integrating on [0, s], we get

$$\begin{aligned}&\int _0^s ({\mathbb {B}}\Psi (t)E{\dot{u}}(t),\Psi (t)E\varphi _s(t))_H\,\mathrm {d}t\\&\quad =\int _0^s \left[ \frac{\mathrm {d}}{\mathrm {d}t}({\mathbb {B}}\Psi (t)Eu(t),\Psi (t)E\varphi _s(t))_H-2 ({\mathbb {B}}\Psi (t)Eu(t),{\dot{\Psi }}(t)E\varphi _s(t))_H\right] \,\mathrm {d}t\\&\qquad -\int _0^s({\mathbb {B}}\Psi (t)E\dot{\varphi }_s(t),\Psi (t)E\dot{\varphi }_s(t))_H\mathrm {d}t\\&\quad \le ({\mathbb {B}}\Psi (s)Eu(s),\Psi (s)E\varphi _s(s))_H-({\mathbb {B}}\Psi (0)Eu(0),\Psi (0)E\varphi _s(0))_H]\,\mathrm {d}t\\&\qquad +\int _0^s\left[ 2({\mathbb {B}}\Psi (t)Eu(t),\Psi (t)Eu(t))^{\frac{1}{2}}_H({\mathbb {B}}\dot{\Psi }(t)E\varphi _s(t),\dot{\Psi }(t)E\varphi _s(t))^{\frac{1}{2}}_H\right] \,\mathrm {d}t\\&\qquad -\int _0^s ({\mathbb {B}}\Psi (t)E\dot{\varphi }_s(t),\Psi (t)E\dot{\varphi }_s(t))_H\mathrm {d}t\\&\quad \le \left. \int _0^s\left[ ({\mathbb {B}}\Psi (t)Eu(t),\Psi (t)Eu(t))_H+({\mathbb {B}}\dot{\Psi }(t)E\varphi _s(t),\dot{\Psi }(t)E\varphi _s(t))_H\right] \,\mathrm {d}t\right. \\&\qquad \left. -\,\int _0^s({\mathbb {B}}\Psi (t)E\dot{\varphi }_s(t),\Psi (t)E\dot{\varphi }_s(t))_H\right] \mathrm {d}t\\&\quad \le ||\mathbb B ||_\infty ||{\dot{\Psi }} ||_\infty ^2\int _0^s\Vert E\varphi _s(t)\Vert _H^2\mathrm {d}t, \end{aligned}$$

since $E\varphi _s(s)=0=\Psi (0)Eu(0)$ and $E{\dot{\varphi }}_s=Eu$ in (0, s). By combining the previous inequality with (5.4) and using the coercivity of the tensor ${\mathbb {C}}$, we derive

$$\begin{aligned}&\frac{\lambda _1}{2}\Vert E\varphi _s(0)\Vert ^2_H+\frac{1}{2}\Vert u(s)\Vert _H^2\le \frac{1}{2}(\mathbb CE\varphi _s(0),E\varphi _s(0))_H+\frac{1}{2}\Vert u(s)\Vert _H^2\\&\quad \le ||{\mathbb {B}} ||_\infty ||{\dot{\Psi }} ||_\infty ^2\int _0^s\Vert E\varphi _s(t)\Vert _H^2\mathrm {d}t. \end{aligned}$$

Let us set $\xi (t):=\int _0^t u(\tau )\mathrm {d}\tau$, then

$$\begin{aligned}&\Vert E\varphi _s(0)\Vert _H^2=\Vert E\xi (s)\Vert ^2_H,\quad \Vert E\varphi _s(t)\Vert ^2_H=\Vert E\xi (t)-E\xi (s)\Vert _H^2\le 2\Vert E\xi (t)\Vert ^2_H+2\Vert E\xi (s)\Vert _H^2, \end{aligned}$$

from which we deduce

$$\begin{aligned} \frac{\lambda _1}{2}\Vert E\xi (s)\Vert ^2_H+\frac{1}{2}||u(s) ||_H^2\le C\int _0^s\Vert E\xi (t)\Vert ^2_H\mathrm {d}t+Cs\Vert E\xi (s)\Vert ^2_H, \end{aligned}$$

(5.6)

where $C:=2||{\mathbb {B}} ||_\infty ||{\dot{\Psi }} ||_\infty ^2$. Therefore, if we set $s_0:=\frac{\lambda _1}{4C}$, for all $s\le s_0$, we obtain

$$\begin{aligned} \frac{\lambda _1}{4}\Vert E\xi (s)\Vert ^2_H\le \left( \frac{\lambda _1}{2}- Cs\right) \Vert E\xi (s)\Vert ^2_H\le C\int _0^s\Vert E\xi (t)\Vert ^2_H\mathrm {d}t. \end{aligned}$$

By Gronwall’s lemma, the last inequality implies $E\xi (s)=0$ for all $s\le s_0$. Hence, thanks to (5.6), we get $\Vert u(s)\Vert ^2_H\le 0$ for all $s\le s_0$, which yields $u(s)=0$ for all $s\le s_0$. Since $s_0$ depends only on ${\mathbb {C}}$, ${\mathbb {B}}$, and $\Psi$, we can repeat this argument starting from $s_0$, and with a finite number of steps, we obtain $u\equiv 0$ on [0, T]. $\square$

In order to prove our uniqueness result in the case of a moving crack, we need two auxiliary results, which are [4, Theorem 6.1] and [8, Theorem 4.3]. For the sake of the readers, we rewrite below the statements without proof.

The first one ([4, Theorem 6.1]) is a generalization of the well-known result of finite speed of propagation for the wave equation. Given an open bounded set $U\subset {\mathbb {R}}^d$, we define by $\partial _LU$ the Lipschitz part of the boundary $\partial U$, which is the collection of points $x\in \partial U$ for which there exist an orthogonal coordinate system $y_1,\dots ,y_d$, a neighborhood V of x of the form $A\times I$, with A open in ${\mathbb {R}}^{d-1}$ and I open interval in ${\mathbb {R}}$, and a Lipschitz function $g:A\rightarrow I$, such that $V\cap U:=\{(y_1,\dots ,y_d)\in V:y_d<g(y_1,\dots ,y_{d-1})\}$. Moreover, given a Borel set $S\subseteq \partial _LU$, we define

$$\begin{aligned} H_S(U;{\mathbb {R}}^d):=\{u\in H^1(U;{\mathbb {R}}^d):u=0\text { on }S\}. \end{aligned}$$

Notice that $H_S(U;{\mathbb {R}}^d)$ is a Hilbert space, and we denote its dual by $H^{-1}_S(U;{\mathbb {R}}^d).$

Theorem 5.3

(Finite speed of propagation) Let $U\subset {\mathbb {R}}^d$ be an open bounded set and let $\partial _LU$ be the Lipschitz part of $\partial U$. Let $S_0$ and $S_1$ be two Borel sets with $S_0\subseteq S_1\subseteq \partial _LU$, and let $\mathbb C:U\rightarrow {\mathscr {L}}({\mathbb {R}}^{d\times d}_\mathrm{{sym}};{\mathbb {R}}^{d\times d}_\mathrm{{sym}})$ be a fourth-order tensor satisfying (2.4)–(2.6). Let

$$\begin{aligned} u\in L^2(0,T;H^1_{S_0}(U;{\mathbb {R}}^d))\cap H^1(0,T;L^2(U;{\mathbb {R}}^d))\cap H^2(0,T;H^{-1}_{S_1}(U;{\mathbb {R}}^d)) \end{aligned}$$

be a solution to

$$\begin{aligned} \langle {\ddot{u}}(t), \psi \rangle _{H^{-1}_{S_1}(U;{\mathbb {R}}^d)}+({\mathbb {C}}Eu(t),E\psi )_{L^2(U;{\mathbb {R}}^{d\times d}_\mathrm{{sym}})}=0\quad \text {for every }\psi \in H^1_{S_1}(U;{\mathbb {R}}^d), \end{aligned}$$

with initial conditions $u(0)=0$ and $\dot{u}(0)=0$ in the sense of $L^2(U;{\mathbb {R}}^d)$ and $H^{-1}_{S_1}(U;{\mathbb {R}}^d)$, respectively. Then

$$\begin{aligned} u(t)=0\quad \text {a.e. in }U_t:=\{x\in U:\mathrm{dist}(x,S_1{\setminus } S_0)>t\sqrt{||{\mathbb {C}} ||_\infty }\} \end{aligned}$$

for every $t\in [0,T]$.

Proof

See [4, Theorem 6.1]. $\square$

The second one ([8, Theorem 4.3]) is a uniqueness result for the weak solutions of the wave equation in a moving domain. Let ${\hat{H}}$ be a separable Hilbert space, and let $\{\hat{V}_t\}_{t\in [0,T]}$ be a family of separable Hilbert spaces with the following properties:

(i):

for every $t\in [0,T]$, the space ${\hat{V}}_t$ is contained and dense in ${\hat{H}}$ with continuous embedding;

(ii):

for every $s,t\in [0,T]$, with $s<t$, ${\hat{V}}_s\subset {\hat{V}}_t$ and the Hilbert space structure on ${\hat{V}}_s$ is the one induced by ${\hat{V}}_t$.

Let $a:{\hat{V}}_T\times {\hat{V}}_T\rightarrow {\mathbb {R}}$ be a bilinear symmetric form satisfying the following conditions:

(iii):

there exists $M_0$ such that

$$\begin{aligned} |a(u,v)|\le M_0||u ||_{{\hat{V}}_T}||v ||_{{\hat{V}}_T}\quad \text {for every }u,v\in {\hat{V}}_T; \end{aligned}$$

(iv):

there exists $\lambda _0>0$ and $\nu _0\in {\mathbb {R}}$ such that

$$\begin{aligned} a(u,u)\ge \lambda _0||u ||_{{\hat{V}}_T}^2-\nu _0||u ||_{\hat{H}}^2\quad \text {for every }u\in {\hat{V}}_T. \end{aligned}$$

Assume that

• (U1) for every $t\in [0,T]$, there is a continuous and linear bijective operator $Q_t:{\hat{V}}_t\rightarrow {\hat{V}}_0$, with continuous inverse $R_t:{\hat{V}}_0\rightarrow {\hat{V}}_t$;

• (U2) $Q_0$ and $R_0$ are the identity maps on ${\hat{V}}_0$;

• (U3) there exists a constant $M_1$ independent of t such that

  $$\begin{aligned}&||Q_tu ||_{{\hat{H}}}\le M_1 ||u ||_{{\hat{H}}}\quad \text {for every }u\in {\hat{V}}_t,&||R_tu ||_{{\hat{H}}}\le M_1 ||u ||_{{\hat{H}}}\quad \text {for every }u\in {\hat{V}}_0,\\&||Q_tu ||_{{\hat{V}}_0}\le M_1 ||u ||_{{\hat{V}}_t}\quad \text {for every }u\in {\hat{V}}_t,&||R_tu ||_{{\hat{V}}_t}\le M_1 ||u ||_{{\hat{V}}_0}\quad \text {for every }u\in {\hat{V}}_0. \end{aligned}$$

Since ${\hat{V}}_t$ is dense in ${\hat{H}}$, (U3) implies that $Q_t$ and $R_t$ can be extended to continuous linear operators from ${\hat{H}}$ into itself, still denoted by $Q_t$ and $R_t$. We also require

• (U4) for every $v\in {\hat{V}}_0$, the function $t\mapsto R_tv$ from [0, T] into ${\hat{H}}$ has a derivative, denoted by $\dot{R}_t v$;

• (U5) there exists $\eta \in (0,1)$ such that

  $$\begin{aligned} ||\dot{R}_t Q_tv ||^2_{{\hat{H}}}\le \lambda _0(1-\eta )||v ||_{\hat{V}_t}^2\quad \text {for every }v\in {\hat{V}}_t; \end{aligned}$$

• (U6) there exists a constant $M_2$ such that

  $$\begin{aligned} ||Q_tv-Q_sv ||_{{\hat{H}}}\le M_2||v ||_{\hat{V}_s}(t-s)\quad \text {for every } 0\le s<t\le T \text { and every } v\in \hat{V}_s; \end{aligned}$$

• (U7) for very $t\in [0,T)$ and for every $v\in {\hat{V}}_t$, there exists an element of ${\hat{H}}$, denoted by $\dot{Q}_tv$, such that

  $$\begin{aligned} \lim _{h\rightarrow 0^+}\frac{Q_{t+h}v-Q_tv}{h}=\dot{Q}_t v\text { in }{\hat{H}}. \end{aligned}$$

For every $t\in [0,T]$, define

$$\begin{aligned}&\alpha (t):{\hat{V}}_0\times {\hat{V}}_0\rightarrow {\mathbb {R}}\quad \text {as }\alpha (t)(u,v):=a(R_tu,R_tv)\text { for }u,v\in {\hat{V}}_0,\\&\beta (t):{\hat{V}}_0\times {\hat{V}}_0\rightarrow {\mathbb {R}}\quad \text {as }\beta (t)(u,v):=(\dot{R}_tu,\dot{R}_tv)\text { for }u,v\in {\hat{V}}_0,\\&\gamma (t):{\hat{V}}_0\times {\hat{H}}\rightarrow {\mathbb {R}}\quad \text {as }\gamma (t)(u,v):=(\dot{R}_tu,R_tv)\text { for }u\in {\hat{V}}_0\text { and }v\in {\hat{H}},\\&\delta (t):{\hat{H}}\times {\hat{H}}\rightarrow {\mathbb {R}}\quad \text {as }\delta (t)(u,v):=(R_tu,R_tv)-(u,v)\text { for }u,v\in {\hat{H}}. \end{aligned}$$

We assume that there exists a constant $M_3$ such that

• (U8) the maps $t\mapsto \alpha (t)(u,v)$, $t\mapsto \beta (t)(u,v)$, $t\mapsto \gamma (t)(u,v)$, and $t\mapsto \delta (t)(u,v)$ are Lipschitz continuous and for a.e. $t\in (0,T)$, their derivatives satisfy

  $$\begin{aligned}&|{\dot{\alpha }}(t)(u,v)|\le M_3||u ||_{{\hat{V}}_0}||v ||_{\hat{V}_0}\quad \text {for }u,v\in {\hat{V}}_0,\\&|{\dot{\beta }}(t)(u,v)|\le M_3||u ||_{{\hat{V}}_0}||v ||_{\hat{V}_0}\quad \text {for }u,v\in {\hat{V}}_0,\\&|{\dot{\gamma }}(t)(u,v)|\le M_3||u ||_{{\hat{V}}_0}||v ||_{\hat{H}}\quad \text {for }u\in {\hat{V}}_0\text { and }v\in {\hat{H}},\\&|{\dot{\delta }}(t)(u,v)|\le M_3||u ||_{{\hat{H}}}||v ||_{\hat{H}}\quad \text {for }u,v\in {\hat{H}}. \end{aligned}$$

Theorem 5.4

(Uniqueness for the wave equation) Assume that ${\hat{H}}$, $\{{\hat{V}}_t\}_{t\in [0,T]}$, and a satisfy (i)–(iv) and that (U1)–(U8) hold. Given $u^0\in {\hat{V}}_0$, $u^1\in {\hat{H}}$, and $f\in L^2(0,T;{\hat{H}})$, there exists a unique solution

$$\begin{aligned} u\in \hat{{\mathcal {V}}}:=\{\varphi \in L^2(0,T;{\hat{V}}_T):\dot{u}\in L^2(0,T;{\hat{H}}),\,u(t)\in {\hat{V}}_t\text { for a.e. }t\in (0,T)\} \end{aligned}$$

to the wave equation

$$\begin{aligned} -\int _0^T({\dot{u}}(t),{\dot{\varphi }}(t))_{{\hat{H}}}\,\mathrm {d}t+\int _0^Ta(u(t),\varphi (t))\,\mathrm {d}t=\int _0^T(f(t),\varphi (t))_{\hat{H}}\,\mathrm {d}t\quad \text {for every } \varphi \in \hat{{\mathcal {V}}}, \end{aligned}$$

satisfying the initial conditions $u(0)=u^0$ and $\dot{u}(0)=u^1$ in the sense that

$$\begin{aligned} \lim _{h\rightarrow 0^+}\frac{1}{h}\int _0^h\left( \Vert u(t)-u^0\Vert ^2_{\hat{V}_t}+\Vert {\dot{u}}(t)-u^1\Vert ^2_{{\hat{H}}}\right) \,\mathrm {d}t=0. \end{aligned}$$

Proof

See [8, Theorem 4.3]. $\square$

We now are in position to prove the uniqueness theorem in the case of a moving domain. We consider the dimensional case $d=2$, and we require the following assumptions:

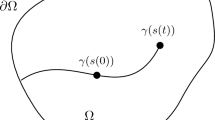
• (H1) there is a $C^{2,1}$ simple curve $\Gamma \subset {{\overline{\Omega }}}\subset {\mathbb {R}}^2$, parametrized by arc-length $\gamma :[0,\ell ]\rightarrow {{\overline{\Omega }}}$, such that $\Gamma \cap \partial \Omega =\gamma (0)\cup \gamma (\ell )$ and $\Omega {\setminus }\Gamma$ is the union of two disjoint open sets with Lipschitz boundary;

• (H2) there exists a non-decreasing function $s:[0,T]\rightarrow (0,\ell )$ of class $C^{1,1}$ such that $\Gamma _t=\gamma ([0,s(t)])$;

• (H3) $|\dot{s}(t)|^2< \frac{\lambda _1}{C_K}$, where $\lambda _1$ is the ellipticity constant of ${\mathbb {C}}$ and $C_K$ is the constant that appears in Korn’s inequality in (2.2).

Notice that hypotheses (H1) and (H2) imply (E1)–(E3). We also assume that $\Psi$ satisfies (5.1) and there exists a constant $\epsilon >0$ such that for every $t\in [0,T]$

$$\begin{aligned} \Psi (t,x)=0\quad \text {for every }x\in \{y\in {{\overline{\Omega }}}:|y-\gamma (s(t))|<\epsilon \}. \end{aligned}$$

(5.7)

Theorem 5.5

Assume $d=2$ and (H1)–(H3), (5.1), and (5.7). Then the system (2.8) with boundary conditions (2.9)–(2.11) has a unique weak solution $u\in {\mathcal {W}}$ which satisfies the initial conditions $u(0)=u^0$ and $\dot{u}(0)=u^1$ in the sense of (2.16).

Proof

As before, let $u_1,u_2\in {\mathcal {W}}$ be two weak solutions to (2.8)–(2.11) with initial conditions (2.12). Then $u:=u_1-u_2$ satisfies (5.2) and (5.3) for every $\varphi \in {\mathcal {V}}^D$ such that $\varphi (T)=0$. Let us define

$$\begin{aligned} t_0:=\sup \{t\in [0,T]:u(s)=0\text { for every }s\in [0,t] \}, \end{aligned}$$

and assume by contradiction that $t_0<T$. Consider first the case in which $t_0>0$. By (H1), (H2), (5.1), and (5.7), we can find two open sets $A_1$ and $A_2$, with $A_1\subset \subset A_2\subset \subset \Omega$, and a number $\delta >0$ such that for every $t\in [t_0-\delta ,t_0+\delta ]$, we have $\gamma (s(t))\in A_1$, $\Psi (t,x)=0$ for every $x\in {\overline{A}}_2$, and $(A_2{\setminus } A_1)\setminus \Gamma$ is the union of two disjoint open sets with Lipschitz boundary. Let us define

$$\begin{aligned} {\hat{V}}^1:=\{u\in H^1((A_2{\setminus } A_1)\setminus \Gamma _{t_0-\delta };{\mathbb {R}}^2): u=0\text { on }\partial A_1\cup \partial A_2\},\quad {\hat{H}}^1:= L^2(A_2{\setminus } A_1;{\mathbb {R}}^2). \end{aligned}$$

Since every function in ${\hat{V}}^1$ can be extended to a function in $V_{t_0-\delta }^D$, by classical results for linear hyperbolic equations (see, e.g., [9]), we deduce ${\ddot{u}}\in L^2(t_0-\delta ,t_0+\delta ;({\hat{V}}^1)')$ and that u satisfies for a.e. $t\in (t_0-\delta ,t_0+\delta )$

$$\begin{aligned} \langle {\ddot{u}}(t), \phi \rangle _{({\hat{V}}^1)'}+({\mathbb {C}}Eu(t),E\phi )_{ {\hat{H}}^1}=0\quad \text {for every }\phi \in {\hat{V}}^1. \end{aligned}$$

Moreover, we have $u(t_0)=0$ as element of ${\hat{H}}^1$ and $\dot{u}(t_0)=0$ as element of $({\hat{V}}^1)'$, since $u(t)\equiv 0$ in $[t_0-\delta ,t_0)$, $u\in C^0([t_0-\delta ,t_0];{\hat{H}}^1)$, and $\dot{u}\in C^0([t_0-\delta ,t_0];({\hat{V}}^1)')$. We are now in position to apply the result of finite speed of propagation of Theorem 5.3. This theorem ensures the existence of the third open set $A_3$, with $A_1\subset \subset A_3\subset \subset A_2$, such that, up to choose a smaller $\delta$, we have $u(t)=0$ on $\partial A_3$ for every $t\in [t_0,t_0+\delta ]$, and both $(\Omega {\setminus } A_3)\setminus \Gamma$ and $A_3{\setminus } \Gamma$ are union of two disjoint open sets with Lipschitz boundary.

In $\Omega {\setminus } A_3$, the function u solves

$$\begin{aligned}&-\int _{t_0-\delta }^{t_0+\delta }\int _{\Omega {\setminus } A_3}\dot{u}(t,x)\cdot {\dot{\varphi }}(t,x)\,\mathrm {d}x\,\mathrm {d}t+\int _{t_0-\delta }^{t_0+\delta }\int _{\Omega {\setminus } A_3}\mathbb C(x)Eu(t,x)\cdot E\varphi (t,x)\,\mathrm {d}x\,\mathrm {d}t\\&\quad +\int _{t_0-\delta }^{t_0+\delta }\int _{\Omega {\setminus } A_3}\mathbb B(x)\Psi (t,x)E\dot{u}(t,x)\cdot \Psi (t,x)E\varphi (t,x)\,\mathrm {d}x\,\mathrm {d}t=0 \end{aligned}$$

for every $\varphi \in L^2(t_0-\delta ,t_0+\delta ;{\hat{V}}^2)\cap H^1(t_0-\delta ,t_0+\delta ;{\hat{H}}^2)$ such that $\varphi (t_0-\delta )=\varphi (t_0+\delta )=0$, where

$$\begin{aligned} {\hat{V}}^2:=\{u\in H^1((\Omega {\setminus } A_3)\setminus \Gamma _{t_0-\delta };{\mathbb {R}}^2): u=0\text { on }\partial _D\Omega \cup \partial A_3\},\quad \hat{H}^2:=L^2(\Omega {\setminus } A_3;{\mathbb {R}}^2). \end{aligned}$$

Since $u(t)=0$ on $\partial _D\Omega \cup \partial A_3$ for every $t\in [t_0-\delta ,t_0+\delta ]$ and $u(t_0-\delta )=\dot{u}(t_0-\delta )=0$ in the sense of (2.16) (recall that $u\equiv 0$ in $[t_0-\delta ,t_0)$), we can apply Lemma 5.2 to deduce $u(t)=0$ in $\Omega {\setminus } A_3$ for every $t\in [t_0-\delta ,t_0+\delta ]$.

On the other hand in $A_3$, by setting

$$\begin{aligned} {\hat{V}}^3_t:=\{u\in H^1(A_3{\setminus }\Gamma _t;{\mathbb {R}}^2): u=0\text { on }\partial A_3\},\quad {\hat{H}}^3:= L^2(A_3;{\mathbb {R}}^2), \end{aligned}$$

we get that the function u solves

$$\begin{aligned} -\int _{t_0-\delta }^{t_0+\delta }\int _{A_3}\dot{u}(t,x)\cdot \dot{\varphi }(t,x)\,\mathrm {d}x\,\mathrm {d}t&+\int _{t_0-\delta }^{t_0+\delta }\int _{ A_3}{\mathbb {C}}(x)Eu(t,x)\cdot E\varphi (t,x)\,\mathrm {d}x\,\mathrm {d}t=0 \end{aligned}$$

for every $\varphi \in L^2(t_0-\delta ,t_0+\delta ;\hat{V}^3_{t_0+\delta })\cap H^1(t_0-\delta ,t_0+\delta ;{\hat{H}}^3)$ such that $\varphi (t)\in {\hat{V}}^3_t$ for a.e. $t\in (t_0-\delta ,t_0+\delta )$ and $\varphi (t_0-\delta )=\varphi (t_0+\delta )=0$. Here, we would like to apply the uniqueness result of Theorem 5.4 for the spaces $\{{\hat{V}}_t^3\}_{t\in [t_0-\delta ,t_0+\delta ]}$ and $\hat{H}^3$, endowed with the usual norms, and for the bilinear form

$$\begin{aligned} a(u,v):=\int _{A_3}{\mathbb {C}}(x)Eu(x)\cdot Ev(x)\mathrm {d}x\quad \text {for every }u,v\in {\hat{V}}^3_{t_0+\delta }. \end{aligned}$$

As shown in [7, Example 2.14], we can construct $\Phi ,\Lambda \in C^{1,1}([t_0-\delta ,t_0+\delta ]\times \overline{A}_3;{\mathbb {R}}^2)$ such that for every $t\in [0,T]$, the function $\Phi (t,\cdot ):{\overline{A}}_3\rightarrow {\overline{A}}_3$ is a diffeomorphism of $A_3$ in itself with inverse $\Lambda (t,\cdot ):{\overline{A}}_3\rightarrow {\overline{A}}_3$. Moreover, $\Phi (0,y)=y$ for every $y\in {\overline{A}}_3$, $\Phi (t,\Gamma \cap {\overline{A}}_3)=\Gamma \cap {\overline{A}}_3$ and $\Phi (t,\Gamma _{t_0-\delta }\cap {\overline{A}}_3)=\Gamma _t\cap {\overline{A}}_3$ for every $t\in [t_0-\delta ,t_0+\delta ]$. For every $t\in [t_0-\delta ,t_0+\delta ]$, the maps $(Q_tu)(y):=u(\Phi (t,y))$, $u\in {\hat{V}}_t^3$ and $y\in A_3$, and $(R_tv)(x):=v(\Lambda (t,x))$, $v\in {\hat{V}}_{t_0-\delta }^3$ and $x\in A_3$, provide a family of linear and continuous operators which satisfy the assumptions (U1)–(U8) of Theorem 5.4 (see [8, Example 4.2]). The only condition to check is (U5). The bilinear form a satisfies the following ellipticity condition

$$\begin{aligned} a(u,u)\ge \lambda _1||Eu ||_{L^2(A_3;{\mathbb {R}}^{2\times 2}_\mathrm{{sym}})}^2\ge \frac{\lambda _1}{{\hat{C}}_k}||u ||_{\hat{V}_{t_0+\delta }^3}^2-\lambda _1||u ||_{{\hat{H}}^3}^2\quad \text {for every }u\in {\hat{V}}_{t_0+\delta }^3, \end{aligned}$$

(5.8)

where ${\hat{C}}_K$ is the constant in Korn’s inequality in $\hat{V}_{t_0+\delta }^3$, namely

$$\begin{aligned} ||\nabla u ||_{L^2(A_3;{\mathbb {R}}^{2\times 2})}^2\le \hat{C}_K(||u ||_{L^2(A_3;{\mathbb {R}}^2)}^2+||Eu ||_{L^2(A_3;{\mathbb {R}}^{2\times 2}_\mathrm{{sym}})}^2)\quad \text {for every }u\in {\hat{V}}_{t_0+\delta }^3. \end{aligned}$$

Notice that for $t\in [t_0-\delta ,t_0+\delta ]$

$$\begin{aligned} (\dot{R}_tv)(x)=\nabla v(\Lambda (t,x)){\dot{\Lambda }}(t,x)\quad \text {for a.e. }x\in A_3, \end{aligned}$$

from which we obtain

$$\begin{aligned} ||\dot{R}_tQ_tu ||_{{\hat{H}}^3}^2\le \int _{A_3}|\nabla u(x)|^2|{\dot{\Phi }}(t,\Lambda (t,x))|^2\,\mathrm {d}x. \end{aligned}$$

Hence, have to show the property

$$\begin{aligned} |{\dot{\Phi }}(t,y)|^2<\frac{\lambda _1}{{\hat{C}}_K}\quad \text {for every } t\in [t_0-\delta ,t_0+\delta ]\text { and } y\in {\overline{A}}_3. \end{aligned}$$

This is ensured by (H3). Indeed, as explained in [7, Example 3.1], we can construct the maps $\Phi$ and $\Lambda$ in such a way that

$$\begin{aligned} |{\dot{\Phi }}(t,y)|^2<\frac{\lambda _1}{C_K}, \end{aligned}$$

since $|\dot{s}(t)|^2<\frac{\lambda _1}{C_K}$. Moreover, every function in $\hat{V}^3_{t_0+\delta }$ can be extended to a function in $H^1(\Omega {\setminus }\Gamma ;{\mathbb {R}}^d)$. Hence, for Korn’s inequality in ${\hat{V}}_{t_0+\delta }^3$, we can use the same constant $C_K$ of $H^1(\Omega {\setminus }\Gamma ;{\mathbb {R}}^d)$. This allows us to apply Theorem 5.4, which implies $u(t)=0$ in $A_3$ for every $t\in [t_0,t_0+\delta ]$. In the case $t_0=0$, it is enough to argue as before in $[0,\delta ]$, by exploiting (5.2). Therefore, $u(t)=0$ in $\Omega$ for every $t\in [t_0,t_0+\delta ]$, which contradicts the maximality of $t_0$. Hence $t_0=T$, that yields $u(t)=0$ in $\Omega$ for every $t\in [0,T]$. $\square$

Remark 5.6

Also Theorem 5.5 is true in the antiplane case, with essentially the same proof. Notice that, when the displacement is scalar, we do not need to use Korn’s inequality in (5.8) to get the coercivity in ${\hat{V}}_{t_0+\delta }^3$ of the bilinear form a defined before. Therefore, in this case in (H3), it is enough to assume $|\dot{s}(t)|^2<\lambda _1$.

6 A moving crack satisfying Griffith’s dynamic energy-dissipation balance

We conclude this paper with an example of a moving crack $\{\Gamma _t\}_{t\in [0,T]}$ and weak solution to (2.8)–(2.12) which satisfy the energy-dissipation balance of Griffith’s dynamic criterion, as happens in [4] for the purely elastic case. In dimension $d=2$, we consider an antiplane evolution, which means that the displacement u is scalar, and $\Omega :=\{x\in {\mathbb {R}}^2:|x|<R\}$, with $R>0$. We fix a constant $0<c<1$ such that $cT<R$, and we set

$$\begin{aligned} \Gamma _t:=\{(\sigma ,0)\in {{\overline{\Omega }}}\,:\sigma \le ct\}. \end{aligned}$$

Let us define the following function

$$\begin{aligned} S(x_1,x_2):=\text {Im}(\sqrt{x_1+ix_2})=\frac{1}{\sqrt{2}}\frac{x_2}{\sqrt{|x|+x_1}}\quad x\in {\mathbb {R}}^2{\setminus }\{(\sigma ,0):\sigma \le 0\}, \end{aligned}$$

where $\text {Im}$ denotes the imaginary part of a complex number. Notice that the function S satisfies $S\in H^1(\Omega \setminus \Gamma _0)\setminus H^2(\Omega \setminus \Gamma _0)$, and it is a weak solution to

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta S=0 &{}\text {in } \Omega {\setminus } \Gamma _0,\\ \nabla S\cdot \nu =\partial _2S=0 &{}\text {on } \Gamma _0. \end{array}\right. } \end{aligned}$$

Let us consider the function

$$\begin{aligned} u(t,x):=\frac{2}{\sqrt{\pi }}S\left( \frac{x_1-ct}{\sqrt{1-c^2}},x_2\right) \quad t\in [0,T],\,x\in \Omega {\setminus }\Gamma _t \end{aligned}$$

and let w(t) be its restriction to $\partial \Omega$. Since u(t) has a singularity only at the crack tip (ct, 0), the function w(t) can be seen as the trace on $\partial \Omega$ of a function belonging to $H^2(0,T;L^2(\Omega ))\cap H^1(0,T;H^1(\Omega {\setminus }\Gamma _0))$, still denoted by w(t). It is easy to see that u solves the wave equation

$$\begin{aligned} {\ddot{u}}(t)-\Delta u(t)=0\quad \text {in }\Omega {\setminus }\Gamma _t,\,t\in (0,T), \end{aligned}$$

with boundary conditions

$$\begin{aligned}&u(t)=w(t)&\quad \quad \qquad \qquad \text {on } \partial \Omega , t\in (0,T),&\\&\frac{\partial u}{\partial \nu }(t)=\nabla u(t)\cdot \nu =0&\quad \qquad \qquad \text {on } \Gamma _t, \,\, t\in (0,T),&\end{aligned}$$

and initial data

$$\begin{aligned}&u^0(x_1,x_2):=\frac{2}{\sqrt{\pi }}S\left( \frac{x_1}{\sqrt{1-c^2}},x_2\right) \in H^1(\Omega {\setminus }\Gamma _0),\\&u^1(x_1,x_2):=-\frac{2}{\sqrt{\pi }}\frac{c}{\sqrt{1-c^2}}\partial _1 S\left( \frac{x_1}{\sqrt{1-c^2}},x_2\right) \in L^2(\Omega ). \end{aligned}$$

Let us consider a function $\Psi$ which satisfies the regularity assumptions (5.1) and condition (5.7), namely

$$\begin{aligned} \Psi (t)=0\quad \text {on } B_\epsilon (t):=\{x\in {\mathbb {R}}^2:|x-(ct,0)|<\epsilon \} \text { for every } t\in [0,T], \end{aligned}$$

with $0<\epsilon <R-cT$. In this case, u is a weak solution, in the sense of Definition 2.4, to the damped wave equation

$$\begin{aligned} {\ddot{u}}(t)-\Delta u(t)-\mathrm{div}(\Psi ^2(t)\nabla {\dot{u}}(t))=f(t)\quad \text {in }\in \Omega {\setminus }\Gamma _t,\,t\in (0,T), \end{aligned}$$

with forcing term f given by

$$\begin{aligned} f:=-\mathrm{div}(\Psi ^2\nabla \dot{u})=-\nabla \Psi \cdot 2\Psi \nabla \dot{u}-\Psi ^2\Delta \dot{u}\in L^2(0,T;L^2(\Omega )), \end{aligned}$$

and boundary and initial conditions

$$\begin{aligned}&u(t)=w(t)&\qquad \qquad \qquad \qquad \text {on } \partial \Omega , t\in (0,T),&\\&\frac{\partial u}{\partial \nu }(t)+\Psi ^2(t) \frac{\partial \dot{u}}{\partial \nu }(t)=0&\qquad \qquad \quad \text {on } \Gamma _t,\,\, t\in (0,T),&\\&u(0)=u^0,\quad \dot{u}(0)=u^1. \end{aligned}$$

Notice that to derive the homogeneous Neumann boundary conditions on $\Gamma _t$, we used $\frac{\partial \dot{u}}{\partial \nu }(t)=\nabla {\dot{u}}(t)\cdot \nu =\partial _2{\dot{u}}(t)=0$ on $\Gamma _t$. By the uniqueness result proved in the previous section, the function u coincides with that one found in Theorem 3.1. Thanks to the computations done in [4, Section 4], we know that u satisfies for every $t\in [0,T]$ the following energy-dissipation balance for the undamped equation, where ct coincides with the length of $\Gamma _t{\setminus }\Gamma _0$

$$\begin{aligned} \frac{1}{2}||{\dot{u}}(t) ||^2_{L^2(\Omega )}+\frac{1}{2}||\nabla u(t) ||^2_{L^2(\Omega ;{\mathbb {R}}^2)}+ct&=\frac{1}{2}||\dot{u}(0) ||^2_{L^2(\Omega )}+\frac{1}{2}||\nabla u(0) ||^2_{L^2(\Omega ;{\mathbb {R}}^2)}\nonumber \\&\quad +\int _0^t\left( \frac{\partial u}{\partial \nu }(s),\dot{w}(s)\right) _{L^2(\partial \Omega )}\,\mathrm {d}s. \end{aligned}$$

(6.1)

Moreover, we have

$$\begin{aligned} \begin{aligned} \int _0^t\left( \frac{\partial u}{\partial \nu }(s),\dot{w}(s)\right) _{L^2(\partial \Omega )}\,\mathrm {d}s&=\int _0^t(\nabla u(s),\nabla \dot{w}(s))_{L^2(\Omega ;{\mathbb {R}}^2)}\,\mathrm {d}s-\int _0^t (\dot{u}(s),\ddot{w}(s))_{L^2(\Omega )}\,\mathrm {d}s\\&\quad +({\dot{u}}(t),\dot{w}(t))_{L^2(\Omega )}-(\dot{u}(0),\dot{w}(0))_{L^2(\Omega )}. \end{aligned} \end{aligned}$$

(6.2)

For every $t\in [0,T]$, we compute

$$\begin{aligned} (f(t),{\dot{u}}(t)-\dot{w}(t))_{L^2(\Omega )}&=-\int _{(\Omega {\setminus } B_\epsilon (t)){\setminus }\Gamma _t}\mathrm{div}[\Psi ^2(t,x)\nabla \dot{u}(t,x)](\dot{u}(t,x)-\dot{w}(t,x))\,\mathrm {d}x\\&=-\int _{(\Omega {\setminus } B_\epsilon (t)){\setminus }\Gamma _t}\mathrm{div}[\Psi ^2(t,x)\nabla \dot{u}(t,x)(\dot{u}(t,x)-\dot{w}(t,x))]\,\mathrm {d}x\\&\quad +\int _{(\Omega {\setminus } B_\epsilon (t)){\setminus }\Gamma _t}\Psi ^2(t,x)\nabla \dot{u}(t,x)\cdot (\nabla \dot{u}(t,x)-\nabla \dot{w}(t,x))\,\mathrm {d}x. \end{aligned}$$

If we denote by $\dot{u}^\oplus (t)$ and $\dot{w}^\oplus (t)$ the traces of ${\dot{u}}(t)$ and $\dot{w}(t)$ on $\Gamma _t$ from above and by $\dot{u}^\ominus (t)$ and $\dot{w}^\ominus (t)$ the trace from below, thanks to the divergence theorem, we have

$$\begin{aligned}&\int _{(\Omega {\setminus } B_\epsilon (t)){\setminus }\Gamma _t}\mathrm{div}[\Psi ^2(t,x)\nabla \dot{u}(t,x)(\dot{u}(t,x)-\dot{w}(t,x))]\,\mathrm {d}x\\&\quad =\int _{\partial \Omega } \Psi ^2(t,x)\frac{\partial \dot{u}}{\partial \nu }(t,x)(\dot{u}(t,x)-\dot{w}(t,x))\,\mathrm {d}x\\&\qquad +\int _{\partial B_\epsilon (t)} \Psi ^2(t,x)\frac{\partial \dot{u}}{\partial \nu }(t,x)(\dot{u}(t,x)-\dot{w}(t,x))\,\mathrm {d}x\\&\qquad -\int _{(\Omega {\setminus } B_\epsilon (t))\cap \Gamma _t} \Psi ^2(t,x)\partial _2 \dot{u}^\oplus (t,x)(\dot{u}^\oplus (t,x)-\dot{w}^\oplus (t,x))\,\mathrm {d}{\mathcal {H}}^1(x)\\&\qquad +\int _{(\Omega {\setminus } B_\epsilon (t))\cap \Gamma _t} \Psi ^2(t,x)\partial _2 \dot{u}^\ominus (t,x)(\dot{u}^\ominus (t,x)-\dot{w}^\ominus (t,x))\,\mathrm {d}{\mathcal {H}}^1(x)=0, \end{aligned}$$

since $u(t)=w(t)$ on $\partial \Omega$, $\Psi (t)=0$ on $\partial B_\epsilon (t)$, and $\partial _2{\dot{u}}(t)=0$ on $\Gamma _t$. Therefore, for every $t\in [0,T]$, we get

$$\begin{aligned} (f(t),{\dot{u}}(t)-\dot{w}(t))_{L^2(\Omega )}=\Vert \Psi (t)\nabla {\dot{u}}(t)\Vert ^2_{L^2(\Omega ;{\mathbb {R}}^2)}-(\Psi (t)\nabla {\dot{u}}(t),\Psi (t)\nabla \dot{w}(t))_{L^2(\Omega ;{\mathbb {R}}^2)}. \end{aligned}$$

(6.3)

By combining (6.1)–(6.3), we deduce that u satisfies for every $t\in [0,T]$ the following Griffith’s energy-dissipation balance for the viscoelastic dynamic equation

$$\begin{aligned} \begin{aligned}&\frac{1}{2}||{\dot{u}}(t) ||^2_{L^2(\Omega )}+\frac{1}{2}||\nabla u(t) ||^2_{L^2(\Omega ;{\mathbb {R}}^2)}+\int _0^{t} ||\Psi (s) \nabla {\dot{u}}(s) ||^2_{L^2(\Omega ;{\mathbb {R}}^2)}\,\mathrm {d}s+ct\\&\quad = \frac{1}{2}||\dot{u}(0) ||^2_{L^2(\Omega )}+\frac{1}{2}||\nabla u(0) ||^2_{L^2(\Omega ;{\mathbb {R}}^2)}+{\mathcal {W}}_\mathrm{{tot}}(t), \end{aligned} \end{aligned}$$

(6.4)

where in this case, the total work takes the form

$$\begin{aligned} {\mathcal {W}}_\mathrm{{tot}}(t)&:=\int _0^t \left[ (f(s),\dot{u}(s)-\dot{w}(s))_{L^2(\Omega )}+(\nabla u(s),\nabla \dot{w}(s))_{L^2(\Omega ;{\mathbb {R}}^2)}\right] \,\mathrm {d}s\\&\quad +\int _0^t(\Psi (s)\nabla \dot{u}(s),\Psi (s)\nabla \dot{w}(s))_{L^2(\Omega ;{\mathbb {R}}^2)}\mathrm {d}s\\&\quad -\int _0^t (\dot{u}(s),{\ddot{w}}(s))_{L^2(\Omega )}\,\mathrm {d}s+({\dot{u}}(t),\dot{w}(t))_{L^2(\Omega )}-(\dot{u}(0),\dot{w}(0))_{L^2(\Omega )}. \end{aligned}$$

Notice that equality (6.4) gives (1.6). This shows that in this model Griffith’s dynamic energy-dissipation balance can be satisfied by a moving crack, in contrast with the case $\Psi =1$, which always leads to (1.3).