Resolvability in circulant graphs

Abstract

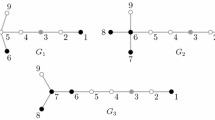
A set W of the vertices of a connected graph G is called a resolving set for G if for every two distinct vertices u, υ ∈ V (G) there is a vertex w ∈ W such that d(u,w) ≠ d(υ,w). A resolving set of minimum cardinality is called a metric basis for G and the number of vertices in a metric basis is called the metric dimension of G, denoted by dim(G). For a vertex u of G and a subset S of V (G), the distance between u and S is the number min_s∈S d(u, s). A k-partition Π = {S ₁, S ₂, …, S _k } of V (G) is called a resolving partition if for every two distinct vertices u, v ∈ V (G) there is a set S _i in Π such that d(u, S _i ) ≠ d(v, S _i ). The minimum k for which there is a resolving k-partition of V (G) is called the partition dimension of G, denoted by pd(G). The circulant graph is a graph with vertex set ℤ _n , an additive group of integers modulo n, and two vertices labeled i and j adjacent if and only if i − j (mod n) ∈ C, where C ∈ ℤ _n has the property that C = −C and 0 ∉ C. The circulant graph is denoted by X _n,Δ where Δ = |C|. In this paper, we study the metric dimension of a family of circulant graphs X _n,3 with connection set $C = \left\{ {1,\tfrac{n} {2},n - 1} \right\}$ and prove that dim(X _n,3) is independent of choice of n by showing that

$$\dim \left( {X_{n,3} } \right) = \left\{ \begin{gathered} 3 for all n \equiv 0 (mod 4), \hfill \\ 4 for all n \equiv 2 (mod 4). \hfill \\ \end{gathered} \right.$$

We also study the partition dimension of a family of circulant graphs X _n,4 with connection set C = {±1,±2} and prove that pd(X _n,4) is independent of choice of n and show that pd(X _5,4) = 5 and

$$pd\left( {X_{n,4} } \right) = \left\{ \begin{gathered} 3 for all odd n \geqslant 9, \hfill \\ 4 for all even n \geqslant 6 and n = 7. \hfill \\ \end{gathered} \right.$$

.