Bipolar method and its modifications

Abstract

Bipolar is one of the multiple criteria decision analysis methods, proposed by Konarzewska-Gubała (in Archiwum Automatyki i Telemechaniki 32(4):289–300, 1987). The main feature of the method is that alternatives are not compared directly with each other, but they are confronted to the two reference sets of objects: desirable and non-acceptable. Practical application of the method revealed its shortcomings, therefore improvements of the method were desirable. The aim of the paper is to formulate some modifications of the classical Bipolar approach and consider a case where reference sets are numerous. Unified Bipolar procedure which contains classical Bipolar method as well as the modifications described in the paper is given. Numerical illustrations of the modifications and unified approach are also presented.

1 Introduction

One of the multiple criteria decision analysis (MCDA) methods is Bipolar proposed by Konarzewska-Gubała (1987). The method is based on the concept of two bipolar sets of reference objects. The practical application of the method revealed its shortcomings, therefore improvements of the method were desirable. The aim of the paper is to formulate some modifications of the classical Bipolar approach, which will help to overcome the difficulties encountered. In one of the modifications we consider a case where reference sets are numerous. Unified Bipolar procedure which contains classical Bipolar method as well as all the modifications described in the paper is given.

The paper consists of nine sections. Section 2 is an overview of MCDM methods and a comparison of the main notions of the Bipolar method with those methods. In Sect. 3 a formal presentation of the classical Bipolar method, based on the description presented in Trzaskalik and Sitarz (2012) is given. The first suggestion presented in Sect. 4 refers to the modification of one of the reference sets. In the second suggestion, the set of categories used in bipolar sorting is enlarged. New propositions are illustrated by simple numerical examples. Section 5 suggests a modification of the method of comparing decision variants with the elements of the reference system and of the method of determining the position of the decision variant with respect to a bipolar reference system. Section 6 suggests a method of aiding a decision maker in the determination of criteria weights and veto threshold values. Section 7 presents a procedure to be applied in the Bipolar method which takes into account the modifications suggested in the paper. Section 8 presents a numerical example that includes the modifications of the methods introduced in Sects. 5 and 6. The concluding remarks, which include references to applications of Bipolar methodology and directions of further research, end the paper. Early versions of the paper can be found in Trzaskalik and Sitarz (2012) and Trzaskalik et al. (2013).

2 The Bipolar approach as compared with other MCDA methods

2.1 Overview of MCDA methods

Discrete multi-criteria problems can be formulated as follows: given a finite set of alternatives which are evaluated using certain criteria, the decision maker intends to achieve one of the following goals (Figueira et al. 2005):

• Select the alternative which best corresponds to his/her preferences (the problem of selection);

• Order the alternatives from the best to the worst (the problem of ordering);

• Assign each alternative to one of predefined classes (the problem of multi-criteria classification).

Among multi-criteria problems one can distinguish deterministic, stochastic, and fuzzy problems. In deterministic problems, the evaluations of alternatives with respect to criteria are numbers. The set of all evaluations forms the decision table. In stochastic problems, the evaluation of each alternative with respect to the criteria is a discrete random variable with a known probability distribution. To compare decision variants, selection rules based on stochastic dominations are most often used. In fuzzy problems, the evaluations of alternatives are fuzzy numbers (usually triangular fuzzy numbers). The problems are usually solved in two stages. In the first stage the decision variants are compared using certain criteria. In the second stage, a synthesis of the results is performed, in various ways (Trzaskalik 2014).

Among the oldest multi-criteria methods are additive methods, such as the SAW method (Simple Additive Weighting Method) (Churchman and Ackoff 1954). The decision maker’s preferences are modeled using an additive linear function. An extension of this method is the F-SAW method (Fuzzy Simple Additive Weighing Method) (Tzeng and Huang 2011), in which triangular fuzzy numbers are used, and their parameters can be obtained through a dialogue with an expert. In both the SMART method (Simple Multi-Attribute Ranking Technique) (Edwards 1971), and in the SMARTER method (Simple Multi-Attribute Ranking Technique Exploiting Ranks) (Edwards and Barron 1994) the weights of criteria are obtained by comparing the changes of states from the least desired to the most desired with respect to one criterion, with those with respect to another criterion. The final evaluation is interpreted as the global utility of the given variant.

Analytical hierarchization and related methods are commonly used, in particular the AHP method (Analytical Hierarchy Process) (Saaty 1980). This method allows to form a scale vector whose components permit to order decision variants and to select the best one. The vector is formed using verbal pairwise comparisons of the criteria and of the decision variants with respect to the criteria. Fuzzy versions of this method also exist, such as F-AHP (Fuzzy Analytic Hierarchy Process) (Mikhailov and Tzvetinov 2004).

In the REMBRANDT method (Ratio Estimation in Magnitudes or deciBells to Rate Alternatives which are Non-DominaTed) method (Lootsma 1992), the Saaty scale is replaced by the logarithmic scale, and the Perron-Frobenius eigenvalue method, by the logarithmic least squares method. This method constitutes a reply to the criticism of AHP, concerning the evaluation scale used, the method of obtaining a synthetic evaluation of the variants, and the possible changes in the ranking when a new variant is added. In the ANP method (Analytic Network Process) (Saaty 1996), the assumption of the preferential independence of criteria—used in other methods—is abandoned, which allows to take into account relationships among the criteria and between the criteria and the alternatives. An example of the fuzzy variant of this method is F-ANP (Fuzzy Analytic Network Process) (Tzeng and Huang 2011). In the MACBETH method (Measuring Attractiveness by a Categorical Based Evaluation TecHnique) (Bana e Costa and Vansnick 1993), the relative attractiveness of the elements compared (ordinal evaluation) is determined, and then—when the given elements are not regarded as equally attractive—a qualitative evaluation of the difference between the more attractive and the less attractive elements is expressed using a set of six semantic categories.

Verbal Decision Analysis (VDA) is used to analyze unstructured problems, with mostly qualitative parameters, for which there is no objective model of aggregation. It uses verbal evaluations to which no quantitative operations can be applied. The ZAPROS method (Russian: ЗAмкнyтыe ПPoцeдypы y Oпopныx Cитyaций, Closed Procedures at Reference Situations) (Larichev and Moskovich 1995) and its modification, ZAPROS III, use verbal ordinal scales. In the method proposed by Larichev (2001), the Joint Ordinal Scale is created on the basis of the decision maker’s preferences and a partial ordering on the set of decision variants is formed.

Methods from the ELECTRE family (fr. ELimination Et Choix Traduisant la REalia), developed by B. Roy and his collaborators, play an important role in the development of multi-criteria methods. Roy suggests to extend the set of basic preference situations so as to include the situations of equivalence, weak preference, strong preference, and incomparability. Moreover, he defines grouped relations, which—together with the application of equivalence and preference thresholds, as well as of the principle of limited compensation—allows to define a fuzzy relation called the outranking relation. An entire family of methods, which includes ELECTRE I, ELECTRE Iv, ELECTRE Is, ELECTRE III, ELECTRE TRI, ELECTRE IV (Roy and Bouyssou 1993), had been created using these assumptions. An approach combining ELECTRE with stochastic dominations can be found in the papers (Zaras and Martel 1994; Nowak 2005).

The methods from the PROMETHEE (Preference Ranking Organisation METHod for Enrichment Evaluations) group take into account the differences between the evaluations of alternatives for all criteria. The greater the difference between the evaluations, the stronger (with respect to the given criterion) the preference for one of the alternatives. Each criterion has a preference function assigned, with values from the interval [0, 1], measuring the strength of the preference. A characteristic feature here is the use of preference flows. Among basic methods in this group are: PROMETHEE I (Brans 1982), which allows to partially order the alternatives, and PROMETHEE II, which allows to order them completely. A method proposed in the paper (Górecka and Muszyńska 2011) combines elements of ELECTRE and PROMETHEE II, with veto thresholds added. Another modification is the EXPROM method (EXtension of the PROMethee method) (Diakoulaki and Koumoutsos 1991), which uses the ideal and anti-ideal variants. Adding veto thresholds to EXPROM has been suggested in the paper (Górecka and Szalucka 2013). A stochastic variant of PROMETHEE II with veto thresholds and stochastic dominations has been proposed in the paper (Nowak 2005). An extension of the EXPROM II method, on the other hand, with veto thresholds and stochastic dominations, can be found in the papers (Górecka 2010a, b).

Using an interactive approach, we assume that the decision maker is able to supply local information, that is, to evaluate an individual alternative or a small subset of alternatives. Each iteration consists of two stages: dialogue with the decision maker and calculations. In the dialogue stage the decision maker is asked to express his/her preferences by formulating an opinion about the values of the parameters which describe the consequences of the selection of the proposed decision variants. The decision makers reveals his/her preferences by evaluating the proposed solution and indicating how it can be improved. The process is continued until a solution satisfactory for the decision maker is found. Interactive stochastic methods include: STEP-DPR (STEP Method for Discrete Decision Making Problems under Risk) (Nowak 2008), INSDECM (INteractive Stochastic DECision Making Procedure) (Nowak 2006), ATO-DPR (Analysis of Trade-Offs for Discrete Decision Making Problems under Risk) (Nowak 2010).

A very popular approach, which is the focus of our attention in this paper, is an approach using reference points. One of the best known methods of this kind is the TOPSIS method (Technique for Order Preference by Similarity to Ideal Solution) (Hwang and Yoon 1981), in which the alternatives considered are compared with abstract weighed reference solutions: ideal and anti-ideal. It has a fuzzy counterpart, namely F-TOPSIS (Fuzzy Technique for Order Preference by Similarity to Ideal Solution) (Jahanshahloo et al. 2006). The values of the criteria characterizing the alternatives are given as triangular fuzzy numbers. The VIKOR method (Serbian: VIseKriterijumska Optimizacija I Kompromisno Resenje, Multicriteria Optimization and Compromise Solution) (Opricovic 1998) is very often used, thanks to the paper (Opricovic and Tzeng 2004), whose authors compare it to TOPSIS. The ideal and anti-ideal variants are the reference points. Combining the three methods: DEMATEL, ANP i VIKOR (Tzeng and Huang 2011) allows to consider decision problems with interdependent criteria and variants. The first one, DEMATEL (DEcision Making Trial and Evaluation Laboratory) (Gabus and Fontela 1973), explains the interdependencies among the model’s elements without the need to perform tedious pairwise comparisons. To obtain the limit supermatrix, the ANP method is used, while the final ordering is obtained using the VIKOR method.

2.2 The Bipolar method

Let us focus on Bipolar method (Konarzewska-Gubała 1987, 1989). To accept the notion of bipolar reference system, applied in the method, it is worth while to follow the evolution of the notion of the ideal solution, which can be traced in a large variety of papers in different fields: goal programming, compromise programming, multidimensional statistical analysis or game theory. The author of the method claims that due to the large number of ideals, as well as to the fuzziness and imprecision of their definitions, the ideal “point” is not perceived as a point but, rather, as a set (“cloud”). The question arises: do humans try to reach success (“ideal”) with the same intensity as they want to avoid failure (“anti-ideal”). It follows from the descriptive models that the motivation to reach success and the motivation to avoid failure are not entirely symmetrical. Therefore, the final evaluation of an alternative is based on its independent “position” with regard to both subsets called “ideal” and “anti-ideal” (Konarzewska-Gubała 1987, 1989).

The main feature of the analysis in the Bipolar method is that the decision alternatives are not compared directly with each other, but by means of two sets of reference objects: desirable (“good”) and non-acceptable (“bad”). These two disjoint sets form the bipolar reference system. It is assumed that the decision maker applying the Bipolar method in practice, on the basis of her/his experience, opinions gathered and studies undertaken, is able to create such a system.

In the first phase of the Bipolar method alternatives are compared to reference objects and, as a result, outranking indicators and preference structure in the reference system are established. In this phase the notions of concordance and veto thresholds, introduced in Electre methodology (Roy 1985) can be recognized. In the second phase of the method the position of each alternative with respect to the bipolar reference system is established. This phase is influenced by algorithms of confrontation (Merighi 1980). Finally, in the third phase a bipolar partial preordering is obtained, as the intersection of two mono-sortings of alternatives into specified categories and two partial preorderings (mono-orders) introduced independently in the set of alternatives.

The Bipolar method has been applied in modeling of multi-stage multi-criteria decision processes (Trzaskalik 1987). Modifications of this approach also exist (Górecka 2009). The changes, as compared with the original BIPOLAR method, consist in using, in the first stage of the procedure, the distributions of the evaluations of variants with respect to each criterion and in the application of SD (Stochastic Dominance) rules, as well as in the application of the notion of a pseudo-criterion and the determination of the position of the variants investigated with respect to the bipolar reference system. (Here, the idea behind the PROMETHEE II method can be recognized.) BIPOLAR MIX (Górecka 2017a, b) is another methodological proposal, which allows to use data in various forms.

The Bipolar method belongs to a group of methods that involve reference objects for comparison of alternatives. We can also mention to other bi-reference methods described in the papers Michałowski and Szapiro (1992) and Skulimowski (1996). Decision support system reference sets and the rough sets methodology is described in (Greco et al. 2002). More recently the paper Chen (2011) develops optimistic and pessimistic estimations with several fuzzy point operators. A new notion of a bipolar query against collections of textual documents is introduced in Zadrożny et al. (2012). The paper Bouzarour-Amokrane et al. (2015) addresses collaborative group decision making problems using a consensus process to achieve a joint legitimate solution. The proposed resolution model is based on individual bipolar assessments. The model proposed in Shen and Tzeng (2016) provides a bipolar approach to guide businesses towards systematic improvements. In Wang et al. (2018) MCDM methods are investigated in a bipolar neutrosophic environment. Bipolar 2-tuple linguistic aggregation operators are developed in Lu et al. (2017) for aggregation operations. The paper Liu et al. (2018) aims to develop a dynamic linguistic multi-criteria decision making model dealing with bipolar linguistic scales in which both alternatives and criteria may vary across time.

In the classical Bipolar procedure, described in Konarzewska-Gubała (1987, 1989), some alternatives can be evaluated as better than “good” objects from the reference system. Such alternatives are named “overgood”. Other alternatives can be evaluated as worse than “bad” objects from the reference system. Such alternatives are named “underbad”. A question arises: is it possible for an alternative to be “overgood” and “underbad” simultaneously? The author claims that if the reference sets of “bad” and “good” objects are disjoint and Assumption 2, formulated as follows.

there does not exist a “good” reference object and a “bad” reference object such that the “good” reference object is dominated (in the sense of the classical domination relation) by the “bad” reference object.

holds, then such a situation (which at first seems unreasonable) cannot occur.

Attempts at using the Bipolar method in practice together with Assumption 2—particularly when the sets of reference objects are created using historical data—have shown that it was frequently possible for some alternatives to be “underbad” and “overgood” simultaneously. This feature was pointed out by Dominiak (1996) in the application of the method to the selection of securities at a stock exchange. The situation in question is eliminated if Assumption 1, formulated as follows:

each “good” reference object dominates each “bad” reference object.

is satisfied.

Assumption 1 is over-restrictive, therefore it is often impossible for decision makers to apply the approach in real-life decision problems. It seems that it is necessary to include new concepts in the Bipolar methodology. Hence, the present paper formulates modifications of the classical Bipolar approach. The selection of one or several of the presented possibilities should be performed together with a decision maker willing to apply the Bipolar approach. The present paper will also consider a case where reference sets are large (as it may happen when they are created from historical data) and suggest changes to the original version of the Bipolar method.

3 The classical Bipolar method

In this section a formal presentation of the classical Bipolar method is given. Such a new description [prepared by the authors of the paper and first presented in Trzaskalik and Sitarz (2012)] seems necessary for the presentation of modifications to the Bipolar method, presented in the next sections of the paper.

It is assumed, that there are given: the set of decision alternatives A = {a¹, a²,…, a^m} and the set of criteria functions F = {f₁,…,f_n}, where f_k: A→ K_k for k = 1, …, n, and K_k is a cardinal, ordinal or binary scale. Criteria are defined in such a way that higher values are preferred to lower values.¹ For each criterion the decision maker establishes weight w_k of relative importance (it is assumed, that $\sum\nolimits_{k = 1}^{n} {w_{k} } = 1$ and w_k≥ 0 for each k = 1, …, n), equivalence threshold q_k and veto threshold v_k. The decision maker also establishes minimal criteria values concordance level s as the outranking threshold. It is assumed, that condition 0.5 ≤ s ≤ 1 holds.

The decision maker establishes a bipolar reference system R = G ∪ B, which consists of the set of “good” objects G = {g¹, …, g^g}and the set of “bad” objects B = {b¹, …, b^b}, where g and b denote the number of “good” and “bad” objects, respectively. It is assumed, that G ∩ B = ∅. The number of elements of the set R is equal to g + b. Elements of the set R are denoted as r^h, h = 1, …, g + b. Values f_k(r^h) for k = 1, …, n and h = 1, …, r are known.

We assume, that condition

$$ \forall_{k = 1, \ldots ,n} \forall_{{{\mathbf{g}} \in {\mathbf{G}}}} \forall_{{{\mathbf{b}} \in {\mathbf{B}}}} f_{k} \left( {\mathbf{g}} \right) \ge f_{k} \left( {\mathbf{b}} \right) $$

(1)

holds (Assumption 1).

3.1 Comparison of alternatives to reference objects

3.1.1 Outranking indicators

For the pair (aⁱ, r^j), where aⁱ ∈ A, r^j ∈ R, the following values:

$$ \begin{aligned} c^{ + } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right) = & \sum\limits_{k = 1}^{n} {w_{k} } \varphi_{k}^{ + } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right)\;{\text{where}}\quad \varphi_{k}^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;f_{k} \left( {{\mathbf{a}}^{i} } \right) - f_{k} \left( {{\mathbf{r}}^{j} } \right) > q_{k} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ c^{ - } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right) = & \sum\limits_{k = 1}^{n} {w_{k} } \varphi_{k}^{ - } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right)\;{\text{where}}\quad \varphi_{k}^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;f_{k} \left( {{\mathbf{r}}^{j} } \right) - f_{k} \left( {{\mathbf{a}}^{i} } \right) > q_{k} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ c^{ = } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right) = & \sum\limits_{k = 1}^{n} {w_{k} } \varphi_{k}^{ = } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right)\;{\text{where}}\quad \varphi_{k}^{ = } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {{\text{if}}\;\left| {f_{k} \left( {{\mathbf{r}}^{j} } \right) - f_{k} \left( {{\mathbf{a}}^{i} } \right)} \right| \le q_{k} } \hfill \\ {0,} \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. \\ \end{aligned} $$

are calculated.

The value $c^{ + } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right)$ is the sum of the criteria weights for which aⁱ is preferred to r^j with equivalence threshold q_k; the value $c^{ - } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right)$ is the sum of the criteria weights for which r^j is preferred to aⁱ with equivalence threshold q_k; and the value $c^{ = } \left( {{\mathbf{a}}^{i} ,\,{\mathbf{r}}^{j} } \right)$ is the sum of the criteria weights for which aⁱ is equal to r^j with equivalence threshold q_k.

Sets of indices:

$$ I^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = \left\{ {k:\;\varphi_{k}^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 1} \right\}\quad I^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = \left\{ {k:\,\,\varphi_{k}^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 1} \right\} $$

are determined.

The set $I^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right)$ consists of those criteria indices for which aⁱ is preferred to r^j, while the set $I^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right)$ consists of those criteria indices for which r^j is preferred to aⁱ.

Let ν_k be threshold values given for k = 1, …, n by the decision maker. Condition

$$ \mathop \forall \limits_{{k \in I^{ - } \,}} f_{k} \left( {{\mathbf{a}}^{i} } \right) > v_{k} $$

is called the veto test.

For $k \in I^{ - }$, the veto test is positively verified if r^j is preferred to aⁱ and the value of the criteria function is greater than the given threshold ν_k.

Conditions

$$ \mathop \forall \limits_{{k \in I^{ - } }} \quad f_{k} \left( {{\mathbf{a}}^{i} } \right) > v_{k} \quad \quad \mathop \forall \limits_{{k \in I^{ + } }} \quad f_{k} \left( {{\mathbf{a}}^{i} } \right) > v_{k} $$

are called non-discordance tests. The interpretation of non-discordance tests is analogous to that of the veto test.

Case 1 c⁺(aⁱ, r^j) > c⁻(aⁱ, r^j).

• If for the pair (aⁱ, r^j) veto test is positively verified, then outranking indicators are defined as follows:

  $$ d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = c^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) + c^{ = } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right),\quad d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 0 $$

• If for the pair (aⁱ, r^j) veto test is not positively verified, then outranking indicators are defined as follows:

  $$ d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 0,\quad d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 0 $$

Case 2 c⁺(aⁱ, r^j) < c⁻(aⁱ, r^j).

• If for the pair (aⁱ, r^j) veto test is positively verified, then outranking indicators are defined as follows:

  $$ d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 0,\quad d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = c^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) + c^{ = } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) $$

• If for the pair (aⁱ, r^j) veto test is not positively verified, then outranking indicators are defined as follows:

  $$ d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 0\quad d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 0 $$

Case 3 c⁺(aⁱ, r^j) = c⁻(aⁱ, r^j).

• If for the pair (aⁱ, r^j) two non-discordance tests are positively verified, then outranking indicators are defined as follows:

  $$ d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = c^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) + c^{ = } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right)\quad d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = c^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) + c^{ = } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) $$

• For the pair (aⁱ, r^j) at least one of non-discordance tests is not positively verified, then outranking indicators are defined as follows:

  $$ d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 0,\quad d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) = 0. $$

The outranking indicators defined above are measures of being better (d⁺) or being worse (d⁻), with equivalence threshold q_k and veto threshold ν_k. Moreover, they satisfy the following conditions: d⁺(aⁱ, r^j) ∈ [0, 1] and d⁻(aⁱ, r^j) ∈ [0, 1].

3.1.2 Preference structure

By means of outranking indicators three relationships: large preference L_s, indifference I_s and incomparability R_s are defined as follows:

$$ \begin{aligned} & {\mathbf{a}}^{i} {\text{L}}_{\text{s}} {\mathbf{r}}^{h} \quad {\text{iff}}\;d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{h} } \right) > {\text{s}} \wedge d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{h} } \right) = 0 \\ & {\mathbf{r}}^{j} {\text{L}}_{\text{s}} {\mathbf{a}}^{i} \quad {\text{iff}}\;d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{h} } \right) = 0 \wedge d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{h} } \right) > {\text{s}} \\ & {\mathbf{a}}^{i} {\text{I}}_{\text{s}} {\mathbf{r}}^{h} \quad {\text{iff}}\;d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{h} } \right) > {\text{s}} \wedge d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{h} } \right) > {\text{s}} \\ & {\mathbf{a}}^{i} {\text{R}}_{\text{s}} {\mathbf{r}}^{j} \quad {\text{otherwise}} \\ \end{aligned} $$

The interpretations of these relations are as follows:

• Large preference (aⁱ L_sr^h) means that aⁱ is preferred to r^h with outranking threshold s ∈ [0.5, 1]. We interpret large preference (r^j L_saⁱ) analogically.

• Indifference aⁱ I_sr^h means that aⁱ is indifferent to r^h with outranking threshold s. This can only hold if c⁺(aⁱ, r^j) = c⁻(aⁱ, r^j) and two non-discordance tests are positively verified.

• Incomparability aⁱ R_sr^j means that aⁱ and r^h are incomparable.

3.2 Position of an alternative in relation to the bipolar reference system

3.2.1 Success achievement degree

For a given aⁱ ∈ A auxiliary sets of indices are defined as follows:

$$ \begin{aligned} L_{s} \left( {{\mathbf{a}}^{i} ,{\mathbf{G}}} \right) = & \left\{ {h:{\mathbf{a}}^{i} {\text{L}}_{\text{s}} {\mathbf{g}}^{h} ,{\mathbf{g}}^{h} \in {\mathbf{G}}} \right\} \\ I_{s} \left( {{\mathbf{a}}^{i} ,{\mathbf{G}}} \right) = & \left\{ {h:{\mathbf{a}}^{i} {\text{I}}_{\text{s}} {\mathbf{g}}^{h} ,{\mathbf{g}}^{h} \in {\mathbf{G}}} \right\} \\ L_{s} \left( {{\mathbf{G}},{\mathbf{a}}^{i} } \right) = & \left\{ {h:{\mathbf{g}}^{h} {\text{L}}_{\text{s}} {\mathbf{a}}^{i} ,{\mathbf{g}}^{h} \in {\mathbf{G}}} \right\} \\ \end{aligned} $$

In the set L_s(aⁱ, G) there are included these indices of “good” objects, for whom the statement aⁱ L_sg^h is true. The two remaining sets are defined similarly.

Defining the position of an alternative aⁱ in relation to the set G we consider three possibilities:

Case S1 L_s(aⁱ, G) ∪ I_s (aⁱ, G) ≠ ∅.

The value

$$ d_{\text{G}}^{ + } \left( {{\mathbf{a}}^{i} } \right) = { \hbox{max} }\left\{ {d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{g}}^{h} } \right):h \in L_{s} \left( {{\mathbf{a}}^{i} ,{\mathbf{G}}} \right) \cup I_{s} \left( {{\mathbf{a}}^{i} ,{\mathbf{G}}} \right)} \right\} $$

is calculated. The success achievement degree d_S(aⁱ) is defined to be equal to d ⁺ _G (aⁱ).

Case S2 L_s(aⁱ, G) ∪ I_s(aⁱ, G) = ∅ ^ L_s(G, aⁱ) ≠ ∅.

The value

$$ d_{{\mathbf{G}}}^{ - } \left( {{\mathbf{a}}^{i} } \right) = { \hbox{min} }\left\{ {d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{g}}^{h} } \right):h \in L_{s} ({\mathbf{G}},{\mathbf{a}}^{i} )} \right\} $$

is calculated. The success achievement degree d_S(aⁱ) is defined to be equal to d ⁻ _G (aⁱ).

Case S3 If conditions described in Cases S1 and S2 are not fulfilled, then the success achievement degree d_S(aⁱ) is defined to be equal to 0.

3.2.2 Failure avoidance degree

For a given aⁱ ∈ A auxiliary sets of indices are defined as follows:

$$ \begin{aligned} L_{s} \left( {{\mathbf{B}},{\mathbf{a}}^{i} } \right) & = \left\{ {h:{\mathbf{b}}^{h} {\text{L}}_{\text{s}} {\mathbf{a}}^{i} ,{\mathbf{b}}^{h} \in {\mathbf{B}}} \right\} \\ I_{s} \left( {{\mathbf{B}},{\mathbf{a}}^{i} } \right) & = \left\{ {h:{\mathbf{b}}^{i} {\text{I}}_{\text{s}} {\mathbf{a}}^{h} ,{\mathbf{b}}^{h} \in {\mathbf{B}}} \right\} \\ L_{s} ({\mathbf{a}}^{i} ,{\mathbf{B}}) & = \left\{ {h:{\mathbf{b}}^{i} {\text{L}}_{\text{s}} {\mathbf{b}}^{h} ,{\mathbf{b}}^{h} \in {\mathbf{B}}} \right\} \\ \end{aligned} $$

In the set L_s(B, aⁱ) there are included these numbers of “bad” objects, for whom the statement b^hL_saⁱ is true. The two remaining sets are interpreted similarly.

Defining the position of an alternative aⁱ in relation to the set B we consider three possibilities:

Case F1 L_s(B, aⁱ) ∪ I_s(B, aⁱ) = ∅ ^ L_s(aⁱ, B) ≠ ∅.

The value

$$ d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) = { \hbox{min} }\left\{ {d^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{b}}^{h} } \right):h \in L_{s} ({\mathbf{a}}^{i} ,{\mathbf{B}})} \right\} $$

is calculated. The failure avoidance degree d_F(aⁱ) is defined to be equal to d ⁺_B (aⁱ).

Case F2 L_s(B, aⁱ) ∪ I_s(B, aⁱ) ≠ ∅.

The value

$$ d_{\text{B}}^{ - } \left( {{\mathbf{a}}^{i} } \right) = { \hbox{max} }\left\{ {d^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{b}}^{h} } \right):h \in L_{s} \left( {{\mathbf{B}},{\mathbf{a}}^{i} } \right) \cup I_{s} \left( {{\mathbf{B}},{\mathbf{a}}^{i} } \right)} \right\} $$

is calculated. The failure avoidance degree d_F(aⁱ) is defined to be equal to d ⁻ _B (aⁱ).

Case F3 If conditions described in Cases S1 and S2 are not fulfilled, then the failure avoidance degree d_F(aⁱ) is defined to be equal to 0.

3.3 Relationships in the set of alternatives

3.3.1 Mono-sortings and mono-rankings

According to the success achievement degree the alternatives from the set A are sorted to the three categories:

Category S1 consists of the “overgood” alternatives, for which condition, formulated in Case S1 is fulfilled.

Category S2 consists of the alternatives, for which condition, formulated in Case S2 is fulfilled.

Category S3 consists of the alternatives, for which condition, formulated in Case S3 is fulfilled (decision variants non-comparable with G).

A way of building above categories implies that each alternative from the Category S1 should be preferred to any alternative from the Category S2. Decision variants are ordered as follows:

$$ \begin{aligned} & {\mathbf{a}}^{i} \;{\text{is}}\;{\text{preferred}}\;{\text{to}}\;{\mathbf{a}}^{j} (i \ne j,i,j = 1, \ldots ,m),\;{\text{iff}} \\ & \quad \left[ {d_{\text{S}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{S}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{j} } \right) \wedge \left( {d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) > d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{j} } \right)} \right)} \right] \\ & \quad \quad \vee \left[ {d_{\text{S}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{S}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{G}}}^{ - } \left( {{\mathbf{a}}^{j} } \right)} \right] \\ & \quad \quad \vee \left[ {d_{\text{S}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{G}}}^{ - } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{S}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{G}}}^{ - } \left( {{\mathbf{a}}^{j} } \right) \wedge \left( {d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) < d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{j} } \right)} \right)} \right] \\ & {\mathbf{a}}^{i} \;{\text{is}}\;{\text{equivalent}}\;{\text{to}}\;{\mathbf{a}}^{j} ,\;{\text{iff}} \\ & \quad \left[ {d_{\text{S}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{S}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{j} } \right) \wedge d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{j} } \right)} \right] \\ & \quad \quad \vee \left[ {d_{\text{S}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{G}}}^{ - } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{S}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{G}}}^{ - } \left( {{\mathbf{a}}^{j} } \right) \wedge d_{{\mathbf{G}}}^{ - } \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{G}}}^{ - } \left( {{\mathbf{a}}^{j} } \right)} \right] \\ \end{aligned} $$

According to the failure avoidance degree the alternatives from the set A are sorted to the three categories:

Category F1 consists of the alternatives, for which condition, formulated in Case F1 is fulfilled.

Category F2 consists of “underbad” alternatives, for which condition, formulated in Case F2 is fulfilled.

Category F3 consists of the alternatives, for which condition, formulated in Case F3 is fulfilled (alternatives non-comparable with B).

A way of building above categories implies that each alternative from the Category F1 should be preferred to any alternative from Category F2. Alternatives are ordered as follows:

$$ \begin{aligned} & {\mathbf{a}}^{i} \;{\text{is}}\;{\text{preferred}}\;{\text{to}}\;{\mathbf{a}}^{j} ,\;{\text{iff}} \\ & \quad \left[ {d_{\text{F}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{F}} \left( {a^{j} } \right) = d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{j} } \right) \wedge d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) \, > d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{j} } \right)} \right] \\ & \quad \quad \vee \left[ {d_{\text{F}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{F}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{j} } \right)} \right] \\ & \quad \quad \vee \left[ {d_{\text{F}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{F}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{j} } \right) \wedge d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{i} } \right) \, < d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{j} } \right)} \right] \\ & {\mathbf{a}}^{i} \;{\text{is}}\;{\text{equivalent}}\;{\text{to}}\;{\mathbf{a}}^{j} ,\;{\text{iff}} \\ & \quad \left[ {d_{\text{F}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{F}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{j} } \right) \wedge d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{j} } \right)} \right] \\ & \quad \quad \vee \left[ {d_{\text{F}} \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{B}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) \wedge d_{\text{F}} \left( {{\mathbf{a}}^{j} } \right) = d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{j} } \right) \wedge d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{i} } \right) = d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{j} } \right)} \right] \\ \end{aligned} $$

3.3.2 Bipolar-sorting and Bipolar-ranking

Considering jointly evaluation of success achievement degree and failure avoidance degree, three categories of alternatives are defined:

Category B1 consists of such alternatives aⁱ, that d ⁺ _G (aⁱ) > 0 ∧ d ⁺ _B (aⁱ) > 0.

Category B2 consists of such alternatives aⁱ, that d ⁻ _G (aⁱ) > 0 ∧ d ⁺ _B (aⁱ) > 0.

Category B3 consists of such alternatives aⁱ, that d ⁻ _G (aⁱ) > 0 ∧ d ⁻ _B (aⁱ) > 0.

Assuming, that each alternative from the Category B1 is preferred to any alternative from Category B2 and each alternative from Category B2 is preferred to any alternative from Category B3, linear order is given in each category as follows:

• For aⁱ, a^j ∈ B1

  • aⁱ is preferred to a^j, iff d_S(aⁱ) + d_F(aⁱ)> d_S(a^j) + d_F(a^j)

  • aⁱ equivalent to a^j, iff d_S(aⁱ) + d_F(aⁱ)= d_S(a^j) + d_F(a^j)

• For aⁱ, a^j ∈ B2

  • aⁱ is preferred to a^j, iff 1 − d_S(aⁱ) + d_F(aⁱ)>1 − d_S(a^j) + d_F(a^j)

  • aⁱ is equivalent to a^j, iff 1 − d_S(aⁱ) + d_F(aⁱ) =1 − d_S(a^j) +d_F(a^j)

• For aⁱ, a^j ∈ B3

  • aⁱ is preferred to a^j, iff d_S(aⁱ)+ d_F(aⁱ)< d_S(a^j)+ d_F(a^j)

  • aⁱ is equivalent to a^j, iff d_S(aⁱ)+ d_F(aⁱ)= d_S(a^j) + d_F(a^j)

4 Modifications of reference sets and categories

Let D be classical domination relation:

$$ f\left( {\mathbf{b}} \right){\text{D}}\;f\left( {\mathbf{g}} \right) \Leftrightarrow \forall_{k = 1, \ldots ,n} \quad f_{k} \left( {\mathbf{b}} \right) \ge f_{k} \left( {\mathbf{g}} \right) \wedge \exists_{l = 1, \ldots ,n} \;f_{l} \left( {\mathbf{b}} \right) > f_{l} \left( {\mathbf{g}} \right). $$

Up to now we have assumed that condition (1) holds. Now we will assume, that condition

$$ \sim\exists_{{{\mathbf{g}} \in {\mathbf{G}}}} \sim\exists_{{{\mathbf{b}} \in {\mathbf{B}}}} \quad f\left( {\mathbf{b}} \right){\text{D}}\;f\left( {\mathbf{g}} \right) $$

(2)

is fulfilled (Assumption 2).

Example 1

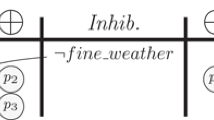
We have four alternatives, four “good” objects and three “bad” objects. Values of criteria functions for these data are presented in Fig. 1. Other parameters are as follows: v₁ = 1, v₂ = 1, w₁ = 0.7, w₂ = 0.3, s = 0.6 q₁ = 0.3 and q₂ = 0.3.

Fig. 1

Values of criteria for alternatives and reference objects

We can easily check that condition (1) does not hold (for example ~ [f(g²) D f(b³)]). Applying the Bipolar method presented in Sect. 3 we obtain the following bipolar ranking:

$$ \begin{aligned} & 1 :\;{\mathbf{a}}^{4} \\ & 2 :\;{\mathbf{a}}^{2} ,{\mathbf{a}}^{3} ({\text{equivalent}}\;{\text{alternatives}}) \\ \end{aligned} $$

Let us notice that alternative a¹ is not included, because for a¹ we have $d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{1} } \right)$ > 0 and $d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{1} } \right)$ > 0. It means that a¹ is “overgood” and “underbad” simultaneously. To exclude such situations we propose below suitable modifications.

4.1 Modification of the reference system

We check if condition (1) is fulfilled. If it is not, we modify the reference set of “good” objects or reference set of “bad” objects (Trzaskalik and Sitarz 2012).

4.1.1 Modification of the reference set of “good” objects

Let $\mathop {{\mathbf{f}}^{{\mathbf{B}}} }\limits^{ \wedge }$ denote the ideal vector in the reference set of “bad” objects, hence

$$ \mathop {f_{k}^{{\mathbf{B}}} }\limits^{ \wedge } = max\left\{ {f_{k} \left( {\mathbf{b}} \right):{\mathbf{b}} \in {\mathbf{B}}} \right\} $$

We replace the set G by the set $\overline{{\mathbf{G}}}$ = {$\overline{{\mathbf{g}}}^{1}$, …, $\overline{{\mathbf{g}}}^{g}$}, changing these evaluations, which are too low according to ideal solutions in the set B, that is

$$ f_{k} \left( {\overline{{\mathbf{g}}} } \right) = \left\{ {\begin{array}{*{20}l} {f_{k} \left( {\mathbf{g}} \right),} \hfill & {if\;f_{k} \left( {\mathbf{g}} \right) \ge \mathop {f_{k}^{{\mathbf{B}}} }\limits^{ \wedge } } \hfill \\ {\mathop {f_{k}^{{\mathbf{B}}} }\limits^{ \wedge } ,} \hfill & {if\;f_{k} \left( {\mathbf{g}} \right) < \mathop {f_{k}^{{\mathbf{B}}} }\limits^{ \wedge } } \hfill \\ \end{array} } \right. $$

(3)

Let us notice, that if f(g) dominates all “bad” objects, then f($\overline{{\mathbf{g}}}$) = f(g). In the opposite case we increase the appropriate components of vector f(g).

Example 1a

We consider data presented in Example 1. We have: f(g¹) = (0, 6), f(g²) = (1, 6), f(g²) = (5, 6), f(g³) = (5, 0) and $\mathop {f_{1}^{{\mathbf{B}}} }\limits^{ \wedge }$ = 2, $\mathop {f_{2}^{{\mathbf{B}}} }\limits^{ \wedge }$ = 2. According to the formula (3) we obtain: f($\overline{{\mathbf{g}}}^{1}$) = (2, 6), f($\overline{{\mathbf{g}}}^{2}$) = (2, 6), f($\overline{{\mathbf{g}}}^{3}$) = (5, 6), f($\overline{{\mathbf{g}}}^{4}$) = (5, 2). Modifications of “good” objects are shown in Fig. 2.

Fig. 2

Modification of reference set G

4.1.2 Modification of the reference set of “bad” objects

Let $\mathop {{\mathbf{f}}_{{}}^{\text{D}} }\limits^{ \vee }$ denote nadir vector in the reference set of “good” objects, hence

$$ \mathop {f_{k}^{{\mathbf{G}}} }\limits^{ \vee } = { \hbox{min} }\left\{ {f_{k} \left( {\mathbf{g}} \right):{\mathbf{g}} \in {\mathbf{G}}} \right\} $$

We replace the set B by the set $\overline{{\mathbf{B}}}$ = { $\overline{{\mathbf{b}}}^{1}$, …, $\overline{{\mathbf{b}}}^{b}$ } changing these evaluations, which are too high according to nadir solution in the set G, that is

$$ f_{k} \left( {\overline{{\mathbf{b}}} } \right) = \left\{ {\begin{array}{*{20}l} {f_{k} \left( {\mathbf{b}} \right),} \hfill & {if\;f_{k} \left( {\mathbf{b}} \right) \le \mathop {f_{k}^{{\mathbf{G}}} }\limits^{ \vee } } \hfill \\ {\mathop {f_{k}^{{\mathbf{G}}} }\limits^{ \vee } ,} \hfill & {if\;f_{k} \left( {\mathbf{b}} \right) > \mathop {f_{k}^{{\mathbf{G}}} }\limits^{ \vee } } \hfill \\ \end{array} } \right. $$

(4)

Let us notice, that if f(b) is dominated by all “bad” objects, then f($\overline{{\mathbf{b}}}$) = f(b). In the opposite case we decrease the appropriate components of vector f(b).

Example 1b

We consider data presented in Example 1. We have: f(b¹) = (0, 2), f(b²) = (1, 1), f(b²) = (0, 2), and $\mathop {f_{1}^{{\mathbf{G}}} }^{ \vee }$ = 0, $\mathop {f_{2}^{{\mathbf{G}}} }^{ \vee }$ = 0. According to the formula (4) we obtain: f($\overline{{\mathbf{b}}}^{1}$) = (0, 0), f($\overline{{\mathbf{b}}}^{2}$) = (0, 0), f($\overline{{\mathbf{b}}}^{3}$) = (0, 0). Modifications of “bad” objects are shown in Fig. 3.

Fig. 3

Modification of the reference set B

4.2 Modification of categories in bipolar ranking

The idea of this approach comes from (Trzaskalik and Sitarz 2012). We introduce a new category B2’ which includes alternatives, which are simultaneously “overgood” and “underbad”:

$$ {\mathbf{a}}^{i} \in \text{B}2^{\prime } \;{\text{iff}}\;d_{{\mathbf{G}}}^{ + } \left( {{\mathbf{a}}^{i} } \right) > 0 \wedge d_{{\mathbf{B}}}^{ - } \left( {{\mathbf{a}}^{i} } \right) > 0. $$

From this point of view category B1 consists of alternatives which are better than “good” and “bad” objects simultaneously; category B2 consists of alternatives which are worse than “good” objects and better than “bad” objects. Category B3 consists of alternatives which are worse than “good” and “bad” objects simultaneously. Thus, we can place category B2’ between categories B1 and B3. Categories B2 and B2’ are on the same level. To rank alternatives in category B2’ we proceed as described in Sect. 3.3.2. Summarizing this approach, dependences among categories in the bipolar sorting system can be presented in the way shown in Fig. 4.

Fig. 4

Dependences among categories in bipolar sorting system

Example 1c

In this example we consider data presented in Example 1 with category B2’. In this situation category B2’ consists of one alternative—a¹.

4.3 Numerical results

Table 1 presents the results of computations conducted for Examples 1, 1a1b and 1c. Let us notice that alternative a¹ is ranked in Examples 1a, 1b and 1c but not in Example 1.

Table 1 Results of computations for Examples 1, 1a, 1b, 1c

5 Modifications for numerous reference sets

Let us assume that reference sets are numerous and values of all the criteria are given on number scales. In the first proposed modification it is assumed that the weight of considered criterion depends on the values of the “bad” reference objects. Functions of local preference will describe that kind of dependence. The second modification refers to position description for alternatives in relation to the reference system.

5.1 Local preference function

Let us denote as {δ ^G_0k , δ ^G_1k , …, δ ^G_10,k } and {δ ^B_0k , δ ^B_1k , …, δ ^B_10,k } subsequent deciles in sets G and B. Functions ξ^G(x) and ξ^B(x) are defined as follows:

$$ \xi^{{\mathbf{B}}} \left( x \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\;{\text{x}} < \delta_{0}^{{\mathbf{B}}} \, } \hfill \\ {\mathop {\hbox{max} }\limits_{q} \left\{ {\delta_{q - 1}^{{\mathbf{B}}} \le {\text{ x}} < \delta_{q}^{{\mathbf{B}}} } \right\}} \hfill & {{\text{if}}\;\delta_{q - 1}^{{\mathbf{B}}} \le {\text{ x}} < \delta_{q}^{{\mathbf{B}}} } \hfill \\ {10} \hfill & {{\text{if}}\;{\text{x}} \ge \delta_{{{\kern 1pt} 10}}^{{\mathbf{B}}} } \hfill \\ \end{array} } \right.,\quad \xi^{{\mathbf{G}}} \left( x \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {{\text{if}}\;{\text{x}} < \delta_{0}^{{\mathbf{G}}} \, } \hfill \\ {\mathop {\hbox{max} }\limits_{q} \left\{ {\delta_{q - 1}^{{\mathbf{G}}} \le {\text{ x}} < \delta_{q}^{{\mathbf{G}}} } \right\}} \hfill & {{\text{if}}\;\delta_{q - 1}^{{\mathbf{G}}} \le {\text{ x}} < \delta_{q}^{{\mathbf{G}}} } \hfill \\ {10} \hfill & {{\text{if}}\;{\text{x}} \ge \delta_{{{\kern 1pt} 10}}^{{\mathbf{G}}} } \hfill \\ \end{array} } \right. $$

The local preference function is defined on values f_k(aⁱ) for a considered criterion and subsequent alternatives aⁱ as follows.

$$ \eta_{k} \left[ {f_{k} \left( {{\mathbf{a}}^{i} } \right)} \right] = w_{k} \xi^{{\mathbf{B}}} \left[ {f_{k} \left( {{\mathbf{a}}^{i} } \right)} \right]/10 $$

The value of function η_k is equal to w_k, if the value of the criterion number k for the considered alternative aⁱ is greater or equal to the highest value of that criterion on the reference set B. On the other hand, the value of that function is equal to 0, if the value of the criterion number k for the considered decision variant aⁱ is smaller than the lowest value of the criterion number k on the reference set B. It means, that if the value of the k-th criterion for the considered decision variant is lower than the best value of that criterion for some (or all) objects from the set B, the value of the local preference function weakens the weight of that criterion, given by the decision maker.

We propose to take into account local preference functions, when calculating coefficients c⁺(aⁱ, r^j), c⁻(aⁱ, r^j) oraz c⁼(aⁱ, r^j). Modified formulas are as follows:

$$ \begin{aligned} c^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) & = \sum\limits_{k = 1}^{n} {\eta_{k} \left[ {f_{k} \left( {{\mathbf{a}}^{i} } \right)} \right]\varphi_{k}^{ + } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right)} \\ c^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) & = \sum\limits_{k = 1}^{n} {\eta_{k} \left[ {f_{k} \left( {{\mathbf{a}}^{i} } \right)} \right]\varphi_{k}^{ - } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right)} \\ c^{ = } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right) & = \sum\limits_{k = 1}^{n} {\eta_{k} \left[ {f_{k} \left( {{\mathbf{a}}^{i} } \right)} \right]\varphi_{k}^{ = } \left( {{\mathbf{a}}^{i} ,{\mathbf{r}}^{j} } \right)} \\ \end{aligned} $$

5.2 Modification of position definition for an alternative in relation to the reference system

We assume that the considered alternative outranks a reference set, if the number of objects outranked by that variant is greater than the number of objects from that set which outranked the considered alternative. Otherwise we assume that the reference set outranks the considered decision variant. As a measure of outranking we consider the ratio of the difference between these values to the number of elements of the reference set.

We denote:

$$ \begin{aligned} g^ + \left( {{{\bf{a}}^i}} \right) &= card\left\{ {{\varvec{g}^j} \in \varvec{G}:{{\bf{a}}^i}{{\rm{L}}_{\rm{s}}}{\varvec{g}^j}} \right\}\quad g^ - \left( {{{\bf{a}}^i}} \right) = card\left\{ {{\varvec{g}^j} \in \varvec{G}:{\varvec{g}^j}{{\rm{L}}_{\rm{s}}}{{\bf{a}}^i}} \right\} \\ b^ + \left( {{{\bf{a}}^i}} \right) &= card\left\{ {{\varvec{b}^j} \in \varvec{B}:{{\bf{a}}^i}{{\rm{L}}_{\rm{s}}}{\varvec{b}^j}} \right\} \quad b^ - \left( {{{\bf{a}}^i}} \right) = card\left\{ {{\varvec{b}^j} \in \varvec{G}:{\varvec{b}^j}{{\rm{L}}_{\rm{s}}}{{\bf{a}}^i}} \right\} \end{aligned} $$

Coefficients of success achievement degree and failure avoidance degree are modified as follows:

$$ d_{S} \left( {{\mathbf{a}}^{i} } \right) = \frac{{g^{ + } \left( {{\mathbf{a}}^{i} } \right) - g^{ - } \left( {{\mathbf{a}}^{i} } \right)}}{{card\;{\mathbf{G}} }} \in \left[ { - 1,1} \right]\quad d_{N} \left( {{\mathbf{a}}^{i} } \right) = \frac{{b^{ + } \left( {{\mathbf{a}}^{i} } \right) - b^{ - } \left( {{\mathbf{a}}^{i} } \right)}}{{card\;{\mathbf{B}} }} \in \left[ { - 1,1} \right]. $$

6 Determining criteria weights and veto thresholds

Let us assume again that reference sets are numerous and values of all the criteria are given on number scales.

6.1 Criteria weights

For each criterion we compute the value

$$ \mu_{k} = \sum\limits_{q = 1}^{10} {\mathop \xi \nolimits_{{}}^{{\mathbf{G}}} \left( {\delta_{qk}^{{\mathbf{G}}} } \right)} $$

The value of coefficient μ_k is from the range from 0 to 100. If the value of all deciles of the k-th criterion in the set f(G) are greater than the highest value of that criterion in the set f(B), then μ_k = 100. That situation is the most profitable. If the values of all deciles of the k-th criterion in the set f(G) are smaller than the highest value of that criterion in the set f(B), then μ_k = 0. Such a result indicates that the decision maker should remove that criterion from the further considerations. If deciles distributions for a chosen criterion in the both sets are identical or close each other, then μ_k = 55. It occurs, if

$$ \mathop \forall \limits_{{q \in \{ 0, \ldots ,10\} }} \mathop {\xi^{{\mathbf{G}}} \left( {\delta_{qk}^{{\mathbf{G}}} } \right)}\nolimits_{{}} = q $$

If μ_k ≤ 55, such a situation is unfavorable and the decision maker is advised to remove that criterion from the further considerations. We assume, that the criterion weight should be higher, if the values of the considered criterion is more differentiated between sets f(B) and f(G). To set up weights we propose to apply the formula:

$$ w_{k} = {{\mu_{k} } \mathord{\left/ {\vphantom {{\mu_{k} } {\sum\limits_{p = 1}^{n} {\mu_{p} } }}} \right. \kern-0pt} {\sum\limits_{p = 1}^{n} {\mu_{p} } }} $$

Applying the coefficient

$$ \omega = \sum\limits_{p = 1}^{n} {\mu_{p} } /100n $$

we determine the degree of values differentiation in reference sets. The value of that coefficient belongs to the interval [0, 1]. The higher value ω the better considered criteria reflect preference structure, represented by means of reference sets. Calculated weights and the value ω are presented to the decision maker. She/he can accept proposed values or modify them. The decision maker should verify the set of criteria, especially if the weights for some criteria should be close or equal to zero.

6.2 Veto thresholds

We propose to define a veto threshold for k-th criterion as follows:

$$ v_{k} = \mathop \delta \nolimits_{qk}^{{\mathbf{G}}} $$

Value of q (the same for all the considered criteria) is arbitrarily determined by the decision maker. Defining the number of deciles in the set f(G) the decision maker determines such a value of considered criterion, which is better than the value of that criterion for q × 10% objects in that set.

7 Modified Bipolar procedure

We consider the situation, when all the considered criteria are on the number scale. To give a possibility for a decision maker to apply the modifications described above as well as the classical Bipolar approach we propose a procedure, elaborated below. The block-scheme of the procedure is given in Fig. 5.

Fig. 5

Modified Bipolar block scheme

• Start

  • 1. Establish sets A, G, B.

  • 2. Is condition (1) fulfilled? Yes—go to 10. No—go to 3.

  • 3. Do you want to modify reference sets? Yes—go to 4. No—go to 6.

  • 4. Do you want to modify the set G? Yes—go to 7. No—go to 5.

  • 5. Do you want to modify set B? Yes—go to 8. No—go to 10.

  • 6. Do you want to extend the set of Bipolar categories? Yes—go to 9. No—go to 10.

  • 7. Modify the set G according to 3.1.1. Go to 10.

  • 8. Modify the set B according to 3.1.2. Go to 10.

  • 9. Extend the set of categories in Bipolar ranking according to 3.2. Go to 10.

  • 10. Do you want to apply the possibility of decision support for establishing weights? Yes—go to 12. No—go to 11.

  • 11. Establish weights, k = 1, …, n and concordance level s. Go to 13.

  • 12. Establish weights according to 5.1 and concordance level s. Go to 13.

  • 13. Do you want to apply possibility of decision support for establishing veto thresholds? Yes—go to 15. No—go to 14.

  • 14. Establish veto thresholds. Go to 16.

  • 15. Establish veto thresholds according to 5.2. Go to 16.

  • 16. Do you want to apply local preference functions to determine outranking coefficients? Yes—go to 17. No—go to 18.

  • 17. Determine outranking coefficients according to 4.1. Go to 20.

  • 18. Determine outranking coefficients according to 2.1.1. Go to 20.

  • 19. Determine preference structure according to 2.1.2. Go to 20.

  • 20. Do you want to apply modification of position definition for aⁱ in relation to R? Yes—go to 22. No—go to 21.

  • 21. Determine the position aⁱ in relation to R according to 2.2. Go to 23.

  • 22. Determine the position aⁱ in relation to R according to 4.2. Go to 23.

  • 23. Perform mono-sortings and mono-rankings according to 2.3.1. Go to 24.

  • 24. Perform Bipolar-sorting and Bipolar-ranking according to 2.3.2. Go to Stop.

• Stop

8 Illustrative numerical examples

We will consider two examples. In both of them the reference system consists of 20 “good” objects and 20 “bad” objects, while the set of alternatives consists of 10 elements. Values of 3 criteria are real numbers. Numerical data are given in Table 2.

Table 2 Values of criteria for reference objects and alternatives

In the first of considered examples (Example 2) we will apply modifications, described in Chapters 4 and 5, whereas in the second one (Example 2a) for the same set of data we will perform calculations according the classical version of the method.

Example 2

• Start

  • 1. We establish sets A, G, B (Table 2).

  • 2. Condition (1) is not fulfilled [condition (2) holds]. We go to 3.

  • 3. We do not want to modify reference sets and go to 6.

  • 6. We do not want to extend set of Bipolar categories and go 10.

  • 10. We will apply possibility of decision support for establishing the weights.

    Subsequent deciles in the sets B and G are given in Table 3. Determining deciles we apply linear interpolation. We go to 12.

    Table 3 Deciles distributions in the sets G and B

  • 12. We apply decision support in establishing weights and calculate coefficients μ₁ = 99, μ₂ = 74, μ₁ = 92, weights: w₁ = 0.374, w₂ = 0.279, w₃ = 0.347, and coefficient ω = 0.883. It is seen, that the obtained value of ω confirms, that reference sets B and G has been established properly. We establish s = 0.5 and go to 13.

  • 13. We do not want to apply decision support for establishing veto thresholds and go to 14.

  • 14. We establish veto thresholds v₁ = 1, v₂ = 1, v₃ = 1 and go to 16.

  • 16. We want to apply the local preference function and go to 17.

  • 17. We determine outranking coefficients according to 4.1. Auxiliary values are shown in Table 4. We go to 20.

    Table 4 Auxiliary calculations

  • 20. We want to apply modification of position definition for aⁱ in relation to R and go to 22.

  • 21. We determine the position aⁱ in relation to R according to 4.2. and go to 23.

  • 23. We perform mono-sortings and mono-rankings according to 2.3.1. Results are given in Table 5. We go to 24.

    Table 5 Categories and rankings in Examples 2 and 2a

  • 24. We perform Bipolar-sorting and Bipolar-ranking according to 2.3.2. Results are given in Table 5. Go to Stop.

• Stop

Example 2a

• Start

  We perform steps 1, 2, 3, 6, 10, 12, 13, 14 in the same way, as in Example 2

  • 16. We do not want to apply the local preference function and go to 18.

  • 18. We determine outranking coefficients according to 2.1.1 and go to 20.

  • 20. We do not want to apply modification of position definition for aⁱ in relation to R and go to 21.

  • 21. We determine the position aⁱ in relation to R according to 2.2 and go to 23.

  • 23. We perform mono-sortings and mono-rankings according to 2.3.1. Results are given in Table 5. We go to 24.

  • 24. We perform Bipolar-sorting and Bipolar-ranking according to 2.3.2. Results are given in Table 5. We go to Stop.

• Stop

Comparing results obtained in Examples 2a and 2 it is seen that four alternatives: a⁴, a⁵, a⁶ and a⁸ are simultaneously “overgood” and “underbad”. Applying proposed modifications they become comparable with the rest of the alternatives and are classified in the class B2. It is worth to notice reverse of classification in mono-sortings (column 1 and 3—for alternatives a⁴, a⁵, a⁶, a⁷, a⁸) and bipolar sorting (column 5 for alternative a⁷).

9 Concluding remarks

The present paper presents some modifications of the Bipolar method which are optional and complement the classical version of the procedure. They can be treated as a decision support tool when formula (1) is not satisfied.

Inconsistency of preference can be removed by the application of modifications described in Sect. 4.1.1 for “good” objects and in Sect. 4.1.2 for “bad” objects. When discussing modifications of categories in bipolar ranking it should be noted that despite of the supposition that no alternative can be both “overgood” and “underbad”, such situations occur in practical applications. It may be difficult (or impossible) to modify the reference sets, hence—if the decision maker does not want to disregard such an alternative—we propose an (optional) procedure of ranking alternatives, presented in Sect. 4.2.

Examples 1a, 1b and 1c illustrate the possibility of a rational solution of the problem of bipolar incomparability of one alternative that is observed when the classical version of the Bipolar method is applied. On the other hand, a comparison of the results obtained when analyzing Examples 2 and 2a shows that the modifications suggested in Sects. 5 and 6 allow for a rational solution of the problem of bipolar incomparability of some alternatives and also for working out a ranking.

In the present paper the criteria were measured on a number scale. It is a limitation which we want to overcome in further research. We will consider criteria measured on an ordinal or binary scale. Another direction of research is to consider the possibility of applying an interactive approach both for the creation of reference sets and during the procedure itself.

The Bipolar method has been already applied to solve some real-life problems: for instance, to create a job characteristics of a “good” physics teacher (Jakubowicz 1987; Jakubowicz and Konarzewska-Gubała 1989), to support an effective performance appraisal system (Konarzewska-Gubała 1996), in multi-criteria decision support for portfolio selection using the idea of reference solutions (Dominiak 1997; Trzaskalik 2014). Multiple Criteria company benchmarking (Konarzewska-Gubała 2002). Modifications of Bipolar methodology proposed by D. Górecka were used for the evaluation and ranking of the European projects (Górecka 2009, 2010a, b, 2011, 2012, 2014, 2017a, b). The development of applications is the next direction of further research.