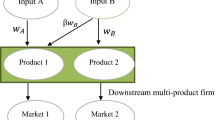
Abstract
This article presents a model in which two downstream firms compete in a differentiated product market and choose whether to adopt new advanced inputs supplied by the monopolist or competitively supplied standard inputs. When the downstream firms are independent of the monopolistic supplier, from the welfare viewpoint, the incentive to adopt the new inputs is insufficient (can be excessive) given that the rival firm does not (does) adopt. When the monopoly supplier and one downstream firm merge, such integration increases the unintegrated downstream firm’s incentive to adopt the new input supplied by the rival, spreading new inputs in the industry. We emphasize the price-increasing effect under the commitment to procure advanced inputs and show that vertical integration can be harmful to welfare despite the increase in product quality and the reduction in the welfare loss due to double marginalization.



Similar content being viewed by others
Notes
It may be risky because there might be cannibalization effect between its own products and hold-up problem in which outsourcing suppliers may name high-input prices in the future after the firms have already invested and locked in this input. See Jungbauer et al. (2021) for empirical discussions on the organization of innovation.
We can interpret our model as one with a make-or-buy decision in which each firm chooses whether it procures the high quality inputs that enhance its demand from outside and saves the maintenance cost of production technology or maintains its production ability and continues to make low quality inputs inside. For a discussion on the make-or-buy decisions, see Sappington (2005), Arya et al. (2008), and Loertscher and Riordan (2019). In Sect. 6, we examine the hold-up problem wherein input suppliers name their prices first before downstream firms choose whether to purchase the specific input, and then they might change their prices later.
The literature suggests how vertical integration alters pricing incentives in relevant upstream and downstream markets. It emphasizes the efficiencies of the elimination of double marginalization but features trade-off between efficiencies and anticompetitive effects. We discuss the differences between our analysis and that of the previous literature later.
Manasakis et al. (2013, 2014) and Liu et al. (2015) explicitly considered the market-expanding effect of CSR and examined certificates and market structure. Lee and Park (2019) and Hirose et al. (2017, 2020) also included the welfare effects of environmental CSR. For intensive discussions of qualitative and empirical works on CSR, see Schreck (2011) and Kitzmueller and Shimshack (2012) for excellent reviews.
The analysis of vertical integration and exclusive contracts yield important insights on the anti-competitive effects. Since Rasmusen et al. (1991), recent developments of exclusion by adopting exclusive contracts include Chen and Riordan (2007), Wright (2009), Kitamura (2010), Allain et al. (2016), Kitamura et al. (2017), and so on. For more discussions on anti-competitive vertical integration, see Matsushima and Pan (2016) and the studies cited therein.
In Sect. 6, we examine a hold-up problem by incorporating a standard timing sequence and show that the input supplier might commit to its price to induce the adoption of the new input and vertical integration might still affect the adoption pattern of the unintegrated firm in the equilibrium.
Note that the commitment to procure high quality inputs has recently been influential given the popularity of CSR activities and non-GMO concerns.
Instead, we can interpret our model as a model with a make-or buy-decision. See footnote 2.
It may be natural to assume that the production cost for the advanced input is higher than that for the standard input. Suppose that the cost difference between them is c. All of lemmas and propositions hold if we replace A* with A** = A*—c. In other words, we can interpret A* as the net benefit (i.e., the demand-expanding effect minus the additional production cost of the input) of adopting the high-quality input.
The first digit in the bracket indicates the decision of firm \(i\) on high-quality procurement, and the second digit indicates the decision of firm \(j\) on high-quality procurement. For example, \({\pi }_{i}(\mathrm{1,0})\) denotes the profit of firm \(i\) when only firm i adopts the high-quality input.
We can show that the upstream firm always provides the specific input to the downstream firms when they commit to adopting, i.e., \({\pi }_{U}\left(\mathrm{1,1}\right)>{\pi }_{U}\left(\mathrm{1,0}\right)\) for \(A<{A}^{*}<\bar{A}\) and \(\beta \in \left(\mathrm{0,1}\right)\). Thus, the upstream firm has no incentive to restrict the input provisions under the exclusive contracts.
All the proofs of lemmas and propositions are provided in the Appendix.
Note that there exist threshold values of market enhancing effect, \({A}^{*}\), which satisfy \(W\left(\mathrm{0,0}\right)<W\left(\mathrm{1,0}\right)<W(\mathrm{1,1})\). For more details, see the proofs in Appendix.
For a discussion of the business-stealing effect, see Mankiw and Whinston (1986).
This is because firm 1 can offer a sufficiently high price in the third stage. If firm 2 expects firm 1 to set such a high price, it never chooses to adopt the high quality input.
\({{\pi }_{1}}^{M}\left(1,1\right)>{{\pi }_{1}}^{M}\left(1,0\right)\) for \(A<{A}^{*}<\overline{A}\ \mathrm{ and }\ \beta \in \left(\mathrm{0,1}\right)\). Thus, the integrated firm has no incentive to restrict the input provisions under the exclusive contracts.
It is easy to see that \({{P}_{1}}^{M}\left(\mathrm{1,0}\right)<{{P}_{1}}^{M}(\mathrm{1,1})\) and \({{P}_{2}}^{M}\left(\mathrm{1,0}\right)<{{P}_{2}}^{M}\left(\mathrm{1,1}\right).\)
It is also practical if the downstream firm has to invest in the capacities of producing the input materials after adopting the new inputs under the contract agreed. In the following analysis, we do not consider the other case of a hold-up problem that once downstream firm committed to adopting new inputs it can break up its agreement after the upstream firm changes the input price. This case also corresponds to the case where the switching cost of downstream firms is small. Thus, after the downstream firm announces to adopt the new inputs, it can negotiate the input prices or may give up the adoption when the input prices are changed. For example, Chen (2001) showed that the anti-competitive effects of an integration depend on the cost of switching suppliers and the degree of downstream product differentiation.
Note that we have the profits of the firms under case (a), i.e., \({\pi }_{U}(\mathrm{1,1})=\frac{{{A}^{*}}^{2}}{2(2-\beta )(1+\beta )}\), \({\pi }_{i}(\mathrm{1,1})=\frac{(1-\beta ){{A}^{*}}^{2}}{4{(2-\beta )}^{2}(1+\beta )}\), and under case (b), i.e., \({\pi }_{U}(\mathrm{1,1})=\frac{2A({A}^{*}-A)}{(2-\beta )(1+\beta )}\), \({\pi }_{i}(\mathrm{1,1})=\frac{{A}^{2}(1-\beta )}{{(2-\beta )}^{2}(1+\beta )}\), respectively.
Note thatwe have the profits of the firms under case (a), i.e., \({{\pi }_{1}}^{M}(\mathrm{1,1})=\frac{(12+\beta (4+\beta +{\beta }^{2})){({A}^{*})}^{2}}{4(1+\beta )(8+{\beta }^{2})}\) and \({{\pi }_{2}}^{M}(\mathrm{1,1})=\frac{\left(1-\beta \right){\left(2+{\beta }^{2}\right)}^{2}{\left({A}^{*}\right)}^{2}}{\left(1+\beta \right){\left(8+{\beta }^{2}\right)}^{2}},\) and under case (b), i.e., \({\pi }_{1}(\mathrm{1,1})=\frac{(16-16\beta -48{\beta }^{2}+28{\beta }^{3}+28{\beta }^{4}-14{\beta }^{5}-5{\beta }^{6}+2{\beta }^{7}){({A}^{*})}^{2}+A(2-{\beta }^{2})(2(8+{\beta }^{2}(2-\beta (1+(1-\beta )\beta ))){A}^{*}-A(2-{\beta }^{2})(8+{\beta }^{2}))}{4{(4-5{\beta }^{2}+{\beta }^{4})}^{2}}\) and \({\pi }_{2}(\mathrm{1,1})=\frac{{(A(2-{\beta }^{2})-\beta {A}^{*})}^{2}}{(1-{\beta }^{2}){(4-{\beta }^{2})}^{2}}\), respectively.
Note that under the alternative time line, vertical integration cannot affect social welfare if the new input supplier with or without merge can credibly commit to its price before the decision on the adoption of new input. Note also that from Lemmas 9 and 10, vertical integration increases the threshold of price discount (i.e., \(\frac{(2-{\beta }^{2})({A}^{*}-A)}{2-2{\beta }^{2}}>{A}^{*}-A\)).
References
Allain ML, Chambolle C, Rey P (2016) Vertical integration as a source of hold-up. Rev Econ Stud 83(1):1–25
Arya A, Mittendorf B, Sappington DE (2008) Outsourcing, vertical integration, and price versus quantity competition. Int J Ind Organ 26(1):1–16
Chen Y (2001) On vertical mergers and their competitive effects. Rand J Econ 32(4):667–685
Chen Y (2010) Strategic outsourcing between rivals. Ann Econ Finance 11(2):301–311
Chen Y, Riordan M (2007) Vertical integration, exclusive dealing, and ex post cartelization. RAND J Econ 38(1):1–21
Flath D (1989) Vertical integration by means of shareholding interlocks. Int J Ind Organ 7(3):369–380
Greenlee P, Raskovich A (2006) Partial vertical ownership. Eur Econ Rev 50(4):1017–1041
Harbour PJ, Koslov TI (2010) Section 2 in a Web 2.0 World: an expanded vision of relevant product markets. Antitrust Law J 76(3):769–797
Hirose K, Lee SH, Matsumura T (2017) Environmental corporate social responsibility: a note on the first-mover advantage under price competition. Econ Bull 37(1):A20
Hirose K, Lee SH, Matsumura T (2020) Noncooperative and cooperative environmental corporate social responsibility. J Inst Theor Econ 176(3):549–571
Hunold M, Stahl K (2016) Passive vertical integration and strategic delegation. Rand J Econ 47(4):891–913
Jungbauer T, Nicholson S, Pan J, Waldman M (2021) The organization of innovation: property rights and the outsourcing decision. NBER working paper 28379
Kitamura H (2010) Exclusionary vertical contracts with multiple entrants. Int J Ind Organ 28(3):213–219
Kitamura H, Matsushima N, Sato M (2017) Exclusive contracts and bargaining power. Econ Lett 151:1–3
Kitzmueller M, Shimshack J (2012) Economic perspectives on corporate social responsibility. J Econ Lit 50(1):51–84
Lee SH, Park CH (2019) Eco-firms and sequential adoption of environmental corporate social responsibility in the managerial delegation. B.E. J Theor Econ 19(1):20170043
Liu CC, Wang LF, Lee SH (2015) Strategic environmental corporate social responsibility in a differentiated duopoly market. Econ Lett 129:108–111
Loertscher S, Riordan MH (2019) Make and buy: outsourcing, vertical integration, and cost reduction. Am Econ J Microecon 11(1):105–123
Manasakis C, Mitrokostas E, Petrakis E (2013) Certification of corporate social responsibility activities in oligopolistic markets. Can J Econ 46(1):282–309
Manasakis C, Mitrokostas E, Petrakis E (2014) Strategic corporate social responsibility activities and corporate governance in imperfectly competitive markets. Manag Decis Econ 35(7):460–473
Mankiw NG, Whinston MD (1986) Free entry and social inefficiency. Rand J Econ 17(1):48–58
Matsushima N, Pan C (2016) Strategic perils of outsourcing: Sourcing strategy and product positioning. ISER discussion paper 983
Moresi S, Schwartz M (2017) Strategic incentives when supplying to rivals with an application to vertical firm structure. Int J Ind Organ 51:137–161
Ordover JA, Saloner G, Salop SC (1990) Equilibrium vertical foreclosure. Am Econ Rev 80(1):127–142
Rasmusen EB, Ramseyer JM, Wiley JS Jr (1991) Naked exclusion. Am Econ Rev 81(5):1137–1145
Sappington DE (2005) On the irrelevance of input prices for make-or-buy decisions. Am Econ Rev 95(5):1631–1638
Schreck P (2011) Reviewing the business case for corporate social responsibility: new evidence and analysis. J Bus Ethics 103(2):167
Wright J (2009) Exclusive dealing and entry, when buyers compete: comment. Am Econ Rev 99(3):1070–1081
Acknowledgements
We would like to thank Hiroshi Kitamura, Noriaki Matsushima, Woohyung Lee, and the participants of the Industrial Organization and Competition Policy Workshop at Kyoto Sangyo University and a seminar at the University of Tokyo. We are also benefitted from the constructive comments by the two referees. All remaining errors are ours. This work was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea (NRF-2021S1A5B5A16076177), JSPS KAKENHI of Japan (18K01500, 21K01398) and Murata Science Foundation of Japan. We thank Editage for English language editing.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs of Propositions and Lemmas
Appendix: Proofs of Propositions and Lemmas
1.1 Proof of Lemma 1
Suppose that firm j does not adopt the high-quality input. Then, we obtain \(\pi_{i} \left( {1,0} \right) - \pi_{i} \left( {0,0} \right) = \frac{{\left( {\left( {2 - \beta^{2} } \right)A^{*} - A\left( {4 - \beta - 2\beta^{2} } \right)} \right)\left( {A\left( {4 - \beta \left( {3 + 2\beta } \right)} \right) + \left( {2 - \beta^{2} } \right)A^{*} } \right)}}{{4\left( {4 - \beta^{2} } \right)^{2} \left( {1 - \beta^{2} } \right)}} > 0\) if and only if \(A^{*} > A_{\pi } \left( {1,0} \right) = \frac{{A\left( {4 - \beta - 2\beta^{2} } \right)}}{{2 - \beta^{2} }}\). This implies (1).
Suppose that firm j adopts the high-quality input. Then, we obtain \(\pi_{i} \left( {1,1} \right) - \pi_{i} \left( {0,1} \right) = \frac{{\left( {2 - \beta^{2} } \right)^{3} \left( {2 - \beta \left( {2 + \beta } \right)} \right)\left( {A^{*} } \right)^{2} + 2\beta \left( {2 - \beta^{2} } \right)\left( {8 - 9\beta^{2} + 2\beta^{4} } \right)AA^{*} - \left( {8 - 9\beta^{2} + 2\beta^{4} } \right)^{2} A^{2} }}{{4\left( {1 - \beta^{2} } \right)\left( {8 - 6\beta^{2} + \beta^{4} } \right)^{2} }} > 0\) if and only if \(A^{*} > A_{\pi } \left( {1,1} \right) = \frac{{A\left( {8 - 9\beta^{2} + 2\beta^{4} } \right)}}{{\left( {2 - \beta^{2} } \right)^{2} }}\). This implies (3).
Finally, \(A_{\pi } \left( {1,1} \right) - A_{\pi } \left( {1,0} \right) = \frac{{A\beta \left( {1 - \beta } \right)\left( {2 + \beta } \right)}}{{\left( {2 - \beta^{2} } \right)^{2} }} > 0.\) This implies (2).
1.2 Proof of Lemma 2
\(\pi_{i} \left( {1,0} \right) - \pi_{j} \left( {1,0} \right) = \frac{{\left( {2 - \beta^{2} } \right)^{2} \left( {A^{*} } \right)^{2} + 2\beta \left( {2 - \beta^{2} } \right)AA^{*} - \left( {4 + \beta - 2\beta^{2} } \right)\left( {4 - \beta - 2\beta^{2} } \right)A^{2} }}{{4\left( {4 - \beta^{2} } \right)\left( {2 - \beta^{2} } \right)^{2} }}\) > 0 if and only if \(A^{*} > \frac{{A\left( {4 - \beta - 2\beta^{2} } \right)}}{{2 - \beta^{2} }} = A_{\pi } \left( {1,0} \right).\)
1.3 Proof of Lemma 3
Define \(A_{W} \left( {1,0} \right)\) and \(A_{W} \left( {1,1} \right)\), which satisfy \(W\left( {1,0} \right)\frac{ > }{ < }W\left( {0,0} \right) \Leftrightarrow A^{*} \frac{ > }{ < }A_{W} \left( {1,0} \right)\) and \(W\left( {1,1} \right)\frac{ > }{ < }W\left( {1,0} \right) \Leftrightarrow A^{*} \frac{ > }{ < }A_{W} \left( {1,1} \right)\). We have \(A_{W} \left( {1,0} \right) = A\frac{{\beta \left( {36 - 31\beta^{2} + 6\beta^{4} } \right) + 2\left( {1 - \beta } \right)\left( {2 + \beta } \right)\sqrt {\sigma \left( {1,0} \right)} }}{{\left( {2 - \beta^{2} } \right)\left( {28 - 21\beta^{2} + 4\beta^{4} } \right)}}\) and \(A_{W} \left( {1,1} \right) = A\frac{{\left( {2 + \beta } \right)\sqrt {\sigma \left( {1,1} \right)} - \beta \left( {36 - 31\beta^{2} + 6\beta^{4} } \right)}}{{\left( {2 - \beta^{2} } \right)\left( {28 - \beta \left( {32 + \beta \left( {21 - 2\beta \left( {5 + 2\beta } \right)} \right)} \right)} \right)}}\) where \(\sigma \left( {1,0} \right) = \left( {2 + \beta } \right)\left( {2 - \beta^{2} } \right)\left( {84 - \beta \left( {70 + \beta \left( {62 - \beta \left( {53 + 8\left( {1 - \beta } \right)\beta } \right)} \right)} \right)} \right) > 0\) and \(\sigma \left( {1,1} \right) = 2\left( {1 - \beta } \right)\left( {672 - \beta \left( {768 + \beta \left( {1140 - \beta \left( {1320 + \beta \left( {653 - 2\beta \left( {398 + \beta \left( {69 - \beta \left( {97 + 4\beta - 8\beta^{2} } \right)} \right)} \right)} \right)} \right)} \right)} \right)} \right) > 0\). We also have \(\left. {A_{W} \left( {1,0} \right)} \right|_{\beta = 0} = \left. {A_{W} \left( {1,1} \right)} \right|_{\beta = 0} = 2A\sqrt{\frac{3}{7}} \approx 1.31\), and \(\frac{{\partial A_{W} \left( {1,0} \right)}}{\partial \beta } < 0\), \(\frac{{\partial A_{W} \left( {1,1} \right)}}{\partial \beta } > 0\) for \(\beta \in \left( {0,1} \right)\). Then, \(A < A_{W} \left( {1,0} \right) < A_{W} \left( {1,1} \right)\) for \(\beta \in \left( {0,1} \right).\)
1.4 Proof of Lemma 4
We have \(A_{\pi } \left( {1,0} \right) - A_{W} \left( {1,0} \right) = \frac{2A}{{\left( {2 - \beta^{2} } \right)^{2} \left( {28 - 21\beta^{2} + 4\beta^{4} } \right)}}\left( {B - \sqrt C } \right)\), where \(B = \left( {7 - 11\beta + 4\beta^{2} } \right)\left( {4 + 2\beta - 2\beta^{2} - \beta^{3} } \right)^{2}\) > 0 and \(C = \left( {1 - \beta } \right)^{2} \left( {4 + 2\beta - 2\beta^{2} - \beta^{3} } \right)^{3} \left( {84 - 70\beta - 62\beta^{2} + 53\beta^{3} + 8\beta^{4} - 8\beta^{5} } \right)\) > 0. Because \(B^{2} - C = 2\left( {1 - \beta } \right)^{2} \left( {2 + \beta } \right)^{3} \left( {2 - \beta^{2} } \right)^{3} \left( {\left( {2 - \beta } \right)\left( {28 - 21\beta^{2} + 4\beta^{4} } \right)} \right) > 0.\) This implies (1).
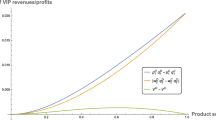
We have \(\left. {A_{W} \left( {1,1} \right)} \right|_{\beta = 0} = 2A\sqrt{\frac{3}{7}} \approx 1.31A < \left. {A_{\pi } \left( {1,1} \right)} \right|_{\beta = 0} = 2A\), \(\frac{{\partial A_{W} \left( {1,1} \right)}}{\partial \beta } > 0\), \(\frac{{\partial A_{\pi } \left( {1,1} \right)}}{\partial \beta } < 0\) for \(\beta \in \left( {0,1} \right)\) and \(\left. {A_{\pi } \left( {1,1} \right)} \right|_{\beta = 1} = A\). Then, \(A_{W} \left( {1,1} \right)\) and \(A_{\pi } \left( {1,1} \right)\) are crossed at \(\left( {\beta , A^{*} } \right) = \left( {0.85, 1.54A} \right)\). This implies (2). Figure 1 shows an example that \(A_{W} \left( {1,1} \right) > A_{\pi } \left( {1,1} \right)\) and \(A_{W} \left( {1,1} \right) < A_{\pi } \left( {1,1} \right)\) are possible.
1.5 Proof of Lemma 5
We obtain \(\pi_{2}^{M} \left( {1,1} \right) - \pi_{2}^{M} \left( {1,0} \right) = \frac{DE}{{\left( {1 - \beta^{2} } \right)\left( {32 - 4\beta^{2} - \beta^{4} } \right)^{2} }}\), where \(D = \left( {8 + \beta^{2} \left( {2 - \beta \left( {1 + \left( {1 - \beta } \right)\beta } \right)} \right)} \right)A^{*} - A\left( {2 - \beta^{2} } \right)\left( {8 + \beta^{2} } \right)\) and \(E = A\left( {2 - \beta^{2} } \right)\left( {8 + \beta^{2} } \right) - \left( {\beta \left( {16 + \left( {2 - \beta } \right)\beta \left( {\beta + \beta^{2} - 1} \right)} \right) - 8} \right)A^{*}\). Then, D > 0 if and only if \(A^{*} > \frac{{A\left( {2 - \beta^{2} } \right)\left( {8 + \beta^{2} } \right)}}{{8 + \beta^{2} \left( {2 - \beta \left( {1 + \left( {1 - \beta } \right)\beta } \right)} \right)}} = A_{\pi }^{M} \left( {1,1} \right)\) and E > 0 if and only if \(A^{*} < \frac{{A\left( {2 - \beta^{2} } \right)\left( {8 + \beta^{2} } \right)}}{{\beta \left( {16 + \left( {2 - \beta } \right)\beta \left( {\beta + \beta^{2} - 1} \right)} \right) - 8}}\). Note that \(\overline{A} < \frac{{A\left( {2 - \beta^{2} } \right)\left( {8 + \beta^{2} } \right)}}{{\beta \left( {16 + \left( {2 - \beta } \right)\beta \left( {\beta + \beta^{2} - 1} \right)} \right) - 8}}\), which is sufficient to prove the result.
1.6 Proof of Lemma 6
Define \(A_{W}^{M} \left( {0,0} \right)\) and \(A_{W}^{M} \left( {1,0} \right)\), which satisfy \(W^{M} \left( {1,1} \right)\frac{ > }{ < }W\left( {0,0} \right) \Leftrightarrow A^{*} \frac{ > }{ < }A_{W}^{M} \left( {0,0} \right)\) and \(W^{M} \left( {1,1} \right)\frac{ > }{ < }W^{M} \left( {1,0} \right) \Leftrightarrow A^{*} \frac{ > }{ < }A_{W}^{M} \left( {1,0} \right)\). We have \(A_{W}^{M} \left( {0,0} \right) = A\frac{{2\left( {8 + \beta^{2} } \right)\sqrt {6 - 4\beta } }}{{\left( {2 - \beta } \right)\sqrt {304 + 48\beta + 108\beta^{2} + 16\beta^{3} + 11\beta^{4} - \beta^{5} } }}\) and \(A_{W}^{M} \left( {1,0} \right) = A\frac{{2\left( {8 + \beta^{2} } \right)\left( {\left( {4 - \beta^{2} } \right)\sqrt {\sigma^{M} \left( {1,0} \right)} - 2\beta \left( {8 + \beta^{2} } \right)\left( {8 - 3\beta^{2} } \right)} \right)}}{{4\left( {448 - 1024\beta + 16\beta^{2} + 144\beta^{3} - 60\beta^{4} + 72\beta^{5} + 6\beta^{6} + \beta^{7} - 3\beta^{9} } \right) - \beta^{8} \left( {21 - \beta^{2} } \right)}}\) where \(\sigma^{M} \left( {1,0} \right) = \left( {1 - \beta } \right)\left( {2\left( {672 - 864\beta - 496\beta^{2} + 104\beta^{3} - 6\beta^{4} + 80\beta^{5} + 11\beta^{8} - \beta^{9} } \right) + 19\beta^{6} \left( {7 + 3\beta } \right)} \right) > 0.\)
We have \(\frac{{\partial A_{W}^{M} \left( {1,0} \right)}}{\partial \beta } > 0\), \(\frac{{\partial^{2} A_{W}^{M} \left( {1,0} \right)}}{{\partial \beta^{2} }} > 0\), \(\left. {A_{W}^{M} \left( {1,0} \right)} \right|_{\beta = 0} = 2A\sqrt{\frac{3}{7}} \approx 1.31A\), \(\frac{{\partial A_{W}^{M} \left( {0,0} \right)}}{\partial \beta }\frac{ > }{ < }0\) and \(\frac{{\partial^{2} A_{W}^{M} \left( {0,0} \right)}}{{\partial \beta^{2} }} < 0\) for \(\beta \in \left( {0,1} \right)\). Moreover, we have \(\left. {A_{W}^{M} \left( {0,0} \right)} \right|_{\beta = 0} = 2A\sqrt{\frac{6}{19}} \approx 1.12A\) and \(\left. {A_{W}^{M} \left( {0,0} \right)} \right|_{\beta = 1} = \frac{2A}{{\sqrt 3 }} \approx 1.15A\), meaning \(A_{W}^{M} \left( {0,0} \right)\) has the maximum value, 1.17A at \(\beta \approx 0.74\). Then, \(A_{W}^{M} \left( {0,0} \right) < A_{W}^{M} \left( {1,0} \right)\). Figure 2 shows that \(A_{W}^{M} \left( {0,0} \right) < A_{W}^{M} \left( {1,0} \right)\) for \(\beta \in \left( {0,1} \right).\)
1.7 Proof of Lemma 7
We have \(\frac{{\partial A_{\pi }^{M} \left( {1,1} \right)}}{\partial \beta } < 0\) for \(\beta \in \left( {0,1} \right)\), \(\left. {A_{\pi }^{M} \left( {1,1} \right)} \right|_{\beta = 0} = 2A\) and \(\left. {A_{\pi }^{M} \left( {1,1} \right)} \right|_{\beta = 1} = A\), meaning that \(A_{\pi }^{M} \left( {1,1} \right)\) is a monotonically decreasing function with respect to β, from A to 2A. From Lemma 6, the intersection between \(A_{W}^{M} \left( {1,0} \right)\) and \(A_{\pi }^{M} \left( {1,1} \right)\) is \(\left( {\beta , A^{*} } \right) = \left( {0.55, 1.67A} \right)\) and that of between \(A_{W}^{M} \left( {0,0} \right)\) and \(A_{\pi }^{M} \left( {1,1} \right)\) is \(\left( {\beta , A^{*} } \right) = \left( {0.77, 1.39A} \right).\) Figure 2 shows an example that (1) and (2) are possible.
1.8 Proof of Lemma 8
\(A_{\pi } \left( {1,1} \right) - A_{\pi }^{M} \left( {1,1} \right) = \frac{{\beta^{2} \left( {1 - \beta } \right)\left( {1 + \beta } \right)\left( {2 + \beta } \right)\left( {16 - 12\beta - \beta^{2} + 5\beta^{3} - 2\beta^{4} } \right)}}{{\left( {2 - \beta^{2} } \right)^{2} \left( {8 + 2\beta^{2} - \beta^{3} - \beta^{4} + \beta^{5} } \right)}}\) > 0 for \(\beta \in \left( {0,1} \right).\)
1.9 Proof of Proposition 4
We consider the eight adoption combinations between the integration and non-integration cases.
(1) Suppose that both firms adopt the high-quality input without integration. Then, from Proposition 2, both adopt the high-quality input with integration, too. Therefore, we obtain
(2) Suppose that only firm 1 adopts the high-quality input with and without integration. This happens only when \(A^{*} < A_{\pi }^{M} \left( {1,1} \right)\). Then, we have \(\pi_{2}^{M} \left( {1,0} \right) > \pi_{2} \left( {1,0} \right)\) if and only if \(A^{*} > \frac{{A\left( {16 - 17\beta^{2} + 4\beta^{4} } \right)}}{{6\beta - 3\beta^{3} }}\). Because \(\frac{{A\left( {16 - 17\beta^{2} + 4\beta^{4} } \right)}}{{6\beta - 3\beta^{3} }} > A_{\pi }^{M} \left( {1,1} \right),\) we can show that \(\pi_{2}^{M} \left( {1,0} \right) > \pi_{2} \left( {1,0} \right)\) never holds in this case.
(3) Suppose that only firm 1 adopts the high-quality input with integration, and both adopt the high-quality input without integration. This contradicts Proposition 2, and thus it never takes place.
(4) Suppose that both firms adopt the high-quality input with integration, but only firm 1 adopts the high-quality input without integration. This happens only when \(A^{*} > A_{\pi } \left( {1,1} \right)\). We obtain \(\pi_{2}^{M} \left( {1,1} \right) > \pi_{2} \left( {1,0} \right)\) if and only if \(A^{*} > \frac{{A\left( {8 + \beta^{2} } \right)\left( {8 - 9\beta^{2} + 2\beta^{4} } \right)}}{{\left( {2 - \beta^{2} } \right)\left( {16 - \beta \left( {8 - \beta \left( {4 - \beta \left( {3 + 2\left( {1 - \beta } \right)\beta } \right)} \right)} \right)} \right)}}\). Because \(\frac{{A\left( {8 + \beta^{2} } \right)\left( {8 - 9\beta^{2} + 2\beta^{4} } \right)}}{{\left( {2 - \beta^{2} } \right)\left( {16 - \beta \left( {8 - \beta \left( {4 - \beta \left( {3 + 2\left( {1 - \beta } \right)\beta } \right)} \right)} \right)} \right)}} > A_{\pi } \left( {1,1} \right)\), \(\pi_{2}^{M} \left( {1,1} \right) > \pi_{2} \left( {1,0} \right)\) never holds in this case.
(5) Suppose that only firm 2 adopts the high-quality input without integration and only firm 1 adopts the high-quality input with integration. Then, we have \(\pi_{2} \left( {0,1} \right) - \pi_{2}^{M} \left( {1,0} \right) = \frac{{6AA^{*} \beta \left( {2 - \beta^{2} } \right) + \left( {A^{*} } \right)^{2} \left( {4 - 8\beta^{2} + \beta^{4} } \right) - A^{2} \left( {16 - 17\beta^{2} + 4\beta^{4} } \right)}}{{4\left( {4 - \beta^{2} } \right)^{2} \left( {1 - \beta^{2} } \right)}}\). Then, \(\pi_{2} \left( {0,1} \right) < \pi_{2}^{M} \left( {1,0} \right)\) if \(A^{*} < \frac{{\left( {4 + \beta - 2\beta^{2} } \right)}}{{2 + 2\beta - \beta^{2} }}\) or \(A^{*} > \frac{{\left( {4 - \beta - 2\beta^{2} } \right)}}{{ - 2 + 2\beta + \beta^{2} }}\). Because \(\frac{{\left( {4 + \beta - 2\beta^{2} } \right)}}{{2 + 2\beta - \beta^{2} }} < A_{\pi } \left( {1,0} \right)\) and \(\frac{{\left( {4 - \beta - 2\beta^{2} } \right)}}{{ - 2 + 2\beta + \beta^{2} }} > \overline{A}\) for \(\beta \in \left( {0,1} \right)\), \(\pi_{2} \left( {0,1} \right) < \pi_{2}^{M} \left( {1,0} \right)\) never holds in this case. Furthermore, as we showed in Lemma 2, in the non-integration case, the firm that does not adopt the high-quality input obtains smaller profits. In addition, firm 1’s marginal cost is lower under integration. Both effects reduce firm 2’s profit, whereas there is no effect of increasing firm 2’s profit. Therefore, firm 2’s profit is smaller with integration.
(6) Suppose that only firm 2 adopts the high-quality input without integration, and both firms adopt the high-quality input with integration. Then, firm 2 earns a larger profit than when only firm 1 adopts the high-quality input without integration from Lemma 2. We also showed in (4) that integration reduces firm 2’s profit even when only firm 1 adopts the high-quality input without integration. These two facts imply that integration reduces firm 2’s profit in this case, too.
(7) Suppose that no firm adopts the high-quality input without integration and only firm 1 adopts the high-quality input with integration. We have \(\pi_{2} \left( {0,0} \right) - \pi_{2}^{M} \left( {1,0} \right) = \frac{{\left( {A^{*} - A} \right)\beta \left( {A\left( {4 - \beta - 2\beta^{2} } \right) - \beta A^{*} } \right)}}{{\left( {4 - \beta^{2} } \right)^{2} \left( {1 - \beta^{2} } \right)}}\). Then, \(\pi_{2} \left( {0,0} \right) < \pi_{2}^{M} \left( {1,0} \right)\) if and only if \(A^{*} > A\frac{{4 - \beta - 2\beta^{2} }}{\beta }\). Because \(A\frac{{4 - \beta - 2\beta^{2} }}{\beta } > \overline{A}\) for \(\beta \in \left( {0,1} \right)\), \(\pi_{2} \left( {0,0} \right) < \pi_{2}^{M} \left( {1,0} \right)\) never holds in this case. Furthermore, the adoption of the high-quality input by firm 1 reduces firm 2’s profit, and vertical integration reduces firm 1’s cost, making firm 1 stronger. Both effects reduce firm 2’s profit, whereas there is no effect of increasing firm 2’s profit. Therefore, firm 2’s profit is smaller with integration.
(8) Suppose that no firm adopts the high-quality input without integration, and both firms adopt the high-quality input with integration. This happens only when \(A^{*} < A_{\pi } \left( {1,0} \right).\) \(\pi_{2}^{M} \left( {1,1} \right) > \pi_{2} \left( {0,0} \right)\) if and only if \(A^{*} > \frac{{A\left( {8 + \beta^{2} } \right)}}{{4 - 2\beta + 2\beta^{2} - \beta^{3} }}\). Because \(\frac{{A\left( {8 + \beta^{2} } \right)}}{{4 - 2\beta + 2\beta^{2} - \beta^{3} }} > A_{\pi } \left( {1,0} \right),\) \(\pi_{2}^{M} \left( {1,1} \right) > \pi_{2} \left( {0,0} \right)\) never holds in this case.
1.10 Proof of Proposition 5
(1) First, suppose that both firms adopt the high-quality input with and without integration. Then, we obtain
Second, suppose that only firm 1 adopts the high-quality input with and without integration. This happens only when \(A_{\pi } \left( {1,0} \right) \leqq A^{*}\). We obtain
Thus, we have \(W^{M} \left( {1,0} \right) > W\left( {1,0} \right)\) if and only if \(A^{*} > A\frac{{\beta \left( {36 - 35\beta^{2} + 8\beta^{4} } \right)}}{{\left( {2 - \beta^{2} } \right)\left( {20 - 15\beta^{2} + 4\beta^{4} } \right)}}\). Because \(A_{\pi } \left( {1,0} \right) - A\frac{{\beta \left( {36 - 35\beta^{2} + 8\beta^{4} } \right)}}{{\left( {2 - \beta^{2} } \right)\left( {20 - 15\beta^{2} + 4\beta^{4} } \right)}} = \frac{{2A\left( {1 - \beta } \right)\left( {2 + \beta } \right)\left( {20 - 4\beta - 17\beta^{2} + 2\beta^{3} + 4\beta^{4} } \right)}}{{\left( {2 - \beta^{2} } \right)\left( {20 - 15\beta^{2} + 4\beta^{4} } \right)}} > 0\), we can show that this always holds.
(2) Fig. 3 shows that \(A_{\pi } \left( {1,1} \right) > A_{\pi }^{M} \left( {1,1} \right)\), but both \(A_{\pi }^{M} \left( {1,1} \right) > A_{W}^{M} \left( {1,0} \right)\) and \(A_{\pi }^{M} \left( {1,1} \right) < A_{W}^{M} \left( {1,0} \right)\) are possible.
1.11 Proof of Lemma 9
First, when firm j adopts the standard input, firm i adopts the high-quality input if and only if \(\pi_{i} \left( {1,0} \right) \ge \pi_{i} \left( {0,0} \right)\), which requires \(r \le A^{*} - A\). Second, when firm j adopts the high-quality input, firm i also adopts the high-quality input if and only if \(\pi_{i} \left( {1,1} \right) \ge \pi_{i} \left( {0,1} \right)\), which requires \(r \le A^{*} - A\). Hence, both firms adopt the high-quality input in the equilibrium if and only if \(r \le A^{*} - A.\)
1.12 Proof of Lemma 10
In the second stage, after observing r, firm 2 adopts the high-quality input if and only if \(\pi_{2}^{M} \left( {1,1} \right) > \pi_{2}^{M} \left( {1,0} \right)\), which requires \(A^{*} < \overline{A} = A\left( {\frac{{2 - \beta^{2} }}{\beta }} \right)\). Thus, we have the input price constraint that \(r \le \frac{{\left( {2 - \beta^{2} } \right)\left( {A^{*} - A} \right)}}{{\left( {2 - 2\beta^{2} } \right)}}\). Otherwise, firm 2 adopts the standard input.
Rights and permissions
About this article
Cite this article
Park, CH., Matsumura, T. & Lee, SH. Procurement of advanced inputs and welfare-reducing vertical integration. J Econ 135, 255–283 (2022). https://doi.org/10.1007/s00712-021-00759-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00712-021-00759-3