Skip to main content
Springer Nature Link
Log in

Stability of natural convection in a vertical layer of Brinkman porous medium

  • Original Paper
  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

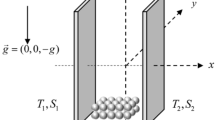
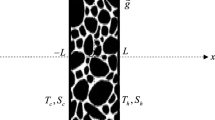
A classical linear stability theory is applied to emphasize the effect of inertia on the stability of buoyancy-driven parallel shear flow in a vertical layer of porous medium. The Lapwood–Brinkman model with fluid viscosity different from effective viscosity is used to describe the flow in a porous medium. The resulting eigenvalue problem is solved numerically using the Chebyshev collocation method. The critical Darcy–Rayleigh number \(R_\mathrm{Dc} \), the critical wave number \(a_\mathrm{c}\) and the critical wave speed \(c_\mathrm{c}\) are computed over a wide range of values of the Darcy–Prandtl number \(Pr_\mathrm{D}\) and the Darcy number \({\tilde{D}}a\). Depending on the choice of physical parameters, instability occurs due to the presence of inertia. The value of \(Pr_\mathrm{D}\) at which the transition from stationary to traveling-wave mode instability takes place increases with decreasing \({\tilde{D}}a\). Besides, the effect of decreasing \({\tilde{D}}a\) shows destabilizing effect if the instability is via stationary mode, and on the contrary, it exhibits a dual behavior if the instability is through traveling-wave mode. The streamlines and isotherms presented herein demonstrate the development of complex dynamics at the critical state. In the energy spectrum, transition of instability from one type to another is found to take place as a function of \(Pr_\mathrm{D}\). The disturbance kinetic energy due to surface drag and viscous force plays no significant role in the stability of flow throughout the domain of \(Pr_\mathrm{D}\) considered.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

Abbreviations

a :

Vertical wave number

c :

Wave speed

\(c_r\) :

Phase velocity

\(c_i\) :

Growth rate

\(D=\mathrm{d}/\mathrm{d}x\) :

Differential operator

\({\tilde{D}}a\) :

Darcy number

\(E_\mathrm{b}, E_\mathrm{d}, E_\mathrm{D}, E_\mathrm{s}\) :

Disturbance kinetic energies

\({\vec {g}}\) :

Acceleration due to gravity

h :

Half-width of the porous layer

\({\hat{i}}\) :

Unit vector in the x-direction

\({\hat{k}}\) :

Unit vector in the z-direction

k :

Permeability

p :

Pressure

\(Pr_\mathrm{D}\) :

Darcy–Prandtl number

\({\vec {q}}=(u,v,w)\) :

Velocity vector

\(R_\mathrm{D}\) :

Darcy–Rayleigh number

t :

Time

T :

Temperature

\(T_\mathrm{c}, T_\mathrm{d}\) :

Disturbance thermal energies

\(T_1\) :

Temperature of the left boundary

\(T_2\) :

Temperature of the right boundary

\(W_\mathrm{b}\) :

Basic velocity

\(\left( {x,y,z} \right) \) :

Cartesian coordinates

\(\alpha \) :

Thermal diffusivity

\(\beta \) :

Volumetric expansion coefficient

\(\theta \) :

Amplitude of the perturbed temperature

\(\mu \) :

Fluid viscosity

\(\mu _\mathrm{e}\) :

Effective fluid viscosity

\(\nu \) :

Kinematic viscosity

\(\rho \) :

Fluid density

\(\rho _0\) :

Reference density at \(T_0\)

\(\varphi _\mathrm{p}\) :

Porosity of the porous medium

\(\chi \) :

Ratio of heat capacities

\(\psi \left( {x,z,t} \right) \) :

Stream function

\(\Psi \) :

Amplitude of the perturbed stream function

References

  1. Helmig, R.: Multiphase Flow and Transport Processes in the Subsurfaces. Springer, Berlin (1997)

    Book  Google Scholar 

  2. Koponen, A., Kandhai, D., Helle’n, E., Alava, M., Hoekstra, A., Kataja, M.: Permeability of three dimensional random fiber webs. Phys. Rev. Lett. 80, 716 (1998)

    Article  Google Scholar 

  3. King, P., Buldyrev, S.V., Dokholyan, N.V., Havlin, S., Lee, Y., Paul, G.: Applications of statistical physics to the oil industry: predicting oil recovery using percolation theory. Phys. A 274, 60 (1999)

    Article  Google Scholar 

  4. Dando, P.R., Stuben, D., Varnavas, S.P.: Hydrothermalism in the Mediterranean Sea. Prog. Oceanogr. 44, 333 (1999)

    Article  Google Scholar 

  5. Straughan, B.: Stability and Wave Motion in Porous Media. Springer, New York (2008)

    MATH  Google Scholar 

  6. Straughan, B.: The Energy Method, Stability, and Non-linear Convection. Springer, New York (2004)

    Book  MATH  Google Scholar 

  7. Turcotte, D.L., Schubert, G.: Geodynamics, 3rd edn. Cambridge University Press, Cambridge (2014)

    Google Scholar 

  8. Shiina, Y., Inagaki, T.: Study on the efficiency of effective thermal conductivities on melting characteristics of latent heat storage capsules. Int. J. Heat Mass Transf. 48, 373 (2005)

    Article  MATH  Google Scholar 

  9. Makinde, O.D.: On the Chebyshev collocation spectral approach to stability of fluid flow in a porous medium. Int. J. Numer. Methods Fluids 59, 791 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hill, A.A., Straughan, B.: Stability of Poiseuille flow in a porous medium. In: Rannacher, R., Sequeria, A. (eds.) Advanced Mathematical Fluid Mechanics, pp. 287–293. Springer, New York (2010)

    Chapter  Google Scholar 

  11. Rudraiah, N., Shankar, B.M., CO, Ng: Electrohydrodynamic stability of couple stress fluid flow in a channel occupied by a porous medium. Spec. Top. Rev. Porous Med. 2, 11 (2011)

    Article  Google Scholar 

  12. Shankar, B.M., Kumar, J., Shivakumara, I.S., CO, Ng: Stability of fluid flow in a Brinkman porous medium—a numerical study. J. Hydrodyn. 26, 681 (2014)

    Article  Google Scholar 

  13. Gill, A.E.: A proof that convection in a porous vertical slab is stable. J. Fluid Mech. 35, 545 (1969)

    Article  MATH  Google Scholar 

  14. Wolanski, E.J.: Convection in a vertical porous slab. Phys. Fluids 16, 2014 (1973)

    Article  MATH  Google Scholar 

  15. Straughan, B.: A nonlinear analysis of convection in a porous vertical slab. Geophys. Astrophys. Fluid Dyn. 42, 269 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  16. Flavin, J.N., Rionero, S.: Nonlinear stability for a thermofluid in a vertical porous slab. Contin. Mech. Thermodyn. 11, 173 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  17. Kwok, L.P., Chen, C.F.: Stability of thermal convection in a vertical porous layer. ASME J. Heat Trans. 109, 889–893 (1987)

    Article  Google Scholar 

  18. Qin, Y., Kaloni, P.N.: A nonlinear stability problem of convection in a porous vertical slab. Phys. Fluids A 5, 2067–2069 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  19. Lewis, S., Bassom, A.P., Rees, D.A.S.: The stability of vertical thermal boundary layer flow in a porous medium. Eur. J. Mech. B 14, 395 (1995)

    MathSciNet  MATH  Google Scholar 

  20. Kumar, J., Bera, P., Khalili, A.: Influence of inertia and drag terms on the stability of mixed convection in a vertical porous medium channel. Int. J. Heat Mass Transf. 53, 5261 (2010)

    Article  MATH  Google Scholar 

  21. Rees, D.A.S.: The effect of local thermal nonequilibrium on the stability of convection in a vertical porous channel. Transp. Porous Med. 87, 459 (2011)

    Article  MathSciNet  Google Scholar 

  22. Scott, N.L., Straughan, B.: A nonlinear stability analysis of convection in a porous vertical channel including local thermal nonequilibrium. J. Math. Fluid Mech. 15, 171 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  23. Barletta, A.: A proof that convection in a porous vertical slab may be unstable. J. Fluid Mech. 770, 273 (2015)

    Article  MathSciNet  Google Scholar 

  24. Barletta, A.: Instability of stationary two-dimensional mixed convection across a vertical porous layer. Phys. Fluids 28, 014101 (2016)

    Article  Google Scholar 

  25. Gershuni, G.Z.: On the stability of plane convective motion of a liquid. Zh. Tekh. Fiz. 23, 1838 (1953)

    Google Scholar 

  26. Birikh, R.V.: On small perturbations of a plane parallel flow with cubic velocity profile, Prikl. Mat. Mekh. 30, 356 (1966). Appl. Math. Mech., 30, 432 (1966)

  27. Gotoh, K., Satoh, M.: The stability of a natural convection between two parallel vertical planes. J. Phys. Soc. Jpn. 21, 542 (1966)

    Article  Google Scholar 

  28. Rudakov, R.N.: Spectrum of perturbations and stability of convective motion between vertical planes, Prikl. Mat. Mekh. 31, 349 (1967). (Appl. Math. Mech., 31, 376 (1967))

  29. Vest, C.M., Arpaci, V.S.: Stability of natural convection in a vertical slot. J. Fluid Mech. 36, 1 (1969)

    Article  MATH  Google Scholar 

  30. Gill, A.E., Kirkham, C.C.: A note on the stability of convection in a vertical slot. J. Fluid Mech. 42, 125 (1970)

    Article  Google Scholar 

  31. Birikh, R.V., Gershuni, G.Z., Zhukhovitskii, E.M., Rudakov, R.N.: On oscillatory instability of plane-parallel convective motion in a vertical channel, Prikl. Mat. Mekh. 36, 745 (1972). (Appl. Math. Mech. 36, 707 (1972))

  32. Korpela, S.A., Gozum, D., Baxi, C.B.: On the stability of the conduction regime of natural convection in a vertical slot. Int. J. Heat Mass Transf. 16, 1683 (1973)

    Article  Google Scholar 

  33. Bergholz, R.F.: Instability of steady natural convection in a vertical fluid layer. J. Fluid Mech. 84, 743 (1978)

    Article  Google Scholar 

  34. Ruth, D.W.: On the transition to transverse rolls in an infinite vertical fluid layer—a power series solution. Int. J. Heat Mass Transf. 22, 1199 (1979)

    Article  MATH  Google Scholar 

  35. McBain, G.D.: Fully developed laminar buoyant flow in vertical cavities and ducts of bounded section. J. Fluid Mech. 401, 365 (1999)

    Article  MATH  Google Scholar 

  36. McBain, G.D., Armfield, S.W.: Natural convection in a vertical slot: accurate solution of the linear stability equations. ANZIAM J. 45, 92 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  37. Shankar, B.M., Kumar, Jai, Shivakumara, I.S.: Stability of natural convection in a vertical couple stress fluid layer. Int. J. Heat Mass Transf. 78, 447 (2014)

    Article  Google Scholar 

  38. Shankar, B.M., Kumar, Jai, Shivakumara, I.S.: Stability of natural convection in a vertical dielectric couple stress fluid layer in the presence of a horizontal ac electric field. Appl. Math. Model. 40, 5462 (2016)

    Article  MathSciNet  Google Scholar 

  39. Shiina, Y., Hishida, M.: Critical Rayleigh number of natural convection in high porosity anisotropic horizontal porous layers. Int. J. Heat Mass Transf. 53, 1507 (2010)

    Article  MATH  Google Scholar 

  40. Givler, R.C., Altobelli, S.A.: Determination of the effective viscosity for the Brinkman–Forchheimer flow model. J. Fluid Mech. 258, 355 (1994)

    Article  Google Scholar 

  41. Nield, D.A., Bejan, A.: Convection in Porous Media, 4th edn. Springer, New York (2013)

    Book  MATH  Google Scholar 

  42. Drazin, P.G., Reid, W.H.: Hydrodynamic Stability. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  43. Su, Y.C., Chung, J.N.: Linear stability analysis of mixed-convection flow in a vertical pipe. J. Fluid Mech. 422, 141 (2000)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, PES University, Bangalore, 560 085, India

    B. M. Shankar

  2. ISRO Satellite Centre, Bangalore, 560 017, India

    Jai Kumar

  3. Department of Mathematics, Bangalore University, Bangalore, 560 056, India

    I. S. Shivakumara

Authors
  1. B. M. Shankar
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Jai Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. I. S. Shivakumara
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to B. M. Shankar.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shankar, B.M., Kumar, J. & Shivakumara, I.S. Stability of natural convection in a vertical layer of Brinkman porous medium. Acta Mech 228, 1–19 (2017). https://doi.org/10.1007/s00707-016-1690-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-016-1690-6

Profiles

  1. B. M. Shankar View author profile