Skip to main content
SpringerLink
Log in

Dynamic stress in a semi-infinite solid with a cylindrical nano-inhomogeneity considering nanoscale microstructure

  • Published:
Acta Mechanica Aims and scope Submit manuscript

Abstract

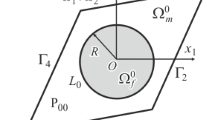
In this paper, the dynamic stress around a cylindrical nano-inhomogeneity embedded in a semi-infinite solid under anti-plane shear waves is investigated. The surface/interface stress effects around the nano-inhomogeneity and at the straight edge of the semi-infinite solid are both considered. The boundary condition at the straight edge of the semi-infinite solid with surface/interface effects is satisfied by the image method. The incident, scattered and refracted displacement fields in the nano-sized composites are expressed by employing the wave function expansion method. The addition theorem for a cylindrical wave function is applied to accomplish the superposition of wave fields in the two semi-infinite solids. Analyzes show that the effect of interface properties, especially that at the straight edge, on the dynamic stress is significant, and the effect increases noticeably due to the nanoscale of the structure. The incident frequency and angle of waves and the shear modulus ratio of the nano-inhomogeneity to matrix also show a pronounced effect on the dynamic stress distribution if the semi-infinite solid shrinks to nanoscale.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Tan E.P.S., Lim C.T.: Mechanical characterization of nano fibers—a review. Compos. Sci. Technol. 66, 1102–1111 (2006)

    Article  Google Scholar 

  2. Sharma P., Ganti S., Bhate N.: Effect of surfaces on the size-dependent elastic state of nano-inhomogeneities. Appl. Phys. Lett. 82, 535–537 (2003)

    Article  Google Scholar 

  3. Sharma P., Ganti S.: Interfacial elasticity corrections to size-dependent strain-state of embedded quantum dots. Phys. Stat. Sol. 234, 10–12 (2002)

    Article  Google Scholar 

  4. Mogilevskaya S.G., Crouch S.L., Stolarski H.K.: Multiple interacting circular nano-inhomogeneities with surface/interface effects. J. Mech. Phys. Solids 56, 2298–2327 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  5. Fang Q.H., Liu Y.W.: Size-dependent elastic interaction of a screw dislocation with a circular nano-inhomogeneity incorporating interface stress. Scr. Mater. 55, 99–102 (2006)

    Article  Google Scholar 

  6. Wang G.F., Wang T.J., Feng X.Q.: Surface effects on the diffraction of plane compressional waves by a nanosized circular hole. J. Appl. Phys. 89, 231923 (2006)

    Google Scholar 

  7. Wang G.F., Feng X.Q., Yu S.W.: Interface effects on the diffraction of plane compressional waves by a nanosized spherical inclusion. J. Appl. Phys. 102, 043533 (2007)

    Article  Google Scholar 

  8. Guz I.A., Rushchitsky J.J.: Computational simulation of harmonic wave propagation in fibrous micro- and nanocomposites. Compos. Sci. Technol. 67, 861–866 (2007)

    Article  Google Scholar 

  9. Fang X.Q., Liu J.X., Yang S.P., Zhang L.L.: Effect of surface/interface on the dynamic stress of two interacting cylindrical nano-inhomogeneities under compressional waves. Thin Solid Films 518, 6938–6944 (2010)

    Article  Google Scholar 

  10. Fang X.Q., Wang X.H., Zhang L.L.: Interface effect on the dynamic stress around an elliptical nano-inhomogeneity subjected to anti-plane shear waves. CMC Comput. Mater. Contin. 16, 229–246 (2010)

    Google Scholar 

  11. Hasheminejad S.M., Avazmohammadi R.: Size-dependent effective dynamic properties of unidirectional nanocomposites with interface energy effects. Comp. Sci. Technol. 69, 2538–2546 (2009)

    Article  Google Scholar 

  12. Mi C., Kouris D.: Nanoparticles under the influence of surface/interface elasticity. J. Mech. Mater. Struct. 1, 763–791 (2006)

    Article  Google Scholar 

  13. Jammes M., Mogilevskaya S.G., Crouch S.L.: Multiple circular nano-inhomogeneities and/or nano-pores in one of two joined isotropic elastic half planes. Eng. Anal. Bound. Elem. 33, 233–248 (2009)

    Article  MathSciNet  Google Scholar 

  14. Avazmohammadi R., Yang F., Abbasion S.: Effect of interface stresses on the elastic deformation of an elastic half-plane containing an elastic inclusion. Int. J. Solid. Struct. 46, 2897–2906 (2009)

    Article  MATH  Google Scholar 

  15. Gurtin M.E., Murdoch A.I.: A continuum theory of elastic material surfaces. Arch. Ration. Mech. Anal. 57, 291–323 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  16. Pao Y.H., Mow C.C.: Diffraction of Elastic Waves and Dynamic Stress Concentration. Crane, Russak, New York (1973)

    Google Scholar 

  17. Stratton J.A.: Electromagnetic Theory. McGraw-Hill, New York (1941)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Civil Engineering, Shijiazhuang Tiedao University, Shjiazhuang, 050043, People’s Republic of China

    Q. Yang

  2. Department of Engineering Mechanics, Shijiazhuang Tiedao University, Shijiazhuang, 050043, People’s Republic of China

    J. X. Liu & X. Q. Fang

Authors
  1. Q. Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. X. Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. X. Q. Fang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. X. Liu.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yang, Q., Liu, J.X. & Fang, X.Q. Dynamic stress in a semi-infinite solid with a cylindrical nano-inhomogeneity considering nanoscale microstructure. Acta Mech 223, 879–888 (2012). https://doi.org/10.1007/s00707-012-0613-4

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00707-012-0613-4

Keywords

Search

Navigation