1 Introduction

Thermal loadings are becoming recurrent in many subsurface operations. From oil and gas (O&G) exploitation to geological Carbon dioxide (CO2) and hydrogen storage, through steam assisted gravity drainage (SAGD) and radioactive waste management, the wellbore, the host rock and their surroundings face several temperature variations, with amplitude up to 90 °C or higher (Butler 1994; Finsterle et al. 2019; Torp and Gale 2004; Wiktorski et al. 2019). In the case of geological storage of CO2, the temperature of injected CO2 is usually lower than that of the in-situ formation. For offshore transport by ship, CO2 can stay  at a temperature as low as − 50 °C (Vilarrasa and Rutqvist 2017). Thus, the temperature of CO2 is warmed up above 0 °C before its injection to prevent the formation of hydrate or freezing of the pore network and thus the decreasing of injectivity (Hoteit et al. 2019; Möller et al. 2014). However, even in this case, the temperature of CO2 at wellhead which can be around 25 °C (or lower) is still lower than that of the in-situ reservoir (around 105 °C or higher) and still lower that of the rock formation behind the casing (Loeve et al. 2014; Paterson et al. 2010; Thompson et al. 2021). This temperature gap between the injected CO2 and the reservoir as well as the borehole and its surrounding will therefore lead to thermal loadings on the in-situ formations (including the caprock) consisting of cooling during injection and heating back when the injection must be paused (e.g., due to batchwise injection procedure or to technical issues). For O&G exploitation, thermal variations in the wellbore occur from drilling to production. The produced hydrocarbon is under high temperature in the reservoir and by being produced up transfers part of that heat to the completion fluid, the casing, the cement sheath, and the rock nearby. In the case of SAGD, the reservoir containing heavy oil is warmed up with steam at higher temperature to reduce the oil's viscosity and enhance its production. By doing so, the reservoir rock and the formations around it may undergo significant thermal loading cycles. In the above-mentioned operations, shale, or clay-rich formations, which play an important role as they are usually the sealing caprock barriers, are submitted to several thermal loadings with various temperature amplitudes. The structural integrity of the storage site therefore also lies in the capacity of these formations to withstand various thermal loadings. As they are porous media, the investigation of their thermal behaviour within the framework of poromechanics is therefore of great importance.

The evaluation of temperature effects on wellbore and in-situ formation, which is usually based on theoretical prediction and numerical simulations, requires the knowledge of thermo-poroelastic parameters for their validation, as it can be noticed in investigations (Ghabezloo 2011; Ghabezloo et al. 2009; Thompson et al. 2021; Vu 2012). The poroelastic parameters derived under isothermal conditions initially derived by Biot (1941, 1957) followed by Rice and Cleary (1976), and Zimmerman et al. (1986), have been extended to account for temperature effects on the pore fluid and the matrix (Cheng 2016; Ghabezloo et al. 2009; McTigue 1986; Palciauskas and Domenico 1982). Theoretical derivations and experiments have shown that undrained thermal loadings in low-permeability materials, such as shales or cement pastes, not only result in strain variation, but also lead to pressure variation (Ghabezloo and Sulem 2008). The parameter relating the variation of pore pressure to that of the temperature is called the thermal pressurization coefficient and has been evaluated in several experiments and for various types of materials (Ghabezloo and Sulem 2008; Ghabezloo et al. 2009; Ghabezloo 2011; Monfared et al. 2011; Mohajerani et al. 2012, 2013; Menaceur et al. 2015; Armand et al. 2017; Belmokhtar et al. 2017; Zhang et al. 2017; Braun et al. 2019). It is well known that the thermal expansion coefficient of a pore fluid is significantly higher compared to that of the solid. On one hand, during a thermal heating, the pore pressure is expected to increase and under drained conditions, the pore fluid is expulsed from the pore space keeping the pore pressure constant. Sulem et al. (2004, 2007) showed that a low permeable clayey fault gouge (~ 10–20 m2), displayed a contracting behaviour both during heating and cooling in drained condition at 1.2 °C/h. This contraction observed during heating is usually known as thermal compaction (Bauer et al. 2014) and has the expulsion of the pore fluid from pore space as one of the main driving mechanisms. Its interpretation can be made difficult if the thermal loading rate is too high [e.g. ~ 0.78 °C/h or higher under drained conditions (Sultan et al. 2002)] to permit pore pressure and/or temperature equilibrium within the porous material during the loading. The authors therefore advised to pay high attention on the effect of thermal loading rate on the observed behaviour (Sultan et al. 2002; Xu et al. 2011). On the other hand, during a thermal cooling at a certain loading rate, since the volume reduction of the pore fluid is higher than that of the solid part, the pore pressure is expected to decrease; under drained conditions, fluid is taken into the pore network maintaining its pressure constant. This intake of pore fluid may lead to macroscopic volume increase during a thermal cooling, as has been observed on a clay-rich sample by Sultan et al. (2002) and Xu et al. (2011). The temperature was also shown to affect both the stress–strain behaviour and the elastic properties of the low-permeability materials (Xu et al. 2011). McTigue (1986) and Blond et al. (2003) presented a theorical solution for a half-space porous material, with open boundaries, submitted to thermal loading. They concluded that the amplitude of pore pressure variation is not only due to the temperature change, but also depends on other parameters such as the loading rate and the ratio between the hydraulic diffusivity and the thermal diffusivity of the porous medium. Within the framework of thermo-poroelasticity, Ghabezloo et al. (2008, 2009) derived and experimentally investigated the thermal expansion and thermal pressurization coefficients of isotropic porous materials such as hardened cement paste and sandstone. From undrained heating loadings, the authors showed that the thermal pressurization coefficient varies with temperature and can be as high as 0.22 MPa/°C in a sandstone and 0.57 MPa/°C in a cement paste. The induced pore pressure due to this thermal pressurization decreases the effective stress and can lead to shear failure or hydraulic fracturing of the loaded porous material (Ghabezloo and Sulem 2008). The thermal expansion coefficients were also found to be dependent of the temperature. Monfared et al. (2011, 2012, 2013), Belmokhtar et al. (2017) and Braun et al. (2019) conducted a succession of studies to experimentally investigate the thermo-mechanical behaviour of claystone and shale. The thermal expansion and thermal pressurization coefficients were also measured, as well as other poroelastic parameters such the Skempton coefficients, the drained and undrained bulk modulus.

However, the equations describing the material behaviour in the above-mentioned investigations have been derived within isotropic thermo-poroelasticity. Since many rocks such as claystone and shale are anisotropic, the full evaluation of their thermo-poroelastic parameters should be done within the framework of anisotropy. Giot et al. (2018) derived a transversely isotropic thermo-poroelastic model for claystone, in which the thermal expansion coefficients were described as a function of anisotropic poroelastic parameters. A good match was found between the analytical solution and the numerical simulation for an inclined well. Recently Braun et al. (2021) evaluated the transversely isotropic thermo-poroelastic parameters of a Callovo–Oxfordian claystone sample. The results showed high difference between the thermal expansion coefficients in the plane of symmetry and along the axis, both for drained and undrained loadings. These coefficients were shown to have a rather limited increase with temperature. These studies still need to be performed on various porous materials with properties close to those of caprock or reservoir formations. In this paper, the thermo-poroelastic parameters of the outcrop Pierre II shale are evaluated. The samples, considered as anisotropic and prepared with zero orientation bedding (plug axis parallel to the bedding plane normal), are submitted to two groups of loading paths. In the first groups, three samples undergo CIU (consolidated isotropic undrained) tests at room temperature and under different confining pressure. In the second group, one sample undergoes complex loading paths combining isotropic compression, thermal cycles and deviatoric loading. This combination of loading paths permitted not only to evaluate various thermo-poroelastic parameters of the studied samples, but also to analyse the effect of thermal loadings on stress–strain behaviour. This paper is divided into three main sections. After this introduction, a theorical thermo-poroelastic description for anisotropic materials is given. From the general anisotropy, simplified equations are successively given for orthotropic, transverse isotropic and isotropic symmetries. This is followed by the presentation of the experimental setups, the tested materials as well as the experimental results and discussion. The paper ends with a few conclusions.

2 Theoretical Description

2.1 Thermo-Poroelasticity of Anisotropic Materials

Unlike the isotropic materials which properties are independent of the direction in which they are measured, for anisotropic rock, their measured properties are direction-dependent (Jaeger et al. 2007). The generalized Hooke's law for such materials have more than two independent elastic parameters. The general relationship between strain tensor \({{\varvec{\upvarepsilon}}}\) and stress tensor \({{\varvec{\upsigma}}}\) is usually expressed with a fourth-order tensor \({\mathbf{c}}\), such as \({{\varvec{\upvarepsilon}}} = {\mathbf{c\sigma }}\). The tensor \({\mathbf{c}}\) has 81 components and is known as tensor of elastic compressibility. The strain and stress tensors are symmetric, and each has only six independent components. Therefore, the independent components of \({\mathbf{c}}\) cannot exceed 36 (Jaeger et al. 2007). Voigt (1928) suggested a notation in which the stress and strain tensors are reduced to 6 × 1 row vectors, rather than 3 × 3 matrix and \({\mathbf{c}}\) to a 6 × 6 matrix. The Voigt notation is given by: \(11 \equiv xx \to 1\), \(22 \equiv yy \to 2\), \(33 \equiv zz \to 3\), \(23 \equiv yz \to 4\), \(13 \equiv xz \to 5\), \(12 \equiv xy \to 6\). From this notation, the stress–strain is given in relation (1), and the matrix of elastic compressibility which appears in that equation is always symmetric (Jaeger et al. 2007). The total number of independent parameters for elastic anisotropic materials is reduced to 21.

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\varepsilon_{zz} } \\ {2\varepsilon_{yz} } \\ {2\varepsilon_{xz} } \\ {2\varepsilon_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {c_{11} } & {c_{12} } & {c_{13} } & {c_{14} } & {c_{15} } & {c_{16} } \\ {c_{12} } & {c_{22} } & {c_{23} } & {c_{24} } & {c_{25} } & {c_{26} } \\ {c_{13} } & {c_{23} } & {c_{33} } & {c_{34} } & {c_{35} } & {c_{36} } \\ {c_{14} } & {c_{24} } & {c_{34} } & {c_{44} } & {c_{45} } & {c_{46} } \\ {c_{15} } & {c_{25} } & {c_{35} } & {c_{45} } & {c_{55} } & {c_{56} } \\ {c_{16} } & {c_{26} } & {c_{36} } & {c_{46} } & {c_{56} } & {c_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{yy} } \\ {\sigma_{zz} } \\ {\sigma_{yz} } \\ {\sigma_{xz} } \\ {\sigma_{xy} } \\ \end{array} } \right]$$
(1)

When taking into account the pore space, and according to Cheng (1997), the linear stress–strain relation of a reversible deformation process (small deformation) with a poroelastic framework can be constructed from the generalized Hooke’s law, and can be given by:

$$d\varepsilon_{ij} = c_{ijkl} \left( {d\sigma_{kl} - b_{kl} dp} \right)$$
(2)

where \(\sigma_{ij}\) and \(\varepsilon_{ij}\) are components of the stress and strain tensor, respectively; \(c_{ijkl}\) components of the compressibility tensor with 21 independent values, \(b_{ij}\) are those of the Biot's coefficients tensor, which is symmetric and thus has 6 independent coefficients; \(p\) is the pore pressure. The reference state is unstressed and unstrained, and its perturbation is given by Lagrangian increment \(d\chi\) (\(\chi = \varepsilon_{ij} ,\;\;\sigma_{ij} \;{\text{or}}\;p\)). In Eq. (2), Einstein's notation is used, in which repeated subscripts (e.g. i, j, k, l) in a parameter or in a multiplication of parameters means summation from 1 to 3. The repeated subscripts \(kl\) (on the right hand) means:

$$c_{ijkl} \left( {d\sigma_{kl} - b_{kl} dp} \right) = \sum\limits_{k = 1}^{3} {\sum\limits_{l = 1}^{3} {c_{ijkl} \left( {d\sigma_{kl} - b_{kl} dp} \right)} }$$
(3)

The pore pressure can be related to the stresses by the following expression (Jaeger et al. 2007):

$$dp = \frac{1}{3}B_{ij} d\sigma_{ij}$$
(4)

where \(B_{ij}\) represent the Skempton’s pore pressure coefficients (Skempton 1954). From relation (4), it is seen that excess pore pressure can also be generated by shear stresses. For an isotropic material, one has \(B_{ij,i \ne j} = 0\), and \(B_{xx} = B_{yy} = B_{zz} = B\), and Eq. (4) becomes \(dp = {{Bd\sigma_{ii} } \mathord{\left/ {\vphantom {{Bd\sigma_{ii} } 3}} \right. \kern-\nulldelimiterspace} 3}\) showing that the pore pressure is only affected by normal stresses.

When the thermal behaviour is considered, 6 independent coefficients describing the thermal expansion of the material are added to Eq. (2). The thermos-poroelastic behaviour of an anisotropic porous material saturated with a single pore fluid, is then given by Eq. (5) (Aichi and Tokunaga, 2012):

$$d\varepsilon_{ij} = c_{ijkl} \left( {d\sigma_{kl} - b_{kl} dp} \right) - \alpha_{ij} dT$$
(5)

where \(\alpha_{ij}\) are the 6 components of the drained linear thermal expansivity tensor, and \(T\) the temperature. It can also be demonstrated that the variation of porosity within the thermo-poroelastic framework is given by the following expression (Jaeger et al., 2007; Aichi and Tokunaga, 2012).

$$d\phi = - b_{ij} c_{ijkl} d\sigma_{kl} + \left( {b_{ij} c_{ijkk} - \phi^{0} c_{\phi } } \right)dp + \phi^{0} \alpha_{\phi } dT$$
(6)

where the first expression in the right-hand side reflects the mechanical loading under drained and isothermal conditions, the second expression shows the effect of the pore pressure while the third one presents the effect of temperature. The porosity increases with the increase of the pore pressure, therefore \(b_{ij} c_{ijkk} - \phi^{0} c_{\phi } \ge 0\).

2.2 Transverse Isotropic Materials

If the rock has a rotational symmetry, in which all directions perpendicular to its axis are elastically equivalent, it is known as a transversely isotropic material. The non-zero components of the compressibility tensor are reduced to \(c_{11}\), \(c_{22}\), \(c_{33}\), \(c_{12}\), \(c_{13}\), \(c_{23}\), \(c_{44}\), \(c_{55}\) and \(c_{66}\) (Jaeger et al. 2007; Fjaer et al. 2008). The non-zero Biot's coefficients and thermal expansion coefficients are \(b_{ii}\) and \(\alpha_{ii}\), respectively (Giot et al., 2018). The following stress–strain relation is obtained under thermo-poroelastic consideration, which is a kind of extended Hooke's law.

$$\left[ {\begin{array}{*{20}c} {d\varepsilon_{xx} } \\ {d\varepsilon_{yy} } \\ {d\varepsilon_{zz} } \\ {2d\varepsilon_{yz} } \\ {2d\varepsilon_{xz} } \\ {2d\varepsilon_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {c_{11} } & {c_{12} } & {c_{13} } & 0 & 0 & 0 \\ {c_{12} } & {c_{22} } & {c_{23} } & 0 & 0 & 0 \\ {c_{13} } & {c_{23} } & {c_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {c_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {c_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {c_{66} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {d\sigma_{xx} - b_{xx} dp} \\ {d\sigma_{yy} - b_{yy} dp} \\ {d\sigma_{zz} - b_{zz} dp} \\ {d\sigma_{yz} } \\ {d\sigma_{xz} } \\ {d\sigma_{xy} } \\ \end{array} } \right] - \, \left[ {\begin{array}{*{20}c} {\alpha_{xx} } \\ {\alpha_{yy} } \\ {\alpha_{zz} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]dT$$
(7)

The compressibility components \(c_{ij}\) are related to the elastic properties by:

$$c_{11} = \frac{1}{{E_{xx} }};\;\;\;c_{22} = \frac{1}{{E_{yy} }};\; \, c_{33} = \frac{1}{{E_{zz} }}$$
(8)
$$c_{12} = - \frac{{\nu_{yx} }}{{E_{yy} }}; \, c_{13} = - \frac{{\nu_{zx} }}{{E_{zz} }}; \, c_{23} = - \frac{{\nu_{zy} }}{{E_{zz} }}$$
(9)
$$c_{44} = \frac{1}{{G_{yz} }}; \, c_{55} = \frac{1}{{G_{xz} }}; \, c_{66} = \frac{1}{{G_{xy} }}$$
(10)

With the following correspondence:

$$\frac{{\nu_{xy} }}{{E_{xx} }} = \frac{{\nu_{yx} }}{{E_{yy} }}; \, \frac{{\nu_{xz} }}{{E_{xx} }} = \frac{{\nu_{zx} }}{{E_{zz} }}; \, \frac{{\nu_{yz} }}{{E_{yy} }} = \frac{{\nu_{zy} }}{{E_{zz} }}$$
(11)

where \(E_{ij}\), \(\nu_{ij}\) and \(G_{ij}\) are the Young moduli, Poisson's ratios and shear moduli, respectively.

Due to that fact that the stored strain energy function should be positive-definite, the following constraints are obtained on the elastic properties (Jaeger et al. 2007):

$$\begin{gathered} E_{xx} ,\; \, E_{yy} ,\; \, E_{zz} ,\; \, G_{yz} ,\; \, G_{xz} ,\; \, G_{xy} > 0 \hfill \\ \nu_{xy} \nu_{yx} < 1,\; \, \nu_{zy} \nu_{yz} < 1,\; \, \nu_{xz} \nu_{zx} < 1 \hfill \\ \nu_{xy} \nu_{yx} + \nu_{zy} \nu_{yz} + \;\nu_{xz} \nu_{zx} + \nu_{yx} \nu_{xz} \nu_{zy} + \nu_{zx} \nu_{xy} \nu_{yz} < 1 \hfill \\ \end{gathered}$$
(12)

Let the z axis be the axis of symmetry, the x- and y-axis are therefore equivalent. Consequently, the properties within the plane xy are equal: \(E_{xx} = E_{yy} = E_{h}\); \(\nu_{xy} = \nu_{yx} { = }\nu_{h}\). Similarly, the properties along the axis of symmetry are also equal: \(G_{xz} = G_{yz} = G_{z}\); \(\nu_{xz} = \nu_{yz}\) and \(\nu_{zx} = \nu_{zy} = \nu_{z}\) The stiffness coefficients are invariant to any rotation around the z axis, and results to \(E_{h} = 2G_{h} \left( {1 + \nu_{h} } \right)\), with \(G_{h} = G_{xy}\). The drained linear thermal expansion coefficients as well as the tensor of Biot coefficients are also reduced to \(\alpha_{xx} = \alpha_{yy} = \alpha_{h}\), \(\alpha_{zz} = \alpha_{z}\), \(b_{xx} = b_{yy} = b_{h}\) and \(b_{zz} = b_{z}\). From Eqs. (8)–(11), it yields that \(c_{11} = c_{22}\), \(\, c_{13} = c_{23}\), \(c_{44} = c_{55}\) and Eq. (7) leads to the following expression:

$$\left[ {\begin{array}{*{20}c} {d\varepsilon_{xx} } \\ {d\varepsilon_{yy} } \\ {d\varepsilon_{zz} } \\ {2d\varepsilon_{yz} } \\ {2d\varepsilon_{xz} } \\ {2d\varepsilon_{xy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{1 \mathord{\left/ {\vphantom {1 {E_{h} }}} \right. \kern-\nulldelimiterspace} {E_{h} }}} & { - {{\nu_{h} } \mathord{\left/ {\vphantom {{\nu_{h} } {E_{h} }}} \right. \kern-\nulldelimiterspace} {E_{h} }}} & { - {{\nu_{z} } \mathord{\left/ {\vphantom {{\nu_{z} } {E_{z} }}} \right. \kern-\nulldelimiterspace} {E_{z} }}} & 0 & 0 & 0 \\ { - {{\nu_{h} } \mathord{\left/ {\vphantom {{\nu_{h} } {E_{h} }}} \right. \kern-\nulldelimiterspace} {E_{h} }}} & {{1 \mathord{\left/ {\vphantom {1 {E_{h} }}} \right. \kern-\nulldelimiterspace} {E_{h} }}} & { - {{\nu_{z} } \mathord{\left/ {\vphantom {{\nu_{z} } {E_{z} }}} \right. \kern-\nulldelimiterspace} {E_{z} }}} & 0 & 0 & 0 \\ { - {{\nu_{z} } \mathord{\left/ {\vphantom {{\nu_{z} } E}} \right. \kern-\nulldelimiterspace} E}_{z} } & { - {{\nu_{z} } \mathord{\left/ {\vphantom {{\nu_{z} } {E_{z} }}} \right. \kern-\nulldelimiterspace} {E_{z} }}} & {{1 \mathord{\left/ {\vphantom {1 {E_{z} }}} \right. \kern-\nulldelimiterspace} {E_{z} }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 {G_{z} }}} \right. \kern-\nulldelimiterspace} {G_{z} }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 {G_{z} }}} \right. \kern-\nulldelimiterspace} {G_{z} }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {{1 \mathord{\left/ {\vphantom {1 {G_{h} }}} \right. \kern-\nulldelimiterspace} {G_{h} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {d\sigma_{xx} - b_{h} dp} \\ {d\sigma_{yy} - b_{h} dp} \\ {d\sigma_{zz} - b_{z} dp} \\ {d\sigma_{yz} } \\ {d\sigma_{xz} } \\ {d\sigma_{xy} } \\ \end{array} } \right] - \, \left[ {\begin{array}{*{20}c} {\alpha_{h} } \\ {\alpha_{h} } \\ {\alpha_{z} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right]dT$$
(13)

It can also be shown that the non-zero components of the Skempton tensor are \((B_{ii} )\), so that on can pose: \(B_{xx} = B_{yy} = B_{h} , \, B_{zz} = B_{z}\).

The variation of pore pressure with principal stresses was expressed by Skempton (1954) in term of two independent parameter noted here as \(A\) and \(B\) so that:

$$dp = B\left[ {d\sigma_{{\text{c}}} + A\left( {d\sigma_{{\text{a}}} - d\sigma_{{\text{c}}} } \right)} \right]$$
(14)

where \(\sigma_{{\text{c}}} \equiv \sigma_{xx}\) and \(\sigma_{{\text{a}}} \equiv \sigma_{zz}\) represent the confining and axial stress applied during the experiment, respectively. Under transverse symmetry, Eq. (4) becomes:

$$dp = \frac{{2B_{h} }}{3}d\sigma_{{\text{c}}} + \frac{{B_{z} }}{3}d\sigma_{{\text{a}}}$$
(15)

Combining equations (14) and (15), Skempton \(A\) and \(B\) are expressed by:

$$B = \frac{{2B_{h} + B_{z} }}{3};\;\;\;\;\;A = \frac{{B_{z} }}{3B}$$
(16)

The explicit form of Eq. (13) is given in the following relations:

$$d\varepsilon_{xx} = \frac{1}{{E_{h} }}\left( {d\sigma_{xx} - b_{h} dp} \right) - \frac{{\nu_{h} }}{{E_{h} }}\left( {d\sigma_{yy} - b_{h} dp} \right) - \frac{{\nu_{z} }}{{E_{z} }}\left( {d\sigma_{zz} - b_{z} dp} \right) - \alpha_{h} dT$$
(17)
$$d\varepsilon_{yy} = - \frac{{\nu_{h} }}{{E_{h} }}\left( {d\sigma_{xx} - b_{h} dp} \right) + \frac{1}{{E_{h} }}\left( {d\sigma_{yy} - b_{h} dp} \right) - \frac{{\nu_{z} }}{{E_{z} }}\left( {d\sigma_{zz} - b_{z} dp} \right) - \alpha_{h} dT$$
(18)
$$d\varepsilon_{zz} = - \frac{{\nu_{z} }}{{E_{z} }}\left( {d\sigma_{xx} - b_{h} dp} \right) - \frac{{\nu_{z} }}{{E_{z} }}\left( {d\sigma_{yy} - b_{h} dp} \right) + \frac{1}{{E_{z} }}\left( {d\sigma_{zz} - b_{z} dp} \right) - \alpha_{z} dT$$
(19)
$$d\varepsilon_{yz} = \frac{1}{{2G_{z} }}d\sigma_{yz} {; }d\varepsilon_{xz} = \frac{1}{{2G_{z} }}d\sigma_{xz} {; }d\varepsilon_{xy} = \frac{1}{{2G_{h} }}d\sigma_{xy}$$
(20)

From Eqs. (17)–(19) the volumetric strain is given by:

$$d\varepsilon_{{\text{v}}} = \left( {\frac{{1 - \nu_{h} }}{{E_{h} }} - \frac{{\nu_{z} }}{{E_{z} }}} \right)\left( {d\sigma_{xx} + d\sigma_{yy} - 2b_{h} dp} \right) + \frac{{1 - 2\nu_{z} }}{{E_{z} }}\left( {d\sigma_{zz} - b_{z} dp} \right) - \left( {2\alpha_{h} + \alpha_{z} } \right)dT$$
(21)

2.2.1 Drained, Isothermal, Deviatoric Experiment

Under these conditions, we have \(\Delta \sigma_{xx} = \Delta \sigma_{yy} = 0\), \(\Delta p = 0\), \(\Delta T = 0\) and shear stress. The elastic constants \(\nu_{z}\) and \(E_{z}\) can therefore be evaluated.

$$\Delta \varepsilon_{zz} = \frac{1}{{E_{z} }}\Delta \sigma_{zz}$$
(22)
$$\Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = - \nu_{z} \Delta \varepsilon_{zz}$$
(23)

unlike \(d\chi\) which is the instantaneous variation of the variable \(\chi\) at a given point, \(\Delta \chi\) is its variation over an interval of time.

2.2.2 Undrained, Isothermal, Deviatoric Loading

Under these conditions, one has \(\Delta \sigma_{xx} = \Delta \sigma_{yy} = 0\), \(dT = 0\), and there is shear stress. From equation (15), the pore pressured during this deviatoric phase is given by the following expression:

$$\Delta p = \frac{{B_{z} }}{3}\Delta \sigma_{zz}$$
(24)
$$\begin{gathered} \Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = \left[ { - \frac{{b_{h} }}{{E_{h} }}\left( {1 - \nu_{h} } \right)\frac{{B_{z} }}{3} - \frac{{\nu_{z} }}{{E_{z} }}\left( {1 - b_{z} \frac{{B_{z} }}{3}} \right)} \right]\Delta \sigma_{zz} \hfill \\ \Delta \varepsilon_{zz} = \left[ {2\frac{{\nu_{z} }}{{E_{z} }}b_{h} \frac{{B_{z} }}{3} + \frac{1}{{E_{z} }}\left( {1 - b_{z} \frac{{B_{z} }}{3}} \right)} \right]\Delta \sigma_{zz} \hfill \\ \end{gathered}$$
(25)

Which can be further reduced to:

$$\Delta \varepsilon_{zz} = \frac{1}{{E_{z}^{u} }}\Delta \sigma_{zz} ,\;\;\;\;\frac{1}{{E_{z}^{u} }} = \frac{1}{{E_{z} }}\left( {1 + 2\nu_{z} \frac{{b_{h} B_{z} }}{3} - \frac{{b_{z} B_{z} }}{3}} \right)$$
(26)
$$\Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = - \nu_{z}^{u} \Delta \varepsilon_{zz}$$
(27)

where \(E_{z}^{u}\) and \(\nu_{z}^{u}\) are the undrained Young's modulus and the undrained Poisson's ratio along the axis of symmetry, respectively. They are the undrained versions of the expressions given in (23) and (22). It can be demonstrated that the shear modulus along the axis of symmetry is related to the Young's modulus and Poisson's ratio along the same axis through the following known relation:

$$G_{z} = \frac{{E_{z} }}{{2\left( {1 + \nu_{z} } \right)}} = \frac{{E_{z}^{u} }}{{2\left( {1 + \nu_{z}^{u} } \right)}}$$
(28)

2.2.3 Isothermal, Unjacketed Isotropic Compression

One has \(\Delta \sigma_{xx} = \Delta \sigma_{yy} = \Delta \sigma_{zz} = \Delta \sigma = \Delta p\), \(\Delta T = 0\) and no shear stress. Equations (17)–(19) and (21) lead to:

$$\Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = \left[ {\frac{{\left( {1 - b_{h} } \right)\left( {1 - \nu_{h} } \right)}}{{E_{h} }} - \frac{{\nu_{z} \left( {1 - b_{z} } \right)}}{{E_{z} }}} \right]\Delta \sigma$$
(29)
$$\Delta \varepsilon_{zz} = \frac{{\left( {1 - b_{z} } \right) - 2\nu_{z} \left( {1 - b_{h} } \right)}}{{E_{z} }}\Delta \sigma$$
(30)
$$\Delta \varepsilon_{{\text{v}}} = c_{{\text{s}}} \Delta \sigma \;\;;\;\;\;c_{{\text{s}}} = \frac{{2\left( {1 - \nu_{h} } \right)\left( {1 - b_{h} } \right)}}{{E_{h} }} + \frac{{\left( {1 - 2\nu_{z} } \right)\left( {1 - b_{z} } \right) - 2\nu_{z} \left( {1 - b_{h} } \right)}}{{E_{z} }}$$
(31)

where \(c_{{\text{s}}}\) is the compressibility of the solid grain.

2.2.4 Drained, Isothermal, Isotropic Compression

One has \(\Delta \sigma_{xx} = \Delta \sigma_{yy} = \Delta \sigma_{zz} = \Delta \sigma\), \(\Delta p = 0\), \(\Delta T = 0\), and there is no shear stress in material equations (17)–(19) and (21) lead to:

$$\Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = \left( {\frac{{1 - \nu_{h} }}{{E_{h} }} - \frac{{\nu_{z} }}{{E_{z} }}} \right)\Delta \sigma$$
(32)
$$\Delta \varepsilon_{zz} = \frac{{1 - 2\nu_{z} }}{{E_{z} }}\Delta \sigma$$
(33)
$$\Delta \varepsilon_{{\text{v}}} = c_{{\text{d}}} \Delta \sigma \;\;;\;\;\;\;c_{{\text{d}}} = \frac{{2\left( {1 - \nu_{h} } \right)}}{{E_{h} }} + \frac{{1 - 4\nu_{z} }}{{E_{z} }}$$
(34)

where \(c_{{\text{d}}}\) is the drained compressibility. Combining (31) and (34), the Biot coefficient \(b\) becomes a complex combination of its components along different directions and that of the Young's moduli and Poisson's ratios, and is given in the following expression:

$$\;1 - \frac{{c_{{\text{s}}} }}{{c_{{\text{d}}} }} = \frac{{2\left( {1 - \nu_{h} } \right)b_{h} }}{{c_{{\text{d}}} E_{h} }} + \frac{{\left( {1 - 2\nu_{z} } \right)b_{z} - 2\nu_{z} b_{h} }}{{c_{{\text{d}}} E_{z} }}$$
(35)

2.3 Undrained, Isothermal, Isotropic Compression

Under these conditions, \(\Delta \sigma_{xx} = \Delta \sigma_{yy} = \Delta \sigma_{zz} = \Delta \sigma = \Delta \sigma_{{\text{a}}} = \Delta \sigma_{{\text{c}}}\), \(\Delta T = 0\) and no shear stress is present. From Eq. (14) the pore pressure is then related to the applied stress by:

$$\Delta p = B\Delta \sigma$$
(36)

And from Eqs. (17)–(19), one has:

$$\Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = c_{h}^{u} \Delta \sigma ,\;\;\;\;c_{h}^{u} = \frac{{\left( {1 - b_{h} B} \right)\left( {1 - \nu_{h} } \right)}}{{E_{h} }} - \frac{{\nu_{z} \left( {1 - b_{z} B} \right)}}{{E_{z} }}$$
(37)
$$\Delta \varepsilon_{zz} = c_{z}^{u} \Delta \sigma ,\;\;\;c_{z}^{u} = \frac{{\left( {1 - b_{z} B} \right) - 2\nu_{z} \left( {1 - b_{h} B} \right)}}{{E_{z} }}$$
(38)
$$\Delta \varepsilon_{{\text{v}}} = c_{{\text{u}}} \Delta \sigma \;\;;\;\;\;c_{{\text{u}}} = \frac{{2\left( {1 - \nu_{h} } \right)\left( {1 - b_{h} B} \right)}}{{E_{h} }} + \frac{{\left( {1 - 2\nu_{z} } \right)\left( {1 - b_{z} B} \right) - 2\nu_{z} \left( {1 - b_{h} B} \right)}}{{E_{z} }}$$
(39)

where \(c_{{\text{u}}}\) is the undrained bulk compressibility, \(c_{h}^{u}\) and \(c_{z}^{u}\) are the undrained compressibilities in the plane of symmetry and along the axis, respectively.

2.3.1 Undrained Thermal Loading Under Constant Stress

Under these conditions, we have \(\Delta \sigma_{xx} = \Delta \sigma_{yy} = \Delta \sigma_{zz} = 0\). The pore pressure and temperature are also related through a positive coefficient \(\Lambda\) known as the thermal pressurization, which gives the variation of the pore pressure with temperature during an undrained thermal experiment under constant applied stresses (Ghabezloo 2011), so that:

$$\Delta p = \Lambda \Delta T$$
(40)

From Eqs. (17)–(19), the following expression is obtained:

$$\Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = - \alpha_{h}^{u} \Delta T,\;\;\;\;\alpha_{h}^{u} = \alpha_{h} + \left[ {\frac{{b_{h} \left( {1 - \nu_{h} } \right)}}{{E_{h} }} - \frac{{\nu_{z} b_{z} }}{{E_{z} }}} \right]\Lambda$$
(41)
$$\Delta \varepsilon_{zz} = - \alpha_{z}^{u} \Delta T,\;\;\;\;\alpha_{z}^{u} = \alpha_{z} + \frac{{\left( {b_{z} - 2\nu_{z} b_{h} } \right)\Lambda }}{{E_{z} }}$$
(42)
$$\Delta \varepsilon_{{\text{v}}} = - \alpha_{{\text{u}}} \Delta T,\;\;\;\;\alpha_{{\text{u}}} = \alpha_{z}^{u} + 2\alpha_{h}^{u} = \left( {\alpha_{z} + 2\alpha_{h} } \right) + 2b_{h} \Lambda \left( {\frac{{1 - \nu_{h} }}{{E_{h} }} - \frac{{\nu_{z} }}{{E_{z} }}} \right) + \frac{{\left( {1 - 2\nu_{z} } \right)b_{z} \Lambda }}{{E_{z} }}$$
(43)

where \(\alpha_{{\text{u}}}\) is the undrained volumetric thermal expansion coefficient, \(\alpha_{z}^{u}\) and \(\alpha_{h}^{u}\) the undrained versions of \(\alpha_{z}\) and \(\alpha_{h}\), respectively.

2.3.2 Drained Thermal Loading Under Constant Stress

Under these conditions, we have \(\Delta \sigma_{xx} = \Delta \sigma_{yy} = \Delta \sigma_{zz} = 0\) and \(dp = 0\), Eqs. (17)–(19) lead to the following expressions from which are obtained linear and volumetric drained expansion coefficients.

$$\Delta \varepsilon_{xx} = \Delta \varepsilon_{yy} = - \alpha_{h} \Delta T$$
(44)
$$\Delta \varepsilon_{zz} = - \alpha_{z} \Delta T$$
(45)
$$\Delta \varepsilon_{{\text{v}}} = - \alpha_{{\text{d}}} \Delta T,\;\;\;\alpha_{{\text{d}}} = \alpha_{z} + 2\alpha_{h}$$
(46)

where \(\alpha_{{\text{d}}}\) is the volumetric drained thermal expansion coefficient of the frame.

2.4 Isotropic Materials

For isotropic materials, one has: \(b_{h} = b_{z} = b\), \(\alpha_{h} = \alpha_{z} = \alpha\), \(E_{h} = E_{z} = E\), \(\nu_{h} = \nu_{z} = \nu\), \(G_{h} = G_{z} = G\), \(B_{h} = B_{z} = B\) and \(A = \frac{1}{3}\). They can be introduced in relations (17) to (21) for further simplifications. The variations of porosity and of volumetric strain presented in relations (6) and (21) become:

$$d\varepsilon_{{\text{v}}} = c_{{\text{d}}} \left( {d\sigma - bdp} \right) - \alpha_{{\text{d}}} dT$$
(47)
$$d\phi = - bc_{{\text{d}}} d\sigma + \left( {bc_{{\text{d}}} - \phi^{0} c_{\phi } } \right)dp + \phi^{0} \alpha_{\phi } dT$$
(48)

where \(d\sigma = \frac{1}{3}\left( {d\sigma_{xx} + d\sigma_{yy} + d\sigma_{zz} } \right)\) is the mean stress,\(\;c_{{\text{d}}} = \frac{{3\left( {1 - 2\nu } \right)}}{E}\) and \(\alpha_{{\text{d}}} = 3\alpha\). Relations (47) and (48) are the usual equations found for volumetric strain and porosity variation for isotropic materials (Zimmerman et al. 1986; Ghabezloo 2011; Agofack et al. 2020).

3 Tested Material and Used Devices

3.1 Material Tested and Sample Preparation

The Pierre II claystone is used in this experiment. It is an outcrop and a homogeneous anisotropic shale with a porosity of 40.3% and a permeability perpendicular to the bedding of 1.47 × 10–20 m2 (0.147 μDarcy). Its bulk and grain densities are 2.03 g/cm3 and 2.77 g/cm3, respectively. From mercury intrusion porosimeter, the average pore diameter is 27.6 nm with very little number of pores larger than 100 nm. The material is also characterized by a total organic carbon (TOC) of 1.2%, BET surface area of 27.4 m2/g and pore water concentration of 3.5%wt. NaCl (weight percentage). The XRD experiment presented in Table 1 shows that this material is composed of more than 50% clay with 26.7% mixed layer/smectite, 18.6% illite/mica and 2.9% kaolinite (Duda et al. 2021).

Table 1 XRD mineralogical composition of Pierre II claystone
Full size table

During sample preparation, the material was continuously kept in inert oil (Marcol 82) to prevent any change in its moisture content. Sample extraction is made by coring, using a core barrel with industrial diamond cutting interface, followed by end-grinding to achieve flat and parallel end surfaces better than 0.02 mm. An oil-cooling core barrel is used to core the plug. Four samples with bedding orientation parallel to plug cross section were tested. Three small samples had dimensions of around 15 mm diameter and around 30 mm length, the fourth sample had dimensions of 25.53 mm diameter and 51.30 mm length. Following measurement of dimensions, the samples were photographed prior to testing. From solid's and fluid's mass balance, the relation between the degree of saturation of brine, the porosity, the bulk, and grain densities are given in equation (49).

$$S = \frac{{\rho_{b} - \rho_{s} \left( {1 - \phi } \right)}}{{\phi \rho_{f} }} \times 100,\;\;[{\text{in }}\% ]$$
(49)

where \(S\) is the degree of saturation which represent the ratio of fluid volume over the pore volume. \(\rho_{b}\) is the bulk density,\(\rho_{s}\) the grain density and \(\rho_{f}\) the density of the fluid (assumed 1 g/cm3 for 3.5%NaCl brine), the void density is neglected. With the values densities and porosity given above, the initial degree of saturation of the sample is 93.4%.

3.2 Experimental Setups

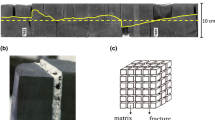
A hydraulic servo-controller load frame was used for the described tests. Its confining pressure vessel can handle a confining pressure of 140 MPa and pore pressure up to 140 MPa. Two high precision Kistler zero dead-volume pressure transducers (one for inlet and one for outlet) were used to measure the pore pressure. These transducers have a maximum working pressure of 50 MPa, and they do not have any dead volume. In addition, they are placed very close to the sample to minimize the minimize the dead volume. The tests were computer-controlled, allowing the user to pre-programme complex loading paths, but also with the possibility of manually modifying the paths during the test. Pressure intensifiers are used to monitor the confining and the pore pressures. The dead-volume of the pore fluid system is around 1.4 ml. To achieve this small dead volume, stainless steel tubing of 0.5 mm inner diameter (1/16" or 1.6 mm outer diameter) are used to connect the tested sample to the pore pressure transducers. The total length of the pore fluid line from sample to the pressure transducer is around 1.5 m. The above-estimated dead volume is the upper limit and include the compressibility of tubes as well as the metal mesh around the lateral surface on the sample (as presented in Fig. 1). Based on the size of the tested sample; a ratio of 1/7.4 of dead volume to pore volume is obtained. Such a small ratio permits to directly measure pore pressure changes of 0.01 MPa or less (Duda et al. 2021). An internal heating element and an external cooling jacket are used on the confining vessel to monitor the temperature. Two thermocouples (one on the electric heater and another close to the sleeve surface) are used to control and monitor the thermal loading paths during the experiment. The instrumentation also included fitting the sample with four strips of metal mesh in the vertical direction along the outside, overlaying drainage holes in each end piston to facilitate communication with the pore pressure. Pressure transducers are connected to each end piston. The radial displacement is measured in two orthogonal directions at mid length of the sample using a strain gauge cantilever. The FEP heat shrink Teflon sleeve is used to avoid pore fluid absorption which affects the pore pressure. The FEP sleeve shrinks at 110 °C and is therefore not expected to be influenced by the temperature range applied in these experiments. Axial deformation is measured by three Linear Variable Differential Transformers (LVDT) placed every 120° around the sample. A photograph of the triaxial test setup with a mounted sample is shown in Fig. 1. Each end piston is fitted with compressional (P-wave) ultrasonic crystals measuring the ultrasonic velocity in the axial direction.

Fig. 1
figure 1

Photographs showing: a The two endcaps with the drainage hole on their sections (both endcaps are similar). b An endcap with side drainage hole all around. c The four strips of metal mesh overlaying the side drainage holes on the two endcaps, and it goes through the lateral surface of the sample. d A sample mounted between endcaps and ready for testing. The four-metal mesh is visible on the lateral surface of the black sample, and both are covered by the transparent heat shrink sleeve. Radial deformation is measured in two orthogonal directions by a cantilever setup and the axial deformation is measured by LVDT's. The ultrasonic transducers measuring P-wave velocity are also connected. The pore pressure lines (stainless steel of 0.5 mm inner diameter) are also visible

Full size image

The three small samples were used for CIU (consolidated isotropic undrained) tests as described in Agofack et al. (2019), which briefly consisted of consolidating the sample at given confining and pore pressures, followed by an undrained deviatoric phase until peak stress, and with possible post-peak mechanical cycle (see Fig. 2). These samples were tested at room temperature and under different confining pressures and are considered as reference tests. The fourth sample was submitted to complex loadings including thermal cycles with amplitude up to 60 °C. For the sake of simplicity, only the calibration and the loading paths of this last experiment are fully described in the next section. This last sample will later be referred to as the “thermally-affected sample”.

Fig. 2
figure 2

Typical loading path for the reference CIU tests

Full size image

4 Results and Discussion

4.1 Calibration and Loading Paths

A fused quartz sample with known thermal properties and similar sizes as those of our sample, was used for calibration. The thermal loading (including rate and amplitude) defined for the shale sample was applied to this quartz. It was therefore possible to derive the mechanical and thermal correction factors for the load cell, axial strain and radial strain. The loading paths applied to the shale sample are displayed in Fig. 3 showing the temperature, pressures, and axial stress as function of time. The points P1 to P21 are only to ease the reading of the figures. After mounting the sample into the triaxial cell, a confining pressure of around 3 MPa was applied. The back pressure controller was set to 1 MPa and the pore fluid (brine at 3.5%wt. NaCl) was circulated (from the bottom to the top) to saturate the sample and remove possible air bubbles in the pore lines. After few hours, the valve connected to back pressure controller was closed and the confining pressure was increased to 10 MPa under isothermal drained conditions. Time was then given for consolidation (between P1 and P2 in the Figure). The end of consolidation, as well as the consolidation time were evaluated using the procedure described by Agofack et al. (2019). The estimation of that time is presented in Fig. 4. After the complete consolidation (with a sqrt of time in minutes at 15.5, which is around 4 h), a slight increase of the volumetric strain can be observed. It is most likely related to creep deformation, which is one of the main characteristics of shale rocks.

Fig. 3
figure 3

Loading paths given the confining pressure, pore pressure and temperature as function of time. The points P1–P21 are to facilitate the reading of timeline. Figures a and b are a continuous experiment with the same sample, P13 follows P12

Full size image
Fig. 4
figure 4

Estimation of the consolidation under a confining pressure of 10 MPa and pore pressure of 2 MPa

Full size image

At the end of the consolidation, an undrained loading was applied by increasing the confining pressure from 10 to 45 MPa (P2 P3). The pore pressure then increased from 2 to 35.15 MPa and slightly increased to 35.46 MPa while the confining pressure was kept at 45 MPa. This little increase of the pore pressure with constant confining pressure under undrained condition is probably related to some creep effects. Time was again given for additional consolidation and a slight creep was also observed. After stabilization of deformations, the temperature was increased from 22 to 90 °C with a rate of 0.9 °C/h, at undrained conditions and constant confining pressure. After the stabilisation of the pore pressure, the confining pressure was then decreased to 10 MPa at undrained condition. It was then followed by an undrained thermal cycle consisting of decreasing the temperature from 90 °C to 30 °C and increase back to 90 °C (see P5 P7). The confining pressure was successively increased to 20 MPa and to 45 MPa under undrained conditions and a similar thermal cycle was applied at each stage. These thermal cycles at different confining pressure are used to evaluate the effect of in-situ stress on thermo-poroelastic parameters. After reducing the confining pressure and temperature to 10 MPa and 30 °C (P11  P12), respectively, an unjacketed loading was applied by increasing simultaneously the confining pressure and pore pressure from 10 to 13 MPa and 2.85 to 5.85, respectively. This was followed by a drained isotropic compression where the confining pressure was further increased up to 20 MPa (P14  P15). A drained thermal cycle (30 °C → 90 °C → 30 °C) was then applied. The undrained deviatoric loading was then applied by increasing the axial stress from 20 to 30 MPa by strain control, at confining pressure of 20 MPa and temperature of 30 °C. After reaching the peak (see P19), the axial stress was then reduced to 25 MPa below it. An undrained thermal cycle (from P20) was applied to investigate the post-failure parameters, and the test was ended. Except the deviatoric phase which strain control, all the mechanical loadings were stress-control with a rate of around 4 MPa/h.

Table 2 summarized the different loading paths and the thermo-poroelastic properties that the loading path helps accessing.

Table 2 Different loading paths and evaluated thermo-poroelastic properties
Full size table

4.2 Results and Discussion

The response of the material in terms of strains and P-wave velocity for the thermally-affected sample is given in Fig. 5 as function of time. The points P1–P21, like those of Fig. 3, are only used to ease the reading of the figures. The axial strain \(\varepsilon_{{\text{a}}}\) is the average strain from the three axial LVDT, while the radial strain \(\varepsilon_{{\text{r}}}\) is the average of the radial strains provided by the cantilevers at 0 and 90° azimuth. The volumetric strain \(\varepsilon_{{\text{v}}}\) is calculated from the axial and radial ones using the following expression \(\varepsilon_{{\text{v}}} = \varepsilon_{{\text{a}}} + 2\varepsilon_{{\text{r}}}\). During the first undrained heating (from P3), the volumetric strain decreases, meaning expansion of the sample. When the temperature reached 90 °C and was kept constant, a slight increase of the strains is observed, correlating the decrease observed on pore pressure at the stage inducing an increase of the effective stress. This slight decrease of the pore pressure of around 0.25 MPa over a period 45 h has not yet found a proper explanation. The opposite is observed after cooling. After taking the temperature down from 90 °C and holding at 30 °C (P12–P13), a slight decrease is observed. This opposite variation eliminates the leakage as the source of the observation. Even if a proper explanation has not yet been found, an experimental artefact might be more plausible. Fortunately, they are very limited and insignificant during the mechanical or thermal loadings, and thus do not affect the results presented here. The ultrasonic P-wave velocity at 500 kHz varies between 2000 and 2300 m/s during the mechanical and thermal loadings. The P-wave velocity increases with the increase of volumetric compaction of the sample (increase of \(\varepsilon_{{\text{v}}}\)) and decreases when \(\varepsilon_{{\text{v}}}\) decreases. All the four tested samples are assumed transverse isotropic along the z axis, the equations developed in (13)–(46) are used to evaluate the poromechanical and thermal parameters.

Fig. 5
figure 5

The responses (of loading path presented in Fig. 3) in terms of axial, radial and volumetric strain, as well as the P-wave velocity as function of time. The points P1–P21 are to facilitate the reading of the timeline

Full size image

The strains and induced pore pressure are given in Fig. 6 during the deviatoric and thermal loadings for the thermally affected sample and one reference which was tested under similar confining pressure. For these two samples as well as the other reference sample, a cycle loading/unloading/reloading is applied in the beginning of the deviatoric phase. This cycle is used to estimate the elastic parameters \(\chi_{{\_{\text{elastic}}}}\) (\(\chi\) being \(E_{z}^{u}\), \(\nu_{z}^{u}\), \(G_{z}\) or \(B_{z}\)). The material was then loaded until the peak deviatoric stress. The parameters \(\chi_{\_50}\) can then be evaluated and represent the estimation of \(\chi\) at 50% of peak, which can be different to \(\chi_{{\_{\text{elastic}}}}\). Because the deviatoric phase was strain-controlled (rate of 1.2 × 10–5 mm/s), it was possible to observe the post-peak behaviour. Some samples were also submitted to mechanical and/or thermal loadings during the post-peak stage. A post-peak value \(\chi_{{{\text{\_postpeak}}}}\) could also be estimated. All these parameters, evaluated at different stages during the deviatoric phase are presented in Table 3. The stress–strain curves for the two samples show some discrepancies, which are probably related to their loading history. The induced pore pressure is around 7 MPa for thermally-affected sample and is around 9 MPa for reference sample. An increase of this pore pressure is even observed during the post-peak, with negative variation of the volumetric strain (meaning volume expansion). This is probably due to the pore collapsing effect. In the elastic regime, such volume expansion under undrained condition is generally linked to pore pressure decrease. The post-peak behaviour observed here is related to the plastic behaviour of the material. During the thermal heating cycle at the post-peak, the pore pressure induced during the heating phase is 5 MPa and it is around 6.6 MPa during the cooling. This irreversible behaviour of pore pressure further highlights the creep in post-yield of the material. The photos of the thermally-affected sample before and after experiment are given in Fig. 7 where a clear failure plane can be observed (photo on the right).

Fig. 6
figure 6

Stress–strain behaviour and induced pore pressure during the deviatoric phase: comparison between the thermally-affected sample and a reference sample under similar confining pressure. The induced pore pressure for the thermally-affected sample is composed of two portions related to mechanical (TRX) and thermal loadings

Full size image
Table 3 Parameters evaluated the undrained deviatoric phase. For the Young modulus, shear modulus, Poisson's ratio and Skempton's cofficient A, three different values are provided with subscripts "_elqstic", "_50", "_postpeak representing the the corresponding value evaluated in the elastic region, at 50% of the maximum deviatoric stress and after the peak of deviatoric stress, respectively
Full size table
Fig. 7
figure 7

Thermally-affected sample: before experiment (left), after experiment (right)

Full size image

Parameters such as the Young's modulus, shear modulus, Poisson's ratio and Skempton coefficient A evaluated on the deviatoric before and after the peak are summarized in Table 3 for the two groups of tests. For the three reference samples, the maximum axial stress, as expected, increases with the initial net mean stress, which is the net mean stress at the beginning of the deviatoric phase. This is a well-known behaviour of sedimentary rock, reflecting the fact that under higher net stress, the rock is more compact and thus displays higher maximum deviatoric stress. The same trend is also observed for the elastic undrained Young’s modulus, shear modulus and Poisson ratio showing a stiffer material after higher compaction. These elastic properties evaluated during the deviatoric loading cycle are in accordance with what could be expected. However, the parameters evaluated at 50% of the maximum deviatoric stress and within an interval of 2 MPa seem to an unexpected trend showing that the material at that stress level has already developed some inelastic strain. For the thermally-affected sample, it appears that this loading history has changed these poromechanical properties of this material and has made it stiffer. The parameter \(A\) for thermally-affected sample shows values slightly lower than those obtained on reference samples. They all show higher values compared to those of reference samples.

The curves analysed in the q – p' plane are presented in Fig. 8, which give the maximum shear stress and effective mean stress at the failure. These curves are typical responses for deviatoric undrained tests on normally consolidated claystone materials (Fjaer et al. 2008). The maximum shear stress of the thermally-affected sample is slightly lower than the expected value, probably due to the loading history which has reduced its yield stress. Using the Drucker-Prager criterion, which the generalization of the Mohr–Coulomb one, q is related to p' by the following expression (Drucker and Prager 1952; Jaeger et al. 2007; Fjaer et al. 2008).

$$q^{2} = \frac{1}{2}C_{1}^{2} \left( {3p^{\prime} + C_{2} } \right)^{2}$$
(50)

When \(q\), \(C_{1}\) and \(3p^{\prime} + C_{2}\) are positive, expression (50) becomes:

$$q = \frac{1}{2}C_{1} \left( {3p^{\prime} + C_{2} } \right)$$
(51)
Fig. 8
figure 8

Drucker-Prager criterion in the q–p' plane during the deviatoric phase (p' init represents the value of p' at the beginning of the deviatoric phase)

Full size image

where \(q\) is the generalized shear stress, p' the effective (or net) mean stress. \(C_{1}\) is dimensionless while \(C_{2}\) has a dimension of stress. q and p' are given by:

$$q = \frac{1}{\sqrt 2 }\sqrt {\left( {\sigma^{\prime}_{1} - \sigma^{\prime}_{2} } \right)^{2} + \left( {\sigma^{\prime}_{2} - \sigma^{\prime}_{3} } \right)^{2} + \left( {\sigma^{\prime}_{3} - \sigma^{\prime}_{1} } \right)^{2} } ;\;\;\;\;\;p^{\prime} = \frac{1}{3}\left( {\sigma^{\prime}_{1} + \sigma^{\prime}_{2} + \sigma^{\prime}_{3} } \right)$$
(52)

In the deviatoric phase of triaxial experiment where \(\sigma^{\prime}_{2} = \sigma^{\prime}_{3}\), \(q\) and \(p^{\prime}\) become:

$$q = \sigma^{\prime}_{1} - \sigma^{\prime}_{3} \;;\;\;\;p^{\prime} = \frac{1}{3}\left( {\sigma^{\prime}_{1} + 2\sigma^{\prime}_{3} } \right)$$
(53)

Combining equation (51) and (53), the following relation is obtained between \(\sigma^{\prime}_{1}\) and \(\sigma^{\prime}_{3}\):

$$\sigma^{\prime}_{1} = \frac{{C_{1} C_{2} }}{{2 - C_{1} }} + \sigma^{\prime}_{3} \frac{{1 + C_{1} }}{{1 - {{C_{1} } \mathord{\left/ {\vphantom {{C_{1} } 2}} \right. \kern-\nulldelimiterspace} 2}}}$$
(54)

The Mohr–Coulomb criteria is expressed by (Jaeger et al. 2007; Fjaer et al. 2008):

$$\sigma^{\prime}_{1} = C_{0} + \sigma^{\prime}_{3} \tan^{2} \beta$$
(55)

where \(C_{0}\) is the uniaxial compressive strength (UCS), related to cohesion \(S_{0}\) by \(C_{0} = 2S_{0} \tan \beta\) and \(\beta\) the angle where the failure criterion is fulfilled, which is related to internal friction angle \(\varphi\) by \(\beta = \frac{\pi }{4} + \frac{\varphi }{2}\). Using equation (51) and Fig. 8, the constants \(C_{1}\) and \(C_{2}\) equal 0.16 and 33.88 MPa, respectively. From equations (54) and (55), \(C_{0}\) is equal to 2.95 MPa, \(\beta\) to 48.31°, \(S_{0}\) to 1.31 MPa and \(\varphi\) to 6.62°.

As displayed in Fig. 3 and described in Sect. 4.1 for the thermally-affected sample, the different mechanical and thermal loadings, applied prior to the deviatoric phase, are used to evaluate other thermo-poroelastic properties of this material. The variation of the pore pressure with the confining pressure is used to evaluate the Skempton coefficient, while that of the confining pressure with the volumetric strain permits to estimate the undrained bulk modulus (\(K_{{\text{u}}} = 1/c_{{\text{u}}}\)), as it is presented in Fig. 9 for example.

Fig. 9
figure 9

Evaluation of bulk undrained modulus and Skempton B during the first undrained loading (P2  P3)

Full size image

The variation of the pore pressure (resp. of the volumetric strain) as a function of temperature is used to determine the thermal pressurization coefficient (resp. the undrained thermal coefficient). They are presented in Figs. 10, 11, 12, 13 as a function of net mean stress. Since the net mean stress changed during some loading phases, its value used in these Figures is that in the beginning of the phase where the specific parameter is evaluated. The undrained bulk modulus increases with the net mean stress from 5 to 6 (Fig. 10). Its value evaluated during the first compression at room temperature is higher than the subsequent values when the temperature of the sample was increased to 90 °C. The Skempton coefficient \(B\) varies between 0.94 and 0.98 and is rather poorly affected by the net stress (Fig. 11). Even if the increase of B with the net mean stress is very limited, the opposite was expected (decrease of B while increasing the neat mean stress). However, even though the reported values are given at 90 °C, they were each measured after submitting the sample to different thermal loading cycles. The actual trend is more corelated with the number of thermal cycles submitted to the sample (the higher the number, the higher the B value). \(B\) remains lower than 1 event if its values in the plan or along the axis of symmetry can be higher than 1. These values of Skempton \(B\) are higher than those found by Duda et al. (2021) at room temperature on the same sample material. \(B\) is therefore affected by loading history and tend to increase after thermal exposure.

Fig. 10
figure 10

Undrained bulk modulus as function of net mean stress

Full size image
Fig. 11
figure 11

Skempton's coefficient B as function of the net mean stress

Full size image
Fig. 12
figure 12

Undrained volumetric thermal expansion coefficient as function of net mean stress

Full size image
Fig. 13
figure 13

Thermal pressurization coefficient as function of net mean stress

Full size image

The volumetric undrained thermal expansion coefficient (resp. thermal pressurization coefficient) also shows some slight variation with the differential mean stress. From Figs. 12 and 13, it can be seen that the net stress at the beginning of the cooling phase is lower than that at the beginning of the heating. This is due to undrained isotropic cooling phase being preceded by heating during which the induced pore pressure increase contributed to the net stress reduction, and vice-versa. The plots show that \(\alpha_{{\text{u}}}\)(resp. \(\Lambda\)) slightly decreases (resp. increases) with the increase of the net mean stress both during the cooling and the heating phases. For a given thermal cooling/heating cycle, the value of these coefficients evaluated on the cooling phase is similar to that evaluated on the heating phase. At the post-peak stage, \(\alpha_{{\text{u}}}\) (resp. \(\Lambda\)) evaluated under anisotropic stress state is 3.07 × 10–4 /°C (resp. 0.92 MPa/°C), which is higher than (resp. within the same range as) the values presented in Figs. 12 and 13. The pressurization coefficient found is lower than that found on hardened cement paste. Ghabezloo et al. (2011) found \(\Lambda\) equal to 0.62 MPa/°C for the heating phase and 0.57 MPa/°C for the cooling phases on a hardened cement paste cured and aged at 90 °C. In wellbore condition with low permeable materials like cement or shale, the temperature decrease following the injection of CO2 will result in pore pressure decrease and thus an increase of effective stress, which will tend to preserve the material from tensile failure. Unlike the CO2 injection, in some other operations like SAGD, the pore pressure will increase due to temperature increase and this could likely lead to failure, first in the cement sheath as shown by Roy et al. (2016, 2018). This change of effective stress following heating or cooling is sketched in Fig. 14. It can be seen that an initial sample that did not fail can be moved to shear failure due to pore pressure increase following heating.

Fig. 14
figure 14

Possible change in Mohr–Coulomb circles after cooling or heating

Full size image

Similarly, the responses of other loading types were used to evaluate the corresponding parameters like the bulk drained modulus (\(K_{{\text{d}}} = 1/c_{{\text{d}}}\)) from drained compression and the solid grain modulus (\(K_{{\text{s}}} = 1/c_{{\text{s}}}\)) from unjacketed loading. These results are summarised in Table 4 together with the averaged values of \(K_{{\text{u}}}\), \(B\), \(\alpha_{{\text{u}}}\), and \(\Lambda\), and their standard deviation. For anisotropic material, the standard relations between its elastic parameters are not anymore valid. For example, the Biot coefficient \(b \ne 1 - {{K_{{\text{d}}} } \mathord{\left/ {\vphantom {{K_{{\text{d}}} } {K_{{\text{s}}} }}} \right. \kern-\nulldelimiterspace} {K_{{\text{s}}} }}\) (see Eq. (35)). For a full characterized TI material, components \(b_{h}\) and \(b_{z}\) could have been measured during the deviatoric undrained phase using equations (25) if the drained Young moduli (\(E_{h}\) and \(E_{z}\)) and drained Poisson ratios (\(\nu_{h}\) and \(\nu_{z}\)) are known. Such values could have been used to evaluate \(b\) for anisotropic and compare it to the isotropic case.

Table 4 Average valued of other thermo-poroelastic parameters evaluated on unjacketed, drained, undrained compression, and thermal loading phases during the fourth experiment
Full size table

5 Conclusions

This paper investigated the thermo-poromechanical properties of an anisotropic material and analysed the effect of thermal loading on the elastic properties, failure envelope and post-failure behaviour. A theorical description was provided with the thermo-poroelastic derivations for transverse isotropic (TI) and isotropic porous material was derived as well as the relations between different thermo-poroelastic properties. For the experiment, a Pierre II shale was assumed having TI symmetry. Samples with bedding plane parallel to the cross Sect. (0° bedding) were prepared and submitted to various mechanical and thermal loadings. The thermo-poroelastic properties were evaluated. They include the Skempton coefficients A and B, the drained, undrained, and solid phase compressibilities, the coefficients of thermal expansion (both drained and undrained), the thermal pressurization coefficient as well as the undrained Young's modulus and Poisson's ratio along the axis of symmetry. The undrained bulk modulus tended to increase with the net mean stress and decrease when increasing the temperature from room to 90 °C. The Skempton B coefficient which usually decrease with increase of the net mean stress, showed an opposite trend. It appeared that the number of thermal cycles that the sample has been submitted to has higher effect on B than the net mean stress. Even though the thermal loadings appeared to significant effect on the poroelastic properties, its effects on the failure envelop were rather limited.