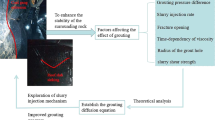
Abstract
A systematic presentation of the analytic relations of grout spread to the time period is established. They are divided following the nature of the flow, the property of the mix and the driving process. This includes channel flow between parallel plates and radial flow between parallel discs, nonlinear Newtonian fluids like silica solution, polyurethane and epoxy, and Bingham material like cement-based grout, and three grouting processes at a constant flow rate, constant pressure and constant energy. The analytic relations for the constant energy process are new and complete the relations of the constant flow rate and constant pressure processes. The well-known statement that refusal cannot be obtained during finite time for any injected material at a constant flow rate or constant injection pressure is extended to include the energy process. The term refusal pressure or energy cannot be supported for stop criteria. Stop criteria have to be defined considering confirmed relation of the spread to the time period and of the flow rate to the pressure and spread. It is shown that it is always possible to select a grouting process along which the work will exceed any predefined energy, the consequence of which is that jacking is related to the applied forces and not to the injected energy. Furthermore, a clarification is undertaken concerning the radial flow rate of a Bingham material since there are two different formulations. Their difference is explained and quantified. Finally, it is shown that the applied Lugeon theory is not supported by the analytic relations and needs to be substantially modified.






Similar content being viewed by others
Abbreviations
- A i , A 0, A 1 :
-
A(0), A(t 0), A(t 1) of any time function A(t)
- a :
-
Radius of the injection hole
- b :
-
Radius of the mix at the front
- c :
-
Yield stress or cohesion
- f :
-
Ratio of the viscosity to its initial value
- f, f′:
-
Local function and derivative defined in Appendix
- F :
-
Driving relation
- F :
-
Function
- F (0), F (1) :
-
Zero order, first-order approximation of F
- F a , F b , F c :
-
Local function defined in Appendix
- G :
-
Driving energy
- H :
-
Half-thickness of the planar fracture
- L, L 0 :
-
Spread of the mix and initial spread
- Li2 :
-
Dilogarithm function
- N :
-
Number of fractures
- n :
-
Integer index used in Appendix
- p :
-
Pressure
- P :
-
Injection pressure
- Q :
-
Flow rate
- r :
-
Radial coordinate
- R :
-
Reach
- S :
-
Span
- Sp:
-
Spence’s function
- T :
-
Maturity time
- t :
-
Time
- t 0 :
-
Initial time
- t G :
-
Gel time
- t P :
-
Pot life
- u :
-
Dummy variable
- V :
-
Volume of the mix
- w :
-
Width
- W :
-
Work
- x :
-
Dummy variable in Appendix
- z :
-
Local variable in Appendix
- α :
-
Fitting parameter
- β :
-
Ratio of the pseudo-core thickness to the fracture thickness
- η :
-
Dynamic viscosity
- η i :
-
Initial dynamic viscosity
- π :
-
Pi
- ξ :
-
Ratio of the spread to the span
- ξ 0 :
-
Spread ratio at t 0
- ξ a :
-
Ratio of the injection hole radius to the spread
- ξ r :
-
Ratio of the spread to the reach
- ξ r0 :
-
Ratio of the spread to the reach at t 0
- ξ ra :
-
Ratio of the radius of the injection hole to the reach
References
Andersson HMK, Borchardt PJ, Bruce DA (2001) The use of polyurethane resins in tunnel grouting. In: Rapid excavation and tunneling conference, San Diego, CA, June 11–13, 18 pp
Brantberger M, Stille H, Eriksson M (2000) Controlling grout spreading in tunnel grouting—analyses and developments of the GIN-method. Tunn Undergr Space Technol 15(4):343–352
Bruce DA (2011) Rock grouting for dams and the need to fight regressive thinking. Geotech News 29(2):23–30
Bruce DA (2013) Refusal and closure in rock grouting: let’s get it right! Geotech News 31(2):24–25
Bruce DA, de Porcellinis P (1990) Structural repair of major concrete dams through epoxy resin bonding. Concrete Repair Bull 22:4–5
Cambefort H (1961) L’injection et ses problèmes. Bull Tech Suisse Roman 87(19):329–341
Carino LJ, Lew HS (2001) The maturity method: from theory to application. In: Proceedings of the 2001 structures congress and exposition, pp 1–19, ASCE, Washington, DC
Dai G, Bird R (1981) Radial flow of a Bingham fluid between two fixed circular disks. J Non-Newton Fluid Mech 8:349–355
El Tani M (2009) Grout-time to break through the SL dispute. Geotech News 27(3):41–48
El Tani M (2012) Grouting rock fractures with cement grout. Rock Mech Rock Eng 45:547–561
El Tani M (2013) Grouting emancipation. Geotech News 31(3):38–42
El Tani M, Bremen R, Katterbach M (2014) Stop criterion for GIN. In: 8th Asian rock mechanics symposium, Sapporo, ISRM/One Petro, pp 447–456
Frigaard IA, Paso KG, de Souza Medes KG (2017) Bingham’s model in the oil and gas industry. Rheol Acta 56(3):259–282
Funehag J, Axelsson M (2003) Hydrogeological characterisation and sealing of narrow fractures in hard rock. Mater Geoenviron 60:121–124
Funehag J, Gustafsson G (2008) Design of grouting with silica sol in hard rock. Part I. TUST 23:1–8
Gustafson G, Claesson J (2005) Steering parameters for rock grouting. Unpublished paper submitted to the international journal of rock mechanics and mining sciences (IJRMMS), pp 19
Gustafson G, Stille H (2005) Stop criteria for cement grouting. Felsbau 25(3):62–68
Håkansson U (1993) Rheology of fresh cement-based grouts. Thesis KTH, Stockholm, Sweden, p 154
Hässler L (1991) Grouting of rock—simulation and classification. PhD thesis, Royal Institute of Technology, Sweden, p 159
Hatem M, Pusch M, Knutsson S (2015) Study of cement-grout penetration into fractures under static and oscillatory conditions. TUST 45:10–19
Houlsby AC (1990) Construction and design of cement grouting. Wiley, New York, p 442
Karol RH (2003) Chemical grouting and soil stabilization, 3rd edn. Dekker
Ladiges S, Willey J, Norbert M, Barclay A (2013) Case studies of foundation grouting using the GIN method at the enlarged Cotter Dam, 18p, ANCOLD conference 2013
Lombardi G, Deere D (1993) Grouting design and control using the GIN principle. Water Power Dam Constr 45(6):15–22
Naudts A (2004) Contemporary issues in rock grouting and formulation of engineered cement based suspension grouts, 14 p, Montreal
Rafi JY, Stille H (2015) Applicability of using GIN method, by considering theoretical approach of grouting design. Geotech Geol Eng 33(6):1431–1448
Stille H (2015) Rock grouting theories and application, pp 140. Befo Stockholm. ISBN: 978-91-88257-46-8
Stille B, Stille H, Gustafson G, Kobayashi S (2009) Experience with the real time grouting control method. Geomech Tunn 2:447
Teyssandier F, Ivankovic M, Love BJ (2010) Modeling the effect of the curing conversion on the dynamic viscosity of epoxy resins cured by an anhydride curing agent. J Appl Polym Sci 115:1671–1674
Wallner M (1976) Propagation of sedimentation stable cement pastes in jointed rock. Rock Mech Waterw Constr 2:449–461
Walz AH, Wilson DB, Bruce DA, Hamby JA (2003) Grouted seepage cutoffs in karstic limestone. In: 3rd international conference on grouting and ground treatment, New Orleans, ASCE, vol 120, pp 967–978
Weaver K, Bruce D (2007) Dam foundation grouting, revised and expanded. ASCE, press, New York
Zagier D (2006) The dilogarithm function. In: Frontiers in number theory physics and geometry, vol II, pp 3–65, Springer, Berlin. doi:10.1007/978-3-540-30308-4
Author information
Authors and Affiliations
Corresponding author
Appendices
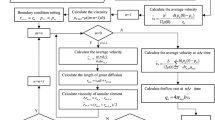
Appendix 1: Time–Spread Closed Form
The integration of the right-hand side of Eq. (50) leads to
with,
in which Sp is Spence’s function. Spence’s function is
Spence’s function has different appellations since it has many discoverers or re-discoverers (Zagier 2006). Spence’s function can be calculated using the dilogarithm function that is defined in the interval (−1, 1) as
Their relations are
Appendix 2: Time–Spread First-Order Approximation
The first-order approximations of Eq. (50) in the interval (0, ξ) is
in which
The integration is straightforward and leads to F (1) = F (0) + ∆F with
F (0) is the zero-order approximation.
Rights and permissions
About this article
Cite this article
El Tani, M., Stille, H. Grout Spread and Injection Period of Silica Solution and Cement Mix in Rock Fractures. Rock Mech Rock Eng 50, 2365–2380 (2017). https://doi.org/10.1007/s00603-017-1237-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00603-017-1237-8