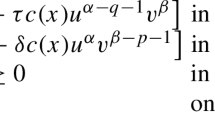Skip to main content
SpringerLink
Log in

Lack of coercivity in a concave–convex type equation

  • Published:
Calculus of Variations and Partial Differential Equations Aims and scope Submit manuscript

Abstract

Existence and multiplicity of non-negative solutions are investigated for the concave–convex type equation

$$-\Delta_p u +V(x)u^{p-1}=\lambda a(x) u^{r-1}+b(x)u^{q-1},\quad u\in W_0^{1,p}(\Omega),$$

where Ω is a bounded domain and 1 < r < p < q < p*. By minimization on the Nehari manifold, we find conditions on V, a, and b that yield up to four non-negative solutions when the left-hand side of the equation has a non-coercive behavior, a and b are sign-changing, and λ is positive and sufficiently small.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Allegretto W., Huang Y.-X.: A Picone’s identity for the p-Laplacian and applications. Nonlinear Anal. Theory Methods Appl. 32(7), 819–830 (1998)

    Article  MATH  MathSciNet  Google Scholar 

  2. Ambrosetti A., Brezis H., Cerami G.: Combined effect of concave and convex nonlinearities in some elliptic problems. J. Funct. Anal. 122, 519–543 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  3. Ambrosetti A., Azorero J.G., Peral I.: Multiplicity results for some nonlinear elliptic equations. J. Funct. Anal. 137(1), 219–242 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  4. Ambrosetti A., Azorero J.G., Peral I.: Existence and multiplicity results for some nonlinear elliptic equations: a survey. Dedicated to the memory of Gaetano Fichera (Italian). Rend. Mat. Appl. 20(7), 167–198 (2000)

    MATH  MathSciNet  Google Scholar 

  5. Azorero J.G., Alonso I.P.: Multiplicity of solutions for elliptic problems with critical exponent or with a nonsymmetric term. Trans. Am. Math. Soc. 323(2), 877–895 (1991)

    Article  MATH  Google Scholar 

  6. Azorero J.G., Alonso I.P.: Some results about the existence of a second positive solution in a quasilinear critical problem. Indiana Univ. Math. J. 43(3), 941–957 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  7. Birindelli I., Demengel F.: Existence of solutions for semilinear equations involving the p-Laplacian: the non coercive case. Calc. Var. 20, 343–366 (2004)

    MATH  MathSciNet  Google Scholar 

  8. Brown K.J.: The Nehari manifold for a semilinear elliptic equation involving a sublinear term. Calc. Var. Partial Differ. Equ. 22(4), 483–494 (2005)

    Article  MATH  Google Scholar 

  9. Brown K.J., Zhang Y.: The Nehari manifold for a semilinear elliptic equation with a sign-changing weight function. J. Differ. Equ. 193(2), 481–499 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  10. Brown K.J., Wu T.-F.: A fibering map approach to a semilinear elliptic boundary value problem. Electron. J. Differ. Equ. 2007(69), 1–9 (2007) (electronic)

    MathSciNet  Google Scholar 

  11. Cuesta M., Ramos Quoirin H.: A weighted eigenvalue problem for the p-Laplacian plus a potential. Nonlinear Differ. Equ. Appl. - NoDEA 16(4), 469–491 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  12. De Figueiredo D.G., Gossez J.-P., Ubilla P.: Local superlinearity and sublinearity for indefinite semilinear elliptic problems. J. Funct. Anal. 199(2), 452–467 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  13. De Figueiredo D.G., Gossez J.-P., Ubilla P.: Multiplicity results for a family of semilinear elliptic problems under local superlinearity and sublinearity. J. Eur. Math. Soc. (JEMS) 8(2), 269–286 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  14. De Figueiredo D.G., Gossez J.-P., Ubilla P.: Local “superlinearity” and “sublinearity” for the p-Laplacian. J. Funct. Anal. 257(3), 721–752 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  15. Drabek P., Pohozaev S.I.: Positive solutions for the p-Laplacian: application of the fibrering method. Proc. R. Soc. Edinburgh 127, 703–726 (1997)

    MATH  MathSciNet  Google Scholar 

  16. Guedda M., Véron L.: Quasilinear elliptic equations involving critical Sobolev exponents. Nonlinear Anal. Theory Methods Appl. 13(8), 879–902 (1989)

    Article  MATH  Google Scholar 

  17. Il’yasov Y.: On positive solutions of indefinite elliptic equations. C. R. Acad. Sci. Paris Ser. I Math. 333(6), 533–538 (2001)

    MATH  MathSciNet  Google Scholar 

  18. Il’yasov Y.: On nonlocal existence results for elliptic equations with convex–concave nonlinearities. Nonlinear Anal. 61(1–2), 211–236 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  19. Serrin J.: Local behavior of solutions of quasilinear equations. Acta Math. 111, 247–302 (1962)

    Article  MathSciNet  Google Scholar 

  20. Tarantello G.: On nonhomogeneous elliptic equations involving critical Sobolev exponent. Ann. Inst. Henri Poincaré Anal. Non Linéaire 9(3), 281–304 (1992)

    MATH  MathSciNet  Google Scholar 

  21. Trudinger N.S.: On Harnack type inequalities and their application to quasilinear elliptic equations. Comm. Pure Appl. Math. 20, 721–747 (1967)

    Article  MATH  MathSciNet  Google Scholar 

  22. Wu T.-F.: Multiplicity of positive solution of p-Laplacian problems with sign-changing weight functions. Int. J. Math. Anal. (Ruse) 1(9–12), 557–563 (2007)

    MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Université Libre de Bruxelles, CP 214, 1050, Bruxelles, Belgium

    Humberto Ramos Quoirin

Authors
  1. Humberto Ramos Quoirin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Humberto Ramos Quoirin.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ramos Quoirin, H. Lack of coercivity in a concave–convex type equation. Calc. Var. 37, 523–546 (2010). https://doi.org/10.1007/s00526-009-0275-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00526-009-0275-9

Mathematics Subject Classification (2000)

Search

Navigation