Skip to main content
SpringerLink
Log in

Quasiconvexification of sets in optimal design

  • Published:
Calculus of Variations and Partial Differential Equations Aims and scope Submit manuscript

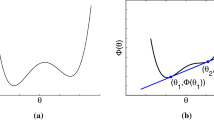
Abstract

By a suitable reformulation of a typical optimal design problem in conductivity, we treat the issue of determining the quasiconvexification (to fixed volume fraction) of certain sets of matrices that are union of two manifolds. By means of a helpful lemma, we are able to explicitly compute such hulls in a rather straightforward fashion without the need of seeking laminates by hand, and hence avoiding some tedious computations. We examine the linear case, both elliptic and hyperbolic, in 2 and higher dimension (by looking at a div–curl situation), as well as an interesting non-linear example that provides some clue as to what kind of characterization one may hope for in non-linear situations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Allaire G. (2002) Shape optimization by the homogenization method. Springer, Heidelberg

    MATH  Google Scholar 

  2. Boussaid, O.: Relaxation results for functions depending on polynomials changing sign on rank-one matrices (submitted)

  3. Faraco, D.: Beltrami operators and microstructure. Ph.D. Thesis, University of Helsinki (2002)

  4. Fonseca I., Müller S. (1999) A-quasiconvexity, lower semicontinuity and young measures. SIAM Math. Anal. 30(6): 1355–1390

    Article  MATH  Google Scholar 

  5. Maestre, F., Münch, A., Pedregal, P.: A spatio-temporal design problem for a damped wave equation. SIAM Appl. Math. (in press)

  6. Milton G.W. (2002) The Theory of Composites. Cambridge Monographs on Applied and Computational Mathematics, 6. Cambridge University Press, Cambridge

    Google Scholar 

  7. Milton G.W., Serkov S.K. (2000) Bounding the current in nonlinear conducting composites. The J. R. Willis 60th anniversary volume. J. Mech. Phys. Solids 48(6–7): 1295–1324

    Article  MATH  MathSciNet  Google Scholar 

  8. Münch A., Pedregal P., Periago F. (2006) Optimal design of the damping set for the stabilization of the wave equation. J. Differ. Equ. 231: 331–358

    Article  MATH  Google Scholar 

  9. Murat F. (1987) A survey on compensated compactness. In: Cesari L. (eds) Contributions to the modern calculus of variations. Pitman, London, pp 145–183

    Google Scholar 

  10. Pedregal P. (2005) Vector variational problems and applications to optimal design. ESAIM-COCV 11(3): 357–381

    Article  MATH  MathSciNet  Google Scholar 

  11. Pedregal P. (2007) div–curl young measures and optimal design in any dimension. Rev. Univ. Complutense 20(1): 239–255

    MATH  MathSciNet  Google Scholar 

  12. Tartar L. (1979) Compensated compactness and applications to partal differential equations, nonlinear analysis and mechanics: Heriot-Watt Symposium. In: Knops R. (eds) Research Notes in Mathematics, vol. IV, 39. Pitman, London, pp 136–212

    Google Scholar 

  13. Tartar L. (2000) An introduction to the homogenization method in optimal design. Springer Lect. Notes Math. 1740: 47–156

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculté des Sciences et Sciences de L’ingénieur, Université de Chlef, 02000, Chlef, Algeria

    Omar Boussaid

  2. Universidad de Castilla-La Mancha, ETSI Industriales, 13071, Ciudad Real, Spain

    Pablo Pedregal

Authors
  1. Omar Boussaid
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pablo Pedregal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pablo Pedregal.

Additional information

This work was supported by the research projects MTM2007-62945 of the MCyT (Spain) and PCI08-0084-0424 of the JCCM (Castilla-La Mancha).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Boussaid, O., Pedregal, P. Quasiconvexification of sets in optimal design. Calc. Var. 34, 139–152 (2009). https://doi.org/10.1007/s00526-008-0178-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00526-008-0178-1

Keywords

Search

Navigation