Skip to main content
SpringerLink
Log in

Polynomial dendritic neural networks

  • Original Article
  • Published:
Neural Computing and Applications Aims and scope Submit manuscript

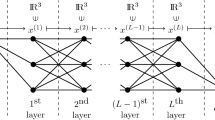
Abstract

Although many artificial neural networks have achieved success in practical applications, there is still a concern among many over their “black box” nature. Why and how do they work? Recently, some interesting interpretations have been made through polynomial regression as an alternative to neural networks. Polynomial networks have thus received more and more attention as generators of polynomial regression. Furthermore, some special polynomial works, such as dendrite net (DD) and Kileel et al.’s deep polynomial neural networks, showed that some single neurons have powerful computability. This agrees with a recent discovery on biological neurons, that is, a single biological neuron can perform XOR operations. Inspired by such works, we propose a new model called the polynomial dendritic neural network (PDN) in this article. The PDN achieves powerful computability on a single neuron in a neural network. The output of a PDN is a high degree polynomial of the inputs. To obtain its parameter values, we took PDN as a neural network and employed the back-propagation method. As shown in this context, PDN contains more polynomial outputs than DD and deep polynomial neural networks. We deliberately studied two special PDNs called the exponential PDN (EPDN) and asymptotic PDN (APDN). For interpretability, we proposed a feature analysis method based on the coefficients of the polynomial outputs of such PDNs. The EPDN and APDN showed satisfactory accuracy, precision, recall, F1 score, and AUC in several experiments. Furthermore, we found the coefficient-based interpretability to be effective on some actual health cases.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Abdelouahab K, Pelcat M, Berry F (2017) Why tanh can be a hardware friendly activation function for CNNs. In: Proceedings of the 11th international conference on distributed smart cameras, pp 199–201

  2. Adebayo J, Gilmer J, Muelly M, Goodfellow I, Hardt M, Kim B (2018) Sanity checks for saliency maps. In: Proceedings of the 32nd international conference on neural information processing systems, NeurIPS’18, pp 9525–9536

  3. Bahdanau D, Cho K, Bengio Y (2015) Neural machine translation by jointly learning to align and translate. ICLR

  4. Bowman S, Angeli G, Potts C, Manning C (2015) A large annotated corpus for learning natural language inference. In: Proceedings of the 2015 conference on empirical methods in natural language processing, pp 632–642

  5. Chen X, Duan Y, Houthooft R, Schulman J, Sutskever I, Abbeel P (2016) Infogan: interpretable representation learning by information maximizing generative adversarial nets. In: Proceedings of the 30th international conference on neural information processing systems, pp 2180–2188

  6. Dahl G, Yu D, Deng L, Acero A (2011) Context-dependent pre-trained deep neural networks forlarge-vocabulary speech recognition. IEEE Trans Audio Speech Lang Proces 20(1):30–42

    Article  Google Scholar 

  7. Dong Y, Hang S, Zhu J, Bo Z (2017) Improving interpretability of deep neural networks with semantic information. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 4306–4314

  8. Emschwiller M, Gamarnik D, Kızıldaǧ E, Zadik I (2020) Neural networks and polynomial regression. Demystifying the overparametrizaiotn phenomena. arXiv preprint arXiv:2003.10523

  9. Ghorbani A, Abid A, Zou J (2019) Interpretation of neural networks is fragile. In: Proceedings of the AAAI conference on artificial intelligence, vol 33, issue no 1, pp 3681–3688

  10. Gidon A, Zolnik TA, Fidzinski P, Bolduan F, Larkum M (2020) Dendritic action potentials and computation in human layer 2/3 cortical neurons. Science 367(6473):83–87

    Article  Google Scholar 

  11. Goodfellow I, Bengio Y, Courville A (2016) Deep learning. MIT press (2016)

  12. Guidotti R, Monreale A, Ruggieri S, Turini F, Giannotti F, Pedreschi D (2018) A survey of methods for explaining black box models. ACM Comput Surv 51(5):1–42

    Article  Google Scholar 

  13. He K, Zhang X, Ren S, Sun J (2015) Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In: Proceedings of the IEEE international conference on computer vision, pp 1026–1034

  14. Higgins I, Matthey L, Pal A, Burgess C, Glorot X, Botvinick M, Mohamed S, Lerchner A (2017) beta-vae: Learning basic visual concepts with a constrained variational framework. In: 5th International conference on learning representations, conference track proceedings

  15. Huang W, Oh S, Pedrycz W (2014) Design of hybrid radial basis function neural networks (HRBFNNs) realized with the aid of hybridization of fuzzy clustering method (FCM) and polynomial neural networks (PNNs). Neural Netw 60:166–181

    Article  Google Scholar 

  16. Huang G, Liu Z, Laurens V, Weinberger K (2017) Densely connected convolutional networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp 4700–4708

  17. Hui Z, Zhu J, Rosset S, Hastie T (2009) Multi-class adaboost. Stat. Interface 2(3):349–360

    MathSciNet  MATH  Google Scholar 

  18. Hyvarinen A, Oja E (2000) Independent component analysis: algorithms and applications. Neural Netw 13(4):411–430

    Article  Google Scholar 

  19. Kileel J, Trager M, Bruna J (2019) On the expressive power of deep polynomial neural networks. Adv Neural Inf Process Syst 32:10310–10319

    Google Scholar 

  20. Kingma D, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980

  21. Kingma D, Welling M (2013) Auto-encoding variational bayes, 2013. arXiv preprint arXiv:1312.6114

  22. Klambauer G, Unterthiner T, Mayr A, Hochreiter S (2017) Self-normalizing neural networks. In: Proceedings of the 31st international conference on neural information processing systems, pp 972–981

  23. Kramer O (2016) Machine learning for evolution strategies, vol 20. Springer, Switzerland

    MATH  Google Scholar 

  24. Liu G, Wang J (2021) Dendrite net: a white-box module for classification, regression, and system identification. IEEE Trans Cybern 1–14

  25. Luxburg U (2004) A tutorial on spectral clustering. Stat Comput 17(4):395–416

    Article  MathSciNet  Google Scholar 

  26. Menon A, Mehrotra K, Mohan C, Ranka S (1996) Characterization of a class of sigmoid functions with applications to neural networks. Neural Netw 9(5):819–835

    Article  Google Scholar 

  27. Park C, Choi E, Han K, Lee H, Rhee T, Lee S, Cha M, Lim W, Kang S, Oh S (2017) Association between adult height, myocardial infarction, heart failure, stroke and death: a Korean nationwide population-based study. Int J Epidemiol 47(1):289–298

    Article  Google Scholar 

  28. Safavian S, Landgrebe D (1991) A survey of decision tree classifier methodology. IEEE Trans Syst Man Cybern 21(3):660–674

    Article  MathSciNet  Google Scholar 

  29. Sainath T, Vinyals O, Senior A, Sak H (2015) Convolutional, long short-term memory, fully connected deep neural networks. In: 2015 IEEE international conference on acoustics, speech and signal processing (ICASSP), pp 4580–4584

  30. Selvaraju R, Cogswell M, Das A, Vedantam R, Parikh D, Batra D (2017) Grad-cam: visual explanations from deep networks via gradient-based localization. In: Proceedings of the IEEE international conference on computer vision, pp 618–626

  31. Simonyan K, Vedaldi A, Zisserman A (2014) Deep inside convolutional networks: Visualising image classification models and saliency maps. In: Workshop at international conference on learning representations

  32. Springenberg J, Dosovitskiy A, Brox T, Riedmiller M (2014) Striving for simplicity: The all convolutional net. arXiv preprint arXiv:1412.6806

  33. Sundararajan M, Taly A, Yan Q (2016) Gradients of counterfactuals. arXiv preprint arXiv:1611.02639

  34. Sweller J (1988) Cognitive load during problem solving: effects on learning. Cogn Sci 12(2):257–285

    Article  Google Scholar 

  35. Vaswani A, Shazeer N, Parmar N, Uszkoreit J, Jones L, Gomez A, Kaiser Ł, Polosukhin I (2017) Attention is all you need. In: Advances in neural information processing systems, pp 5998–6008

  36. Veličković P, Cucurull G, Casanova A, Romero A, Liò P, Bengio Y (2018) Graph attention networks. In: International conference on learning representations

  37. Wold S, Esbensen K, Geladi P (1987) Principal component analysis. Chemom Intell Lab Syst 2(1–3):37–52

    Article  Google Scholar 

  38. Xi C, Khomtchouk B, Matloff N, Mohanty P (2018) Polynomial regression as an alternative to neural nets. arXiv preprint arXiv:1806.06850

  39. Yang S, Ho C, Lee C (2006) HBP: improvement in BP algorithm for an adaptive MLP decision feedback equalizer. IEEE Trans Circuits Syst II Express Briefs 53(3):240–244

    Article  Google Scholar 

  40. Zeiler M, Fergus R (2014) Visualizing and understanding convolutional networks. In: European conference on computer vision, pp 818–833

  41. Zjavka L, Pedrycz W (2016) Constructing general partial differential equations using polynomial and neural networks. Neural Netw 73:58–69

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful to Professors Peng Tang and Bin Yi, in Southwest Hospital, Third Military Medical University, for their professional explanations for the breast cancer and cardiovascular disease results.

Author information

Authors and Affiliations

  1. Chongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences, Chongqing, China

    Yuwen Chen & Jiang Liu

  2. Chengdu Institute of Computer Applications, Chinese Academy of Sciences, Chengdu, China

    Yuwen Chen

Authors
  1. Yuwen Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jiang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiang Liu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This work was partially supported by the National Key R&D Program of China (No. 2018YFC0116704), NSF of China (No. 61672488), Science and Technology Service Network Initiative (No. KFJ-STS-QYZD-2021-01-001), Youth Innovation Promotion Association of Chinese Academy of Sciences (No. 2020377).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, Y., Liu, J. Polynomial dendritic neural networks. Neural Comput & Applic 34, 11571–11588 (2022). https://doi.org/10.1007/s00521-022-07044-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00521-022-07044-4

Keywords

Mathematics Subject Classification

Search

Navigation