1 Introduction

In most of the optimization problems, multi-objective optimization problems (MOPs) are required to be tackled and in particular in the case of having conflicting objectives (Coello 2018). The methods of single objective problems cannot solve these problems. One of the amazing characteristics of the MOPs is that there is no unique solution but a tradeoff between set of points. With each tradeoff point, there is a different solution. These points are called Pareto optimal set or non-dominated set (Rostami et al. 2020).

Most of the optimization techniques are designed to solve single objective problems (Kotb et al. 2019). The designers develop new techniques or modify the available ones to solve MOPs. There are three procedures according to the designer options (priori, posteriori and advanced) (Wang et al. 2020). In the first procedure, the designer transfers the multi-objectives into a unique equation including a set of weights. These weights are changing each run according to the importance of each objective. The most popular examples for this procedure are ε-constraint and weighted sum methods (Cunha et al. 2022). However, there are two drawbacks of this category: a unique solution for each run is cropped; the Pareto set is obtained after several runs, and it cannot solve all problems. In the posteriori, the Pareto set after a single run is obtained. One of the obtained solutions is carefully picked up according to the designer preferences after obtaining the Pareto set. The drawbacks of this category are the complexity and the expensive cost to obtain the Pareto set.

The examples for posteriori methods are multi-objective particle swarm algorithm (MOPSO) (Zain et al. 2018), non-dominated sorting genetic algorithm (NSGA) (Labbi et al. 2020) and multi-objective salp swarm algorithm (MOSSA) (Mirjalili et al. 2017a). For advanced procedure, the designer set his preference during the optimization process. Due to the demerits of the classical methods such as trapping in local optima and the dependency on the derivative method, the researchers have been developed a significant number of algorithms in the last decades such as vector evaluated genetic algorithm (Kou et al. 2021), niched Pareto genetic algorithm (NPGA) (Wu et al. 2020), strength Pareto evolutionary algorithm (SPEA) (Jiang and Yang 2017), multi-objective genetic algorithm (Guariso and Sangiorgio 2020), multi-objective bee algorithm (Zarea et al. 2018), multi-objective ant lion optimizer (Mirjalili et al. 2017b) and multi-objective equilibrium algorithm (Rizk-Allah and Hassanien 2022).

The researchers continuously develop more techniques or improve the current algorithms to solve MOPs. When the technique solves some problems efficiently, it does not guarantee its effectiveness in different sets of test problems according to the No-Free-Lunch theory (Adam et al. 2019). This is the basic motivation of this research.

Tunicate swarm algorithm (TSA) is mathematically described by Kaur et al. (2020a) as one of the simplest bio-inspired meta-heuristics algorithms. It was mathematically modeled based on the swarm behavior and jet propulsion. It was proved its efficacy by solving 74 test functions such as (CEC2017, classical, and CEC2015), and was applied to different engineering problems. To avoid the demerits of the original TSA, enhancing the convergence performance and satisfying a suitable balance between exploitation and exploration (Wilson et al. 2021), some improved variants have been developed. For instance, Fetouh et al. emerged levy flight with TSA and proved its high quality by testing optimal distribution network reconfiguration (DNR) with control of the switched capacitor banks and taking distribution generator into account (Fetouh and Elsayed 2020). In Houssein et al. (2021), a local operator is combined with the original TSA to enhance its quality of the solution. Rizk-Allah et al. developed an enhanced TSA based on a novel searching mechanism to enhance the searching ability (Rizk-Allah et al. 2021). Li et al. proposed an improved TSA for solving dynamic economic and emission dispatch using three test systems (Li et al. 2021). Dogra et al. used TSA to optimize a way for elongation network lifetime and improve various performance metrics (Dogra et al. 2021). A. Sharma et al. employed the TSA to evaluate the preferred value of the unknown parameters of a PV cell/module under standard temperature conditions comparing with four different algorithms (Sharma et al. 2021). Arabali et al. (2022) introduced an adaptive TSA for finding the optimum design of a shallow spread foundation with solving some global optimization problems. They confirmed the efficacy of their methodology by using a set of 23 mathematical test functions and they compare the results with other algorithms. Yadav et al. developed an improved TSA to deal with the weapon target assignment (WTA) (Yadav et al. 2022), where they prove its efficacy by the comparisons with different algorithms.

Chaos theory is a deterministic nonlinear system with stochastic and ergodic properties which is depended on the initial conditions. It was described by Hénon and Lorenz (Hénon 1976; Lorenz 1995). There are many important applications that use it such as physics, meteorology, biology, economics, sociology, and engineering. In the last years, chaos is embedded with multi-objective techniques to enhance the convergence and diversity of the non-dominated solutions which use the different chaotic maps (Chen and Hu 2017). Many designers developed a combination between chaos theory and different multi-objective techniques to avoid the demerits of the traditional techniques. Ammaruekarat et al. proposed a technique that combined between chaos and memetic algorithm (MA) (Neri and Cotta 2021) for solving MOPs. The comparative results showed the efficient performance (Ammaruekarat and Meesad 2012). In (Shayeghi and Ghasemi 2014; Seuci 2015), the researchers developed a new multi-objective technique that embedded chaos search to a modified artificial bee colony. Ahmed et al. developed a new methodology that chaos methods are embedded with a binary MOPSO to find optimal maintenance for pavement (Ahmed et al. 2019). The results showed the significant effect of the proposed methodology comparing with other algorithms (Ahmed et al. 2019). Although, the above-mentioned techniques have confirmed their effectiveness in solving MPOs, there is still needed to introduce robust algorithms that can efficiently converge and approximate the true Pareto front (Arora et al. 2020; Moysis et al. 2020; Ryu and Kim 2020).

In this research, a chaos-enhanced multi-objective tunicate swarm algorithm (CMOTSA) is proposed with the aim to enhance the diversification and intensification features of the classical TSA towards an efficient Pareto front. To prove the validation of CMOTSA, it is applied on ZDT functions with different characteristics and compared with other techniques from the literature. The applicability is confirmed by solving the combined economic-emission dispatch (CEED) problem using different systems 6-units, 10-units and 14-units system.

The main contributions of this work are as follows: (i) Chaotic map is embedded to enrich the diversity of solutions, thus enhancing the exploration ability of the proposed CMOTSA, (ii) Exponential strategy- based neighborhood searching pattern is designed to facilitate the exploitation capacity, which leads to boost the quality of solutions, (iii) The effectiveness of CMOTSA is illustrated through the investigation on ZDT functions with large-scale aspect, where the comparisons against other competitors have proven that the CMOTSA provides a good convergence and well-distributed solutions in terms of GD and IGD metrics, and (v) The CMOTSA is applied to CEED including valve ripples by using three different system topologies, and results exhibited its competitive performance.

The coming sections are prearranged as follows: the mathematical definition of MOPs and solution indices are in Sect. 2. The fundamentals of TSA and the CMOTSA are shown in Sect. 3. The experiments and results are introduced in Sect. 4. Then, the CMOTSA is applied to CEED problem in Sect. 5 plus analysis and discussion of results. Finally, conclusion and future work are announced in Sect. 6.

2 Preliminaries and model adaption

The mathematical definition of the MOPs and some solution concepts are introduced in this section.

2.1 Problem definition

A MOP consists of more than one objective function. These objective functions need to be optimized simultaneously with satisfying some constraints. The mathematical definition of the MOP is as follows:

$$ {\text{Minimize}}\quad \left( {f\left( v \right)} \right) = {\text{Min}}\left( {f_{1} \left( v \right),f_{2} \left( v \right), \ldots \ldots ..,f_{m} \left( v \right)} \right),\quad v = \left\{ {v_{1} ,v_{2} , \ldots \ldots .v_{q} } \right\} $$

Subject to:

$$ \begin{gathered} h_{p} \left( v \right) \le 0 ,\quad \forall p \in n \hfill \\ q_{l} \left( v \right) = 0 ,\quad \forall l \in s \hfill \\ v_{i}^{\min } \le v_{i} \le v_{i}^{\max } \hfill \\ \end{gathered} $$
(1)

where \(h_{p} \left( v \right)\) is the inequality the \(p{\text{th}}\) constraint, \(q_{l} \left( v \right)\) is the \(l{\text{th}}\) equality constraints, \(v\) defines the control variable vector, \(m\) is the number of fitness functions, \(n\) defines the number of inequality constraints, \(s\) is the number of equality constraints,\( q\) is the number of variables and \(v_{i}^{\min } ,v_{i}^{\max }\) are the boundaries (min and max) for the \(i{\text{th}}\) variable.

In single objective problems, the traditional operators compare the solutions based on only one objective, and thus one solution becomes the better if its fitness function is less than the other members. In MOP, the Pareto dominance is performed to compare the solutions with each other. Some solution concepts to understand the MOP are shown below (Rostami et al. 2020).

Concept 1 Pareto optimal dominance: Assuming \(v_{1} ,v_{2 }\) are two vectors. It can be said that \(v_{1}\) dominates \(v_{2} \left( {v_{1} > v_{2} } \right) \) if the two rules are satisfied.

$$ \begin{gathered} \forall j:f_{j} \left( {v_{1} } \right) \le f_{j} \left( {v_{2} } \right),\quad \forall j \in m \hfill \\ \exists i: f_{i} \left( {v_{1} } \right) < f_{i} \left( {v_{2} } \right),\quad \forall j \in m \hfill \\ \end{gathered} $$
(2)

Concept 2 Pareto optimality. One can say that the solution \(A \in V\) is a Pareto optimal if \(\exists C \in V:A > C\), then \(V\) can be defined as a feasible region

$$ V = \left\{ {v:h_{p} \left( v \right) \le 0 \forall p;\;q_{l} \left( v \right) = 0 \forall l;v_{i}^{\min } \le v_{i} \le v_{i}^{\max } \forall i } \right\} $$
(3)

Concept 3 Pareto optimal set. The set that contains all the Pareto optimal solutions

$$ P_{set} = \left\{ {v :\neg \exists v^{\prime} \in V, v^{\prime} > v} \right\} $$
(4)

Concept 4 Pareto optimal front. The set that contains the fitness functions of all Pareto optimal solutions set

$$ {\text{PF}} = \left\{ {f\left( {v_{i} } \right)|v_{i} \in P_{{{\text{set}}}} } \right\} $$
(5)

2.2 Mathematical definition of CEED

CEED problem is considered as a nonlinear bi-objective optimization problem (economic dispatch, and emission dispatch). The values of the generation powers are varied with the aim to minimize the two conflicting objective functions (the cost of generation and the emission of pollutants) with satisfying the demand power and the generation boundaries constraints.

2.2.1 Economic dispatch

The first fitness function of CEED is to minimize the generation cost. The generation cost function can be formulated in two forms (with and without valve ripple effect). For simple problem, it is considered as quadratic and convex function. In real economic dispatch, the fuel cost is represented as a non-convex and nonlinear function because of steam which appears as a ripple or a sinusoidal part (Elhameed and El-Fergany 2017).

$$ \min \left( {f_{c} } \right) = \left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{i = 1}^{G} \partial_{i} {\text{GE}}_{i}^{2} + \propto_{i} {\text{GE}}_{i} + \varepsilon_{i} } & {{\text{Without}}\;{\text{valve}}\;{\text{effect}}} \\ {\mathop \sum \limits_{i = 1}^{G} \partial_{i} {\text{GE}}_{i}^{2} + \propto_{i} {\text{GE}}_{i} + \varepsilon_{i} + \left| {\theta_{i} \times \sin \left\{ {\beta_{i} \left( {{\text{GE}}_{i}^{\min } - {\text{GE}}_{i} } \right)} \right\}} \right|} & {{\text{With}}\;{\text{valve}}\;{\text{effect}}} \\ \end{array} } \right. $$
(6)

where \(\partial_{i} , \propto_{i} ,\varepsilon_{i} ,\theta_{i} ,\& \beta_{i}\) are the fuel cost coefficients, \({\text{GE}}_{i}\) is the generation power for the \(i{\text{th}}\) unit and \(G\) is the number of units.

2.2.2 Emission Dispatch

Minimizing the pollutants emission is the second fitness function of CEED problem. There are many emissions which are released from the power plants to the atmosphere such as \({\text{NO}}_{x}\). The mathematical definition of these pollutants can be considered as expressed in Eq. (7).

$$ \min \left( {E_{P} } \right) = \mathop \sum \limits_{i = 1}^{G} A_{i} {\text{GE}}_{i}^{2} + B_{i} {\text{GE}}_{i} + C_{i} + \omega_{i} \exp \left( {\mu_{i} {\text{GE}}_{i} } \right) $$
(7)

where \( A_{i} ,B_{i} ,C_{i} ,\omega_{i} , \& \mu_{i}\) are the coefficients of the total emissions.

The system must satisfy the following constraints:

2.2.2.1 The balance of power constraint

The total power of generators must equal the sum of the demand power \( D_{{{\text{power}}}}\) and the losses of transmission \( \left( {P_{{{\text{loss}}}} } \right)\).

$$ \mathop \sum \limits_{i = 1}^{G} {\text{GE}}_{i} = D_{{{\text{power}}}} + P_{{{\text{loss}}}} $$
(8)
$$ P_{{{\text{loss}}}} = \mathop \sum \limits_{u = 1}^{G} \mathop \sum \limits_{k = 1}^{G} {\text{GE}}_{iu} B_{uk} {\text{GE}}_{iu} + \mathop \sum \limits_{u = 1}^{G} B_{Ou} {\text{GE}}_{iu} + B_{OO} $$
(9)

where \({B}_{uk},{B}_{Ou},{\& B}_{OO}\) are the coefficients of the transmission losses.

2.2.2.2 The boundaries constraints

Each generator must satisfy its min/max boundaries.

$$ {\text{GE}}_{i}^{\min } \le {\text{GE}}_{i} \le {\text{GE}}_{i}^{\max } \forall i \in G $$
(10)

2.3 Quality metrics

There are many quality metrics to assess the solutions of MOPs. In this research, two of them are employed which are widely used, namely the inverted generational distance (IGD) and generational distance (GD) metrics.

2.3.1 Inverted generational distance

The IGD takes the optimal \(PF\) as a standard and computes the Euclidean distance of each point of it to the evaluated \(PF\). With the IGD, the convergence and diversity of the proposed methodology can be evaluated. The mathematical definition of the IGD is (Sun et al. 2019):

$$ {\text{IGD}} = \frac{1}{{{\text{NS}}}}\sqrt {\mathop \sum \limits_{i = 1}^{{{\text{NS}}}} \left( {D_{i}^{2} } \right)} $$
(11)

where \({\text{NS}}\) is the number of the solutions in optimal \({\text{PF}}\) and \(D_{i}\) is the Euclidean distance between each point of optimal \({\text{PF}}\) to the evaluated \({\text{PF}}\).

2.3.2 Generational distance

The GD shows the ability of the proposed technique to produce the \({\text{PF }}\) at a closest distance to the optimal \({\text{ PF}}\). The technique with a minimum GD has the good convergence to optimal \({\text{PF}}\). The mathematical definition of GD is (Liu et al. 2019):

$$ {\text{GD}} = \frac{1}{{{\text{NT}}}}\sqrt {\mathop \sum \limits_{i = 1}^{{{\text{NT}}}} \tilde{D}_{i}^{2} } $$
(12)

where \({\text{NT}}\) is the number of solutions in the evaluated \({\text{ PF}}\) and \(\tilde{D}_{i} \) is the Euclidean distance of each point of the evaluated \( {\text{PF }}\) to the closest point of the optimal \({\text{ PF}}\).

3 The proposed method

This section introduces the basics of tunicate swarm algorithm (TSA), the concept of chaos theory, and the proposed methodology (CMOTSA) with details.

3.1 The classical TSA

S. Kaur et al. proposed the TSA for solving different optimization problems. Tunicates with the cylindrical shape and the tunic in each one can move through the ocean using fluid jet and join with each other. Tunicates use two important techniques to navigate and reach to the food source (swarm behavior and jet propulsion). In jet propulsion, the tunicates must prevent the collision between them, move to the optimal one and must be near to the best. There is a vector \(\vec{N}\) which is emerged to compute a new position of tunicate to prevent the collision between them. It is described as follows:

$$ \vec{N} = \frac{{r_{2} + r_{3} - 2r_{1} }}{{S_{\min } + r_{1} \left( {S_{\max } - S_{\min } } \right)}} $$
(13)

where \( r_{1} ,r_{2} ,r_{3} \) are random between (0,1) and \(S_{\min } ,\;S_{\max }\) are lower and upper tunicates speed.

The tunicates update its positions according to the best one using the swarm behavior which is described as follows:

$$ P_{{{\text{pos}}}} \left( {t + 1} \right) = \frac{{P_{{{\text{pos}}}} \left( t \right) + P_{{{\text{pos}}}} \left( {t + 1} \right)}}{{2 + r_{1} }} $$
(14)
$$ P_{{{\text{pos}}}} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {F_{{{\text{pos}}}} + \vec{N}.DF\quad {\text{if}}\; rand \ge 0.5} \\ {F_{{{\text{pos}}}} - \vec{N}.DF\quad {\text{if}}\; rand \le 0.5} \\ \end{array} } \right. $$
(15)

\({\text{where}}\;F_{{{\text{pos}}}} { }\) is the food position, and \({\text{DF}}\) is the distance between each tunicate and \(F_{{{\text{pos}}}}\). Here \(P_{{{\text{pos}}}} \left( {t + 1} \right)\) denotes the updated position of tunicates, \(t\) denotes the present iteration, and \(P_{{{\text{pos}}}} \left( t \right)\) defines the present position of tunicates.

The algorithmic steps and practical formulation of the classical TSA are framed as follows:

  1. 1.

    Insert the basic parameter for TSA, max. number of generations

  2. 2.

    Produce a random population of tunicates

  3. 3.

    Compute the objective functions of tunicates and specify the tunicate with the best fitness

  4. 4.

    Update the tunicates positions by Eq. (14)

  5. 5.

    Compute the objective function of each tunicate according to the updated position

  6. 6.

    Check the boundaries for each tunicate

  7. 7.

    Update the optimal tunicate

3.2 Chaos theory

Many practical applications used chaos theory as it is one of the important optimization techniques. Chaos can be considered as natural nonlinear phenomena with high sensitivity to the initial conditions. Chaos causes a large variation in the results with a small difference in the initial variables. It appears as probabilistic and random, but it is a deterministic theory which uses different maps. Each map has maximum number of iterations (\({\text{CT}}\)). Logistic map is the most popular map, where its mathematical definition is expressed as follows:

Logistic map is the most used in different techniques. It converts the simple formulation into a complex system with deterministic sequence. It can be defined as follows:

$$ c_{n + 1} = \alpha c_{n} \left( {1 - c_{n} } \right) $$
(16)

where \(c_{n}\) defines chaotic variable, \(n\) is chaotic iteration number, \(\alpha\) is a control factor with \(c_{o} \in \left( {0,1} \right) \;{\text{and}}\; c_{o} \notin \left\{ {0.0, 0.25, 0.5, 0.75, 1} \right\}. \) Fig. 1 shows the chaotic values of the logistic map with initial chaotic value \((c_{o} ) = 0.7\) and \(CT\) = 150 iterations.

Fig. 1
figure 1

Dynamics of logistic map

Full size image

3.3 Chaotic multi-objective TSA (CMOTSA)

This subsection is exhibited the proposed CMOTSA that is embedded with the chaotic sequence map and the exponential neighborhood searching strategy. Instead of the random search, the chaotic values of the logistic map are used in this methodology. The chaotic search is inserted to enhance the diversity and convergence of the technique. Moreover, the exponential neighborhood searching strategy is presented to enhance the exploitation ability. The main steps of the CMOTSA can be stated as follows.

  • Step 1: Initialization Enter the basic parameters such as maximum number of iterations (\(T\)), population size (\({\text{PS}}\)) and maximum size of archive (\({\text{RS}}\)). Randomly initialize a population of tunicates.

  • Step 2: Evaluation The fitness functions of each tunicate are computed and then obtained the non-dominated tunicates in archive. Then update the archive with the non-dominated solutions or Pareto solutions that are obtained using Pareto dominance concepts.

  • Step 3: Chaotic search. Insert the initial value of the map \((c_{o} )\), maximum number of chaotic iterations (\({\text{CT}}\)). The mapping Eq. (16) is used to generate the chaotic values (\(c\)) until reach to the chaotic maximum iterations.

  • Step 4: Exponential neighborhood searching phase In this step, a new exponential equation based on the chaotic values is adapted to enhance the exploitation and explore new solutions. For each iteration (\(t\)), each tunicate position in the strategy is modified by an exponential function depending on the chaotic numbers. The modified equation is represented as follows:

    $$ P_{{{\text{pos}}}} \left( {n + 1} \right) = P_{{{\text{pos}}}} \left( n \right) - c*\exp \left( { - \frac{t}{T}} \right)*\emptyset $$
    (17)

    where \( \emptyset\) is the dynamic difference between the maximum and minimum of the tunicate positions. It can be represented as follows:

    $$ \emptyset = P_{{{\text{pos}}}}^{\max } - P_{{{\text{pos}}}}^{\min } $$
    (18)

    In each iteration, the obtained result from the modified search and the result before it are compared. If the new value dominated the first one, add the new one to the archive.

    During this step, the obtained results are compared with all results in the storage and updated continuously with the obtained non-dominated tunicates until the archive reaches to its max. size.

  • Step 5: Managing the size of archive The ranking of the tunicate solutions is performed within the archive based on the crowding of tunicates. The most crowding of tunicates takes the highest rank. After this a roulette wheel selection is applied to choose at least one of them to be deleted with when the archive becomes full. The solution in the crowded region (the highest rank) is the best choice to remove it.

  • Step 6 Update the tunicates population according to Eq. (14) and Eq. (17) and make sure that all the boundaries are satisfied.

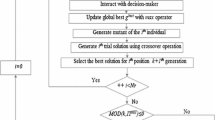
The steps from 2 to 6 are repeated until reaching to \( T\). Lastly, the storage containing the non-dominated tunicates is obtained. One of the challenges in MOPs is choice of the compromise solution from the Pareto solutions rather that exhibiting all Pareto solutions and thus facilitates the mission of the designer to perform his/her task. The flowchart of the CMOTSA is presented in Fig. 2.

Fig. 2
figure 2

The flowchart of CMOTSA

Full size image

3.4 Experiments and results

To verify the good performance of CMOTSA, it is applied on ZDT functions which have different \({\text{PF }}\) characteristics (discrete, non-convex, and convex). The mathematical formulation of these functions is illustrated in Table 1. Then, its results are compared with the original MOTSA and other techniques from the literature review. The proposed algorithms are implemented for 20 independent runs. Table 2 contains the different parameters of the used techniques. By using GD and IGD, the proposed CMOTSA proved its robustness when comparing with other techniques. MATLAB R2015b with 64-bit, Core i7, 2.60 GHz and 8 GB internal memory is employed to implement the proposed algorithms.

Table 1 The mathematical formulation of ZDT functions
Full size table
Table 2 Techniques parameters for ZDT functions evaluation
Full size table

3.5 ZDT functions results

The CMOTSA is applied to the well-known ZDT functions, and its results are compared with the traditional MOTSA. The IGD and GD metrics are used to show the validation of the suggested algorithms, where the ZDT1-ZDT3, and ZDT6 functions are optimized with 30 control variables. Then, the statistical results (maximum, minimum, average, median and standard deviation) are reported for GD and IGD in Table 3 which shows that the suggested algorithm has the best results for all functions. The best results are marked with bold font. The evaluated \({\text{PF }}\) with the true one of these functions are compared as depicted in Fig. 3. The figure shows the good convergence and well diversity of the proposed CMOTSA against the true \({\text{PF}}\). The most important property of chaotic search is that it enhances the convergence, increases the diversity of the evaluated Pareto solutions, explores more solutions, and makes the evaluated \( PF \) approach to the True one.

Table 3 GD and IGD statistical results for all functions
Full size table
Fig. 3
figure 3

Evaluated \(PF\) for CMOTSA and MOTSA against the true \(PF\)

Full size image

3.6 Comparing ZDT results with the literature review

In this subsection, the performance of the suggested algorithms is investigated through ZDT functions by using GD and IGD values, where lower values of them show the good performance of the suggested technique. The results of the suggested CMOTSA are compared with some recent techniques which are taken from the literature including the multi-objective crow search algorithm based orthogonal strategy (M2O-CSA) (Rizk-Allal et al. 2020), multi-objective crow search algorithm MOCSA (Hinojosa et al. 2018) and chaotic MOCSA (MOCCSA) (Hinojosa et al. 2018), and their results are recorded in Table 4. In which, the superiority of the suggested technique in GD for most functions plus the results of IGD values are pointed out which verify that the proposed CMOTSA gets the best results for all functions. The best results are marked with bold font.

Table 4 Comparing results of GD values and IGD values with literature review
Full size table

3.7 Analysis of computation time

The consumed time by the proposed techniques for all functions is shown in Table 5. The CMOTSA consumed less time than the traditional MOTSA for most functions. Due to the chaos theory strategy, the proposed algorithm reaches to the uniformity PF after little iterations. On the other hand, the computation time of CMOTSA for ZDT1 is slightly larger than the traditional technique. Although the CMOTSA consumes more computational time for ZDT1 than the traditional MOTSA, it can provide more accurate Pareto front than the traditional MOTSA. Moreover, the superiority of the proposed CMOTSA is affirmed through providing less computation time for most of the test functions.

Table 5 The computational time for all functions
Full size table

4 Investigation on the CEED problem

The CEED problem is a MOP with two conflicting fitness functions. In this research, the two fitness functions (cost of fuel and emission of pollutants) are solved simultaneously with an external archive to store the evaluated Pareto solutions. To satisfy the validation of the suggested technique, the proposed methods is applied and tested on three systems (IEEE 30-bus 6 units with and without losses and 10 units systems, IEEE 118-bus with fourteen units without valve point effect). The number of tunicates is set to 40 with 20 independently runs and the number of iterations is set to 200. To make sure that the proposed CMOTSA can deal with important constrained problem, the evaluated results are compared and appraised with the traditional MOTSA and other algorithms from the literature.

4.1 Results of CEED problem

In this subsection, the results of CEED problem are demonstrated for two cases (minimum of emission and minimum of cost) according to the preference of the decision maker.

4.1.1 System 1: 6 generating units

In this case, 6-unit system is used with the total demand of power 2.834 pu with 100 MVA base. The coefficients of cost and emission as well as the boundaries of generation and losses coefficients are taken from Gong et al. (2010). The results have been taken in two cases without and with losses, the end points or anchor points of \({\text{PF}}\) are shown in Tables 6 and 7, respectively. The \({\text{PF}}\) of this system is shown in Figs. 4 and 5, respectively. For the first case (6 units without losses), the minimum cost of CMOTSA is 600.1127 $/h and 0.1942 ton/h for the minimum emission. For the second case, the minimum cost is 604.7077 $/h and 0.1942 ton/h for minimum emission. The performance of CMOTSA is also demonstrated by comparing it with other algorithms from the literature which are taken from Xu et al. (2020). The results of CMOTSA are compared with the multi-objective learning backtracking search algorithm (MOLBSA) (Xu et al. 2020), multi-objective backtracking search algorithm (MOBSA) (Maani et al. 2019), multi-objective stochastic search technique (MOSST) (Srinivas et al. 2007), NSGA (Labbi et al. 2020), NPGA (Wu et al. 2020), SPEA (Jiang and Yang 2017), NSGA-II (Farag et al. 2020), fuzzy clustering-based PSO (FCPSO) (Agrawal et al. 2008) as revealed in Tables 8 and 9, respectively. It is shown that CMOTSA gives the minimum cost and the second optimizer for the minimum emission.

Table 6 The results for 6-unit system without losses
Full size table
Table 7 The results for 6-unit system with losses
Full size table
Fig. 4
figure 4

\(\mathrm{PF}\) for 6-units without losses

Full size image
Fig. 5
figure 5

\(PF\) for 6-units with losses

Full size image
Table 8 Comparing the results for 6-units system without losses against other algorithms
Full size table
Table 9 Comparing the results for 6-units system with losses against other algorithms
Full size table

4.1.2 System 2: 10 generating units

This system considers 10 generation units with the total power 2000 MW. The best results of this case are reported in Table 10. The \({\text{PF }}\) of this case is depicted in Fig. 6 which shows its uniformity and the diversity. All the coefficients of this system are taken from Xu et al. (2020). The proposed CMOTSA gives 105,660 $/h for minimum cost and 3650.1 ton/h for minimum emission. To validate the performance of the suggested algorithm, the results are compared with MOFFA (Spea 2021) and PHOA (Rizk-allah et al. 2018) that are shown in Table 11. A closer look to Table 11, it is observed that the proposed CMOTSA dominates the other competing methods regarding the minimum cost and minimum emission.

Table 10 The results for 10-units system without losses
Full size table
Fig. 6
figure 6

The obtained Pareto front for 10 units system

Full size image
Table 11 Comparing the results for 10-units system without losses with other algorithms
Full size table

4.1.3 System 3: 14 generating units

In this system (118-bus, 14 units), the total demand is considered as 2000 MW (Srinivas et al. 2007; El-Fergany and Hasanien 2018) without valve point effect. The statistical results and the anchor points are reported in Table 12. The \({\text{PF}}\) of CMOTSA is depicted in Fig. 7. The CMOTSA gives the minimum cost of 8741.3 $/h and the minimum emission of 2747.6 ton/h. The results of the CMOTSA are compared with MNSGAII-MPVDE (Rajesh and Visali 2020), SPEA2 (Kaur et al. 2020b), MODE (Hancer 2020), MOPSO (Zain et al. 2018), and FCPSO (Agrawal et al. 2008) as in Table 13. Based on the reported results, it can be observed that the proposed CMOTSA outperforms all algorithms in terms of minimum values of total cost and total emission.

Table 12 The results for 14-units system without valve point effect
Full size table
Fig. 7
figure 7

The obtained Pareto front for 14 units system

Full size image
Table 13 Comparing the results for 14-units system without valve point effect with other algorithms
Full size table

4.2 Selection of compromise solution by TOPSIS technique

After evaluating the non-dominated solutions, ranking process is performed to the compromise solution according to the preference of the decision maker. In this work, a practical and robust technique has been used for ranking the evaluated Pareto solution by the proposed CMOTSA for CEED problem called TOPSIS (Technique for order performance by similarity to ideal solution). TOPSIS is a multi-attribute decision analysis technique that is developed by Hwang and Yoon (Bozorg-Haddad et al. 2021). It is depended on evaluating the compromise solution that has the longest length from the negative ideal solution (\({\text{IS}}^{ - }\)) and the closest to the positive ideal solution (\({\text{IS}}^{ + }\)). The steps of TOPSIS can be described as follows:

Step 1: Enter the decision matrix that contains all the objective functions of the Pareto solutions in the storage (\({\text{PM}}_{{{\text{ab}}}}\)). Whereas \(\left( {a \in {\text{NS}}} \right) \;{\text{and}}\; \left( {b \in m} \right)\). \({\text{NS}}\) is the number of Pareto solutions. Each row indicates to one alternative and each column indicates to one objective function.

Step 2: Enter the weight factors \(\left( {w_{1} ,w_{2} } \right)\) according to the preference of the decision maker but all alternatives must satisfy this equation: \( w_{1} + w_{2} = 1\).

Step 3: Due to the different measurement unit for each objective function, the decision matrix is normalized to obtain a new normalized matrix (\(NM_{ab} )\) using the following formula:

$$ {\text{NM}}_{{{\text{ab}}}} = \frac{{{\text{PM}}_{{{\text{ab}}}} }}{{\sqrt {\mathop \sum \nolimits_{a = 1}^{{{\text{NS}}}} {\text{PM}}_{{{\text{ab}}}}^{2} } }} $$
(19)

Step 4: Obtain the weighted normalized matrix by the following equation:

$$ {\text{WM}}_{{{\text{ab}}}} = w_{b} \times {\text{NM}}_{{{\text{ab}}}} $$
(20)

Step 5: Compute the \(IS^{ - }\) and \(IS^{ + }\) by using the following formulas:

$$ \left[ {\begin{array}{*{20}c} {{\text{IS}}^{ + } } \\ {{\text{IS}}^{ - } } \\ \end{array} } \right] = \left\{ {\begin{array}{*{20}c} {\min \left( {{\text{WM}}_{11} , \ldots \ldots {\text{WM}}_{a1} } \right),\min \left( {{\text{WM}}_{21} , \ldots \ldots {\text{WM}}_{2b} } \right) } \\ { \max \left( {{\text{WM}}_{11} , \ldots \ldots {\text{WM}}_{a1} } \right),\max \left( {{\text{WM}}_{21} , \ldots \ldots {\text{WM}}_{2b} } \right) } \\ \end{array} } \right. $$
(21)

Step 6: Calculate the distance between the ideal option and each weighted normalized one as follows:

$$ \left( {D_{a}^{ + } } \right) = \sqrt {\mathop \sum \limits_{b = 1}^{m} \left( {{\text{WM}}_{{{\text{ab}}}} - {\text{IS}}^{ + } } \right)^{2} } $$
(22)
$$ \left( {D_{a}^{ - } } \right) = \sqrt {\mathop \sum \limits_{b = 1}^{m} \left( {{\text{WM}}_{{{\text{ab}}}} - {\text{IS}}^{ - } } \right)^{2} } $$
(23)

Step 7: Compute the relative proximity factor (\({\text{RF}}\)) or the relative closeness for each alternative that can be calculated as follows:

$$ {\text{RF}} = \frac{{D_{a}^{ - } }}{{D_{a}^{ + } + D_{a}^{ - } }} $$
(24)

Step 8: According to the values of \({\text{RF}}\), rank its values in descending order and the first one is selected as the compromise solution.

All these steps are applied to the non-dominated solutions by CMOTSA for all systems. Here \( w_{1}\) is considered as the weight factor of fuel cost and \(w_{2}\) as the weight factor of emission. The weight factor of cost portion is changed \(\left( {{\text{i}}.{\text{e}}.{ }w_{1} = 0, 0.2, 0.4, 0.6, 0.8, 1} \right)\), then the weight factor of emission is evaluated by the following equation:\( w_{2} = 1 - w_{1}\).

For 6 units system, TOPSIS calculates the compromise solution according to the relative weight factors. Tables 14 and 15 give the different values of weight factors and the compromise solutions according to each weight for 6 units system with and without losses. The end points of \({\text{PF}}\) at \( w_{1} = 0\; {\text{and}} \;1\) are cropped. All the values of two cases of 6 units system are shown in Figs. 8 and 9, respectively.

Table 14 The compromise solution by TOPSIS for 6 units system without losses
Full size table
Table 15 The compromise solution by TOPSIS for 6 units system with losses
Full size table
Fig. 8
figure 8

The compromise solution for 6 units system without losses according to \({w}_{1}\)

Full size image
Fig. 9
figure 9

The compromise solution for 6 units system with losses according to \({w}_{1}\)

Full size image

For 10 units system, TOPSIS is employed with different weight factors and all results are reported in Table 16. Figure 10 illustrates the different values of two objective functions according to the different weight factors. The results for 14 units system are reported in Table 17. All best results are depicted in Fig. 11.

Table 16 The compromise solution by TOPSIS for 10 units system
Full size table
Fig. 10
figure 10

The compromise solutions for 10 units system according to \({w}_{1}\)

Full size image
Table 17 The compromise solution by TOPSIS for 14 units system
Full size table
Fig. 11
figure 11

The compromise solutions for 14 units system according to \({w}_{1}\)

Full size image

4.3 Analysis, discussion of results, and limitations of proposed approach

In this study, two novel conceptions, chaotic sequence-based mapping function and exponential searching-based neighborhood strategy, are synchronously embedded into TSA to promote the inclusive the features of exploration and exploitation search of the basic version. In addition, the experimental simulations obtained by CMOTSA are assessed using the IGD and GD metrics through the comparison with other common optimizers. Firstly, it is applied to ZDT functions (ZDT1-ZDT3, ZDT6) with large-scale dimensions. The average, the best, the worst, the standard deviation, and median values of GD and IGD are computed for all functions. All results are compared with different algorithms that show the minimum values for the proposed algorithm. The results have affirmed the superiority of the proposed CMOTSA. Additionally, the computational efforts for the presented algorithms are recorded, and the obtained results revealed that the proposed saves the computational time than the traditional technique for most functions. Furthermore, the applicability of the CMOTSA is confirmed by the investigation on the CEED problem as the challenge task for the operation of the electrical power stations. Three systems are considered (IEEE 30-bus with 6 generators system, 10 units system and IEEE 118-bus with 14 generating units). The cropped results affirm that the proposed algorithm can provide competitive results in terms of converge and coverage towards the Pareto optimal front. Also, the analysis of solution is performed through implementing algorithm with different weights to help the designer or operator with the behavior of the objectives to decide the best operating points. On the other hand, the TOPSIS technique is adopted to automatically get the compromise solution based on the distance functions which help the inexperience operator to obtain the best choice.

Although, the CMOTSA performs well in obtaining the Pareto optimal solutions for MOPs and CEED problem, there is still potential for enhancement in some respects. Firstly, the CMOTSA cannot deal with all optimization tasks, and the problems in this study are specific in nature. Second, the algorithm suggested in this study can further enhance the performance using other searching strategies, particularly in terms of time effectiveness. Additionally, as the CMOTSA is a stochastic method, it is prone for the possibility of stagnation dilemma, especially while tackling with more complex practical tasks. Finally, other fascinating tasks of applying the CMOTSA can be explored, including, multi-objective optimal power flow, reactive power dispatch with ramp rates and prohibited zones, economic power dispatch based on hybrid renewable energy systems, and economic dispatch in large-scale smart grids.

5 Conclusion and future work

In this paper, a novel chaos-enhanced multi-objective tunicate swarm algorithm (CMOTSA) for CEED problem is proposed. To enhance the exploration and exploitation trends of the basic tunicate swarm algorithm (TSA), an exponential-based neighborhood searching strategy and chaotic logistic pattern are incorporated. The CMOTSA was investigated on ZDT functions set and was compared with several other competing algorithms. The strict simulation results illustrate that the CMOTSA has outperformed other counterparts in terms of IGD and GD metrics, which means that the diversification and intensification capacities regarding Pareto optimal front of the basic MOTSA have been strengthened, efficiently. In addition, The CMOTSA also was applied to address the solution of three practical systems of CEED problem. The final outcomes show that the CMOTSA can supply robust assistance for dealing with CEED problem by comparing with other advanced optimization methods and it has the potential to be very helpful in addressing more real-world CEED issues with complicated operational conditions as well. Although the chaotic search improved the searching performance, it suffers from elapsing more time for ZDT1 function and some complexity due to the chaotic search. Taking more real constraints such as the unit’s reactive power limits, ramp rates and prohibited zones of generating units represents the future extension of this current effort and the applications to larger systems as well.