Abstract
Using methods from classical absolute stability theory, combined with recent results on input-to-state stability (ISS) of Lur’e systems, we derive necessary and sufficient conditions for a class of Lur’e systems to have the converging-input converging-state (CICS) property. In particular, we provide sufficient conditions for CICS which are reminiscent of the complex Aizerman conjecture and the circle criterion and connections are also made with small gain ISS theorems. The penultimate section of the paper is devoted to non-negative Lur’e systems which arise naturally in, for example, ecological and biochemical applications: the main result in this context is a sufficient criterion for a so-called “quasi CICS” property for Lur’e systems which, when uncontrolled, admit two equilibria. The theory is illustrated with numerous examples.
Similar content being viewed by others
1 Introduction
We consider forced Lur’e systems in continuous-time of the form
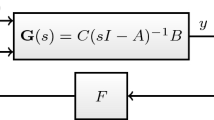
where A, B and C are appropriately sized matrices, f is a (nonlinear) function, x denotes the state and v is a control function (also interpreted as and named a disturbance, forcing term or input). Differential equations of the form (1.1) often arise as closed-loop systems obtained by the application of output feedback with nonlinear “characteristic” f to the linear system specified by (A, B, C), namely
where u and y denote the input and output variables, respectively, see Fig. 1. Lur’e systems are a common and important class of nonlinear systems and are at the centre of the classical subject of absolute stability theory which includes the well-known real and complex Aizerman conjectures, circle and Popov criteria, see [13, 14, 18, 20, 23, 24, 45, 47]. An absolute stability criterion for (1.1) is a sufficient condition for stability, usually formulated in terms of frequency-domain properties of the linear system given by (A, B, C) and sector or boundedness conditions for f, guaranteeing stability for all nonlinearities f satisfying these conditions.
Block diagram of the controlled Lur’e system (1.1)
Traditionally, Lyapunov approaches to the stability theory of systems of the form (1.1) consider the uncontrolled (\(v=0\)) case, whilst Lur’e systems with forcing (usually acting through B, that is, v is of the form \(v=Bw\) for some w) have been studied using the input–output framework initiated by Sandberg and Zames in the 1960s; see, for example, [11, 45]. More recently, forced Lur’e systems have been analyzed in the context of input-to-state stability (ISS) theory, see [4, 19, 20, 36]. Whilst ISS is a concept for general controlled nonlinear systems (first formulated in [38]), in our context, ISS is a stability property of an equilibrium pair of (1.1), where \((x^\mathrm{e}, v^\mathrm{e})\) is an equilibrium pair if \(Ax^\mathrm{e}+Bf(Cx^\mathrm{e})+v^\mathrm{e}=0\). Loosely speaking, \((x^\mathrm{e}, v^\mathrm{e})\) is ISS if the map \((x^0 - x^\mathrm{e},v-v^\mathrm{e})\mapsto x(t; x^0, v) - x^\mathrm{e}\) has “nice” boundedness and asymptotic properties (see (2.2)), where \(x(\cdot \,; x^0, v)\) denotes the solution of (1.1). In particular, if an equilibrium pair \((x^\mathrm{e}, v^\mathrm{e})\) is ISS, then \(x(t; x^0, v)\rightarrow x^\mathrm{e}\) as \(t\rightarrow \infty \) for all \(x^0\in {\mathbb {R}}^n\) and all (essentially) bounded v such that \(\lim _{t\rightarrow \infty }v(t)=v^\mathrm{e}\). For surveys of ISS theory the reader is referred to [9, 42].
In the present paper, we investigate the following problem (and variations thereof): given \(v^\infty \in {\mathbb {R}}^n\), find conditions (necessary or sufficient) for the existence of \(x^\infty \in {\mathbb {R}}^n\) such that, for every \(x^0\) and every v with \(v(t)\rightarrow v^\infty \) as \(t\rightarrow \infty \), the solution x of (1.1) converges to \(x^\infty \). In particular, we consider the so-called converging-input converging-state (CICS) property: (1.1) is said to have the CICS property if, for every \(v^\infty \in {\mathbb {R}}^n\), there exists \(x^\infty \in {\mathbb {R}}^n\) such that \(\lim _{t\rightarrow \infty }x(t)=x^\infty \) for all \(x^0\) and all inputs v converging to \(v^\infty \).
For background and motivation, we comment that if (1.1) is linear and asymptotically stable, that is, for some matrix F, we have that \(f(z)=Fz\) and \(A+BFC\) is Hurwitz (meaning every eigenvalue has negative real part), then (1.1) has the CICS property. Indeed, it is well known that, for given \(v^\infty \), the state x and output y of (1.1) have respective limits
for every initial vector \(x^0\) and every v converging to \(v^\infty \). The matrices \(-(A+BFC)^{-1}\) and \(-C(A+BFC)^{-1}\) are sometimes referred to as “steady-steady gains” and provide linear maps \(v^\infty \mapsto x^\infty \) and \(v^\infty \mapsto y^\infty \). If system (1.1) has the CICS property, then the steady-steady gain concept extends to Lur’e systems in the sense that there are explicit formulae for the nonlinear functions \(v^\infty \mapsto x^\infty \) and \(v^\infty \mapsto y^\infty \) which map input limits to state limits and output limits, respectively (see Sect. 4).
The main contribution of this paper is the establishment of sufficient conditions for the CICS property which are reminiscent of the complex Aizerman conjecture [17, 18, 20, 36], the circle criterion for ISS [19, 20, 36] and the “nonlinear” ISS small-gain condition for Lur’e systems [36] and involve the transfer function matrix of the linear system (A, B, C) and an incremental condition (in terms of norm or sector inequalities) on the nonlinearity f. Recent ISS results for Lur’e systems [36] play a key role in the development of the CICS theory in Sect. 4. We demonstrate that our sufficient CICS conditions also ensure that the nonlinear steady-state gains are continuous maps—further mirroring the linear case. We emphasize that CICS is a system property, whereas ISS relates to stability properties of an equilibrium pair of (1.1). In contrast to linear systems, Lur’e systems which admit a globally asymptotically stable equilibrium when uncontrolled (\(v = 0\)) need not have the CICS property. Indeed, there may exist convergent inputs such that, for some initial states, the corresponding state trajectory is asymptotically divergent (see part (b) of Example 4.5).
In certain circumstances, it is of interest to relax the CICS concept and restrict attention to convergent forcing terms v with limits \(v^\infty \) belonging to a subset of \({\mathbb {R}}^n\), perhaps just a singleton. For example, assuming that \(f(0) =0\), the so-called 0-CICS property requires that \(x(t;x^0,v)\rightarrow 0\) as \(t\rightarrow \infty \) for every \(x^0\in {\mathbb {R}}^n\) and every \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) such that \(v(t)\rightarrow 0\) as \(t\rightarrow \infty \). In deriving sufficient conditions for the “global” CICS property, we present a “local” CICS result in Theorem 4.3 (local in the limiting values \(v^\infty \) of the forcing functions v), see also Examples 4.6.
In the context of general nonlinear systems, CICS-type properties (including 0-CICS) have been studied in [2, 34, 41]. Concepts related to or reminiscent of the CICS property have been introduced in [3, 40]. Whilst [2, 3, 34, 40] have little overlap with the material presented here, [41] plays an important role in the proof of statement (1) of Theorem 4.3, one of the main results in the current paper. To the best of our knowledge, there is not much previous work on CICS properties for Lur’e systems, exceptions include [7, 31, 35]. Of these works, [35] is, by some margin, the closest in spirit to the present paper and we provide detailed comments on the relation of the contribution in [35] to our results after the proof of Corollary 4.16. The papers [7, 31] develop stability criteria from the perspective of incremental stability and convergent dynamics [1, 30, 33, 46] and touch upon aspects of CICS for Lur’e systems, but there is very little intersection with the systematic theory developed here.
We also study the CICS property for a class of Lur’e systems which is a variation of (1.1), namely
where the interpretation of the terms in (1.2) is the same as that in (1.1). System (1.2) can be thought of as a closed-loop system obtained by linear feedback applied to the linear system (A, B, C) subjected to an input nonlinearity f:
see Fig. 2. We derive a CICS criterion for Lur’e systems of the form (1.2) and use it to generalize a well-known result on integral control for linear systems to this class of nonlinear systems.
Block diagram of the controlled Lur’e system (1.2)
Furthermore, we consider a class of non-negative (also known as positive) Lur’e systems, cf. [6, 36, 37, 44]. As an instance of a positive control system [15], these arise naturally in a variety of applied contexts: a common key feature is that their state variables, which may represent population abundances, chemical concentrations or economical quantities (such as prices) are, necessarily, non-negative. In a population model, the nonlinear term f may describe Allee effects [8] or density-dependent recruitment owing to decreased survival rates or increased competition for resources at lower and higher population abundances, respectively. In a chemical reaction model, f may describe a nonlinear reaction rate between certain reagents. Unforced biological, ecological and chemical models often admit (at least) two equilibria: the zero equilibrium and some non-zero equilibrium, the latter corresponding to the co-existence of populations or chemical compounds. The control v in (1.1) may model immigration in a population model or the addition of a new reagent in a chemical reaction model. Our main result for non-negative Lur’e systems is a sufficient condition for a “quasi CICS” property which, for zero control \(v=0\), have two equilibria (see Theorem 6.6). In this context, we shall make contact with recent work [6] on stability properties of non-negative Lur’e systems: a certain “repeller” or “persistence” property established in [6] will play a pivotal role in the proof of Theorem 6.6.
The paper is organized as follows. In Sects. 2 and 3, we discuss a number of preliminaries and prove necessary conditions for CICS, respectively. Section 4 is devoted to sufficient conditions for the CICS property for (1.1), the main result being Theorem 4.3, from which several CICS criteria are derived as corollaries. These criteria have the flavour of well-known absolute stability results (complex Aizerman conjecture, circle criterion and small gain). Sections 5 and 6 consider systems of the form (1.2) and non-negative versions of (1.1), respectively. We present some concluding comments in Sect. 7.
Notation and terminology For a set S, the symbol \(\#S\) denotes the cardinality of S (if S is infinite, then we write \(\#S=\infty \)). The set of positive integers is denoted by \({\mathbb {N}}\) and \({\mathbb {R}}\) and \({\mathbb {C}}\) denote the fields of real and complex numbers, respectively. We set \({\mathbb {R}}_+:=\{r\in {\mathbb {R}}:r\ge 0\}\). For \(n \in {\mathbb {N}}, {\mathbb {R}}^n\) and \({\mathbb {C}}^n\) denote the usual real and complex n-dimensional vector spaces, respectively, both equipped with the 2-norm denoted by \(\Vert \cdot \Vert \).
For \(m \in {\mathbb {N}}\), let \({\mathbb {R}}^{n \times m}\) and \({\mathbb {C}}^{n \times m}\) denote the normed linear spaces of \(n \times m\) matrices with real and complex entries, respectively, both equipped with the operator norm induced by the 2-norm, also denoted by \(\Vert \cdot \Vert \). Given \(M \in {\mathbb {R}}^{m \times n}\), we let \(\mathrm{im}\, M \) denote the image of M, that is, the linear subspace spanned by the columns of M. A matrix \(M\in {\mathbb {C}}^{n\times n}\) is said to be Hurwitz if all its eigenvalues have negative real parts. Note that Hurwitz matrices are necessarily invertible. If M is additionally real, with components \(m_{ij}\), then it is said to be reducible if there exist non-empty disjoint subsets \(J_1,J_2 \subseteq \{1,\ldots ,n\}\) such that \(J_1\cup J_2=\{1,\ldots ,n\}\) and \(m_{ij}=0\) for all \((i,j)\in J_1\times J_2\). We say that M is irreducible if M is not reducible. We refer the reader to [5, 27] for more details on irreducible matrices.
Let \(M=(m_{ij})\in {\mathbb {R}}^{n\times m}\) and \(N=(n_{ij})\in {\mathbb {R}}^{n\times m}\). We write
We say that M is non-negative if \(M\ge 0\). The matrix M is called positive if \(M\gg 0\). A square matrix \(M=(m_{ij})\in {\mathbb {R}}^{n\times n}\) is said to be Metzler (or essentially non-negative or quasi positive) if all its off-diagonal entries of M are non-negative, that is, \(m_{ij}\ge 0\) for all \(1\le i,j\le n\) with \(i\ne j\). It is well known (and straightforward to prove) that \(M\in {\mathbb {R}}^{n\times n}\) is Metzler if, and only if, \(\mathrm{e}^{Mt}\xi \in {\mathbb {R}}^n_+\) for all \(\xi \in {\mathbb {R}}^n_+\) and all \(t\ge 0\) (see, for example, [26]).
For \(K\in {\mathbb {C}}^{m\times p}\) and \(r>0\), set
the open (complex) ball in \({\mathbb {C}}^{m\times p}\), centred at K and of radius r.
A square rational matrix-valued function \(s \mapsto \mathbf{H}(s)\) of a complex variable s is said to be positive real if for every \(s\in {\mathbb {C}}\) with \(\mathrm{Re}\,s\ge 0\), which is not a pole of \(\mathbf{H}\), the matrix \([\mathbf{H}(s)]^*+ \mathbf{H}(s)\) is positive semi-definite. As usual, if \(\mathbf{H}\) is a proper rational matrix-valued function which does not have any poles in the closed right-half plane \(\mathrm{Re}\,s\ge 0\), then we define its \(H^\infty \)-norm by
More details on \(H^\infty \)-norms can be found in, for example, [29].
We recall the definitions of certain classes of comparison functions. Let \({{\mathcal {K}}}\) denote the set of all continuous functions \(\varphi :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) such that \(\varphi (0)=0\) and \(\varphi \) is strictly increasing. Moreover,
We denote by \({{\mathcal {K}}}{{\mathcal {L}}}\) the set of functions \(\psi :{\mathbb {R}}_+\times {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+\) with the following properties: \(\psi (\cdot \,, t)\in {{\mathcal {K}}}\) for every \(t\ge 0\), and \(\psi (s,\cdot \,)\) is non-increasing with \(\lim _{t\rightarrow \infty } \psi (s, t) = 0\) for every \(s\ge 0\). Following the convention of [39], we do not impose continuity in the definition of a \({{\mathcal {K}}}{{\mathcal {L}}}\) function. By [39, Proposition 7], it follows that a discontinuous \({{\mathcal {K}}}{{\mathcal {L}}}\)-function can be bounded from above by a continuous one. For more details on comparison functions the reader is referred to [22].
The linear space of (equivalence classes of) locally essentially bounded functions \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}^n\) is denoted by \(L^\infty _\mathrm{loc}({\mathbb {R}}_+, {\mathbb {R}}^n)\). If \(f\in L^\infty _\mathrm{loc}({\mathbb {R}}_+, {\mathbb {R}}^n)\), then
As usual, \(L^\infty ({\mathbb {R}}_+, {\mathbb {R}}^n)\) denotes the space of all essentially bounded functions \({\mathbb {R}}_+\rightarrow {\mathbb {R}}^n\). For \(f\in L^\infty ({\mathbb {R}}_+, {\mathbb {R}}^n)\), we write
Finally, we use the symbol \(\theta \) to denote the constant function \({\mathbb {R}}_+\rightarrow {\mathbb {R}}\) given by \(\theta (t)=1\) for all \(t \ge 0\).
2 Preliminaries and definitions
Consider the forced Lur’e system (1.1), where \(A\in \mathbb {R}^{n\times n}, B\in \mathbb {R}^{n\times m}, C\in \mathbb {R}^{p\times n}, f:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) is locally Lipschitz, \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}^n)\) is a control (forcing, input) function. If \(v=0\), then we will refer to (1.1) as the uncontrolled system (1.1). Frequently, the input v will be of the form \(v=Ew\), where \(E\in {\mathbb {R}}^{n\times q}\) and \(w\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}^q)\). If \(q=m\) and \(E=B\), then (1.1) can be written in the form
Let \(x(\cdot \,;x^0,v)\) denote the unique maximally defined forward solution of the initial-value problem (1.1). We say that \((x^\mathrm{e},v^\mathrm{e})\in {\mathbb {R}}^n\times {\mathbb {R}}^n\) is an equilibrium pair of (1.1) if \(Ax^\mathrm{e}+Bf(Cx^\mathrm{e})+v^\mathrm{e}=0\), that is, if \(x^\mathrm{e}\) is an equilibrium of the (autonomous) differential equation
It is clear that if, for some \(v^\infty \in {\mathbb {R}}^n\) and \(x^0\in {\mathbb {R}}^n, x(t;x^0,v^\infty \theta )\) converges to \(x^\infty \) as \(t\rightarrow \infty \), then \((x^\infty ,v^\infty )\) is an equilibrium pair of (1.1). An equilibrium pair \((x^\mathrm{e},v^\mathrm{e})\) is said to be globally asymptotically stable (GAS), if \(x^\mathrm{e}\) is a globally asymptotically stable equilibrium of (2.1). Obviously, if (0, 0) is an equilibrium pair of (1.1), then (0, 0) is GAS if, and only, if the equilibrium 0 of the uncontrolled Lur’e system (1.1) is GAS. We say that an equilibrium pair \((x^\mathrm{e},v^\mathrm{e})\) of (1.1) is input-to-state stable (ISS) if there exist \(\psi \in {{\mathcal {K}}}{{\mathcal {L}}}\) and \(\varphi \in {{\mathcal {K}}}\) such that, for every \(x^0\in {\mathbb {R}}^n\), every \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}^n)\), and all \(t \ge 0\),
In the following, let \(\mathbf{G}\) be the transfer function of the linear system specified by the triple (A, B, C), that is, \(\mathbf{G}(s)=C(sI-A)^{-1}B\), where s is a complex variable. Applying output feedback of the form \(u=Ky+w\) to (A, B, C), where \(K\in {\mathbb {R}}^{m\times p}\) and w is an input signal, leads to the closed-loop linear system specified by \((A+BKC,B,C)\), the transfer function of which shall be denoted by \(\mathbf{G}_K\). It is readily seen that
where, for notational convenience, we have set \(A_K:=A+BKC\).
Let \({\mathbb {S}}_{\mathbb {C}}(A,B,C)\) denote the set of complex stabilizing output feedback gains for the linear system (A, B, C), that is,
Moreover, we define
the set of real stabilizing output feedback gains for (A, B, C). Note that \({\mathbb {S}}_{\mathbb {R}}(A,B,C)\) and \({\mathbb {S}}_{\mathbb {C}}(A,B,C)\) may be empty. In principle, the Nyquist stability criterion can be used to check for non-emptiness of \({\mathbb {S}}_{\mathbb {R}}(A,B,C)\) or \({\mathbb {S}}_{\mathbb {C}}(A,B,C)\): this is particularly straightforward in the case \(m=p=1\). If A is Hurwitz, then trivially \({\mathbb {S}}_{\mathbb {R}}(A,B,C)\) is non-empty. Furthermore, if \(m=p, (A,B,C)\) is stabilizable and detectable and \(\mathbf{G}+cI\) is positive real for some \(c>0\), then \({\mathbb {B}}_{\mathbb {C}}(-\rho I,\rho )\subseteq {\mathbb {S}}_{\mathbb {C}}(A,B,C)\), where \(\rho :=1/(2c)\).
The next theorem is a stability result for Lur’e systems that will be a key tool throughout this paper.
Theorem 2.1
Let \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\) and set \(\gamma :=1/\Vert \mathbf{G}_K\Vert _{H^\infty }\) (where \(\gamma :=\infty \) if \(\Vert \mathbf{G}_K\Vert _{H^\infty }=0\)). The following statements hold.
-
1.
If \(\gamma <\infty \) and
$$\begin{aligned} \Vert f(z) - Kz\Vert <\gamma \Vert z\Vert \quad \forall \,z\in {\mathbb {R}}^p,\ z\not =0, \end{aligned}$$then the equilibrium 0 of the uncontrolled system (1.1) is GAS.
-
2.
If \(\gamma <\infty \) and there exists \(\alpha \in {{\mathcal {K}}}_\infty \) such that
$$\begin{aligned} \Vert f(z) - Kz\Vert \le \gamma \Vert z\Vert - \alpha (\Vert z\Vert )\quad \forall \,z\in {\mathbb {R}}^p, \end{aligned}$$then the equilibrium pair (0, 0) of (1.1) is ISS.
-
3.
If \(\gamma =\infty \), then the conclusions in statements (1) and (2) hold for every locally Lipschitz \(f:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) such that \(f(0)=0\).
Statements (1) and (2) are consequences results in [17, 18] and [36], respectively. The scenario considered in statement (3), wherein \(\Vert \mathbf{G}_K\Vert _{H^\infty }=0\) (or, equivalently, \(\mathbf{G}_K(s)\equiv 0\)), is not very interesting, but is included for mathematical completeness. Note that \(\Vert \mathbf{G}_K\Vert _{H^\infty }=0\) if, and only if, \(\Vert \mathbf{G}\Vert _{H^\infty }=0\). Consequently, if (A, B) is controllable ((C, A) is observable) and \(C\not =0\) (\(B\not =0\)), then \(\Vert \mathbf{G}_K\Vert _{H^\infty }\not =0\). A proof of Theorem 2.1 can be found in the Appendix.
The following proposition is a special case of a well-known result from ISS theory.
Proposition 2.2
Assume that (0, 0) is an ISS equilibrium pair of (1.1). Then (1.1) has the 0-converging-input converging-state property: for every \(x^0\in {\mathbb {R}}^n\) and for every \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) such that \(v(t)\rightarrow 0\) as \(t\rightarrow \infty ,\) we have that \(x(t;x^0,v)\rightarrow 0\) as \(t\rightarrow \infty \).
We emphasize that ISS is not a necessary condition for (1.1) to have the 0-converging-input converging-state property (0-CICS property), see Example 4.5 further below. We now introduce a concept which strengthens the notion of the 0-CICS property and is the primary focus of the present paper.
Definition 2.3
We say that (1.1) has the converging-input converging-state property (CICS property) if, for every \(v^\infty \in {\mathbb {R}}^n\), there exists \(x^\infty \in {\mathbb {R}}^n\) such that, for all \(x^0\in {\mathbb {R}}^n\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) with \(\lim _{t\rightarrow \infty }v(t)=v^\infty \),Footnote 1
If (1.1) has the CICS property and if \(f(0)=0\) (that is, the origin is an equilibrium of the uncontrolled Lur’e system (1.1)), then clearly (1.1) has the 0-CICS property.
The CICS property enables us to define steady-state gains for the Lur’e system (1.1). Indeed, assuming that (1.1) has the CICS property, the map
is well defined and is said to be the input-to-state steady-state gain (ISSS gain). The map
is said to be the input-to-output steady-state gain (IOSS gain). In particular, if (1.1) has the CICS property, then, for every \(v^\infty \), the point \(x^\infty :=\Gamma _\mathrm{is}(v^\infty )\) is a globally attractive equilibrium of the system
3 A necessary condition for CICS
In this short section, we derive a necessary condition for the CICS property. In the following, the map
where \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\), will play a key role. For a set \(W\subseteq {\mathbb {R}}^p\), we shall denote the preimage of W under \(F_K\) by \(F_K^{-1}(W)\). For \(w\in {\mathbb {R}}^p\), it is convenient to set \(F_K^{-1}(w):=F_K^{-1}(\{w\})\). We note two simple, but important, properties of \(F_K\):
a proof of which is contained in the Appendix. The next proposition describes properties of the map \(F_K\) and shows how \(F_K\) relates to equilibrium pairs \((x^\infty , v^\infty )\) of (1.1).
Proposition 3.1
Assume that \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\).
-
1.
Let \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) have a limit \(v^\infty := \lim _{t\rightarrow \infty }v(t)\) and assume that, for some \(x^0\in {\mathbb {R}}^n\), the limit \(x^\infty :=\lim _{t\rightarrow \infty }x(t;x^0,v)\) exists. Then \((x^\infty ,v^\infty )\) is an equilibrium pair of (1.1),
$$\begin{aligned} x^\infty =-A_K^{-1}\big (B(f(Cx^\infty )-KCx^\infty )+v^\infty \big ),\quad \end{aligned}$$(3.2)where \(A_K:=A+BKC\), and \(F_K(Cx^\infty )=-CA_K^{-1}v^\infty \).
-
2.
Let \(v^\infty \in {\mathbb {R}}^n\) and assume that there exists \(x^\infty \in {\mathbb {R}}^n\) such that, for all \(x^0\in {\mathbb {R}}^n, x(t;x^0,v^\infty \theta )\rightarrow x^\infty \) as \(t\rightarrow \infty \). Then \(\#F_K^{-1}(-CA_K^{-1}v^\infty )=1\).
-
3.
Let \(v^\infty \in {\mathbb {R}}^n, y^\infty \in F_K^{-1}(-CA_K^{-1}v^\infty )\) and set \(x^\infty :=-A_K^{-1}(B(f(y^\infty )-Ky^\infty )+v^\infty )\). Then \(Cx^\infty =y^\infty \) and \((x^\infty ,v^\infty )\) is an equilibrium pair of (1.1).
Proof of Proposition 3.1
To prove statement (1), set \(x(t):=x(t;x^0,v)\) and note that x satisfies
Since \(A_K\) is Hurwitz, it follows immediately that (3.2) holds. As an immediate consequence of (3.2), we have
showing that \((x^\infty ,v^\infty )\) is an equilibrium pair of (1.1). Furthermore, applying C to both sides of (3.2) and rearranging shows that \(F_K(Cx^\infty )=-CA_K^{-1}v^\infty \).
We proceed to prove statement (2). By statement (1), \(x^\infty \) satisfies (3.2), and \(Cx^\infty \in F_K^{-1}(-CA_K^{-1}v^\infty )\), showing that \(F_K^{-1}(-CA_K^{-1}v^\infty ) \not =\emptyset \). Let \(y_1,y_2\in F_K^{-1}(-CA_K^{-1}v^\infty )\). It remains to show that \(y_1=y_2\). To this end, set
Then
But \(F_K(y_i)=-CA_K^{-1}v^\infty \) for \(i\in \{1,2\}\) and so, \(y_i=C\xi _i\) for \(i\in \{1,2\}\). Consequently, by (3.3),
and so
showing that \((\xi _1,v^\infty )\) and \((\xi _2,v^\infty )\) are equilibrium pairs of (1.1). Hence, \(x(t;\xi _i,v^\infty \theta )=\xi _i\) for all \(t\ge 0\) and it follows from the hypothesis that \(\xi _1=x^\infty =\xi _2\). Thus, \(y_1=C\xi _1=C\xi _2=y_2\), completing the proof.
To prove statement (3), note that
Therefore,
showing that \((x^\infty ,v^\infty )\) is an equilibrium pair of (1.1). \(\square \)
The following consequence of Proposition 3.1 provides, in terms of \(F_K\), a necessary condition for the CICS property to hold.
Corollary 3.2
Let \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\). If the Lur’e system (1.1) has the CICS property, then \(\#F_K^{-1}(z)=1\) for all \(z\in \mathrm{im}\, C\).
It follows from (3.1) and Corollary 3.2 that, if (1.1) has the CICS property, then the restriction of \(F_K\) to \(\mathrm{im}\,C\) provides a bijection from the subspace \(\mathrm{im}\,C\) into itself.
Proof of Corollary 3.2
Let \(z\in \mathrm{im}\, C\). Then there exists \(v^\infty \in {\mathbb {R}}^n\) such that \(z=-CA_K^{-1}v^\infty \). By the CICS property, it is clear that there exists \(x^\infty \in {\mathbb {R}}^n\), such that for all \(x^0\in {\mathbb {R}}^n, x(t;x^0,v^\infty \theta )\rightarrow x^\infty \) as \(t\rightarrow \infty \). Hence, by statement (2) of Proposition 3.1, \(\#F_K^{-1}(z)=\#F_K^{-1}(-CA_K^{-1}v^\infty )=1\). \(\square \)
4 Sufficient conditions for CICS
In this section, we provide conditions which ensure that the Lur’e system (1.1) has the CICS property. The main result is Theorem 4.3 which, in turn, yields a host of sufficient conditions for the CICS property, formulated as Corollaries 4.8, 4.10, 4.11, 4.15 and 4.16.
The next result provides conditions which guarantee certain surjectivity and injectivity properties of the map \(F_K\). We denote the restriction of \(F_K\) to \(\mathrm{im}\,C\) by \({\hat{F}}_K\). It follows from (3.1) that \({\hat{F}}_K\) maps into \(\mathrm{im}\,C\) and we define the co-domain of \({\hat{F}}_K\) to be equal to \(\mathrm{im}\,C\).
Proposition 4.1
Let \(Y\subseteq \mathrm{im}\,C\) be nonempty, \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C),\) set \(\gamma :=1/\Vert \mathbf{G}_K\Vert _{H^\infty }\) (where \(\gamma :=\infty \) if \(\Vert \mathbf{G}_K\Vert _{H^\infty }=0\)) and assume that f satisfies the condition :
(A) \(\Vert f(z+\xi )-f(\xi )-Kz\Vert <\gamma \Vert z\Vert \) for all \(\xi \in Y\) and all \(z\in {\mathbb {R}}^p, z\not =0\).
The following statements hold.
-
1.
\(\# F_K^{-1}(z)=1\) for every \(z\in \mathrm{im}\,C\) such that \(F_K^{-1}(z)\cap Y\not =\emptyset \).
-
2.
If
$$\begin{aligned} \Vert \mathbf{G}_K(0)\Vert <\Vert \mathbf{G}_K\Vert _{H^\infty }, \end{aligned}$$(4.1)then \(F_K\) is surjective.
-
3.
If there exists \(\zeta \in {\mathbb {R}}^p\) such that
$$\begin{aligned} \gamma \Vert z\Vert -\Vert f(z+\zeta )-f(\zeta )-Kz\Vert \rightarrow \infty \quad \hbox { as } \Vert z\Vert \rightarrow \infty , \end{aligned}$$(4.2)then \(F_K\) is surjective.
-
4.
If \(Y=\mathrm{im}\,C\) and (4.1) or (4.2) hold, then \({\hat{F}}_K\) is bijective.
Before we prove Proposition 4.1, we state and prove a simple lemma which will be a convenient tool in the following. In particular, it will be useful in the proof of Proposition 4.1.
Lemma 4.2
Let \(g:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) be an arbitrary function and let \(r>0\).
-
1.
If there exists \(\zeta \in {\mathbb {R}}^p\) such that
$$\begin{aligned} r\Vert z\Vert -\Vert g(z+\zeta )-g(\zeta )\Vert \rightarrow \infty \quad \hbox {as } \Vert z\Vert \rightarrow \infty , \end{aligned}$$(4.3)then, for every \(\xi \in {\mathbb {R}}^p,\)
$$\begin{aligned} r\Vert z\Vert -\Vert g(z+\xi )-g(\xi )\Vert \rightarrow \infty \quad \hbox {as }\Vert z\Vert \rightarrow \infty . \end{aligned}$$ -
2.
If g is continuous, \(\Vert g(z)\Vert <r\Vert z\Vert \) for all non-zero \(z\in {\mathbb {R}}^p\) and \(r\Vert z\Vert -\Vert g(z)\Vert \rightarrow \infty \) as \(\Vert z\Vert \rightarrow \infty ,\) then there exists \(\alpha \in {{\mathcal {K}}}_\infty \) such that \(\Vert g(z)\Vert \le r\Vert z\Vert -\alpha (\Vert z\Vert )\) for all \(z\in {\mathbb {R}}^p\).
Proof
To prove statement (1), let \(\xi \in {\mathbb {R}}^p\), set \(w:=z+\xi -\zeta \) and note that
Consequently,
and since \(\Vert w\Vert \rightarrow \infty \) as \(\Vert z\Vert \rightarrow \infty \), the claim follows from (4.3).
To prove statement (2), define \(\beta :{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) by
Then \(\beta \) is continuous (by the continuity of g), \(\beta (0)=0, \beta (s)>0\) for \(s>0, \beta \) is nondecreasing, \(\beta (s)\rightarrow \infty \) as \(s\rightarrow \infty \) and \(\Vert g(z)\Vert \le r\Vert z\Vert -\beta (\Vert z\Vert )\) for all \(z\in {\mathbb {R}}^p\). Therefore, setting \(\alpha (s):=(1-\mathrm{e}^{-s})\beta (s)\), it is clear that \(\alpha \in {{\mathcal {K}}}_\infty \) and \(\Vert g(z)\Vert \le r\Vert z\Vert - \alpha (\Vert z\Vert )\) for all \(z\in {\mathbb {R}}^p\), completing the proof. \(\square \)
Proof of Proposition 4.1
If \(\mathbf{G}_K(0)=0\), then \(F_K(z)=z\) for all \(z\in {\mathbb {R}}^p\). Consequently, the maps \(F_K\) and \({\hat{F}}_K\) are bijective and there is nothing to prove. Let us now assume that \(\mathbf{G}_K(0)\not =0\). Then, \(\Vert \mathbf{G}_K\Vert _{H^\infty }\not =0\), and so, \(0<\gamma <\infty \).
To prove statement (1), let \(z\in \mathrm{im}\,C\) and assume that \(F_K^{-1}(z)\cap Y\not =\emptyset \). Let \(\xi _1\in F_K^{-1}(z)\cap Y\) and \(\xi _2\in F_K^{-1}(z)\). To establish that \(\# F_K^{-1}(z)=1\), it suffices to show that \(\xi _1=\xi _2\). Since \(F_K(\xi _1)=F_K(\xi _2)\), it follows that
If \(\xi _1\not =\xi _2\), then, by condition (A),
which is impossible. Hence, \(\xi _1=\xi _2\).
We proceed to prove statement (2). To show surjectivity of \(F_K\), note that, by [32, Theorem 9.36], it is sufficient to prove that \(F_K\) is coercive, that is,
To establish (4.4), we note that, for all \(z\in {\mathbb {R}}^p\),
and hence
where \(\xi \in Y\). By condition (A),
Consequently, for all \(z\in {\mathbb {R}}^p\),
and thus,
Setting
and invoking (4.5) and (4.6), we conclude that
Now, by hypothesis, \(\Vert \mathbf{G}_K(0)\Vert <\Vert \mathbf{G}_K\Vert _{H^\infty }\), or, equivalently, \(1-\gamma \Vert \mathbf{G}_K(0)\Vert >0\), implying that (4.4) holds, and so surjectivity of \(F_K\) follows.
To prove statement (3), let \(\xi \in Y\). By hypothesis and statement (1) of Lemma 4.2 (applied to \(g(z)=f(z)-Kz\)),
Together with assumption (A) and an application of statement (2) of Lemma 4.2 this shows that there exists \(\alpha \in {{\mathcal {K}}}_\infty \) such that
An argument very similar to that leading to (4.6) yields
Together with (4.5) this implies
with \(\kappa \) defined by (4.7). Now \(1-\gamma \Vert \mathbf{G}_K(0)\Vert \ge 1-\gamma \Vert \mathbf{G}_K\Vert _{H^\infty }=0\) and (4.4) follows, showing that \(F_K\) is coercive and hence surjective.
Finally, to prove statement (4), assume that \(Y=\mathrm{im}\,C\) and that (4.1) or (4.2) are satisfied. Then the map \(F_K\) is surjective (as follows from statement (2) if (4.1) holds and from statement (3) if (4.2) holds). Surjectivity of \(F_K\), (3.1) and statement (1) guarantee that \(\# F_K^{-1}(z)=1\) for all \(z\in \mathrm{im}\,C\). Writing \(F_K^{-1}(z)=\{y_z\}\) for every \(z\in \mathrm{im}\,C\) and, once again, invoking (3.1), we conclude that \(y_z\in \mathrm{im}\,C\) and bijectivity of \({\hat{F}}_K\) follows. \(\square \)
For \(\tau \ge 0\), we define the left-shift operator \(\Lambda _\tau \) by \((\Lambda _\tau v)(t)=v(t+\tau )\) for all \(t\ge 0\), where v is an arbitrary function \({\mathbb {R}}_+\rightarrow {\mathbb {R}}^n\). A subset \({{\mathcal {V}}}\subseteq L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) is said to be equi-convergent to \(v^\infty \in {\mathbb {R}}^n\) if, for every \(\varepsilon >0\), there exists \(\tau \ge 0\) such that
The following theorem is the main result of this section.
Theorem 4.3
Let \(Y\subseteq \mathrm{im}\,C\) be nonempty, \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C), v^\infty \in {\mathbb {R}}^n\) and set \(\gamma :=1/\Vert \mathbf{G}_K\Vert _{H^\infty }\) (where \(\gamma :=\infty \) if \(\Vert \mathbf{G}_K\Vert _{H^\infty }=0\)). Assume that condition (A) holds and that \(F_K^{-1}(-CA_K^{-1}v^\infty )\cap Y\not =\emptyset \). Then \(\# F_K^{-1}(-CA_K^{-1}v^\infty )=1\) and, writing \(\{y^\infty \}= F_K^{-1}(-CA_K^{-1}v^\infty ),\) the pair \((x^\infty ,v^\infty ),\) where
is an equilibrium pair of system (1.1). Furthermore, \(Cx^\infty =y^\infty \) and the following statements hold.
-
1.
The equilibrium pair \((x^\infty ,v^\infty )\) is GAS, and, for every \(x^0\in {\mathbb {R}}^n\) and every \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) such that \(\lim _{t\rightarrow \infty } v(t)=v^\infty ,\) we have that either \(x(t;x^0,v)\rightarrow x^\infty \) or \(\Vert x(t;x^0,v)\Vert \rightarrow \infty \) as \(t\rightarrow \infty \).
-
2.
Under the additional assumption that, for some \(\zeta \in {\mathbb {R}}^p,\)
$$\begin{aligned} \gamma \Vert z\Vert -\Vert f(z+\zeta )-f(\zeta )-Kz\Vert \rightarrow \infty \quad \hbox {as}\ \Vert z\Vert \rightarrow \infty , \end{aligned}$$(4.9)\((x^\infty ,v^\infty ),\) with \(x^\infty \) given by (4.8), is an ISS equilibrium pair of (1.1) and there exist \(\psi _1, \psi _2\in {{\mathcal {K}}}{{\mathcal {L}}}\) and \(\varphi \in {{\mathcal {K}}}\) such that, for all \((x^0,v) \in {\mathbb {R}}^n\times L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) and all \(t\ge 0,\)
$$\begin{aligned} \Vert x(t;x^0,v)-x^\infty \Vert\le & {} \psi _1(\Vert x^0-x^\infty \Vert ,t)+ \psi _2(\Vert v-v^\infty \theta \Vert _{L^\infty },t)\nonumber \\&+\,\varphi (\Vert \Lambda _{t/2}(v-v^\infty \theta )\Vert _{L^\infty }). \end{aligned}$$(4.10)
In particular, for every \(x^0\in {\mathbb {R}}^n\) and every \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) such that \(\lim _{t\rightarrow \infty } v(t)=v^\infty ,\)
and the convergence is uniform in the following sense : given a set of inputs \({{\mathcal {V}}}\subseteq L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) which is equi-convergent to \(v^\infty \) and \(\kappa >0,\) then the set of solutions
is equi-convergent to \(x^\infty \).
Before proving Theorem 4.3, we provide some commentary.
Remark 4.4
- (a):
-
Assumption (A) is an incremental condition which is weaker than a global Lipschitz condition, since (A) only needs to hold for all \(\xi \in Y\). We mention that the number \(1/\Vert \mathbf{G}_K\Vert _{H^\infty }\) appearing on the right-hand side of the inequality in assumption (A) is equal to the structured complex stability radius of the Hurwitz \(A+BKC\) with respect to the perturbation structure given by B and C, see [16].
- (b):
-
The set \(Y\subseteq \mathrm{im}\,C\) should be interpreted as the set of all “achievable” output limits. Indeed, if \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\), condition (A) is satisfied and there exists \(\zeta \) such that (4.9) holds, then, for every \(y^\infty \in Y\), there exists \(v^\infty \in {\mathbb {R}}^n\) such that \(F_K(y^\infty )=-CA_K^{-1}v^\infty \) and, by Theorem 4.3, \(Cx(t;x^0,v)\rightarrow y^\infty \) as \(t \rightarrow \infty \) for every \(x^0\) and every v convergent to \(v^\infty \).
- (c):
-
It may appear that \(y^\infty \) and \(x^\infty \) depend on K, but this is not the case. Indeed, let non-empty \(Y\subseteq \mathrm{im}\,C\) and \(v^\infty \in {\mathbb {R}}^n\) be given, let \(K_1,K_2\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\) and set \(\gamma _i:=1/\Vert \mathbf{G}_{K_i}\Vert _{H^\infty }\), where \(i=1,2\). Assume that condition (A) holds with \(K=K_i\) and \(\gamma =\gamma _i\) and \(F_{K_i}^{-1}(-CA_{K_i}^{-1}v^\infty )\cap Y\not =\emptyset \) for \(i=1,2\). By Theorem 4.3, the pre-image \(F^{-1}_{K_i}(-CA^{-1}_{K_i}v^\infty )\) is a singleton, the element of which we denote by \(y^\infty _i\). Defining, as in (4.8),
$$\begin{aligned} x_i^\infty :=-A_{K_i}^{-1}(B(f(y_i^\infty )-K_iy_i^\infty )+v^\infty ),\quad i=1,2, \end{aligned}$$it follows from Theorem 4.3 that \((x^\infty _1,v^\infty )\) and \((x^\infty _2,v^\infty )\) are globally asymptotically stable equilibrium pairs, which obviously implies that \(x^\infty _1=x^\infty _2\). Consequently, \(y^\infty _1=Cx^\infty _1= Cx^\infty _2=y^\infty _2\). In particular, if \(Y=\mathrm{im}\,C\) and there exists \(\zeta _i\in {\mathbb {R}}^p\) such that (4.9) holds with \(K=K_i\) and \(\zeta =\zeta _i\) for \(i=1,2\), the map \({\hat{F}}_{K_i}\) is bijective for \(i=1,2\) (by Proposition 4.1) and \({\hat{F}}^{-1}_{K_1}(CA^{-1}_{K_1}w)= {\hat{F}}^{-1}_{K_2}(CA^{-1}_{K_2}w)\) for all \(w\in {\mathbb {R}}^n\).
- (d):
-
A (conservative) sufficient condition for (4.9) is that there exists \(\rho \in (0, \gamma )\) and \(\zeta \in {\mathbb {R}}^p\) such that
$$\begin{aligned} \Vert f(z+\zeta )-f(\zeta )-Kz\Vert \le \rho \Vert z\Vert \quad \forall \, z \in {\mathbb {R}}^p. \end{aligned}$$(4.11)We give a simple example which satisfies (4.9), but for which there does not exist \(\rho \in (0, \gamma )\) such that (4.11) holds. Consider \(p = m = \gamma =1, K=0\) and
$$\begin{aligned} f: {\mathbb {R}}_+ \rightarrow {\mathbb {R}}_+,\quad z\mapsto 0.9z + 0.1(z\sin z-\ln (1+z)), \end{aligned}$$and note that
$$\begin{aligned} \vert z \vert - \vert g(z) \vert = 0.1z(1-\sin z) + 0.1\ln (1+z) \ge 0.1 \ln (1+z)\quad \forall \,z\in {\mathbb {R}}. \end{aligned}$$Consequently, the divergence condition (4.9) holds (as does condition (A)), but there does not exist \(\rho \in (0,1)\) such that (4.11) holds.
- (e):
-
The estimate (4.10) is the result of a suitable modification of an ISS estimate (see the proof below for details). The three terms on the right-hand side, all of which converge to 0 as \(t\rightarrow \infty \), relate, respectively, to the initial “error” \(x^0 - x^\infty \), the \(L^\infty \)-norm of \(v - v^\infty \theta \) over the entire time interval \([0,\infty )\) and the \(L^\infty \)-norm of \(v - v^\infty \theta \) over \([t/2,\infty )\) (the latter converging to 0 as \(t\rightarrow \infty \)). Note that the \({{\mathcal {K}}}{{\mathcal {L}}}\)-functions \(\psi _1\) and \(\psi _2\) and the \({{\mathcal {K}}}\)-function \(\varphi \) only depend on \(v^\infty \) and \(x^\infty \) and hence (4.10) is uniform in \(x^0\) and v. Furthermore, (4.10) evidently implies CICS and the equi-convergence property formulated towards the end of statement (2) of Theorem 4.3.\(\Diamond \)
Proof of Theorem 4.3
By hypothesis, assumption (A) holds and \(F_K^{-1}(-CA_K^{-1}v^\infty )\cap Y\not = \emptyset \), and thus, statement (1) of Proposition 4.1 yields that \(\#F_K^{-1}(-CA_K^{-1}v^\infty )=1\). For \(x^\infty \) given by (4.8), it follows from statement (3) of Proposition 3.1 that \((x^\infty ,v^\infty )\) is an equilibrium pair of (1.1) and \(Cx^\infty =y^\infty \). Define \({\tilde{f}}:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) by
A straightforward calculation shows that
Moreover, since \(y^\infty \in Y\), it follows from assumption (A) that
To prove statement (1), note that, by (4.12), a function x satisfies
if, and only if, \({\tilde{x}}:=x-x^\infty \theta \) satisfies
Consequently, the equilibrium \(x^\infty \) of (4.14) is GAS if, and only if, the equilibrium 0 of (4.15) is GAS. Invoking (4.13) in conjunction with statements (1) and (3) of Theorem 2.1 shows that the equilibrium 0 of (4.15) is GAS and hence, \(x^\infty \) is a GAS equilibrium of system (4.14). An application of [41, Theorem 1] (or, alternatively, of [25, Theorem 4.3]) allows us to conclude that, for \(x^0\in {\mathbb {R}}^n\) and \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) with \(v(t)\rightarrow v^\infty \) as \(t\rightarrow \infty \), we have that either \(x(t;x^0,v)\rightarrow x^\infty \) or \(\Vert x(t;x^0,v)\Vert \rightarrow \infty \) as \(t\rightarrow \infty \), completing the proof of statement (1).
We proceed to prove statement (2). To this end, let \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}^n)\) and set \({\tilde{v}}=v-v^\infty \theta \). Invoking (4.12) shows that a function x solves (1.1) if, and only if, \({\tilde{x}}:=x-x^\infty \theta \) solves
Consequently, the equilibrium pair \((x^\infty ,v^\infty )\) of (1.1) is ISS if, and only if, the equilibrium pair (0, 0) of (4.16) is ISS. By (4.9) and statement (1) of Lemma 4.2,
This, together with (4.13) and statement (2) of Lemma 4.2, shows that there exists \(\alpha \in {{\mathcal {K}}}_\infty \) such that \(\Vert {\tilde{f}}(z)-Kz\Vert \le \gamma \Vert z\Vert -\alpha (\Vert z\Vert )\) for \(z\in {\mathbb {R}}^p\). Statements (2) and (3) of Theorem 2.1 now show that (0, 0) is an ISS equilibrium pair of the system (4.16) and thus, the equilibrium pair \((x^\infty ,v^\infty )\) of (1.1) is ISS. Consequently, there exist \(\psi \in {{\mathcal {K}}}{{\mathcal {L}}}\) and \(\varphi \in {{\mathcal {K}}}\) such that
It remains to show that (4.10) holds. To this end, let \(x^0\in {\mathbb {R}}^n\) and \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) and note that, by the state transition property of system (1.1),
Hence, by (4.17),
Another application of (4.17) yields
Consequently, defining \(\psi _1,\psi _2\in {{\mathcal {K}}}{{\mathcal {L}}}\) by
we obtain, for \(t\ge 0\),
which is (4.10). \(\square \)
We illustrate the conclusions of Theorem 4.3 with some simple examples.
Example 4.5
Consider the one-dimensional Lur’e system
Note that here \(n=1, A=-1\) and \(B=C=1\). We choose \(K=0\) and so
Since \(\Vert \mathbf{G}\Vert _{H^\infty }=\mathbf{G}(0)=1\), we have \(\gamma =1\).
-
(a)
Let \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) be given by
$$\begin{aligned} f(z)=z-\mathrm{sign}(z)(1-\mathrm{e}^{-|z|})\quad \,\forall \,z\in {\mathbb {R}}. \end{aligned}$$(4.19)Since
$$\begin{aligned} f'(z)=1-\mathrm{e}^{-|z|}\quad \forall \,z\in {\mathbb {R}}, \end{aligned}$$the mean-value theorem guarantees that
$$\begin{aligned} |f(z+\xi )-f(\xi )|<|z|\quad \forall \,\xi ,z\in {\mathbb {R}},\ z\not =0. \end{aligned}$$Furthermore,
$$\begin{aligned} F_0(z)=z-f(z)=\mathrm{sign}(z)(1-\mathrm{e}^{-|z|})\quad \forall \,z\in {\mathbb {R}}, \end{aligned}$$and so, \(F_0({\mathbb {R}})=(-1,1)\). Setting \(Y:=\mathrm{im}\,C={\mathbb {R}}\), we see that, for every \(v^\infty \in (-1,1)\), the assumptions of statement (1) of Theorem 4.3 are satisfied. Therefore, if \(v^\infty \in (-1,1)\), then, for all \(x^0\in {\mathbb {R}}\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}})\) such that \(\lim _{t\rightarrow \infty }v(t)=v^\infty \), we have that either \(x(t;x^0,v)\rightarrow x^\infty =F_0^{-1}(v^\infty )\) or \(|x(t;x^0,v)|\rightarrow \infty \) as \(t\rightarrow \infty \). We show that divergence is not possible. Seeking a contradiction, suppose that there exist \(v^\infty \in (-1,1), v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}})\) with \(\lim _{t\rightarrow \infty }v(t)= v^\infty \) and \(x^0\in {\mathbb {R}}\) such that \(|x(t;x^0,v)|\rightarrow \infty \) as \(t\rightarrow \infty \). Setting \(x(t):=x(t;x^0,v)\), we have that either \(x(t)\rightarrow \infty \) or \(x(t)\rightarrow -\infty \) as \(t\rightarrow \infty \). If \(x(t)\rightarrow \infty \) as \(t\rightarrow \infty \), then there exists \(\tau \ge 0\) such that
$$\begin{aligned} \dot{x}(t)=-1+\mathrm{e}^{-x(t)}+v(t)\le (v^\infty -1)/2<0\quad \forall \,t\ge \tau . \end{aligned}$$But this implies that \(x(t)\rightarrow -\infty \) as \(t\rightarrow \infty \), providing the desired contradiction. Similarly, if \(x(t)\rightarrow -\infty \) as \(t\rightarrow \infty \), then there exists \(\tau \ge 0\) such that
$$\begin{aligned} \dot{x}(t)=1-\mathrm{e}^{x(t)}+v(t)\ge (v^\infty +1)/2>0\quad \forall \,t\ge \tau , \end{aligned}$$showing that \(x(t)\rightarrow \infty \) as \(t\rightarrow \infty \), which is impossible. The above analysis shows in particular that the system (4.18) has the 0-CICS property. Note that the equilibrium pair (0, 0) of (4.18) is not ISS (since the input \(v(t)\equiv 1+\varepsilon , \varepsilon >0\), produces an unbounded solution).
-
(b)
Consider again system (4.18), but now with \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) given by
$$\begin{aligned} f(z)=z-\mathrm{sat}(z)\mathrm{e}^{-|z|},\quad \forall \,z\in {\mathbb {R}}, \end{aligned}$$where \(\mathrm{sat}(z):=z\) for \(|z|\le 1\) and \(\mathrm{sat}(z):=\mathrm{sign}(z)\) for \(|z|>1\). Set \(Y:=\{0\}\) and let \(v^\infty =0\). Since,
$$\begin{aligned} |f(z)|<|z|\quad \forall \,z\not =0, \end{aligned}$$the assumptions of statement (1) of Theorem 4.3 are satisfied and it follows that \(y^\infty =x^\infty =0\), the equilibrium 0 of the uncontrolled system (4.18) is GAS, and, for every \(x^0\in {\mathbb {R}}\) and every \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}})\) with \(\lim _{t\rightarrow \infty }v(t)=0\), either \(x(t;x^0,v)\rightarrow 0\) or \(|x(t;x^0,v)|\rightarrow \infty \) as \(t\rightarrow \infty \). Divergence is possible: indeed, with v given by \(v(t)=2/(t+e)\), it is straightforward to verify that \(x(t;1,v)=\ln (t+e)\). \(\Diamond \)
Example 4.6
Consider the two-dimensional Lur’e system
with nonlinearity \(f\in {{\mathcal {F}}}\), where \({{\mathcal {F}}}\) is the set of all of continuously differentiable functions \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) such that
Setting
it is clear that system (4.20) is of the form (1.1). The matrix A is Hurwitz (\(-2\) is an eigenvalue of algebraic multiplicity two) and the transfer function of the linear system (A, B, C) is \(\mathbf{G}(s)=(s+4)/(s+2)^2\). Choosing \(K=0\), we have
and thus, \(\gamma =1\). It follows from (4.21) that \(|z|-|f(z)|\rightarrow \infty \) as \(|z|\rightarrow \infty \) and so, (4.9) holds with \(\zeta =0\). Using elementary calculus, it is not difficult to show that, for every \(\xi \in {\mathbb {R}}\backslash (1,6)\), there exists \(a_\xi \in (0,1)\) such that
Hence, condition (A) holds with \(Y:={\mathbb {R}}\backslash (1,6)\). Furthermore, \(F_0(z)=F_K(z)=z-f(z)\), and so, using (4.21),
According to statement (2) of Theorem 4.3, for every \(v^\infty =(v^\infty _1,v^\infty _2)^\mathrm{T}\in {\mathbb {R}}^2\) such that
there exists \(x^\infty \in {\mathbb {R}}\) such that, for all \(x^0\in {\mathbb {R}}\) and all \(v\in \ L^\infty ({\mathbb {R}}_+,{\mathbb {R}})\) with \(\lim _{t\rightarrow \infty }v(t)=v^\infty \), the solution \(x(t,x^0,v)\) of (4.20) converges to \(x^\infty \) as \(t\rightarrow \infty \).
Let \(\xi _0\in (1,6)\). Then it is not difficult to show that there exists \(f\in {{\mathcal {F}}}\) such that
and it is clear that condition (A) does not hold for \(\xi =\xi _0\). We claim that, for \(v^\infty =(v^\infty _1,v^\infty _2)^\mathrm{T}\in {\mathbb {R}}^2\) such that
there does not exist \(x^\infty \in {\mathbb {R}}^2\) such that \(\lim _{t\rightarrow \infty }x(t,x^0,v) =x^\infty \) for all \(x^0\in {\mathbb {R}}^2\) and all \(v\in \ L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^2)\) with \(\lim _{t\rightarrow \infty }v(t)=v^\infty \). To this end note that, by (4.22), there exists \(z_0\not =0\) such that
and thus
Now (4.21) guarantees that
and hence there exists \(\xi _1\not =\xi _0\) such that \(F_0(\xi _0)=F_0(\xi _1)\). As a consequence, \(\#F_0^{-1}(-CA^{-1}v^\infty )>1\), and so, by statement (2) of Proposition 3.1, it follows that there does not exist \(x^\infty \in {\mathbb {R}}^2\) such that \(\lim _{t\rightarrow \infty }x(t,x^0,v)=x^\infty \) for all \(x^0\in {\mathbb {R}}^2\) and all \(v\in \ L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^2)\) with \(\lim _{t\rightarrow \infty }v(t)=v^\infty \).
To illustrate the last point, we consider a specific example: fix \(\xi _0 = 7/2\in (1,6)\) and let \(f \in {{\mathcal {F}}}\) be given by
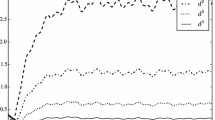
where \(q(z):=-2z^3 +21z^2 -143z/2 +81\) (Fig. 3).
Graph of f from (4.24)
It is straightforward to verify that the function f belongs to \({{\mathcal {F}}}\), in particular:
The last identity shows that condition (4.22) holds. Moreover, \(F_0(\xi _0) = \xi _0 - f(\xi _0)=5/4\), and thus, \(v^\infty := (2,-5/3)^\mathrm{T}\) satisfies (4.23). A straightforward argument shows that \(F_0^{-1}(5/4)= \{5/2,7/2,9/2\}\). Calculating \(x^\infty =-A^{-1}(Bf(y^\infty )+v^\infty )\) for \(y^\infty \in \{5/2,7/2,9/2\}\), we see that \((x^\infty ,v^\infty )\) is an equilibrium pair for every \(x^\infty \) of the form
In particular, there does not exist \(x^\infty \in {\mathbb {R}}^2\) such that \(\lim _{t\rightarrow \infty }x(t,x^0,v)=x^\infty \) for all \(x^0\in {\mathbb {R}}^2\) and all \(v\in \ L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^2)\) with \(\lim _{t\rightarrow \infty }v(t)=v^\infty \). \(\Diamond \)
The following corollary is a consequence of statement (1) of Theorem 4.3.
Corollary 4.7
Let \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C),\) set \(\gamma :=1/\Vert \mathbf{G}_K\Vert _{H^\infty }\) (where \(\gamma :=\infty \) if \(\Vert \mathbf{G}_K\Vert _{H^\infty }=0\)), assume that (A) holds with \(Y:=F_K^{-1}(\mathrm{im}\,C) \subseteq \mathrm{im}\,C\) and set \(V:=\{w\in {\mathbb {R}}^n:-CA_K^{-1}w\in F_K(Y)\}\). Furthermore, assume that, for every \(x^0\in {\mathbb {R}}^n\) and every \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) such that \(\lim _{t\rightarrow \infty } v(t)=v^\infty \in V,\) the function \(Cx(\cdot \,;x^0,v)\) is bounded. Then, for every \(v^\infty \in V, \# F_K^{-1}(-CA_K^{-1}v^\infty )=1\) and, for every \(x^0\in {\mathbb {R}}^n\) and every \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) such that \(\lim _{t\rightarrow \infty } v(t)=v^\infty \in V,\) we have that \(x(t;x^0,v)\rightarrow x^\infty \) as \(t\rightarrow \infty ,\) where \(x^\infty :=-A_K^{-1}(B(f(y^\infty )-Ky^\infty )+v^\infty )\) with \(y^\infty \) given by \(\{y^\infty \}=F_K^{-1}(-CA_K^{-1}v^\infty )\).
Note that usually \(\mathrm{rank}\, C=p\), in which case \(\mathrm{im}\,C={\mathbb {R}}^p, Y={\mathbb {R}}^p\) and \(F_K(Y)=F_K({\mathbb {R}}^p)=\mathrm{im}\,F_K\).
Proof of Corollary 4.7
Let \(v^\infty \in V\) and set \(z:=-CA_K^{-1}v^\infty \). Obviously, \(z\in \mathrm{im}\,C\) and it follows from the definitions of the sets Y and V that \(F_K^{-1}(z)\cap Y\not =\emptyset \). Consequently, by Proposition 4.1, \(\# F_K^{-1}(-CA_K^{-1}v^\infty ) =\# F_K^{-1}(z)=1\).
To prove the convergence property, let \(x^0\in {\mathbb {R}}^n, v^\infty \in V\) and let \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) be such that \(v(t)\rightarrow v^\infty \) as \(t\rightarrow \infty \) and write \(x(t):=x(t;x^0,v)\). By hypothesis, Cx is bounded, and so, since x satisfies \(\dot{x}=A_Kx+B(f(Cx)-KCx)+v\), the Hurwitz property of \(A_K\) guarantees that x is bounded. An application of statement (1) of Theorem 4.3 shows that \(x(t)\rightarrow x^\infty \) as \(t\rightarrow \infty \), completing the proof. \(\square \)
The next result, a corollary of statement (2) of Theorem 4.3, provides a sufficient condition for the CICS property.
Corollary 4.8
Let \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\) and set \(\gamma :=1/\Vert \mathbf{G}_K\Vert _{H^\infty }\) (where \(\gamma :=\infty \) if \(\Vert \mathbf{G}_K\Vert _{H^\infty }=0\)). If there exists \(\zeta \in {\mathbb {R}}^p\) such that (4.9) holds and f satisfies
(B) \(\Vert f(z+\xi )-f(\xi )-Kz\Vert <\gamma \Vert z\Vert \) for all \(\xi \in \mathrm{im}\,C\) and all \(z\in {\mathbb {R}}^p, z\not =0,\) then (1.1) has the CICS property.
Proof
The map \(F_K\) is surjective, as follows from hypothesis (B), (4.9) and statement (3) of Proposition 4.1. Hence, by (3.1),
Invoking statement (2) of Theorem 4.3 (with \(Y=\mathrm{im}\,C\)) shows that the Lur’e system (1.1) has the CICS property. \(\square \)
As an illustration of Corollary 4.7, consider the system (4.18) with f given by (4.19) and \(K=0\), see part (a) of Example 4.5. In this case, \(\gamma =1, Y={\mathbb {R}}\) and \(V=F_0({\mathbb {R}})=(-1,1)\). As has been shown in part (a) of Example (4.5), assumption (A) holds with \(Y={\mathbb {R}}\) and \(Cx(\cdot \,;x^0,v)=x(\cdot \,;x^0,v)\) is bounded for all \(x^0\in {\mathbb {R}}\) and all convergent \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) with limit in \((-1,1)\). Consequently, all assumptions of Corollary 4.7 are satisfied and so, for all \(x^0\in {\mathbb {R}}\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\) such that \(\lim _{t\rightarrow \infty }v(t)=v^\infty \), we have that \(\lim _{t\rightarrow \infty }x(t;x^0,v)=x^\infty \), where \(x^\infty \) is given by \(\{x^\infty \}=F_0^{-1}(v^\infty )\). Note that the system does not have the CICS property, since the input \(v(t)\equiv 1+\varepsilon , \varepsilon >0\), generates a divergent state trajectory. Moreover, note that Corollary 4.8 does not apply: whilst assumption (B) is satisfied, there does not exist \(\zeta \in {\mathbb {R}}\) such that (4.9) holds.
We give a sufficient condition for (B) to hold. The proof is routine and is, therefore, left to the reader.
Lemma 4.9
Assume that \(f:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) is continuously differentiable, with derivative denoted by Df. Let \(\Delta \subseteq {\mathbb {R}}^p\) be a set which does not have any accumulation points. If
then condition (B) holds.
In the following, we shall derive a number of further corollaries which will provide “interpretations” of Corollary 4.8 in terms of the complex Aizerman conjecture, small-gain theorems and circle criteria, respectively.
The next result is reminiscent of the complexified Aizerman conjecture [17, 18, 36].
Corollary 4.10
Let \(K\in {\mathbb {R}}^{m\times p}, r>0\) and assume that \({\mathbb {B}}_{\mathbb {C}}(K,r) \subseteq {\mathbb {S}}_{\mathbb {C}}(A,B,C)\). If
and there exists \(\zeta \in {\mathbb {R}}^p\) such that
then (1.1) has the CICS property.
Corollary 4.10 says, roughly speaking, that linear stability (namely \({\mathbb {B}}_{\mathbb {C}}(K, r)\subseteq {\mathbb {S}}_{\mathbb {C}}(A,B,C)\)) implies CICS for all nonlinearities f satisfying the “incremental” ball condition (4.25) and the divergence property (4.26).
Proof of Corollary 4.10
By hypothesis \({\mathbb {B}}_{\mathbb {C}}(K,r)\subseteq {\mathbb {S}}_{\mathbb {C}}(A,B,C)\) and so, \(A_K=A+BKC\) is Hurwitz and \({\mathbb {B}}_{\mathbb {C}}(0,r)\subseteq {\mathbb {S}}_{\mathbb {C}}(A_K,B,C)\). Thus, appealing to elementary stability radius theory [16, 18] (see also the proof of Theorem 2.1 in the Appendix), we have that \(r\le 1/\Vert \mathbf{G}\Vert _{H^\infty }\). The claim follows now from Corollary 4.8. \(\square \)
Consider the following incremental small-gain condition:
(\(\mathbf{B}^\prime \)) For every \(\xi \in \mathrm{im}\,C\), there exists \(\alpha _\xi \in {{\mathcal {K}}}_\infty \) such that
We are now in the position to state a “nonlinear” small-gain criterion for the CICS property.
Corollary 4.11
Let \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\). If f satisfies \((\mathrm{B}^\prime ),\) then (1.1) has the CICS property.
Proof
It is clear that if (\(\hbox {B}^\prime \)) is satisfied, then (B) and (4.9) hold. Thus, the claim follows from Corollary 4.8. \(\square \)
Note that (\(\hbox {B}^\prime \)) is not a small-gain condition in the sense of classical input–output theory of feedback systems (as presented, for example, in [11, 13, 14, 23, 45]): whilst, for every fixed \(\xi \in \mathrm{im}\,C\), the right-hand side of (4.27) is smaller than 1 for all \(z\not =0\), it is in general not uniformly bounded away from 1. Indeed, it is possible that, for fixed \(\xi \), the right-hand side of (4.27) is converging to 1 as \(\Vert z\Vert \rightarrow 0\) or \(\Vert z\Vert \rightarrow \infty \). Therefore, rather than comparing Corollary 4.11 with classical small-gain theorems [11, 13, 14, 23, 45], it is more appropriate to view it in the context of “modern” nonlinear ISS small-gain results, see for example [10, 21, 36, 43].
If \(\mathrm{im}\,C={\mathbb {R}}^p\), then condition (B) implies that \(f_K:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m, z\mapsto f(z)-Kz\) is globally Lipschitz and \(\gamma \) is a Lipschitz constant for \(f_K\). If the map \(f_K\) is globally Lipschitz and has a Lipschitz constant \(\lambda <\gamma \), then
This inequality, a (incremental) small-gain condition in the sense of classical input–output theory, is sufficient for (\(\hbox {B}^\prime \)) to hold. Consequently, (4.28) is a sufficient condition for the CICS property.
In the following example, we present a simple nonlinearity f such that f satisfies condition (B), \(f_K\) has minimal Lipschitz constant equal to \(\gamma \) and (4.9) holds.
Example 4.12
Let
The characteristic polynomial of A is \(\det (sI-A)=(s+1)^3\). Hence, A is Hurwitz and so may choose \(K=0\), leading to
A routine argument shows that
and thus \(\gamma =1/\Vert \mathbf{G}\Vert _{H^\infty }=1\). In the following, we consider the Lur’e system
The function f is continuously differentiable and
It follows from Lemma 4.9 that condition (B) is satisfied. Moreover, trivially, \(|z|-|f(z)|\rightarrow \infty \) as \(|z|\rightarrow \infty \), and so, Corollary 4.8 guarantees that (4.29) has the CICS property. Finally, note that f is globally Lipschitz with minimal Lipschitz constant equal to \(\gamma =1\). \(\Diamond \)
Remark 4.13
If the assumptions of Corollary 4.8 hold, then, by Proposition 4.1, the map \({\hat{F}}_K:\mathrm{im}\,C\rightarrow \mathrm{im}\,C\) restricting \(F_K\) to \(\mathrm{im}\,C\) is bijective and the ISSS gain of (1.1) can be written as
where \(f_K(z):=f(z)-Kz\). Similarly, the IOSS gain of (1.1) can expressed as
Note that if A is Hurwitz, \(f=0\) and \(K=0\), then (1.1) “collapses” to the linear system
which has transfer function \(\mathbf{H}(s)=C(sI-A)^{-1}\). In this case, \(F_K(z)=F_0(z)=z\) for all \(z\in {\mathbb {R}}^n\) and \(\Gamma _\mathrm{io}(z)=-CA^{-1}z=\mathbf{H}(0)z\), that is, the familiar linear steady-state gain is recovered. \(\Diamond \)
Statement (1) of the next proposition demonstrates that, under the assumptions of Corollary 4.8, the maps \(\Gamma _\mathrm{is}\) and \( \Gamma _\mathrm{io}\) (the steady-state gains) are continuous.
Proposition 4.14
Let \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\) and set \(\gamma :=1/\Vert \mathbf{G}_K\Vert _{H^\infty }\) (where \(\gamma :=\infty \) if \(\Vert \mathbf{G}_K\Vert _{H^\infty }=0\)).
-
1.
If the assumptions of Corollary 4.8 hold, then the steady-state gains \(\Gamma _\mathrm{is}\) and \( \Gamma _\mathrm{io}\) are continuous.
-
2.
If the map \({\mathbb {R}}^p\rightarrow {\mathbb {R}}^m,\,z \mapsto f(z) - Kz\) is globally Lipschitz with Lipschitz constant \(\lambda <\gamma ,\) then \(\Gamma _\mathrm{is}\) and \( \Gamma _\mathrm{io}\) are globally Lipschitz.
Proof
To prove statement (1), we note that, in light of Remark 4.13, it is sufficient to show that \({\hat{F}}_K^{-1}:\mathrm{im}\,C\rightarrow \mathrm{im}\,C\) is continuous. To this end, let \(w \in \mathrm{im}\,C\) be fixed, but arbitrary, set \(\xi := {\hat{F}}_K^{-1} (w) \in \mathrm{im}\,C\) and define \({\tilde{f}}: {\mathbb {R}}^p \rightarrow {\mathbb {R}}^p\) by \({\tilde{f}}(z):= f(z+\xi ) - f(\xi )\) for all \(z\in {\mathbb {R}}^p\). Invoking the divergence assumption (4.9) and statement (1) of Lemma 4.2 shows that
and so by statement (2) of Lemma 4.2, there exists \(\alpha \in {{\mathcal {K}}}_\infty \) such that
We now use (4.32) to estimate
Thus,
where \(\alpha ^{-1} \in {{\mathcal {K}}}_\infty \), as \(\alpha \in {{\mathcal {K}}}_\infty \). Invoking the invertibility of \({\hat{F}}_K\) and the definition of \(\xi \), we see that
In particular, we obtain that \({\hat{F}}_K^{-1}\) is continuous at w. As \(w \in \mathrm{im}\,C\) was arbitrary, continuity of \({\hat{F}}_K^{-1}\) follows.
The proof of statement (2) is similar to that of statement (1). Indeed, we have that
which implies that
showing that \({\hat{F}}_K^{-1}\) is globally Lipschitz. Consequently, invoking formulas (4.30) and (4.31), the steady-state gains \(\Gamma _\mathrm{is}\) and \( \Gamma _\mathrm{io}\) inherit the global Lipschitz property from that of their constituents. \(\square \)
Next we present, in form of two corollaries, sufficient conditions for the CICS property which are reminiscent of the well-known circle criterion (see, for example, [14, 23, 36, 45]).
Corollary 4.15
Let \(K_1, K_2\in {\mathbb {R}}^{m \times p}\). Assume that (A, B, C) is stabilizable and detectable, \((I - K_2\mathbf{G})(I - K_1\mathbf{G})^{-1}\) is positive real,
and there exist \(\zeta \in {\mathbb {R}}^p\) and \(\alpha \in {{\mathcal {K}}}_\infty \) such that
Then the Lur’e system (1.1) has the CICS property.
Proof
We shall rewrite the Lur’e system in a form which will allow the application of Corollary 4.8. For \(\xi \in {\mathbb {R}}^p\), define \(f_\xi :{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) by
Setting
we have that
Note that in conjunction with (4.33) (or, alternatively, (4.34) could be invoked) this implies \(\ker L = \{0\}\). Thus \(L^*L\) is invertible and \(L^{\sharp } := (L^*L)^{-1}L^* \in {\mathbb {R}}^{p \times m}\) is a left inverse of L. Define the nonlinearity \(g:{\mathbb {R}}^m\rightarrow {\mathbb {R}}^m\) by \(g(z):=f(L^{\sharp }z) - K_1L^{\sharp }z\) for all \(z\in {\mathbb {R}}^m\) and consider the Lur’e system
where \(A_{K_1}:=A+BK_1C\). The linear state space system \((A_{K_1},B,LC)\) has transfer function
It is obvious that x is solves the original Lur’e system \(\dot{x}=Ax+Bf(Cx)+v\) if, and only if, x solves (4.36). Therefore, it is sufficient to show that (4.36) has the CICS property. To this end, set \(K:=-LL^\sharp \). Using, mutatis mutandis, arguments from [36, proof of Corollary 3.10], it follows that \(K\in {\mathbb {S}}_{\mathbb {R}}(A_{K_1},B,LC)\),
there exists \(\beta \in {{\mathcal {K}}}_\infty \) such that
and
Consequently, the assumptions of Corollary 4.8 are satisfied in the context of the Lur’e system (4.36) and therefore, (4.36) has the CICS property, completing the proof. \(\square \)
Recall that a rational square matrix \(\mathbf{H}\) is said to be strictly positive real if there exists \(\varepsilon >0\) such the rational matrix function \(s\mapsto \mathbf{H}(s-\varepsilon )\) is positive real.
Corollary 4.16
Let \(K_1, K_2\in {\mathbb {R}}^{m \times p}\). Assume that \(\ker (K_1-K_2)=\{0\}, (A,B,C)\) is stabilisable and detectable, \((I - K_2\mathbf{G})(I - K_1\mathbf{G})^{-1}\) is strictly positive real and
Then the Lur’e system (1.1) has the CICS property.
Proof
Set \(M:=K_2-K_1\), let \(\xi \in \mathrm{im}\,C\) and define \(f_\xi :{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) by (4.35). Then, mutatis mutandis, arguments from [36, proof of Corollary 3.13] can be invoked to show that there exists \(k>0\) and \(\mu >0\) such that, for all \(\kappa \in (0,k)\), the rational matrix function
is positive real and
It follows that the conditions of Corollary 4.15 hold (with \(\alpha (s)=\mu \kappa (\kappa +1)s\) and \(K_1\) and \(K_2\) replaced by \(K_1-\kappa M\) and \(K_2+\kappa M\), respectively). Hence, (1.1) has the CICS property. \(\square \)
Note that the assumptions in Corollary 4.16 are essentially identical to those in the “classical” circle criterion which guarantees global asymptotic stability (see [13, Theorem 5.1], [14, Corollary 5.8] and [23, Theorem 7.1], the only difference being that (4.37) is the incremental version of the standard sector condition in the circle criterion.
We further note that Corollary 4.16 is reminiscent of the main result in [35] which provides a description of the steady-state error of single-input single-output Lur’e systems of the form (1.2) in response to a class of polynomial inputs (including unbounded signals such as ramps) under the assumption that the conditions of the SISO circle criterion are met. Whilst the CICS property is not mentioned in [35], part (1) of [35, Theorem] can be interpreted in CICS terms.
We emphasize that Corollaries 4.15 and 4.16 are not equivalent. Indeed, the latter is more conservative than the former as is illustrated by the following simple example.
Example 4.17
Consider the one-dimensional Lur’e system
with \(f:{\mathbb {R}}\rightarrow {\mathbb {R}}\) given by \(f(z)=-\mathrm{sign}(z)\ln (1+|z|)\). The function f is continuously differentiable, \(f'(0)=-1\) and \(-1<f'(z)<0\) for all \(z\not =0\). Obviously, (4.38) is of the form (1.1) with \((A,B,C)=(0,1,1)\), and so \(\mathbf{G}(s)=1/s\). Let \(K_1<K_2\) and note that
is (strictly) positive real if, and only if, \(K_2\le 0\, (K_2<0)\).
Now if \(K_1<K_2<0\), then, for every \(\xi \in {\mathbb {R}}\),
and we conclude that Corollary 4.16 does not apply.
However, choosing \(K_1<-1\) and \(K_2=0\), it is not difficult to show that the conditions of Corollary 4.15 are satisfied. Indeed, for \(K_1<-1\) and \(K_2=0\), the rational function in (4.39) is positive real and, by the mean-value theorem for differentiation,
Furthermore, it is clear that
which, together with (4.40), shows that there exists \(\alpha \in {{\mathcal {K}}}_\infty \) such that
We have now established that the assumptions of Corollary 4.15 hold (with \(K_1<-1, K_2=0\) and \(\zeta =0\)) and consequently, system (4.38) has the CICS property. \(\Diamond \)
5 The CICS property for another class of Lur’e systems
In this short section, we consider forced Lur’e systems of the form
where, as in Sects. 2–4, \(A\in \mathbb {R}^{n\times n}, B\in \mathbb {R}^{n\times m}, C\in \mathbb {R}^{p\times n}, f:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m, y\) denotes the output and \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}^p)\) is the control (forcing, input) function. In the uncontrolled case (\(v=0\)), the Lur’e systems (1.1) and (5.1) are identical. As has been pointed out in Sect. 1, the Lur’e system (5.1) can be thought of as a closed-loop system obtained by applying the linear feedback \(w=y-v\) to the system \(\dot{x}=Ax+Bf(w)\) (a linear system with input nonlinearity), see Fig. 2.
Let \({\hat{x}}(\cdot \,;x^0,v)\) denote the unique maximally defined forward solution of the initial-value problem (5.1). The CICS property can be defined as before: Lur’e system (5.1) is said to have the CICS property if, for every \(v^\infty \in {\mathbb {R}}^p\), there exists \(x^\infty \in {\mathbb {R}}^n\) such that \(\lim _{t\rightarrow \infty }{\hat{x}}(t;x^0,v) =x^\infty \) for all \(x^0\in {\mathbb {R}}^n\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^p)\) with \(\lim _{t\rightarrow \infty }v(t)=v^\infty \).
The following corollary provides a sufficient condition for (5.1) to have the CICS property.
Proposition 5.1
Let \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C),\) assume that \(\Vert \mathbf{G}_K\Vert _{H^\infty }>0\) and set \(\gamma :=1/\Vert \mathbf{G}_K\Vert _{H^\infty }\). Furthermore, assume that there exists \(\zeta \in {\mathbb {R}}^p\) such that (4.9) holds and f satisfies
(C) \(\Vert f(z+\xi )-f(\xi )-Kz\Vert <\gamma \Vert z\Vert \) for all \(\xi , z\in {\mathbb {R}}^p, z\not =0\).
Then the map \(F_K\) is bijective and, for all \(v^\infty \in {\mathbb {R}}^p,\) all \(x^0\in {\mathbb {R}}^n\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^p)\) with \(\lim _{t\rightarrow \infty }v(t)=v^\infty ,\)
where \(y^\infty \in {\mathbb {R}}^p\) is given by \(y^\infty :=F_K^{-1}(-(I+\mathbf{G}_K(0)K) v^\infty )+v^\infty \) and satisfies \(y^\infty =Cx^\infty \). In particular, the Lur’e system (5.1) has the CICS property.
Remark 5.2
Note that under the assumptions of Proposition 5.1, it is natural to define the IOSS gain of (5.1) to be the map \(v^\infty \mapsto F_K^{-1}\big (-(I+\mathbf{G}_K(0)K)v^\infty \big )+v^\infty \). Proposition 5.1 allows us to extend a classical result on integral control to Lur’e systems of the form (5.1). To this end, assume that the assumptions of Proposition 5.1 are satisfied, \(f(0)=0\) and the linear system (A, B, C) contains an integrator, that is, \(\mathbf{G}\) has a Laurent expansion of the form
where \(G_j\in {\mathbb {R}}^{p\times m}\) and \(G_{-1}\not =0\). If \(G_{-1}K\) is invertible, then \(\mathbf{G}_K(0)K=-I\) and so, \(y^\infty =F_K^{-1}(0)+v^\infty =v^\infty \) (where we have used that \(f(0)=0\)), showing that every input v with limit \(v^\infty \) produces an output y converging also to \(v^\infty \), or equivalently, the IOSS gain of (5.1) is equal to the identity. \(\Diamond \)
Proof of Proposition 5.1
It follows from statement (3) of Proposition 4.1 that \(F_K\) is surjective. Injectivity of \(F_K\) can be shown by an argument similar to that used in the proof of statement (1) of Proposition 4.1.
To prove the convergence property, let \(x^0\in {\mathbb {R}}^n, v^\infty \in {\mathbb {R}}^p\) and \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^p)\) such that \(v(t)\rightarrow v^\infty \) as \(t\rightarrow \infty \). Setting \({\tilde{x}}(t):={\hat{x}}(t;x^0,v)-x^\infty , {\tilde{v}}(t):=v(t)-v^\infty \) and \({\tilde{f}}(z):=f(z+y^\infty -v^\infty )-f(y^\infty -v^\infty )\), a routine calculation shows that \({\tilde{x}}\) satisfies
Consequently, writing \(w:=B\big [f(C{\tilde{x}}-{\tilde{v}})- f(C{\tilde{x}})\big ]\), it follows that
and we note that (5.2) is a forced Lur’e system of the form (1.1). Note that the hypotheses on f combined with Lemma 4.2 guarantee that there exists \(\alpha \in {{\mathcal {K}}}_\infty \) such that \(\Vert {\tilde{f}}(z)-Kz\Vert \le \gamma \Vert z\Vert -\alpha (\Vert z\Vert )\) for all \(z\in {\mathbb {R}}^p\). Consequently, by Theorem 2.1, the equilibrium pair (0, 0) of (5.2) is ISS. Moreover, hypothesis (C) implies that
showing that \(w(t)\rightarrow 0\) as \(t\rightarrow \infty \) (note that \(\gamma <\infty \) by hypothesis). An application of Proposition 2.2 now shows that \({\tilde{x}}(t)\rightarrow 0\) as \(t\rightarrow \infty \) and thus, \({\hat{x}}(t;x^0,v)\rightarrow x^\infty \) as \(t\rightarrow \infty \).
It remains to show that \(y^\infty =Cx^\infty \). To see this, note that \(Cx^\infty =\mathbf{G}_K(0)(f(y^\infty -v^\infty )-Ky^\infty )\). Hence,
and so,
But \(F_K(y^\infty -v^\infty )=-(I+\mathbf{G}_K(0)K)v^\infty \), implying that \(y^\infty =Cx^\infty \). \(\square \)
6 CICS properties for non-negative Lur’e systems
In this section, we study non-negative Lur’e systems, which, as has already been indicated in Sect. 1, arise naturally in a variety of applied contexts, such as population dynamics and chemical reaction models, cf. [6, 36, 37, 44]. We will restrict attention to models with scalar feedback f (\(m=p=1\) and f is a scalar function), that is, we consider forced Lur’e systems of the form
so that, in particular, the linear system \((A,b,c^\mathrm{T})\) is a single-input, single-output (SISO) system. We assume that the following positivity conditions hold:
- (P1):
-
\(A\in {\mathbb {R}}^{n\times n}\) is Metzler and \(b,c\in {\mathbb {R}}_+^n, b,c >0\),
- (P2):
-
\(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) is locally Lipschitz.
Furthermore, we only consider non-negative control (forcing, input) functions, that is, \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}_+^n)\).
As before, we denote the unique maximally defined forward solution of the initial-value problem (6.1) by \(x(\cdot \,;x^0,v)\). It is well known that if (P1) and (P2) hold, then for all non-negative initial states \(x^0\in {\mathbb {R}}_+^n\) and \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}_+^n)\), the solution \(x(t;x^0,v)\) remains in the non-negative orthant \({\mathbb {R}}_+^n\) for all \(t\in [0,\omega )\), where \([0,\omega ), 0<\omega \le \infty \) denotes the maximal interval of existence. If \(\omega <\infty \), then \(\Vert x(t;x^0,v)\Vert \rightarrow \infty \) as \(t\rightarrow \omega \). If (P1) and (P2) hold, then we will refer to (6.1) as a non-negative Lur’e system.
For later purposes, we introduce a further positivity assumption on the linear system \((A,b,c^\mathrm{T})\).
- (P3):
-
The matrix \(A+bc^\mathrm{T}\) is irreducible.
Note that \(A+bc^\mathrm{T}\) is irreducible if, and only, if \(A+kbc^\mathrm{T}\) is irreducible for every \(k>0\).
Let \(s \mapsto \mathbf{G}(s)=c^\mathrm{T}(sI-A)^{-1}b\) denote the transfer function of the linear SISO system \((A,b,c^\mathrm{T})\). A proof of the following result can be found in [6].
Proposition 6.1
If A is Hurwitz and (P1) holds, then
Under the additional assumption that (P3) is satisfied we have
It follows from Proposition 6.1 that if A is Hurwitz, (P1) holds and (A, b) is controllable or \((c^\mathrm{T},A)\) is observable, then \(\mathbf{G}(0)>0\).
Theorem 6.2
Let \(Y\subseteq {\mathbb {R}}_+\) be nonempty and assume that (P1) and (P2) hold and A is Hurwitz. Set \(\gamma :=1/\mathbf{G}(0)\) (where \(\gamma :=\infty \) if \(\mathbf{G}(0)=0\)) and assume further that
and
Then the following statements hold.
-
1.
The map
$$\begin{aligned} F:{\mathbb {R}}_+\rightarrow {\mathbb {R}},\quad z\mapsto z-\mathbf{G}(0)f(z) \end{aligned}$$(6.4)has the following properties : \({\mathbb {R}}_+\subseteq F({\mathbb {R}}_+)\) and \(\# F^{-1}(z)=1\) for every \(z\in {\mathbb {R}}\) such that \(F^{-1}(z)\cap Y\not =\emptyset \).
-
2.
Let \(v^\infty \in {\mathbb {R}}_+\) and assume that \(F^{-1}(-c^\mathrm{T}A^{-1}v^\infty ) \cap Y\not =\emptyset \). Then, \(\# F^{-1}(-c^\mathrm{T}A^{-1}v^\infty )=1\) and, for all \(x^0\in {\mathbb {R}}^n\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}_+^n)\) such that \(\lim _{t\rightarrow \infty } v(t)=v^\infty \),
$$\begin{aligned} \lim _{t\rightarrow \infty }x(t;x^0,v)=-A^{-1}(bf(y^\infty )+v^\infty ) =:x^\infty \in {\mathbb {R}}_+^n, \end{aligned}$$where \(\{y^\infty \}=F^{-1}(-c^\mathrm{T}A^{-1}v^\infty )\) and \(x^\infty \) satisfies \(c^\mathrm{T}x^\infty =y^\infty \ge 0\).
Proof
We extend f to \({\mathbb {R}}\) by defining
Using (6.2), it is straightforward to show that
Consequently,
Furthermore, by (6.3),
Defining \({\tilde{F}}:{\mathbb {R}}\rightarrow {\mathbb {R}}\) by \(F(z)=z-\mathbf{G}(0){\tilde{f}}(z)\), an application of Proposition 4.1 shows that \({\tilde{F}}\) is surjective and
Now \({\tilde{F}}(z)<-\mathbf{G}(0)f(0)\le 0\) for all \(z<0\) and so surjectivity of \({\tilde{F}}\) implies that \({\mathbb {R}}_+\subseteq {\tilde{F}}({\mathbb {R}}_+)=F({\mathbb {R}}_+)\). Moreover, let \(z\in {\mathbb {R}}\) be such that \(F^{-1}(z)\cap Y\not =\emptyset \). If \(w\in F^{-1}(z)\subseteq {\mathbb {R}}_+\), then \(z=F(w)={\tilde{F}}(w)\), and so \(F^{-1}(z) \subseteq {\tilde{F}}^{-1}(z)\). Consequently, \({\tilde{F}}^{-1}(z)\cap Y\not =\emptyset \), whence, by (6.7), \(\# F^{-1}(z)=\#{\tilde{F}}^{-1}(z)=1\), completing the proof of statement (1).
To prove statement (2), let \(v^\infty \in {\mathbb {R}}_+\) be such that \(F^{-1}(-c^\mathrm{T}A^{-1}v^\infty ) \cap Y\not =\emptyset \). It follows from the proof of statement (1) that
Let \(x^0\in {\mathbb {R}}_+^n\) and let \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}_+^n)\) be such that \(\lim _{t\rightarrow \infty } v(t)=v^\infty \). Setting \(x(t):=x(t;x^0,v)\), it is clear that \(x(t)\in {\mathbb {R}}_+^n\) for \(t\ge 0\), implying that \(c^\mathrm{T}x(t) \ge 0\) for all \(t\ge 0\). Consequently, x is a solution of
Appealing to (6.5), (6.6) and (6.8), an application of statement (2) of Theorem 4.3 to the Lur’e system (6.9) then shows that
and
where \(\{y^\infty \}={\tilde{F}}^{-1}(-c^\mathrm{T}A^{-1}v^\infty )\). By hypothesis, \(F^{-1}(-c^\mathrm{T}A^{-1}v^\infty )\cap Y\not =\emptyset \) and thus, invoking (6.8) and (6.10), we obtain that
Finally, since \(-c^\mathrm{T}A^{-1}v^\infty \ge 0\), we have \(y^\infty \ge 0\), implying that \(f(y^\infty )={\tilde{f}}(y^\infty )\) and \(\{y^\infty \}=F^{-1}(-c^\mathrm{T}A^{-1}v^\infty )\). In particular, the right-hand side of (6.11) is equal to \(-A^{-1}\big (b f(y^\infty )+v^\infty \big )\) and the proof is complete. \(\square \)
As an immediate consequence of Theorem 6.2 we obtain the following result.
Corollary 6.3
Assume that (P1) and (P2) hold and A is Hurwitz. Set \(\gamma :=1/\mathbf{G}(0)\) (where \(\gamma :=\infty \) if \(\mathbf{G}(0)=0\)) and assume further that
and (6.3) is satisfied. Then, for every \(v^\infty \in {\mathbb {R}}_+^n, \# F^{-1}(-c^\mathrm{T}A^{-1}v^\infty )=1,\) with F given by (6.4), and the non-negative Lur’e system (6.1) has the CICS property : for all \(x^0\in {\mathbb {R}}_+^n\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}_+^n)\) with \(\lim _{t\rightarrow \infty } v(t)=v^\infty ,\)
where \(\{y^\infty \}=F^{-1}(-c^\mathrm{T}A^{-1}v^\infty )\).
The following lemma (which is an immediate consequence of the mean-value theorem for differentiation) provides a sufficient condition for (6.12) to hold.
Lemma 6.4
Assume that \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) is continuously differentiable and let \(\Delta \subseteq {\mathbb {R}}_+\) be a subset which does not have any accumulation points. If
then (6.12) holds for all \((\xi ,z)\in {\mathbb {R}}_+\times {\mathbb {R}}_+\) such that \(z\not =\xi \).
Example 6.5
Non-negative Lur’e systems of the form (6.1) with
where \(a_i>0\) for all \(i\in \{1,\ldots , 2n-1\}\) and \(b_1>0\), arise in both, population modelling [12] and reaction kinetics, see, for example, [28, Section 7.2]. Obviously, A is Metzler and Hurwitz. In a population dynamics context, the \(a_{2k-1}\) represent mortality rates, the \(a_{2k}\) represent growth rates into the next stage class and f models nonlinear recruitment. The function v could model, for example, immigration effects.
Here we consider the following specific example of the above structure.
Then,
and a routine argument shows that
whence \(\gamma =1/\Vert \mathbf{G}\Vert _{H^\infty }=1/2\). We consider the non-negative Lur’e system
for three different nonlinearities \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\).
-
(a)
Let \(f(z)=z/(z+2)\) for \(z\ge 0\). Then, \(f'(z)=2(z+2)^{-2}\) and so,
$$\begin{aligned} f'(0)=\frac{1}{2}\quad \hbox {and}\quad f'(z)<\frac{1}{2},\ \forall \,z>0. \end{aligned}$$By Lemma 6.4, condition (6.12) holds. Furthermore, (6.3) is trivially satisfied. Consequently, Corollary 6.3 guarantees that (6.14) has the CICS property.
-
(b)
Let \(f(z)=1/(z+2)\) for \(z\ge 0\). Then, \(f'(z)=-(z+2)^{-2}\), and, arguing as in part (a), we see that (6.14) has the CICS property.
a State components generated by input signal shown in b and given by (6.15). The non-zero initial states \(x^0\) have been chosen randomly
Figure 4a displays numerical simulations of the state trajectories generated by the input signals \(v^1\) and \(v^2\) given by
where \(\lfloor z \rfloor \in {\mathbb {N}}_0\) denotes the largest integer less or equal to \(z\in {\mathbb {R}}_+\) and the “switching function” \(S:{\mathbb {R}}_+\rightarrow \{0,1\}\) is defined by
The functions \(w_1\) and \(w_2\) are plotted in Fig. 4b. Obviously, \(w_1(t)\rightarrow 1\) and \(w_2(t)\rightarrow 1\) as \(t\rightarrow \infty \), and so
By the CICS property, the limit
exists, is independent of \(j\in \{1,2\}\) and the initial condition \(x^0\) and is given by \(x^\infty =-A^{-1}\big (bf(y^\infty )+v^\infty \big )\), where \(\{y^\infty \}=F^{-1}(-c^\mathrm{T}A^{-1}v^\infty )\) (see Corollary 6.3). The condition for \(y^\infty \) can be expressed in the form
which is a quadratic equation in \(y^\infty \) and has non-negative solution \(y^\infty = 1.5616\). Now \(x^\infty \) can be computed and we obtain
see Fig. 4a for an illustration.
-
(c)
Let \(f(z)=2z/(z+1)\) for \(z\ge 0\), in which case
$$\begin{aligned} f(z)-f(\xi )=\frac{2(z-\xi )}{(z+1)(\xi +1)}\quad \forall \, (\xi ,z)\in {\mathbb {R}}_+\times {\mathbb {R}}_+. \end{aligned}$$Note that, for any \(\xi \in [0,3]\), there exists \(z\ge 0, z\not =\xi \), such that
$$\begin{aligned} \left| \frac{f(z)-f(\xi )}{z-\xi }\right| \ge \frac{1}{2}=\gamma . \end{aligned}$$In particular, for \(\xi =3\):
$$\begin{aligned} \frac{f(3)}{3}=\frac{f(0)-f(3)}{0-3}=\frac{1}{2}=\gamma . \end{aligned}$$On the other hand, for every \(\xi >3\):
$$\begin{aligned} \left| \frac{f(z)-f(\xi )}{z-\xi }\right| <\frac{1}{2}=\gamma \quad \forall \,z\ge 0. \end{aligned}$$It is obvious that \(z/2-f(z)\rightarrow \infty \) as \(z\rightarrow \infty \), and so, Theorem 6.2, with \(Y:=(3,\infty )\), can be applied to (6.14). To this end, note that the function \(F:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) is given by
$$\begin{aligned} F(z)=z-\mathbf{G}(0)f(z)=z-\frac{4z}{z+1}, \end{aligned}$$and so, \(F(Y)=(0,\infty )\). Now,
$$\begin{aligned} A^{-1}:=\begin{pmatrix} -1 &{}\quad 0 &{}\quad 0\\ -2 &{}\quad -2 &{}\quad 0\\ -1 &{}\quad -1 &{}\quad -1/2 \end{pmatrix}, \end{aligned}$$and thus, \(-c^\mathrm{T}A^{-1}=(1,1,1/2)\), showing that
$$\begin{aligned} -c^\mathrm{T}A^{-1}v^\infty >0\quad \forall \,v^\infty \in {\mathbb {R}}_+^3\backslash \{0\}. \end{aligned}$$Consequently,
$$\begin{aligned} F^{-1}(-c^\mathrm{T}A^{-1}v^\infty )\cap Y\not =\emptyset \quad \forall \,v^\infty \in {\mathbb {R}}_+^3\backslash \{0\}. \end{aligned}$$Theorem 6.2 guarantees that, for every \(v^\infty \in {\mathbb {R}}_+^3\backslash \{0\}\), there exists \(x^\infty \in {\mathbb {R}}_+^3\) such that \(\lim _{t\rightarrow \infty }x(t;x^0,v)=x^\infty \) for all \(x^\infty \in {\mathbb {R}}_+^3\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}_+^3)\) with \(\lim _{t\rightarrow \infty } v(t)=v^\infty \).
To consider a specific numerical example, let
in which case, \(-c^\mathrm{T}A^{-1}v^\infty =1\). Now \(F^{-1}(1)=\{2+\sqrt{5}\}\), and so \(y^\infty =2+\sqrt{5}, f(y^\infty )=(1+\sqrt{5})/2\), and
Finally, we comment on input functions v which converge to 0: there does not exist \(x^\infty \) such that \(\lim _{t\rightarrow \infty }x(t;x^0,v)=x^\infty \) for all \(x^0\in {\mathbb {R}}_+^3\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}_+^3)\) with \(\lim _{t\rightarrow \infty } v(t)=0\). Indeed, this follows from the fact that, for \(v=0\), the system (6.14) has two equilibria in \({\mathbb {R}}_+^3\), namely (0, 0, 0) and \((3,6,3)^\mathrm{T}\). Also note that \(F^{-1}(0)=\{0,3\}\) and thus \(\#F^{-1}(0)>1\) (cf. Proposition 3.1). \(\Diamond \)
In the context of the Lur’e system discussed in part (c) of Example 6.5, it is interesting to note that the non-zero equilibrium \(x^*=(3,6,3)^\mathrm{T}\) of the uncontrolled system is asymptotically stable with region of attraction equal to \({\mathbb {R}}_+^3\backslash \{0\}\). This gives rise to the following question: does \(x(t;x^0,v)\) converge to \(x^*\) for all non-zero initial conditions \(x^0\in {\mathbb {R}}_+^3\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}_+^3)\) with \(\lim _{t\rightarrow \infty } v(t)=0\)? We shall now state and prove a CICS result which implies that the answer to the question is “yes”.
Theorem 6.6
Assume that (P1)–(P3) hold and A is Hurwitz. Set \(\gamma :=1/\mathbf{G}(0)\) and assume further that \(f(0)=0,\) there exists \(y^*>0\) such that \(f(y^*)=\gamma y^*,\) (6.3) is satisfied,
and
Then the following statements hold.
-
1.
The points 0 and \(x^*:=-\gamma y^*A^{-1}b\) are equilibria of the uncontrolled system \(\dot{x}=Ax+bf(c^\mathrm{T}x)\).
-
2.
The map
$$\begin{aligned} F^*:[y^*,\infty )\rightarrow {\mathbb {R}}_+,\quad z\mapsto z-\mathbf{G}(0)f(z) \end{aligned}$$is a bijection.
-
3.
The non-negative Lur’e system (6.1) has the following “quasi-CICS” property : for all \(x^0\in {\mathbb {R}}_+^n,\) all \(v^\infty \in {\mathbb {R}}_+^n\) and all \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}_+^n)\) such that \(\Vert x^0\Vert +\Vert v\Vert _{L^\infty }>0\) and \(\lim _{t\rightarrow \infty } v(t)=v^\infty ,\)
$$\begin{aligned} \lim _{t\rightarrow \infty }x(t;x^0,v)=-A^{-1}(bf(y^\infty )+v^\infty ) =x^\infty \in {\mathbb {R}}_+^n, \end{aligned}$$where \(y^\infty =F^{*\,-1}(-c^\mathrm{T}A^{-1}v^\infty )\). In particular, if \(v^\infty =0,\) then \(y^\infty =y^*\) and \(x^\infty =x^*=-\gamma y^*A^{-1}b\).
Proof
Since \(f(0)=0\), it is obvious that 0 is an equilibrium of \(\dot{x}=Ax+bf(c^\mathrm{T}x)\). Invoking the hypothesis that \(f(y^*)=\gamma y^*\), a straightforward calculation shows that \(x^*\) is also an equilibrium of \(\dot{x}=Ax+bf(c^\mathrm{T}x)\), completing the proof of statement (1).
To prove statements (2) and (3), let \(x^0,v^\infty \in {\mathbb {R}}_+^n\) and \(v\in L^\infty ({\mathbb {R}}_+,{\mathbb {R}}_+^n)\) be such that \(\Vert x^0\Vert +\Vert v\Vert _{L^\infty }>0\) and \(\lim _{t\rightarrow \infty } v(t)=v^\infty \). We consider two cases: \(x^0\not =0\) and \(x^0=0\).
Case 1: \(x^0\not =0\).
Invoking (P1)–(P3) and conditions (6.16) and (6.17), it follows from [6, Proposition 4.12] that there exist \({\varepsilon }\in (0,y^*)\) and \(\tau \ge 0\) such that
Consider
and
and note that, since \(f(y^*)=\gamma y^*\),
In particular, \({\tilde{F}}(0)=0\) and, by (6.3) and (6.17),
implying that \({\tilde{F}}({\mathbb {R}}_+)={\mathbb {R}}_+\) and so
Next, we prove that
To see this, let \(\xi \ge 0\). Then, invoking (6.17), we obtain that, for non-zero \(z\ge -(\xi +y^*)+{\varepsilon }\),
Furthermore, for \(z<-(\xi +y^*)+{\varepsilon }\), we have \(|z|=-z>\xi +y^*-{\varepsilon }>0\) and so
where the last inequality follows from (6.17). Therefore, (6.21) holds. Consequently,
Moreover, by (6.3),
Setting \(x^*:=-A^{-1}bf(y^*)=-\gamma y^*A^{-1}b\) and
we have, by (6.18),
where we have used that \(c^\mathrm{T}x^*=y^*\). Consequently,
and so, \({\tilde{x}}\) satisfies
where, as before, \(\Lambda _\tau \) denotes the left-shift by \(\tau \). Appealing to (6.20), (6.22) and (6.23), we may apply Theorem 4.3 (with \(K=0\) and \(Y={\mathbb {R}}_+\)) in the context of the controlled Lur’e system (6.24) and obtain that
and
where \(\{{\tilde{y}}^\infty \}={\tilde{F}}^{-1}(-c^\mathrm{T}A^{-1}v^\infty \}\). Equations (6.19), (6.20) and (6.25) show that \(F^*\) is a bijection. Finally, setting \(y^\infty :={\tilde{y}}^\infty +y^*\), we obtain from (6.19), that \(y^\infty =F^{*\,-1}(-c^\mathrm{T}A^{-1}v^\infty )\), and, by (6.26),
as \(t\rightarrow \infty \).
Case 2: \(x^0=0\).
Then, by hypothesis, \(\Vert v\Vert _{L^\infty }>0\) and thus, there exists \(t_0\ge 0\) such that
The function \(\zeta \) defined by \(\zeta (t):=x(t+t_0;0,v)\) satisfies
and so, by case 1,
completing the proof. \(\square \)
Example 6.7
Here we re-visit part (c) of Example 6.5: A, b and c are given by (6.13) and \(f(z)=2z/(z+1)\) for all \(z\ge 0\). It is readily verified that \(A+bc^\mathrm{T}\) is irreducible, that is, condition (P3) is satisfied. We recall that the uncontrolled Lur’e system (6.14) has two equilibria, namely 0 and \(x^*=(3,6,3)^\mathrm{T}\) (the latter being asymptotically stable with domain of attraction \({\mathbb {R}}^{3}_+\backslash \{0\}\), as follows from [6]) and that \(\gamma =1/\Vert G\Vert _{H^\infty }=1/2\). We note that \(f(3)=3/2=3\gamma , \liminf _{z\rightarrow 0}(f(z)/z)=f'(0)=2\), and
We may now apply Theorem 6.6 (with \(y^*=3\)) and obtain that the Lur’e system under consideration has the quasi-CICS property (in the sense of Theorem 6.6).
Consider the input signals \(v^1\) and \(v^2\) given by \(v^j(t)=w_j(t)(0,1,0)^\mathrm{T}\), where
see panel (b) of Fig. 5 for an illustration. Note that \(v^1(t) \rightarrow (0,1,0)^\mathrm{T}\) and \(v^2(t)\rightarrow (0,0,0)^\mathrm{T}\) as \(t\rightarrow \infty \). By Theorem 6.6, for all \(x^0\in {\mathbb {R}}^3_+, x(t;x^0,v^1)\rightarrow x^\infty \) and \(x(t;x^0,v^2)\rightarrow x^*\) as \(t\rightarrow \infty \), where
Panel (a) of Fig. 5 shows plots of \(\Vert x(t;x^0,v^1) - x^\infty \Vert _2\) (solid line) and \(\Vert x(t;x^0,v^2) - x^*\Vert _2\) (dotted line) for \(x^0=0\). In particular, we see that the state trajectory \(x(t;0,v^2)\) is at the zero equilibrium for \(0 \le t \le 10\) since the input \(v^2\) is zero in this time interval. On the interval \((10,10+25\pi /2), v^2\) is positive and correspondingly, \(x(t;0,v^2)\) moves away from the origin and eventually converges to \(x^*\). \(\Diamond \)
We state a lemma which provides a sufficient condition for (6.17) to hold. The proof of the lemma is given in the Appendix.
Lemma 6.8
Assume that \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) is continuously differentiable, \(f(0)=0, f'(z)\ge 0\) for all \(z\ge 0, f'(0)>\gamma , f'\) is non-increasing and \(\lim _{z\rightarrow \infty }f'(z)<\gamma \). Then there exists \(y^*>0\) such that \(f(y^*)=\gamma y^*\) and
The next lemma specifies an interval such that, for all \(\gamma \) in that interval, the so-called Ricker nonlinearity, relevant in the context of models from ecology and population dynamics, satisfies condition (6.17). As with Lemma 6.8, the proof of Lemma 6.9 may be found in the Appendix.
Lemma 6.9
Let \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) be given by
where \(\rho >0\) is a parameter, and let \(\gamma \in [\mathrm{e}^{-2},1)\). Then \(y^* := 1/\rho \ln (1/\gamma ) >0\) is the unique positive solution of \(f(y^*)=\gamma y^*\) and (6.17) holds.
Example 6.10
Consider the Lur’e system (6.14) in Example 6.5, with A, b and c given by (6.13). Let \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}_+\) be the Ricker nonlinearity given by (6.27), where \(\rho >0\) is fixed, but arbitrary. Then conditions (P1)–(P3) hold, A is Hurwitz and \(\gamma =1/\Vert \mathbf{G}\Vert _{H^\infty }=1/2\). Furthermore,
and, by Lemma 6.9, (6.17) is satisfied. Consequently, the Lur’e system (6.14) has the quasi-CICS property in the sense of Theorem 6.6. \(\Diamond \)
7 Conclusions
We have considered the CICS property for forced Lur’e systems and have derived a number of necessary and sufficient conditions for CICS. Our motivation has been to study to what extent the appealing CICS property exhibited by linear systems extends to Lur’e systems, and, more broadly, to investigate the effect of convergent additive forcing on the state and output of Lur’e systems. The CICS property for Lur’e systems leads to explicit formulae for the resulting asymptotic state \(x^\infty \) and output \(y^\infty \) in terms of the input limit \(v^\infty \) and enabled us to extend the concept of steady-state gain to Lur’e systems. The theory developed is in the spirit of absolute stability theory and makes use of recent ISS results for Lur’e systems [36]. In particular, several of our sufficient conditions for CICS are reminiscent of the complex Aizerman conjecture, the circle criterion and nonlinear ISS small gain theorems. Finally, for non-negative Lur’e systems, we have derived a “quasi CICS” property which applies to systems which when uncontrolled have two equilibria (one of which is the origin), a common scenario in the context of biological, ecological and chemical models. The proof of our quasi CICS result rests on a recent persistence result [6] for non-negative Lur’e systems.
In future work on forced Lur’e systems, we are planning to investigate the relationship between the concepts of CICS, convergent systems [30] and various notions of incremental stability [2]. One aim is to derive sufficient conditions for the response to (almost) periodic inputs to be asymptotically (almost) periodic.
Notes
As an element in \(L^\infty ({\mathbb {R}}_+,{\mathbb {R}}^n)\), strictly speaking, v is not a function, but an equivalence class of functions. Therefore, we should clarify what we mean by

We say that (\(*\)) holds, if \(\Vert v-v^\infty \theta \Vert _{L^\infty (t,\infty )} \rightarrow 0\) as \(t\rightarrow \infty \), or equivalently, if there exists a representative w in the equivalence class v such that \(w(t)\rightarrow v^\infty \) as \(t\rightarrow \infty \).
References
Aminzarey Z, Sontag ED (2014) Contraction methods for nonlinear systems: a brief introduction and some open problems. In: Proceedings of 53rd IEEE conference on decision and control (CDC), Los Angeles, California, pp 3835–3847
Angeli D (2002) A Lyapunov approach to incremental stability properties. IEEE Trans Autom Control 47:410–421
Angeli D, De Leenheer P, Sontag ED (2004) A small-gain theorem for almost global convergence of monotone systems. Syst Control Lett 52:407–414
Arcak M, Teel A (2002) Input-to-state stability for a class of Lurie systems. Automatica 38:1945–1949
Berman A, Plemmons RJ (1994) Nonnegative Matrices in the Mathematical Sciences. Classics in Applied Mathematics. SIAM, Philadelphia
Bill A, Guiver C, Logemann H, Townley S (2016) Stability of non-negative Lur’e systems. SIAM J Control Optim 54:1176–1211
Chaillet A, Pogromsky AY, Rüffer BS (2013) A Razumikhin approach for the incremental stability of delayed nonlinear systems. In: Proceedings of 52nd IEEE conference on decision and control (CDC), Florence, Italy, pp 1596–1601
Courchamp F, Berec L, Gascoigne J (2008) Allee effects in ecology and conservation. Environ Conserv 36:80–85
Dashkovskiy SN, Efimov DV, Sontag ED (2011) Input-to-state stability and allied system properties. Autom Remote Control 72:1579–1614
Dashkovskiy SN, Rüffer BS, Wirth FR (2007) An ISS small gain theorem for general networks. Math Control Signals Syst 19:93–122
Desoer CA, Vidyasagar M (1975) Feedback systems: input–output properties. Academic Press, New York
Gouzé JL, Rapaport A, Hadj-Sadok HZ (2000) Interval observers for uncertain biological systems. Ecol Model 133:45–56
Haddad WM, Bernstein DS (1993) Explicit construction of quadratic Lyapunov functions for the small gain, positivity, circle, and Popov theorems and their application to robust stability (part I: continuous-time theory). Int J Robust Nonlinear Control 3:313–339
Haddad WM, Chellaboina V (2008) Nonlinear dynamical systems and control. Princeton University Press, Princeton
Haddad WM, Chellaboina V, Hui Q (2010) Non-negative and compartmental dynamical systems. Princeton University Press, Princeton
Hinrichsen D, Pritchard AJ (1986) Stability radius for structured perturbations and the algebraic Riccati equation. Syst Control Lett 8:105–113
Hinrichsen D, Pritchard AJ (1992) Destabilization by output feedback. Differ Integral Equ 5:357–386
Hinrichsen D, Pritchard AJ (2005) Mathematical systems theory I. Springer, Berlin
Jayawardhana B, Logemann H, Ryan EP (2009) Input-to-state stability of differential inclusions with applications to hysteretic and quantized feedback systems. SIAM J Control Optim 48:1031–1054
Jayawardhana B, Logemann H, Ryan EP (2011) The circle criterion and input-to-state stability: new perspectives on a classical result. IEEE Control Syst Mag 31:32–67
Jiang ZP, Teel AR, Praly L (1994) Small-gain theorem for ISS systems and applications. Math Control Signals Syst 7:95–120
Kellet CM (2014) A compendium of comparison function results. Math Control Signals Syst 26:339–374
Khalil HK (2002) Nonlinear systems, 3rd edn. Prentice-Hall, Upper Saddle River
Liberzon MR (2006) Essays on absolute stability theory. Autom Remote Control 67:1610–1644
Logemann H, Ryan EP (2003) Non-autonomous systems: asymptotic behaviour and weak invariance principles. J Differ Equ 189:440–460
Luenberger DG (1979) Introduction to dynamical systems. Wiley, New York
Mayer CD (2000) Matrix analysis and applied linear algebra. SIAM, Philadelphia
Murray JD (2002) Mathematical biology I, 3rd edn. Springer, New York
Partington JP (2004) Linear operators and linear systems. Cambridge University Press, Cambridge
Pavlov A, van de Wouw N, Nijmeijer H (2006) Uniform output regulation of nonlinear systems: a convergent dynamics approach. Birkhäuser Boston, Boston
Pogromsky AY, Matveev MS (2013) A non-quadratic criterion for stability of forced oscillations. Syst Control Lett 62:408–412
Renardy M, Rogers RC (1993) An introduction to partial differential equations. Springer, New York
Rüffer BS, van de Wouw N, Mueller M (2013) Convergent systems vs. incremental stability. Syst Control Lett 62:277–285
Ryan EP, Sontag ED (2006) Well-defined steady-state response does not imply CICS. Syst Control Lett 55:707–710
Sandberg IW, Kramer Johnson K (1992) Steady-state errors in nonlinear control systems. IEEE Trans Autom Control 37:1985–1989
Sarkans E, Logemann H (2015) Input-to-state stability for Lur’e systems. Math Control Signals Syst 27:439–465
Smith HL, Thieme HR (2013) Persistence and global stability for a class of discrete time structured population models. Discrete Contin Dyn Syst 33:4627–4646
Sontag ED (1989) Smooth stabilization implies coprime factorization. IEEE Trans Autom Control 34:435–443
Sontag ED (1998) Comments on integral variants of ISS. Syst Control Lett 34:93–100
Sontag ED (2002) Asymptotic amplitudes and Cauchy gains: a small-gain principle and an application to inhibitory biological feedback. Syst Control Lett 47:167–179
Sontag ED (2003) A remark on the converging-input converging-state property. IEEE Trans Autom Control 48:313–314
Sontag ED (2006) Input to state stability: basic concepts and results. In: Nistri P, Stefani G (eds) Nonlinear and optimal control theory. Springer, Berlin, pp 163–220
Sontag ED, Ingalls B (2002) A small-gain theorem with applications to input/output systems, incremental stability, detectability, and interconnections. J Frankl Inst 339:211–229
Townley S, Rebarber R, Tenhumberg B (2012) Feedback control systems analysis of density dependent population dynamics. Syst Control Lett 61:309–315
Vidyasagar M (1993) Nonlinear systems analysis, 2nd edn. Prentice-Hall, Englewood Cliffs
Yakubovich VA (1964) Matrix inequalities method in stability theory for nonlinear control systems: I. Absolute stability of forced vibrations. Autom Remote Control 7:905–917
Yakubovich VA, Leonov GA, Gelig AKh (2004) Stability of stationary sets in control systems with discontinuous nonlinearities. World Scientific, Singapore
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by the UK EPSRC—Engineering and Physical Sciences Research Council—(Grant EP/I019456/1).
Appendix A
Appendix A
In this Appendix, we give proofs of Theorem 2.1, Lemma 6.8 and Lemma 6.9. We also derive the inclusions in (3.1).
Proof of Theorem 2.1
Since \(K\in {\mathbb {S}}_{\mathbb {R}}(A,B,C)\), the matrix \(A_K=A+BKC\) is Hurwitz. The structured complex stability radius of \(A_K\) with respect to the weights B and C is defined by
It is well known [16, 18] that
To prove statements (1) and (2), let \(x^0\in {\mathbb {R}}^n\) and write \(x(t):=x(t;x^0,0)\). Obviously, x satisfies \(\dot{x}=A_Kx+Bf_K(Cx)\), where \(f_K:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) is defined by
By hypothesis, \(\Vert f_K(z)\Vert <\gamma \Vert z\Vert \) for all non-zero \(z\in {\mathbb {R}}^p\) and thus the claim follows from (A.1) and [18, Theorem 5.6.22] or [17, Corollary 3.15]. Moreover, by (A.1), \({\mathbb {B}}_{\mathbb {C}}(K,\gamma )\subseteq {\mathbb {S}}_{\mathbb {C}}(A,B.C)\), and thus, statement (2) is a consequence of [36, Theorem 3.2].
We proceed to prove statement (3). To this end, let \(f:{\mathbb {R}}^p\rightarrow {\mathbb {R}}^m\) be locally Lipschitz and such that \(f(0)=0\). We show that the equilibrium pair (0, 0) of (1.1) is ISS. Let \(x^0\in {\mathbb {R}}^n\) and \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}^n)\) be arbitrary and set \(x(t):=x(t;x^0,v)\). Then \(\dot{x}=A_Kx+Bf_K(Cx)+v\), where \(f_K\) is defined by (A.2). Thus, by the variation-of-parameters formula,
where \(0<\omega \le \infty \) and \([0,\omega )\) is the maximal interval of existence of the forward solution x. Note that, since f is not necessarily affine linearly bounded, finite escape time cannot be ruled out at this stage. Now \(C\mathrm{e}^{A_K t}B\) is the inverse Laplace transform of \(\mathbf{G}_K\) and hence \(C\mathrm{e}^{A_K t}B=0\) for all \(t\in {\mathbb {R}}\). Consequently, it follows from (A.3),
Since \(A_K\) is Hurwitz, it follows that Cx is bounded on any bounded subinterval of \([0,\omega )\) and thus, by (A.3), x is also bounded on any bounded subinterval of \([0,\omega )\). We may, therefore, conclude that \(\omega =\infty \).
By the Hurwitz property of \(A_K\), there exist \(M\ge 1\) and \(\mu >0\) such that
Combining this with (A.4) shows that there exist positive constants \(M_1\) and \(M_2\) such that, for all \(x^0\in {\mathbb {R}}^n\) and \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}^n)\),
Moreover, let \(\eta \in {{\mathcal {K}}}\) be such that
The existence of such a function \(\eta \) follows from the continuity of \(f_K\) and the fact that \(f_K(0)=0\). Invoking (A.5) and (A.6), we obtain
where the \({{\mathcal {K}}}\)-functions \(\eta _1\) and \(\eta _2\) are defined by \(\eta _1(s)=\eta (2M_1s)\) and \(\eta _2(s)=\eta (2M_2s)\).
Next we estimate the term \(I(t):=\int _0^t\mathrm{e}^{A_K(t-s)}Bf_K(Cx(s))\mathrm{d}s\). To this end, writing
we note that, by (A.7),
Consequently,
Furthermore,
and therefore, by (A.3),
Hence, defining \(\psi \in {{\mathcal {K}}}{{\mathcal {L}}}\) and \(\varphi \in {{\mathcal {K}}}\) by
respectively, we conclude that, for every \(x^0\in {\mathbb {R}}^n\) and every \(v\in L^\infty _\mathrm{loc}({\mathbb {R}}_+,{\mathbb {R}}^n)\),
showing that the equilibrium pair (0, 0) of (1.1) is ISS. \(\square \)
Proof of (3.1)
To prove the first inclusion, let \(z \in \mathrm{im}\, C\), so that \(z = Cw\) for some \(w \in {\mathbb {R}}^n\). Then
For the proof of the second inclusion assume that \(z \in F_K^{-1}(\mathrm{im}\, C)\), so that \(F_K(z) = C w\), for some \(w \in {\mathbb {R}}^n\). Then
as required. \(\square \)
Proof of Lemma 6.8
It follows immediately from the hypotheses that there exist \(y^*>y_*>0\) such that \(f(y^*)=\gamma y^*, f'(y_*)=\gamma , f'(z)>\gamma \) if \(z\in [0,y_*)\) and \(f'(z)<\gamma \) if \(z>y_*\). We consider two cases.
Case 1: \(\xi \ge y^*\) and \(z>y_*, z\not =\xi \).
In this case,
Case 2: \(\xi \ge y^*\) and \(z\in (0,y_*]\).
Note that, by Case 1, \(|f(y^*)-f(\xi )|\le \gamma |y^*-\xi |\) and thus,
Now
and we conclude that
In both cases we have
completing the proof. \(\square \)
Proof of Lemma 6.9
Note that, as z decreases from \(2/\rho \) to \(0, f(z)/z=\mathrm{e}^{-\rho z}\) increases strictly monotonically from \(\mathrm{e}^{-2}\) to 1. Consequently, for every, \(\gamma \in [\mathrm{e}^{-2},1)\), there exists a unique \(y^*\in (0,2/\rho ]\) such that \(f(y^*)=\gamma y^*\).
To prove that (6.17) holds, we initially assume that \(\gamma \in (\mathrm{e}^{-2},1)\) and deal with the case \(\gamma =\mathrm{e}^{-2}\) separately. We proceed in several steps.
Step 1 A routine calculation shows
Since \(\gamma >\mathrm{e}^{-2}\), we conclude that
and hence, by the mean-value theorem for differentiation,
Step 2 Note that \(f'(z)<\gamma \) for all \(z\in [y^*,2/\rho ]\) (which follows because \(f'(0)>\gamma , f'\) is non-increasing on \([0,2/\rho ]\) and \(f(y^*)=\gamma y^*\)). Since \(f'(z)<0<\gamma \) for all \(z>2/\rho \), we obtain, via the mean-value theorem for differentiation,
Step 3 Let \(\xi \ge y^*\) and \(z\in (0,y^*)\). By (A.9) and (A.10),
Moreover, invoking again (A.9) and using that \(f(z)>\gamma z\), we obtain
and so
Now \(|f(z)-f(\xi )|\le |f(z)-f(y^*)|+|f(y^*)-f(\xi )|\), and thus, by (A.11) and (A.12),
Since \(z<y^*\le \xi \), we have \(|z-y^*|+|y^*-\xi |=|z-\xi |\) and conclude
Step 4 Combining (A.9), (A.10) and (A.13), we arrive at
which is (6.17).
Finally, let us consider the case wherein \(\gamma =\mathrm{e}^{-2}\). Then \(y^*=2/\rho \) and so \(f'(y^*)=f'(2/\rho )=-\mathrm{e}^{-2}=-\gamma \), implying that (A.8) does not hold for \(z=y^*\). We will show that nevertheless (A.9) remains valid in this case. To this end, note that
From the mean-value theorem we immediately obtain that
Let \(z\in (0,y^*)\) and \(\xi \ge y^*\). Then
where we have used (A.15). Yet another application of the mean-value theorem shows that there exists \(\theta \in (z,y^*)\) such that
where the inequality follows from (A.14). Consequently, \(f(z)-f(y^*)<\gamma (y^*-z)\), and so, invoking (A.16), we arrive at \(f(z)-f(\xi )<\gamma (\xi -z)\), or equivalently,
We have now shown that (A.9) still holds in the case wherein \(\gamma =\mathrm{e}^{-2}\). Steps 2–4 remain valid without change and, therefore, we conclude that (6.17) is satisfied in the case under consideration, completing the proof. \(\square \)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bill, A., Guiver, C., Logemann, H. et al. The converging-input converging-state property for Lur’e systems. Math. Control Signals Syst. 29, 4 (2017). https://doi.org/10.1007/s00498-016-0184-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s00498-016-0184-3
Keywords
- Absolute stability
- Circle criterion
- Converging-input converging-state property
- Input-to-state stability
- Lur’e systems
- Non-negative systems