1 Introduction

A growing interest is observed, in the last few decades, on the parametric (Bosq 2000) and nonparametric (Ferraty and Vieu 2006) spatiotemporal data analysis based on infinite-dimensional spatial models. Particularly, the field of Functional Data Analysis (FDA) has been nurtured by various disciplines, including probability in abstract spaces (see, e.g., Ledoux and Talagrand 1991). The most recent contributions are developed in the framework of stochastic partial differential and pseudodifferential equations (see, e.g., Ruiz-Medina 2022). Particularly in the Gaussian random field context, it is well-known that Gaussian measures in Hilbert spaces and associated infinite-dimensional quadratic forms play a crucial role (see Da Prato and Zabczyk 2002). The tools developed have recently been exploited in several statistical papers on spatiotemporal modeling under the umbrella of infinite-dimensional inference, based on statistical analysis of infinite-dimensional multivariate data and stochastic processes (see, e.g., Frías et al. 2022; Ruiz-Medina 2022; Torres-Signes et al. 2021). In particular, statistical distance based approaches are often adopted in hypothesis testing (see, e.g., Ruiz-Medina 2022, where an estimation methodology based on a Kullback–Leibler divergence-like loss operator is proposed in the temporal functional spectral domain). This methodology has been also exploited in structural complexity analysis based on sojourn measures of spatiotemporal Gaussian and Gamma-correlated random fields. Indeed, there exists a vast literature in the context of stochastic geometrical analysis of the sample paths of random fields based on these measures (see, e.g., Bulinski et al. 2012; Ivanov and Leonenko 1989, among others). Special attention has been paid to the asymptotic analysis of long-range dependent random fields (see Leonenko 1999; Leonenko and Olenko 2014; Makogin and Spodarev 2022). Recently, in Leonenko and Ruiz-Medina (2023), new spatiotemporal limit results have been derived to analyze, in particular, the limit distribution of Minkowski functionals, in the context of Gaussian and Chi-Square subordinated spatiotemporal random fields.

The geometrical interpretation of these functionals, which, for instance in 2D, is related to the total area of all hot regions, and the total length of the boundary between hot and cold regions, as well as the Euler–Poincaré characteristic, counting the number of isolated hot regions minus the number of isolated cold regions within the hot regions, has motivated several statistical approaches, adopted, for instance, in the Cosmic Microwave Background (CMB) evolution modeling and data analysis (see, e.g., Marinucci and Peccati 2011).

The present work continues the above-referred research lines in relation to structural complexity analysis of long-range dependent Gaussian and Chi-Square subordinated spatial and spatiotemporal random fields. Indeed, a more general random field framework is considered, defined from the Lancaster–Sarmanov random field class.

The approach adopted here is based on the quantitative assessment in terms of appropriate information-theoretic measures, a framework which has played a fundamental role, with a very extensive related literature, in the probabilistic and statistical characterization and description of structural aspects inherent to stochastic systems arising in a wide variety of knowledge areas. More precisely, the asymptotic behavior, for infinitely increasing distance, of divergence-based Shannon and Rényi mutual information measures, which are formally and conceptually connected to certain forms of ‘complexity’ and ‘diversity’ (see, for instance, Angulo et al. 2021, and references therein), is derived for this random field class. This behavior is characterized by the long-range dependence (LRD) parameter, that in this context determines the global diversity loss, associated with lower values of such a parameter. The deformation parameter \(q \ne 1\) involved in the definition of Rényi mutual information also modulates the power rate of decay of this structural dependence indicator as the distance between the considered spatial location increases. As is well-known, the derived asymptotic analysis results based on Shannon mutual information arise as limiting cases, for \(q \rightarrow 1\), of the ones obtained based on Rényi mutual information. The spatiotemporal case is analyzed in an infinite-dimensional spatial framework. In particular, related spatiotemporal extensions of the Lancaster–Sarmanov random field class, as well as of divergence-based mutual information measures, are formalized under a functional approach. A simulation study is undertaken showing, in particular, that the same asymptotic orders as in the purely spatial case hold for the infinite-dimensional versions of divergence measures here considered (see, e.g., Angulo and Ruiz-Medina 2023).

The main results of this paper, Theorem 1 and 2, illustrate the asymptotic behavior derived in reduction theorems for local means of nonlinear transformation of Gaussian and Chi-Square random fields (see, e.g., Leonenko et al. 2017). Specifically, a suitable scaling depending on the LRD parameter allows convergence in the second Wiener chaos in the case of quadratic transformations of Gaussian random fields. That is the case of Chi-Square subordinated random fields. In our framework this fact is reflected in the convergence to zero of the statistical distance, evaluated from mutual information, according to a power law decay involving the LRD parameter. The asymptotic self-similarity of the family of nonlinear random field models analyzed here allows to establish asymptotic equivalence between the transition rate from spatial dependence to independence and from spatial correlation to uncorrelation, in terms of a power law decay. This fact has also clear implications in the transition to asymptotic spatial linear association between the spatial components of the nonlinear transformation of LRD Gaussian random fields in the family studied. The approach presented has indeed interesting applications in mutual information analysis of nonlinear groundwater stochastic fields; see, e.g., Butera et al. (2018), where these aspects are addressed through the uncertainty coefficient in an alternative modeling framework.

The paper content is structured as follows. Section 2 provides the preliminary elements on the analyzed class of Lancaster–Sarmanov random fields, as well as the introduction of information-complexity measures. The main results derived on the asymptotic large scale behavior of Shannon and Rényi mutual information measures, involving the bivariate distributions of the Lancaster–Sarmanov subordinated random field class studied, are obtained in Sect. 3. These aspects are illustrated in terms of some numerical examples in subsection 3.3. The functional approach to the spatiotemporal case based on an infinite-dimensional spatial framework is addressed in Sect. 4. Final comments, with a reference to open research lines, are given in Sect. 5.

2 Preliminaries

Let \((\Omega , {\mathcal {A}},P)\) be the basic complete probability space, and denote by \({\mathcal {L}}^{2}(\Omega ,{\mathcal {A}},P)\) the Hilbert space of equivalence classes (with respect to P) of zero-mean second-order random variables on \((\Omega , {\mathcal {A}},P)\). Consider \(X=\{ X({\textbf{z}}),\ {\textbf{z}}\in {\mathbb {R}}^{d}\}\) to be a zero-mean spatial homogeneous and isotropic mean-square continuous second-order random field, with correlation function \(\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )=\text{ Corr }\left( X({\textbf{x}}),X({\textbf{y}})\right)\). Assume that the marginal probability distributions are absolutely continuous, having probability density p(u) with support included in (a, b), \(-\infty \le a<b\le \infty\). Let now \(L^{2}((a,b), p(u)du)\) be the Hilbert space of equivalence classes of measurable real-valued functions on the interval (a, b) which are square-integrable with respect to the measure \(\mu (du)=p(u)du\).

2.1 Lancaster–Sarmanov random field class

Assume that there exists a complete orthonormal basis \(\{e_{k},\ k\ge 0\}\), with \(e_{0}\equiv 1\), of the space \(L^{2}((a,b), p(u)du)\) such that

$$\begin{aligned} & \frac{\partial ^{2}}{\partial u\partial v}P\left[ X({\textbf{x}})\le u,X({\textbf{y}})\le v\right] ~ =: ~ p(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert ) \nonumber \\= & p(u)~p(v)~\left[ 1+\sum _{k=1}^{\infty }\gamma ^{k} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{k}(u)~e_{k}(v)\right] , \; \forall {\textbf{x}}, {\textbf{y}} \in {\mathbb {R}}^{d} . \nonumber \\ \end{aligned}$$
(1)

The family of random fields X satisfying the above conditions is known as the Lancaster–Sarmanov random field class (see, e.g., Lancaster 1958; Sarmanov 1963). Gaussian and Gamma-correlated random fields are two important cases within this class, with \(\{e_{k},\ k\ge 0\}\) being given by the (normalized) Hermite polynomial system in the Gaussian case (see, for example, Peccati and Taqqu 2011), and by the generalized Laguerre polynomials in the Gamma-correlated case. An interesting special case of the latter is defined by the Chi-Square random field family.

Remark 1

Equation (1) constitutes a particular case of the more general construction introduced in Sarmanov (1963) involving the series expansion of transition probability functions of Markov processes (e.g., in the particular framework of diffusion processes). This construction is based on the orthonormal polynomials of the infinitesimal generator (respectively, forward operator) in the \(l^{2}(m)\) space of square integrable functions with respect to the invariant measure m. Specifically, in the spirit of this pioneer paper, one can consider the Hilbert–Schmidt integral operator \({\mathcal {K}}\) on \(l^{2}(m)\) with kernel

$$\begin{aligned} K(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )=\frac{p(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{\sqrt{p(u)~p(v)}}, \end{aligned}$$

satisfying

$$\begin{aligned} \int _{a}^{b}\int _{a}^{b}K^{2}(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )p(u)~p(v)~du~dv<\infty . \end{aligned}$$
(2)

Hence, the symmetric kernel

$$\begin{aligned} Q(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )=\frac{p(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{p(u)~p(v)} \end{aligned}$$
(3)

admits the following series expansion (see, e.g., equation (5) in Leonenko et al. 2017):

$$\begin{aligned} Q(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )=\sum _{k=0}^{\infty }r_{k}(\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{k}(u)~e_{k}(v), \end{aligned}$$
(4)

with \(\sum _{k=0}^{\infty }r_{k}^{2}(\Vert {\textbf{x}}-{\textbf{y}}\Vert )<\infty .\) In the context of Markov processes, \(\left\{ e_{k}(u) \right\}\) are the orthonormal eigenfunctions (polynomials) of the infinitesimal generator, and p(u)du plays the role of invariant measure (see also Theorem 1 in Ascione et al. 2022, for the case of solvable birth-death processes, in the special case of state space \(E=(a,b)\)).

Additionally to the case analyzed here where \(r_{k}(\Vert {\textbf{x}}-{\textbf{y}}\Vert )=\gamma ^{k} (\Vert {\textbf{x}}-{\textbf{y}}\Vert ),\) one can see alternative interesting examples of the sequence of functions \(\left\{ r_{k}(\Vert {\textbf{x}}-{\textbf{y}}\Vert ),\ k\ge 0\right\}\) in Sarmanov (1963) by changing the invariant measure, leading to different definitions of the infinitesimal generator. That is the case, for \(d = 1\), of the Jacobi Markovian diffusion with beta marginal distributions, and Jacobi orthogonal polynomials, where \(r_{k}(\Vert {\textbf{x}}-{\textbf{y}}\Vert )\) are negative exponents of eigenvalues of generators, which depend on k as quadratic functions (see equation (66) in Sarmanov 1963).

It is well-known (see, e.g., Leonenko et al. 2017, and references therein) that nonlinear transformations of these random fields can be approximated in terms of the above series expansions: For every \(\varphi \in L^{2}((a,b), p(u)du)\),

$$\begin{aligned} \varphi (x)=\sum _{k=0}^{\infty }C_{k}^{\varphi }e_{k}(x),\; \text{ with } \; C_{k}^{\varphi } =\int _a^b \varphi (u)~e_{k}(u)~p(u)~du,\ k\ge 0. \end{aligned}$$
(5)

In particular, \(C_{0}^{\varphi } = E_p[\varphi (X)]\). The maximum integer m such that \(C_{k}^{\varphi } = 0\) for all \(1 \le k \le m-1\) represents the rank of function \(\varphi\) in the orthonormal basis \(\{e_{k},\ k\ge 0\}\) of the space \(L^{2}((a,b), p(u)du)\); that is,

$$\begin{aligned} \varphi (x)=C_{0}^{\varphi }+\sum _{k=m}^{\infty }C_{k}^{\varphi } e_{k}(x). \end{aligned}$$
(6)

In the cases of Gaussian and Gamma-correlated subordinated random fields we will refer to the Hermite and generalized Laguerre ranks, respectively, of function \(\varphi\).

An interesting example is Minkowski functional \(M_{0}(\nu ; X,D)\) providing the random volume of the set of spatial points within D (usually a bounded subset of \({\mathbb {R}}^{d}\)) where random field X crosses above a given threshold \(\nu\). That is, denoting by \(\lambda\) the Lebesgue measure on \({\mathbb {R}}^{d}\),

$$\begin{aligned} M_{0}(\nu ; X,D)=\int _{D}1_{\nu }(X({\textbf{y}}))~d{\textbf{y}}=\lambda (S_{X,D}(\nu )), \end{aligned}$$
(7)

where

$$\begin{aligned} S_{X,D}(\nu )=\left\{ {\textbf{z}}\in D:\ X({\textbf{z}})\ge \nu \right\} = \left\{ {\textbf{z}}\in D:\ 1_{\nu }(X({\textbf{z}})) = 1 \right\} , \end{aligned}$$
(8)

hence with \(\varphi (x)=1_{\nu }(x)\), the indicator function based on threshold \(\nu\), i.e., \(1_{\nu }(x)= 1\) if \(x\ge \nu\), and \(1_{\nu }(x)= 0\) otherwise.

In the Gaussian standard case, since \(p(u)=\frac{1}{\sqrt{2\pi }}\exp (-u^{2}/2)\), Eq. 5 leads to

$$\begin{aligned} 1_{\nu }(x)=\sum _{k=0}^{\infty }\frac{G_{k}(\nu )}{k!}{\mathcal {H}}_{k}(x), \end{aligned}$$

where \(\{ {\mathcal {H}}_k, \ k \ge 0 \}\) denotes the basis of (non-normalized) Hermite polynomials, with

$$\begin{aligned} G_{k}(\nu )= & {} \left\langle 1_{\nu }, {\mathcal {H}}_{k}\right\rangle _{ L^{2}((a,b), p(u)du)}\\= & {} \frac{1}{\sqrt{2\pi }}\exp (-\nu ^{2}/2){\mathcal {H}}_{k-1}(\nu ),\quad k\ge 1, \end{aligned}$$

and \(G_{0}(\nu )=\frac{1}{\sqrt{2\pi }}\int _{\nu }^{\infty }\exp (-u^{2}/2)du= 1- \Phi (\nu )\), with \(\Phi\) denoting the probability distribution function of a standard normal random variable, and hence, \(1- \Phi (\nu )\) being the value of the decumulative normal distribution at \(\nu .\) Therefore,

$$\begin{aligned} M_{0}(\nu ; X,D)=\sum _{k=0}^{\infty }\frac{G_{k}(\nu )}{k!}\int _{D}{\mathcal {H}}_{k}(X({\textbf{y}}))~d{\textbf{y}} \end{aligned}$$

(see Leonenko and Ruiz-Medina 2023).

The following assumption on the large-scale behavior of the correlation function \(\gamma\) is considered:

Assumption I.

$$\begin{aligned} \gamma (\Vert {\textbf{z}}\Vert )= & {} {\mathcal {O}}\left( \Vert {\textbf{z}}\Vert ^{-\varrho }\right) ,\quad \text{ as } \quad\Vert {\textbf{z}}\Vert \rightarrow \infty ,\quad \varrho \in (0,d). \end{aligned}$$
(9)

2.2 Information-complexity measures

Since the seminal paper by Shannon (1948), arisen in the context of communications, Information Theory has extraordinarily grown as a fundamental scientific discipline, with a wide projection in many diverse fields of application. In particular, a variety of information and complexity measures have been proposed and thoroughly studied, with the aim of characterizing the uncertain behavior inherent to random systems.

Although most concepts have a simpler interpretation in the case of systems with a finite number of states, in this preliminary introduction, and in the sequel, we directly refer to definitions for the continuous case, as is the object of this paper. Accordingly, for a continuous multivariate probability distribution with density function \(\{f({\textbf{x}}), {\textbf{x}} \in {\mathbb {R}}^n\}\), Shannon entropy (also called ‘differential entropy’ in this continuous case) is defined as

$$\begin{aligned} H(f) := - \int _{{\mathbb {R}}^n}\ln (f({\textbf{x}})) ~ f({\textbf{x}})~ d{\textbf{x}} = E_{f}[-\ln (f)]. \end{aligned}$$

As is well known, the infimum and supremum of H(f) over the family of probability density functions on \({\mathbb {R}}^n\) are \(-\infty\) and \(\infty\), respectively. In fact, some examples of distributions where the infimum is attained can be found, for instance, in Cadirci et al. (2020), Appendix A, and references therein. Shannon entropy satisfies ‘extensivity’, i.e., additivity for independent (sub)systems.

Among various generalizations of Shannon entropy, Rényi entropy (Rényi 1961), based on a deformation (distortion) parameter, constitutes the most representative one under preservation of extensivity. For a continuous multivariate distribution with probability density function \(\{f({\textbf{x}}), {\textbf{x}} \in {\mathbb {R}}^n\}\), Rényi entropy of order q is defined as

$$\begin{aligned} H_q(f):= & {} \frac{1}{1-q} \ln \left( \int _{{\mathbb {R}}^n} f^q({\textbf{x}})~ d{\textbf{x}} \right) \\= & {} \frac{1}{1-q}\ln \left( E_{f}[f^{q-1}]\right) \qquad (q\ne 1). \end{aligned}$$

As before, the infimum and supremum of \(H_q(f)\) are \(-\infty\) and \(+ \infty\), respectively. Shannon entropy H(f) is the limiting case of Rényi entropy \(H_q(f)\) as \(q\rightarrow 1\), hence also denoted as \(H_1(f)\).

In particular, Rényi entropy constitutes the basis for the formal definition of the two-parameter generalized complexity measures proposed by López-Ruiz et al. (2009), given by

$$\begin{aligned} C_{\alpha , \beta }(f) := e^{H_{\alpha }(f)-H_{\beta }(f)}, \end{aligned}$$

for \(0< \alpha , \beta < \infty\).

Campbell (1968) justified the interpretation of Shannon and Rényi entropies in exponential scale (both in the discrete and continuous cases) as an index of ‘diversity’ or ‘extent’ of a distribution. For the continuous case, the diversity index of order q,

$$\begin{aligned} DI_{q}(f) = e^{H_q(f)}, \end{aligned}$$

then varies between 0 and \(+\infty\), and

$$\begin{aligned} C_{\alpha , \beta }(f) = \frac{DI_{\alpha }(f)}{DI_{\beta }(f)}, \end{aligned}$$

which leads to the interpretation of this concept of complexity in terms of sensitivity of the diversity index of order q with respect to the deformation parameter; see Angulo et al. (2021).

Beyond the assessment on global uncertainty, divergence measures are defined for comparison of two given probability distributions at state level. As before, we here directly focus on versions for the continuous case. For two density functions \(\left\{ f({\textbf{x}}), {\textbf{x}} \in {\mathbb {R}}^n \right\}\) and \(\left\{ g({\textbf{x}}), {\textbf{x}} \in {\mathbb {R}}^n \right\}\), with f being absolutely continuous with respect to g, Kullback and Leibler (1951), following the same conceptual approach leading to the definition of Shannon entropy, introduced the (directed) divergence of f from g as

$$\begin{aligned} KL(f\Vert g)&:= \int _{{\mathbb {R}}^n} f({\textbf{x}})~ \ln \left( \frac{f({\textbf{x}})}{g({\textbf{x}})} \right) ~ d{\textbf{x}} = E_{f}\left[ \ln \left( \frac{f}{g}\right) \right] , \end{aligned}$$

which, among other uses, has been widely adopted as a meaningful reference measure for inferential optimization purposes. Correspondingly, a generalization is given by Rényi (1961) divergence of order q, defined as

$$\begin{aligned} H_q(f\Vert g)&:= \frac{1}{q-1} \ln \left( \int _{{\mathbb {R}}^n} f({\textbf{x}})~ \left( \frac{f({\textbf{x}})}{g({\textbf{x}})} \right) ^{q-1} d{\textbf{x}}\right) \nonumber \\&= \frac{1}{q-1} \ln \left( E_{f}\left[ \left( \frac{f}{g} \right) ^{q-1}\right] \right) \qquad (q\ne 1). \end{aligned}$$

For \(q \rightarrow 1\), \(H_q(f\Vert g)\) tends to \(KL(f\Vert g)\) (also denoted as \(H_1(f\Vert g)\)).

Angulo et al. (2021) proposed a natural formulation of a ‘relative diversity’ index of order q as

$$\begin{aligned} DI_q(f\Vert g) = e^{H_q(f\Vert g)}, \end{aligned}$$

meaning the structural departure of f from g in terms of the state-by-state probability contribution to diversity. This also gives a complementary interpretation, in terms of sensitivity with respect to the deformation parameter of Rényi divergence, for the two-parameter generalized relative complexity measure introduced by Romera et al. (2011):

$$\begin{aligned} C_{\alpha , \beta }(f\Vert g) := e^{H_{\alpha }(f\Vert g)-H_{\beta }(f\Vert g)} = \frac{DI_{\alpha }(f\Vert g)}{DI_{\beta }(f\Vert g)}, \end{aligned}$$

for \(0< \alpha , \beta < \infty\).

A further step, aiming at quantifying stochastic dependence between two random vectors, is achieved in terms of mutual information measures. From the point of view of departure from independence, divergence measures constitute, in particular, a direct instrumental approach, comparing the (true) joint distribution to the product of the corresponding marginal distributions (hypothetical case of independence). Thus, in the continuous case, for two random vectors \(X\sim f_X\) and \(Y\sim f_Y\), with \((X,Y)\sim f_{XY}\), the Rényi-divergence-based measure of mutual information of order q is defined as

$$\begin{aligned} I_q(X,Y)&:= H_q(f_{XY}\Vert f_X f_Y), \end{aligned}$$
(10)

including the special case

$$\begin{aligned} I(X,Y)&:= KL(f_{XY}\Vert f_X f_Y)=H(X) + H(Y) - H(X,Y) \end{aligned}$$
(11)

(with the last equality not being similarly satisfied, in general, for \(q \ne 1\)). Here, \(H(X,Y)=E_{f_{XY}}\left[ - \ln \left( f_{XY}\right) \right] .\)

Related concepts and interpretations can be derived in relation to ‘mutual complexity’ and ‘mutual diversity’ (see, e.g., Alonso et al. 2016; Angulo et al. 2021).

These elements are applied in the next sections to studying, under the informational approach, the large-scale asymptotic behavior of real and infinite-dimensional valued (for the spatiotemporal case) random fields of Lancaster–Sarmanov type.

3 Methodology: mutual information dependence assessment

In this section, we apply Eq. 9 in the derivation of the asymptotic order characterizing the spatial large scale behavior of mutual information between the marginal spatial components of Lancaster–Sarmanov subordinated random fields. Under Assumption I, this asymptotic order is related to the LRD parameter \(\varrho\) of the underlying Lancaster–Sarmanov random field. Note that the lower values of \(\varrho\) correspond to higher asymptotic structural diversity loss. Such an asymptotic order is evaluated in Sect. 3.1, in particular, for mutual information based on Shannon entropy.

3.1 Asymptotic analysis from Shannon mutual information

Let \(\{X({\textbf{x}}),\ {\textbf{x}}\in {\mathbb {R}}^d\}\) be an element of the Lancaster–Sarmanov random field class. From Eq. 1, mutual information between component r.v.’s \(X({\textbf{x}})\) and \(X({\textbf{y}})\) can be expressed as follows:

$$\begin{aligned}{} & {} I(X({\textbf{x}}),X({\textbf{y}})) \nonumber \\{} & {} \quad = \int _{a}^{b} \int _{a}^{b} p(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )~ \ln \left( \frac{p(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{p(u)~p(v)}\right) ~dudv \nonumber \\{} & {} \quad = \int _{a}^{b} \int _{a}^{b} p(u)~p(v)~\left[ 1+\sum _{k=1}^{\infty }\gamma ^{k} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{k}(u)~e_{k}(v)\right] \nonumber \\{} & {} \quad \quad \times \ln \left( 1+\sum _{k=1}^{\infty }\gamma ^{k} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{k}(u)~e_{k}(v)\right) ~dudv. \end{aligned}$$
(12)

The following lemma shows that, under Assumption I, the asymptotic behavior of \({\mathcal {S}}_{\varrho }(\Vert {\textbf{x}}-{\textbf{y}}\Vert ) := I(X({\textbf{x}}),X({\textbf{y}}))\), when \(\Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty\), involves the LRD parameter \(\varrho\), thus providing an indicator of diversity loss at large scale, with higher values attained as \(\varrho\) gets closer to 0.

Lemma 1

Under Assumption I, the following asymptotic behavior holds:

$$\begin{aligned} {\mathcal {S}}_{\varrho }(\Vert {\textbf{z}}\Vert ) = {\mathcal {O}}\left( \Vert {\textbf{z}}\Vert ^{-\varrho }\right) , \quad \text{ as }\quad\Vert {\textbf{z}}\Vert \rightarrow \infty . \end{aligned}$$
(13)

Proof

Note that \(p(u)\in L^{2}((a,b), p(u)du)\) admits the series expansion

$$\begin{aligned} p(u)=\sum _{k=0}^{\infty }C_{k}^{p}e_{k}(u),\quad \text{ with } \quad C_{k}^{p}=\int _{a}^{b}[p(u)]^{2}~e_{k}(u)~du,\quad k\ge 0. \end{aligned}$$

From Eq. 12, applying Taylor series expansion of logarithmic function at a neighborhood of 1, keeping in mind that \(\sum _{k=0}^{\infty }\left[ C_{k}^{p}\right] ^{2}<\infty ,\) we obtain

$$\begin{aligned} {\mathcal {S}}_{\varrho }(\Vert {\textbf{x}}-{\textbf{y}}\Vert )= & {} I(X({\textbf{x}}),X({\textbf{y}})) \nonumber \\\simeq & {} \int _{a}^{b}\int _{a}^{b}\left[ \sum _{k=0}^{\infty }C_{k}^{p}~e_{k}(u)\right] \left[ \sum _{l=0}^{\infty }C_{l}^{p}~e_{l}(v)\right] \nonumber \\{} & {} \times \left[ 1+\sum _{i=1}^{\infty }\gamma ^{i} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{i}(u)~e_{i}(v)\right] \nonumber \\{} & {} \left[ \sum _{j=1}^{\infty }\gamma ^{j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{j}(u)~e_{j}(v)\right] ~dudv\nonumber \\= & {} \sum _{j=1}^{\infty }\gamma ^{j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\left[ C_{j}^{p}\right] ^{2} \nonumber \\{} & {} +\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }\gamma ^{i+j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert ) \nonumber \\{} & {} \times \int _{a}^{b}\int _{a}^{b}~e_{i}(u)~e_{i}(v)~e_{j}(u)~e_{j}(v)~\nonumber \\{} & {} p(u)~p(v)~dudv\nonumber \\= & {} \sum _{j=1}^{\infty }\gamma ^{j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\left[ C_{j}^{p}\right] ^{2} \nonumber \\{} & {} +\sum _{i=1}^{\infty }\sum _{j=1}^{\infty }\gamma ^{i+j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~\delta _{i,j} \end{aligned}$$
(14)
$$\begin{aligned}= &\; {} \sum _{j=1}^{\infty }\gamma ^{j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\left[ C_{j}^{p}\right] ^{2}+\sum _{i=1}^{\infty }\gamma ^{2i}(\Vert {\textbf{x}}-{\textbf{y}}\Vert )\nonumber \\\le & {} \left( \sup _{j\ge 1}\left[ C_{j}^{p}\right] ^{2}\right) \sum _{j=1}^{\infty }\gamma ^{j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert ) \nonumber \\{} & {} +\sum _{i=1}^{\infty }\gamma ^{2i}(\Vert {\textbf{x}}-{\textbf{y}}\Vert ) \nonumber \\= & {} \left( \sup _{j\ge 1}\left[ C_{j}^{p}\right] ^{2}\right) \frac{\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{1-\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )} \nonumber \\{} & {} + \frac{\gamma ^{2} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{1-\gamma ^{2} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )} \nonumber \\= & {} \;{\mathcal {O}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert ^{-\varrho }\right) ,\quad \text{ as }\quad\Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty , \end{aligned}$$
(15)

where in (14) we have applied the orthonormality of the basis \(\{e_{j}(\cdot )\}_{j\ge 0}\) in the space \(L^{2}\left( (a,b), p(u)du\right) ,\) and \(\simeq\)’ denotes the local approximation obtained when \(\Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty ,\) since \(\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\rightarrow 0,\) and \(\left[ 1+\sum _{i=1}^{\infty }\gamma ^{i} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{i}(u)~e_{i}(v)\right] \rightarrow 1.\) Hence, for \(\Vert {\textbf{x}}-{\textbf{y}}\Vert\) sufficiently large, one can consider the local approximation provided by Taylor expansion at a neighborhood of 1.

Similarly,

$$\begin{aligned} {\mathcal {S}}_{\varrho }(\Vert {\textbf{x}}-{\textbf{y}}\Vert )= & {}\; I(X({\textbf{x}}),X({\textbf{y}})) \nonumber \\ \simeq & {} \sum _{j=1}^{\infty }\gamma ^{j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\left[ C_{j}^{p}\right] ^{2}+\sum _{i=1}^{\infty }\gamma ^{2i}(\Vert {\textbf{x}}-{\textbf{y}}\Vert )\nonumber \\\ge & {} \sum _{j=1}^{\infty }\gamma ^{j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\left[ C_{j}^{p}\right] ^{2}\nonumber \\\ge & {} \left( \inf _{j\ge 1}\left[ C_{j}^{p}\right] ^{2}\right) \sum _{j=1}^{\infty }\gamma ^{j} (\Vert {\textbf{x}}-{\textbf{y}}\Vert ) \nonumber \\= &\; {} {\mathcal {O}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert ^{-\varrho }\right) ,\quad \text{ as } \quad\Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty , \end{aligned}$$
(16)

where we have applied the fact that the rank of function \(p\in L^{2}((a,b), p(u)du)\) is equal to 1. \(\square\)

For \(\varphi \in L^{2}((a,b), p(u)du)\), a similar asymptotic behavior is displayed by mutual information \(I(\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}})))\) when \(\Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty\), involving the LRD parameter \(\varrho\) scaled by the rank m of function \(\varphi\) in the orthonormal basis \(\{e_{k},\ k\ge 0\}\) (Hermite and generalized Laguerre ranks in the Gaussian and Gamma-correlated cases, respectively). This fact is proved in the following result.

Theorem 1

Let p(u) be, as before, the probability density characterizing the marginal probability distributions of the Lancaster–Sarmanov random field \(X=\{ X({\textbf{z}}),\ {\textbf{z}}\in {\mathbb {R}}^{d}\}\). Assume that \(\varphi \in L^{2}((a,b), p(u)du)\) has rank m, and is such that \(\varphi (X({\textbf{z}}))\) is a discrete random variable whose state space is finite (with cardinal N), for \({\textbf{z}}\in {\mathbb {R}}^{d}.\) The following asymptotic behavior then holds:

$$\begin{aligned} I\left( \varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))\right) = {\mathcal {O}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert ^{-m\varrho }\right) ,\; \text{ as } \; \Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty . \end{aligned}$$
(17)

Remark 2

Note that applying variable change theorem, Eq. 17 is also satisfied in the case where, for every \({\textbf{z}}\in {\mathbb {R}}^{d},\) \(\varphi (X({\textbf{z}}))\) is a continuous random variable and \(\varphi\) admits an inverse function \(\varphi ^{-1}\) having non-null derivatives over \(\varphi ((a,b)).\) Identity (17) also holds when \(\varphi\) is non injective but a countable set \(\{\varphi _{k}^{-1}({\textbf{y}}),\ k\in {\mathbb {N}}\}\) of preimages is associated with every point \({\textbf{y}}\in \varphi ((a,b)),\) with \(\varphi _{k}^{-1}\) having non-null derivatives over \(\varphi ((a,b)),\) for \(k\in {\mathbb {N}}.\)

Proof

Under Assumption I, applying Jensen’s inequality, since \(\{e_{k},\ k\ge 0\}\) is an orthonormal basis of the space \(L^{2}((a,b), p(u)du),\)

$$\begin{aligned}{} & {} I\left( \varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))\right) \nonumber \\{} & {} \quad = \sum _{i=1}^{N}\sum _{j= 1 }^{N}\ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i},\varphi _{j})}{p_{\varphi (X({\textbf{x}}))}(\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi_{j})} \right] \nonumber \\{} & {} \quad \quad \times \int _{\varphi ^{-1}(\varphi _{i})\times \varphi ^{-1}(\varphi _{j})}p(u)~p(v) ~\nonumber \\{} & {} \qquad \left[ 1+\sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{h}(u)~e_{h}(v)\right] ~dudv\nonumber \\{} & {} \quad \le \sup _{i,j} \left( \ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i},\varphi _{j})}{p_{\varphi (X({\textbf{x}}))} (\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi _{j})} \right] \right) \nonumber \\{} & {} \quad \quad \times\quad N^{2}\left[ 1 +\sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\nonumber \right. \\{} & {} \left. \quad \quad \int _{a}^{b}\int _{a}^{b} p(u)~p(v)~ e_{h}(u)~e_{h}(v)~dudv\right] \nonumber \\{} & {} \quad = \sup _{i,j}\left( \ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i}, \varphi _{j})}{p_{\varphi (X({\textbf{x}}))}(\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi _{j})} \right] \right) \nonumber \\{} & {} \quad \quad \times \quad N^{2}\left[ 1 +\sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\left( E_{p}\left[ e_{h}(\cdot )\right] \right) ^{2}\right] \nonumber \\{} & {} \quad \le \sup _{i,j}\left( \ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i},\varphi _{j})}{p_{\varphi (X({\textbf{x}}))} (\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi _{j})} \right] \right) \nonumber \\{} & {} \qquad \times \quad N^{2}\left[ 1 +\sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\Vert e_{h}\Vert _{L^{2}((a,b), p(u)du)}^{2}\right] \nonumber \\{} & {} \quad = \sup _{i,j}\left( \ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i},\varphi _{j})}{p_{\varphi (X({\textbf{x}}))}(\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi _{j})} \right] \right) \nonumber \\{} & {} \quad \quad \times \quad N^{2}\left[ \gamma ^{0} (\Vert {\textbf{x}}-{\textbf{y}}\Vert ) +\sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\right] \nonumber \\{} & {} \quad = {\mathcal {O}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert ^{-m\varrho }\right) ,\quad \text{ as } \quad\Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty . \end{aligned}$$
(18)

From (1), the following lower bound is obtained:

$$\begin{aligned}{} & {} I\left( \varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))\right) \nonumber \\{} & {} \quad = \sum _{i=1}^{N}\sum _{j= 1 }^{N}\ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i},\varphi _{j})}{p_{\varphi (X({\textbf{x}}))} (\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi _{j})} \right] \nonumber \\{} & {} \quad \quad \times \int _{\varphi ^{-1}(\varphi _{i})\times \varphi ^{-1}(\varphi _{j})}p(u)~p(v)~\nonumber \\{} & {} \qquad \left[ 1+\sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{h}(u)~e_{h}(v)\right] ~dudv\nonumber \\{} & {} \quad \ge \inf _{i,j}\left( \ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i},\varphi _{j})}{p_{\varphi (X({\textbf{x}}))}(\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi _{j})} \right] \right) \nonumber \\{} & {} \quad \quad \times \quad N^{2}\left[ 1 + \left[ \sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\right] \nonumber \right. \\{} & {} \left. \qquad \int _{{\mathcal {S}}\times {\mathcal {S}}}e_{h}(u)~e_{h}(v)~p(u)~p(v)~dudv\right] \nonumber \\{} & {} \quad = \inf _{i,j}\left( \ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i},\varphi _{j})}{p_{\varphi (X({\textbf{x}}))}(\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi _{j})} \right] \right) \nonumber \\{} & {} \quad \quad \times \quad N^{2}\left[ \left( E_{p}[1_{{\mathcal {S}}}e_{h}(\cdot )]\right) ^{2} \right. \nonumber \\{} & {} \left. \qquad + \left[ \sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\right] \left( E_{p}[1_{{\mathcal {S}}}e_{h}(\cdot )]\right) ^{2}\right] \nonumber \\{} & {} \quad \ge \inf _{i,j}\left( \ln \left[ \frac{p_{\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))}(\varphi _{i},\varphi _{j})}{p_{\varphi (X({\textbf{x}}))}(\varphi _{i})~p_{\varphi (X({\textbf{y}}))}(\varphi _{j})} \right] \right) \nonumber \\{} & {} \quad \quad \times \quad \left[ N\left( \inf _{h\ge m}E_{p}[1_{{\mathcal {S}}}e_{h}(\cdot )]\right) \right] ^{2} \nonumber \\{} & {} \qquad \left[ \gamma ^{0} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )+ \sum _{h=m}^{\infty }\gamma ^{h} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )\right] \nonumber \\{} & {} \quad = {\mathcal {O}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert ^{-m\varrho }\right) ,\quad \text{ as } \quad \Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty , \end{aligned}$$
(19)

where \({\mathcal {S}}\subseteq (a,b)\) satisfies \(p({\mathcal {S}})=\inf _{i=1,\dots ,N} p(\varphi ^{-1}(\varphi _{i}))>0 ,\) and in the last inequality we have applied that \(1_{{\mathcal {S}}}\in L^{2}((a,b), p(u)du)\) with \(\Vert 1_{{\mathcal {S}}}\Vert _{L^{2}((a,b), p(u)du)}>0,\) and \(E_{p}[1_{{\mathcal {S}}}e_{m}(\cdot )]>0\), \(\forall m\), hence \(\inf _{h\ge m}E_{p}[1_{{\mathcal {S}}}e_{h}(\cdot )]>0.\) From (18) and (19), Eq. 17 holds. \(\square\)

3.2 Asymptotic analysis from Rényi mutual information

This section extends the asymptotic analysis derived in the previous section beyond the special limit case based on Shannon entropy to the framework of Rényi mutual information. Hence, several interpretations arise in terms Campbell’s diversity indices for generalized complexity measures.

From Eq. 1, for any \({\textbf{x}},{\textbf{y}}\in {\mathbb {R}}^d\), Rényi mutual information between random components \(X({\textbf{x}})\) and \(X({\textbf{y}})\) of random field X in the Lancaster–Sarmanov class is given by

$$\begin{aligned}{} & {} I_{q}(X({\textbf{x}}),X({\textbf{y}})) \nonumber \\{} & {} \quad = \frac{1}{q-1}\ln \left( \int _{a}^{b}\int _{a}^{b}\left[ \frac{p(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{p(u)~p(v)}\right] ^{q-1}\right. \nonumber \\{} & {} \left. \quad \quad p(u,v,\Vert {\textbf{x}}-{\textbf{y}}\Vert )~dudv\right) , \end{aligned}$$
(20)

for any \(q\ge 0,\) with \(q\ne 1.\)

Theorem 2

Under the conditions assumed in Lemma 1, if

$$\begin{aligned} \sup _{(k_{1},\dots , k_{L})\in {\mathbb {N}}^{L}}\left( E_{p}\left[ \prod _{i=1}^{L}e_{k_{i}}(\cdot )\right] \right) ^{2}<\infty \end{aligned}$$
(21)

for a given integer \(L>1\), then, for any \(q\le L\),

$$\begin{aligned} I_{q}(X({\textbf{x}}),X({\textbf{y}}))= {\mathcal {O}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert ^{-q\varrho }\right) ,\quad \text{ as } \quad \Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty . \end{aligned}$$
(22)

Here, as before, \(E_{p}[\cdot ]\) denotes the expectation with respect to the marginal probability density p.

Proof

Under the conditions of Lemma 1, from Eqs. 1 and 20, and assumption (21), applying the orthogonality of the basis \(\{e_{k},\ k\ge 0\}\) in the space \(L^{2}((a,b), p(u)du)\), for any \({\textbf{x}},{\textbf{y}}\in {\mathbb {R}}^d\), and for any integer \(q \in \{1,\dots ,L\}\), we obtain

$$\begin{aligned}{} & {} I_{q}(X({\textbf{x}}),X({\textbf{y}})) \\{} & {} \quad = \frac{1}{q-1}\ln \left( \int _{a}^{b}\int _{a}^{b}\left[ 1+\sum _{k=1}^{\infty }\gamma ^{k} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{k}(u)~e_{k}(v)\right] ^{q}\right. \\{} & {} \qquad \left. p(u)~p(v)~dudv\right) \\{} & {} \quad = \frac{1}{q-1}\ln \left( 1+\int _{a}^{b}\int _{a}^{b} |{\mathcal {Q}}_{\Vert {\textbf{x}}-{\textbf{y}}\Vert }(u,v)|^{q}p(u)~p(v)~dudv\right) \\{} & {} \quad =\frac{1}{q-1}\ln \left( 1+\sum _{k_{1},\dots ,k_{q}}\gamma ^{k_{1}+\dots +k_{q}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert \right) \right. \\{} & {} \quad \quad \times \left. \int _{a}^{b}\int _{a}^{b}\prod _{i=1}^{q}e_{k_{i}}\otimes e_{k_{i}}(u,v) ~ p\otimes p(u,v)~dudv\right) \\{} & {} \quad =\frac{1}{q-1}\ln \left( 1+\sum _{k_{1},\dots ,k_{q}}\gamma ^{k_{1}+\dots +k_{q}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert \right) \right. \\{} & {} \qquad \left. \left[ E_{p}\left[ \prod _{i=1}^{q}e_{k_{i}}(\cdot )\right] \right] ^{2}\right) \\{} & {} \quad \simeq \frac{1}{q-1}\left( \sum _{k_{1},\dots ,k_{q}}\gamma ^{k_{1}+\dots +k_{q}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert \right) \right. \\{} & {} \qquad \left. \left[ E_{p}\left[ \prod _{i=1}^{q}e_{k_{i}}(\cdot )\right] \right] ^{2}\right) \\{} & {} \quad \le \frac{1}{q-1}\sup _{(k_{1},\dots , k_{q})\in {\mathbb {N}}^{q}}\\{} & {} \qquad \left( E_{p}\left[ \prod _{i=1}^{q}e_{k_{i}}(\cdot )\right] \right) ^{2}\left[ \frac{\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{1-\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}\right] ^{q}\\{} & {} \quad = C_1(q) \left[ \frac{\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{1-\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}\right] ^{q} \\{} & {} \quad = {\mathcal {O}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert ^{-q\varrho }\right) ,\quad \text{ as } \quad \Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty . \end{aligned}$$

Here, \({\mathcal {Q}}_{\Vert {\textbf{x}}-{\textbf{y}}\Vert }(u,v)\) denotes the kernel \(\sum _{k=1}^{\infty }\gamma ^{k} (\Vert {\textbf{x}}-{\textbf{y}}\Vert )~e_{k}(u)~e_{k}(v),\) for \(u,v\in (a,b)\).

Similarly, the following asymptotic behavior is obtained:

$$\begin{aligned}{} & {} I_{q}(X({\textbf{x}}),X({\textbf{y}})) \\{} & {} \quad \simeq \frac{1}{q-1}\left( \sum _{k_{1},\dots ,k_{q}}\gamma ^{k_{1}+\dots +k_{q}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert \right) \right. \\{} & {} \qquad \left. \left[ E_{p}\left[ \prod _{i=1}^{q}e_{k_{i}}(\cdot )\right] \right] ^{2}\right) \\{} & {} \quad = \frac{1}{1-q} \ln \left[ 1 + \sum _{(k_1,\dots ,k_q) \in E_1} \gamma ^{k_{1}+\dots +k_{q}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert \right) \right. \\{} & {} \qquad \left[ E_{p}\left[ \prod _{i=1}^{q}e_{k_{i}}(\cdot )\right] \right] ^{2} \\{} & {} \quad \quad \left. + \sum _{(k_1,\dots ,k_q) \in {\mathbb {N}^{q}} \setminus (E_1 \cup \{(0,\dots ,0)\})} \gamma ^{k_{1}+\dots +k_{q}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert \right) \right. \\{} & {} \qquad \left. \left[ E_{p}\left[ \prod _{i=1}^{q}e_{k_{i}}(\cdot )\right] \right] ^{2} \right] \\{} & {} \quad \ge \frac{1}{q-1}\inf _{(k_{1},\dots , k_{q})\in {\mathbb {N}}^{q}}\left[ E_{p}\left[ \prod _{i=1}^{q}e_{k_{i}}(\cdot )\right] \right] ^{2}\\{} & {} \qquad \left[ \frac{\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{1-\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}\right] ^{q}\\{} & {} \quad = C_2(q) \left[ \frac{\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{1-\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}\right] ^{q} \\{} & {} \quad = {\mathcal {O}}\left( \Vert {\textbf{x}}-{\textbf{y}}\Vert ^{-q\varrho }\right) ,\quad \Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty , \end{aligned}$$

where \(E_1 = \{(k_{1},\dots , k_{q})\in {\mathbb {N}}^{q}: \ \exists ! \ l \in \{1,\dots ,q\} \ \text{ with } \ k_l \ge 1 \ \text{ and } \ k_i = 0, \ i \in \{1,\dots ,q\} \setminus \{l\}\}.\) Noting that, as \(\Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty\),

$$\begin{aligned} \sup _{q \in \{1,\dots ,L\}} C_1(q) \,\ge & {} \ \left[ \frac{1-\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}{\gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )}\right] ^{q} I_{q}(X({\textbf{x}}),X({\textbf{y}})) \ \\\ge & {} \ \inf _{q \in \{1,\dots ,L\}} C_2(q), \end{aligned}$$

and applying Dominated Convergence Theorem, we have that Eq. 22 holds for \(q \in [1,L]\). For \(q \in [0,1]\), the result also holds from Theorem 1, applying a similar argument, as \(I_{0}(X({\textbf{x}}),X({\textbf{y}})) \equiv 0\). \(\square\)

Remark 3

Condition (21) is satisfied, for example, when the moment generating function of the marginal probability distributions exists. That is the case of Gaussian and Gamma-correlated random fields.

3.3 Simulations

Let \(\{X({\textbf{x}}),\ {\textbf{x}}\in {\mathbb {R}}^{d}\}\) be a measurable zero-mean Gaussian homogeneous and isotropic mean-square continuous random field on a probability space \((\Omega ,{\mathcal {A}},P),\) with \(\textrm{E}[Y^{2}({\textbf{x}})]=1,\) for all \({\textbf{x}}\in {\mathbb {R}}^{d},\) and correlation function \(\textrm{E}[X( {\textbf{x}})X({\textbf{y}})]\) \(=B(\Vert {\textbf{x}}-{\textbf{y}}\Vert )\) of the form:

$$\begin{aligned} B(\Vert {\textbf{z}}\Vert )=\frac{{\mathcal {L}}(\Vert {\textbf{z}}\Vert )}{\Vert {\textbf{z}}\Vert ^{\alpha }},\quad {\textbf{z}}\in {\mathbb {R}}^{d},\quad 0<\alpha < d/2. \end{aligned}$$
(23)

The correlation B of X is a continuous function of \(r=\Vert {\textbf{z}}\Vert .\) It then follows that \({\mathcal {L}}(r)={\mathcal {O}}(r^{\alpha }),\) \(r\rightarrow 0.\) Note that the covariance function

$$\begin{aligned} B(\Vert {\textbf{z}}\Vert )=\frac{1}{(1+\Vert {\textbf{z}}\Vert ^{\beta })^{\gamma }},\quad 0<\beta \le 2,\quad \gamma >0, \end{aligned}$$
(24)

is a particular case of the family of covariance functions (23) studied here with \(\alpha = \beta \gamma ,\) and

$$\begin{aligned} {\mathcal {L}}(\Vert {\textbf{z}}\Vert )=\frac{\Vert {\textbf{z}}\Vert ^{\beta \gamma }}{(1+\Vert {\textbf{z}} \Vert ^{\beta })^{\gamma }}. \end{aligned}$$
(25)

In the present simulation study, we restrict our attention to such a family of covariance functions. Specifically, we have considered the parameter values \(\beta = \gamma =0.2,\) in the generations of Gaussian random field X with covariance function (24) (see Fig. 1). From ten independent copies \(X_{i},\) \(i=1,\dots ,10,\) of random field X a \(\chi _{10}^{2}\) random field is also generated from the identity

$$\begin{aligned} \chi _{10}^{2}({\textbf{x}})=\frac{1}{2}\left[ X_{1}^{2}({\textbf{x}})+\dots +X_{10}^{2}({\textbf{x}})\right] ,{\textbf{x}}\in {\mathbb {R}}^{d}. \end{aligned}$$

Its correlation function \(\gamma\) is given by

$$\begin{aligned} \gamma (\Vert {\textbf{x}}-{\textbf{y}}\Vert )=\frac{\text{ Cov }(\chi _{10}^{2}({\textbf{x}}), \chi _{10}^{2}({\textbf{y}}))}{\text{ Var }(\chi _{10}^{2}({\textbf{0}}))}=B^{2}(\Vert {\textbf{z}}\Vert ), \end{aligned}$$

where \(B^{2}(\Vert {\textbf{z}}\Vert )\) has been introduced in (24).

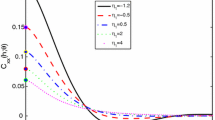
The results derived in Lemma 1, and Theorems 1 and 2 are illustrated for both models, computing Shannon and Rényi mutual informations for the corresponding original random variables, and for their transformed versions in terms of indicator functions, considering an increasing sequence of distances between the involved random variables. Specifically, a truncated version of \(I(X({\textbf{x}}),X({\textbf{y}})),\) and \(I_{q}(X({\textbf{x}}),X({\textbf{y}})),\) based on \(M=5\) Hermite and Laguerre polynomials, respectively, is computed for spatial distances \(d_{n}=\Vert {\textbf{x}}_{n}-{\textbf{y}}_{n}\Vert ,\) \(d_{n}=1,\dots ,1000.\) The derived lower and upper bounds are represented as well. In particular, Fig. 2 displays in green dashed line \(I(X({\textbf{x}}),X({\textbf{y}}))\) (top-left), and \(I(\chi _{10}^{2}({\textbf{x}}),\chi _{10}^{2}({\textbf{y}}))\) (top-right), \(I(\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}})))\) (bottom-left), and \(I(\varphi (\chi _{10}^{2}({\textbf{x}})),\varphi (\chi _{10}^{2}({\textbf{y}})))\) (bottom-right). Here, \(\varphi (x)=1_{\nu }(x),\) \(\nu =0.95.\) The upper and lower bounds are represented in dashed red and blue lines, respectively. The values of \(I_{q}(X({\textbf{x}}),X({\textbf{y}})),\) \(q=1.5,~2.10,~2.25;\) \(I_{q}(\chi _{10}^{2}({\textbf{x}}),\chi _{10}^{2}({\textbf{y}})),\) \(q=2,~2.05,~2.10;\) \(I_{q}(\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))),\) \(q=1.5,~1.75,~1.95;\) and \(I_{q}(\varphi (\chi _{10}^{2}({\textbf{x}})),\varphi (\chi _{10}^{2}({\textbf{y}}))),\) \(q=1.75,~1.85,~ 1.95;\) for \(\varphi (x)=1_{\nu }(x),\) \(\nu =0.95,\) are also plotted in Fig. 3. It must be observed that, as we have checked through a large number of simulations, sensitivity at shorter distances with respect to the deformation parameter q depends on the polynomial basis and the truncation order selected.

Fig. 1
figure 1

Covariance function of X (left-hand side), and covariance function of \(\chi _{10}^{2}\) (right-hand side) for a regular grid of \(20\times 20\) spatial locations, with respect to distances in horizontal axis

Full size image
Fig. 2
figure 2

In green color, truncated \(I(X({\textbf{x}}),X({\textbf{y}}))\) (top-left), and \(I(\chi _{10}^{2}({\textbf{x}}),\chi _{10}^{2}({\textbf{y}}))\) (top-right), \(I(\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}})))\) (bottom-left), and \(I(\varphi (\chi _{10}^{2}({\textbf{x}})),\varphi (\chi _{10}^{2}({\textbf{y}})))\) (bottom-right). The upper and lower bounds are represented in red and blue colors, respectively. Here, \(\varphi (x)=1_{\nu }(x),\) \(\nu =0.95\)

Full size image
Fig. 3
figure 3

In green color, truncated \(I_{q}(X({\textbf{x}}),X({\textbf{y}})),\) \(q=1.5,~2.10,~2.25\) (top-row); \(I_{q}(\chi _{10}^{2}({\textbf{x}}),\chi _{10}^{2}({\textbf{y}})),\) \(q=2,~2.05,~2.10\) (second row); \(I_{q}(\varphi (X({\textbf{x}})),\varphi (X({\textbf{y}}))),\) \(q=1.5,~1.75,~1.95\) (third row), and \(I_{q}(\varphi (\chi _{10}^{2}({\textbf{x}})),\varphi (\chi _{10}^{2}({\textbf{y}}))),\) \(q=1.75,~1.85,~1.95\) (fourth row). The upper and lower bounds are represented in red and blue colors, respectively. As before, \(\varphi (x)=1_{\nu }(x),\) \(\nu =0.95\)

Full size image

4 Spatiotemporal case: functional approach

In this section, we consider the extension of the above introduced concepts and elements in an infinite-dimensional framework. In this sense, a wider concept of diversity is adopted for functional systems characterized by separable non-countable families of infinite-dimensional random variables, and their measurable functions.

Specifically, the departure from independence of the components of a functional system, as displayed by spatial white noise random fields, is measured in terms of diversity loss in the spatial functional sample paths. Equivalently, diversity loss is induced here by the strong interrelations displayed by the functional random components of such systems.

4.1 Mutual information in an infinite-dimensional framework

The formulation of mutual information as a measure for spatiotemporal structural complexity analysis can be addressed for the general class of Lancaster–Sarmanov random fields adopting the infinite-dimensional spatial framework introduced in Angulo and Ruiz-Medina (2023).

Let \(X=\{X_{{\textbf{x}}}(\cdot ),\ {\textbf{x}}\in {\mathbb {R}}^d \}\) be a zero-mean homogeneous and isotropic spatial functional random field on the separable Hilbert space \((H, <\cdot ,\cdot >_H)\), mean-square-continuous w.r.t. the H norm. In the following, we will assume that \(H=L^{2}({\mathcal {T}}),\) with \({\mathcal {T}}\subseteq {\mathbb {R}}_{+}\). For every \({\textbf{x}},{\textbf{y}}\in {\mathbb {R}}^d\), \(\left( X_{{\textbf{x}}}(\cdot ),X_{{\textbf{y}}}(\cdot )\right) ^{T}\) is a random element in the separable Hilbert space \(\left( H^{2}, \left\langle \cdot ,\cdot \right\rangle _{H^{2}}\right)\) of vector functions \({\textbf{f}}=(f_{1},f_{2})^{T}\), with the inner product given by \(\left\langle {\textbf{f}},{\textbf{g}}\right\rangle _{H^2}=\sum _{i=1}^{2}\left\langle f_{i}, g_{i}\right\rangle _{H},\ \forall {\textbf{f}},{\textbf{g}}\in H^{2}\). Thus, for every \({\textbf{x}},{\textbf{y}}\in {\mathbb {R}}^d\), we consider the measurable function

$$\begin{aligned} \left( X_{{\textbf{x}}}(\cdot ),X_{{\textbf{y}}}(\cdot )\right) ^{T}: \;(\Omega ,{\mathcal {A}}, P)\longrightarrow \left( H^{2},{\mathcal {B}}(H^{2}),P_{\Vert {\textbf{x}}-{\textbf{y}}\Vert }(dh_{1},dh_{2})\right) . \end{aligned}$$

Let us denote by \(\{P_{X_{{\textbf{x}}}(\cdot )}(dh),\ {\textbf{x}}\in {\mathbb {R}}^d\}\) the marginal infinite-dimensional probability distributions, with \(P_{X_{{\textbf{x}}}(\cdot )}(dh)=P(dh),\) for every \({\textbf{x}}\in {\mathbb {R}}^d.\) Let \(L^{2}(H,P(dh))\) be the space of measurable functions \(\varphi :\ H \longrightarrow {\mathbb {R}}\) such that \(\int _{H}|\varphi (h)|^{2}P(dh)<\infty .\) Assume that there exists an orthonormal basis \(\{{\mathcal {B}}_{k},\ k\ge 0\}\) of \(L^{2}(H,P(dh))\) such that the Radon-Nikodym derivative of the bivariate infinite-dimensional probability distribution \(P_{\Vert {\textbf{x}}-{\textbf{y}}\Vert }(dh_{1},dh_{2})\) can be written in terms of the corresponding marginals as (see, e.g., Ledoux and Talagrand 1991), for \(n,m\ge 1,\)

$$\begin{aligned}{} & {} p_{\Vert {\textbf{x}}-{\textbf{y}}\Vert ,n,m}(h_{1},h_{2}) \, \\{} & {} \quad = \ p(h_{1})p(h_{2}) \\{} & {} \quad \quad \times \left[ 1+\sum _{k\ge 1} \left[ \int _{H}\left\langle X_{{\textbf{x}}}(\cdot ),\phi _{n}(\cdot )\right\rangle _{L^{2}({\mathcal {T}})} \left\langle X_{{\textbf{y}}}(\cdot ),\phi _{m}(\cdot )\right\rangle _{L^{2}({\mathcal {T}})} \right. \right. \\{} & {} \quad \left. \quad P_{\Vert {\textbf{x}}-{\textbf{y}}\Vert } (dX_{{\textbf{x}}}(\cdot ),dX_{{\textbf{y}}}(\cdot ))\right] ^{k} \\{} & {} \qquad \left. {\mathcal {B}}_{k}(h_{1}) {\mathcal {B}}_{k}(h_{2})\right] \mu (dh_{1}, dh_{2}), \end{aligned}$$

for a given orthonormal basis \(\{ \phi _{n},\ n \ge 1\}\) of H,  with

$$\begin{aligned} \gamma _{\Vert {\textbf{x}}-{\textbf{y}}\Vert }(\phi _{n})(\phi _{m}) \,= & {} \ \text{ Corr } (X_{{\textbf{x}}}(\phi _{n}), X_{{\textbf{y}}}(\phi _{m})) \\= & {} \int _{H}\left\langle X_{{\textbf{x}}}(\cdot ),\phi _{n}(\cdot )\right\rangle _{L^{2}({\mathcal {T}})} \left\langle X_{{\textbf{y}}}(\cdot ),\phi _{m}(\cdot )\right\rangle _{L^{2}({\mathcal {T}})} \\{} & {} P_{\Vert {\textbf{x}}-{\textbf{y}}\Vert } (dX_{{\textbf{x}}}(\cdot ),dX_{{\textbf{y}}}(\cdot )) \end{aligned}$$

being the spatial correlation operator applied to the elements \(\phi _{n}\) and \(\phi _{m}\) of the orthonormal basis \(\{ \phi _{n},\ n \ge 1\},\) for every \({\textbf{x}},{\textbf{y}}\in {\mathbb {R}}^d.\) Here, p(h) denotes the Radon–Nikodym derivative of the absolutely continuous marginal infinite-dimensional probability measure P(dh),  with respect to the uniform probability measure \(\mu (dh)\) in H,  constructed from the uniform measure on cylinder sets of H,  defined from Riesz Theorem (see, e.g., Gel’fand and Vilenkin 1968, and Ledoux and Talagrand 1991). The bivariate uniform measure on \(H^{2}\) is denoted as \(\mu (dh_{1}, dh_{2}).\)

Under the above setting of conditions, the resulting class of spatial functional random fields defines the infinite-dimensional version of Lancaster–Sarmanov random fields. In the simulation study undertaken in the next section, we analyze the asymptotic behavior of the Shannon entropy based mutual information between two random components of an element of this functional random field class. Specifically, from the infinite-dimensional formulation of Kullback–Leibler divergence established in Angulo and Ruiz-Medina (2023), we consider the following version of Shannon mutual information operator as a functional counterpart of Eq. 12: For \({\textbf{x}},{\textbf{y}}\in {\mathbb {R}}^d\), and \(n,m\ge 1,\)

$$\begin{aligned}{} & {} {\mathcal {S}}_{\varrho }(\Vert {\textbf{x}}-{\textbf{y}}\Vert ,n,m) \ \nonumber \\{} & {} \quad := \ {\mathcal {S}}_{\varrho }(\Vert {\textbf{x}}-{\textbf{y}}\Vert )(\phi _{n})(\phi _{m}) \nonumber \\{} & {} \quad = \int _{H^{2}} P_{\Vert {\textbf{x}}-{\textbf{y}}\Vert ,n,m}(dh_{1}, dh_{2}) \ln \left( \frac{p_{\Vert {\textbf{x}}-{\textbf{y}}\Vert ,n,m}(h_{1},h_{2})}{p(h_{1})p(h_{2})}\right) \nonumber \\{} & {} \quad = \int _{H^{2}} p(h_{1})~p(h_{2})~\nonumber \\{} & {} \qquad \left[ 1+\sum _{k=1}^{\infty }[\gamma _{\Vert {\textbf{x}}-{\textbf{y}}\Vert }(\phi _{n})(\phi _{m})]^{k}~{\mathcal {B}}_{k}(h_{1}) {\mathcal {B}}_{k}(h_{2})\right] \nonumber \\{} & {} \quad \quad \times \ln \left( 1+\sum _{k=1}^{\infty }[\gamma _{ \Vert {\textbf{x}}-{\textbf{y}}\Vert }(\phi _{n})(\phi _{m})]^{k}~{\mathcal {B}}_{k}(h_{1}) {\mathcal {B}}_{k}(h_{2})\right) \mu (dh_{1}, dh_{2}). \nonumber \\ \end{aligned}$$
(26)

4.2 Simulation study

Let \(\Upsilon (u)\), \(u\ge 0\), be a completely monotone function, and suppose further that \(\psi (u)\), \(u\ge 0\), is a positive function with a completely monotone derivative (such functions are also called Bernstein functions). Consider the function

$$\begin{aligned} C(\left\| \textbf{z}\right\| ,\tau )=\frac{\sigma ^{2}}{[\psi (\tau ^{2})]^{d/2}} \Upsilon \left( \frac{\left\| \textbf{z}\right\| ^{2}}{\psi (\tau ^{2})}\right) , \text { }\sigma ^{2}\ge 0,\text { }(\textbf{z},\tau )\in {\mathbb {R}}^{d}\times {\mathbb {R}}. \end{aligned}$$
(27)

Hence C is a covariance function under Gneiting’s criterion (see Gneiting 2002). Let now consider the special case of functions \(\Upsilon\) and \(\psi\) given by

$$\begin{aligned} \Upsilon (u)= & {} \frac{1}{(1+cu^{\gamma })^{\delta }},u>0,c>0,0<\gamma \le 1,\delta>0\nonumber \\ \psi (u)= & {} (1+au^{\alpha })^{\beta },\text { }a>0,\text { }0<\alpha \le 1,\text { }0<\beta \le 1,\text { }u\ge 0.\nonumber \\ \end{aligned}$$
(28)

Note that, functions \(\Upsilon\) and \(\psi\) can also be written as

$$\begin{aligned} \Upsilon (u)= & {} \frac{{\mathcal {L}}_{1}(u)}{u^{\gamma \delta }},\quad {\mathcal {L}}_{1}(u)=\frac{u^{\gamma \delta }}{(1+cu^{\gamma })^{\delta }}\nonumber \\ \psi (u)= & {} \left[ \frac{{\mathcal {L}}_{2}(u)}{u^{\alpha \beta }}\right] ^{-1},\quad {\mathcal {L}}_{2}=\frac{u^{\alpha \beta }}{(1+au^{\alpha })^{\beta }}, \end{aligned}$$
(29)

where \({\mathcal {L}}_{i},\) \(i=1,2,\) represent positive continuous slowly varying function at infinity, satisfying

$$\begin{aligned} \lim _{T\rightarrow \infty }\frac{{\mathcal {L}}_{i}\left( T\Vert \textbf{z}\Vert \right) }{{\mathcal {L}}\left( T\right) }=1, \quad i=1,2, \end{aligned}$$
(30)

for every \(\textbf{z}\in {\mathbb {R}}^{d}\), \(d\ge 1\), \(\textbf{z} \ne \textbf{0}\).

Applying Tauberian Theorems (see Doukhan et al. 1996; see also Leonenko and Olenko 2013, and Theorems 4 and 11 in Leonenko and Olenko 2014), their corresponding Fourier transforms satisfy

$$\begin{aligned} {\widehat{\Upsilon }}(\boldsymbol{\lambda} )= & {} \int _{{\mathbb {R}}^{d}}\exp \left( -i\left\langle \boldsymbol{\lambda} , \textbf{z}\right\rangle \right) \Upsilon (\Vert \textbf{z}\Vert ^{2})d\textbf{z} \nonumber \\\sim & {} c(1,2\gamma \delta ) \frac{{\mathcal {L}}_{1}\left( \frac{1}{\Vert \boldsymbol{\lambda} \Vert }\right) }{\Vert \boldsymbol{\lambda}\Vert^{d-2\gamma \delta } },\quad \text{ as } \Vert \boldsymbol{\lambda} \Vert \rightarrow \textbf{0}\nonumber \\ {\widehat{\psi }}(\omega )= & {} \int _{{\mathbb {R}}}\exp \left( -i\left\langle \omega , t\right\rangle \right) \psi (|t|^{2})dt \nonumber \\\sim & {} c(1,2\alpha \beta )\frac{{\mathcal {L}}_{2}\left( \frac{1}{|\omega |}\right) }{|\omega |^{1-2\alpha \beta }},\quad \text{ as } |\omega | \rightarrow 0,\nonumber \\ \end{aligned}$$
(31)

where \(c\left( d,\theta \right) =\frac{\Gamma \left( \frac{d-\theta }{2}\right) }{\pi ^{d/2}2^{\theta }\Gamma (\theta /2)},\) with \(\theta =2\gamma \delta ,\) and \(\theta =2\alpha \beta ,\) for \(0< 2\gamma \delta <d,\) and \(0<2\alpha \beta <1.\)

Figure 4 displays color plots surfaces of the Gaussian spatiotemporal random field, generated with covariance function in the Gneiting class for \(\alpha =0.3,\) \(\beta = 0.7,\) \(\gamma =0.2,\) and \(\delta =0.35,\) at times \(t=25, 50, 75,100.\) Shannon mutual information surfaces are evaluated from the reconstruction formula

$$\begin{aligned} {\mathcal {K}}_{{\mathcal {S}}_{\Vert {\textbf{x}}-{\textbf{y}}\Vert }}(t,s)=\sum _{n=1}^{M}\sum _{m=1}^{M}{\mathcal {S}}_{\varrho }(\Vert {\textbf{x}}-{\textbf{y}}\Vert )(\phi _{n})(\phi _{m}) \phi _{n}\otimes \phi _{m}(t,s) \end{aligned}$$

implemented for \(M=100.\) Figure 4 displays spatial cross–sections \({\mathcal {K}}_{{\mathcal {S}}_{\Vert {\textbf{x}}_{i}-{\textbf{y}}_{i}\Vert }}(t,s)\) corresponding to spatial nodes (i, 1),  \(i=1,2,3,4,5\) (labeled at the x-axis), and (i, 1),  \(i=6,7,8,9,10\) (labeled at the y-axis), at \((t,s)\in [1,100]\times [1,100].\) It can be observed the same power law in the decay of \({\mathcal {K}}_{{\mathcal {S}}_{\Vert {\textbf{x}}-{\textbf{y}}\Vert }}(t,s)\) as \(\Vert {\textbf{x}}-{\textbf{y}}\Vert \rightarrow \infty ,\) for each fixed \((t,s) \in [1,100]\times [1,100].\)

Fig. 4
figure 4

The surfaces values at times \(t=25, 50, 75,100\) of the Gaussian spatiotemporal random field generated with covariance function in the Gneiting class are displayed

Full size image
Fig. 5
figure 5

Shannon mutual information surfaces corresponding to crossing two random components respectively located at spatial nodes (i, 1),  \(i=1,2,3,4,5\) (values labeled at the x-axis), and (i, 1),  \(i=6,7,8,9,10\) (values labeled at the y-axis) of the \(10\times 10\) spatial regular grid considered, for crossing times in the set \(\left[ \{59,\dots , 99\}\right] ^{2}.\)

Full size image

5 Conclusion

This paper focuses on the asymptotic mutual information based analysis of a class of spatial and spatiotemporal LRD Lancaster–Sarmanov random fields, as well as their subordinated forms. Persistence of memory in space is characterized in terms of the LRD parameter, modeling the mutual information decay representing spatial structure dissipation at large scales. Random field subordination affects this decay rate when the rank m of the function \(\varphi\) involved is larger than one. Hence, large scale aggregation is lost up to order m. Faster decay to zero is then observed in the corresponding asymptotic order modeling a faster spatial structure dissipation from intermediate scales. However, when the rank is equal to one, as illustrated here in the case of \(\varphi\) being the indicator function, spatial structure dissipation occurs at the same rate, for the original and transformed random variables. The structural index provided by Rényi mutual information reflects some different behaviors depending on the characteristics of the polynomial basis (in our simulation study, Hermite or generalized Laguerre polynomials), as well as on the range analyzed for the q deformation parameter. Particularly, this range induces strong changes at small spatial scales, but the general shape of the curves reflecting asymptotic decay is invariant, and displays a power law involving the LRD and the deformation parameters.

In the spatiotemporal case, the class of Lancaster–Sarmanov random fields is introduced in a spatial functional framework. The simulation study undertaken shows a similar asymptotic behavior at spatial large scale level, i.e., power law decay of the mutual information surfaces, which is accelerated at coarser temporal scales. Thus, time varying asymptotic orders are obtained characterizing the spatial diversity loss in a functional framework, under an increasing domain asymptotics. Similar results will be derived, in a subsequent paper, regarding the asymptotic analysis of Shannon and Rényi mutual information measures, in an infinite-dimensional framework, in terms of time-varying spatial local complexity orders associated with a fixed domain asymptotics, reflecting limiting behaviors at high resolution levels.