Skip to main content
Springer Nature Link
Log in

Information measures through velocity time series in a seepage affected alluvial sinuous channel

  • Original Paper
  • Published:
Stochastic Environmental Research and Risk Assessment Aims and scope Submit manuscript

Abstract

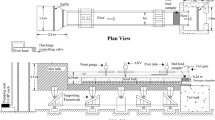
Alluvial channels with sinuosity follow an altered flow behavior, contradictory to straight flows. At the interface of surface water and groundwater, seepage is a significant phenomenon occurring at the boundary of alluvial channels. The study of turbulence in seepage affected sinuous alluvial channels would thus provide us with a better insight into their hydro-morphological behavior. To address the nature of turbulence in sinuous channel with downward seepage an experimental framework was design. The paper reports the structure of turbulence in the sinuous channel for no seepage and seepage flow. With downward seepage, there is a noticeable shift of Reynolds shear stress at near-bed, which reports more momentum transport. The average streamwise and transverse turbulence intensity increased by 3.8–18.5% and 4–10.6%, respectively with downward seepage. Calculation of Kolmogorov complexity and the Kolmogorov complexity spectrum suggests higher randomness in the outer region, which can be associated with excess momentum transport. In the lower flow depth \( \left( {{\text{z}}/{\text{h}}} = 0.2 \right)\), the randomness in the transverse velocities is higher in the outer region of the bend for about 25% and 38% compared to the central and inner region of the bend, respectively. With downward seepage, randomness increased especially in the outer region. This increase in randomness may report the erosive action in the outer part of the bend. Permutation entropy provided an informative measure to study the complex behavior of the transverse velocity time-series, which we found to be higher in the outer flow zone. For downward seepage, mean of entropy increased across the bend. The turbulent flow alterations and increase in randomness with seepage may be helpful to understand the flow in seepage affected sinuous alluvial channels.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Abad JD, Garcia MH (2009) Experiments in a high-amplitude Kinoshita meandering channel: 1. Implications of bend orientation on mean and turbulent flow structure. Water Resour Res. https://doi.org/10.1029/2008WR007016

    Article  Google Scholar 

  • Anwar HO (1986) Turbulent structure in a river bend. J Hydraul Eng 112(8):657–669

    Google Scholar 

  • Azami H, Escudero J (2016) Improved multiscale permutation entropy for biomedical signal analysis: interpretation and application to electroencephalogram recordings. Biomed Signal Process Control 23:28–41

    Google Scholar 

  • Bandt C, Pompe B (2002) Permutation entropy: a natural complexity measure for time series. Phys Rev Lett 88(17):174102

    Google Scholar 

  • Blanckaert K (2002) Secondary currents measured in sharp open-channel bends. In: 5th international conference on hydroinformatics river flow 2002

  • Blanckaert K, De Vriend HJ (2004) Secondary flow in sharp open-channel bends. J Fluid Mech 498:353–380

    Google Scholar 

  • Booij R (2003) Modeling the flow in curved tidal channels and rivers. In: Proceedings of the international conference on estuaries and coasts, pp 786–794

  • Callander RA (1978) River meandering. Annu Rev Fluid Mech 10(1):129–158

    Google Scholar 

  • Camporeale C, Perona P, Porporato A, Ridolfi L (2007) Hierarchy of models for meandering rivers and related morphodynamic processes. Rev Geophys. https://doi.org/10.1029/2005RG000185

    Article  Google Scholar 

  • Cao D, Chiew Y-M (2013) Suction effects on sediment transport in closed-conduit flows. J Hydraul Eng 140(5):4014008

    Google Scholar 

  • Chen X, Chiew Y-M (2004) Velocity distribution of turbulent open-channel flow with bed suction. J Hydraul Eng 130(2):140–148

    Google Scholar 

  • Crosato A (2008) Analysis and modelling of river meandering. Doctoral thesis, Universitá degli Studi di Padova geboren te Bolzano, Italië. IOS press (ISBN:978-1-58603-915-8)

  • de Vriend HJ, Geldof HJ (1983) Main flow velocity in short river bends. J Hydraul Eng 109(7):991–1011

    Google Scholar 

  • Deshpande V, Kumar B (2016) Turbulent flow structures in alluvial channels with curved cross-sections under conditions of downward seepage. Earth Surf Proc Land 41(8):1073–1087

    Google Scholar 

  • Dietrich WE, Dungan Smith J, Dunne T (1979) Flow and sediment transport in a sand bedded meander. J Geol 87(3):305–315

    Google Scholar 

  • Esfahani FS, Keshavarzi A (2011) Effect of different meander curvatures on spatial variation of coherent turbulent flow structure inside ingoing multi-bend river meanders. Stoch Environ Res Risk Assess 25(7):913–928

    Google Scholar 

  • Esfahani FS, Keshavarzi A (2013) Dynamic mechanism of turbulent flow in meandering channels: considerations for deflection angle. Stoch Environ Res Risk Assess 27(5):1093–1114

    Google Scholar 

  • Ferenets R et al (2006) Comparison of entropy and complexity measures for the assessment of depth of sedation. IEEE Trans Biomed Eng 53(6):1067–1077

    Google Scholar 

  • Goring DG, Nikora VI (2002) Despiking acoustic doppler velocimeter data. J Hydraul Eng 128(1):117–126

    Google Scholar 

  • Graf WH, Blanckaert K (2002) Flow around bends in rivers. In: 2nd international conference new trends in water and environmental engineering for safety and life: eco-compatible solutions for aquatic environments, pp 1–9

  • Henry M, Judge G (2019) Permutation entropy and information recovery in nonlinear dynamic economic time series. Econometrics 7(1):10

    Google Scholar 

  • Herrera-Granados O, Kostecki SW (2017) Experimental study of the influence of small upward seepage on open-channel flow turbulence. J Hydraul Eng 143(8):6017009

    Google Scholar 

  • Hu J, Gao J, Principe JC (2006) Analysis of biomedical signals by the Lempel–Ziv complexity: the effect of finite data size. IEEE Trans Biomed Eng 53(12):2606–2609

    Google Scholar 

  • Ichimiya M, Nakamura I (2013) Randomness representation in turbulent flows with Kolmogorov complexity (in mixing layer). J Fluid Sci Technol 8(3):407–422

    Google Scholar 

  • Lade AD, Mihailović A, Mihailović DT, Kumar B (2019) Randomness in flow turbulence around a bridge pier in a sand mined channel. Physica A Stat Mech Appl 535:122426

    Google Scholar 

  • Leopold LB, Langbein WB (1966) River Meanders. Sci Am 214(6):60–73

    Google Scholar 

  • Li X, Ouyang G, Richards DA (2007) Predictability analysis of absence seizures with permutation entropy. Epilepsy Res 77(1):70–74

    Google Scholar 

  • Li X, Cui S, Voss LJ (2008) Using permutation entropy to measure the electroencephalographic effects of sevoflurane. Anesthesiol J Am Soc Anesthesiol 109(3):448–456

    CAS  Google Scholar 

  • Li Y et al (2018) A fault diagnosis scheme for planetary gearboxes using adaptive multi-scale morphology filter and modified hierarchical permutation entropy. Mech Syst Signal Process 105:319–337

    Google Scholar 

  • Liu XX, Chiew Y-M (2012) Effect of seepage on initiation of cohesionless sediment transport. Acta Geophys 60(6):1778–1796

    Google Scholar 

  • Maclean AG (1991) Open channel velocity profiles over a zone of rapid infiltration. J Hydraul Res 29(1):15–27

    Google Scholar 

  • McKeogh EJ, Kiely GK (1989) Experimental study of the mechanisms of flood flow in meandering channels. In: Proceeding of 23rd IAHR Congress, Ottawa, Canada, pp 491–498

  • McLelland SJ, Nicholas AP (2000) A new method for evaluating errors in high-frequency ADV measurements. Hydrol Process 14(2):351–366

    Google Scholar 

  • Michael S (2005) Applied nonlinear time series analysis: applications in physics, physiology and finance. World Scientific, Singapore

    Google Scholar 

  • Mihailović DT, Nikolić-Dorić E, Drešković N, Mimić G (2014) Complexity analysis of the turbulent environmental fluid flow time series. Physica A Stat Mech Appl 395:96–104

    Google Scholar 

  • Mihailović D, Mimić G, Drešković N, Arsenić I (2015a) Kolmogorov complexity based information measures applied to the analysis of different river flow regimes. Entropy 17(5):2973–2987

    Google Scholar 

  • Mihailović DT, Mimić G, Nikolić-Djorić E, Arsenić I (2015b) Novel measures based on the Kolmogorov complexity for use in complex system behavior studies and time series analysis. Open Phys 13:1. https://doi.org/10.1515/phys-2015-0001

    Article  Google Scholar 

  • Mihailović D et al (2017) Randomness representation of turbulence in canopy flows using Kolmogorov complexity measures. Entropy 19(10):519

    Google Scholar 

  • Oldenziel DM, Brink WE (1974) Influence of suction and blowing on entrainment of sand particles. J Hydraul Div 100(7):935–949

    Google Scholar 

  • Omidvarnia A, Mesbah M, Pedersen M, Jackson G (2018) Range entropy: a bridge between signal complexity and self-similarity. Entropy 20(12):962

    Google Scholar 

  • Pincus SM (1991) Approximate entropy as a measure of system complexity. Proc Natl Acad Sci 88(6):2297–2301

    CAS  Google Scholar 

  • Pincus S (1995) Approximate entropy (ApEn) as a complexity measure. Chaos Interdiscip J Nonlinear Sci 5(1):110–117

    Google Scholar 

  • Radhakrishnan N, Wilson JD, Loizou PC (2000) An alternate partitioning technique to quantify the regularity of complex time series. Int J Bifurc Chaos 10(07):1773–1779

    Google Scholar 

  • Rao AR, Sreenivasulu G (2009) Design of plane sand-bed channels affected by seepage. Period Polytech Civ Eng 53(2):81–92

    Google Scholar 

  • Richardson JR, Abt SR, Richardson EV (1985) Inflow seepage influence on straight alluvial channels. J Hydraul Eng 111(8):1133–1147

    Google Scholar 

  • Richman JS, Moorman JR (2000) Physiological time-series analysis using approximate entropy and sample entropy. Am J Physiol Heart Circul Physiol 278(6):H2039–H2049

    CAS  Google Scholar 

  • Rozovskiῐ IL (1957) Flow of water in bends of open channels. Academy of Sciences of the Ukrainian SSR, Kiev

    Google Scholar 

  • Schumm SA (1963) Sinuosity of alluvial rivers on the Great Plains. Geol Soc Am Bull 74(9):1089–1100

    Google Scholar 

  • Sen AK (2009) Complexity analysis of riverflow time series. Stoch Environ Res Risk Assess 23(3):361–366

    Google Scholar 

  • Sharma A, Mihailović DT, Kumar B (2018) Randomness representation of turbulence in an alluvial channel affected by downward seepage. Physica A Stat Mech Appl 509:74–85

    Google Scholar 

  • Song Y, Crowcroft J, Zhang J (2012) Automatic epileptic seizure detection in EEGs based on optimized sample entropy and extreme learning machine. J Neurosci Methods 210(2):132–146

    Google Scholar 

  • Sreenivasulu G, Kumar B, Rao AR (2011) Variation of stream power with seepage in sand-bed channels. Water SA. https://doi.org/10.4314/wsa.v37i1.64115

    Article  Google Scholar 

  • Srinivasan V, Eswaran C, Sriraam N (2007) Approximate entropy-based epileptic EEG detection using artificial neural networks. IEEE Trans Inf Technol Biomed 11(3):288–295

    Google Scholar 

  • Sukhodolov A, Kaschtschejewa E (2010) Turbulent flow in a meander bend of a lowland river: field measurements and preliminary results. In: River flow, pp 309–316

  • Taye J, Barman J, Kumar B, Oliveto G (2020) Deciphering morphological changes in a sinuous river system by higher-order velocity moments. Water 12(3):772

    Google Scholar 

  • Tennekes H, Lumley JL, Lumley JL et al (1972) A first course in turbulence. MIT Press, Cambridge

    Google Scholar 

  • Termini D (2009) Experimental observations of flow and bed processes in large-amplitude meandering flume. J Hydraul Eng 135(7):575–587

    Google Scholar 

  • Thorne CR et al (1985) Direct measurements of secondary currents in a meandering sand-bed river. Nature 315(6022):746

    Google Scholar 

  • Xu K, Wang J (2017) Weighted fractional permutation entropy and fractional sample entropy for nonlinear Potts financial dynamics. Phys Lett A 381(8):767–779

    CAS  Google Scholar 

  • Yalin MS, da Silva AMF (2001) Fluvial processes. IAHR monograph. International Association for Hydraulic Research, Delft

    Google Scholar 

  • Zhang X-S, Roy RJ, Jensen EW (2001) EEG complexity as a measure of depth of anesthesia for patients. IEEE Trans Biomed Eng 48(12):1424–1433

    CAS  Google Scholar 

  • Zhou S et al (2018) A novel bearing multi-fault diagnosis approach based on weighted permutation entropy and an improved SVM ensemble classifier. Sensors 18(6):1934

    Google Scholar 

  • Zhu X, Xu H, Zhao J, Tian J (2017) Automated epileptic seizure detection in scalp EEG based on spatial-temporal complexity. Complexity. https://doi.org/10.1155/2017/5674392

    Article  Google Scholar 

  • Zunino L et al (2009) Forbidden patterns, permutation entropy and stock market inefficiency. Physica A Stat Mech Appl 388(14):2854–2864

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil Engineering, Indian Institute of Technology, Guwahati, Guwahati, 781039, India

    Jyotismita Taye, Abhijit D. Lade & Bimlesh Kumar

  2. Novi Sad, Serbia

    Anja Mihailović

  3. Faculty of Science, Department of Physics, University of Novi Sad, D. Obradovića Sq. 3, 21000, Novi Sad, Serbia

    Dragutin T. Mihailović

Authors
  1. Jyotismita Taye
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Abhijit D. Lade
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Anja Mihailović
    View author publications

    You can also search for this author inPubMed Google Scholar

  4. Dragutin T. Mihailović
    View author publications

    You can also search for this author inPubMed Google Scholar

  5. Bimlesh Kumar
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Bimlesh Kumar.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Taye, J., Lade, A.D., Mihailović, A. et al. Information measures through velocity time series in a seepage affected alluvial sinuous channel. Stoch Environ Res Risk Assess 34, 1925–1938 (2020). https://doi.org/10.1007/s00477-020-01849-2

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00477-020-01849-2

Keywords