Skip to main content
Springer Nature Link
Log in

CVaR-based factorial stochastic optimization of water resources systems with correlated uncertainties

  • Original Paper
  • Published:
Stochastic Environmental Research and Risk Assessment Aims and scope Submit manuscript

Abstract

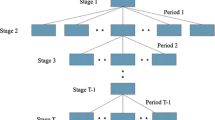
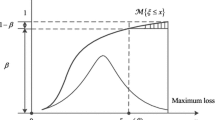
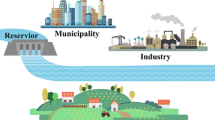
In this paper, a conditional value-at-risk based factorial stochastic programming approach is proposed to address random uncertainties and their interactions in a systematic manner. Random variables can be addressed through a risk-averse method within the two-stage stochastic programming framework. Interactions between random variables are examined through conducting a multi-level factorial analysis. The proposed approach is applied to a case study of water resources management to demonstrate its validity and applicability. A number of decision alternatives are obtained under different risk coefficients, which are useful for decision-makers to make sound water management plan and to perform an in-depth analysis of trade-offs between economic objectives and associated risks. Results obtained from the factorial experiment uncover the multi-level interactions between uncertain parameters and their contributions to the variability of net benefits. The performance of the proposed approach is compared with a factorial two-stage stochastic programming method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  • Ahmed S (2006) Convexity and decomposition of mean-risk stochastic programs. Math Program 106(3):433–446

    Article  Google Scholar 

  • Birge JR, Louveaux FV (1988) A multicut algorithm for two-stage stochastic linear programs. Eur J Oper Res 34(3):384–392

    Article  Google Scholar 

  • Carneiro MC, Ribas GP, Hamacher S (2010) Risk management in the oil supply chain: a CVaR approach. Ind Eng Chem Res 49(7):3286–3294

    Article  CAS  Google Scholar 

  • Chan TC, Mahmoudzadeh H, Purdie TG (2014) A robust-CVaR optimization approach with application to breast cancer therapy. Eur J Oper Res 238(3):876–885

    Article  Google Scholar 

  • Claessens S, Kreuser J (2004) A framework for strategic foreign reserves risk management. European Central Bank, Germany

    Google Scholar 

  • Ezenwaji EE, Anyadike RN, Igu NI (2014) Optimal allocation of public water supply to the urban sectors of Enugu, Nigeria: a linear programming approach. Appl Water Sci 4(1):73–78

    Article  Google Scholar 

  • Fan YR, Huang GH, Guo P, Yang AL (2012) Inexact two-stage stochastic partial programming: application to water resources management under uncertainty. Stoch Environ Res Risk Assess 26(2):281–293

    Article  Google Scholar 

  • Ganji A, Khalili D, Karamouz M, Ponnambalam K, Javan M (2008) A fuzzy stochastic dynamic Nash game analysis of policies for managing water allocation in a reservoir system. Water Resour Manag 22(1):51–66

    Article  Google Scholar 

  • Han Y, Huang Y, Wang G (2011) Interval-parameter linear optimization model with stochastic vertices for land and water resources allocation under dual uncertainty. Environ Eng Sci 28(3):197–205

    Article  CAS  Google Scholar 

  • Haro D, Paredes J, Solera A, Andreu J (2012) A model for solving the optimal water allocation problem in river basins with network flow programming when introducing non-linearities. Water Resour Manag 26(14):4059–4071

    Article  Google Scholar 

  • Huang GH (1996) IPWM: an interval parameter water quality management model. Eng Optim + A35 26(2):79–103

    Article  Google Scholar 

  • Huang GH, Chang NB (2003) The perspectives of environmental informatics and systems analysis. J Environ Inf 1(1):1–7

    Article  Google Scholar 

  • Huang GH, Loucks DP (2000) An inexact two-stage stochastic programming model for water resources management under uncertainty. Civ Eng Syst 17(2):95–118

    Article  Google Scholar 

  • Karamouz M, Houck MH (1987) Comparision of stochastic and deterministic dynamic programming for reservoir operating rule generation. J Am Water Resour Assoc 23:1–9

    Article  Google Scholar 

  • Lewis SM, Dean AM (2001) Detection of interactions in experiments on large numbers of factors. J R Stat Soc Ser B Stat Methodol 63(4):633–672

    Article  Google Scholar 

  • Li CY, Zhang L (2015) An inexact two-stage allocation model for water resources management under uncertainty. Water Resour Manag 29(6):1823–1841

    Article  Google Scholar 

  • Li YP, Huang GH, Huang YF, Zhou HD (2009) A multistage fuzzy-stochastic programming model for supporting sustainable water-resources allocation and management. Environ Model Softw 24(7):786–797

    Article  CAS  Google Scholar 

  • Li W, Li YP, Li CH, Huang GH (2010) An inexact two-stage water management model for planning agricultural irrigation under uncertainty. Agric Water Manag 97(11):1905–1914

    Article  Google Scholar 

  • Li W, Wang B, Xie YL, Huang GH, Liu L (2015) An inexact mixed risk-aversion two-stage stochastic programming model for water resources management under uncertainty. Environ Sci Pollut Res 22(4):2964–2975

    Article  CAS  Google Scholar 

  • Luo B, Maqsood I, Yin YY, Huang GH, Cohen SJ (2003) Adaption to climate change through water trading under uncertainty: an inexact two-stage nonlinear programming approach. J Environ Inf 2(2):58–68

    Article  Google Scholar 

  • Maqsood I, Huang GH (2003) A two-stage interval-stochastic programming model for waste management under uncertainty. J Air Waste Manag Assoc 53(5):540–552

    Article  Google Scholar 

  • Maqsood I, Huang G, Huang Y, Chen B (2005) ITOM: an interval-parameter two-stage optimization model for stochastic planning of water resources systems. Stoch Environ Res Risk Assess 19(2):125–133

    Article  Google Scholar 

  • Montgomery DC (2000) Design and analysis of experiments, 5th edn. Wiley, New York

    Google Scholar 

  • Montgomery DC, Runger GC (2003) Applied statistics and probability for engineers, 3rd edn. Wiley, New York

    Google Scholar 

  • Qin XS, Huang GH, Chakma A (2008) Modeling groundwater contamination under uncertainty: a factorial-design-based stochastic approach. J Environ Inf 11(1):11–20

    Article  Google Scholar 

  • Quaranta AG, Zaffaroni A (2008) Robust optimization of conditional value at risk and portfolio selection. J Bank Finance 32(10):2046–2056

    Article  Google Scholar 

  • Reca J, Roldán J, Alcaide M, López R, Camacho E (2001) Optimisation model for water allocation in deficit irrigation systems: I. Description of the model. Agric Water Manag 48(2):103–116

    Article  Google Scholar 

  • Rockafellar RT, Uryasev S (2000) Optimization of conditional value-at-risk. J Risk 2:21–42

    Article  Google Scholar 

  • Rockafellar RT, Uryasev S (2002) Conditional value-at-risk for general loss distributions. J Bank Finance 26(7):1443–1471

    Article  Google Scholar 

  • Wang S, Huang GH (2013a) Interactive fuzzy boundary interval programming for air quality management under uncertainty. Water Air Soil Pollut 224(5):1–16

    Article  Google Scholar 

  • Wang S, Huang GH (2013b) An interval-parameter two-stage stochastic fuzzy program with type-2 membership functions: an application to water resources management. Stoch Environ Res Risk Assess 27(6):1493–1506

    Article  Google Scholar 

  • Wang S, Huang GH (2013c) A coupled factorial-analysis-based interval programming approach and its application to air quality management. J Air Waste Manag Assoc 63(2):179–189

    Article  CAS  Google Scholar 

  • Wang S, Huang GH (2015) A multi-level Taguchi-factorial two-stage stochastic programming approach for characterization of parameter uncertainties and their interactions: an application to water resources management. Eur J Oper Res 240(2):572–581

    Article  Google Scholar 

  • Wang S, Huang GH (2016) Risk-based factorial probabilistic inference for optimization of flood control systems with correlated uncertainties. Eur J Oper Res. 249(1): 258–269 doi:10.1016/j.ejor.2015.08.023

    Google Scholar 

  • Wang S, Huang GH, Baetz BW, Huang W (2015) A polynomial chaos ensemble hydrologic prediction system for efficient parameter inference and robust uncertainty assessment. J Hydrol 530:716–733

    Article  Google Scholar 

  • Wang LZ, Fang L, Hipel KW (2003) Water resources allocation: a cooperative game theoretic approach. J Environ Inf 2(2):11–22

    Article  Google Scholar 

  • Wang JF, Cheng GD, Gao YG, Long AH, Xu ZM, Li X et al (2008) Optimal water resource allocation in arid and semi-arid areas. Water Resour Manag 22(2):239–258

    Article  CAS  Google Scholar 

  • Wang X, Cui Q, Li S (2012) An optimal water allocation model based on water resources security assessment and its application in Zhangjiakou region, northern china. Resour Conserv Recycl 69(12):57–65

    Google Scholar 

  • Wang YY, Huang GH, Wang S, Li W (2015) A stochastic programming with imprecise probabilities model for planning water resources systems under multiple uncertainties. Stoch Environ Res Risk Assess 1–10

  • Wang YY, Huang GH, Wang S, Li W, Guan PB (2016) A risk-based interactive multi-stage stochastic programming approach for water resources planning under dual uncertainties. Adv Water Resour 94:217–230

    Article  CAS  Google Scholar 

  • Webby RB, Adamson PT, Boland J, Howlett PG, Metcalfe AV, Piantadosi J (2007) The Mekong—applications of value at risk (VaR) and conditional value at risk (CVaR) simulation to the benefits, costs and consequences of water resources development in a large river basin. Ecol Model 201(1):89–96

    Article  Google Scholar 

  • Xevi E, Khan S (2005) A multi-objective optimization approach to water management. J Environ Manag 77(4):269–277

    Article  CAS  Google Scholar 

  • Zhou Y, Huang GH (2011) Factorial two-stage stochastic programming for water resources management. Stoch Environ Res Risk Assess 25(1):67–78

    Article  Google Scholar 

  • Zhou Y, Huang GH, Yang B (2013) Water resources management under multi-parameter interactions: a factorial multi-stage stochastic programming approach. Omega 41(3):559–573

    Article  Google Scholar 

Download references

Acknowledgments

This research was supported by the National Natural Science Foundation of China (51225904, 51190095 and 51109077), the 111 Project (B14008), and the Fundamental Research Funds for the Central Universities (2014XS69). The authors would like to express thanks to the editor and the anonymous reviewers for their constructive comments and suggestions.

Author information

Authors and Affiliations

  1. MOE Key Laboratory of Regional Energy Systems Optimization, S&C Resources and Environmental Research Academy, North China Electric Power University, Beijing, 102206, China

    Y. Y. Wang

  2. Faculty of Engineering and Applied Science, University of Regina, Regina, SK, S4S 0A2, Canada

    G. H. Huang & S. Wang

Authors
  1. Y. Y. Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. G. H. Huang
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. S. Wang
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to G. H. Huang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Y.Y., Huang, G.H. & Wang, S. CVaR-based factorial stochastic optimization of water resources systems with correlated uncertainties. Stoch Environ Res Risk Assess 31, 1543–1553 (2017). https://doi.org/10.1007/s00477-016-1276-9

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00477-016-1276-9

Keywords