Abstract
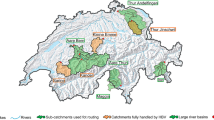
With the potentially devastating consequences of flooding, it is crucial that uncertainties in the modelling process are quantified in flood simulations. In this paper, the impact of uncertainties in design losses on peak flow estimates is investigated. Simulations were carried out using a conceptual rainfall–runoff model called RORB in four catchments along the east coast of New South Wales, Australia. Monte Carlo simulation was used to evaluate parameter uncertainty in design losses, associated with three loss models (initial loss–continuing loss, initial loss–proportional loss and soil water balance model). The results show that the uncertainty originating from each loss model differs and can be quite significant in some cases. The uncertainty in the initial loss–proportional loss model was found to be the highest, with estimates up to 2.2 times the peak flow, whilst the uncertainty in the soil water balance model was significantly less, with up to 60 % variability in peak flows for an annual exceedance probability of 0.02. Through applying Monte Carlo simulation a better understanding of the predicted flows is achieved, thus providing further support for planning and managing river systems.








Similar content being viewed by others
Explore related subjects
Discover the latest articles and news from researchers in related subjects, suggested using machine learning.References
Beven K (2006) A manifesto for the equifinality thesis. J Hydrol 320(1–2):18–36. doi:10.1016/j.jhydrol.2005.07.007
Blong R (2005) Natural hazards risk assessment—an Australian perspective. Issues in Risk Science 4. Benfield Hazard Research Centre. London. p 28. http://www.preventionweb.net/english/professional/publications/v.php?id=2954. Accessed 10 June 2013
Bureau of Infrastructure, Transport and Regional Economics (BITRE) (2008) About Australia’s regions 2008. Department of Infrastructure, Transport and Regional Economics. Canberra, Australia. http://www.bitre.gov.au/publications/2008/files/other_005_RegStats_2008.pdf. Accessed 4 April 2011
Caballero WL, Rahman A (2013) Development of regionalized joint probability approach to flood estimation: a case study for eastern New South Wales. Hydrol Process, Australia. doi:10.1002/hyp.9919
Charalambous J, Rahman A, Carroll D (2013) Application of Monte Carlo simulation technique to design flood estimation: a case study for North Johnstone River in Queensland, Australia. Water Resour Manag. doi:10.1007/s11269-013-0398-9
Cordery I (1970) Antecedent wetness for design flood estimation. Civil Eng Trans CE12:181–184
Dyer BG, Nathan RJ, McMahon TA, O’Neill IC (1994) Development of regional prediction equations for the RORB runoff routing model. CRC for catchment hydrology. Report 94/1
Haddad K, Rahman A, Weinmann PE, Kuczera G, Ball JE (2010) Streamflow data preparation for regional flood frequency analysis: lessons from South-East Australia. Aust J Water Resour 14(1):17–32
Hill PI, Maheepala U, Mein RG (1996) Empirical analysis of data to derive losses: methodology, programs and results. CRC for catchment hydrology. Working Document 96/5
Hill PI, Graszkiewicz, Z, Sih K, Rahman A (2013) Project 6: loss models for catchment simulation—rural catchments. Report prepared by Sinclair Knight Merz for the Institution of Engineers, Australia. http://www.ncwe.org.au/arr/comm_report.html. Accessed 13 March 2013
Huang M, Liang X (2006) On the assessment of the impact of reducing parameters and identification of parameter uncertainties for a hydrologic model with applications to ungauged basins, J Hydrol 320(1–2):37–61. http://dx.doi.org/10.1016/j.jhydrol.2005.07.010
Ilahee M (2005) Modelling Losses in Flood Estimation. Doctoral Dissertation. School of Urban Development, University of Queensland, St Lucia
Jothityangkoon C, Sivapalan M (2003) Towards estimation of extreme floods: examination of the roles of runoff process changes and floodplain flows. J Hydrol 281(3):206–229. doi:10.1016/S0022-1694(03)00237-3
Kavetski D, Kuczera G, Franks SW (2006) Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory. Water Resour Res. doi:10.1029/2005WR004368
Koehler MA, Linsley RK (1951) Predicting the runoff from storm rainfall. Research Paper no. 34. Weather Bureau, US Dept of Commerce. Washington
Kuczera G (1999) Comprehensive at-site flood frequency analysis using Monte Carlo Bayesian inference. Water Resour Res 35(5):1551–1557. doi:10.1029/1999WR900012
Laurenson EM, Mein RG, Nathan RJ (2010) RORB version 6 runoff routing program: User manual. Monash University and Sinclair Knight Merz, Melbourne
Levy JK, Hall J (2005) Advances in flood risk management under uncertainty. Stoch Environ Res Risk Assess 19:375–377. doi:10.1007/s00477-005-0005-6
Loveridge M, Rahman A, Hill P, Babister M (2013) Investigation into probabilistic losses for design flood estimation: a case study for the Orara River catchment, NSW. Aust J Water Resour 17(1):13–24. doi:10.7158/W12-034.2013.17.1
Mein RG, Nandakumar N, Siriwardena L (1995) Estimation of initial loss from soil moisture indices (Pilot Study). CRC for catchment hydrology. Working Document 95/1
Minty LJ, Meighen J (1999) Rainfall antecedent to large and extreme rainfall bursts over southeast Australia. Hydrology Report Series, Report No. 6. Bureau of Meteorology, Melbourne
Moore RJ, Clarke RT (1981) A distribution function approach to rainfall–runoff modelling. Water Resour Res 17:1367–1382
Murphy R, Graszkiewicz Z, Hill PI, Neal B, Nathan R (2011) Project 7: baseflow for catchment simulation. Report prepared by Sinclair Knight Merz for the Institution of Engineers, Melbourne. http://www.ncwe.org.au/arr/comm_report.html. Accessed 12 October 2012
Pilgrim DH (ed) (1987) Australian rainfall and runoff: A guide to flood estimation, vol 1. Institution of Engineers Australia, Canberra
Pilgrim DH, Robinson DK (1988) Flood Estimation in Australia - Progress to the Present, Possibilities for the Future. Civil Eng Trans CE30:87–206
Rahman A, Weinmann PE, Hoang TMT, Laurenson EM (2002a) Monte Carlo simulation of flood frequency curves from rainfall. J Hydrol 256(3–4):196–210. doi:10.1016/S0022-1694(01)00533-9
Rahman A, Weinmann E, Mein RG (2002b) The use of probability-distributed initial losses in design flood estimation. Aust J Water Resour 6(1):17–29
Refsgaard JC, van der Sluijsb JP, Brownc J, van der Keur P (2006) A framework for dealing with uncertainty due to model structure error. Adv Water Resour 29(11):1586–1597. http://dx.doi.org/10.1016/j.advwatres.2005.11.013
Tian Y, Booij MJ, Xu YP (2013) Uncertainty in high and low flows due to model structure and parameter errors. Stoch Environ Res Risk Assess. doi:10.1007/s00477-013-0751-9
Tularam GA, Ilahee M (2007) Initial loss estimates for tropical catchments of Australia. Environ Impact Assess Rev 27:493–504. doi:10.1016/j.eiar.2006.12.006
Vrugt JA, ter Braak CJF, Gupta HV, Robinson BA (2008) Equifinality of formal (DREAM) and informal (GLUE) Bayesian approaches in hydrologic modeling? Stoch Environ Res Risk Assess 23(7):1011–1026. doi:10.1007/s00477-008-0274-y
Wagener T, Gupta H (2005) Model identification for hydrological forecasting under uncertainty. Stoch Environ Res Risk Assess 19:378–387. doi:10.1007/s00477-005-0006-5
Water and Rivers Commission (2003) SWMOD A rainfall loss model for calculating rainfall excess User Manual (Version 2.11). Prepared by Hydrology and Water Resources Branch Resource Science Division
Zhao RJ, Zhuang Y-L, Fang L-R, Liu X-R, Zhang Q-S (1980) The Xinanjiang model. Hydrological forecasting. International Association of Hydrological Sciences (IAHS) Press, Wallingford, pp 51–356
Acknowledgments
The authors wish to thank Peter Hill, Mark Babister and Dharma Hagare for their constructive comments to this research. They would also like to acknowledge Sinclair Knight Merz (SKM) for providing an enhanced version of the RORB model for use in this study.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Loveridge, M., Rahman, A. Quantifying uncertainty in rainfall–runoff models due to design losses using Monte Carlo simulation: a case study in New South Wales, Australia. Stoch Environ Res Risk Assess 28, 2149–2159 (2014). https://doi.org/10.1007/s00477-014-0862-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00477-014-0862-y