Skip to main content

Advertisement

Springer Nature Link
Log in

A stochastic model for optimal operation of inter-basin water allocation systems: a case study

  • Original Paper
  • Published:
Stochastic Environmental Research and Risk Assessment Aims and scope Submit manuscript

Abstract

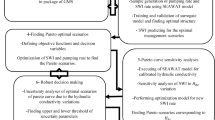
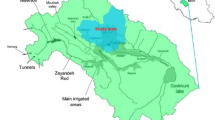
This paper presents a new methodology for optimal operation of inter-basin water transfer systems by conjunctive use of surface water resources in water donor basin and groundwater resources in water receiving basin. To incorporate the streamflow uncertainty, an integrated stochastic dynamic programming (ISDP) model is developed. In the ISDP, the monthly inflow to the reservoir in the water donor basin, the water storage of the reservoir, and the water storage of the aquifer in the water receiving basin are considered as state variables. A water allocation optimization model is embedded in the main structure of ISDP and a new ensemble streamflow prediction model based on K-nearest-neighbourhood algorithm is also developed and linked to the ISDP. By using a new reoptimization process, the ISDP model provides monthly policies for water allocation to users in water donor and receiving basins. As water users can form a coalition to increase their benefits, several solution concepts in cooperative game theory, namely Nash–Harsanyi, Shapley, Nucleolus, Weak Nucleolus, Proportional Nucleolus, Separable Costs Remaining Benefits (SCRBs) and Minimum Costs Remaining Savings are utilized to determine the profit of each water user. In the last step, stakeholders make negotiation over these solution concepts using the Fallback bargaining theory to reach a unanimous agreement on the final distribution of the total benefit. The methodology is applied to an inter-basin water transfer project and the results show that the Shapley and SCRB solutions concepts can provide better distributions for the total benefit and the total benefit of water users is increased by a factor of 1.6 when they participate in a grand coalition.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Explore related subjects

Discover the latest articles and news from researchers in related subjects, suggested using machine learning.

References

  • Abed-Elmdoust A, Kerachian R (2012) Water resources allocation using a cooperative game with fuzzy payoffs and fuzzy coalitions. Water Resour Manag 26(13):3961–3976

    Google Scholar 

  • Abed-Elmdoust A, Kerachian R (2013) Incorporating economic and political considerations in inter-basin water allocations: a case study. Water Resour Manag 27(3):859–870

    Google Scholar 

  • Ben Alaya A, Souissi A, Tarhouni J, Ncib K (2003) Optimization of Nebhana reservoir water allocation by stochastic dynamic programming. Water Resour Manag 17(4):259–272

    Article  Google Scholar 

  • Brams SJ, Kilgour MD (2001) Fallback bargaining. Group Decis Negot 10:287–316

    Article  Google Scholar 

  • Dinar A, Howitt RE (1997) Mechanisms for allocation of environmental control cost: empirical tests of acceptability and stability. J Environ Manag 49:183–203

    Article  Google Scholar 

  • Eum HI, Kim YO, Palmer RN (2011) Optimal drought management using sampling stochastic dynamic programming with a hedging rule. J Water Resour Plan Manag 137:113–122

    Article  Google Scholar 

  • Faber BA, Stedinger JR (2001) Reservoir optimization using sampling SDP with ensemble streamflow prediction (ESP) forecasts. J Hydrol 249:113–133

    Article  Google Scholar 

  • Fan YR, Huang GH, Guo P, Yang AL (2012) Inexact two-stage stochastic partial programming: application to water resources management under uncertainty. Stoch Environ Res Risk Assess 26(2):281–293

    Article  Google Scholar 

  • Fu DZ, Li YP, Huang GH (2012) A fuzzy-Markov-chain-based analysis method for reservoir operation. Stoch Environ Res Risk Assess 26(3):375–391

    Article  Google Scholar 

  • Guo P, Huang GH (2009) Two-stage fuzzy chance-constrained programming: application to water resources management under dual uncertainties. Stoch Environ Res Risk Assess 23(3):349–359

    Article  Google Scholar 

  • Guo P, Chen X, Li M, Li J (2013) Fuzzy chance-constrained linear fractional programming approach for optimal water allocation. Stoch Environ Res Risk Assess 1-12

  • Han JC, Huang GH, Zhang H (2012) Fuzzy constrained optimization of eco-friendly reservoir operation using self-adaptive genetic algorithm: a case study of a cascade reservoir system in the Yalong River, China. Ecohydrology 5:768–778

    Article  Google Scholar 

  • Harsanyi JC (1959) A bargaining model for the cooperative n-person game. In: Tucker AW, Luce DR (eds) Contributions to the theory of games, vol 4. Princeton University Press, Princeton, pp 324–356

    Google Scholar 

  • Heaney JP, Dickinson RE (1982) Methods for apportioning the cost of a water resource project. Water Resour Res 18:476–482

    Article  Google Scholar 

  • Jafarzadegan K, Abed-Elmdoust A, Kerachian R (2013) A fuzzy variable least core game for inter-basin water resources allocation under uncertainty. Water Resour Manag 27(9):3247–3260

    Google Scholar 

  • Kang P, Cho S (2008) Locally linear reconstruction for instance-based learning. J Pattern Recognit 41:3507–3518

    Article  Google Scholar 

  • Karlsson M, Yakowitz S (1987) Nearest neighbour methods for time series with application to rainfall–runoff prediction. In: MacNeil JB, Humphries GH (eds) Stochastic hydrology. D. Reidel, Hingham, pp 149–160

    Google Scholar 

  • Kerachian R, Karamouz M (2007) A stochastic conflict resolution model for water quality management in reservoir–river systems. Adv Water Resour 30(4):866–882

    Article  Google Scholar 

  • Kim Y, Eum H, Lee E, Ko I (2007) Optimizing operational policies of a Korean multireservoir system using sampling stochastic dynamic programming with ensemble streamflow prediction. J Water Resour Plan Manag 133:4–14

    Article  Google Scholar 

  • Lejano RP, Davos CA (1995) Cost allocation of multiagency water resource projects: game-theoretic approaches and case study. Water Resour Res 31:1387–1393

    Article  Google Scholar 

  • Li YP, Huang GH, Chen X (2009) Multistage scenario-based interval-stochastic programming for planning water resources allocation. Stoch Environ Res Risk Assess 23(6):781–792

    Article  Google Scholar 

  • Liu P, Zhao J, Li L, Shen Y (2012) Optimal reservoir operation using stochastic dynamic programming. J Water Resour Prot 4(6):342–345

    Article  Google Scholar 

  • Madani K, Dinar A (2011) Exogenous regulatory institutions for sustainable management of common pool resources. Working Paper 01-0311. Water Science and Policy Center, University of California, Riverside

    Google Scholar 

  • Madani K, Dinar A (2012a) Cooperative institutions for sustainable common pool resource management: application to groundwater. Water Resour Res 48(9):W09553. doi:10.1029/2011WR010849

    Article  Google Scholar 

  • Madani K, Dinar A (2012b) Non-cooperative institutions for sustainable common pool resource management: application to groundwater. Ecol Econ 74:34–45. doi:10.1016/j.ecolecon.2011.12.006

    Article  Google Scholar 

  • Madani K, Shalikarian L, Naeeni STO (2011) Resolving hydro-environmental conflicts under uncertainty using Fallback bargaining procedure. In: Proceeding of the 2011 international conference on environment science and engineering (ICESE 2011), Bali Island, Indonesia, pp 192–196

  • Mahjouri N, Ardestani M (2010) A game theoretic approach for interbasin water resources allocation considering the water quality issues. Environ Monit Assess 167:527–544

    Article  Google Scholar 

  • Mahjouri N, Ardestani M (2011) Application of cooperative and non-cooperative games in large-scale water quantity and quality management: a case study. Environ Monit Assess 172:157–169

    Article  Google Scholar 

  • Mahjouri N, Bizhani-Manzar M (2013) Waste load allocation in rivers using Fallback bargaining. Water Resour Manag 27(7):2125–2136

    Google Scholar 

  • Maqsood I, Huang GH, Huang Y, Chen B (2005) ITOM: an interval-parameter two-stage optimization model for stochastic planning of water resources systems. Stoch Environ Res Risk Assess 19(2):125–133

    Article  Google Scholar 

  • Mousavi S, Karamouz M, Menhadj M (2004) Fuzzy-state stochastic dynamic programming for reservoir operation. Water Resour Plan Manag 130(6):460–470

    Article  Google Scholar 

  • Mujumdar PP, Ramesh TSV (1997) Real-time reservoir operation for irrigation. Water Resour Res 33:1157–1164

    Article  Google Scholar 

  • Nikoo MR, Kerachian R, Poorsepahy-Samian H (2012) An interval parameter model for cooperative inter-basin water resources allocation considering the water quality issues. Water Resour Manag 26(1):3329–3343

    Google Scholar 

  • Sadegh M, Kerachian R (2011) Water resources allocation using solution concepts of fuzzy cooperative games: fuzzy least core and fuzzy weak least core. Water Resour Manag 25:2543–2573

    Article  Google Scholar 

  • Schmeidler D (1969) The nucleolus of a characteristic function game. SIAM J Appl Math 17(6):1163–1170

    Article  Google Scholar 

  • Shapley LS (1953) A value for n-person games, in contribution to the theory of games II. In: Kuhn HW, Tucker AW (eds) Annals math studies, vol 28. Princeton University Press, Princeton

    Google Scholar 

  • Sheikhmohammady M, Madani K (2008) Bargaining over the Caspian Sea—the largest lake on the earth. In: Babcock RW, Walton R (eds) Proceeding of the 2008 world environmental and water resources congress, Honolulu, Hawaii. ASCE. doi:10.1061/40976(316)262

  • Tejada-Guibert JA, Johnson SA, Stedinger JR (1993) Comparison of two approaches for implementing multireservoir operating policies derived using stochastic dynamic programming. Water Resour Res 29:3969–3980

    Article  Google Scholar 

  • Umamahesh NV, Sreenivasulu P (1997) Two-phase stochastic dynamic programming model for optimal operation of irrigation reservoir. Water Resour Manag 11:395–406

    Article  Google Scholar 

  • Vedula S, Mujumdar PP (1992) Optimal reservoir operation for irrigation of multiple crops. Water Resour Res 28:1–9

    Article  Google Scholar 

  • Young HP, Okada N, Hashimoto T (1982) Cost allocation in water resources development. Water Resour Res 18:463–475

    Article  Google Scholar 

  • Zhou Y, Huang GH (2011) Factorial two-stage stochastic programming for water resources management. Stoch Environ Res Risk Assess 25(1):67–78

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Civil Engineering, College of Engineering, University of Tehran, Tehran, Iran

    Keighobad Jafarzadegan & Armaghan Abed-Elmdoust

  2. Center of Excellence for Engineering and Management of Civil Infrastructures, School of Civil Engineering, College of Engineering, University of Tehran, Tehran, Iran

    Reza Kerachian

Authors
  1. Keighobad Jafarzadegan
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Armaghan Abed-Elmdoust
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Reza Kerachian
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Reza Kerachian.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jafarzadegan, K., Abed-Elmdoust, A. & Kerachian, R. A stochastic model for optimal operation of inter-basin water allocation systems: a case study. Stoch Environ Res Risk Assess 28, 1343–1358 (2014). https://doi.org/10.1007/s00477-013-0841-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00477-013-0841-8

Keywords

Profiles

  1. Reza Kerachian View author profile